Estimation and selection of complex covariate effects in pooled nested case–control studies with heterogeneity

Abstract

A major challenge in cancer epidemiologic studies, especially those of rare cancers, is observing enough cases. To address this, researchers often join forces by bringing multiple studies together to achieve large sample sizes, allowing for increased power in hypothesis testing, and improved efficiency in effect estimation. Combining studies, however, renders the analysis difficult owing to the presence of heterogeneity in the pooled data. In this article, motivated by a collaborative nested case–control (NCC) study of ovarian cancer in three cohorts from United States, Sweden, and Italy, we investigate the use of penalty regularized partial likelihood estimation in the context of pooled NCC studies to achieve two goals. First, we propose an adaptive group lasso (gLASSO) penalized approach to simultaneously identify important variables and estimate their effects. Second, we propose a composite agLASSO penalized approach to identify variables with heterogeneous effects. Both methods are readily implemented with the group coordinate gradient decent algorithm and shown to enjoy the oracle property. We conduct simulation studies to evaluate the performance of our proposed approaches in finite samples under various heterogeneity settings, and apply them to the pooled ovarian cancer study.

1. Introduction

Cancer is both a rare and a complex disease and thus a large number of subjects are often needed to elucidate the relationship between the disease and risk factors. As a single study is unlikely to be sufficient or definitive, researchers have devoted increasing efforts to build large pooled datasets by bringing multiple studies together, such as the projects in the NIH/NCI Cohort Consortium (http://epi.grants.cancer.gov/Consortia/cohort.html). The pooling strategy has allowed researchers to examine rare cancers, rare exposures, risk factors with small effects, and the interplay among multiple risk factors.

The motivating study for this paper is a collaboration between the New York University Women's Health Study (NYUWHS), the Northern Sweden Health and Disease Study (NSHDS), and the Italian Hormones and Diet in the Etiology of Cancer Study (ORDET) to assess the effects of circulating levels of inflammation markers on the risk of invasive epithelial ovarian cancer (Clendenen and others, 2011). This joint effort identified 230 cases from the three cohorts and, for each case, 2 controls were selected from the same cohort using the nested case–control (NCC) sampling design (Thomas, 1979). The inflammatory markers were measured from stored blood samples collected at enrollment, and other risk factors were assembled from the questionnaires. We know that heterogeneity is often present in pooled observational epidemiological studies (Friedenreich, 1993; Ioannidis and others, 2002). The potential source of heterogeneity for our study included recruitment, disease ascertainment methods, and sample types (serum/plasma). Implementing the NCC design that selected cases and controls nested within the same cohort facilitated the pooling and reduced the heterogeneity in our study. But we still found that some markers exhibited heterogeneous effects across cohorts when examining the heterogeneity using a likelihood ratio test comparing models with and without biomarker × cohort-membership interaction terms (Clendenen and others, 2011).

Statistical methods for pooled studies need to recognize heterogeneity. A commonly used method for pooled analysis is the two-stage method to combine study-specific results using either a fixed-effects model (Hedges and Olkin, 1985) or a random-effects model (DerSimonian and Laird, 1986). The method originates from the meta-analysis of randomized clinical trials and has been extended to meta-regression to adjust heterogeneous study characteristics (Greenland, 1994; Thompson and Higgins, 2002). Bayesian approaches to random-effects meta-analysis (Smith and others, 1995) and a Bayesian hierarchical model (Liu and others, 2011) have also been proposed to integrate multiple studies and accommodate heterogeneity. In recent papers focusing on variable selection in pooled genetic studies, group penalty regularized regressions that consider the effects of a genetic variant over multiple studies in a group manner have been adopted, e.g. the group lasso (gLASSO) penalized regression for genome-wide mapping in ancestry admixed population (Puniyani and others, 2010); gene selection in pooled microarray studies using the group minimax concave penalty (Ma and others, 2011) or the group bridge penalty (Ma and others, 2011).

In this article, we propose two approaches based on penalized partial likelihood with group selection feature to integrate multiple NCC studies with potential heterogeneity. In the first approach, we adopt the adaptive gLASSO (agLASSO) penalty technique proposed by Wang and Leng (2008) to incorporate heterogeneity to the analysis of pooled NCC studies and show that the agLASSO penalty regularized maximum partial likelihood estimators have the oracle property (Fan and Li, 2001) for selection and estimation. Furthermore, identifying covariates with heterogeneous effects has great implications for building accurate cancer risk prediction models. Statistical tests for heterogeneity, such as Cochran Q-test (Cochran, 1954) and 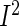-test (Higgins and Thompson, 2002), often have low power. In our second approach, we introduce a hierarchical structure over a variable's effects by modeling heterogeneous effects through interactions of the variable with cohort-membership indicators, and propose a composite agLASSO (cagLASSO) method to identify this hierarchical structure for variables with heterogeneous effects. Our cagLASSO method generalizes Zhao and others (2009) by applying data-adaptive weights to different components in the cagLASSO penalty and can achieve a consistent selection for heterogeneous effects.

The rest of the article is organized as follows. In Section 2, we propose the agLASSO and cagLASSO approaches for pooled NCC studies with heterogeneity, and establish asymptotic properties for our proposed estimators. Numerical simulations and the analysis of the ovarian cancer study are presented in Section 3. A discussion with concluding remarks is presented in Section 4.

2. Penalized partial likelihood approaches for pooled NCC studies

Consider a pooled NCC study from K parent cohorts with each size of 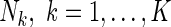. Let 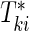be the failure time and 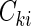be the censoring time for the ith subject in cohort k. Denote the observed time-to-event by 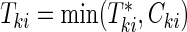, failure status by 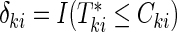, and the counting process by N_ki(t)=δ_kiI(T^*_ki≤t)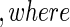I(⋅) denotes the indicator function throughout. Within cohort k, cases are identified as subjects with 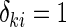, and for a given case i, the NCC design randomly samples m controls without replacement from the risk set at 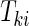excluding the case itself. Let denote the indices of the case and its m selected controls. Covariates of interest 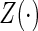are ascertained for each case–control set at the case failure time.

2.1. Variable selection and effect estimation

In each cohort k, the failure time follows a Cox proportional hazards (PHs) model (Cox, 1972):

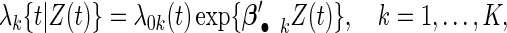(2.1)

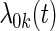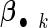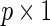where is the cohort-specific baseline hazard function, and is a vector of coefficients characterizing the effects of covariates in cohort k. Parameters of interest are

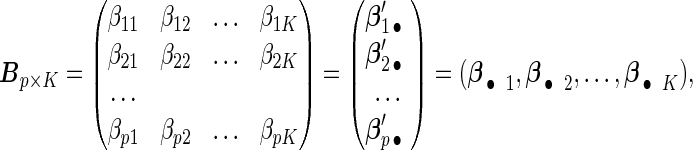where each row β_j •′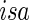K×1 vector denoting the effects of the jth covariate across K studies. The Cox PH model assumes that covariates have multiplicative effects on the hazard function of failure time and yields interpretation of the coefficients as hazard ratios. Furthermore, the Cox PH model is commonly used to analyze NCC data because of its easy implementation using the partial likelihood technique (Thomas, 1979; Oakes, 1981). Under the Cox PH model and time-invariant covariates, the expression of Thomas’ partial likelihood function is equivalent to the conditional logistic likelihood. The study-specific log partial likelihood takes the form of

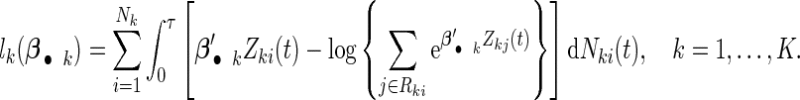(2.2)

Researchers often think that covariates have similar effects across pooled studies while acknowledging the existence of heterogeneity. This is essentially the idea behind the meta-analysis random-effects method in which study-specific effects are assumed to distribute around a central effect. Thus, it is natural to impose a group structure to each covariate's effects over K studies and select the covariate in the group manner. Denote the 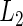-norm of 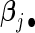by 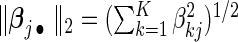. The proposed agLASSO penalized partial likelihood estimator is defined as

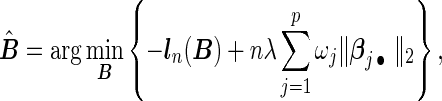(2.3)

where 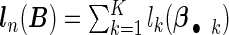, n is the sample size of the pooled NCC studies, λ is a tuning parameter controlling the sparseness of the model, and 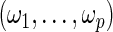are data-dependent weights reflecting the relative importance of covariates. We choos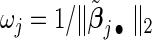e where and 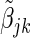is the jth element of the maximum partial likelihood estimator for (2.2) within cohort k.

The convexity of the negative of log partial likelihood functions (2.2) (Goldstein and Langholz, 1992) and of the agLASSO penalty facilitates the optimization in (2.3). Meier and others (2008) propose a group coordinate gradient descent algorithm for the logistic regression with gLASSO penalty, and have implemented it in R-package grplasso. Using a quadratic approximation for the log-likelihood function, the algorithm iterates through each covariate group by first examining the penalized approximation function via the Karush–Kuhn–Tucker (KKT) condition to either set the coefficients to be exact zeros or estimate them to be non-zero, and then supplements the non-zero estimates with an inexact line search until convergence. We adapt the algorithm to our context with the partial likelihood function for NCC data and with adaptive weights.

To select the tuning parameter, we use a BIC-type criterion because of its consistence property for the adaptive LASSO estimation with least square approximation (Wang and Leng, 2007). Our numerical experiences also suggest the superior performance of the BIC-type criterion. Specifically, 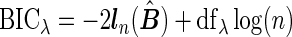, where the degree of freedom 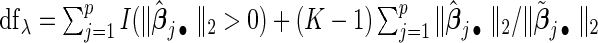following Yuan and Lin (2006) for the gLASSO estimatorsQ6.

The proposed agLASSO method selects important variables that have large group norms of their effects over K studies and accommodates heterogeneity by allowing the variable to have different magnitudes or directions for its effects across studies. Sometimes it is also important to know which covariates have heterogeneous effects for model building using the pooling strategy, because heterogeneous effects need to be modeled by distinct parameters to avoid misrepresenting effects; the homogenous effect can be represented by a common coefficient across studies to reduce the model's complexity and improve efficiency. Therefore, we next develop a method to identify variables with heterogeneous effects.

2.2. Identification of heterogeneous effects

We reparameterize the cohort-specific Cox model (2.1) into

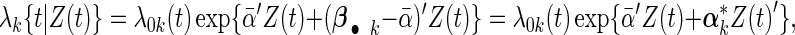(2.4)

where the 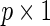vector 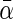denotes the average covariate effects and 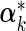denotes the deviation of covariate effects in cohort k from 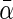. To incorporate the constraint of 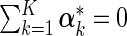, we use the “sum to zero contrast” matrix 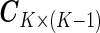(e.g. contr.sum in R) and transform the original parameter matrix 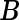into

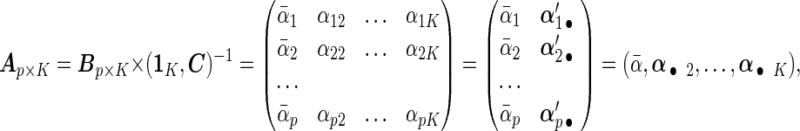where 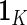is a vector of 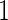's. Now heterogeneous effects of each variable are represented by the coefficients of interaction terms of the variable with the contrast created from cohort membership, motivating us to consider the hierarchical selection method with composite absolute penalty (CAP) for identifying interactions (Zhao and others, 2009). We propose to estimate 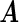by minimizing the following cagLASSO penalized partial likelihood function, i.e.

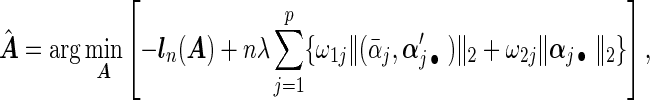(2.5)

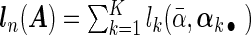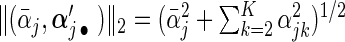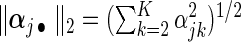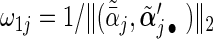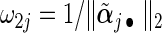where , , , and weights and with 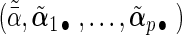being the maximizer of 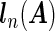. The two penalty terms in (2.5) have overlap on α_j • and thus can yield a hierarchical selection that once heterogeneous effects α_j • deviate from zero, both 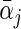and α_j • will be estimated to be non-zero together (Zhao and others, 2009). The extra penalty on α_j • leads to the identification of only a non-zero average effect without heterogeneous effects.

The calculation of (2.5) can be carried out by slightly modifying the algorithm described in Section 2.1. Specifically, in each iteration over the group of coefficients of the jth covariate, we examine the penalized approximation function via two KKT conditions to either set both 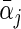and α_j • to be zero, or only set α_j •=0 and obtain a non-zero estimate for 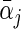, or estimate both to be non-zero. We apply the inexact line search to the non-zero estimates and iterate the algorithm until convergence. The tuning parameter is selected using 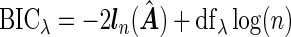with the .

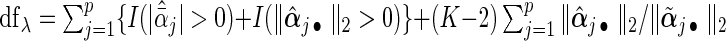2.3. Theoretical properties

We study the asymptotic properties of the proposed agLASSO and cagLASSO estimators, with respect to estimation consistency, selection consistency, and oracle property. For the discussion of the agLASSO estimator, we assume that the first 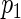rows of the true parameter matrix 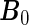are the effects of important variables, i.e. ∥β_0j •∥₂>0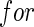j≤p₁ and for 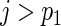. We reorganize the parameters into a vector form as β=(β′_1 •,…,β′_p •)′ and decompose it into β_a=(β′_1 •,…,β′_p1 •)′ and β_b=(β′_(p1+1) •,…,β′_p •)′. Accordingly, we have β₀=(β′_0a,β′_0b)′ and 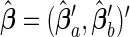. We denote the Fisher information matrix of 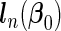by 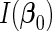, which is positive-definite under the regularity conditions (1)–(6) given in Goldstein and Langholz (1992). Let 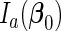denote the upper left submatrix of 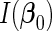. 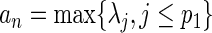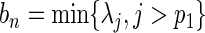Following the arguments in Wang and Leng (2008), we define and where .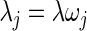

Theorem 2.1 —

Under the regularity conditions, the agLASSO estimator in (2.3) satisfies:

(a. Estimation consistency) if , then ;

(b. Selection consistency) if and , then ;

(c. Oracle property) if and , then .

For the ease of discussion of the cagLASSO estimator, we assume that the first 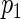rows of true parameter matrix 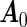have ∥α′_0j •∥₂>0 the next p₂ rows have 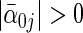and ∥α′_0j •∥₂=0; the remaining rows have 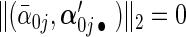. Then we denote the vector form of 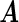by 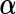and decompose it into two parts: 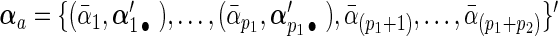and 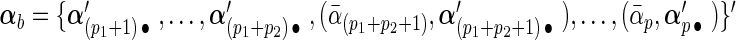. Accordingly, let 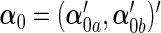, , 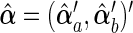and 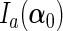be the upper left 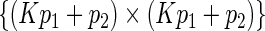submatrix of the Fisher information matrix 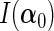. We further define 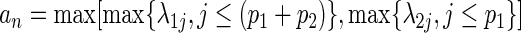and .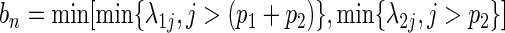

Theorem 2.2 —

Under the regularity conditions, the cagLASSO estimator in (2.5) satisfies:

(a. Estimation consistency) if , then ;

(b. Selection consistency) if and , then ;

(c. Oracle property) if and , then .

Proofs for the theorems are given in Appendix of supplementary material available at Biostatistics online. The theorems show that the agLASSO and cagLASSO estimators consistently select and estimate variables, and, furthermore, the cagLASSO estimator consistently identifies covariates with heterogeneous effects or with non-zero average effects. We estimate the covariance of the proposed estimators using the local quadratic approximation method proposed by Fan and Li (2001) to incorporate the penalty effect on finite sample estimation. We denote the non-zero components of the agLASSO estimator by 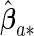and estimate its covariance matrix by the following sandwich formula:

(2.6)

where 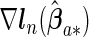, 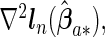and 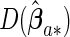are the corresponding components of sample estimates for the gradient vector ∇l_n(β)=∂l_n(β)/∂β, hessian matrix ∇²l_n(β)=∂²l_n(β)/∂β∂β′, and D(β)=diag(ω₁1_K/∥β_1 •∥₂,…,ω_p1_K/∥β_p •∥₂). For the cagLASSO estimator 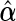, denote its non-zero components by 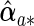and estimate its covariance using (2.6) with D(β)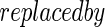D(α)=diag{D₁(α),…,D_p(α)} where .

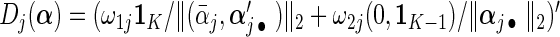3. Numerical studies

3.1. Simulations to evaluate the agLASSO method

We simulated a pooled study consisting of NCC samples from three parent cohorts with sample sizes of 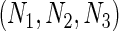. For subjects in cohort k, we generated failure times from the Cox PH model 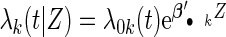, where covariate vector Z was a 20D multivariate normal random vector with mean of 1, variance of 1, and pairwise correlation of 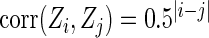. Four covariates 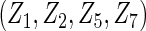were associated with disease risk and the rest were assumed to be null covariates. Specifically, β_1 •=(0.4,0.4,0.4) represented a homogeneous effect; β_2 •=(0.4,0.6,0.3) was heterogeneous with small differences; β_5 •=(−0.4,0,−0.3) was heterogeneous with moderate differences and had one zero effect; β_7 •=(0,−0.7,0) was heterogeneous with big differences and had two zero effects. Four settings were used: (i) equal cohort size of 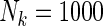and an equal baseline rate 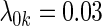; (ii) 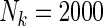and equal baseline rate 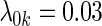; (iii) different a cohort sizes of 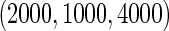and equal baseline disease rate of 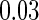; and (iv) different cohort sizes of 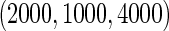and different baseline disease rates of 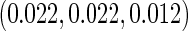. Censoring times were generated from a uniform distribution 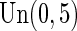and yielded censoring rates ranging from 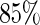to 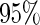with different settings. We conducted 200 runs of simulations for each setting.

We compared the performance of our proposed agLASSO method with (i) cohort-specific method analyzing each cohort separately; (ii) pooled method ignoring any heterogeneity; (iii) meta-analyses using random- and fixed- effects models; and (iv) the gLASSO method. The cohort-specific method selects variables based on the 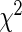-test combining cohort-specific estimates, and the pooled and meta-analysis methods select variables based on the Wald test, all at the 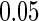significance level. Table 1 summarizes the model selection results. The average mean squared error (MSE) 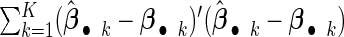is used to measure the prediction accuracy, and the relative MSE (RMSE) with respect to the result of the cohort-specific method is also reported. Overall, our proposed method outperforms all other competitors in terms of being the closest to the true model size, the smallest number of false positives, the highest percentage of correctly fitted models, and having the smallest MSE. The proposed agLASSO method improves its performance as sample size increases, and handles different situations of heterogeneity reasonably well. Although the cohort-specific method is unbiased for estimation, it shows the largest MSEs in all settings due to large variances from only using the data of each sub-study. The meta-analysis methods generally improves the model selection, but the random-effects method can be very conservative, partially because when large heterogeneous effects are modeled by a random effect, the estimated variance for the random effect would mask the central effect. The gLASSO method tends to over-select variables with large numbers of false positives.

Table 1.

Simulation results on model selection and MSE

Method	No. of identified variables	No. of false positives	No. of false negatives	Under-fitted%	Over-fitted%	Correct-fitted%	MSE	RMSE%
Cohort specific	4.700	1.045	0.345	31.0	38.5	30.5	2.273	REF
Pooled analysis	4.190	0.835	0.645	55.0	25.0	20.0	1.024	45.1
Meta-random	2.915	0.645	1.730	98.0	1.5	0.5	1.203	52.9
Meta-fixed	4.050	0.860	0.810	64.5	18.0	17.5	1.170	51.5
gLASSO	4.350	0.550	0.200	18.5	37.0	44.5	0.532	23.4
agLASSO	3.635	0.140	0.505	38.0	9.5	52.5	0.489	21.5
Cohort specific	4.840	0.860	0.020	2.0	51.0	47.0	0.887	REF
Pooled analysis	4.625	0.700	0.075	7.5	46.5	46.0	0.717	80.8
Meta-random	3.065	0.600	1.535	99.5	0.5	0	0.758	85.5
Meta-fixed	4.700	0.805	0.105	10.5	49.5	40.0	0.751	84.7
gLASSO	4.850	0.855	0.005	0.5	61.5	38.0	0.295	33.3
agLASSO	3.945	0.045	0.100	10.0	4.5	85.5	0.218	24.6
Different cohort sizes
Cohort specific	4.865	0.930	0.065	6.5	58.0	35.5	1.212	REF
Pooled analysis	4.280	0.900	0.620	62.0	21.5	16.5	0.750	61.9
Meta-random	3.240	0.645	1.405	99.5	0	0.5	0.759	62.6
Meta-fixed	4.185	0.905	0.750	72.0	18.0	10.0	0.793	65.4
gLASSO	4.840	0.840	0.001	0	58.5	41.5	0.347	28.6
agLASSO	4.105	0.150	0.045	4.0	14.0	82.0	0.262	21.6
Different cohort sizes and disease rates
Cohort specific	4.600	0.860	0.260	24.5	41.5	34.0	1.926	REF
Pooled analysis	4.100	0.790	0.690	63.5	17.5	19.0	0.877	45.5
Meta-random	3.070	0.595	1.525	98.0	0.5	1.5	0.973	50.5
Meta-fixed	3.965	0.790	0.825	76.0	9.0	15.0	0.970	50.4
gLASSO	4.765	0.810	0.045	4.0	52.0	44.0	0.457	23.7
agLASSO	3.910	0.225	0.315	28.5	16.5	55.0	0.413	21.4

“Cohort specific” refers to the method treating each cohort separately and the significance test is based on the χ²-test combining cohort-specific results; “Pooled analysis” refers to the pooled analysis ignoring any heterogeneity; “Meta-random” refers to the meta-analysis with random-effects modeling; “Meta-fixed” refers to the meta-analysis with fixed-effects modeling; “gLASSO” refers to the group LASSO method; “agLASSO” refers to the adaptive group LASSO method; “No. of identified variables” refers to the average number of identified variables by each method in 200 runs of simulations; “No. of false positive” refers to the average number of selected variables out of those true values being 0 by each method in 200 runs of simulations; “No. of false negatives” refers to the average number of missed variables out of those true non-zero values by each method in 200 runs of simulations; “Under-fitted%” refers to the percentage of simulation runs that miss at least one true variable; “Over-fitted%” refers to the percentage of simulation runs that include all true variables and at least one null covariate; “Correct-fitted%” refers to the percentage of simulation runs that correctly identify all variables.

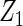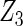Table 2 presents the results on selecting individual variables. For covariates and where effect signals are strong with no or minor heterogeneity, all methods can pick up the signal with good power. For null covariates and 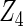, the proposed agLASSO method shows the best performance excluding these variables. For covariates 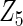and 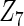with moderate or large heterogeneity, the cohort-specific method, and the penalized methods of gLASSO and agLASSO perform well. The pooled analysis method deteriorates dramatically for 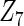under the settings of different cohort sizes and/or different disease rates that aggravate the heterogeneity across cohorts. Meta-analysis methods yield unsatisfactory results as well.

Table 2.

Simulation results on individual variable selection frequency

Method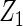
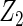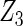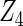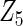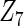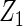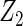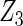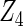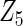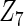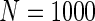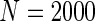Cohort specific	98.0	98.5	5.0	8.5	75.5	93.5	100	100	8.0	5.0	98.0	100
Pooled analysis	99.5	99.0	4.0	3.0	67.5	69.5	100	100	4.0	4.0	96.0	96.5
Meta-random	97.5	89.5	2.0	3.5	35.5	4.5	100	97.5	4.0	5.0	47.5	1.5
Meta-fixed	99.0	98.5	2.5	4.0	67.0	54.5	100	100	6.0	6.0	96.5	93.0
gLASSO	100	99.5	4.0	3.5	82.0	98.5	100	100	5.0	3.5	99.5	100
agLASSO	91.5	96.5	1.0	1.5	68.0	93.5	100	100	0.0	0.0	90.0	100
	Different cohort sizes						Different cohort sizes and disease rates
Cohort specific	100	100	4.5	4.0	99.0	94.5	100	100	6.5	5.5	89.0	85.0
Pooled analysis	100	100	5.5	4.0	99.5	38.5	100	100	6.0	4.0	91.5	39.5
Meta-random	100	98.5	3.5	3.5	60.0	1.0	97.5	94.0	4.0	4.0	53.5	2.5
Meta-fixed	100	100	4.0	4.0	99.5	28.5	100	100	4.5	5.5	91.0	26.5
gLASSO	100	100	3.5	3.0	100	100	100	100	5.0	5.0	97.0	98.5
agLASSO	100	99.5	1.0	1.0	96.5	99.5	98.0	99.5	0.5	0.5	79.5	91.5

“Cohort specific” refers to the method treating each cohort separately and the significance test is based on the χ²-test combining cohort-specific results; “Pooled analysis” refers to the pooled analysis ignoring any heterogeneity; “Meta-random” refers to the metaanalysis with random-effects modeling; “Meta-fixed” refers to the meta-analysis with fixed-effects modeling; “gLASSO” refers to the group LASSO method; “agLASSO” refers to the adaptive group LASSO method.

To examine the accuracy of the proposed variance calculation in Section 2.3, we compare the sample standard deviation of estimates over simulations and the average formula-based estimates of standard errors in Table 3. First, the proposed agLASSO method shows smaller standard errors than the cohort-specific method across the board, indicating that our proposed method can improve efficiency by integrating information across multiple studies. Second, when heterogeneity is small in 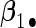and 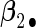, the agLASSO asymptotic variance estimates are close to their sample counterparts, especially when the sample size is large. 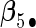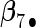Third, for and with moderate or large heterogeneity, the agLASSO asymptotic variance estimates display some discrepancy with the sample standard deviations. One explanation could be that applying the same group penalty to a heterogeneous vector tends to penalize the small coefficients more than the large ones, and thus the estimates for small coefficients demonstrate smaller variability.

Table 3.

Simulation results on the standard errors for the estimates

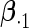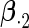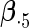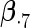Method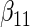
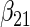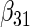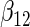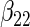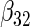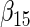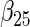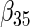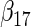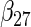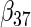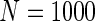Cohort specific	0.184	0.193	0.184	0.211	0.205	0.191	0.188	0.201	0.193	0.174	0.229	0.195
	0.166	0.173	0.165	0.186	0.199	0.183	0.185	0.188	0.182	0.180	0.202	0.180
agLASSO	0.134	0.139	0.132	0.127	0.160	0.121	0.101	0.071	0.093	0.085	0.153	0.085
	0.124	0.124	0.125	0.124	0.126	0.125	0.119	0.119	0.121	0.115	0.118	0.117
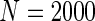Cohort specific	0.108	0.101	0.124	0.119	0.119	0.124	0.121	0.116	0.119	0.116	0.125	0.118
	0.109	0.113	0.110	0.121	0.129	0.120	0.121	0.123	0.121	0.119	0.131	0.119
agLASSO	0.094	0.090	0.103	0.098	0.111	0.090	0.095	0.047	0.082	0.068	0.104	0.067
	0.092	0.093	0.093	0.092	0.094	0.092	0.086	0.086	0.086	0.084	0.087	0.085
Different cohort sizes
Cohort specific	0.108	0.189	0.078	0.119	0.209	0.086	0.121	0.185	0.086	0.116	0.195	0.088
	0.109	0.172	0.075	0.121	0.196	0.083	0.121	0.187	0.083	0.119	0.200	0.082
agLASSO	0.095	0.127	0.079	0.102	0.145	0.079	0.094	0.080	0.067	0.062	0.152	0.039
	0.091	0.120	0.068	0.092	0.122	0.068	0.085	0.116	0.062	0.084	0.117	0.062
Different cohort sizes and disease rates
Cohort specific	0.135	0.229	0.126	0.139	0.238	0.139	0.157	0.255	0.147	0.136	0.289	0.121
	0.128	0.203	0.120	0.141	0.233	0.131	0.142	0.222	0.131	0.139	0.238	0.130
agLASSO	0.115	0.142	0.110	0.114	0.162	0.106	0.105	0.079	0.080	0.067	0.179	0.060
	0.104	0.134	0.099	0.104	0.135	0.099	0.098	0.132	0.093	0.096	0.131	0.092

“Cohort specific” refers to the method treating each cohort separately; “agLASSO” refers to the adaptive group LASSO method. For each parameter's estimate, sample standard deviation of estimates is on the top and the average of estimated standard errors is at the bottom.

Additional simulations with a cohort size of 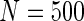were also conducted and showed that all methods had low power to select important variables when the sample size is small. The penalized methods of gLASSO and agLASSO generally exhibited better performances than others, but the superiority of the agLASSO over gLASSO was not obvious under situations with low sample size.

3.2. Simulations to evaluate the cagLASSO method

We compared the proposed cagLASSO method, the interaction method including marker×cohort-membership terms, and the CAP method with group -penalties (Zhao and others, 2009), regarding their performance for identifying important variables and variables with heterogeneous effects. Data generation remained the same as in Section 3.1. Tables 4 and 5 summarize the results on overall model selection and individual variable selection, respectively. The proposed cagLASSO approach accurately selects the four important variables and yields the smallest MSE under all settings (Table 4). Note that three out of the four important variables have heterogeneous effects and demonstrate different magnitudes of heterogeneity. Although the cagLASSO method seems to be inferior to the other two methods in selecting variables with heterogeneous effects, it has comparable performance for selecting the correct heterogeneous variables. From Table 5, we note that the cagLASSO method has the lowest false-positive rate to correctly recognize the absence of heterogeneity in 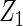. For 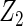with small heterogeneous effects, none of the methods detects the heterogeneity signal with good power. 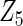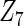For variables of and with moderate or large heterogeneity, the cohort-specific method works generally well, but performances by the CAP estimator and the cagLASSO estimator fluctuate. In general, we find that the cagLASSO estimator shows better performance than the CAP method for 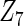with large heterogeneity but lower selection frequency for 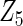with moderate heterogeneity. This observation can be due to the fact that, in finite samples, the data-adaptive weight 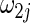in (2.5) may over-penalize the heterogeneous effects when the group norm of heterogeneous effect is small.

Table 4.

Simulation results on model selection and identification of heterogeneous effects

Method	No. of identified variable (4)	No. of correct variable	No. of identified hetero. eff. (3)	No. of correct hetero. eff.	MSE
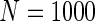Cohort interaction	4.350	3.295	2.500	1.425	1.242
CAP	4.255	3.690	1.565	1.480	0.333
cagLASSO	3.910	3.670	1.325	1.280	0.280
Cohort interaction	4.720	3.910	2.840	1.930	0.497
CAP	4.575	3.985	2.220	2.080	0.234
cagLASSO	4.105	3.960	1.740	1.730	0.164
Different cohort sizes
Cohort interaction	4.715	3.805	2.640	1.650	0.708
CAP	4.265	3.690	1.580	1.400	0.327
cagLASSO	3.950	3.760	1.240	1.180	0.259
Different cohort sizes and disease rates
Cohort interaction	4.312	3.497	2.382	1.372	1.147
CAP	4.106	3.613	1.327	1.201	0.362
cagLASSO	3.900	3.678	1.186	1.106	0.293

“Cohort interaction” refers to the pooled analysis using the interaction terms of covariates with cohort-specific membership indicators; “CAP” refers to the composite absolute penalty method; “cagLASSO” refers to the composite adaptive group lasso penalty method; “No. of identified variable” refers to the average number of identified important variables with non-zero effect by each method in 200 runs of simulations; “No. of correct variable” refers to the average number of identified variables with non-zero effect out of those with true non-zero effects; “No. of identified hetero. eff.” refers to the average number of identified variables with non-zero heterogeneous effect by each method in 200 runs of simulations; “No. of correct hetero. eff.” refers to the average number of identified variables with non-zero heterogeneous effect out of those with true non-zero heterogeneous effects.

Table 5.

Simulation results on the variable selection frequency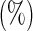

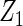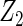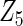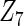Method	Ave. (0.4)	Hetero. (0, 0)	Ave. (0.43)	Hetero. (0.17, −0.13)	Ave. (−0.23)	Hetero. (0.23, −0.06)	Ave. (−0.23)	Hetero. (−0.47, 0.23)
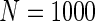Cohort interaction	99.0	8.5	98.5	19.0	67.0	36.5	65.0	87.0
CAP	100	2.0	99.0	19.0	82.0	42.5	88.0	86.5
cagLASSO	99.0	1.5	98.5	10.5	77.5	33.0	92.0	84.5
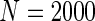Cohort interaction	100	5.0	100	35.0	95.5	58.0	95.5	100
CAP	100	5.5	100	32.5	98.5	75.5	100	100
cagLASSO	100	0.0	100	19.0	96.0	54.5	100	99.5
Different cohort sizes
Cohort interaction	100	6.5	100	29.0	88.0	40.0	92.5	96.0
CAP	100	4.0	100	26.5	100	44.5	69.0	69.0
cagLASSO	100	1.5	100	19.0	99.5	23.5	76.5	75.5
Different cohort sizes and different disease rates
Cohort interaction	100	6.5	100	23.0	71.5	31.5	78.5	82.5
CAP	100	4.0	100	18.0	97.5	38.0	64.0	64.0
cagLASSO	100	1.5	100	15.0	93.0	23.0	75.0	72.5

“Cohort interaction” refers to the pooled analysis using the interaction terms of covariates with cohort-specific membership indicators; “CAP” refers to the composite absolute penalty method; “cagLASSO” refers to the composite adaptive group LASSO penalty method; “Ave.” refers to the average effect of the covariate and its true value is listed below in the parenthesis; “Hetero.” refers to the heterogeneous effects of the covariate and the true values are listed below in the parenthesis.

3.3. The pooled ovarian cancer study

We applied the proposed agLASSO method to the pooled NCC study on ovarian cancer to identify important risk factors and compared its results with those from the cohort-specific analysis, pooled analysis, meta-analysis with random-effects and fixed-effects models, and gLASSO method. Specifically, we considered all 17 inflammation markers and 6 potential confounders including pregnancy history, use of oral contraceptive, use of hormone replacement therapy, age at menarche, body mass index, and current smoking status. The analysis was based on 229 ovarian cancer cases and 429 matched controls (NYUWHS: 81 cases and 160 controls; ORDET: 41 cases and 82 controls; NSHDS: 107 cases and 187 controls). Four subjects were removed due to missing data. All biomarker data were log-transformed and standardized within each cohort.

Both the gLASSO and agLASSO methods select interleukin-4 (IL4) as an important risk factor for ovarian cancer and thus we present the results from different methods focused on IL4 in Table 6. The cohort-specific method indicates that IL4 may have heterogeneous effects across three cohorts: it shows positive association with disease risk in NYUWHS and NSHDS but negative association in ORDET although the results from NSHDS and ORDET are not statistically significant. The results are consistent with the findings in Clendenen and others (2011). The proposed agLASSO method reaches a similar conclusion as the cohort-specific analysis but with more regularized estimates and tighter confidence intervals by integrating three studies together. Under this pattern of heterogeneity, however, the pooled analysis or meta-analysis does not show any significant result. Furthermore, our proposed cagLASSO method also demonstrates the existence of heterogeneity in IL4 effects across three cohorts and estimates (in the log of hazards ratio scale) the average effect as 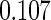and the heterogeneous effects as 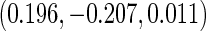for NYUWHS, ORDET, and NSHDS, respectively.

Table 6.

Results on estimation of the effects of IL4 in the ovarian cancer study

Method	HR	95% CI
Cohort specific
NYU	2.596	(1.211, 5.565)*
ORDET	0.568	(0.278, 1.161)
NSHDS	1.833	(0.822, 4.086)
Pooled analysis	1.260	(0.905, 1.755)
Meta-random	1.377	(0.551, 3.439)
Meta-fixed	1.326	(0.856, 2.053)
agLASSO
NYU	1.343	(1.033, 1.747)*
ORDET	0.847	(0.614, 1.168)
NSHDS	1.088	(0.872, 1.357)

“HR” refers to the hazards ratio estimate corresponding to 1 standard deviation increase of the IL4 level (in the logscale); “95% CI” refers to the 95% confidence interval. *The statistical significance at 0.05 level.

4. Discussion

In this article, we develop the penalized partial likelihood methods for variable selection and estimation of the Cox PH model in pooled NCC studies. The proposed methods can be easily extended to pooled analysis of other types of data, or even for combining studies with different designs, such as matched case–control and unmatched case–control studies. Other choices of penalty function can also be used to incorporate investigators’ prior knowledge on the magnitude or structure of heterogeneity. For example, we can use the group L_q penalty with 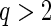to shrink coefficients toward the diagonal and thus can encourage similarity of effects across multiple studies; the proposed cagLASSO method can adopt other penalties with hierarchical structure induced from a directed graph. Also from our numerical experience, when the sample size is sufficiently large, the simple definition for the degree of freedom that counts the number of non-zero coefficient estimates (Wang and others, 2007) can be used for calculating the BIC to select the final model. After significant heterogeneity is detected across studies, the sparse gLASSO penalty also can be used to select cohort-specific important variables.

Using the adaptive weights in our penalized methods is important for achieving the oracle property and good practical performance. When the number of covariates is large, the data-dependent weights from the cohort-specific estimates may not always be estimable. We can use some initial estimates that are zero-consistent as the weights (Huang and others, 2006). Some other non-convex penalty regularized methods also have the oracle property, such as using the group bridge penalty (Ma and others, 2011), however, are more complex in terms of both numerical implementation and theory. In addition, when small heterogeneous effects are present, a very large sample would be necessary for the proposed methods to achieve a perfect fit on all variables.

Lastly, it is of great interest to study other survival models that can relax the PHs assumption for the analysis of pooled NCC studies with heterogeneity. The inverse selection probability weighted technique (Samuelsen, 1997) potentially can be used for this purpose, but the construction of an effective loss function that can simultaneously accommodate the selection weights and couple with penalties needs further investigation.

Supplementary material

Supplementary material is available at http://biostatistics.oxfordjournals.org.

Funding

This work was supported by the National Cancer Institute (R01 CA140632, R03 CA153083, R21 CA116585, R21 CA169739).