Abstract
Visual perception depends strongly on spatial context. A classic example is the tilt illusion where the perceived orientation of a central stimulus differs from its physical orientation when surrounded by tilted spatial contexts. Here we show that such contextual modulation of orientation perception exhibits trait-like interindividual diversity that correlates with interindividual differences in effective connectivity within human primary visual cortex. We found that the degree to which spatial contexts induced illusory orientation perception, namely, the magnitude of the tilt illusion, varied across healthy human adults in a trait-like fashion independent of stimulus size or contrast. Parallel to contextual modulation of orientation perception, the presence of spatial contexts affected effective connectivity within human primary visual cortex between peripheral and foveal representations that responded to spatial context and central stimulus, respectively. Importantly, this effective connectivity from peripheral to foveal primary visual cortex correlated with interindividual differences in the magnitude of the tilt illusion. Moreover, this correlation with illusion perception was observed for effective connectivity under tilted contextual stimulation but not for that under iso-oriented contextual stimulation, suggesting that it reflected the impact of orientation-dependent intra-areal connections. Our findings revealed an interindividual correlation between intra-areal connectivity within primary visual cortex and contextual influence on orientation perception. This neurophysiological-perceptual link provides empirical evidence for theoretical proposals that intra-areal connections in early visual cortices are involved in contextual modulation of visual perception.
Introduction
Visual perception is rarely a true reflection of an object's physical properties but is often biased by the spatial contexts surrounding the object (Schwartz et al., 2007). Such contextual influence is widespread in everyday perception and can be easily demonstrated by contextual illusions. For example, in the tilt illusion, the perceived orientation of an object is shifted away from its physical orientation when surrounded by a tilted context (Fig. 1A). Despite its importance, little is known about the neural mechanisms underlying contextual modulation of visual perception. It has been suggested that contextual information modulates perception through cortical connections, such as intra-areal connections in early visual cortices (Tolhurst and Thompson, 1975; Lamme et al., 1998; Schwartz et al., 2007; Schwartz et al., 2009). These hypotheses are largely based on animal studies showing the involvement of cortical connections in modulating neural activity in early visual cortices. Yet, contextual modulation of visual perception does not necessarily follow similar mechanisms, particularly because neural activity and visual perception exhibit different dependence on the contents of spatial contexts (Schwartz et al., 2007). Despite that, due to the difficulty of assessing perceptual contents in animals and intra-areal connectivity in humans, there has been no direct test for the involvement of cortical connections in contextual modulation of visual perception.
Figure 1.
Contextual induction of tilt illusion. A, The perceived orientation of a grating differs from its physical orientation when surrounded by a tilted context. As illustrated here, the central grating in the left panel and the grating in the right panel are physically identical yet appear perceptually different in orientation. The physical orientation difference between these two gratings was varied (indicated by *) to measure the 50% threshold point, where the two gratings appeared perceptually equal in orientation, that quantified the magnitude of the tilt illusion. B, A group of 40 participants were shown the same tilt illusion stimulus, yet the magnitude of the tilt illusion differed across participants more than ninefold, illustrating interindividual variability in contextual modulation of orientation perception. C, D, We measured the magnitude of the tilt illusion under several stimulus configurations that differed in overall stimulus size (small vs big) or overall stimulus orientation (oblique vs cardinal). The measures were compared against each other and were highly correlated across participants, indicating that interindividual variability in contextual modulation of orientation perception reflected a stimulus-independent personal trait. Bar chart represents the mean ± SEM across participants (N = 20), and statistical values were calculated using paired t test. In the scatter plot, each point represents a single participant (N = 20), and the statistical values were calculated using Pearson's r.
Recent advances in applying dynamic causal modeling (DCM) to functional magnetic resonance imaging (fMRI) blood-oxygen-level dependent (BOLD) signals offer a noninvasive measure of cortical effective connectivity. By taking the biophysical basis of BOLD signals and the temporal dynamics of neural interactions into consideration, DCM estimates the effective strength of synaptic connections from one neural population to another, referred to as effective connectivity (Friston et al., 2003). In contrast to functional connectivity that simply describes the statistical dependencies among observed data (e.g., BOLD signals), effective connectivity represents inferences of the coupling between (hidden) neural states that underlie the observed data (Friston, 2011). The method has been validated by concurrent fMRI-intracranial recordings demonstrating the consistency between DCM-fMRI measure of effective connectivity and intracranial measure of directional neural coupling (David et al., 2008).
Using DCM-fMRI, we measured intra-areal, feedback, and feedforward connectivity between foveal and peripheral regions of early retinotopic visual cortices (V1, V2, and V3) that responded to a central stimulus and its surrounding context, respectively. We asked whether visual cortical connectivity correlated with the degree of contextual modulation on orientation perception, assessed by the tilt illusion magnitude. A classical approach to vary the illusion magnitude is to change the orientation of the tilted context (Schwartz et al., 2007). However, as the perceptual change is accompanied by a physical change in visual stimuli, this approach makes it difficult to determine whether any observed relationship between cortical effective connectivity and tilt illusion magnitude reflects the effect from stimuli or perception. To dissociate perception from visual stimuli, we took a novel approach using the fact that different individuals perceive the same visual stimulus differently (Kanai and Rees, 2011). For a group of 40 healthy human adults, we measured their perception of the same tilt illusion stimuli. We then studied whether interindividual variability in tilt illusion magnitude was correlated with interindividual differences in effective connectivity in early retinotopic visual cortices.
Materials and Methods
A group of 40 healthy human volunteers with normal or corrected to normal vision (21 females, 19 males; age 19–35 years) gave written informed consent to take part in this study approved by University College London ethics committee. For each participant, we assessed contextual modulation of orientation perception using the tilt illusion stimulus where the surrounding grating tilted away from the central grating by 15 degrees and induced the maximum illusion (Wenderoth et al., 1986; Wenderoth and Johnstone, 1988; Schwartz et al., 2007). As the magnitude of tilt illusion depends on the stimulus size and stimulus contrast and differs between oblique versus cardinal stimulus (oblique effect) (Leibowitz and Toffey, 1966; Oyama, 1975; Ninio and O'Regan, 1996; Smith and Wenderoth, 1999), we tested whether the variability across individuals in the illusion magnitude was stimulus specific or stimulus independent. We divided the group of 40 participants into a main group of 20 participants (10 females, 10 males; age 19–34 years) and a second group of 20 participants (11 females, 9 males; age 21–35 years). We further measured the tilt illusion magnitude under a stimulus of different size for the main group of participants, a different contrast for 10 participants from the main group, and a different orientation for the second group of participants.
The main group of participants also took part in fMRI experiments, where we measured intra-areal, feedforward, and feedback connectivity in early retinotopic visual cortices (V1, V2, and V3) through DCM analysis (Friston et al., 2003; Friston, 2009, 2011). To test whether our measure of effective connectivity was robust against fMRI experimental task, we ran two separate fMRI experiments that used the same stimulus configuration but involved passive viewing and active judgment of the stimulus orientation, respectively. All 20 participants from the main group took part in the fMRI experiment with the passive viewing task, whereas 10 participants among them further took part in the fMRI experiment with the orientation judgment task.
Psychophysical experiment
Apparatus and stimulus.
Psychophysical experiments took place in a dark room with computer monitor providing the only significant source of light. Visual stimuli were presented on a 22 inch calibrated CRT monitor (size 41 cm × 30.6 cm, viewing distance 67 cm) and viewed through a chin-and-forehead rest. The interindividual variability in tilt illusion magnitude was assessed using the illusion stimulus where the central and surrounding gratings had a contrast of 70%, were oriented at 45 and 60 degrees, respectively, and covered eccentricities of 0–0.75 and 0.75–3 degrees, respectively.
To test whether interindividual variability in the tilt illusion magnitude was dependent on stimulus size, for the main group of 20 participants, we further measured the tilt illusion magnitude under a new stimulus configuration where the central and surrounding gratings had a contrast of 70%, were oriented at 45 and 60 degrees, respectively, and covered eccentricities of 0.25–1.75 and 2.4–7.2 degrees, respectively. To test whether interindividual variability in the tilt illusion magnitude was dependent on the stimulus orientation, for the second group of 20 participants, we further measured the tilt illusion magnitude under a new stimulus configuration where the central and surrounding gratings had a contrast of 70%, were oriented at 0 and 15 degrees, respectively, and covered eccentricities of 0–0.75 and 0.75–3 degrees, respectively.
To test whether interindividual variability in the tilt illusion magnitude was accounted for by individual differences in the effective contrast of foveal and peripheral visual stimulation (Levitt and Lund, 1997; Dragoi and Sur, 2000), for 10 participants from the main group, we measured the magnitude of tilt illusion where the contrasts of the central grating (oriented at 45 degrees, covered eccentricities of 0.25–1.75 degrees) and the surrounding grating (oriented at 60 degrees, covered eccentricities of 2.4–7.2 degrees) were adjusted for each participant to counteract individual differences in effective contrast. The effective contrast was assessed by the contrast detection threshold of foveal and peripheral visual stimulation (measured in an additional psychophysical experiment) or by the size ratio of the foveal to the peripheral retinotopic region (measured in fMRI experiment). Specifically, we measured the magnitude of the tilt illusion under three different stimulus configurations where (1) the contrast of the central and the surrounding gratings was 100 times the foveal and the peripheral contrast detection threshold, (2) the contrast of the central and the surrounding gratings was 50 times the foveal and the peripheral contrast detection threshold, and (3) the contrast of the central grating was 70% and that of the surrounding grating was 70% times the size ratio of the foveal relative to the peripheral retinotopic region.
Measurement of tilt illusion magnitude.
The magnitude of the tilt illusion was measured using the established psychophysical method of constant stimuli. On each trial, two central gratings (one with and one without tilted surrounding grating) were presented in succession for 300 ms each and separated by an interstimulus interval of 500 ms. The interval (first or second) where the surrounding grating appeared was randomized but counterbalanced across trials. Participants made an unspeeded forced-choice response to report whether the central grating in the second interval, compared with the one in the first interval, was rotated clockwise or counterclockwise.
Before the experiment, each participant completed a session that assessed their orientation discrimination threshold through a standard 2-up-1-down staircase procedure, and another session that assessed their point of subjective equality through four trials of manual orientation adjustment for the central grating presented in isolation until it matched the perceived orientation of the central grating presented in tilted context. In the subsequent experiment, the orientation of the central grating presented in tilted context was kept constant, whereas that of the central grating presented in isolation was varied around the premeasured point of subjective equality for seven different levels (step size equaled the orientation discrimination threshold). For each participant and each stimulus configuration, we measured responses on 112 trials (16 trials per orientation level) and fit the data with a logistic psychometric curve y = λ + (1 − 2λ)F(x, α, β) where λ represented the lapse rate and F(x, α, β) a typical logistic function (Wichmann and Hill, 2001). From the psychometric curve, we acquired the 50% threshold point where the two physically different central gratings appeared perceptually equal in orientation and their physical orientation difference represented the magnitude of the tilt illusion (Fig. 1A).
Measurement of contrast detection threshold.
Contrast detection thresholds were measured using a standard 2-up-1-down staircase procedure. On each trial, a low-contrast grating oriented at 45 degrees toward either left or right of the vertical was presented for 300 ms. The orientation (left or right) of the grating was randomized. Participants made an unspeeded forced-choice response to report whether the grating was left or right oriented. Two consecutive correct answers led to the grating contrast in the next trial being one step lower than in the previous trials, whereas one incorrect answer led to an increase in the grating contrast. The experiment stopped after 18 reversals, and the contrast detection threshold was calculated as the grating contrast averaged over the last 10 reversals.
For an accurate measurement of the contrast detection threshold, we applied the Floyd–Steinberg dithering algorithm to create stimulus contrast below the luminance resolution of the monitor display (Floyd and Steinberg, 1976). Specifically, a low-contrast sinusoidal grating was first dithered into a black–white binary grating that was perceptually equal in contrast to the original grating but had a physical contrast of 100%. The physical contrast of this binary grating was then scaled to create gratings with very low contrast. We measured the contrast detection threshold for the foveal stimulation (0.25–1.75 degrees eccentricity) and the peripheral stimulation (2.4–7.2 degrees eccentricity) in separate experiments. In both cases, the staircase procedure began with a contrast of 0.3333% and had a step size of 0.0196%.
fMRI experiment
Apparatus.
fMRI experiments took place in a Siemens Trio 3T MRI scanner with a 32 channel head-coil. The scanner was located in a dark room with the projector providing the only significant source of light. Visual stimuli were projected onto a screen (size 28.6 cm × 21.5 cm) in the back of the scanner and viewed through a mirror on the head-coil (viewing distance 85 cm). The stimuli covered a visual field extending from fixation to 7.2 degrees eccentricity.
Structural MRI data were acquired using a T1-weighted MDEFT sequence (TR: 7.92 ms, TE: 2.48 ms, flip angle: 16 degrees, resolution: 1 mm isotropic, matrix size: 256 × 240 × 176). fMRI data were acquired using a high spatial resolution 3D EPI sequence developed in-house (TR: 3.2 s, TE: 32.86 ms, flip angle: 20 degrees, resolution: 1.5 mm isotropic, matrix size: 128 × 128 × 40, 25% oversampling along the encoding direction to avoid wrap-around artifacts) (Lutti et al., 2013). Parallel imaging was used along the phase encoding direction to accelerate the acquisition, and images were reconstructed using GRAPPA algorithm available on scanner console. fMRI data were preprocessed in SPM8 (http://www.fil.ion.ucl.ac.uk/spm) using intensity bias correction, realignment, unwarping, coregistration with structural MRI images, and physiology noise correction that regressed out cardiac activity, respiratory activity, and head motion to control for hemodynamic artifacts.
Stimulus.
To measure effective connectivity between foveal and peripheral regions in early retinotopic visual cortices (V1, V2, and V3), the foveal and peripheral visual stimulations were designed to cover 0.25–1.75 and 2.4–7.2 visual degree eccentricity, respectively. The gap between the foveal and the peripheral stimulation and the application of a high spatial resolution fMRI sequence contributed to reliable delineation of the foveal–peripheral boundary. Moreover, the hole within the foveal stimulation helped to avoid activation of the foveal confluence where the boundaries between different retinotopic visual cortices were difficult to define.
Block-design fMRI data were acquired when participants viewed a blank screen, a central grating alone (0.25–1.75 degrees eccentricity), a surrounding grating alone (2.4–7.2 degrees eccentricity), or the central grating together with the surrounding grating. We tested two different conditions of contextual stimulation: the tilted condition where the surrounding grating was tilted away from the central grating and affected the perceived orientation of the central grating as well as the iso-oriented condition where the surrounding grating had the same orientation as the central grating and did not affect the perceived orientation of the central grating. In each run, six different stimuli (Fig. 2A, a blank screen, a 45 degree central grating alone, a 60 degree surrounding grating alone, a 45 degree central grating together with a 60 degree surrounding grating, a 45 degree surrounding grating alone, a 45 degree central grating together with a 45 degree surrounding grating) were presented where each stimulus appeared for six blocks (5 volumes per block). Four different runs were acquired with a counterbalanced block sequence across the runs.
Figure 2.
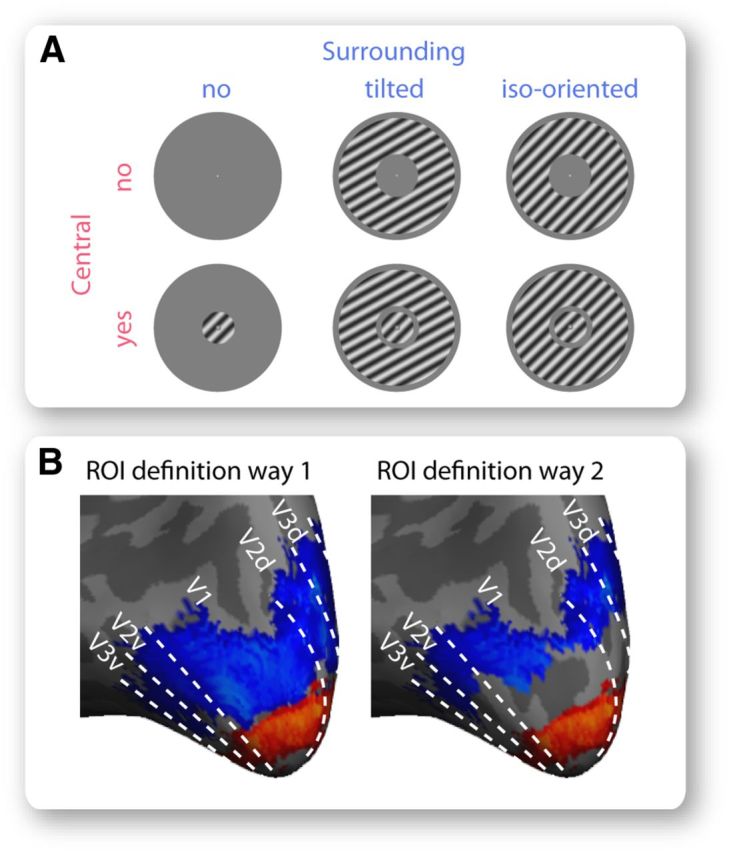
Foveal and peripheral retinotopic regions. A, We acquired fMRI BOLD signals when participants viewed a blank screen, a central grating alone, a surrounding grating alone, or a central grating together with a surrounding grating, in block design. Two different types of surrounding grating were used: a tilted one that differed in orientation from the central grating and affected its perceived orientation, as well as an iso-oriented one that had the same orientation as the central grating and did not affect its perceived orientation. B, We applied two different approaches to define foveal and peripheral ROIs in early retinotopic visual cortices that responded to visual field stimulation by the central and the surrounding grating, respectively. The first approach contrasted BOLD signal evoked by the central grating with that evoked by the surrounding grating at a threshold of p < 0.001 (uncorrected). The second approach further confined foveal and peripheral ROIs by exclusion of voxels whose population receptive field overlapped with the central and the surrounding grating, respectively. Illustrated are the foveal (red) and peripheral (blue) ROIs from a representative participant, where dotted lines represent visual cortical borders delineated from standard retinotopic mapping.
Experimental task.
To test whether the measure of cortical effective connectivity was robust against the fMRI experimental task, we ran two separate fMRI experiments with the same stimulus configuration (see above) but with different tasks. The first fMRI experiment was designed to minimize confounding influences (e.g., attention allocation) on the measure of cortical effective connectivity, and involved passive viewing of the visual stimuli. The second fMRI experiment was designed to match the experimental tasks used in the psychophysical experiments, and involved active judgment of the stimulus orientation.
In the first fMRI experiment, participants passively viewed the grating stimuli while detecting subtle color changes of the central fixation cross throughout the experiment. In the second fMRI experiment, at random temporal intervals, the central grating would rotate either clockwise or counterclockwise (randomized) for 400 ms. Participants reported the direction of the orientation change whenever it happened while maintaining eye fixation at a central cross throughout the experiment (monitored by eye tracker Eyelink 1000). In blocks where no central grating was presented, participants simply maintained eye fixation. To control participants' attention, the orientation change occurred infrequently (0–2 times per block) and the timing of its occurrence was identical across participants. To match the task difficulty level across participants, the degree of the orientation change was adjusted for individual participants according to their orientation discrimination threshold estimated from a preexperiment “mock” run where the orientation change of the central grating was varied in standard 2-up-1-down staircase procedure. Because of the orientation change of the central grating, the fMRI time series from the second experiment contained not only a block component, but also an event-related component associated with participant-specific stimulus (degree of orientation change). As this participant-specific event-related component might confound estimation of interindividual differences in cortical effective connectivity, it was filtered out through a low-pass Butterworth digital filter (stop band frequency > 96 cycles per scan, pass band frequency < 48 cycles per scan).
ROI definition.
We defined six ROIs that represented the foveal or peripheral parts of V1, V2, and V3 (Fig. 2B). Standard phase-encoded retinotopic mapping was used to delineate the boundaries between V1, V2, and V3 (Sereno et al., 1995). To separate the foveal and peripheral retinotopic regions, we used two different approaches. In the first approach, we simply contrasted BOLD signals evoked by foveal stimulation (central grating) with BOLD signals evoked by peripheral stimulation (surrounding grating) at a threshold of p < 0.001 (uncorrected). In the second approach, we further excluded the voxels in the foveal and peripheral ROIs whose population receptive field (Dumoulin and Wandell, 2008) overlapped with peripheral and foveal stimulation, respectively. The population receptive field map, showing the range of visual field locations to which individual fMRI voxels responded, was acquired in a separate experiment. Using this independently acquired map to confine ROIs ensured that the foveal–peripheral boundary was unambiguously defined with no “spill-over” artifacts (Fig. 2B).
To acquire phase-encoded retinotopic maps, participants viewed full-contrast flickered checkerboard wedges (radius 7.2 visual degrees, width 40 degrees) rotating smoothly in clockwise or anti-clockwise direction around a small fixation cross for 10 cycles at a speed of 20 volumes per cycle. At random temporal intervals, the checkerboard stimuli would undergo a small pattern shift for 200 ms, and participants were asked to indicate whenever this happened with a button press while maintaining fixation during the whole experiment. A fast Fourier transform was applied to the BOLD time series to extract the phase and power at the stimulation frequency. The resulting phase maps were displayed on inflated cortical surfaces reconstructed using FreeSurfer (http://surfer.nmr.mgh.harvard.edu). The boundaries between different visual cortices were delineated manually according to mirror reversals in the phase map.
To acquire population receptive field maps, participants viewed full-contrast flickered checkerboard bars (width 1.8 visual degrees) oriented at one of the four orientations (horizontal, vertical, 45 degrees, 135 degrees) and moving along the corresponding orthogonal direction (north/south for horizontal bar, west/east for vertical bar, northwest/southeast for 45 degree bar, northeast/southwest for 135 degree bar) for 8 cycles at a speed of 16 volumes per cycle. A blank screen was inserted into the last quarter of the second, fourth, sixth, and eighth cycles to provide a baseline condition that increased the accuracy of the measure. At random temporal intervals, the fixation cross would change color for 80 ms, and participants were asked to indicate whenever this happened with a button press while maintaining fixation during the whole experiment. The BOLD time series of each voxel was fitted with the predicted response from a population receptive field model. This prediction entailed a 2D Gaussian kernel f(x0, y0, σ) multiplied by the stimulus position function and convolved with the hemodynamic response function, where the center (x0, y0) and the σ of the Gaussian kernel characterized the population receptive field profile. The voxels whose population receptive field (1σ boundary from the center) overlapped with the peripheral and foveal stimulation were excluded from the foveal and peripheral ROIs, respectively.
DCM effective connectivity analysis.
To estimate effective connectivity between the six ROIs (foveal/peripheral V1, V2, and V3) and to study how this effective connectivity changed with visual stimulation, we applied DCM analysis to our fMRI data. DCM is a technique that provides a validated estimate of effective connectivity reflecting the directional coupling between neural populations (Friston et al., 2003; Friston, 2009, 2011). It is important to note that effective connectivity and the more widely used functional connectivity are conceptually different and empirically dissociable (Gerstein and Perkel, 1969; Aertsen and Preissl, 1991; David et al., 2008; Friston, 2011; Smith et al., 2011). Functional connectivity is a descriptive measure of the statistical dependencies (e.g., correlation, Granger causality) among observed data with no inferences about the underlying causes. Such statistical dependencies can arise from confounding causes, such as shared inputs or third connections, other than the underlying neural coupling (David et al., 2008; Friston, 2011; Smith et al., 2011). In contrast, effective connectivity, which originated from single-unit electrophysiology as an attempt to disambiguate the effects of confounding causes from those induced by underlying neural coupling (Gerstein and Perkel, 1969; Aertsen and Preissl, 1991), refers explicitly to the coupling influence that one neural system exerts over another at either synaptic or population level. As such, effective connectivity represents inference of the causes (e.g., neural coupling) underlying the observed data (e.g., BOLD signals) and rests upon the comparison of different models with hypotheses of different causes.
The different nature of the two measures (inferential for effective connectivity and descriptive for functional connectivity) is to be emphasized because it determines the types of questions that each measure is suitable for addressing (Friston, 2011). The analysis of effective connectivity recapitulates the scientific process of hypothesis testing, where one tests different models, each incorporating a hypothesis of neural coupling, that are made to explain the observed data. For example, DCM analysis is typically applied to making inferences about the changes in neural coupling under different experimental conditions, such as under different visual stimuli, by testing models with or without an effect of experimental manipulation on neural coupling. In contrast to the inferential nature of effective connectivity, functional connectivity is a descriptive parameter of the statistical relationships in the observed data. In functional connectivity analysis, no hypothesis of neural coupling is tested; instead, the hypotheses tested are statistical dependency and the null hypothesis of no dependency (Friston, 2011). As such, functional connectivity can be used for identifying statistical patterns, such as covariance networks in the data, but not for drawing inference of the underlying neural coupling. Indeed, concurrent fMRI-intracranial recordings showed that, although the effective connectivity measured from DCM on fMRI data was consistent with directional neural coupling measured from intracranial EEG data, the functional connectivity measured from Granger causality on fMRI data failed because of the confounding hemodynamic variability across cortical regions (David et al., 2008). Thus, existing evidence suggests that, compared with functional connectivity, inference of effective connectivity offers a more reliable estimation of underlying neural states.
As we were interested in the modulations of neural coupling (effective connectivity) by contextual stimulation, DCM analysis provided an appropriate approach. To make inferences concerning neural coupling from the observation of BOLD signals, DCM analysis models the neurovascular basis of BOLD signals through hemodynamic state equations (Friston et al., 2000), and the temporal dynamics of neural coupling through neural state equations that describe how the activity change in one neural population is modulated by the directional connectivity from another neural population multiplied by the activity of that neural population (Deco et al., 2008). Different models incorporating different hypotheses of neural coupling are constructed, and Bayesian model comparison is applied to select the model with the highest posterior probability (Penny et al., 2006; Friston, 2011).
The posterior probability of a model is a function of its prior probability and its model evidence. The model evidence quantifies the probability of the observed data given the model. It is a reflection of both how accurate the model fits the data (the more accurate, the higher the model evidence) and how simple the model structure is (the simpler, the higher the model evidence). The model evidence can be approximated by free energy, Akaike's information criterion, or Bayesian information criterion, and free energy is used in DCM analysis as an approximation to model evidence (Penny, 2012). The prior probability is specified to indicate prior knowledge about the plausibility of model structure. For example, the models with implausible anatomical connections can be given zero prior probability and are thus effectively excluded from the model space. In practice, only the plausible models are included in the model space; moreover, as there usually exists no strong prior against or for specific models, different models are given equal prior probabilities where their posterior probability effectively reflects their model evidence. Because of the nature of Bayesian model comparison, the models with implausible anatomical connections, even when included in the model space and given the same prior probability as the other models, would be less explanatory of the empirical data and have lower posterior probabilities. Notably, the existence of an anatomical connection does not necessarily mean that this connection is effective; conversely, as DCM is usually applied to infer the changes in effective connectivity with experimental conditions, such short-term change is not necessarily accompanied by changes in anatomical connections. As such, although an anatomically constrained model space would enable more efficient Bayesian model comparison, it does not necessarily influence the results of Bayesian model comparison.
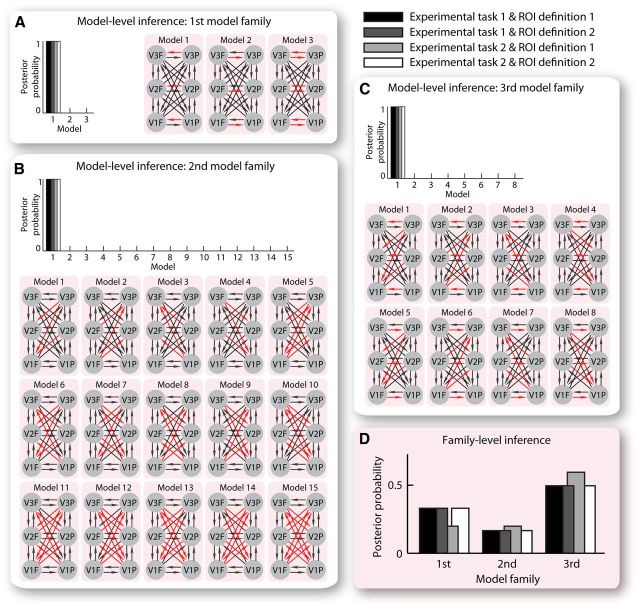
In our DCM analysis, anatomically plausible models comprising six interconnected ROIs (foveal/peripheral V1, V2, and V3) were constructed, where each model tested a different hypothesis of the contextual influence on effective connectivity between foveal and peripheral retinotopic regions. Specifically, we constructed three families of models hypothesizing changes in intra-areal connectivity within each retinotopic visual cortex (the first model family), or interareal connectivity between different retinotopic visual cortices (the second model family), or both (the third model family), when the central stimulus and its surrounding context were present together compared with isolation. Within each model family, different models were constructed with different directionality of hypothesized changes in effective connectivity. The first model family consisted of three different models hypothesizing changes in intra-areal connectivity from peripheral to foveal regions, or intra-areal connectivity from foveal to peripheral regions, or both (Fig. 3A). The second model family consisted of 15 different models hypothesizing changes in feedback connectivity from peripheral to foveal regions, or feedback connectivity from foveal to peripheral regions, or feedforward connectivity from peripheral to foveal regions, or feedforward connectivity from foveal to peripheral regions, or any combination of these (Fig. 3B). The third model family consisted of eight different models hypothesizing a combination of these changes in intra-areal and interareal (feedback, feedforward) connectivity (Fig. 3C). We applied Bayesian model comparison to select the model with the highest posterior probability within each model family (model-level inference) and the model family with the highest posterior probability (family-level inference). The effective connectivity estimation from the “winning” model in the “winning” model family was then linked to interindividual differences in the magnitude of the tilt illusion. Notably, the measure of effective connectivity and that of tilt illusion magnitude were independently acquired from the fMRI experiment (with passive viewing task) and the psychophysical experiment, respectively, which ensured that any observed relationship between the two was unlikely to result from artifacts.
Figure 3.
DCM effective connectivity analysis. We applied DCM analysis to our fMRI data to study the contextual influence on effective connectivity between foveal and peripheral regions of early retinotopic visual cortices (V1, V2, and V3). Three families of models were constructed hypothesizing changes in intra-areal connectivity within each retinotopic visual cortex (A, the first model family), or interareal connectivity between different retinotopic visual cortices (B, the second model family), or both (C, the third model family), when the central and surrounding gratings were presented together compared with isolation. Within each model family, different models were constructed incorporating different directionality of hypothesized changes in effective connectivity, as illustrated by the red arrows in the schematic depictions of model structures. Bayesian model comparison was applied to select the model with the highest posterior probability within each model family (A–C, model-level inference) and the model family with the highest posterior probability (D, family-level inference). DCM analysis for each of the four combinations of ROI definition and experimental task was performed independently and returned highly consistent results.
Results
Contextual induction of tilt illusion
The degree of contextual influence on orientation perception was quantified as the magnitude of the tilt illusion, reflecting the extent to which the perceived orientation of a central stimulus differed from its physical orientation when placed in a tilted context. All 40 participants were shown the same illusion stimulus, but the illusion magnitude differed across them over a remarkably large ninefold range (1.5–14.7 degrees) and followed a Gaussian distribution (Fig. 1B). The illusion magnitude did not covary with the goodness of psychometric curve fitting (r = −0.07, p = 0.76) or with the lapse rate (performance attenuation level) (r = 0.03, p = 0.91).
To test whether this interindividual variability in the magnitude of the tilt illusion was stimulus-dependent, we compared the illusion magnitude measured under different stimulus sizes, orientations, and contrasts. Although increasing the stimulus size led to a weaker tilt illusion (Fig. 1C; t(19) = 3.8, p < 0.005), the illusion magnitudes for small versus large stimuli were correlated across participants (Fig. 1C; r = 0.69, p < 0.001). Similarly, whereas the tilt illusion was 4 times weaker for cardinal stimuli than for oblique stimuli (Fig. 1D; t(19) = 7.5, p < 10−6), the interindividual variability in the illusion magnitude was highly correlated between the two stimulus configurations (Fig. 1D; r = 0.87, p < 10−6). Moreover, even when the contrast of the illusion stimulus was customized for each participant to counteract individual differences in the contrast detection threshold, we still observed substantial interindividual variability in the tilt illusion magnitude that correlated with the one measured with noncustomized stimuli (r = 0.77, p < 0.05). The same results were observed when the contrast of the illusion stimulus was customized according to the size ratio of participants' foveal to peripheral retinotopic regions (r = 0.79, p < 0.01). Thus, perception of the tilt illusion varied across individuals in a trait-like fashion that may reflect interindividual differences in contextual modulation of visual cortical processing.
Contextual modulation of cortical effective connectivity
We applied DCM analysis to study the influences of contextual stimulation on the effective connectivity between the foveal and the peripheral retinotopic regions that responded to the central stimulus and its surrounding context, respectively. Three families of models were constructed, hypothesizing changes in intra-areal connectivity alone (the first model family), or interareal connectivity alone (the second model family), or a combination of intra-areal and interareal connectivity (the third model family), when the central stimulus was presented together with its surrounding context. For each model family, different models were constructed that hypothesized different directionality of changes in effective connectivity.
Within each model family, Bayesian model comparison was applied to select the model with the highest posterior probability (model-level inference). In the first model family (Fig. 3A), the model hypothesizing changes in intra-areal connectivity from peripheral to foveal retinotopic regions had the highest posterior probability, whereas the models hypothesizing changes in intra-areal connectivity of the opposite direction (from foveal to peripheral retinotopic regions) or of both directions had much lower posterior probability. In the second model family (Fig. 3B), the model hypothesizing changes in feedback connectivity from peripheral to foveal retinotopic regions had the highest posterior probability, whereas the models hypothesizing changes in feedback connectivity from foveal to peripheral retinotopic regions, or changes in feedforward connectivity, or changes in any combination of feedback and feedforward connectivity, all had much lower posterior probability. In the third model family (Fig. 3C), the model hypothesizing changes in intra-areal and feedback connectivity from peripheral to foveal retinotopic regions had the highest posterior probability, whereas the models hypothesizing changes in other combinations of intra-areal and interareal connectivity all had much lower posterior probability. Across the model families, Bayesian model comparison was applied to select the model family with the highest posterior probability (family-level inference) and to test the family-wise hypothesis of whether contextual stimulation affected intra-areal connectivity alone (the first model family), or interareal connectivity alone (the second model family), or a combination of both (the third model family). The results showed that the third model family had a higher posterior probability than the other two model families (Fig. 3D).
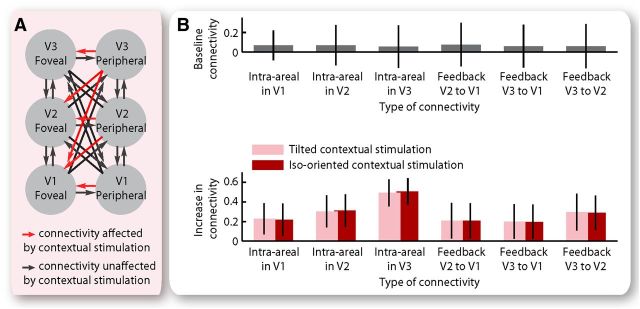
The model-level inference and the family-level inference consistently suggested that contextual stimulation affected both intra-areal and feedback connectivity from peripheral to foveal retinotopic regions, although it had no influence on other intra-areal or interareal connectivity between foveal and peripheral retinotopic regions. These results offered a qualitative estimation of the contextual influence on cortical effective connectivity. Based on the “winning” model in the “winning” model family, we further quantified the contextual influence on intra-areal and feedback connectivity from peripheral to foveal V1, V2, and V3 (Fig. 4A). Specifically, we measured the effective connectivity at the baseline condition where either a blank screen or an isolated central stimulus or an isolated surrounding stimulus was presented, and the changes in effective connectivity from the baseline condition to the contextual stimulation condition where the central stimulus was presented together with its surrounding context. The maximum a posteriori estimates were used for statistical test of the effective connectivity averaged across participants. At the baseline condition, the intra-areal and feedback connectivity from peripheral to foveal retinotopic regions was very weak (Fig. 4B; 95% confidence interval overlapped with zero). However, under contextual stimulation, a substantial increase was observed in intra-areal and feedback connectivity from peripheral to foveal retinotopic regions (Fig. 4B). Moreover, the increase in effective connectivity was observed for both the tilted and the iso-oriented condition where the surrounding context had a different and an identical orientation as the central stimulus, respectively (Fig. 4B). These results revealed a generic (instead of orientation-dependent) modulation of the coupling strength from peripheral to foveal retinotopic regions exerted by contextual stimulation.
Figure 4.
Contextual modulation of cortical effective connectivity. A, The results from Bayesian model comparison suggested contextual modulation of intra-areal and feedback connectivity from peripheral to foveal retinotopic regions, but not of other intra-areal or interareal connectivity between foveal and peripheral retinotopic regions. B, At the baseline condition where either a blank screen or an isolated central grating or an isolated surrounding grating was presented, the intra-areal and feedback connectivity from peripheral to foveal retinotopic regions was not significantly different from zero. Under contextual stimulation, a significant increase was observed in intra-areal and feedback connectivity from peripheral to foveal retinotopic regions, regardless of whether the surrounding and the central gratings had different or identical orientation. Bar chart represents the mean and 95% confidence interval of the maximum a posteriori estimates across participants (N = 20).
Reported above were the results from the DCM analysis on fMRI data where participants passively viewed the visual stimuli and the central versus peripheral ROIs were defined according to general linear model contrast alone. To test whether these results were robust against the stringency of ROI definition and the nature of the fMRI experimental task, we repeated the same DCM analysis twice, first on the BOLD time series extracted from the ROIs stringently confined according to population receptive field map, and then on the BOLD time series acquired from the fMRI experiment where participants actively judged the orientation change of the central stimulus. The results (Fig. 3; Table 1) from these additional DCM analyses were highly consistent with the original ones. Thus, in the context of our study, the measure of cortical effective connectivity was robust against ROI definition criteria and fMRI experimental task.
Table 1.
Influences of ROI definition and experimental task on DCM measure of cortical effective connectivitya
| Type of connectivity | ROI definition 1 versus 2 |
Experimental task 1 versus 2 |
|||
|---|---|---|---|---|---|
| Experimental task 1 | Experimental task 2 | ROI definition 1 | ROI definition 2 | ||
| Baseline condition | Intra-areal in V1 | t(19) = 0.12, p = 0.91 | t(9) = 0.05, p = 0.96 | t(9) = 0.16, p = 0.87 | t(9) = 0.14, p = 0.90 |
| Intra-areal in V2 | t(19) = 0.23, p = 0.82 | t(9) = 0.04, p = 0.97 | t(9) = 0.20, p = 0.85 | t(9) = 0.26, p = 0.80 | |
| Intra-areal in V3 | t(19) = 0.13, p = 0.90 | t(9) = 0.14, p = 0.89 | t(9) = 0.55, p = 0.60 | t(9) = 0.76, p = 0.46 | |
| Feedback V2 to V1 | t(19) = 0.25, p = 0.81 | t(9) = 0.11, p = 0.92 | t(9) = 0.14, p = 0.89 | t(9) = 0.30, p = 0.77 | |
| Feedback V3 to V1 | t(19) = 0.09, p = 0.93 | t(9) = 0.24, p = 0.82 | t(9) = 0.38, p = 0.71 | t(9) = 0.18, p = 0.86 | |
| Feedback V3 to V2 | t(19) = 0.03, p = 0.98 | t(9) = 0.23, p = 0.82 | t(9) = 0.43, p = 0.67 | t(9) = 0.20, p = 0.85 | |
| Tilted contextual stimulation | Intra-areal in V1 | t(19) = 0.07, p = 0.94 | t(9) = 0.06, p = 0.95 | t(9) = 0.35, p = 0.74 | t(9) = 0.36, p = 0.73 |
| Intra-areal in V2 | t(19) = 0.07, p = 0.95 | t(9) = 0.25, p = 0.80 | t(9) = 0.60, p = 0.56 | t(9) = 0.04, p = 0.97 | |
| Intra-areal in V3 | t(19) = 0.21, p = 0.84 | t(9) = 0.08, p = 0.94 | t(9) = 0.46, p = 0.66 | t(9) = 0.26, p = 0.80 | |
| Feedback V2 to V1 | t(19) = 0.04, p = 0.97 | t(9) = 0.01, p = 0.99 | t(9) = 0.24, p = 0.81 | t(9) = 0.04, p = 0.97 | |
| Feedback V3 to V1 | t(19) = 0.00, p = 1.00 | t(9) = 0.04, p = 0.97 | t(9) = 0.44, p = 0.67 | t(9) = 0.77, p = 0.46 | |
| Feedback V3 to V2 | t(19) = 0.07, p = 0.95 | t(9) = 0.22, p = 0.83 | t(9) = 0.78, p = 0.46 | t(9) = 0.35, p = 0.74 | |
| Iso-oriented contextual stimulation | Intra-areal in V1 | t(19) = 0.32, p = 0.75 | t(9) = 0.12, p = 0.91 | t(9) = 0.58, p = 0.58 | t(9) = 0.41, p = 0.69 |
| Intra-areal in V2 | t(19) = 0.09, p = 0.93 | t(9) = 0.03, p = 0.98 | t(9) = 0.74, p = 0.48 | t(9) = 0.50, p = 0.63 | |
| Intra-areal in V3 | t(19) = 0.09, p = 0.93 | t(9) = 0.12, p = 0.90 | t(9) = 0.39, p = 0.70 | t(9) = 0.26, p = 0.80 | |
| Feedback V2 to V1 | t(19) = 0.05, p = 0.96 | t(9) = 0.12, p = 0.91 | t(9) = 0.20, p = 0.85 | t(9) = 0.05, p = 0.96 | |
| Feedback V3 to V1 | t(19) = 0.22, p = 0.83 | t(9) = 0.08, p = 0.94 | t(9) = 0.55, p = 0.60 | t(9) = 0.37, p = 0.72 | |
| Feedback V3 to V2 | t(19) = 0.07, p = 0.94 | t(9) = 0.12, p = 0.91 | t(9) = 0.65, p = 0.53 | t(9) = 0.33, p = 0.75 | |
aTo test whether the measure of cortical effective connectivity was robust against the stringency of ROI definition and the nature of the fMRI experimental task, DCM analysis was independently performed for each of the four combinations of ROI definition and fMRI experimental task. The effective connectivity measure was compared between ROI definition 1 (general linear model contrast) and ROI definition 2 (population receptive field map), or between experimental task 1 (passive viewing of visual stimuli) and experimental task 2 (active judgment of stimulus orientation). The statistical values represent paired t test results.
Correlation between cortical effective connectivity and tilt illusion magnitude
Our DCM-fMRI analysis revealed a contextual modulatory influence on intra-areal and feedback connectivity from peripheral to foveal retinotopic regions. In parallel, our psychophysical experiment demonstrated a contextual modulatory influence on orientation perception. To explore the involvement of visual cortical connections in contextual modulation of visual perception, we studied whether the visual cortical connectivity correlated with the degree of contextual influence on orientation perception, assessed by the magnitude of the tilt illusion. Specifically, we took an individual difference approach examining whether such a correlation between brain signals and perception existed across participants, as this approach dissociated the perceptual effects from the stimulation effects.
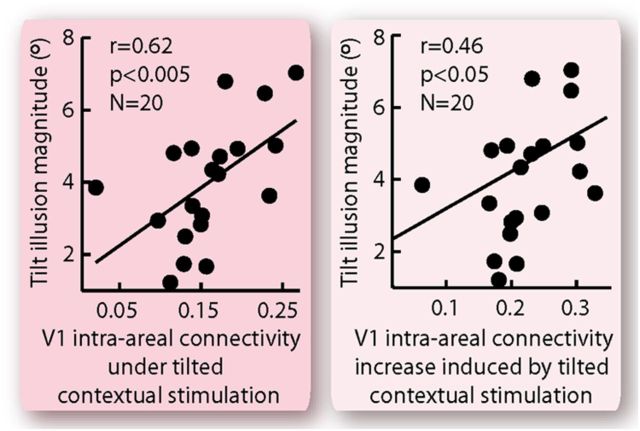
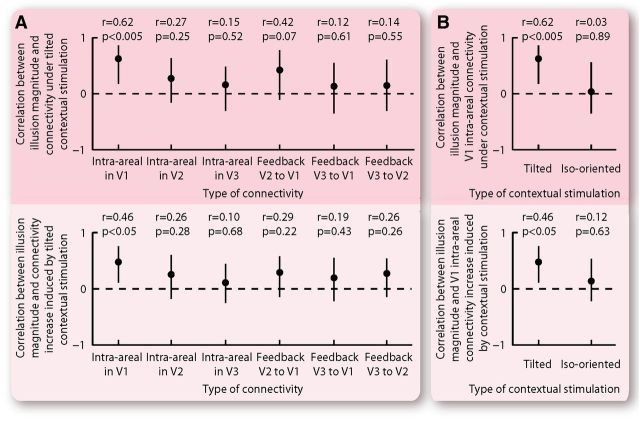
Across participants, we found that the magnitude of the tilt illusion correlated strongly with intra-areal connectivity within primary visual cortex from its peripheral to its foveal regions (Fig. 5). This correlation with the tilt illusion magnitude was observed for both the absolute value of effective connectivity under the tilted contextual stimulation (Fig. 5; r = 0.62, p < 0.005) and the increase in effective connectivity induced by the tilted contextual stimulation (Fig. 5; r = 0.46, p < 0.05). Interestingly, such correlations exhibited traits of circuitry specificity, in that they were observed only for intra-areal connectivity within primary visual cortex and not for other intra-areal or feedback connectivity from peripheral to foveal retinotopic regions (Fig. 6A). Moreover, the correlations exhibited orientation dependency and were specific to effective connectivity under the tilted as opposed to the iso-oriented contextual stimulation (Fig. 6B).
Figure 5.
Correlation between cortical effective connectivity and tilt illusion magnitude. The magnitude of the tilt illusion was plotted against the effective connectivity within primary visual cortex from its peripheral to its foveal region, illustrating a correlation across participants between cortical effective connectivity and tilt illusion magnitude. The correlation was observed regardless of whether the tilt illusion magnitude was linked to the absolute effective connectivity under tilted contextual stimulation or to the increase in effective connectivity induced by tilted contextual stimulation. Each point represents a single participant (N = 20), and the statistical values were calculated using Spearman's ρ.
Figure 6.
Specificity of correlation between cortical effective connectivity and tilt illusion magnitude. A, Contextual stimulation affected intra-areal connectivity within each retinotopic visual cortex from its peripheral to its foveal region, and feedback connectivity between different retinotopic visual cortices from the higher peripheral to the lower foveal region. For each of these affected connectivities, we calculated its interindividual correlation with the tilt illusion magnitude. The correlation was significant only for intra-areal connectivity within V1. B, Contextual stimulation affected cortical effective connectivity regardless of whether the surrounding context had a different and an identical orientation as the central stimulus. For each of these two stimulation conditions, we calculated the interindividual correlation between cortical effective connectivity and tilt illusion magnitude. The correlation was significant for the tilted contextual stimulation but not for the iso-oriented contextual stimulation. The statistical values represent Spearman's ρ and its bootstrap confidence interval with FDR correction for multiple comparisons (α = 0.025).
Reported above were the results from the DCM analysis when the central and peripheral ROIs were defined according to general linear model contrast alone. When the DCM analysis was repeated, but with ROIs now stringently confined according to population receptive field maps, the same relationships between cortical effective connectivity and tilt illusion magnitude were observed (Table 2). The correlation between the effective connectivity within primary visual cortex and the degree of contextual influence on orientation perception provides direct empirical evidence that visual cortical connections are involved in the contextual modulation of visual perception. Moreover, the orientation specificity of this correlation suggests the involvement of orientation-dependent connections in primary visual cortex.
Table 2.
Influences of ROI definition on correlations between cortical effective connectivity and tilt illusion magnitudea
| Type of connectivity | Correlation between illusion magnitude and effective connectivity under tilted contextual stimulation | Correlation between illusion magnitude and effective connectivity increase induced by tilted contextual stimulation |
|---|---|---|
| Intra-areal in V1 | r = 0.61 [0.26, 0.87], p < 0.005 | r = 0.59 [0.19, 0.84], p < 0.01 |
| Intra-areal in V2 | r = 0.09 [−0.31, 0.49], p = 0.70 | r = 0.07 [−0.27, 0.39], p = 0.76 |
| Intra-areal in V3 | r = 0.09 [−0.44, 0.47], p = 0.71 | r = 0.06 [−0.39, 0.49], p = 0.81 |
| Feedback V2 to V1 | r = 0.23 [−0.27, 0.74], p = 0.32 | r = 0.15 [−0.30, 0.59], p = 0.52 |
| Feedback V3 to V1 | r = −0.09 [−0.57, 0.45], p = 0.71 | r = 0.09 [−0.34, 0.40], p = 0.72 |
| Feedback V3 to V2 | r = −0.13 [−0.61, 0.30], p = 0.59 | r = 0.01 [−0.38, 0.32], p = 0.96 |
aThe correlations between cortical effective connectivity and tilt illusion magnitude reported in Figures 5 and 6 are results from DCM analysis on ROIs defined according to general linear model contrast alone (ROI definition 1). The same analysis was repeated on ROIs confined according to population receptive field maps (ROI definition 2), and the results are reported. The statistical values represent Spearman's ρ and its bootstrap confidence interval with FDR correction for multiple comparisons (α = 0.025).
In our study, we used interindividual differences in the tilt illusion magnitude as an approach to create a dissociation of subjective perception from physical stimulation and to induce variability in the degree of perceptual contextual modulation without changing visual stimulation. Nevertheless, the trait-like interindividual diversity in the tilt illusion magnitude is an interesting perceptual phenomenon, and understanding its neural basis is an interesting research topic on its own. Thus, we investigated whether other measures of visual cortical processing from our fMRI data might also correlate with individual differences in the tilt illusion magnitude. We focused on two measures in particular: the level of BOLD activity and the size ratio of peripheral to foveal retinotopic regions. First, we examined the levels of BOLD activity in the six ROIs (foveal/peripheral V1, V2, and V3). The level of BOLD activity under the tilted contextual stimulation and the change in BOLD activity level induced by the presence of tilted context both varied substantially across participants. However, none of these measures correlated with tilt illusion magnitude (all r < 0.20, all p > 0.39) or with cortical effective connectivity (all r < 0.40, all p > 0.08). Next, we looked at the size ratio of peripheral to foveal retinotopic regions. Because this size ratio covaried among V1, V2, and V3 (all r > 0.80, all p < 10−4), we used its average value as the indicator. The size ratio of peripheral to foveal retinotopic regions correlated significantly with the tilt illusion magnitude (r = 0.62, p < 0.005), but not with the effective connectivity between peripheral and foveal retinotopic regions (all r < 0.35, all p > 0.13). This suggested that the intra-areal connectivity within primary visual cortex and the size ratio of peripheral to foveal retinotopic regions were two independent factors that both contributed to interindividual diversity in the tilt illusion magnitude.
Discussion
Contextual modulation is a prominent feature of visual perception. It speaks to the fact that our perception is neither a true reflection of the physical world nor an isolated process that discounts the surrounding information. Not only the perception of but also the neural responses to visual stimuli depend strongly on the spatial contexts surrounding the stimuli (Schwartz et al., 2007). Research on animal models suggests that contextual modulation of neural responses takes place through cortical connections in early visual cortices and, specifically, through intra-areal lateral connections and interareal feedback connections (Lamme et al., 1998; Angelucci and Bullier, 2003; Bair et al., 2003; Schwabe et al., 2006). Inspired by these animal studies on contextual modulation of neural responses, a rich theoretical literature exists that explains the contextual influence on visual perception through modulatory cortical connections (Lamme et al., 1998; Schwartz et al., 2007). However, although visual perception and neural responses are both affected by spatial contexts, their exact dependencies on the contents of spatial contexts are dissociable (Schwartz et al., 2007) and may therefore involve different neural mechanisms.
Despite the long-existing research interest in contextual modulation of visual perception, there has been no direct empirical evidence supporting the role of cortical connections. Such lack of evidence is largely the result of the limitation of noninvasive neuroimaging techniques in characterizing cortical connectivity. In essence, the cortical activity assessed from neuroimaging signals reflects the aggregated contributions of many different cortical connections. Consequently, the conventional approach of linking cortical activity to perceptual contents fails to disentangle the effects of different cortical connections. Moreover, diffusion-weighted MRI measures of anatomical connectivity cannot reveal intra-areal connectivity within gray matter (Gong et al., 2008), whereas the standard measure of functional connectivity can only describe the statistical relationships in the data with no implications of the underlying cortical connectivity (David et al., 2008; Friston, 2011). In contrast, the DCM measure of effective connectivity overcomes these limitations and offers a validated estimation of directional connectivity from one neural population to another (Friston et al., 2003; Friston, 2009, 2011).
Advances in DCM analysis gave us the opportunity to test the involvement of visual cortical connections in contextual modulation of visual perception. As orientation is a visual feature with a well-defined cortical representation, we chose orientation perception and the tilt illusion as the model system. We asked whether the magnitude of the tilt illusion (i.e., the degree to which orientation perception was modulated by spatial contexts) correlated with visual cortical connectivity. Because our research question concerned the neural correlates of perceptual contents, we minimized the confounding influence of visual stimulation on the measure of cortical effective connectivity by taking an individual difference approach. Utilizing the perceptual variability across healthy human individuals (Kanai and Rees, 2011), this approach allowed us to study neural correlates of the tilt illusion magnitude without changing the visual stimulation, such as changing the relative orientation of the tilted context.
Applying DCM analysis to fMRI data, we disentangled signals reflecting intra-areal, feedback, feedforward connectivity between foveal and peripheral retinotopic regions that responded to visual field stimulation by the central stimulus and its surrounding context, respectively. We observed an increase in intra-areal and feedback connectivity from peripheral to foveal retinotopic regions, when the central stimulus and its surrounding context were presented together compared with isolation. Importantly, we found that, across participants, the magnitude of the tilt illusion correlated with the intra-areal connectivity in primary visual cortex from its peripheral to foveal region. This correlation was observed for intra-areal connectivity under the tilted contextual stimulation but not for that under iso-oriented contextual stimulation, suggesting that the estimates of intra-areal connectivity reflected orientation-dependent neural coupling.
Together, these results revealed a link between orientation-dependent connectivity within primary visual cortex and contextual modulation of orientation perception. In primary visual cortex, the intra-areal connections exhibit clear orientation dependency and preferentially link neurons with similar orientation preference (Weliky et al., 1995; Bosking et al., 1997; Dragoi and Sur, 2000; Stettler et al., 2002; Ko et al., 2011). It has been postulated that contextual modulation of orientation perception results from the interactions between neurons with similar orientation preference (Tolhurst and Thompson, 1975; Sengpiel et al., 1997; Bednar and Miikkulainen, 2000; Schwartz et al., 2009). Such interactions can lead to a skew in the population neural activity in a direction repulsive to the orientation of the surrounding context, which via population decoding corresponds to a repulsive shift in the perceived orientation of the central stimulus (Schwartz et al., 2009). Our findings thus provide direct empirical evidence for this theoretical framework that intra-areal connections in primary visual cortex are involved in contextual modulation of orientation perception.
As with most noninvasive techniques, DCM analysis provides an estimate of the effective connectivity at a neural population level. The models tested in DCM analysis constitute macroscopic ROIs (e.g., retinotopic regions). Consequently, the effective connectivity estimate is neither constrained by the detailed mesoscopic/microscopic cortical anatomy nor indicative of the cortical connectivity at a mesoscopic/microscopic level. Our findings showed that such macroscopic estimate of visual cortical connectivity contained a considerable amount of perception-related information that predicted interindividual variability in illusory orientation perception. With advances in two-photon microscopy, synaptic connectivity can now be characterized in behaving animals at a fine resolution of individual dendritic spines (Andermann et al., 2010; Drew et al., 2010). This opens up future research possibility into the relationship between macroscopic estimates of effective connectivity and microscopic measures of synaptic connectivity, the knowledge of which may prove essential for understanding the roles neural connectivity plays in visual perception.
Footnotes
This work was supported by the Brain Research Trust (C.S.), the Wellcome Trust (G.R., D.S.S.), and the Japan Society for the Promotion of Science (R.K.). We thank Karl Friston, Will Penny, and Haidong Lu for helpful discussions; Nikolaus Weiskopf for help with the fMRI sequence; and Sheila Burns, Kristian Johannesson, Ric Davis, Janice Glensman, and Chris Freemantle for help with data collection.
The authors declare no competing financial interests.
References
- Aertsen A, Preissl H. Dynamics of activity and connectivity in physiological neuronal networks. Nonlinear Dynamics Neuronal Networks. 1991:281–301. [Google Scholar]
- Andermann ML, Kerlin AM, Reid RC. Chronic cellular imaging of mouse visual cortex during operant behavior and passive viewing. Front Cell Neurosci. 2010;4:3. doi: 10.3389/fncel.2010.00003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Angelucci A, Bullier J. Reaching beyond the classical receptive field of V1 neurons: horizontal or feedback axons? J Physiol. 2003;97:141–154. doi: 10.1016/j.jphysparis.2003.09.001. [DOI] [PubMed] [Google Scholar]
- Bair W, Cavanaugh JR, Movshon JA. Time course and time-distance relationships for surround suppression in macaque V1 neurons. J Neurosci. 2003;23:7690–7701. doi: 10.1523/JNEUROSCI.23-20-07690.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bednar JA, Miikkulainen R. Tilt aftereffects in a self-organizing model of the primary visual cortex. Neural Comput. 2000;12:1721–1740. doi: 10.1162/089976600300015321. [DOI] [PubMed] [Google Scholar]
- Bosking WH, Zhang Y, Schofield B, Fitzpatrick D. Orientation selectivity and the arrangement of horizontal connections in tree shrew striate cortex. J Neurosci. 1997;17:2112–2127. doi: 10.1523/JNEUROSCI.17-06-02112.1997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- David O, Guillemain I, Saillet S, Reyt S, Deransart C, Segebarth C, Depaulis A. Identifying neural drivers with functional MRI: an electrophysiological validation. PLoS Biol. 2008;23:2683–2697. doi: 10.1371/journal.pbio.0060315. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Deco G, Jirsa VK, Robinson PA, Breakspear M, Friston K. The dynamic brain: from spiking neurons to neural masses and cortical fields. PLoS Comput Biol. 2008;4:e1000092. doi: 10.1371/journal.pcbi.1000092. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dragoi V, Sur M. Dynamic properties of recurrent inhibition in primary visual cortex: contrast and orientation dependence of contextual effects. J Neurophysiol. 2000;83:1019–1030. doi: 10.1152/jn.2000.83.2.1019. [DOI] [PubMed] [Google Scholar]
- Drew PJ, Shih AY, Driscoll JD, Knutsen PM, Blinder P, Davalos D, Akassoglou K, Tsai PS, Kleinfeld D. Chronic optical access through a polished and reinforced thinned skull. Nat Methods. 2010;7:981–984. doi: 10.1038/nmeth.1530. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dumoulin SO, Wandell BA. Population receptive field estimates in human visual cortex. Neuroimage. 2008;39:647–660. doi: 10.1016/j.neuroimage.2007.09.034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Floyd R, Steinberg L. An adaptive algorithm for spatial grey scale. Proc Soc Information Display. 1976;17:75–77. [Google Scholar]
- Friston KJ. Modalities, models, and models in functional Neuroimaging. Science. 2009;326:399–403. doi: 10.1126/science.1174521. [DOI] [PubMed] [Google Scholar]
- Friston KJ. Functional and effective connectivity: a review. Brain Connect. 2011;1:13–36. doi: 10.1089/brain.2011.0008. [DOI] [PubMed] [Google Scholar]
- Friston KJ, Mechelli A, Turner R, Price CJ. Nonlinear responses in fMRI: the balloon model, volterra kernels, and other hemodynamics. Neuroimage. 2000;12:466–477. doi: 10.1006/nimg.2000.0630. [DOI] [PubMed] [Google Scholar]
- Friston KJ, Harrison L, Penny W. Dynamic causal modelling. Neuroimage. 2003;19:1273–1302. doi: 10.1016/S1053-8119(03)00202-7. [DOI] [PubMed] [Google Scholar]
- Gerstein GL, Perkel DH. Simultaneously recorded trains of action potentials: analysis and functional interpretation. Science. 1969;16:828–830. doi: 10.1126/science.164.3881.828. [DOI] [PubMed] [Google Scholar]
- Gong G, He Y, Concha L, Lebel C, Gross DW, Evans AC, Beaulieu C. Mapping anatomical connectivity patterns of human cerebral cortex using in vivo diffusion tensor imaging tractography. Cereb Cortex. 2008;19:524–536. doi: 10.1093/cercor/bhn102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kanai R, Rees G. The structural basis of inter-individual differences in human behaviour and cognition. Nat Rev Neurosci. 2011;12:231–242. doi: 10.1038/nrn3000. [DOI] [PubMed] [Google Scholar]
- Ko H, Hofer SB, Pichler B, Buchanan KA, Sjöström PJ, Mrsic-Flogel TD. Functional specificity of local synaptic connections in neocortical networks. Nature. 2011;473:87–91. doi: 10.1038/nature09880. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lamme VA, Supèr H, Spekreijse H. Feedforward, horizontal, and feedback processing in the visual cortex. Curr Opin Neurobiol. 1998;8:529–535. doi: 10.1016/S0959-4388(98)80042-1. [DOI] [PubMed] [Google Scholar]
- Leibowitz H, Toffey S. The effect of rotation and tilt on the magnitude of the Poggendorf illusion. Vision Res. 1966;6:101–103. doi: 10.1016/0042-6989(66)90018-6. [DOI] [PubMed] [Google Scholar]
- Levitt JB, Lund JS. Contrast dependence of contextual effects in primate visual cortex. Nature. 1997;387:73–76. doi: 10.1038/387073a0. [DOI] [PubMed] [Google Scholar]
- Lutti A, Thomas DL, Hutton C, Weiskopf N. High-resolution functional MRI at 3T: 3d/2d echo-planar imaging with optimized physiological noise correction. Magn Reson Med. 2013;69:1657–1664. doi: 10.1002/mrm.24398. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ninio J, O'Regan JK. The half-zollner illusion. Perception. 1996;25:77–94. doi: 10.1068/p250077. [DOI] [PubMed] [Google Scholar]
- Oyama T. Determinants of the Zollner illusion. Psychol Res. 1975;37:261–280. doi: 10.1007/BF00309038. [DOI] [PubMed] [Google Scholar]
- Penny WD. Comparing dynamic causal models using AIC, BIC and free energy. Neuroimage. 2012;59:319–330. doi: 10.1016/j.neuroimage.2011.07.039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Penny W, Mattout J, Trujillo-Barreto N. Bayesian model selection and averaging. Statistical Parametric Mapping. 2006:1–29. [Google Scholar]
- Schwabe L, Obermayer K, Angelucci A, Bressloff PC. The role of feedback in shaping the extra-classical receptive field of cortical neurons: a recurrent network model. J Neurosci. 2006;26:9117–9129. doi: 10.1523/JNEUROSCI.1253-06.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schwartz O, Hsu A, Dayan P. Space and time in visual context. Nat Rev Neurosci. 2007;8:522–535. doi: 10.1038/nrn2155. [DOI] [PubMed] [Google Scholar]
- Schwartz O, Sejnowski TJ, Dayan P. Perceptual organization in the tilt illusion. J Vis. 2009;9:1–20. doi: 10.1167/9.4.19. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sengpiel F, Sen A, Blakemore C. Characteristics of surround inhibition in cat area 17. Exp Brain Res. 1997;116:216–228. doi: 10.1007/PL00005751. [DOI] [PubMed] [Google Scholar]
- Sereno MI, Dale AM, Reppas JB, Kwong KK, Belliveau JW, Brady TJ, Rosen BR, Tootell RB. Borders of multiple visual areas in human revealed by functional magnetic resonance imaging. Science. 1995;268:889–893. doi: 10.1126/science.7754376. [DOI] [PubMed] [Google Scholar]
- Smith S, Wenderoth P. Large repulsion, but not attraction, tilt illusions occur when stimulus parameters selectively favour either transient (M-like) or sustained (P-like) mechanisms. Vision Res. 1999;39:4113–4121. doi: 10.1016/S0042-6989(99)00118-2. [DOI] [PubMed] [Google Scholar]
- Smith SM, Miller KL, Salimi-Khorshidi G, Webster M, Beckmann CF, Nichols TE, Ramsey JD, Woolrich MW. Network modelling methods for fmri. Neuroimage. 2011;54:875–891. doi: 10.1016/j.neuroimage.2010.08.063. [DOI] [PubMed] [Google Scholar]
- Stettler DD, Das A, Bennett J, Gilbert CD. Lateral connectivity and contextual interactions in macaque primary visual cortex. Neuron. 2002;36:739–750. doi: 10.1016/S0896-6273(02)01029-2. [DOI] [PubMed] [Google Scholar]
- Tolhurst DJ, Thompson PG. Orientation illusions and after-effects: inhibition between channels. Vision Res. 1975;15:967–972. doi: 10.1016/0042-6989(75)90238-2. [DOI] [PubMed] [Google Scholar]
- Weliky M, Kandler K, Fitzpatrick D, Katz LC. Patterns of excitation and inhibition evoked by horizontal connections in visual cortex share a common relationship to orientation columns. Neuron. 1995;15:541–552. doi: 10.1016/0896-6273(95)90143-4. [DOI] [PubMed] [Google Scholar]
- Wenderoth P, Johnstone S. The different mechanisms of the direct and indirect tilt illusions. Vision Res. 1988;28:301–312. doi: 10.1016/0042-6989(88)90158-7. [DOI] [PubMed] [Google Scholar]
- Wenderoth P, O'Connor T, Johnson M. The tilt illusion as a function of the relative and absolute lengths of test and inducing lines. Percept Psychophys. 1986;39:339–345. doi: 10.3758/BF03203001. [DOI] [PubMed] [Google Scholar]
- Wichmann FA, Hill NJ. The psychometric function: I. Fitting, sampling, and goodness of fit. Percept Psychophys. 2001;63:1293–1313. doi: 10.3758/BF03194544. [DOI] [PubMed] [Google Scholar]