Multivariate meta-analysis: a method to summarize non-linear associations

Abstract

Multivariate meta-analysis represents a promising statistical tool in several research areas. Here we provide a brief overview of the application of this methodology to combining complex multi-parameterized relationships, such as non-linear or delayed associations, in multi-site studies. The discussion focuses on the advantages over simpler univariate methods, estimation and computational issues and directions for further research.

In this issue of Statistics in Medicine, Jackson and collaborators offer a comprehensive overview of the recent methodological advancements on multivariate meta-analysis, also highlighting limitations and research directions. Among the potential areas of application illustrated in their examples, we find particularly valuable the use of this methodology to combine multi-parameterized effects in multi-site observational studies, such as time series studies to assess the short term effects of environmental stressors. These studies usually adopt a two-stage approach, where a common first-stage model is applied to different cities or regions to derive site-specific estimates, and a second-stage meta-analysis is performed to combine these effects [4]. The presence of complex regression models with a high number of nuisance parameters to account for confounding factors makes the two-stage analysis attractive, circumventing the specification of a very highly parameterized hierarchical structure in a single multilevel development.

The usual approach proposed so far is based on first-stage models which simplify or summarize the city-specific effect in a single parameter, allowing the application of standard univariate meta-analytic techniques in the second stage. However, in the presence of complex associations, this choice could provide biased results with wrong assumptions about the simplified exposure-response shape (e.g. linear), or offer only a partial description of the phenomenon if the relationship is reduced to simple summaries. Multivariate meta-analysis has been proposed to combine non-linear dependencies [2, 3] and distributed lag structures [1], but there is no overview of methodological options. As a motivating example we illustrate the association between mean daily temperature and all-cause mortality in 108 USA cities [6], estimated through a quadratic B-spline with 5 degrees of freedom (with 3 equally-spaced knots) on lag 0-3. The associations in 4 cities are depicted in Figure 1.

Figure 1.

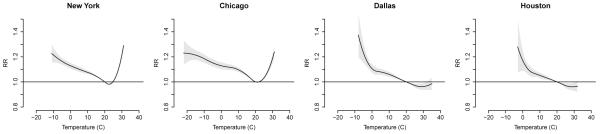
Temperature-mortality relationship (relative risk) in 4 USA cities, with reference at 20° C.

The two-stage approach described above may be applied to model these relationships across cities, assuming that the k estimated parameters ${\widehat{\theta }}_i$ of the B-spline, defining the association in each of the i = 1, …, m cities, follow a multivariate normal distribution with

$${\widehat{\theta }}_i~\mathcal{N}({\text{X}}_i\beta ,{\text{S}}_i+\Sigma )$$ 1

where S_i and Σ are the within and between-city (co)variance matrices, respectively. The term X_i represents a k × kp block-diagonal matrix, with each 1 × p block containing city-specific meta-variables x_i (usually with intercept). The kp-dimensional vector β contains the coefficients specifying the change (effect modification) in each of the k true parameters θ for a unit increase in each of the p meta-variables x_i. When no modifier is included, X_iβ ≡ θ, the vector of true overall (population) parameters, and the model in (1) reduces to Eq. 3 in the paper by Jackson and colleagues.

The need for the more complex meta-regression model in (1), more elaborated than the framework described by the authors for their examples, is motivated by the different focus of the analysis: the main interest here is not to obtain a pooled estimate of the association, but to characterize the heterogeneity of the effects through city-specific meta-variables, while accounting for a random residual component in Σ. In the specific example illustrated in Figure 1, our aim is to model a temperature-mortality relationship reflecting patterns such as shapes relatively similar within pairs of northern (New York and Chicago) and southern cities (Dallas and Houston), but different between them. This pattern may be explained by meta-variables x₁, …, x_p, representing geographical, climatological, demographical or socio-economic determinants. Such analytical proficiency is not obviously achieved with simpler univariate methods.

There are issues of estimation and computation specific to this area of application. Usually, the study design allows complete control of the first-stage model, thus making the within-study covariances in S_i available. However, dimensionality needs to be taken into account: as the association is described by a growing number of parameters θ, estimation of the k(k +1)/2 (co)variance parameters in Σ could be problematic. Potential solutions may involve the simplification of Σ, imposing for example an autoregressive, diagonal or compound-symmetry structure. The problem is worsened by the inclusion of a high number p of meta-variables, involving the estimation of kp coefficients. A simpler alternative is offered by meta-smoothing [7], a method based on a series of univariate meta-analysis of the effects estimated on a grid of exposure values, in order to recover the combined underlying relationship. While this method offers flexibility, an overall estimate of residual heterogeneity and significance tests are not easily provided. Finally, the model in (1) implies that exactly the same function is applied in every city, in order for the parameters ${\widehat{\theta }}_i$ to be meaningfully combined. In the example in Figure 1, the knots of the spline must be placed at the same values and this might represent a problem given the different temperature ranges between cities.

In conclusion, multivariate meta-analysis represents a promising methodology to combine multi-parameterized associations across studies. Compared to other examples described by Jackson and colleagues, the problem here is inherently multivariate, as each parameter is not interpretable on its own, and simplifications or approximations to re-express it in univariate terms are often limited or biased. However, the current framework could be infeasible for complex associations such as distributed lag non-linear relationships, involving a high number of parameters [5]. Further research is needed to address this problem of dimensionality, also providing some guidance on the limitations and comparative performances of different estimation methods in relation to number of studies m, parameters k, modifiers p and complexity of the structure of Σ. This framework applies to other multi-parameter functions summarizing non-linear associations, such as strata or polynomials, and may be extended to other multi-unit studies such as multi-centre randomized controlled trials or multi-country cohort studies.