Detection of submillisecond spike timing differences based on delay-line anticoincidence detection

Abstract

Detection of submillisecond interaural timing differences is the basis for sound localization in reptiles, birds, and mammals. Although comparative studies reveal that different neural circuits underlie this ability, they also highlight common solutions to an inherent challenge: processing information on timescales shorter than an action potential. Discrimination of small timing differences is also important for species recognition during communication among mormyrid electric fishes. These fishes generate a species-specific electric organ discharge (EOD) that is encoded into submillisecond-to-millisecond timing differences between receptors. Small, adendritic neurons (small cells) in the midbrain are thought to analyze EOD waveform by comparing these differences in spike timing, but direct recordings from small cells have been technically challenging. In the present study we use a fluorescent labeling technique to obtain visually guided extracellular recordings from individual small cell axons. We demonstrate that small cells receive 1–2 excitatory inputs from 1 or more receptive fields with latencies that vary by over 10 ms. This wide range of excitatory latencies is likely due to axonal delay lines, as suggested by a previous anatomic study. We also show that inhibition of small cells from a calyx synapse shapes stimulus responses in two ways: through tonic inhibition that reduces spontaneous activity and through precisely timed, stimulus-driven, feed-forward inhibition. Our results reveal a novel delay-line anticoincidence detection mechanism for processing submillisecond timing differences, in which excitatory delay lines and precisely timed inhibition convert a temporal code into a population code.

temporal coding, in which information is encoded into the precise timing of action potentials, is common in sensory systems (VanRullen et al. 2005). In some cases, behavioral sensitivity can reach the submillisecond or even submicrosecond range, several orders of magnitude shorter than a typical action potential (Kawasaki 1997; Moiseff and Konishi 1981; Simmons 1979). Understanding this hyperacute temporal sensitivity provides insight into general properties of temporal processing and the diverse neural mechanisms that can support it (Carr and Friedman 1999).

The best studied examples of submillisecond temporal discrimination involve detection of interaural timing differences (ITDs) for sound localization (Ashida and Carr 2011; Köppl 2009; Schnupp and Carr 2009). In birds and reptiles, ITDs are analyzed through delay-line coincidence detection of binaural excitatory inputs (Carr and Konishi 1990; Carr et al. 2009; Funabiki et al. 2011). In mammals, ITD detection also relies on coincidence detection of binaural excitatory inputs, but the mechanistic basis for ITD tuning remains controversial and cannot be explained by axonal delay lines (Brand et al. 2002; Grothe et al. 2010; McAlpine and Grothe 2003; Roberts et al. 2013; van der Heijden et al. 2013). In both systems, inhibition appears to play important but different roles in shaping binaural processing (Grothe 2003; Roberts et al. 2013; Yamada et al. 2013). One general theme that emerges is that submillisecond temporal processing is implemented using similar neural substrates that are combined in unique ways by different circuits (Carr and Friedman 1999; Carr and Soares 2002; Carr et al. 2001; Kawasaki 2009).

Mormyrid fishes communicate using a species-specific electric organ discharge (EOD) consisting of 1–5 distinct phases and a total duration ranging from ∼0.1 to 20 ms (Carlson et al. 2011; Hopkins 1981). Sharp temporal features of the EOD waveform, particularly the relative timing of phase onsets and offsets, are used for species recognition and mate choice (Arnegard et al. 2006; Feulner et al. 2009; Hopkins and Bass 1981). For example, in the Ivindo River of Gabon there are at least 21 mormyrid species/morphs living in sympatry, each having a distinctive EOD (Arnegard et al. 2010; Carlson et al. 2011; Hopkins 1981). Thus detecting subtle timing differences among EOD waveforms is an essential computation that fish must perform in their natural environment.

EODs are encoded by peripheral electroreceptors distributed throughout the surface of the skin called knollenorgans (KOs), which respond with a single, fixed-latency spike to the onset of inward currents (Bennett 1965; Harder 1968). Variation in the location and orientation of KOs with respect to external electric fields results in different receptors receiving local EOD stimuli with different polarities and intensities (Hopkins 1986; Hopkins and Bass 1981). As a result, different KOs respond to distinct edges of an EOD waveform, thereby encoding EODs into spike timing differences among the population of receptors (Baker et al. 2013).

These timing differences are thought to be analyzed by small cells in the midbrain anterior exterolateral nucleus (ELa; Fig. 1A) (Baker et al. 2013; Xu-Friedman and Hopkins 1999). Small cells receive excitatory inputs from ascending axons and GABAergic input from local interneurons, called large cells, via a calyx synapse (Friedman and Hopkins 1998; George et al. 2011; Mugnaini and Maler 1987). Incoming axons synapse on large cells immediately after entering ELa and then continue on a convoluted path for up to 7 mm, synapsing on dozens of small cells along the way (Friedman and Hopkins 1998). The variable length of the axons projecting to small cells are suggestive of delay-lines that establish variation in the relative timing of excitatory and inhibitory input (Xu-Friedman and Hopkins 1999). This observation led to a delay-line anticoincidence detection model, in which the processing of submillisecond spike timing differences results from a combination of precisely timed inhibition and delayed excitation arising from different receptive fields (Friedman and Hopkins 1998). Unfortunately, it is difficult to record from small cells due to their distinctive anatomic features, so we do not know how they actually perform temporal comparisons. Therefore, we developed a fluorescence-based method to directly target small cell axons for extracellular recording (Lyons-Warren et al. 2013). To determine how small cells code for peripheral timing differences, we recorded responses to spatially uniform, square-pulse electric stimuli that allowed us to precisely manipulate the relative timing of KO responses on opposite sides of the body (Fig. 1A). Our data provide empirical evidence in support of a novel delay-line anticoincidence detection mechanism for processing submillisecond timing differences.

Fig. 1.

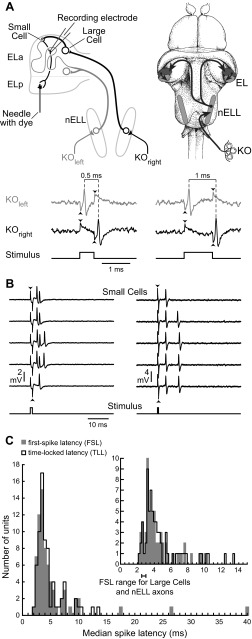
Retrograde labeling allows for visually guided extracellular recordings from small cell axons. A: schematic representation of the knollenorgan (KO) electrosensory pathway. KOs generate short-latency spikes in response to inward current caused by changes in voltage across the skin surface. In response to an electrical stimulus, KOs on opposite sides of the body experience opposite stimulus polarities. Thus, in recordings from a single KO, the responses to normal and reversed polarity stimuli reveal how KOs on opposite sides of the body would respond to a single stimulus (Hopkins and Bass 1981; Lyons-Warren et al. 2012). In the illustration, we show the spiking responses of a single KO, recorded extracellularly, to normal (simulating KO_left) and reversed (simulating KO_right) polarity square pulses of 2 different durations (left, 0.5 ms; right, 1 ms). The stimuli are shown in the bottom trace, and stimulus artifact can be seen at stimulus onset and offset (arrowheads). The difference in spike timing between KO_left and KO_right codes for pulse duration. These spike timing differences are relayed with high temporal fidelity from the hindbrain nucleus of the electrosensory lateral line lobe (nELL) to the midbrain exterolateral nucleus (EL). EL has 2 components, anterior (ELa) and posterior (ELp). nELL axons synapse onto large GABAergic interneurons (large cells) soon after entering ELa and then travel for up to an additional 7 mm, synapsing on dozens of small cells throughout ELa. Small cells also receive GABAergic input from large cell calyx synapses. Small cell axons provide the only projection from ELa to ELp. Thus dye placed in ELp (needle) selectively labels small cells through retrograde transport. B: extracellular recordings from 2 different small cell axons, one showing responses to a 1-ms, 18.4 mV/cm stimulus (left) and a second showing responses to a 0.5-ms, 10 mV/cm stimulus (right). The stimuli are shown in the bottom trace, and stimulus artifact can be seen at stimulus onset and offset (arrowheads). C: histogram of median first-spike latencies (FSL; gray) and time-locked latencies (TLL; black) from the stimulus edge (bin size = 0.5 ms). Inset shows the same result at a finer resolution (bin size = 0.2 ms) for the subset of latencies ranging from 1 to 15 ms. Large cells and nELL axons have an FSL range of 2.5–3 ms (Amagai et al. 1998).

MATERIALS AND METHODS

Animals.

We used developmentally mature individuals of both sexes of the weakly electric mormyrid fish Brienomyrus brachyistius. Fish were purchased from commercial distributors and housed in community aquariums at a temperature of 26–28°C and conductivity of 200–400 μS/cm, with a 12:12-h light-dark cycle. Fish were fed live black worms four times per week. Before all procedures, fish were anesthetized in 300 mg/l tricaine methanesulfonate (MS-222) and then paralyzed with either 20–100 μl of 0.3 mg/ml gallamine triethiodide (for KO recordings) or 100 μl of 3 mg/ml gallamine triethiodide (for evoked potential and small cell recordings). Fish were then placed on a platform, supported with vertical rods, and respirated by a tube placed in the mouth that fed aerated water across the gills. For evoked potential and small cell recordings, we respirated fish under general anesthesia (100 mg/l MS-222) throughout surgery and applied lidocaine as a local anesthetic before performing a craniotomy. Fish were brought out of general anesthesia before all recordings were performed. To monitor fish health during experiments, we recorded the descending EOD command from the spinal cord using a pair of electrodes placed next to the caudal peduncle (Carlson 2003). Fish used for KO recordings were returned to their home tank after recovering from the paralytic. Fish used for small cell and evoked potential recordings were placed back under general anesthesia after all recordings were completed before being euthanized. All procedures were in accordance with guidelines established by the National Institutes of Health (NIH) and were approved by the Animal Care and Use Committee at Washington University in St. Louis.

KO recordings.

We obtained noninvasive, in vivo extracellular recordings from KOs as previously described (Arnegard et al. 2006; Bennett 1965; Hopkins and Bass 1981; Lyons-Warren et al. 2012). We used 3 fish ranging in size from 11.2 to 13.0 cm in standard length. We used relatively large fish for these recordings because larger fish have more KOs and can be more reliably dosed with gallamine triethiodide to allow for a full recovery after the experiment. Previous studies did not find any differences in KO physiology with respect to fish size. Electrodes were forged from 1.0-mm OD, 0.5-mm ID borosilicate glass by heating the distal end and bending the last 1 cm to a 10° angle. The electrode was then filled with tank water, connected to the head stage of a DC amplifier (A-M Systems model 1600), and placed just above an individual KO. Monophasic square-pulse stimuli were generated using isolated square-pulse generators (A-M Systems model 2100), attenuated (Hewlett Packard 350D), and then delivered as a constant-current stimulus directly through the recording electrode, using bridge balance to minimize artifact. Thus KO stimuli consisted of localized current pulses injected directly into the receptor organ and referenced to ground. Stimulus intensities varied from 0.5 to 5.7 nA. For isointensity tuning curves, stimuli were monophasic positive square pulses ranging in duration from 0.01 to 100 ms. For paired-pulse experiments, the stimulus was a 50-ms monophasic positive square pulse followed by a 0.3-ms monophasic positive square pulse with delays of 0.1 to 10 ms between the end of the first pulse and the start of the second pulse. In both experiments, each stimulus was presented for 10, 20, or 30 repetitions. KO electrical activity was amplified 10 times and digitized at 195.3 kHz (Tucker-Davis model RP2.1). Responses were saved using custom software (Matlab).

Small cell recordings.

We obtained extracellular single-unit recordings from 76 retrogradely labeled small cell axons in 37 fish as described in detail in a previous methods article (Lyons-Warren et al. 2013). Individuals ranged from 5.5 to 8.6 cm in standard length. We were limited to using fish ≤8.6 cm in standard length because the compound microscope objective constrained the size of the recording chamber (Lyons-Warren et al. 2013). Sharpened tungsten wires coated in 2 mM dextran-conjugated Alexa Fluor 10,000 MW dye were inserted 1–4 times ∼25 μm deep into the posterior exterolateral nucleus (ELp) for dye placement. Small cells are the only neurons in ELa that project to ELp, so this provided a means of selectively labeling these neurons within ELa (Fig. 1A). Recording electrodes were made from 1-mm OD, 0.58-mm ID borosilicate glass pulled to a 1.0- to 2.4-μm tip, and they were then filled with filtered Hickman's Ringer and connected to a head stage (Axon instruments CV-7B). After 2–6 h for dye uptake and retrograde transport, an electrode under positive pressure was placed next to a labeled axon in ELa visualized using an upright, fixed-stage epifluorescent microscope. Suction was then used to bring the axon into the recording electrode. We attempted to obtain intracellular whole cell recordings from labeled small cell somas, but we were unable to obtain a membrane seal. We also attempted intracellular whole cell recordings from small cells in vitro using both slice (George et al. 2011) and whole brain preparations (Ma et al. 2013). However, even when small cells were visualized at high magnification in vitro, it was difficult to obtain a membrane seal, and on rare instances when a seal was achieved, the resulting intracellular recordings were of low quality (low, unstable resting potential and no ability to drive spiking). Finally, we attempted sharp intracellular recordings from small cells in vitro, but these also resulted in low-quality recordings and an inability to drive spiking with current injection. These difficulties most likely relate to the extensive myelination within ELa, the small size of the cells (diameter = 5–7 μm), and synaptic terminals from other cells covering most of the soma (Friedman and Hopkins 1998; Mugnaini and Maler 1987). Thus we are currently limited to using extracellular recordings from small cells in this study.

Monophasic square-pulse stimuli were generated using isolated square-pulse generators (A-M Systems model 2100), attenuated (Hewlett Packard 350D), and then delivered as global electrosensory stimuli to the tank in one of two orientations, transverse or longitudinal (Lyons-Warren et al. 2013). Transverse stimuli were delivered between three vertically oriented silver wires located on the left wall of the chamber and three vertically oriented silver wires located on the right wall of the chamber, resulting in a uniform electric field vector between the left and right sides of the fish. Longitudinal stimuli were delivered between two vertically oriented silver wires located on the front wall of the chamber and two vertically oriented silver wires located on the back wall of the chamber, resulting in a uniform electric field vector between the head and tail of the fish. After getting a unit, we used both monophasic positive and negative 100-ms square pulses to determine which stimulus orientation (transverse vs. longitudinal), polarity (normal vs. reversed), and intensities elicited a response. We then used the preferred stimulus orientation to assess duration tuning to both stimulus polarities and, when possible, to multiple stimulus intensities. If a unit responded to both stimulus orientations, then duration tuning was assessed for both orientations whenever possible. Stimulus intensities were calibrated in units of millivolts per centimeter at the fish's position but with the fish absent.

The duration tuning of a unit was determined by presenting monophasic positive and negative stimuli ranging in duration from 1 μs to 20 ms. The specific durations presented were chosen to best capture the tuning of each particular unit. Each stimulus was presented as either 1 set of 20 or 4 sets of 5 repetitions each. An inhibitory corollary discharge in the hindbrain timed to the fish's own EOD prevents the KO pathway from responding to stimuli arriving 2–4 ms after the fish's own EOD (Bell and Grant 1989). Therefore, a sweep was discarded if a spinal EOD command occurred during 5-ms windows preceding both stimulus edges.

Responses were obtained using a Multiclamp 700B amplifier (Molecular Devices). Recorded signals were low-pass filtered using a 10-kHz 8-pole Bessel filter, digitized at 166–200 kHz using a Digidata 1322A 16-bit analog-to-digital converter, and acquired in pCLAMP software (Molecular Devices). Pipette capacitance compensation was automatically adjusted using Multiclamp 700B Commander software. Either a threshold or a template search function was used to identify the timing of each spike in each sweep using Clampex software (Molecular Devices). In some recordings, there appeared to be two separate units, likely because of an unlabeled axon in close proximity to the target axon. For these recordings, we used principal components analysis to confirm that multiple units were present and to separate waveforms so that the units could be analyzed separately. We used 12 waveform parameters that resulted in clearly separated units: peak amplitude, time to peak, rise time, rise slope, decay time, decay slope, half-width, area, anti-peak amplitude, time to anti-peak, time to rise to half-amplitude, and time to decay from half-amplitude. We used data from all recorded units in subsequent analyses.

To test for inhibition of small cells, we used two different techniques. First, we used a complex stimulus protocol consisting of a 50-ms monophasic square stimulus (long pulse) at a polarity that elicited a response to the leading edge, followed by a shorter pulse of the same polarity. The duration of the short pulse was the minimum duration that reliably elicited a response when presented alone, which ranged from 0.1 to 0.5 ms depending on the unit. The short pulse was presented at delays ranging from 0.1 to 25 ms after the end of the long pulse. As a control, we presented a 100-ms pulse with a second long pulse timed so the “excitatory” edges occurred at the same intervals as in the paired-pulse experiment but without an “inhibitory” edge between them. Second, we applied SR-95531 (gabazine), a competitive inhibitor of GABA_A receptors (Lindquist et al. 2005). Inhibitory synapses are located on the small cell soma, which is not necessarily proximal to our recording site (Mugnaini and Maler 1987). Therefore, we used bolus application of 5–50 μl of a 1–10 mM solution in Hickman's Ringer (Bremner et al. 2006). The cavity surrounding ELa holds 100–500 μl of Ringer, so we estimate the final concentration of gabazine to be between 100 and 600 μM, which is above saturating levels (Lindquist et al. 2005). In a separate experiment using evoked potential recordings (see below), we demonstrated that the effects of gabazine application on small cell activity are caused by local actions within ELa, not effects on upstream GABAergic synapses.

Spike-response analysis.

To analyze small cell spike times, we generated peristimulus time histograms using a bin size of 1 ms and then divided by the number of stimulus repetitions. The average bin height during the prestimulus baseline period plus three standard deviations was set as a criterion response level. This criterion was then subtracted from the entire histogram, and all bins with a value greater than zero were considered part of the response. First-spike latency (FSL) was calculated as the median latency from stimulus edge to the first spike across repetitions. We also calculated time-locked response latency (TLL). The window for determining TLL was defined as the tallest bin in the peristimulus time histogram plus an additional 0.5 ms on either side of this bin. We then calculated the median and standard deviation of all spike times falling within this window. We used the median rather than the mean to eliminate the effect of outliers in skewing the FSL and TLL. For most units, the mean and median of FSL and TLL were in close agreement. However, some units were more variable in their responses, resulting in large outliers that skewed the mean away from the center of the distribution.

When 100-ms stimuli were tested at multiple intensities, we used the highest intensity tested for analyzing response timing to ensure uniformity. Recordings from KO receptors reveal that response probability and temporal precision increase with stimulus intensity (Lyons-Warren et al. 2012). Response magnitude was determined as the area of all bins poststimulus presentation greater than the baseline criterion, in units of spikes per stimulus. Duration tuning curves were generated by plotting response magnitude as a function of stimulus duration and smoothed using a Savitzky-Golay filter in Matlab with a polynomial order of 1 and a frame size of 3. Tuning categorization was based on which parts of the smoothed curve were greater than 50% of the maximal response. Paired-pulse experiments for both small cells and KOs were analyzed using peristimulus time histograms. We quantified responses to the two pulses as the height of the tallest bin following each stimulus edge and then determined the ratio of the response to the second pulse relative to the first pulse.

Statistical analysis.

All statistical analyses were performed using Statistica 6.1 (StatSoft). Because small cell duration tuning could change with both stimulus intensity and polarity, we treated each tuning curve as an independent sample in statistical analyses of duration tuning. Because of small sample sizes in some cases and deviations from normality in others, we used nonparametric tests for all statistical comparisons between groups. For pair-wise comparisons between independent groups, we used the Mann-Whitney U-test. For pairwise comparisons of repeated measurements, we used the Wilcoxon matched-pairs test. For comparing multiple, independent groups, we used the Kruskal-Wallis one-way ANOVA. We used linear regression to test for correlations between variables. All tests were two-tailed with α = 0.05. We did not perform multiple comparisons on any data set.

Evoked field potential recordings.

Evoked potentials were recorded from the ELa as described previously (Carlson 2009; Lyons-Warren et al. 2012). We recorded from one fish having a standard length of 12.0 cm. We chose a relatively large fish for this because we have found that evoked potential amplitudes in ELa generally scale with fish size. We delivered transverse, 0.5-ms monophasic square pulses at an intensity of 20 mV/cm using 3 vertically oriented silver wires located on the left and right sides of the chamber as described for small cell recordings. Ten repetitions of the stimulus were delivered at a range of latencies after the fish's EOD command. After obtaining baseline responses, we added 15 μl of 5 mM gabazine in Hickman's Ringer to the brain cavity surrounding ELa/ELp. The same stimuli were presented immediately after application and then repeatedly until 5 h after application.

Modeling.

To determine how differences in the latency of excitation relative to inhibition could impact small cell responses to variation in peripheral spike timing differences, we generated leaky integrator neurons (Dayan and Abbott 2001) as

$$C_{\text{m}}\frac{\text{d}{V}_{\text{m}}}{\text{d}t}=I_{\text{E}}(t)+I_{\text{I}}(t)-\frac{V_{\text{m}}}{R_{\text{m}}},$$

where V_m is the membrane potential, C_m is the membrane capacitance (10 μF), R_m is the membrane resistance (200 MΩ), and I_E(t) and I_I(t) represent excitatory and inhibitory synaptic currents. On the basis of the anatomy of the circuit (Friedman and Hopkins 1998; Mugnaini and Maler 1987) and our recordings of small cell responses to square-pulse stimulation, we modeled two conditions: excitatory input in response to one stimulus edge with inhibitory input to the other edge, and separate excitatory inputs in response to both stimulus edges with inhibitory input to a single edge. We varied the latency of excitatory inputs from 0 to 10 ms, and we kept the inhibitory latency constant at 0 ms. This models excitatory latencies that vary from 0 to 10 ms relative to inhibitory latencies, which matches observed anatomic variation in axonal path lengths to small cells (Friedman and Hopkins 1998) and our observed spike latencies. We modeled all synaptic conductances as alpha functions (Dayan and Abbott 2001) using the equation

$$g_{\text{s}}(t)=\frac{g_{\max }t}{{\tau }_{\text{s}}}{e}^{(1-t/{\tau }_{\text{s}})}$$

where g_s is the synaptic conductance, g_max is the maximum conductance, and τ_s is the time constant of the conductance. We set τ_E to 0.5 ms, τ_I to 1 ms, g_maxE to 1 nS, and g_maxI to 10 nS. These values were chosen to reflect inhibition that is slow and strong relative to excitation. Varying these parameters affected the specific quantitative output of the model but did not affect the patterns of duration tuning observed when varying excitatory synaptic latency.

To incorporate the effects of long-pass peripheral filtering by KO electroreceptors on responses to variation in pulse duration (Lyons-Warren et al. 2012), we scaled synaptic conductances using a sigmoidal function:

$$s(d)=\frac{1}{1+e^{-40(d-0.1)}},$$

where d is stimulus duration and s(d) is a scaling factor that varies from 0 to 1. The other parameters were set to replicate the general peripheral filtering observed among KOs (Lyons-Warren et al. 2012).

The excitatory and inhibitory synaptic currents were determined from their respective conductances and driving forces as

$$I_{\text{s}}(t)=g_{\text{s}}(V_{\text{m}}-V_{\text{r}}),$$

where V_r is the reversal potential, which was set at +60 mV depolarized relative to rest for excitatory currents and −20 mV hyperpolarized relative to rest for inhibitory currents. We presented square-pulse stimuli of both polarities ranging in duration from 0.01 to 10 ms. We measured the maximum depolarization of each model neuron as a function of duration and then characterized duration tuning by normalizing the responses of each model neuron to the maximum response. We also characterized the duration tuning of each neuron after removing the inhibitory input to simulate the effects of blocking inhibition on duration tuning.

Stereology counts.

We used Stereo Investigator (MBF Bioscience) to perform stereology counts of nELL and small cell somas from three fish ranging in size from 8.9 to 10.2 cm in standard length (Gundersen et al. 1988). We used 50-μm serial transverse sections from paraformaldehyde-fixed brain tissue stained with cresyl violet. We used every section that included nELL or ELa for generating counts, which ranged from a total of 19–21 sections with nELL and 12–15 sections with ELa. In each section, the region of interest was outlined. Counting grids and frames were selected on the basis of the density and regularity of cells in the region of interest, using a counting grid of 125 × 125 μm for nELL and 150 × 150 μm for ELa. The optical fractionator selected a random box in each grid space at the specified counting frame of 100 × 100 μm for nELL and 50 × 50 μm for ELa. A counter was used to mark the cells of interest. The total number of counters was extrapolated on the basis of the area of the tissue to determine the total number of cells. We repeated this procedure for the left and right nELL and ELa of each fish to estimate the total number of nELL and ELa somas. Gunderson's coefficient of error (m = 1) was ≤0.05 for all counts (Gundersen et al. 1988). To estimate the number of nELL projections to small cells, we multiplied estimates of total nELL soma numbers in each fish by 1.1 to account for the ∼10% of nELL neurons that project bilaterally to ELa (Friedman and Hopkins 1998), and then we multiplied this by 54.5, the median number of small cells that individual nELL axons project to (Friedman and Hopkins 1998). We chose the median rather than the mean because only four nELL axons were systematically analyzed in this previous study (these 4 axons projected to 33, 44, 65, and 72 small cells). For each fish, we then determined the ratio of estimated nELL terminals to small cell somas.

Axonal labeling.

After general anesthesia, two fish (one with a standard length of 6.4 cm and a second of 13.3 cm) were transcardially perfused with ice-cold Hickman's Ringer followed by 4% paraformaldehyde. The brains were postfixed for 24 h at 4°C and then removed from the skull. Dye was placed in the left and right nELL by inserting sharpened tungsten wires coated in DiI or DiO paste throughout the anterior-posterior extent of nELL. The brains were then embedded in a gelatin block and stored in 4% paraformaldehyde at 37–42°C for 14–16 wk to allow for dye transport. We cut 50-μm horizontal sections on a vibratome, washed them in 0.1 M phosphate buffer, and then stained cell nuclei using Hoechst 34580 (2 μg/ml, 5-min incubation at room temperature). Slices were wet mounted in 0.1 M phosphate buffer and coverslipped for imaging on a confocal microscope.

RESULTS

Targeted recordings from small cells.

We obtained extracellular recordings from small cells using a retrograde labeling technique that allowed us to target individual axons (Fig. 1, A and B) (Lyons-Warren et al. 2013). To determine whether excitatory inputs arose from ipsilateral or contralateral receptive fields and characterize their latency, we recorded responses of 70 units to 100-ms square-pulse stimuli presented in a transverse orientation. Although this duration is outside the behaviorally relevant range of EOD durations, it allowed us to distinguish responses to different stimulus edges. Thirty units (42.9%) responded to contralateral-positive (down) edges, 17 (24.3%) responded to ipsilateral-positive (up) edges, and 23 (32.8%) responded to both edges. These numbers roughly agree with anatomic evidence showing twice as many axons from the contralateral vs. ipsilateral hindbrain (Szabo et al. 1983).

FSL, the median time from stimulus edge to the first spike, ranged from 2.2 to 39.8 ms (Fig. 1C). Time-locked latency (TLL), the median time from stimulus edge to spikes that were time-locked to that edge, ranged from 2.2 to 13.4 ms (Fig. 1C). Some units did not respond with a time-locked spike on every stimulus repetition, skewing the FSL to an unreasonably high value due to spontaneous spiking (the reason for calculating TLL). Both distributions exceed the reported FSL values of 2.5–3 ms for incoming axons and large cells, the only other neurons in ELa (Amagai et al. 1998), further demonstrating that our recordings were obtained from small cells. On the basis of an estimated conduction speed of 0.5 m/s for axons <1 μm in diameter (Waxman and Bennett 1972) and axon lengths up to 7 mm (Friedman and Hopkins 1998), we calculated a 14-ms maximum latency difference for excitatory inputs to small cells, close to the observed range of TLL values (11.2 ms). In small-diameter axons, increased axonal length results in increased temporal jitter (Wang et al. 2008). Therefore, if differences in TLL are due to variation in the lengths of nELL axons, units with higher TLL should have increased jitter. Indeed, median TLL was positively correlated with TLL standard deviation for all units that responded with at least 1 spike/stimulus (linear regression: n = 68, r² = 0.34, P < 0.00001).

Small cells are diverse in their responses to peripheral spike timing differences.

We used monophasic square pulses of different durations to measure small cell responses to variation in peripheral spike timing differences. Although square pulses do not capture the complexity of natural EOD waveforms, they can be used to precisely manipulate the relative timing of KO receptor spikes on opposite sides of the body (Fig. 1A). Furthermore, square pulses that elicit the same KO spike timing differences as a natural conspecific EOD elicit similar behavioral responses (Hopkins and Bass 1981).

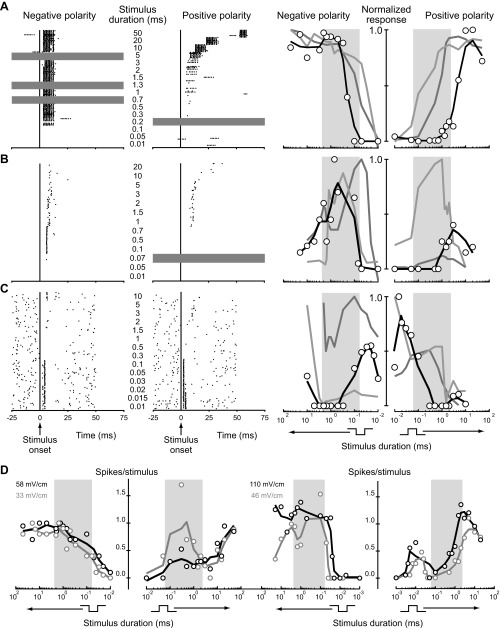
We presented square pulses of both positive and negative polarity ranging in duration from 1 μs to 90 ms at 1 (n = 40), 2 (n = 16) or ≥3 intensities (n = 11). We illustrate the resulting duration tuning curves using two plots (Fig. 2), one on the left representing negative-polarity square pulses and one on the right representing positive-polarity square pulses. The x-axis of the negative-polarity plot on the left is reversed (duration increases to the left). Presented in this way, the two x-axes can be viewed as a single axis that represents the relative timing of upward and downward stimulus edges. Forty-six units had consistent duration tuning to all polarities and intensities tested that elicited a response: 35 (76%) were long-pass tuned (Fig. 2A), 6 (13%) were band-pass tuned, (Fig. 2B), and 5 (11%) were band-stop tuned (Fig. 2C). Twenty of 62 units tested at both polarities (32%) had different duration tuning to positive and negative polarity stimuli (e.g., Fig. 2D); long-pass paired with non-long-pass tuning was the most common (n = 18). Of 27 units tested at multiple intensities, 16 (59%) changed their tuning with changes in intensity (e.g., Fig. 2D).

Fig. 2.

Small cells are diverse in their tuning to peripheral spike timing differences. Shown are raster plots (left) and smoothed tuning curves (right) from representative long-pass small cells (A) that responded preferentially to longer square-pulse durations, band-pass small cells (B) that responded preferentially to intermediate durations, and band-stop small cells (C) that responded preferentially to long and short durations. Rasters show spike times in response to 20 sweeps of each stimulus for both monophasic negative (left portion of raster) and positive (right portion of raster) stimuli (gray horizontal shading indicates durations not tested). Time is relative to stimulus onset. Responses were quantified as the mean number of spikes above baseline per stimulus repetition. The resulting data points (open circles on tuning curves at right) were then scaled to the maximum value within the unit and smoothed (black). In each case, smoothed tuning curves from 2 additional units of the same tuning type (light and dark gray) are also shown. The duration tuning curves are plotted on 2 axes, 1 on the left for negative polarity and 1 on the right for positive polarity, with the x-axis of the negative polarity plot reversed (stimulus duration increases to the left). Together, the 2 plots can be viewed as sharing a single x-axis that represents the relative timing of upward and downward stimulus edges. Background shading on tuning curves indicates the behaviorally relevant range of durations (Lyons-Warren et al. 2012). D: tuning curves (not normalized) of example units that changed tuning with changes in intensity (left) and polarity (left and right).

For most units, responses varied widely over the behaviorally relevant range of durations (Fig. 2), defined as the duration of the shortest EOD phase (60 μs) to the longest total EOD duration (2.37 ms) among conspecific EODs (Carlson et al. 2000). This represents the total possible range of KO receptor spike timing differences in response to conspecific EODs (Lyons-Warren et al. 2012). To determine how much small cell responses varied across this behaviorally relevant range, we calculated the difference between the minimum and maximum responses within this range for all tuning curves (n = 220). On average, responses varied within the behaviorally relevant range by 1.17 ± 0.08 spikes/stimulus (range = 0–6.94 spikes/stimulus).

Primary electroreceptors (KOs) are long-pass tuned at threshold intensities (Lyons-Warren et al. 2012). We confirmed that KOs are also long-pass tuned at higher intensities (not shown). Thus small cell duration tuning is more diverse than receptor duration tuning. Furthermore, small cells are the first place in the circuit where inputs from widely separated receptive fields converge. We therefore hypothesized that small cell duration tuning results from integrating multiple synaptic inputs.

Small cell responses to complex stimuli suggest precisely timed inhibition.

We hypothesized that small cells receive precisely timed inhibition from large cells on the basis of several lines of evidence: large cell axons give rise to large, calyceal synapses onto small cell somas (Friedman and Hopkins 1998; Mugnaini and Maler 1987); large cells are GABAergic (George et al. 2011; Mugnaini and Maler 1987); and large cells respond to stimulus edges with a single, short-latency, time-locked spike (Amagai et al. 1998; Friedman and Hopkins 1998). We used a complex stimulus protocol to test for inhibition in response to the stimulus edge that did not elicit spiking. We presented a 50-ms stimulus that elicited an excitatory response to the leading edge, followed by a shorter pulse at a range of delays following the trailing edge (Fig. 3A, top). A response was consistently seen following the first edge of the long pulse. However, a response to the leading edge of the second pulse only occurred for sufficiently long delays. We determined the minimum delay where the magnitude of the response to the second pulse was >50% of the response to the first pulse, which varied from 0.1 to 25 ms (Fig. 3B, asterisks). As a control, we presented a 100-ms pulse with a second overlapping pulse such that the excitatory edges were presented at the same intervals as in the paired-pulse experiment, but without an inhibitory edge between them (Fig. 3A, bottom). In this case, the response to the second pulse was >50% of the response to the first pulse at all “delays” tested (Fig. 3B).

Fig. 3.

Paired-pulse stimuli suggest functional inhibition of small cells elicited by the nonresponsive stimulus edge. A: representative rasters of the spiking responses of an individual small cell to electrosensory stimulation in paired-pulse (top) and control (bottom) experiments. Time-locked spikes occur following presumed excitatory edges (“e”). The test pulse was presented at varying delays following the presumed inhibitory edge (“i”). B: responses to the paired-pulse (solid) and control (dashed) experiments from 3 representative units showed a failure to respond to the test pulse at varying delays (top). Asterisks indicate shortest delays with a response >50%. Box plots show medians, quartiles, and ranges of shortest delays with a response >50% for all units tested in response to paired-pulse (gray) and control (black) stimuli across 4 different intensities (bottom). Numbers refer to sample size for each condition. C: responses to the paired-pulse (solid) and control (dashed) experiments from 2 representative KOs (top) along with a box plot summary from all recorded KOs (bottom).

We performed the same experiment on KOs. KO responses to the second pulse were also blocked at short delays, but these delays were much shorter than those of small cells (Fig. 3C). Therefore, the blocking of small cell responses cannot be explained by peripheral effects, supporting the hypothesis that small cells receive inhibitory input in response to one edge of a stimulus that is strong enough to block responses to excitatory inputs. It is not clear why different small cells had inhibitory windows of different durations, but this could reflect differences in excitatory latency, differences in the time course of inhibitory postsynaptic potentials (IPSPs), and/or differences in intrinsic physiology. The relatively short range of delays over which KO responses were reduced was likely due to the direct integration of depolarizing and hyperpolarizing currents by KOs. KOs act as AC filters that respond to changes in current intensity (Bennett 1965). Thus the trailing edge of a depolarizing current pulse results in a transient hyperpolarization and decrease in excitability, which would reduce responses to a depolarizing current pulse delivered after a short delay.

GABAergic inhibition reduces spontaneous activity and blocks responses to excitatory input.

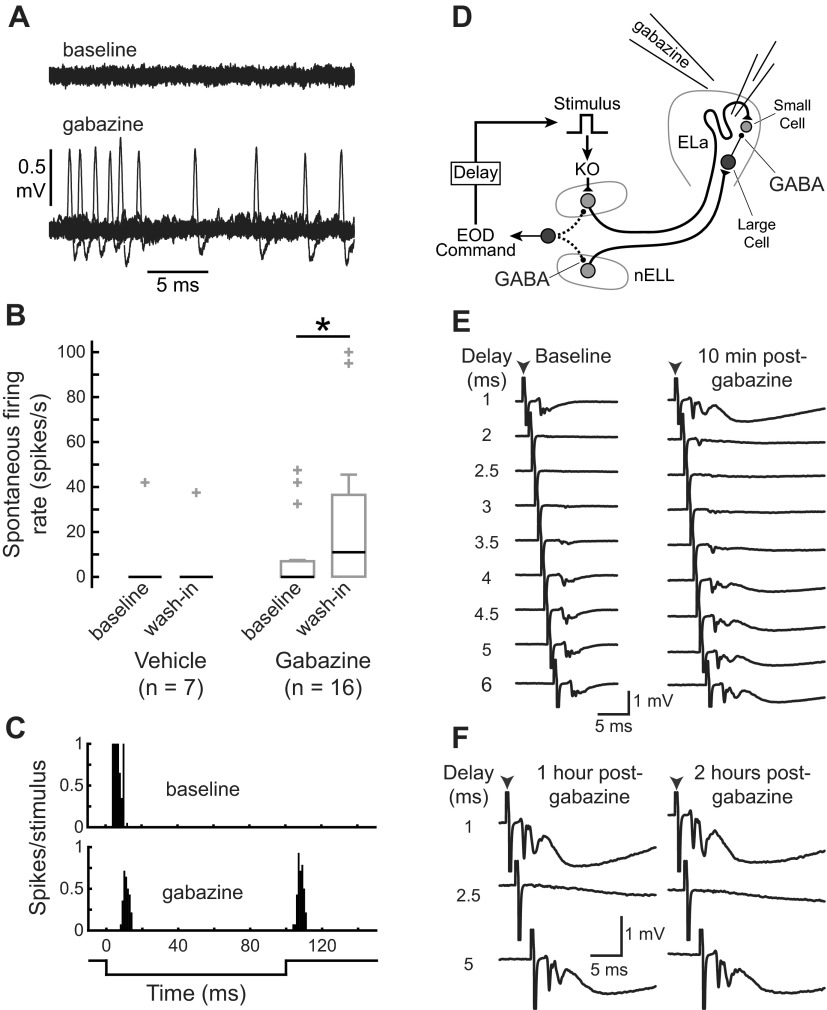
To directly test whether small cells receive functional GABAergic inhibition from large cells, we bath applied SR-95531 (gabazine), a competitive antagonist of GABA_A receptors, to the cavity surrounding ELa (Fig. 4A). We tested seven units with vehicle: six of these had no spontaneous activity before vehicle application, whereas one had relatively high spontaneous activity (Fig. 4B). After vehicle was applied, the six units without spontaneous activity remained silent (Fig. 4B), and there was no significant change in spontaneous activity (Wilcoxon matched-pairs test: n = 7, z = 0, P = 1). We tested 16 units with gabazine: 11 of these had no spontaneous activity before gabazine application, but only 5 of them remained silent after gabazine application (Fig. 4B). Thus gabazine caused a significant increase in the spontaneous activity of small cells (Wilcoxon matched-pairs test: n = 16, z = 2.4, P < 0.05), suggesting they are tonically inhibited at rest. In addition, of three units that responded to only one edge of the 100-ms stimulus before gabazine application, two responded to both edges after gabazine application (e.g., Fig. 4C). This suggests the existence of an excitatory input in response to one of the edges that was previously masked by inhibition.

Fig. 4.

Gabazine affects small cell activity due to local actions in ELa. A: example of increased spontaneous firing rate of a small cell after gabazine application. Twenty repetitions of a 25-ms recording of spontaneous activity are superimposed, revealing an average spontaneous firing rate of 0 spikes/s under baseline conditions (top) and 20 spikes/s after gabazine application (bottom). B: box plots showing spontaneous firing rates of small cells (median is black; quartiles, non-outlier range, and outlier data points are gray) before and after application of gabazine or vehicle reveal a significant increase following gabazine application (Wilcoxon matched-pairs test: n = 16, z = 2.4, P < 0.05) but not vehicle application (Wilcoxon matched-pairs test: n = 7, z = 0, P = 1). C: representative peristimulus histogram of spike times in response to a 100-ms stimulus before (top) and after (bottom) gabazine application from a single unit shows a response to one edge under baseline conditions but a response to both edges in the absence of inhibition. D: schematic representation of the KO pathway leading up to small cells, illustrating the locations of GABAergic synapses and an experiment to test whether gabazine application to ELa affects GABAergic transmission in the hindbrain. The electromotor command that initiates electric organ discharge (EOD) production also triggers inhibitory GABAergic input to the hindbrain nELL through a corollary discharge pathway (dotted lines). This command-triggered inhibition blocks sensory responses in nELL for a brief window of time after each EOD. To assess functional inhibition in nELL, we delivered a sensory stimulus at different delays after the EOD command while recording evoked field potentials in ELa before and after delivering gabazine to the cavity surrounding ELa. E: evoked potentials recorded in ELa in response to a stimulus (0.5 ms, 20 mV/cm, arrowhead indicates stimulus artifact) are blocked at delays of 2–4 ms both before (left) and 10 min after (right) gabazine application, indicating that gabazine is not reaching the hindbrain GABA receptors. F: responses are still blocked at delays of 2–4 ms after 1 (left), 2 (right), and 5 h (not shown) following gabazine application.

Changes in small cell activity following application of gabazine could be due to effects on GABAergic synapses onto small cells or GABAergic synapses in the hindbrain nucleus of the electrosensory lateral line lobe (nELL) (Figs. 1A and 4D). In nELL, GABAergic inhibition triggered by the electromotor command blocks responses to the fish's own EOD (Bell and Grant 1989). Although the fish were paralyzed during our experiments and therefore could not emit EODs, we could record the spinal motor neuron activity representing a fictive EOD (Carlson 2003). To determine whether gabazine application affected GABAergic synapses in nELL, we recorded evoked potentials in ELa in response to a stimulus pulse presented at a range of delays after the fictive EOD (Fig. 4D). Under baseline conditions, the evoked potential was blocked when the stimulus was presented 2–4 ms after the fictive EOD (Fig. 4E), due to the command-triggered GABAergic inhibition in nELL. After application of gabazine, this evoked potential became larger and longer lasting, but it was still blocked at delays of 2–4 ms following the fictive EOD (Fig. 4E), even several hours after gabazine application (Fig. 4F). Therefore, the effects of gabazine application on small cell activity were limited to local actions within ELa. Large cells are the only GABAergic neurons in ELa, and their projections are limited to within ELa (Friedman and Hopkins 1998; George et al. 2011; Mugnaini and Maler 1987). Thus we conclude that the effects of gabazine application on small cell activity are due to blocking inhibition at the large cell-to-small cell synapse.

Some small cells receive multiple excitatory inputs.

Both mammalian and avian sound localization depends critically on binaural excitatory inputs converging onto time comparator neurons (Ashida and Carr 2011; Köppl 2009; Schnupp and Carr 2009). We found that 23 of 70 units (32.8%) exhibited a spiking response to both edges of 100-ms stimuli, suggesting that some small cells likewise receive convergent excitatory inputs originating from the left and right sides of nELL (e.g., Fig. 5A). In some cases, application of gabazine unmasked responses to both stimulus edges (e.g., Fig. 4C). If responses to both edges are driven by excitatory inputs from different axons, each with its own delay, then we would expect no correlation in response latency (TLL) to each edge, which was indeed the case (Fig. 5B; linear regression: n = 23, r² = 0.02, P > 0.4).

Fig. 5.

Some small cells receive multiple excitatory inputs from different receptive fields. A: an example of a unit that responded to both positive-going and negative-going stimulus edges, with different latencies and response strengths. The stimulus (100 ms, 32.6 mV/cm) is shown in the bottom trace, and stimulus artifact can be seen at stimulus onset and offset (arrowheads). B: TLL in response to the edge eliciting a higher magnitude response (strong) was not correlated with TLL to the other edge (weak) (linear regression: n = 23, r² = 0.02, P > 0.4). Dotted line is 1:1 relationship. C: estimated numbers of small cells and nELL axon terminals onto small cells from 3 fish. The numbers of small cells and nELL somas from both sides of the brain were estimated using stereology, and the numbers of axon terminals per nELL soma were estimated using published data on nELL axonal projection patterns (Friedman and Hopkins 1998), as described in materials and methods. D: ipsilateral nELL axons labeled with DiO (green) and contralateral nELL axons labeled with DiI (magenta) colocalized adjacent to individual small cell somas (blue) in the left ELa. The large image at left shows ELa based on a maximum intensity projection from six 2.53-μm slices (scale bar, 100 μm). The adjacent optic tectum (OT) also had labeled axons, likely due to labeling of hindbrain regions other than nELL during dye injection. The smaller images at right show an expanded view of the enclosed box, illustrating colocalization of ipsilateral and contralateral nELL terminals next to small cell nuclei, based on a maximum intensity projection from two 1.14-μm slices (scale bar, 5 μm). Arrowheads indicate putative synaptic boutons; asterisks indicate small cell nuclei where putative ipsilateral and contralateral boutons colocalized. E: labeled axons and small cell nuclei from the right ELa of the same brain, based on a maximum intensity projection from four 1.14-μm slices (scale bar, 5 μm).

To determine whether ELa anatomy would allow for multiple excitatory inputs to individual small cells, we used stereology (Gundersen et al. 1988) to estimate the total numbers of nELL neurons and small cells. Combined with data showing that ∼10% of nELL axons project bilaterally to ELa and that each axon terminates on ∼54.5 small cells (Friedman and Hopkins 1998), the estimated ratio of nELL terminals to small cell somas ranged from 1.4 to 1.5 (Fig. 5C), suggesting that individual small cells receive 1–2 excitatory inputs each.

To further test whether small cells receive multiple excitatory inputs from different receptive fields, we stained the left and right nELLs with different lipophilic dyes. This resulted in densely labeled fiber tracts projecting into ELa and allowed us to distinguish contralateral from ipsilateral axons (Fig. 5, D and E). Small cells are adendritic, and all synaptic inputs to them are therefore on the soma (Friedman and Hopkins 1998; Mugnaini and Maler 1987). Because of their small size, the nuclei of small cells are located within <2 μm of the cell membrane (Mugnaini and Maler 1987). Thus we used a nuclear stain to identify small cells scattered throughout ELa and identified putative synaptic inputs as closely apposed nuclear and punctate axonal stain (Fig. 5, D and E). Electron microscopic studies have demonstrated that about 80% of putative synapses identified on the basis of axonal puncta located close to the cell membrane are functional synapses (Feldmeyer et al. 2002, 2006; Lübke et al. 1996; Markram et al. 1997; Mishchenko et al. 2010; Wang et al. 2002). Using this criterion, we found several labeled small cells that appeared to receive synaptic inputs from both sides of nELL (Fig. 5, D and E), providing an additional piece of evidence for the convergence of bilateral excitatory inputs onto small cells.

Variation among small cells can be explained by differences in excitatory latency.

Unlike the long, winding projections from nELL axons to small cells, the inputs from nELL axons to large cells and from large cells to small cells are both direct (Friedman and Hopkins 1998). This suggests that inhibitory latencies are relatively uniform among small cells and that variation in duration tuning is determined primarily by differences in excitatory latency. Axonal delay lines to small cells (Friedman and Hopkins 1998) and our observed spike latencies (Fig. 1C) suggest that excitatory latencies can vary from about 0 to 10 ms relative to large cell latencies. Finally, some small cells appear to receive separate excitatory inputs in response to the two stimulus edges (Fig. 5). To determine whether these features of synaptic input to small cells could explain the observed diversity of duration tuning, we modeled small cells as leaky integrator neurons receiving excitatory and inhibitory synaptic inputs with different relative latencies (Fig. 6). Each model neuron received excitatory input in response to one stimulus edge and either inhibitory input or both excitatory and inhibitory input in response to the other stimulus edge. We varied the excitatory latencies from 0 to 10 ms relative to the inhibitory latency (set at 0 ms), and we scaled the inhibitory conductances to be larger and longer lasting than the excitatory conductances (see materials and methods for details). Finally, we incorporated a long-pass filter of duration that scaled the synaptic conductances to simulate the observed peripheral filtering imposed by KO electroreceptors (Lyons-Warren et al. 2012).

Fig. 6.

Schematic illustrating the modeling of synaptic integration by small cells. Each cell was modeled as a leaky integrator neuron that received excitation in response to the rising stimulus edge (ipsilateral) and either inhibition only or inhibition plus excitation in response to the falling stimulus edge (contralateral). Inhibitory latencies were set at 0 ms, and excitatory latencies (Δt_ipsi and Δt_contra) were varied from 0 to 10 ms. Synaptic conductances were simulated as alpha functions (see materials and methods for details). These conductances were passed through a sigmoidal filter that modeled the effects of peripheral long-pass filtering by KOs, thereby reducing synaptic input strength at short durations.

The resulting model neurons had the same types of duration tuning observed among actual small cells, including long-pass, band-pass, and band-stop tuning. None of the model cells responded to short durations because of the long-pass peripheral filter. Variation in responses to longer durations among model neurons was caused by differences in excitatory latency, which determined which stimulus durations resulted in overlapping excitation and inhibition, and in the case of model neurons with two excitatory inputs, overlapping excitatory inputs in response to the two edges. To illustrate, we show simulation traces for three different stimuli along with duration tuning curves under three different scenarios (Fig. 7A): ipsilateral excitation (7-ms latency) with contralateral inhibition (0-ms latency) but no contralateral excitation (left); ipsilateral excitation (7-ms latency) with contralateral inhibition (0-ms latency) and contralateral excitation (0-ms latency) (middle); and ipsilateral excitation (7-ms latency) with contralateral inhibition (0-ms latency) and contralateral excitation (5-ms latency) (right). The arrowheads above the duration tuning curves correspond to the example traces shown above.

Fig. 7.

Model neurons that integrate inhibition in response to one stimulus edge and variably delayed excitation in response to one or both stimulus edges recreate the diversity in duration tuning observed among small cells. A: example simulation traces and duration tuning curves from 3 model neurons, each having ipsilateral excitation with Δt_ipsi = 7 ms and contralateral inhibition with 0-ms latency. The model neuron at left does not receive contralateral excitatory input. The other 2 model neurons receive contralateral excitation with Δt_contra set at 0 (middle) or 5 ms (right). For all 3 model neurons, synaptic conductances (g_E-ipsi in blue, g_E-contra in cyan, g_I in red, where E is excitation and I is inhibition) and membrane potential (control V_m in black, V_m without inhibition in gray) are shown in response to a 7-ms reversed polarity stimulus (left), 0.7-ms normal polarity stimulus (middle), and 5-ms normal polarity stimulus (right). Changes in stimulus duration alter the relative timing of different synaptic inputs, and the stimulus durations at which these inputs overlap are determined by their relative latencies. The duration tuning curves show the normalized response of each model neuron for both stimulus polarities for durations ranging from 0.01 to 10 ms under control conditions (black) and after the inhibitory input was removed (gray). Arrowheads indicate the durations corresponding to the sample traces shown above. B: duration tuning changes with variation in excitatory latency. At left is shown the tuning of model neurons that receive ipsilateral excitation and contralateral inhibition only, with Δt_ipsi varying from 0 to 10 ms. Also shown is the tuning of model neurons that also receive contralateral excitation with Δt_contra set at 0 (middle) or 5 ms (right). In the heat maps, the x-axis represents stimulus duration (right plot shows normal polarity, left plot shows reversed polarity) and the y-axis represents Δt_ipsi. Thus each row represents the duration tuning of a single model neuron with a given Δt_ipsi, with responses normalized to its maximum response and colored as indicated in the scale at far right. Plots at bottom illustrate duration tuning of the same model neurons after the inhibitory synaptic input was removed. Asterisks indicate the Δt_ipsi (7 ms) that corresponds to the example traces and tuning curves shown in A.

Figure 7B shows heat maps that illustrate how duration tuning changes with variation in ipsilateral excitatory latency for model neurons under three different scenarios: ipsilateral excitation with contralateral inhibition (0-ms latency) but no contralateral excitation (left); ipsilateral excitation with contralateral inhibition (0-ms latency) and contralateral excitation (0-ms latency) (middle); and ipsilateral excitation with contralateral inhibition (0-ms latency) and contralateral excitation (5-ms latency) (right). In each heat map, the x-axis shows stimulus duration, the y-axis shows ipsilateral excitatory latency, and the color indicates normalized synaptic response. The asterisks to the right of each heat map correspond to the ipsilateral excitatory latencies of the example model neurons shown in Fig. 7A.

Long-pass tuning was always observed at relatively short excitatory latencies, whereas band-pass and band-stop tuning were only observed at longer excitatory latencies (Fig. 7B). When there is a relatively short excitatory latency, contralateral inhibition will block excitation at short stimulus durations (Fig. 8A, top). With longer excitatory latencies, however, inhibition and excitation can interact at longer durations, thereby establishing more complex patterns of tuning (Fig. 8A, bottom). To see whether this prediction held for recordings from actual small cells, we analyzed the relationship between TLL and duration tuning. Extracellular recording does not allow for a direct determination of synaptic latency, but TLL can serve as a proxy for excitatory latency. When the units that only responded to one stimulus edge were considered, the TLL of long-pass tuning curves (n = 68) was significantly shorter than the TLL of band-pass (n = 11) and band-stop (n = 17) tuning curves (Kruskal-Wallis ANOVA: H_2,96 = 14.6, P < 0.001), as predicted by our model (Fig. 8B).

Fig. 8.

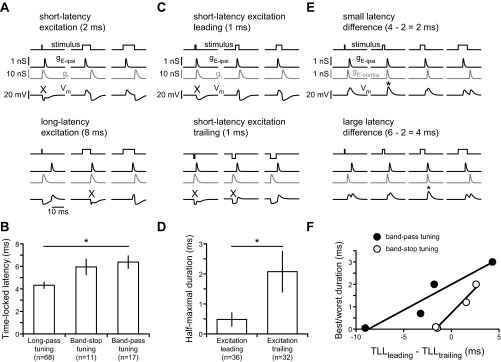
Responses to peripheral spike timing differences are determined by the relative latency of excitation and inhibition. A: model simulations illustrating how short-latency excitation combined with contralateral inhibition gives rise to long-pass tuning (top), whereas long-latency excitation combined with contralateral inhibition gives rise to band-stop tuning (bottom). X indicates stimuli for which excitation is blocked by inhibition, resulting in responses <50% of maximum. B: as predicted by the model, long-pass tuning curves of actual recorded units had significantly shorter TLL than band-stop or band-pass tuning curves (Kruskal-Wallis ANOVA: H_2,96 = 14.6, P < 0.001). C: model simulations illustrating how reversing the sequence of excitation and inhibition by changing stimulus polarity results in responses to shorter durations when excitation is leading (top) compared with when excitation is trailing (bottom). X indicates stimuli for which excitation is blocked by inhibition, resulting in responses <50% of maximum. D: as predicted by the model, long-pass tuning curves of actual recorded units had a significantly shorter minimum duration for eliciting a half-maximal response when excitation was to the trailing, rather than leading, edge of the stimulus (Mann-Whitney U-test: z = 3.5, P < 0.001). E: model simulations illustrating how variation in the relative latencies of 2 excitatory inputs leads to different durations at which these 2 inputs are coincident, resulting in the strongest response (asterisks). F: as predicted by the model for units that responded to both edges, the difference between the TLL of each excitatory edge was significantly correlated with the best duration of band-pass tuning curves (linear regression: r² = 0.90, P < 0.05) and worst duration of band-stop tuning curves (linear regression: r² = 0.97, P < 0.05).

For long-pass tuning curves with relatively short excitatory latencies, our model also predicted differences in tuning curve shape depending on whether excitation was to the leading or trailing edge (Fig. 7B, compare opposite polarity stimuli). When excitation is to the trailing edge of the stimulus, a longer stimulus duration is required to elicit a response compared with when excitation is to the leading edge of the stimulus. The reason for this is that when excitation leads inhibition, the stimulus only needs to be long enough for the excitation to arrive before the onset of inhibition (Fig. 8C, top). When excitation trails inhibition, however, the stimulus needs to be long enough for the excitation to arrive after the inhibitory synaptic potential has ended (Fig. 8C, bottom). To test this hypothesis in our recordings from actual small cells, we compared the minimum duration where responses reached >50% of the maximal response for stimulus polarities in which excitation was to the leading or trailing edge. As predicted by our model, the half-maximal duration of excitation-leading long-pass tuning curves (n = 36) was significantly shorter than the half-maximal duration of excitation-trailing long-pass tuning curves (n = 32) (Fig. 8D; Mann-Whitney U-test: z = 3.5, P < 0.001).

In our model neurons, interactions between separate excitatory inputs to the two stimulus edges also contributed to complex patterns of duration tuning such as band-pass and band-stop tuning (Fig. 7). This is because excitation will be maximal for stimulus durations that cause these two excitatory inputs to arrive simultaneously (Fig. 8E). Therefore, in our recordings from actual band-pass and band-stop small cells that responded to both edges, we compared the difference in TLL to the two edges with their “best” and “worst” stimulus durations, respectively (Fig. 8F). Despite the small number of units that met these criteria (n = 4 each), there was a significant correlation between difference in TLL and best duration of band-pass units (linear regression: r² = 0.90, P < 0.05), as well as worst duration of band-stop units (linear regression: r² = 0.97, P < 0.05). Thus several predictions of our computational model are supported by correlations between TLL and duration tuning among small cells, supporting the hypothesis that variation in excitatory latency contributes to the wide diversity of small cell tuning that we observed. It is important to note, however, that small cells may also differ in other respects, including passive and active membrane properties as well as the strengths and time courses of excitatory and inhibitory synaptic currents. In the absence of intracellular recordings, it is not yet possible to evaluate the potential contribution of these factors to variation in small cell tuning.

Stimulus-driven feed-forward inhibition shapes small cell responses to peripheral spike timing differences.

To directly test the role of GABAergic inhibition from large cells in establishing small cell duration tuning, we quantified tuning before and after gabazine application. Because of space constraints, susceptibility of recordings to mechanical disturbance during drug delivery, and normal difficulties with maintaining stable long-term recordings, it was difficult to hold a unit long enough to get complete tuning curves after drug application. Nevertheless, we were able to collect a total of 32 tuning curves from 5 units after gabazine application. The multiple tuning curves from each unit included tuning curves to both stimulus polarities, as well as to different stimulus intensities, but not repetitions of the same polarity and intensity.

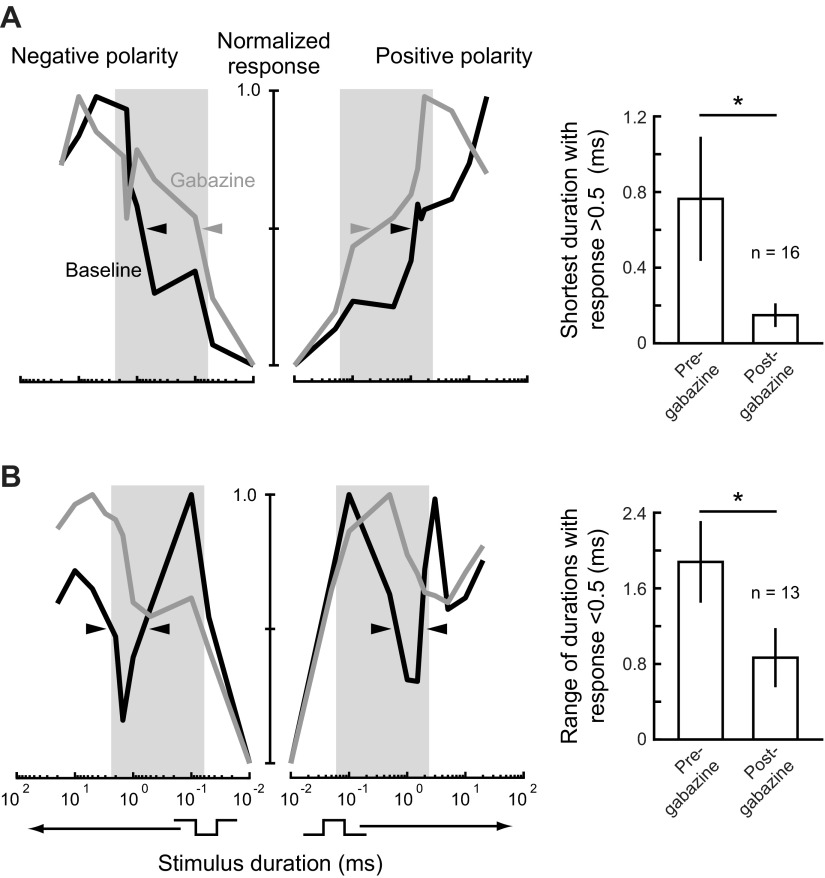
Our modeling results predict that different patterns of duration tuning result from inhibition blocking excitation at different stimulus durations, due to variation in excitatory latency. For long-pass neurons with relatively short excitatory latencies, our model predicts that inhibition blocks excitation only at short durations, thereby increasing the minimum duration for eliciting a response (Figs. 7B and 8A). Thus, after inhibition was removed from long-pass model neurons, there was a decrease in the minimum duration for eliciting a response (Fig. 7B). In recordings from actual long-pass units, blocking inhibition by applying gabazine had a similar effect, leading to increased responses to short stimulus durations (Fig. 9A). Among all long-pass tuning curves tested, gabazine application resulted in a significant decrease in the minimum stimulus duration that elicited a response >50% of the maximum response (Fig. 9A; Wilcoxon matched-pairs test: n = 16, z = 2.9, P < 0.01). This supports our model prediction that inhibition contributes to long-pass tuning by blocking responses to short duration stimuli.

Fig. 9.

Blocking inhibition in ELa affects small cell responses to peripheral spike timing differences. A: smoothed, normalized tuning curves (left) from a representative long-pass small cell before and after gabazine application, presented as in Fig. 2. This cell had long-pass tuning to both stimulus polarities before and after gabazine application. However, the minimum duration eliciting a response >0.5 decreased after gabazine application for both polarities (arrowheads), suggesting that inhibition was affecting excitatory input to the small cell at short durations. The bar graph (right) shows the minimum duration eliciting a response >0.5 (mean ± SE) for all 16 tuning curves that were long-pass before gabazine application. After gabazine application, there was a significant decrease in the minimum duration eliciting a response >0.5 (Wilcoxon matched-pairs test: n = 16, z = 2.9, P < 0.01). B: smoothed, normalized tuning curves (left) from a representative band-stop small cell before and after gabazine application. This cell had band-stop tuning to both stimulus polarities, but the tuning to both polarities changed to long-pass after gabazine application. The band-stop portion of the tuning curves that was <0.5 of the maximum response before gabazine (arrowheads) was no longer present after gabazine application, suggesting that inhibition was responsible for the decreased response at these durations. The bar graph (right) shows the range of durations eliciting a response <0.5 (mean ± SE) for all 13 tuning curves that were either band-pass or band-stop before gabazine application. After gabazine application, there was a significant decrease in the range of durations eliciting a response <0.5 (Wilcoxon matched-pairs test: n = 13, z = 2.4, P < 0.05).

For band-pass and band-stop neurons with relatively long excitatory latencies, our model predicts that inhibition blocks excitation at longer durations (Figs. 7B and 8A). Overall, this results in weak responses to the shortest durations due to the peripheral filter, increasing responses as duration increases, and then decreasing responses due to inhibition as duration increases further (Fig. 7B). Thus, after inhibition was removed from band-pass and band-stop model neurons, the secondary decrease in response at relatively long durations disappeared (Fig. 7B). In recordings from actual band-pass and band-stop units, blocking inhibition by applying gabazine had a similar effect, resulting in an increased response at longer durations that had previously elicited weak responses. For example, the neuron shown in Fig. 9B was band-stop tuned to both polarities, but it became long-pass tuned after gabazine application because the decrease in response to longer duration stimuli no longer occurred. For all band-pass and band-stop tuning curves tested, we identified the minimum duration at which further increases in duration resulted in responses that dropped below 50% of the maximum response. We then determined the total range of durations above this value that elicited a response <50% of the maximum response and compared this to the total range of durations below this criterion after gabazine application. Among all band-pass and band-stop tuning curves tested, gabazine application resulted in a significant decrease in the range of durations that elicited a response <50% of the maximum response (Fig. 9B; Wilcoxon matched-pairs test: n = 13, z = 2.4, P < 0.05). This supports our model prediction that inhibition contributes to band-pass and band-stop tuning by blocking responses to stimuli over a particular range of durations.

DISCUSSION

Small cells are diverse in their responses to variation in peripheral spike timing differences and are the first location where inputs from widely separated receptive fields converge. Our results suggest several factors that determine the responses of individual cells: variation in excitatory latency, likely due to axonal delay lines (Friedman and Hopkins 1998); feed-forward inhibition, likely mediated by large cell calyces (Friedman and Hopkins 1998; George et al. 2011; Mugnaini and Maler 1987); multiple excitatory inputs from different receptive fields for some cells; and variation in the relative timing of excitation and inhibition due to latency differences and the relative timing of stimulus edges.

Variation in excitatory latency determines which peripheral timing differences the cell will respond to. Excitation will be greatest when two excitatory inputs arrive in synchrony, but the strong inhibition from the calyx synapse will effectively silence any excitation. Combined with the peripheral long-pass filter (Lyons-Warren et al. 2012), this mechanism can establish different temporal filters of spike timing differences. Specific predictions of this model regarding the relationship between excitatory latency and duration tuning, as well as the effects of blocking inhibition on duration tuning, were supported by our extracellular data. Our model can also explain changes in tuning with changes in stimulus intensity. As intensity increases, additional receptive fields will be activated, leading to the recruitment of additional inputs.

Mechanisms for detecting submillisecond timing differences have been well studied in auditory pathways that use ITDs to locate azimuthal sound sources (Ashida and Carr 2011; Köppl 2009; Schnupp and Carr 2009). There is strong evidence in birds and reptiles for the canonical Jeffress model (1948), in which a counter-current organization of ipsilateral and contralateral projections to the nucleus laminaris (NL) converts a temporal code into a place code through delay-line coincidence detection (Carr and Konishi 1990; Carr et al. 2009; Funabiki et al. 2011). By contrast, binaural projections to the mammalian medial superior olive (MSO) do not appear to include delay lines (McAlpine and Grothe 2003; Smith et al. 1993). Instead, binaural excitation and inhibition convert a temporal code into a rate code, in which azimuthal sound location is represented by the relative firing rates of neurons in the left and right MSO (Brand et al. 2002; Grothe et al. 2010; van der Heijden et al. 2013). Our data suggest a novel mechanism for processing spike timing differences that combines features of both sound localization pathways, including axonal delay lines and precisely timed feed-forward inhibition. Integration of precisely timed excitation and inhibition is also thought to establish sound duration tuning in the midbrains of mammals and amphibians (Aubie et al. 2009; Leary et al. 2008; Sayegh et al. 2011).

Our results provide empirical support for the delay-line anticoincidence detection model of Friedman and Hopkins (1998). However, our findings also add to this model by revealing multiple excitatory inputs to some cells, an important role for tonic inhibition, and greater diversity of small cell response patterns than first predicted. In its original formulation, the model predicted that all small cells would be long-pass tuned to square-pulse duration, with variation in excitatory latency determining the minimum cutoff duration that small cells would respond to (Xu-Friedman and Hopkins 1999). However, small cell duration tuning was more diverse than this for three reasons. First, the periphery imposes a long-pass filter before stimulus information reaches small cells (Lyons-Warren et al. 2012). Second, relatively long excitatory latencies result in coincident excitation and inhibition at durations that are longer than the cutoff of this peripheral filter. Third, multiple excitatory inputs from different receptive fields result in coincident excitation at certain durations.

Thus, whereas the original model proposed a population code in which the number of responsive small cells codes for square-pulse duration (Xu-Friedman and Hopkins 1999), our present results suggest a distributed population code in which the identity of responsive cells codes for duration. Individual small cells respond equally well to a wide range of stimulus durations, polarities, and intensities such that they cannot individually code for specific stimuli. However, the tuning of each cell is unique, meaning that different stimuli will elicit responses from distinct populations of small cells.

Monophasic square pulses provide a convenient stimulus for precisely manipulating the timing of receptor responses to study the decoding of peripheral timing differences. However, natural EOD waveforms are more complex than square pulses, typically consisting of multiple phases of different durations (Carlson et al. 2011; Hopkins 1981). Variation in the polarity and intensity of an EOD stimulus across the body surface results in a mosaic of peripheral timing differences as opposed to the simple “start-stop” responses to uniform square-pulse stimuli that we elicited (Baker et al. 2013). Thus, in a natural context, the particular timing difference that an individual small cell will experience depends on the receptive fields of its synaptic inputs and on the polarity and intensity of the EOD at those locations. Relative movements of the signaling and receiving fish will further complicate the matter, causing this mosaic of timing differences to shift. Nevertheless, just as changes in square-pulse duration alter the relative timing of peripheral inputs to small cells, so too will changes in EOD waveform and sender position alter the relative timing of these inputs. Thus our findings suggest that both EOD waveform and sender position are represented as a distributed population code among small cells. This contrasts with the mammalian MSO, which converts a temporal code into a rate code, and the avian NL, which converts a temporal code into a place code.

Although the source of much speculation, the reason why different circuits have evolved different mechanisms and recoding strategies for processing submillisecond timing differences remains unclear (Köppl 2009; Schnupp and Carr 2009). Why would mormyrids utilize yet another strategy? We recently found that at near-threshold stimulus intensities, when the temporal code for EOD waveform breaks down, variation in KO tuning establishes a peripheral population code for stimulus duration (Lyons-Warren et al. 2012). Thus there are two peripheral codes operating at different intensities, a population code at low intensities and a temporal code at high intensities. It may be that the temporal code is converted into a population code so that two different peripheral codes come to be represented as a single, unified population code centrally. A similar argument has been proposed to explain different strategies for ITD processing. Mammals use both ITDs and interaural level differences (ILDs) for azimuthal sound localization (Macpherson and Middlebrooks 2002). Because sound intensity is represented using a rate code, the MSO may convert ITDs from a temporal code to a rate code so that both features are in the same “currency” (Schnupp and Carr 2009). Birds, however, use ILDs for elevational sound localization; because ITDs and ILDs represent different information, it may not be necessary to convert them into a common coding scheme.

Another reason that mormyrids may convert a temporal code into a population code is that this circuit must deal with the coding of both spatial and identity information into complex patterns of timing differences among many receptors. By contrast, the mammalian MSO and avian/reptilian NL only need to perform a binaural timing comparison for the sole purpose of azimuthal sound localization. Population codes are able to more efficiently and more accurately represent a large number of stimuli than codes based on individual neurons (Averbeck et al. 2006), and they may be well suited to representing the high dimensionality and variability of electric signals that ELa must deal with.

Multipolar neurons in ELp integrate the outputs of many small cells along their extensive dendritic arbors (Xu-Friedman and Hopkins 1999). This high degree of convergence makes ELp neurons ideally suited to detecting coherent spiking among distinct subpopulations of small cells, and this likely represents the first step in decoding small cell population activity (Amagai 1998). Furthermore, sensory stimulation will result in coherent synaptic input to ELp from many small cells, but spontaneous inputs will be uncorrelated. Thus, even though spontaneous activity among small cells was generally quite low, this convergence should help prevent the propagation of spontaneous activity and ensure reliable sensory coding. Indeed, ELp neurons have low levels of spontaneous synaptic activity and no spontaneous spiking in vivo (Amagai 1998; Carlson 2009).

To our knowledge, this study is the first to document functional roles for an inhibitory calyx. We propose that just as the excitatory calyx of Held functions to increase the reliability of synaptic transmission (Borst and van Hoeve 2012), the calyx structure of the large cell-to-small cell synapse is particularly effective at blocking excitation. It is somewhat puzzling that some small cells receive excitation in response to a stimulus edge that is normally blocked by inhibition in response to that same edge. It may be that coincident excitatory inputs in response to two edges can overcome this inhibition, similar to the anteroventral cochlear nucleus in mice (Chanda and Xu-Friedman 2010). In mammalian MSO neurons, it was recently shown that inhibition increases the linearity and temporal precision of binaural coincidence detection (Roberts et al. 2013). Inhibition in response to the same stimulus edge as excitation could also shorten the window for excitatory integration (Pouille and Scanziani 2001). Conversely, delayed excitation in response to the same stimulus edge as inhibition could effectively shorten the inhibitory window. Finally, even though excitation and inhibition were often elicited by a single stimulus edge in our preparation, these inputs may have arisen through adjacent but separate receptive fields. Slight changes in stimulus orientation during natural social interactions could differentially activate these receptive fields, which would be reflected in the resulting small cell output.

We also found evidence suggesting tonic inhibition of small cells. This could arise through tonic activation of GABA_A receptors by ambient GABA at the large cell terminal, spontaneous miniature IPSPs, spontaneous spiking of large cells, or a separate source of GABAergic inhibition. We consider the latter two possibilities highly unlikely. Intracellular recordings from nELL axons and large cells reveal little, if any, spontaneous firing (Amagai et al. 1998; Friedman and Hopkins 1998). In addition, the cytology and anatomy of ELa has been well described, and there is no evidence for any neurons other than small cells, large cells, and nELL axons (Friedman and Hopkins 1998; George et al. 2011; Mugnaini and Maler 1987). Tonic excitation and inhibition due to low ambient levels of neurotransmitter have been well described (Cavelier et al. 2005; Semyanov et al. 2004). The extensive synaptic cleft formed by the calyx may limit the diffusion and clearance of GABA, resulting in high ambient levels that remain long after presynaptic spiking. Although the exact mechanism remains unknown, it is clear that tonic inhibition of small cells reduces spontaneous firing, which increases the fidelity of stimulus coding by limiting spiking to stimulus-driven events, similar to the effect of tonic inhibition on mechanosensory coding by cerebellar granule cells (Duguid et al. 2012). Furthermore, a tonic inhibitory conductance would decrease the membrane time constant, thereby decreasing temporal integration windows and increasing the precision of coincidence (or anticoincidence) detection (Cavelier et al. 2005; Häusser and Clark 1997).

GRANTS

This research was supported by National Science Foundation Grant IOS-1050701 (to B. A. Carlson), National Institutes of Health (NIH) Grants NS54174 (to S. Mennerick) and F30-DC0111907 (to A. M. Lyons-Warren), NIH Neuroscience Blueprint Center Core Grant P30-NS057105 (to Washington University), the Uehara Memorial Foundation, and the Japan Society for the Promotion of Science Grant G2205 (to T. Kohashi).

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTIONS

A.M.L.-W., T.K., S.M., and B.A.C. conception and design of research; A.M.L.-W., T.K., and B.A.C. performed experiments; A.M.L.-W., T.K., and B.A.C. analyzed data; A.M.L.-W., T.K., S.M., and B.A.C. interpreted results of experiments; A.M.L.-W. and B.A.C. prepared figures; A.M.L.-W. and B.A.C. drafted manuscript; A.M.L.-W., T.K., S.M., and B.A.C. edited and revised manuscript; A.M.L.-W., T.K., S.M., and B.A.C. approved final version of manuscript.