Determination of Primary Spectral Bands for Remote Sensing of Aquatic Environments

Abstract

About 30 years ago, NASA launched the first ocean-color observing satellite: the Coastal Zone Color Scanner. CZCS had 5 bands in the visible-infrared domain with an objective to detect changes of phytoplankton (measured by concentration of chlorophyll) in the oceans. Twenty years later, for the same objective but with advanced technology, the Sea-viewing Wide Field-of-view Sensor (SeaWiFS, 7 bands), the Moderate-Resolution Imaging Spectrometer (MODIS, 8 bands), and the Medium Resolution Imaging Spectrometer (MERIS, 12 bands) were launched. The selection of the number of bands and their positions was based on experimental and theoretical results achieved before the design of these satellite sensors. Recently, Lee and Carder (2002) demonstrated that for adequate derivation of major properties (phytoplankton biomass, colored dissolved organic matter, suspended sediments, and bottom properties) in both oceanic and coastal environments from observation of water color, it is better for a sensor to have ∼15 bands in the 400 – 800 nm range. In that study, however, it did not provide detailed analyses regarding the spectral locations of the 15 bands. Here, from nearly 400 hyperspectral (∼ 3-nm resolution) measurements of remote-sensing reflectance (a measure of water color) taken in both coastal and oceanic waters covering both optically deep and optically shallow waters, first- and second-order derivatives were calculated after interpolating the measurements to 1-nm resolution. From these derivatives, the frequency of zero values for each wavelength was accounted for, and the distribution spectrum of such frequencies was obtained. Furthermore, the wavelengths that have the highest appearance of zeros were identified. Because these spectral locations indicate extrema (a local maximum or minimum) of the reflectance spectrum or inflections of the spectral curvature, placing the bands of a sensor at these wavelengths maximizes the potential of capturing (and then restoring) the spectral curve, and thus maximizes the potential of accurately deriving properties of the water column and/or bottom of various aquatic environments with a multi-band sensor.

1. Introduction

Since the successful demonstration of the Coastal Zone Color Scanner (CZCS) in measuring the spatial and temporal variation of phytoplankton via observation of ocean color (Gordon et al. 1983; Gordon and Morel 1983), the importance of observing ocean and coastal waters with sensors in the visible domain is getting more and more attention from various countries. After the launch of the Sea-viewing Wide Field-of-view Sensor (SeaWiFS) and the Moderate-Resolution Imaging Spectrometer (MODIS) satellites about ten years ago, and the successful and extraordinary results of such data since then, additional satellite sensors have been (or planned to be) launched for the observation of biogeochemical properties via water color. These include the COCTS of China, the MERIS of ESA, the OCM of India, and the GOCI of Korea (IOCCG 1998), to name a few.

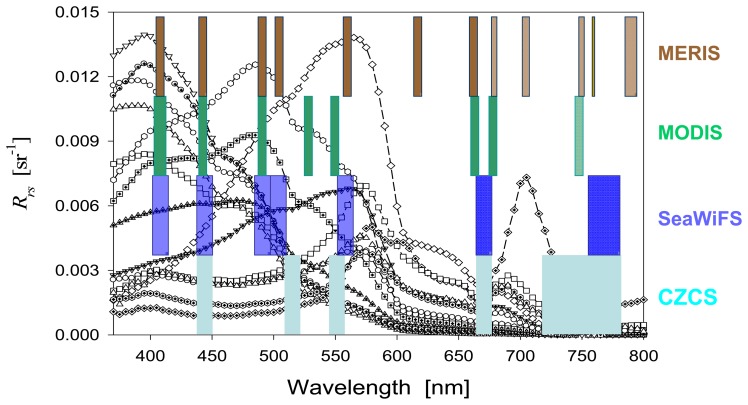
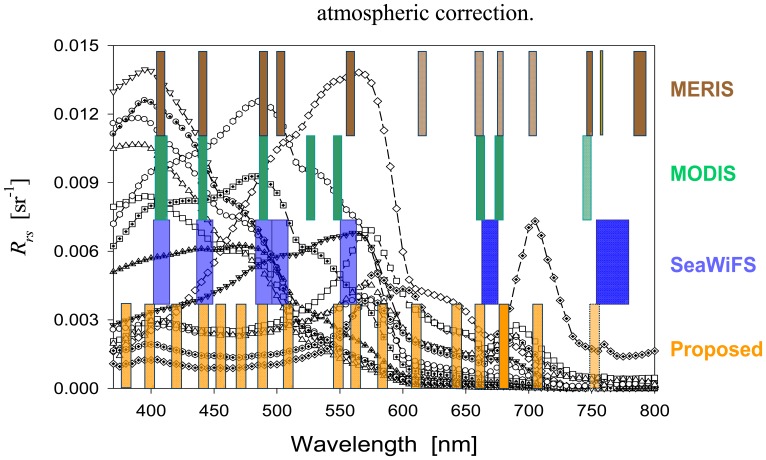
Ideally, to maximize the potential of observing properties of aquatic environments and their temporal and spatial changes, it is best to have a sensor capable of collecting signals with a continuous spectrum. After consideration of data flow, processing, and storage as well as signal-to-noise ratios, satellite sensors commonly have a few bands in the visible and near-IR domain (IOCCG 1998). For instance, the CZCS had five bands, while SeaWiFS and MODIS have seven (or eight) bands (with slightly different configurations). To show the spectral coverage of these operational satellite sensors, Figure 1 presents examples of remote-sensing reflectance spectra, along with the overlaid spectral bands (location and width) of CZCS, SeaWiFS, MODIS, and MERIS. Clearly, for the widely varying reflectance spectra, MERIS collects more spectral information, whereas MODIS and SeaWiFS could miss some important spectral signatures (such as the peak at ∼709 nm and information between 560 – 650 nm), and that CZCS could not observe the reflectance peak at ∼480 nm and the reflectance variation in the blue wavelengths (Carder et al. 1989).

Figure 1.

Examples of measured spectral remote-sensing reflectance (R_rs) used in this study. Overlaid are spectral bands (location and width) of CZCS, SeaWiFS, MODIS, and MERIS.

Selection and positioning of those spectral bands were based on measurements and optical characteristics (both absorption and scattering) of phytoplankton and colored dissolved organic matter (IOCCG 1998). 30 years ago, from 31 measurements of spectral reflectance for waters off the Oregon coast, Mueller (1976) demonstrated that reflectance spectra could be reconstructed with four principal vectors, suggesting that there are only four major variables for reflectance, and thus implying a requirement of 4 bands or so for an ocean color sensor. Similarly, for measurements made in the New York Bight region and also based on principal component analysis, Sathyendranath et al. (1994) concluded that a sensor with 5 bands (413.5, 447, 515, 560, 638.5 nm) can be as effective as 32 bands for the derivation of chlorophyll concentration. Mueller, however, cautiously pointed out that such conclusions are sensitive to the data sets used for the study. For instance, Dekker et al. (1992) indicated that 9 bands in the 500 – 800 nm range are needed to adequately cover the spectral curvatures of inland waters, and Wernand et al (1997) suggested another set of 5 bands (412, 492, 556, 620, and 672 nm) to re-construct hyperspectral reflectance for waters off the coasts of Netherlands. More importantly, the statistically-determined principal vectors are not physically intuitive in interpreting the spectral reflectance (Mueller 1976).

In general, the spectral configurations of current operational satellite sensors are designed for monitoring chlorophyll concentrations (index of phytoplankton) and colored dissolved organic matter (CDOM) in the open oceans, but have not been optimized for remote-sensing of complex coastal waters. Lee and Carder (2002) demonstrated that for adequate remote sensing of major properties (water column and bottom) of both open ocean and complex coastal aquatic environments, a sensor requires ∼ 15 spectral bands in the 400 – 800 nm range in order to obtain similar results as a sensor with 81 consecutive bands with 5-nm spacing. It is not yet clear, however, where the 15 bands should be placed.

In this study, from nearly 400 measurements of hyperspectral remote-sensing reflectance from various oceanic and coastal waters, we derived the spectral locations of the optimal bands via first- and second-order derivatives of the remote sensing reflectance for future advanced multi-band sensors for observing properties of aquatic environments. These bands can thus capture most of the spectral variations in remote-sensing reflectance caused by differing water-column and/or bottom properties, and be sufficient to re-construct hyperspectral remote-sensing reflectance spectra if desired.

2. Data and Methods

Since 1993, for a span of more than 12 years, an extensive remote-sensing-reflectance suite of hyperspectral (∼350 – 900 nm with a resolution ∼3 nm) measurements for various aquatic environments was collected, most of which were taken by the Ocean Optics Lab led by Prof. Kendall Carder at the College of Marine Science of the University of South Florida. Table 1 summarizes the cruises and general information of the various environments. The measured waters included open ocean blue waters to turbid coastal yellowish waters and optically shallow waters (bottom depths in a range ∼ 1 – 25 m). Wide ranges of concentrations of chlorophyll and dissolved organic matter and suspended sediments, along with different types of phytoplankton were encountered during these measurements.

Table 1.

Data used in this study (a total of 384 stations).

Area	Date	# of measurements	[Chl] range (mg/m3)
Gulf of Mexico	Apr. 1993	24	0.07 – 49.0
Florida Keys	July 1994	5	0.06 – 0.5
Arabian Sea	Dec. 1994	20	0.3 – 0.9
Chesapeake Bay	Sept. 1996	36	1.7 – 20.7
Hawaii	Feb. 1997	6	0.1 – 0.3
Florida Keys	May 1997	8	N/A
Bahamas	May 1998	39	0.05 – 1.4
East China Sea	July 1998	37	0.5 – 2.8
California Coast	Oct. 1999	37	0.2 – 9.4
North Atlantic	July 2001	17	4.5 – 13.9
Monterey Bay	Apr. 2003	56	0.1 – 9.7
Ft. Lauderdale	July 2005	52	N/A
Monterey Bay	Sept. 2006	47	0.5 – 500

Spectral remote-sensing reflectance (R_rs(λ)) is defined as the ratio of water-leaving radiance to downwelling irradiance. The R_rs spectrum contains sub-surface information of water constituents and/or bottom properties (when the bottom is optically shallow). Using a handheld spectroradiometer (Spectron Model SE-590 of Spectron Engineering, Inc. before 1997; SPECTRIX (Steward et al. 1994) for 1997 and later), a series (∼ 3 to 5 scans) of upwelling radiance above the surface (L_u(0⁺)) and the downwelling sky radiance (L_sky) were directly measured by the instruments for each station of the many cruises. All these measurements were carried out following the NASA protocols described in Mueller et al. (2002).

The measured L_u is a sum of photons emerged from subsurface scattering (the desired signal) plus surface-reflected sky and solar light (noise). Downwelling irradiance was derived by measuring the radiance (L_R) reflected from a standard diffuse reflector (Spectralon®). For each of the collected scans, hyperspectral total remote-sensing reflectance (T_rs(λ)) and sky reflectance (S_rs(λ)) were derived through

$$T_{rs}=\frac{L_u}{L_R}\frac{R_R}{\pi }\text{and}{S}_{rs}=\frac{L_{\mathit{\text{sky}}}}{L_R}\frac{R_R}{\pi },$$ (1)

with R_R the reflectance of the diffuse reflector (Spectralon, ∼ 10%).

Based on these measured T_rs and S_rs curves, after rejecting obvious outliers, averages of T_rs and S_rs for each station were obtained, respectively, in order to reduce the random variations associated with the measurements. Further, because T_rs is the sum of water-leaving radiance and surface-reflected sky radiance, R_rs(λ) is calculated as (Austin 1974; Carder and Steward 1985)

$$R_{rs}(\lambda )=T_{rs}(\lambda )-F{S}_{rs}(\lambda )-\mathrm{\Delta },$$ (2)

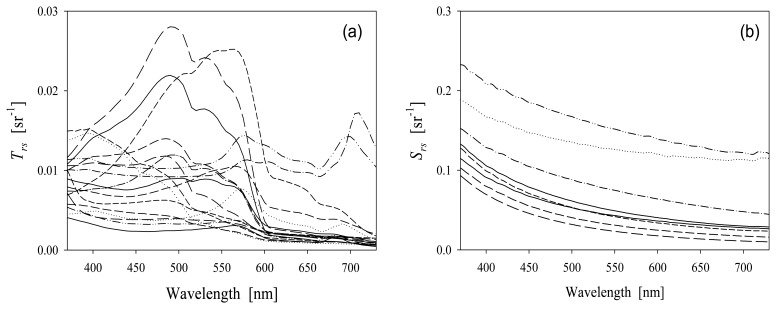
where F is surface Fresnel reflectance (around 0.023 for the viewing geometry), and Δ accounts for the residual surface contribution (glint, etc.). Figure 2 shows some examples of spectral T_rs (Fig. 2a) and S_rs (Fig. 2b). S_rs spectra are monotonic decreasing functions of λ, whereas T_rs spectra, because of the contribution of R_rs, show distinct variations from place to place. In the calculation of R_rs, Δ was determined either by assuming R_rs(750) = 0 (clear oceanic waters) or iteratively derived relative to optical models (coastal turbid waters). Because we are interested in the first- and second-order derivatives of R_rs (see the following for details), inaccurate Δ values have insignificant effects on this study.

Figure 2.

Examples of spectral total remote-sensing reflectance (T_rs, 2a) and sky remote-sensing reflectance (S_rs, 2b).

R_rs is a function of the total absorption and backscattering coefficients (Gordon et al. 1988; Lee et al. 2004; Zaneveld 1995) as well as bottom reflection (Lee et al. 1998; Maritorena et al. 1994). Spectra of backscattering coefficients, although normally stronger at shorter wavelengths, generally do not have strong spectral signatures (Boss et al. 2004; Loisel and Morel 1998; Twardowski et al. 2001). The spectrum of the total absorption coefficient, however, is a sum of the contributions of CDOM, various pigments contained in phytoplankton, plus water molecules (Gordon and Morel 1983; Smith and Baker 1978; Stramski et al. 2001). These contributions are spectrally selective, and thus result in significant variations in the spectral signatures of the total absorption coefficient (Kirk 1994; Mobley 1994). The extreme values (local maximum or minimum) of R_rs(λ) and the inflections of R_rs(λ) indicate the spectral effects of different combinations of those optically active constituents and/or bottom properties. If a sensor has only a few spectral bands and is intended to best capture the spectral signatures of R_rs(λ), then these bands need to be positioned at wavelengths that can match the locations of those extrema and inflections of R_rs(λ), unless the R_rs(λ) values at those bands are perfectly correlated. The spectral locations for such R_rs(λ) values are those wavelengths with zero first- and second-order derivatives of R_rs(λ), respectively.

To locate the optimal spectral positions for all collected samples, we thus carried out the following calculations:

$$\begin{array}{c}\sigma (\lambda )=\frac{d{R}_{rs}(\lambda )}{d\lambda }\\ \varsigma (\lambda )=\frac{d\sigma (\lambda )}{d\lambda }\end{array},$$ (3)

where σ(λ) and ς(λ) are the first- and second-order derivatives of R_rs(λ), respectively. Note that derivative analysis of hyperspectral data is a widely used tool to highlight and enhance the spectral characteristics in various applications (e.g., Holden and LeDrew 1998; Tsai and Philpot 1998). Before calculating the derivatives, R_rs(λ) spectra were interpolated to 1-nm resolution and were smoothed with a 5-nm running average, in order to remove some of the random noises.

3. Results and Discussions

From all of the calculated σ(λ) and ς(λ) spectra, we obtained the spectral distributions (at 1-nm resolution) where σ(λ) and ς(λ) equal zero, respectively. Mathematically, these frequency distributions are,

$$\begin{array}{c}{f}_{\sigma }(\lambda )=\frac{\text{∑}_{i=1}^N{\sigma }_i(\lambda )=0}{N},\\ f_{\varsigma }(\lambda )=\frac{\text{∑}_{i=1}^N{\varsigma }_i(\lambda )=0}{N}.\end{array}$$ (4)

Here σ_i(λ) and ς_i(λ) are the ith σ(λ) and ς(λ) spectrum of the data set, respectively. Figures 3 and 4 show f_σ(λ) and f_ς(λ), after a 5-nm running average was applied to highlight the major bands. The frequency distributions of σ(λ) and ς(λ) for wavelengths longer than 700 nm are not considered here, simply because that for oceanic and most coastal waters the R_rs values in those wavelengths are very small due to the strong absorption of water molecules and limited scatters in the water media. Consequently, R_rs in those wavelengths are either non-informative regarding constituents in water, or too noisy in the measured R_rs, except for highly turbid river plume or inland waters or clear and bright-bottom shallow (< ∼1 m) waters.

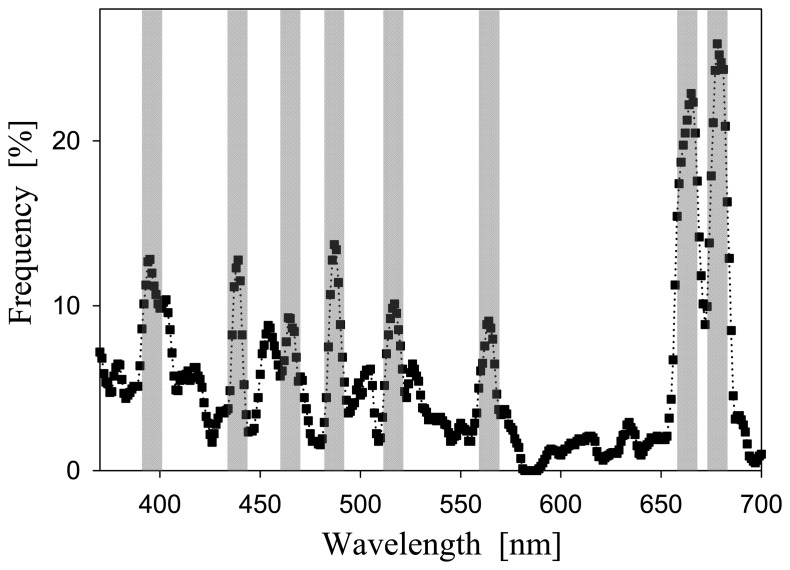
Figure 3.

Spectral distribution of the frequency where the first-order derivative of R_rs(λ) equals 0.

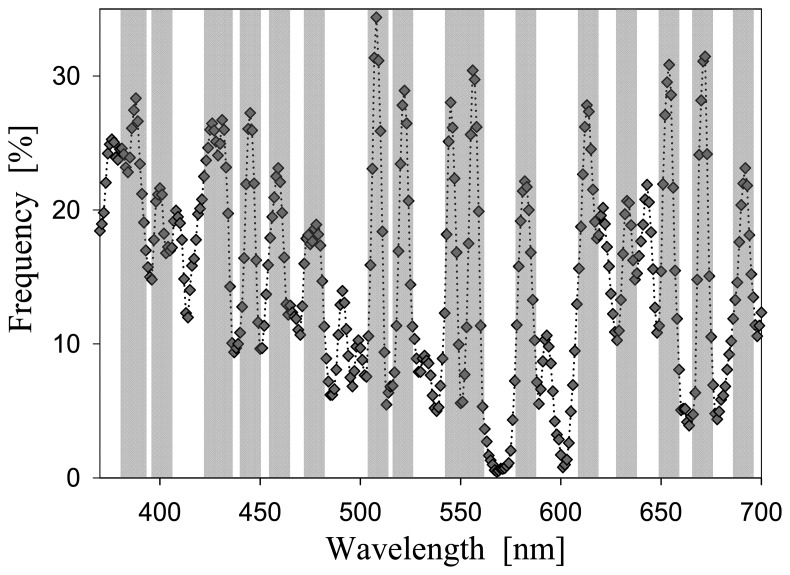
Figure 4.

Spectral distribution of the frequency where the second-order derivative of R_rs(λ) equals 0.

For an R_rs(λ) spectrum, σ_i(λ) = 0 indicates that there is an extremum of R_rs at λ. For various waters, because of the different combinations of water constituents and/or bottom characteristics, the spectral locations of the extrema shift (see Fig. 1). The spectral distribution of f_σ(λ) then summarizes, for all data in this study, the wavelength behavior in capturing the extrema. The greater the f_σ(λ) value, the more appearances of an extrema at that λ. Although each wavelength shows some possibility of capturing extrema of R_rs, apparently, the bands that captured more extrema of R_rs are concentrated in seven bands (in the 360 – 700 nm range) instead of spectrally scattered evenly (see Fig. 3). The seven bands are centered at (rounded to nearest 0 or 5): 395, 440, 490, 515, 565, 665, and 685 nm. Such a result is not surprising. For instance, 440 nm is at the peak absorption of phytoplankton pigments (chlorophyll-a), which can result in a local minimum of R_rs(λ); on the other hand, 685 nm is around the peak of chlorophyll fluorescence, which then contributes a local maximum of R_rs(λ) (see Fig. 1). For the other peaks, such as 490 nm or 515 nm, they normally represent locations of R_rs maximum (see Fig. 1 and Fig. 2a), resulted from minimum absorption coefficients at those wavelengths (Kirk 1994; Mobley 1994). Therefore, a multi-band sensor requires at least these bands to adequately capture the extrema of the various R_rs(λ) spectra.

ς(λ) = 0, on the other hand, indicates an inflection of an R_rs(λ) curvature at λ, normally resulting from different combinations of pigments and water molecules, and/or bottom effects when the water is optically shallow. Table 2 summarizes the wavelengths that capture more inflection points of R_rs(λ) curves (also see Fig. 4). In contrast to the distribution of f_σ(λ), the peak values of f_ς(λ) are much less concentrated spectrally. Interestingly, these bands cover the center wavelengths of the major pigments (Table 2) presented in Hoepffner and Sathyendranath (1991). Such a result supports the inclusiveness of the data set used in this study that covers a wide range of water environments, and encompasses various types of phytoplankton classes (resulting in minor changes in R_rs(λ) curvatures because of different pigment absorptions) and optically shallow environments. For a multi-band sensor, it is necessary to have bands that cover these wavelengths if properties other than chlorophyll concentration (such as pigment composition and/or bottom properties) are also desired from remote sensing of water color.

Table 2.

Bands that capture more extrema and inflections of R_rs(λ).

Wavelength	Fromfσ(λ)	Fromfς(λ)	Proposed Bands	H&S Bands*	MODIS	MERIS
385		x	1	384
395	x		2
400		x		413	412	412
425		x	3
440	x		4	435	443	443
445		x
460		x	5	464
475		x	6
490	x		7	490	488	490
510		x	8			510
515	x
520		x		532	531
545		x	9
555		x			551
565	x		10			560
580		x	11	583
615		x	12	623		620
635		x	13
645		x		644
655		x		655
665	x		14		667	665
670		x		676
685	x		15		678	681
710			16			709
750	For atmosphere correction or turbid river plume water		17		748	754
760	For O2					760
780	For atmosphere correction					779

Consolidating the major bands that have greater values of f_σ(λ) and f_ς(λ) (and considering a 10-20 nm bandwidth for satellite sensors), bands that optimally capture extrema and inflections of spectral R_rs are determined (see Table 2 and Fig. 5). These bands form the basis for a multi-band sensor to monitor aquatic environments (including optically shallow waters), although atmospheric absorption and solar Fraunhofer bands require minor adjustments of band positions for satellite sensors to improve global applicability. Interestingly, the analysis from the first- and second-order derivatives indicates 17 bands in the 385 – 800 nm range for the observation of ocean color, which echoes the findings of Lee and Carder (2002). Bands at 710 and 750 nm are added separately, where 710 nm is important for turbid coastal water and water with extreme phytoplankton blooms (red tide) (Dekker et al. 1992; Gower et al. 1999), and 750 nm and other near-infrared channels (e.g., see MODIS channels) are important/required for atmospheric correction (Gordon and Wang 1994) or for highly turbid inland or river plume waters (Dekker et al. 1992).

Figure 5.

The spectral bands proposed in this study, overlaid are spectral bands of SeaWiFS, MODIS, and MERIS. The 750-nm band with dotted perimeter indicates that this band is mainly used for atmospheric correction.

From Hoepffner and Sathyendranath (1991).

Table 2 also presents, for comparison, the spectral bands of MODIS and MERIS. Clearly, the wavelength selections of those sensors are in general supported by the results presented here. Comparing MODIS bands with those from this study or those of MERIS, the significant shortfall of MODIS (and SeaWiFS) is a band between 551 and 667 nm. Such a band is of great value for remote sensing of suspended sediments (IOCCG 2006) or remote sensing of optically shallow waters (Lee and Carder 2002). On the other hand, the band at 385 nm could be very useful either for the detection of red tide (Kahru and Mitchell 1998) or for atmospheric correction over coastal waters.

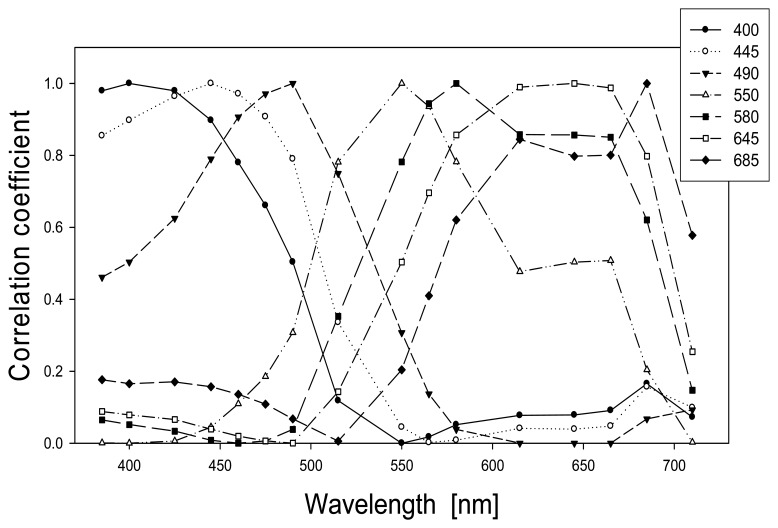
To understand the inter-dependence of R_rs at the selected bands, linear regression analyses of the R_rs at the suggested bands were carried out, and a correlation matrix was obtained. Figure 6 presents a few examples of the correlation spectra. For instance, when R_rs(490) is selected as the independent variable, R_rs at all other bands are considered as dependent, and a correlation spectrum of R_rs is then obtained (Fig. 6). The results from this analysis re-emphasize some known facts: 1) Because the absorption and scattering effects of the individual water constituents are broad-band in nature, the correlation coefficients are high for R_rs(λ) separated by short wavelength distances. 2) Because the absorption coefficients of phytoplankton and CDOM are much stronger in the blue-green region than in the red-infrared region and that they vary independently in general, R_rs in blue-green bands have quite low correlations when compared with R_rs in red-infrared bands (slightly higher correlation for the 670-690 chlorophyll a absorption and fluorescence region). The high correlation coefficients of R_rs at adjacent bands indicate potential redundant measurements when a sensor is exactly equipped with the bands proposed. This is especially true for the bands of 615, 645, and 665 nm where the interdependence is very strong (with correlation coefficients > 0.97). However, as pointed out in the IOCCG Report #1 (1998), “some redundancy is often essential to constrain the solutions”, especially for optically shallow waters where more spectral signal is required in order to adequately separate the information of the water column from that of the bottom. If one band has to be dropped out after considering such high correlation and high overlapping because of 10-20 nm bandwidth of each band, the 645 nm band can be removed from this list. The remaining 615 and 665 nm bands could ensure consistency and continuity with the observations of MODIS and/or MERIS. For waters of Case-1 nature (Morel 1988), however, because the variations of both spectral absorption and backscattering coefficients are determined by chlorophyll concentration alone, R_rs at all wavelengths are correlated (Morel and Maritorena 2001). For such waters and simpler diagnostic requirements, the number of bands can be significantly reduced without losing much information.

Figure 6.

Spectral distributions of correlation coefficients of R_rs(λ) at the bands (see Fig. 5) selected from first- and second-order derivative analyses (see text for details). The bands in the insert indicate the R_rs at those bands was used as the independent variable, respectively, while R_rs at other bands were considered as the dependent variable, a correlation coefficient for linear regression was then obtained for each R_rs pair.

4. Summary

In this study, based on extensive and inclusive measurements of hyperspectral remote-sensing reflectance curves from various aquatic environments, the primary bands (in the ∼ 380 – 800 nm range) that optimally capture the spectral signatures of R_rs are determined via first- and second-order derivatives. These bands in general cover the operational bands of SeaWiFS, MODIS and MERIS, and provide important and useful suggestions and guidance for extra bands of future multi-band sensors, in order to provide more and improved results for remote sensing of oceanic and coastal waters. However, these bands are aimed for general observation of the majority (99% or more) of the global aquatic environments and are derived based on available measurements. As point out in Lee and Carder (2002), sensors with discrete spectral bands are always facing the possibility of missing important spectral features of special cases, such as some coral reefs and/or seagrass beds (e.g., Holden and LeDrew 1998). Sensors with higher spectral resolution (along with high spatial resolution) or specially placed bands could be more helpful for such special and challenging cases.