Neural mechanisms of speed perception: transparent motion

Abstract

Visual motion on the macaque retina is processed by direction- and speed-selective neurons in extrastriate middle temporal cortex (MT). There is strong evidence for a link between the activity of these neurons and direction perception. However, there is conflicting evidence for a link between speed selectivity of MT neurons and speed perception. Here we study this relationship by using a strong perceptual illusion in speed perception: when two transparently superimposed dot patterns move in opposite directions, their apparent speed is much larger than the perceived speed of a single pattern moving at that physical speed. Moreover, the sensitivity for speed discrimination is reduced for such bidirectional patterns. We first confirmed these behavioral findings in human subjects and extended them to a monkey subject. Second, we determined speed tuning curves of MT neurons to bidirectional motion and compared these to speed tuning curves for unidirectional motion. Consistent with previous reports, the response to bidirectional motion was often reduced compared with unidirectional motion at the preferred speed. In addition, we found that tuning curves for bidirectional motion were shifted to lower preferred speeds. As a consequence, bidirectional motion of some speeds typically evoked larger responses than unidirectional motion. Third, we showed that these changes in neural responses could explain changes in speed perception with a simple labeled line decoder. These data provide new insight into the encoding of transparent motion patterns and provide support for the hypothesis that MT activity can be decoded for speed perception with a labeled line model.

visual motion patterns strongly activate neurons in striate and extrastriate cortex both in macaques and humans. Single-cell recordings in macaques have shown that neurons in the middle temporal cortex (MT) are not only highly responsive to motion but also strongly tuned for motion direction and speed, and there is compelling evidence that perceived direction can be decoded from neural activity in MT based on a labeled line model (for review, see Born and Bradley 2005; Parker and Newsome 1998). In this decoding model each neuron represents a certain direction of motion (its label, identified by its preferred direction) and spikes from the neuron represent evidence in favor of that direction of motion.

There is direct evidence that area MT is also involved in speed perception. Lesions in area MT lead to impairments in speed perception (Orban et al. 1995; Pasternak and Merigan 1994), trial-to-trial variations in MT responses are related to speed perception (Liu and Newsome 2005), and microstimulation of groups of neurons that prefer high speeds changes speed perception (Liu and Newsome 2005). Further evidence comes from the use of visual illusions that decrease or increase the perceived speed of moving patterns. The behavioral effect on perceived speed of the step size in apparent motion (Churchland and Lisberger 2001), the contrast of moving sinusoidal gratings (Priebe 2004), motion adaptation (Krekelberg et al. 2006a), acceleration (Schlack et al. 2007, 2008), as well as stimulus size (Boyraz and Treue 2011) can all be linked to firing rate changes in area MT via labeled line models.

Nevertheless, the link between speed-related firing rate changes in area MT and perceived speed is not as clear-cut as for perceived direction. The sensitivity of MT neurons for speed is typically less than the sensitivity of the whole animal, and microstimulation effects on speed judgments are not as prominent as in direction discrimination tasks (Liu and Newsome 2005). In addition, there appears to be an asymmetry in the relationship between neural and behavioral responses that depends on the relationship between the stimulus and the speed preference of the (group of) cells under study. Whereas stimuli with speeds on the ascending flank of the tuning curve show the expected influence of trial-to-trial variability and microstimulation, this association is much weaker (and statistically nonsignificant) for stimuli on the descending flank (Liu and Newsome 2005). Such an asymmetry would not be expected in a labeled line model. Moreover, earlier studies have shown an unexpected monotonic relationship between microstimulation current and perceived speed as measured by oculomotor response (Groh et al. 1997). Finally, we have previously reported evidence against the labeled line model based on a visual illusion that leads to misperceptions in speed (Krekelberg et al. 2006b). Notably, when the luminance contrast of moving random dot patterns is reduced, the subjective speed percept decreases dramatically, but the speed tuning of MT neurons shifts in a direction that is opposite to that predicted by the labeled line model.

While there can be little doubt that area MT plays some role in speed perception, we believe that a better understanding of these discrepancies between changes in MT activity, the labeled line model, and speed perception can provide important insight into the relation between neural activity and behavior. To further constrain this relationship, we investigated the representation of the speed of transparent motion in area MT. When two patterns move transparently in opposite directions, perceived visual speed increases dramatically (up to 50%) compared with the perceived speed of the individual components (De Bruyn and Orban 1999). Such a large perceptual effect should have a clear neural signature.

In our study we first confirmed the behavioral findings by showing a large overestimation of the speed of bidirectional motion patterns in both humans and the macaque monkey. Subsequently, we recorded neural responses to bidirectional patterns and their unidirectional components at different speeds. Finally, we performed a quantitative analysis of the relationship between these responses and behavioral measures of sensitivity and bias in speed perception. Our findings provide clear support for the hypothesis that speed perception is linked to neural activity in area MT via a labeled line decoder model.

MATERIALS AND METHODS

Subjects

Two adult male rhesus monkeys (Macaca mulatta; monkeys M and S) were used in the electrophysiological experiments. Monkey M performed the behavioral experiments. Experimental and surgical protocols were in accordance with the National Institutes of Health (NIH)'s guidelines for humane care and use of laboratory animals and were approved by the local animal use committee.

Five naive human subjects and one author participated in the human psychophysical experiments. All human subject procedures were in accordance with international standards (Declaration of Helsinki) and NIH guidelines and were approved by the institutional review board, and participants gave their informed, written consent. All subjects had normal or corrected-to-normal visual acuity.

Visual Stimulation

All visual stimuli were generated with in-house OpenGL software using a high-resolution graphics display controller (Quadro Pro Graphics card, 1,024 × 768 pixels, 8 bits/pixel). In the experiments with monkey subjects, stimuli were displayed on a 21-in. monitor (Sony GDM-2000TC; 75 Hz, noninterlaced; 1,024 × 768 pixels); in the experiments with human subjects we used a 19-in. Sony Trinitron E500 monitor (75 Hz, noninterlaced, 1,024 × 768 pixels). The output of the video monitor was measured with a PR650 photometer (Photo Research, Chatsworth, CA), and the voltage/luminance relationship was linearized independently for each of the three guns in the CRT. Stimuli were viewed from a distance of 57 cm in a dark room (<0.5 cd/m²).

Monkeys were seated in a standard primate chair (Crist Instruments, Germantown, MD) with the head post rigidly supported by the chair frame. Eye position was sampled at 60 Hz with an infrared video-based system (IScan, Burlington, MA), and the eye position data were monitored and recorded with the CORTEX program (Laboratory of Neuropsychology, National Institute of Mental Health; http://dally.nimh.nih.gov/), which was also used to implement the behavioral paradigm and to control stimulus presentation.

Stimuli and Experimental Paradigms

We used random dot patterns consisting of 100 dots moving within a 10°-diameter circular aperture. The lifetime of the dots was infinite, and they were randomly repositioned after leaving the aperture. Dots were 0.15° in diameter and had a luminance of 30 cd/m². The gray background was 5 cd/m². In the physiological experiments, the direction of motion was adjusted to match the axis of neuronal preferred direction rounded to the nearest multiple of 45°.

Psychophysical paradigm.

Figure 1A shows the paradigm we used to investigate how transparent, bidirectional motion affected perceived speed in humans. Subjects fixated a small red dot at the center of the screen. Two patches of dots appeared 10° left and right of fixation. The subject's task was to determine which of the two patches contained the dots with the fastest speed.

Fig. 1.

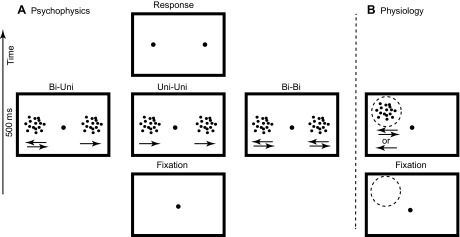
Experimental paradigms. A: sequence of events in the paradigm used for the behavioral experiments. Subjects fixated a red dot, and 2 patterns appeared for 500 ms. In the human behavioral experiments there were 2 conditions. In the first condition a bidirectional motion pattern (2 dot patterns transparently moving in opposite directions) and a unidirectional motion pattern were shown (bi-uni). In the second condition 2 unidirectional motion patterns were shown (uni-uni). In the monkey experiments there was a third condition in which 2 bidirectional motion patterns were shown (bi-bi). In the monkey experiments the bi-uni condition was only shown for a small subset of trials and rewarded randomly. Subjects were instructed to indicate the pattern that moved fastest by a key press (human) or an eye movement to 1 of 2 targets (monkey). B: in the physiological experiments 1 pattern was presented in the receptive field (indicated by dashed line). The only behavioral requirement for the monkey was to fixate the red spot for the duration of the trial.

In one patch (the reference), either all the dots moved rightward [“unidirectional condition” (uni)] or half of the dots moved rightward and the other half moved leftward (bi). The speed of all dots in the reference was the same but varied across conditions (1, 2, 5, 10, 20, 40°/s). In the other patch (the test), all dots moved rightward and their speed was slower or faster than the reference speed by 0%, 10%, 40%, or 80%. Human subjects performed the speed discrimination task comparing unidirectional tests and reference (uni-uni) or a bidirectional reference and a unidirectional test (bi-uni). The 84 test conditions (uni-uni/bi-uni × 6 reference speeds × 7 test speeds) were randomly interleaved.

After the 500-ms stimulus presentation, the dot patterns were extinguished and subjects answered the question “Which pattern moved faster?” by pressing one of two keys on the keyboard. The human subjects received no feedback on their performance, and the next trial started immediately after the subjects' response. The positions of test and reference stimuli were varied randomly across trials. Each comparison of reference speed and test speed was repeated 20 times.

For monkey M we maintained the identical layout and stimuli, but the animal reported which patch moved faster by making an eye movement toward one of two small green dots that appeared 10° left or right of fixation once the moving stimuli were extinguished.

In most trials, the monkey compared a unidirectional reference to a unidirectional test (uni-uni) or a bidirectional reference to a bidirectional test (bi-bi). Because any illusory speed percept would affect both test and reference equally, we rewarded the animal for veridical performance on these trials. On a small subset of trials, the animal compared a bidirectional reference with a unidirectional test of the same physical speed (bi-uni). We expected a potentially large illusory change in perceived speed; hence on these trials we rewarded the animal on 60% of trials, independent of the animal's response on that trial. In our experience, including a large number of randomly rewarded conditions typically leads to random behavior; hence we limited the uni-bi conditions to the comparison of two physically equal speeds (and therefore did not measure the full psychometric curve in this condition). The data reported here (∼16,000 trials) were recorded across 13 days immediately after training on uni-uni and bi-bi comparisons for several weeks.

Electrophysiological paradigm.

We recorded the activity of single units in area MT with tungsten microelectrodes (FHC, 3–5 MΩ) in two monkeys. Neurophysiological signals were filtered, sorted, and stored with the Plexon system (Plexon). We identified area MT physiologically by its characteristically high proportion of cells with directionally selective responses, receptive fields (RFs) that were small relative to those of neighboring area MST, and its location on the posterior bank of the superior temporal sulcus. The typical recording depth agreed well with the expected anatomical location of MT determined from structural MR scans. For more details, see Hartmann et al. (2011) and Richert et al. (2013).

We used automated methods to determine cells' directional selectivity and RF location (Krekelberg and Albright 2005). The approximate RF center and the preferred direction of motion revealed by these methods were used to optimize stimuli for subsequent neuronal response measurements (i.e., we used the preferred direction as estimated by this method rounded to the nearest 45° to align the direction of dot motion with the preferred-antipreferred axis and the location of the coarsely mapped RF to place the dot pattern on its center).

In the main paradigm, we measured speed tuning curves of MT cells, using random dot patterns that appeared 250 ms after the monkey started fixating a central red dot and were extinguished 500 ms later. The range of speeds was 1, 2, 4, 8, 16, 32, and 64°/s, and for each cell we measured the speed tuning curve with unidirectional patterns moving in the preferred direction (uni-pref), unidirectional patterns moving in the antipreferred direction (uni-anti), and bidirectional patterns in which half of the dots moved in the preferred and half of the dots moved in the antipreferred direction (bi). In the bidirectional condition the speed of all dots was always equal.

All conditions were randomly interleaved. Trials in which eye position deviated from a 2°-wide square window centered on the fixation spot were aborted and excluded from analysis. Unless cell isolation was lost prematurely, each condition was repeated 15 times.

Data Analysis

Psychophysical data.

Separately for each combination of reference and test stimulus, we calculated the percentage of trials in which subjects responded that the test stimulus was faster. Using the psignifit MATLAB toolbox (Wichmann and Hill 2001a), we fit these data with cumulative Gaussians and obtained an estimate of the point of subjective equality (PSE), defined as the speed where the fitted curve crossed 50% “test faster,” as well as the sensitivity, defined as the slope of the psychometric curve at the PSE. The Monte Carlo simulations of the pfcmp function in the psignifit toolbox were used to determine whether two psychometric functions (e.g., corresponding to different motion patterns) were significantly different (Wichmann and Hill 2001b).

To estimate the monkey's PSE for uni-bi comparisons based only on the comparison of physically matched uni- and bidirectional speeds, we determined his psychometric curve based jointly on the trials of the uni-uni and bi-bi comparisons and then determined by how much this curve would have to be shifted to explain the performance on the single uni-bi comparison. In other words, for this ballpark estimate we assumed that the animal's psychometric curve in the uni-bi trials was shifted but that its slope was the same as the average slope on the uni-uni and bi-bi comparisons.

Physiological data.

Our primary measure of the neural response was the spike count in the 500 ms following stimulus onset. This window was corrected for each neuron's response latency, which was determined by using a maximum likelihood estimator that assumes Poisson spiking statistics (Friedman and Priebe 1998). (We also performed all analyses with a window starting 200 ms after stimulus onset and ending with stimulus offset; excluding onset transients in this manner led to highly similar effects and did not change any of our conclusions).

As has been shown before, speed tuning curves in MT are well-fit by log-Gaussians (Nover et al. 2005). We parameterized the tuning curves separately for the uni-pref, uni-anti, and bi conditions as $r=\alpha +\beta \times \exp \left[-\frac{1}{2\times {\sigma }^2}{\left({\log }_2\left(s/\delta \right)\right)}^2\right]$ and used a Bayesian method to determine the posterior probability distribution of all such log-Gaussian tuning functions based on the spike count data of all trials and the assumption of Poisson variability (Cronin et al. 2010). In this equation, the parameter α is referred to as the offset (it reflects the part of the response that is not speed tuned), β is the amplitude (it reflects the strength of the speed tuning), σ is a unitless parameter that reflects the (scale invariant) tuning width, and δ is the preferred speed. The Bayesian fitting procedure calculates the posterior probability distribution of all four parameters, which is useful to show the range of tuning curves that are compatible with the data (and the log-Gaussian model) (e.g., Fig. 3). For cell-by-cell comparisons (Fig. 4) and the simulations of Fig. 8, we obtained a point estimate for each of the parameters by taking the median across each of the posterior distributions. We refer to this point estimate as the “best fit.”

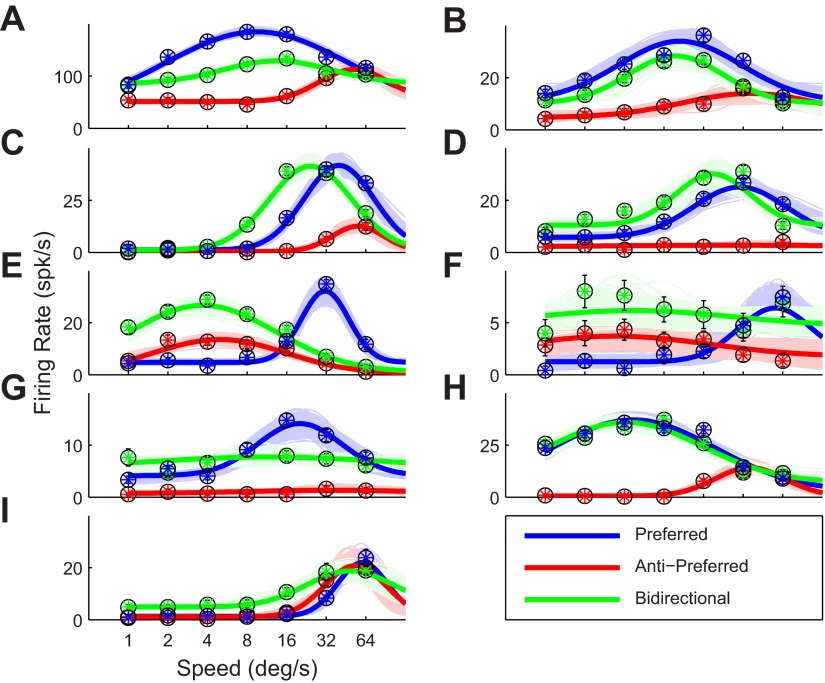
Fig. 3.

Speed tuning curves of 9 example neurons from area MT. In all conditions the dot patterns (in both preferred and antipreferred directions) were moving at the speed indicated on the x-axis. A–I: 9 cells that span the range of effects we found. Error bars on the data points indicate SE. The solid curves represent the best fit; the colored areas around the curves represent the family of tuning curves consistent with the data (see materials and methods). Consistent with previous reports (Snowden et al. 1991), many cells responded less to bidirectional motion than to unidirectional motion. This suppression, however, was not constant across speeds, and most cells also showed enhanced responses to bidirectional motion of certain speeds.

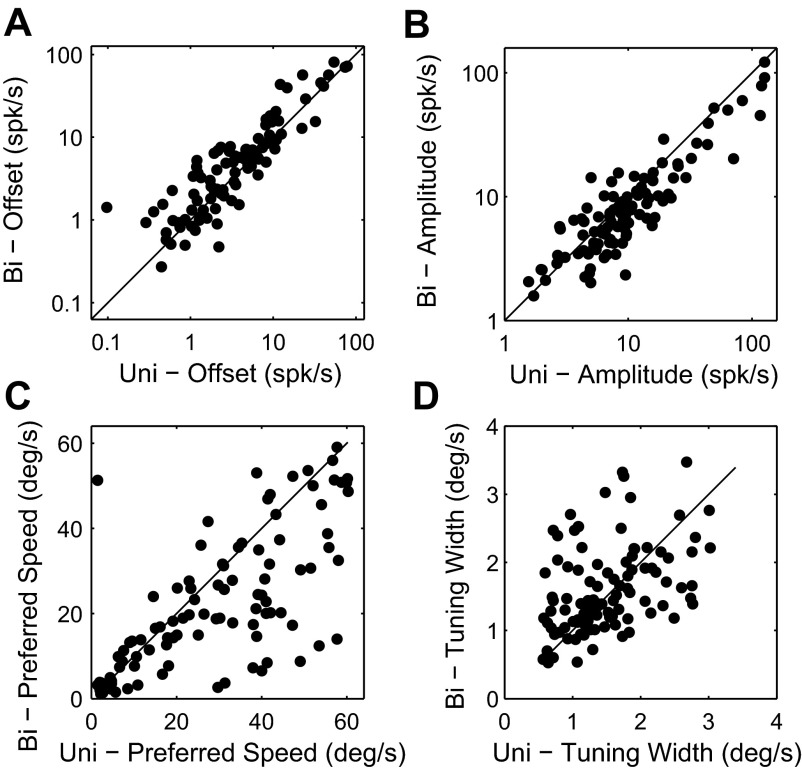
Fig. 4.

Cell-by-cell comparison of tuning parameters. This plot contains only significantly tuned cells (n = 103). A: comparison of the speed-independent (i.e., untuned) response for bidirectional stimuli vs. unidirectional stimuli moving in the preferred direction (offset parameter: α in Eq. 1). B: comparison of the tuning amplitude (β). C: comparison of the preferred speed (δ). D: comparison of the speed tuning width (σ). This figure shows that when a bidirectional stimulus was shown MT neurons typically responded more to all speeds (A) but with a reduced amplitude (B). In addition, most cells preferred lower speeds in bidirectional motion patterns (C).

Fig. 8.

Speed discrimination based on a labeled line model and MT responses. The model used only the responses of 126 MT neurons to determine whether the test patch (moving at speed represented on x-axis) moved faster than the reference patch (moving at a fixed speed of 10°/s). These simulated behavioral experiments match the behavioral experiments shown in Fig. 2. The figure shows that the decoder performed the uni-uni task at a high level of performance. The same decoder, however, had reduced sensitivity for bidirectional stimuli and overestimated the speed of bidirectional patterns compared with unidirectional patterns (red solid line). The dotted and dashed red lines show the results of the bi-uni task when the label of the neurons was based on the preferred speed for bidirectional patterns or the average of the 2 motion types, respectively. These results are in good qualitative agreement with the human and monkey behavioral data of Fig. 2 and support the view that MT responses, decoded with a labeled line decoder, could indeed underlie the perception of speed in uni- and bidirectional patterns.

We compared the log-Gaussian fits with a model in which the spike count was independent of the speed (i.e., untuned) and denoted a cell as speed tuned if the Bayes factor comparing these two models was at least 10 for both the uni-pref and bi conditions (i.e., the log-Gaussian model was at least 10 times more likely to explain the data than the untuned model).

In the nonparametric analyses we determined the median firing rate across trials per cell for each condition. We calculated the direction selectivity index (DSI) on the basis of the median firing rates for the preferred (P) and antipreferred (A) directions per speed as (P − A)/(P + A). The preferred speed was defined as the unidirectional motion pattern that generated the largest median response. To generate population responses, we normalized the firing rate of each cell by its peak response and then determined the median across neurons. To generate a preferred-speed aligned population response, we binned the observed median response across trials as a function of the difference (in octaves) between stimulus speed and preferred speed. In other words, we described the median response as a function of Δspeed = log2(speed) − log2(δ) for each cell, binned this in octaves, and then determined the median across all neurons for every Δspeed bin where we had at least 25 observations (i.e., neurons).

Power-law summation.

In the power-law summation model (Britten and Heuer 1999), the response to a compound stimulus (the bidirectional pattern, r_bi) is determined by a nonlinear summation of the response to the two components (r_uni-pref, the unidirectional preferred and r_uni-anti, the unidirectional antipreferred response):

$$r_{\text{bi}}=a\times {\left[{\left(r_{\text{uni-pref}}\right)}^g+{\left(r_{\text{uni-anti}}\right)}^g\right]}^{\frac{1}{g}}+b$$

The gain (a), power (g), and offset (b) are free parameters, which were determined (per neuron) with least-squares optimization.

Decoding.

We investigated the extent to which a simple labeled line decoding model could relate the neural responses with the behavioral data. In this model a spike from a neuron is interpreted as a vote in favor of the base-2 logarithm of that neuron's preferred speed.

We used the parametric fits of each neuron together with the assumption of Poisson variability to generate simulated population responses for each of the displays that occurred in the behavioral paradigm. In other words, for each (simulated) behavioral trial we generated the response of the 103 speed-tuned neurons to the test stimulus and the response of the same 103 neurons to the reference stimulus.

Note that this relies on the common assumption that for each speed-tuned neuron that we recorded in one hemisphere there exists a neuron with identical properties in the opposite hemisphere (the anti-neuron) and that a perceptual decision is made by comparing the activity in these two groups of neurons. Note also that, because we mapped speed tuning for each neuron in its preferred and antipreferred directions only, our sample contained only neurons that responded maximally to at least one of the directions of motion in the bidirectional pattern. In other words, our decoder used only a slice through the two-dimensional space of neurons with all possible preferred directions and speeds. An optimal decoder, and quite likely the brain, could also use the information provided by neurons whose preferred direction is not matched to any of the directions in the bidirectional stimulus, as well as knowledge about the variability and tuning width of the neurons (Krekelberg et al. 2003; Morris et al. 2013). Given how well the simple decoder worked (see Fig. 8), and because we recorded speed tuning only in two directions, we did not pursue such approaches here.

For each neuron, the response was normalized to its peak response (i.e., divided by the response to the neurons' preferred speed). This resulted in two population vectors: $\overrightarrow{t}$, the response to the test, and $\overrightarrow{r}$, the response to the reference. Each neuron was assigned a label defined by the 2-base log of its preferred speed ($\overrightarrow{l}$; see below). We then calculated the decoded speed as the inner product of the population activity vector and the label vector, normalized by the sum ($\left|\overrightarrow{t}\right|$ or $\left|\overrightarrow{r}\right|$) of the population activity:

$$\begin{array}{cc}{s}_{\text{test}}=\overrightarrow{t}\cdot \overrightarrow{l}/\left|\overrightarrow{t}\right|,& s_{\text{reference}}=\overrightarrow{r}\cdot \overrightarrow{l}/\left|\overrightarrow{r}\right|\end{array}$$

We used this procedure to generate 1,000 synthetic trials for each of the test speeds, and for each motion type, and then compared the decoded test and reference speed to answer the same question that the subjects answered: Was the test faster than the reference (s_test > s_reference)? For each simulated trial this resulted in a binary decision, just like the outcome of a real behavioral trial. To generate psychometric functions we analyzed those binary decisions with procedures identical to those used for the actual behavioral data (see above).

In the first decoder, the population vector of speed labels ($\overrightarrow{l}$) was defined as the base-2 log of each neuron's preferred speed for unidirectional motion. For the second decoder we first used the same Bayesian fitting procedure as described above but now without taking stimulus type (uni- or bidirectional) into account. The label ($\overrightarrow{l}$) was then defined by the preferred speed that resulted from this procedure. Loosely speaking, one can view this as an average preferred speed across the uni- and bidirectional patterns. For the third decoder, we used the preferred speed for bidirectional motion as the label.

RESULTS

The results are divided into three parts. First, we document how transparent motion affected perceived speed in humans and monkeys. Second, we describe how bidirectional, transparent motion influenced responsivity and speed tuning of MT neurons. Third, we present a decoding analysis that links the neural and behavioral data via a labeled line model.

Speed Perception

Previously, De Bruyn and Orban (1999) have shown that the speed of two transparently moving dot patterns is overestimated. To allow a direct comparison of behavioral with physiological data, we replicated their findings using the stimuli we used in the physiological recordings, investigated a wider range of speeds, and obtained behavioral data in healthy human volunteers as well as a monkey. The details of the paradigm are described in materials and methods. Briefly, both the human and monkey subjects viewed two patches of moving random dots and reported which of the two moved faster (Fig. 1A).

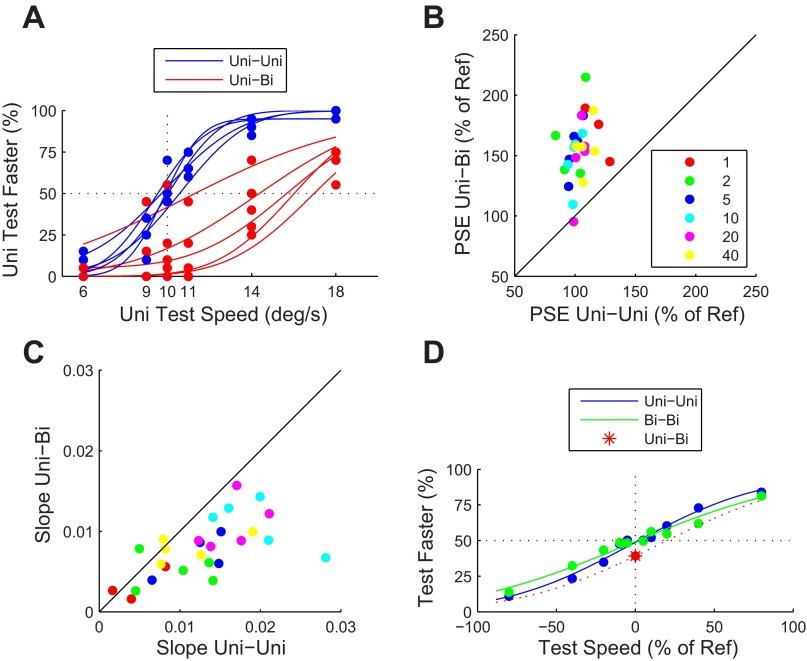
Figure 2 shows the results. The blue psychometric curves in Fig. 2A demonstrate that the five subjects correctly compared the speed of two unidirectional patches while overestimating the speed of bidirectional patches (red curves), compared with unidirectional patches. The shallow slopes of the red curves in Fig. 2A show that sensitivity was reduced for the bidirectional patches compared with the unidirectional patches. Both the increase in PSE (P < 0.001) and the decrease in slope (P < 0.005) were consistent across subjects and reference speeds (Fig. 2, B and C).

Fig. 2.

Perceptual effects of transparency. A: psychometric curves for 5 human subjects. In the uni-uni condition, the subjects compared 2 patches of unidirectional motion, one with a fixed (reference) speed of 10°/s and the other with the variable speed shown on x-axis. In the uni-bi condition, the subjects compared a unidirectional test speed (x-axis) to a bidirectional reference moving at 10°/s. The clear rightward shift of the point of subjective equivalence (PSE) in the uni-bi conditions represents a strong overestimation of the perceived speed of the bidirectional reference. The intersection of the dotted black lines indicates the PSE for veridical speed perception. B: comparison of PSE in the uni-uni and uni-bi conditions for a range of reference speeds. Each data point represents data from a single subject for a single reference speed. Reference speeds (°/s) are color coded according to the key. This plot confirms that the effect shown in A (overestimation of bidirectional speed) was found consistently, and across the range of reference speeds. C: comparison of the sensitivity (the slope of the psychometric function in A at the PSE) in the uni-uni and uni-bi conditions for a range of reference speeds. Sensitivity was consistently higher in the uni-uni condition. D: behavioral data from 1 monkey subject (monkey M). The uni-uni and uni-bi conditions were identical to those of the human subjects. In the bi-bi condition monkey M compared the speed of a bidirectional test stimulus with the speed of a bidirectional reference. The data were averaged over reference speeds, and therefore the test speed on the x-axis is expressed as % of the reference speed. The data show that monkey M was less sensitive for the bi-bi comparison than the uni-uni comparison. Just like the human subjects, monkey M overestimated the speed of bidirectional stimuli compared with unidirectional reference patterns (uni-bi, red asterisk; error bars representing the 95% confidence limits have a length of 4%, which is smaller than the marker). The red dotted line is a psychometric function whose PSE was chosen to match with the uni-bi performance, while the slope was estimated jointly from the uni-uni and bi-bi trials. The intersection of the dotted black lines indicates the PSE for veridical speed perception.

The monkey (Fig. 2D) compared two unidirectional patches (uni-uni; blue curve), two bidirectional patches (bi-bi; green curve), or a unidirectional test with a bidirectional reference whose physical speed was identical (uni-bi; red asterisk). The monkey's sensitivity for bidirectional patches was reduced compared with unidirectional patches (P < 0.001), and, just like the human subjects, he significantly overestimated the speed of the bidirectional reference patch compared with a unidirectional test patch (red asterisk; the unidirectional test was reported as faster in 39% of trials; P < 0.001, binomial test). The red dotted curve in Fig. 2D shows a psychometric curve with a slope determined from the pooled uni-uni and bi-bi comparison trials, while the PSE (20%) was chosen to fit the performance on the uni-bi comparisons (see materials and methods). Hence, a ballpark estimate for the magnitude of speed overestimation by monkey M is 20%.

To summarize, the behavioral data were qualitatively consistent across subjects, species, reference speeds, and replicated previous studies: subjects were less sensitive to bidirectional speed (Verstraten et al. 1996), and they overestimated its speed (De Bruyn and Orban 1999). Next, we describe the neural representation of these motion patterns in macaque MT.

Neural Representation of Speed

We recorded from 126 neurons in area MT of two monkeys (monkey S: 46 cells, monkey M: 80 cells). Their RF eccentricity ranged from 3° to 15°, which was well matched to the position of the stimuli used in the behavioral experiments (10°). Even though the stimuli were not optimized (in size or dot density) per neuron, the responses were clearly direction selective. Direction selectivity depended on the speed of the stimuli. Across all neurons and speeds, the DSI (see materials and methods) had a median of 0.32, while the peak DSI across speeds had a median across the sample of 0.49. (Note that our definition of DSI does not remove the spontaneous firing rate; doing so increases this median peak DSI to 0.86).

In agreement with earlier findings (Lagae et al. 1993; Rodman and Albright 1987), most cells (122/126, 97%) were significantly speed tuned (as defined in materials and methods) for unidirectional patterns. Most of these (103/122, 84%) were also significantly speed tuned for bidirectional patterns. The log-Gaussian was a close fit to the speed tuning curves for unidirectional (R² = 0.9; compatible with earlier reports by Nover et al. 2005) and bidirectional (R² = 0.9) patterns. The distribution of preferred speeds (for unidirectional motion in the preferred direction) was broad; the quartile range extended from 9°/s to 42°/s with a median of 25°/s. These properties are in general agreement with other studies (Churchland and Lisberger 2001; DeAngelis and Uka 2003; Duijnhouwer et al. 2013; Liu and Newsome 2005).

Illustrative example cells.

In each cell, we mapped the speed tuning curve, using unidirectional motion of 100 randomly positioned dots moving in the preferred direction (uni-pref), unidirectional motion in the antipreferred direction (uni-anti), and bidirectional motion with 50 dots moving in the preferred and 50 dots moving in the antipreferred direction (bi). Figure 3 shows these tuning curves for nine example cells that illustrate the range of effects we found in our MT sample.

Figure 3, A and B, show examples that match previous reports on transparent motion (Snowden et al. 1991; van Wezel et al. 1996); bidirectional motion evokes a response in between the response evoked by the preferred and the antipreferred direction of motion. A model in which the bidirectional response is the (weighted) average of the preferred and antipreferred response would fit such cells well (see below for a quantitative treatment). Averaging, however, does not adequately describe the response pattern seen in the remaining panels of Fig. 3. The neurons in Fig. 3, C–E, for instance, reduced their preferred speed when exposed to bidirectional motion. The neurons in Fig. 3, F and G, responded to all speeds of bidirectional patterns and lost their speed tuning. The neuron in Fig. 3H responded to antipreferred motion at high speeds when presented in isolation but responded to the bidirectional stimulus as if it was identical to the preferred stimulus and did not contain any motion in the antipreferred direction (winner-take-all behavior; see below). Finally, the neuron in Fig. 3I was not direction sensitive (red and blue curves overlap), but at low speeds it responded better to bidirectional than unidirectional motion.

Cell-by-cell analysis.

For each cell, we fit a log-Gaussian tuning curve to the responses to motion in the preferred direction and, separately, for bidirectional motion. Figure 4 compares the four parameters of these fits on a cell-by-cell basis for the 103 neurons with significant speed tuning for both uni- and bidirectional patterns. Figure 4A shows that the offset of the tuning curve, which represents the part of the response that is independent of the speed of the stimulus, generally increased for bidirectional motion. This effect was highly significant (sign test; P < 0.01). We used an orthogonal regression to quantify the effect as a 60% increase in the untuned response. Figure 4B compares the amplitude of the speed tuning curves for uni- and bidirectional motion. The amplitude was significantly reduced (sign test; P < 0.01), and, on average, the amplitude of the bidirectional response was 71% of the amplitude of the unidirectional response. Figure 4C shows that the preferred speed for bidirectional stimuli was typically lower than the preferred speed of unidirectional stimuli (sign test; P < 0.01).

These changes in the parameters of the log-Gaussian tuning function go a long way to describe the response changes of the example cells in Fig. 3. For instance, the offset increase can be seen in Fig. 3, D, F, G, and I. A decrease in amplitude is seen in all example cells except Fig. 3, C and H, and a reduced preferred speed is clearly noticeable in Fig. 3, C–E.

The tuning width was characterized by the unitless parameter σ. In our sample σ ranged from 0 to 3 with a median of 1.5 for unidirectional patterns, similar to the values reported by Nover et al. (2005). The scatterplot in Fig. 4D shows that even though bidirectional patterns often induced relatively large changes in tuning width, there was no consistent pattern (sign test; P > 0.8) across the sample. We investigated whether a pattern could be discerned when taking preferred speed into account. For neurons with low preferred speeds tuning was typically broader for bidirectional motion (i.e., σ was reduced), while neurons with high preferred speeds often had narrower tuning for bidirectional motion (i.e., σ was increased). However, this correlation between the change in σ and the preferred speed of the neuron was weak (r = 0.23, P < 0.05); hence most of the variance in tuning width changes induced by bidirectional patterns remains unexplained.

Normalization.

We investigated whether a simple normalization model could describe the relation between the response to the two unidirectional patterns and the response to the bidirectional pattern. Specifically, we used least-squares optimization to fit a power law model to the responses to the bidirectional patterns (see materials and methods). Across our sample of 126 cells this power law model explained little of the variance in the response to bidirectional motion (median explained variance 46%). The model failed entirely (explained variance <10%) for 49 of the neurons (= 39%). Figure 3, A and E–G, show example neurons from this category. For the subset of 37 neurons (= 29%) where the model worked reasonably well (explained variance > 75%), the power parameter (g) was typically above 20, which means that the power-law summation was essentially winner-take-all. Figure 3H shows the speed tuning curves for one of these neurons. This fitting exercise shows that the interaction between the components of bidirectional patterns could in general not be captured by power-law summation. To understand why, we investigated how this interaction was affected by firing rate, direction selectivity, and speed tuning.

Suppression and facilitation.

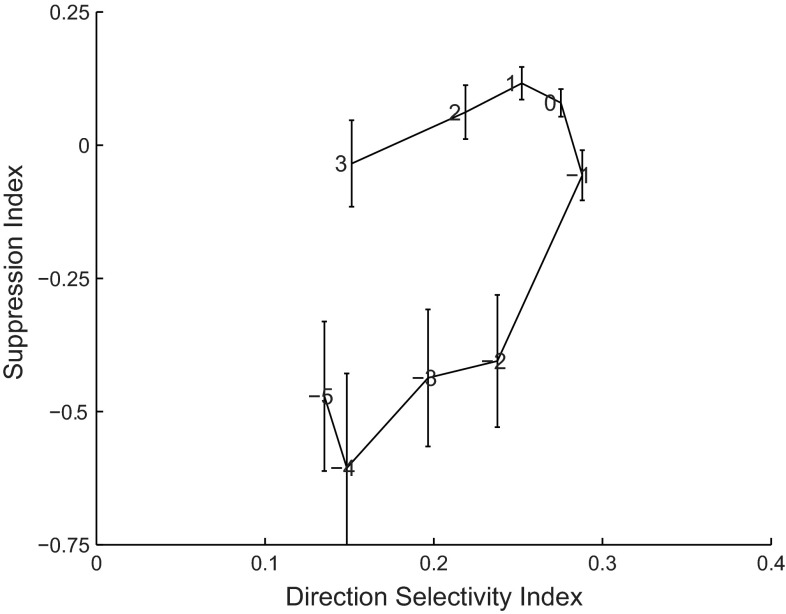
The first study to investigate bidirectional transparent motion in the macaque brain reported mainly suppressive effects (Snowden et al. 1991), which those authors defined as a response to bidirectional motion that was reduced compared with unidirectional preferred motion. We followed their convention and defined an index [suppression index (SI)] as 1 − B/P, where B corresponds to the bidirectional response and P to the unidirectional preferred direction response. We calculated SI for each Δspeed as well as the DSI for each Δspeed. Figure 5 represents the median SI across neurons as a function of DSI (x-axis), while maintaining the dependence on Δspeed (shown as a label near the data point). Clearly, SI typically increased with DSI. (Note that DSI appears relatively low due to the fact that it is an average over the variability induced by different test speeds and because spontaneous firing rate is included in our definition of DSI. The first paragraph of results documents the direction selectivity of these cells.) The fact that the SI depended on DSI is not surprising, as motion opponency increases direction selectivity (Adelson and Bergen 1985; Krekelberg 2008; Krekelberg and Albright 2005) and should increase suppression for bidirectional motion stimuli.

Fig. 5.

Suppression and enhancement. Data points show the median suppression index (SI; y-axis) as a function of the median direction selectivity index (DSI; x-axis). These averages were determined after aligning the tuning curves to the preferred speed (i.e., based on the data shown in Fig. 6B); this allows us to label each data point with the difference between stimulus speed and preferred speed (Δspeed). Error bars show SE across the population. This figure shows that SI depends both on DSI and on Δspeed: suppression increased with direction selectivity but, in addition, decreased for speeds further from the preferred speed.

However, the mapping from DSI to SI is not one-to-one, which implies that stimulus speed also affected the SI. For example, given approximately equal DSI (e.g., 0.2), responses to bidirectional patterns with speeds below the preferred speed (Δspeed = −2) were facilitated (SI < 0), while responses to bidirectional patterns above the preferred speed (Δspeed = 2) were suppressed (SI > 0). This effect is partially captured by the statement that suppression is larger near the preferred speed (Δspeed ∼0) and drops off for speeds above (Δspeed > 0) or below (Δspeed < 0) the preferred speed. For speeds well below the preferred speed the suppression turns into facilitation. A third effect can be inferred from Fig. 5 and Fig. 6: suppression was weaker when firing rates for the preferred and antipreferred motions were lower.

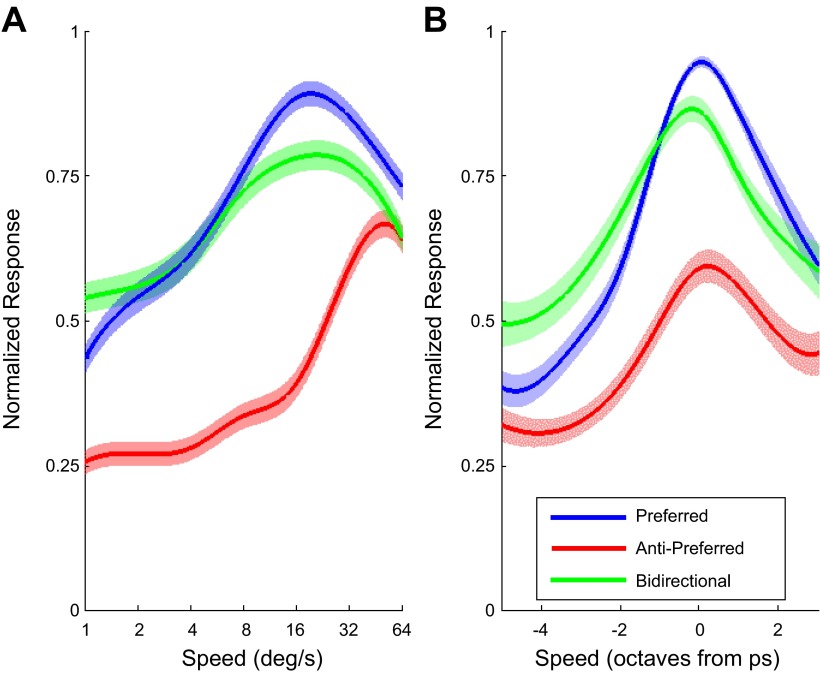
Fig. 6.

Population average speed tuning. A: normalized firing rate averaged over all cells (n = 126). Consistent with the cell-by-cell comparison, bidirectional patches sometimes evoke reduced responses (especially near the preferred speed) but sometimes enhanced responses (at low speeds). B: normalized firing rate after aligning the preferred speeds of each cell. The response to bidirectional patterns was suppressed near the preferred speed and enhanced at lower speeds and showed a reduction in preferred speed.

To quantify these three relationships we determined the linear partial correlation between SI, DSI, Δspeed, and the sum of the response to the preferred and antipreferred stimulus. Suppression was primarily determined by DSI (r = 0.47, P < 0.001), next by the summed firing rate (r = 0.36, P < 0.001), and to a lesser, but statistically significant extent by the difference between the test speed and the preferred speed (r = 0.11, P < 0.005). In words, the data show that the response to bidirectional patterns was suppressed more when they moved at speeds for which the neuron had high direction selectivity, more for speeds that evoked a high firing rate, and more for speeds near the preferred speed. These effects can also be seen in the averaged responses, which we present next.

Average responses.

Figure 6A shows the median normalized response of our sample of MT neurons (all neurons; n = 126) for each speed and in the three motion conditions (uni-pref, uni-anti, bi). This confirms that for some speeds the response to bidirectional patterns is suppressed compared with unidirectional motion in the preferred direction. At low speeds, however, the population response was enhanced in the bidirectional condition.

The speed dependence of suppression is seen more clearly in Fig. 6B, which shows the sample average after aligning the preferred speeds of all cells. Note that, to use the entire population, we defined preferred speed here nonparametrically as the speed that induced the largest response. Using the parametric definition (i.e., Fig. 4C) on the subset of cells that were significantly tuned resulted in a qualitatively similar graph (not shown). Here, we clearly see an enhanced response at low speeds and a suppressed response near the preferred speeds. However, it is also clear from these figures that DSI varied considerably across speeds. Typically DSI was small at low speeds and peaked near the preferred speed. Hence another valid description of the responses to bidirectional patterns is that they are suppressed when neurons are strongly direction selective and enhanced when they are weakly direction selective. The cell-by-cell analysis above quantifies the relative strength of speed tuning, direction selectivity, and the strength of the response on suppression.

Linking Neural and Behavioral Data

Qualitatively, the reduced dynamic range for bidirectional stimuli (Fig. 4B) should result in a loss of sensitivity, and the labeled line decoder predicts that a reduction of the preferred speed for bidirectional stimuli (Fig. 4C) results in an increase of perceived speed. The goal of this section is to make these links quantitative by using a labeled line population decoding algorithm in which each neuron votes for its preferred speed with a weight proportional to its firing rate (see materials and methods).

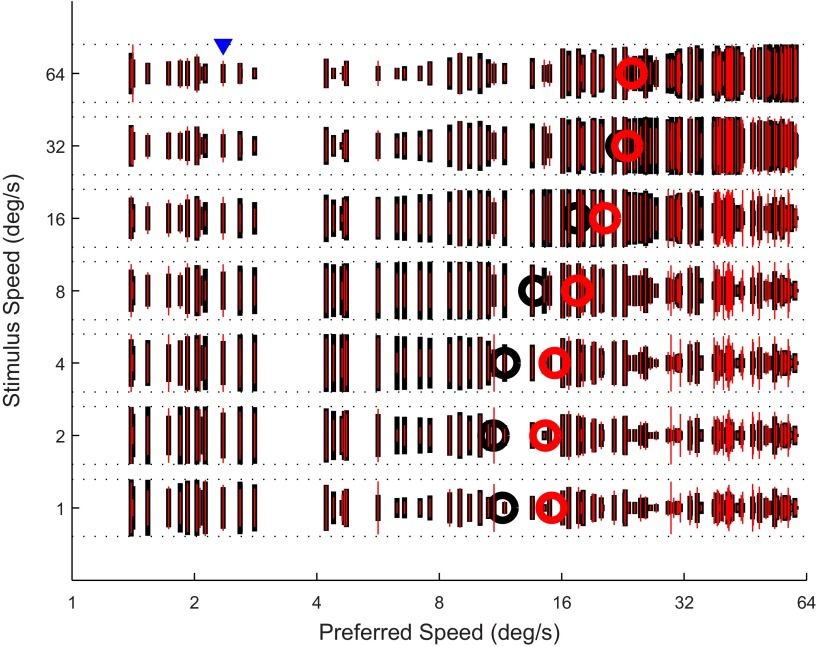
Figure 7 shows the population activity that the decoder used to determine stimulus speed. Specifically, Fig. 7 shows the response of our MT sample to uni- and bidirectional stimuli at seven different speeds. In terms of the decoder, the number along the x-axis corresponds to the label and the length of the vertical lines represents the vote for that label. Clearly, at slow stimulus speeds there were many votes for slow labels (Fig. 7, bottom left), while at high stimulus speeds the votes were predominantly for fast labels (Fig. 7, top right). The circles in Fig. 7 represent the decoded speed for each stimulus speed for unidirectional (black) and bidirectional (red) patterns. The decoder generally overestimated the speed of slow stimuli, while it underestimated the speed of fast stimuli. This is a consequence of the boundaries (e.g., none of our neurons had a preferred speed above 64°/s or below 1°/s; hence our decoder could never decode a speed above 64°/s or below 1°/s) and the fact that more neurons in our sample preferred fast speeds than slow speeds. These decoding biases are well known (Krekelberg et al. 2006b; Priebe and Lisberger 2004); we ignore them here by focusing on decoding relative speeds mainly from the center of the speed range (see discussion).

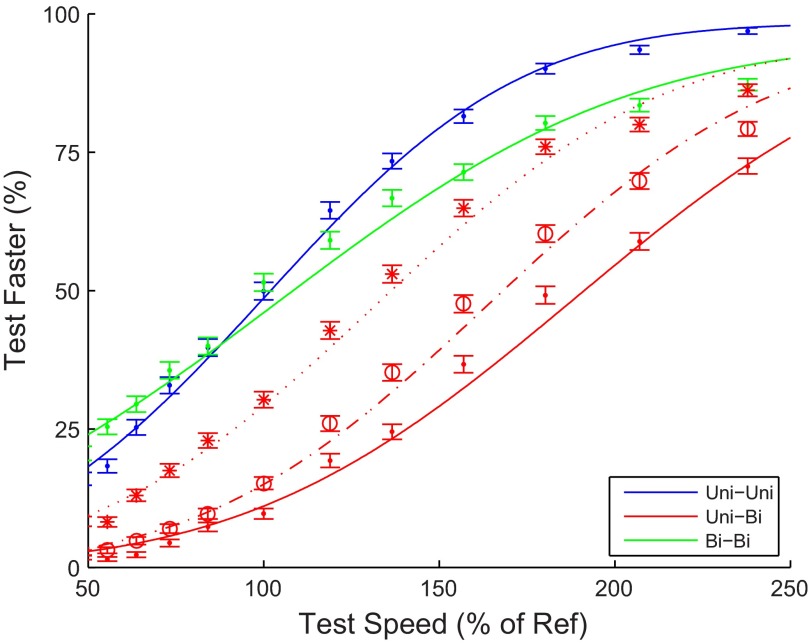
Fig. 7.

MT population activity in response to uni- and bidirectional motion patterns. Each vertical line represents the activity of a single neuron in our sample. Black lines represent the response to unidirectional motion and red lines the response to bidirectional motion. Neurons are sorted by their preferred speed along the x-axis, and stimulus speed is represented along the y-axis. As an example, the arrowhead highlights the response of a neuron with a preferred speed just above 2°/s to stimuli moving at 64°/s. Its response to unidirectional motion (black vertical line) is much less than its maximum response (indicated by horizontal dashed lines). The vertical red line shows that this neuron responds more strongly to bidirectional motion (at 64°/s). (Black lines are thick only to allow us to overlay the response to bidirectional motion with the thin red lines). The circles indicate the decoded speed for each stimulus as determined by the labeled line model (black, unidirectional motion; red, bidirectional motion). This graph shows how increasing the stimulus speed (bottom to top along y-axis) shifts the population activity from low-speed-preferring neurons to high-speed-preferring neurons (left to right along x-axis). This underlies the model's ability to decode speed from the population.

In our first decoder, we equated a neuron's label with its preferred speed for unidirectional motion, generated population responses like those shown in Fig. 7, decoded the speed for a test and a 10°/s reference stimulus, and compared those two decoded speeds to answer the question “Which was faster, the test or the reference?” In terms of Fig. 7 this corresponds to a comparison of two of the circles at different speeds (y-axis), e.g., a black and a red circle for a comparison of uni- and bidirectional motion and two black circles for a uni-uni comparison. Repeating this procedure in 1,000 simulated trials with independent Poisson noise for each neuron resulted in the data points shown as solid circles in Fig. 8. The solid curves show the neurometric curves fitted to these data points. The neurometric curve for bi-bi comparisons (green) was shallower than the curve for uni-uni comparisons (blue). This demonstrates a lower sensitivity for bidirectional than unidirectional motion. Numerically, the slope at the PSE was 0.007 for uni-uni and 0.005 for bi-bi, a 29% loss in sensitivity.

Next, we compared the PSEs. For uni-uni comparisons the PSE was at 101% and for bi-bi comparisons 102%, indicating that the decoder had no bias for such comparisons. For the uni-bi comparisons, however, (red solid line in Fig. 8), the PSE was 189%, showing a large overestimation of the speed of bidirectional motion. (A unidirectional pattern would have to move 89% faster to be decoded as the same speed as a bidirectional pattern).

The choice of each neuron's label in this labeled line decoder is somewhat arbitrary. For instance, one could argue that in a visual system exposed to natural motion, which includes bidirectional motion, the labels should not only be determined by unidirectional motion. As a simple exploration of this possibility, we investigated what would happen if the labels were instead determined by the average of the two motion types (see materials and methods). This decoder still had less sensitivity for bi-bi comparisons than for uni-uni comparisons (10% loss in sensitivity; not shown), and the decoder's PSE for the uni-bi comparison was 163% (dashed-dotted red line in Fig. 8). Finally a decoder based on labels defined by the preferred speed to bidirectional patterns had a slightly increased sensitivity for bi-bi comparisons (5%; not shown) but nevertheless overestimated the speed of bi- compared with unidirectional patterns (PSE 132%; dotted red line in Fig. 8).

Taken together, these decoder simulation results show that reasonable assumptions about the labels used to decode MT are compatible with a loss of sensitivity for bidirectional motion on the order of 25% and an overestimation of the speed of bidirectional patterns on the order of 50%. These estimates are compatible with the measured perceptual effects in Fig. 2. The monkey's sensitivity loss was 23%, and we estimated his overestimation of bidirectional speeds to be 20%. For the human subjects, the sensitivity loss varied between 18% and 50% (quartile range across all data in Fig. 2C) and the overestimation of the speed of bidirectional motion varied between 43% and 76% (quartile range across all data in Fig. 2B). As can be inferred from Fig. 7, however, the decoder predicted that the perceived speed difference between uni- and bidirectional patterns diminishes with increases in the test speed. The behavioral data did not show this effect (Fig. 2B). We return to this issue in discussion.

DISCUSSION

Our behavioral data confirm earlier findings that the speed of bidirectional motion is more difficult to discriminate (Verstraten et al. 1996) and perceived to be faster (De Bruyn and Orban 1999) than unidirectional motion. The speed tuning of neurons in macaque area MT also differed greatly when measured with unidirectional motion or bidirectional motion. Notably, the neurons had a reduced dynamic range and generally preferred lower speeds in the bidirectional motion patterns. Unlike previous reports, we found that the response to bidirectional patterns could be suppressed or enhanced compared with the unidirectional preferred pattern and that this depended on the neurons' direction selectivity, speed preference, and overall firing rate. We were able to link these complex neural responses to our behavioral characterization of perceived speed by a simple labeled line decoder. Just like the human and monkey observers, the decoder performed with high sensitivity for unidirectional patterns, was less sensitive for bidirectional motion, and overestimated the speed of bidirectional motion.

After discussing low-level confounds and alternative interpretations, we discuss the novel insights that our data provide into the processing of transparent motion per se, as well as the relationship between neural activity in MT and the perception of speed.

Alternative Interpretations

Under some conditions—for instance, to make sense of the optic flow created by self-motion—relative motion is more informative than absolute motion. If a neuron encoded relative speed, then the response to a 2°/s bidirectional stimulus should correspond to a 4°/s unidirectional stimulus. In other words, the relative speed assumption predicts a leftward shift of the speed tuning curve by precisely 1 octave. Figure 3C is an example of a neuron that matches this prediction. The overview in Fig. 4C, however, shows that while shifts in preferred speed are predominantly leftward their magnitude is quite variable across the population and the 1-octave shift predicted by the relative speed model does not appear to be particularly common. Hence, our data do not support the idea that MT cells generally respond to relative speed. Determining whether a subset of cells (such as the example cell in Fig. 3C) do represent relative motion would require a more extensive sampling of different combinations of stimulus speeds and directions.

In principle, the substantial inhomogeneities in directional preference across the RF we recently reported (Richert et al. 2013) could contribute to differences in the response to unidirectional and bidirectional stimuli. However, because we repeated each condition on average 12 times, and each repeat consisted of a new set of dots whose starting positions were randomized within the 10° aperture, such variability should average out across multiple trials.

Competitive Interactions in Transparent Motion

Previous work has shown that the percept of transparent motion does not require multiple activity peaks (corresponding to the directions of motion) in the MT population. Instead, the percept of transparent motion can be extracted from the overall pattern of population activity without the need for distinct peaks (Treue et al. 2000). Generation of such patterns of activity can be achieved in models that rely on a local competition between the neurons representing multiple directions of motion (Qian and Andersen 1994; Qian et al. 1994). Neural signatures of competition have been described as a suppression of the neural response to bidirectional motion patterns compared with unidirectional motion in the preferred direction (Snowden et al. 1991; van Wezel et al. 1996). Our examination of bidirectional motion across a range of speeds, however, revealed a much richer repertoire of interactions between opposing directions of motion. These could be understood as the competitive interaction among multiple components that presumably arises as an emergent property of the recurrently connected neural network for motion detection (Grossberg 1973; Krekelberg and Albright 2005).

Our finding that suppression was mainly found near the preferred speed, while enhancement dominated for suboptimal speeds, is reminiscent of the contrast dependence of normalization (Heuer and Britten 2002): two stimuli that each provide weak drive to a neuron sum supralinearly, while stimuli that provide strong drive interact sublinearly. Our analysis of power-law summation, however, shows that a model based solely on untuned normalization cannot capture the complexity found here. The partial correlation analysis clarifies that the response to bidirectional motion of a given speed is determined by the direction selectivity, the total response to each of the unidirectional components, as well as the speed tuning. Hence, a model to capture this complexity would have to be tightly linked with a model for direction selectivity (to explain the dependence on DSI), normalization (to explain the dependence on the total firing rate), and speed tuning (to explain the explicit dependence on the test speed).

Linking with Perception

Our findings add support to the claim that speed perception and neural activity in area MT are causally related via a labeled line decoder. This decoder, however, is far from perfect. Notably, taken at face value, the decoder incorrectly predicted biases in decoding absolute speed (none of the circles in Fig. 7 matches the stimulus speed) and a decrease of the perceived relative speed of uni- and bidirectional patterns with stimulus speed (black and red circles in Fig. 7 move closer together with increasing stimulus speed). At least in part, these decoding errors are due to the overabundance of neurons with high preferred speeds and the absence (in our sample) of neurons with preferred speeds above 64°/s. Such unequal distributions of the label necessarily introduce biases in labeled line decoding (Krekelberg et al. 2006b; Priebe and Lisberger 2004), although they can be reduced by using a weighted and/or nonlinear average across the population (Salinas and Abbott 1994). By focusing our decoding analysis on the center of the range of preferred speeds in our sample, we minimized the influence of these effects and found a good match with the behavioral data in that same range. The visual system, however, has to cope with the full range of speeds in the environment, and it is not clear how it avoids boundary effects (if it uses labeled line decoding). This highlights a conceptual difference between labeled line decoding of a sensory variable that has no boundaries (e.g., direction) and one that has boundaries (e.g., speed has boundaries at zero and at the highest preferred speed in the population). Labeled line averaging works well in the former but can be problematic in the latter sensory domain.

In previous work we have shown that the change in perceived speed induced by manipulating stimulus contrast of random dot patterns is not captured by a labeled line model in area MT (Krekelberg et al. 2006b). Although it is far from the only argument against a labeled line for speed (see introduction), it is clearly the odd one out of studies based on visual illusions. The present study does not resolve this discrepancy, but it does suggest that the influence of stimulus contrast on speed perception may be a special case.

In this context, we note that a striking effect of luminance contrast on neural responses in the visual system is the increase in response latency at low contrasts. Such response latency differences are typically not found in the other manipulations that lead to speed misperceptions (e.g., adaptation, stimulus size, or bidirectional motion). Hence it seems possible that an extension of the labeled line model that takes the latency of the response into account could be fruitful (Chase and Young 2007; Gawne et al. 1996). We note, however, that response latency depends not only on contrast but also on speed and direction tuning, surround interactions, and the magnitude of the response (Raiguel et al. 1989, 1999). Experimentally it is not feasible to control each of these variables independently, which hampers the isolation of a single underlying quantity that identifies perceived speed. Of course, this raises the question of how the brain manages to do so, given that these same confounds exist in everyday life as well. Our findings show that the labeled line model fares well under very constrained conditions (the comparison of bi- and unidirectional patterns of moving dots). Similarly, variants of the labeled line model have been shown to explain the influence of other isolated stimulus manipulations [e.g., apparent motion (Churchland and Lisberger 2001), adapted motion (Krekelberg et al. 2006a), accelerated motion (Schlack et al. 2007), stimulus size (Boyraz and Treue 2011)]. Even though each of these studies used a labeled line model, they are subtly different in the definition of the label, as well as the measure of neural activity that is used in the decoder. Hence it is not clear that a single model could explain all of these data sets in a quantitative manner. The true challenge remains to develop a single model that relates neural activity (in MT or elsewhere) to the perceived speed of natural stimuli in a manner that explains how nuisance features such as luminance, contrast, size, motion direction, and transparency affect the percept of speed.

GRANTS

This research was supported by the National Eye Institute under award number R01 EY-017605.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).

AUTHOR CONTRIBUTIONS

Author contributions: B.K. and R.J.A.v.W. conception and design of research; B.K. and R.J.A.v.W. performed experiments; B.K. and R.J.A.v.W. analyzed data; B.K. and R.J.A.v.W. interpreted results of experiments; B.K. and R.J.A.v.W. prepared figures; B.K. drafted manuscript; B.K. and R.J.A.v.W. edited and revised manuscript; B.K. and R.J.A.v.W. approved final version of manuscript.