Rat primary auditory cortex is tuned exclusively to the contralateral hemifield

Abstract

The rat is a widely used species for study of the auditory system. Psychophysical results from rats have shown an inability to discriminate sound source locations within a lateral hemifield, despite showing fairly sharp near-midline acuity. We tested the hypothesis that those characteristics of the rat's sound localization psychophysics are evident in the characteristics of spatial sensitivity of its cortical neurons. In addition, we sought quantitative descriptions of in vivo spatial sensitivity of cortical neurons that would support development of an in vitro experimental model to study cortical mechanisms of spatial hearing. We assessed the spatial sensitivity of single- and multiple-neuron responses in the primary auditory cortex (A1) of urethane-anesthetized rats. Free-field noise bursts were varied throughout 360° of azimuth in the horizontal plane at sound levels from 10 to 40 dB above neural thresholds. All neurons encountered in A1 displayed contralateral-hemifield spatial tuning in that they responded strongly to contralateral sound source locations, their responses cut off sharply for locations near the frontal midline, and they showed weak or no responses to ipsilateral sources. Spatial tuning was quite stable across a 30-dB range of sound levels. Consistent with rat psychophysical results, a linear discriminator analysis of spike counts exhibited high spatial acuity for near-midline sounds and poor discrimination for off-midline locations. Hemifield spatial tuning is the most common pattern across all mammals tested previously. The homogeneous population of neurons in rat area A1 will make an excellent system for study of the mechanisms underlying that pattern.

previous psychophysical studies have evaluated the ability of carnivores, humans, and other primates to identify or discriminate the locations of sounds (e.g., Heffner and Masterton 1975; Jenkins and Masterton 1982; Makous and Middlebrooks 1990; May and Huang 1996; Nodal et al. 2008; Populin 2006; Tollin et al. 2005). Generally, these species show highest spatial acuity for locations straddling the frontal midline, but they also can discriminate locations within a lateral hemifield (Brown et al. 1982; Heffner and Heffner 1988a, 1990; Kavanagh and Kelly 1987; Middlebrooks and Onsan 2012; Recanzone et al. 1998; Recanzone and Beckerman 2004). In rats spatial acuity around the frontal midline is high like that of other tested animals, but unlike carnivores and primates rats fail to discriminate among lateral locations (Kavanagh and Kelly 1986).

Results from carnivores and primates indicate that firing patterns of cortical neurons can signal sound source locations throughout most of auditory space (e.g., Middlebrooks et al. 1994, 1998; Miller and Recanzone 2009). Here we have examined the spatial sensitivity of neurons in cortical area A1 of the rat. We wished to test the hypothesis that the failure of rats to distinguish lateral source locations is mirrored by an absence of off-midline spatial discrimination by responses of cortical neurons. A second motivation was to obtain descriptive data characterizing cortical spatial sensitivity that would support future study of the cortical mechanisms of spatial hearing in a preparation amenable to modern intracellular, optical imaging, and optogenetic methodologies.

Results demonstrated that every sampled neuron displayed a spatial receptive field favoring the contralateral hemifield, that most showed steepest cutoffs within ∼20° of the midline, and that all showed weak or no responses throughout most of the ipsilateral hemifield. Contralateral-hemifield spatial tuning is the most common pattern seen in the mammals that have been studied thus far. The presence of a largely homogeneous population of neurons showing such spatial tuning in rat A1 will facilitate future study of the mechanisms that underlie that pattern of spatial tuning.

MATERIALS AND METHODS

Animal Preparation

Data presented here are from 15 adult male Sprague-Dawley rats (median age: 18.5 wk) (Charles River Laboratories, Hollister, CA) weighing 245–430 g (median weight: 360 g). All procedures were performed with the approval of the University of California at Irvine Institutional Animal Care and Use Committee according to National Institutes of Health guidelines. Surgical anesthesia was induced with urethane (1.5 g/kg ip) and xylazine (10 mg/kg ip) and supplemented at ∼1-h intervals as needed to maintain an areflexive state. Atropine sulfate (0.1 mg/kg ip) and dexamethasone (0.25 mg/kg ip) were administered at the beginning of the surgery and every 12 h thereafter to reduce the viscosity of bronchial secretions and to prevent brain edema, respectively. Core body temperature was monitored with a rectal thermometer and maintained at ∼37°C with a warm-water heating pad. Respiratory rate, heart rate, and front paw withdrawal reflexes were monitored to ensure that a moderately deep anesthetic state was maintained as uniformly as possible throughout recordings.

A midline incision was made, and the skull was cleared. A flat-head machine screw was fastened to the skull, screw head down, with skull screws and dental acrylic cement. The machine screw was used to support the rat's head. The temporal bone was exposed by partially removing the temporalis muscle. A craniotomy was performed, and the exposed brain was kept moist. Experiments lasted ∼6–18 h.

Experimental Setup and Stimulus Generation

The experimental setup and stimulus generation techniques used here were similar to those described in earlier reports from this lab (Harrington et al. 2008; Middlebrooks et al. 1998; Middlebrooks and Bremen 2013; Stecker et al. 2003, 2005a). Stimulus presentation and data acquisition used System 3 equipment from Tucker-Davis Technologies (TDT, Alachua, FL) controlled by a personal computer running custom MATLAB scripts (The MathWorks, Natick, MA). The animal was positioned in the center of a double-wall sound-attenuating chamber, which was lined with 60-mm-thick absorbent foam (SONEXone, Seattle, WA). The rat's head was supported from behind with a 10-mm-diameter rod that was attached to the screw that was mounted to the head. The area around the head and ears was unobstructed. Sounds were presented one at a time from 8.4-cm two-way coaxial loudspeakers (Pioneer Electronics, Long Beach, CA) that were located 1.2 m from the rat's head and spaced 20° apart on the ear-level horizontal plane. Loudspeaker locations are expressed in degrees of azimuth relative to the loudspeaker directly located in front of the rat's head (0°). Negative azimuths were on the left, contralateral to the right-sided recording sites. The loudspeakers were calibrated to flatten and equalize their frequency responses (Zhou et al. 1992). All stimuli were generated with 24-bit precision at a 97.7-kHz sampling rate. Stimuli were 80-ms Gaussian noise bursts with abrupt onsets and offsets or 80-ms pure tones with 5-ms raised-cosine onset/offset ramps. Noise and tone bursts ranged from −10 to 70 dB SPL and varied in 10-dB steps. Tone frequencies ranged from 1 to 40 kHz.

Experimental Procedure

Extracellular spike activity was recorded with single-shank silicon-substrate probes having sixteen 413-μm² recording sites spaced at 100-μm intervals (NeuroNexus, Ann Arbor, MI). Neural waveforms were digitized and stored for off-line analysis. The 16-channel probes were positioned with cortical surface landmarks, verified by functional properties described below. The probe was aligned visually to be as orthogonal as possible to the cortical surface prior to advancement into the cortex and subsequently was adjusted in depth to maximize the number of recording sites in active cortical layers. Typically, neural spike activity was limited to 12–14 sites, with the most superficial and the deepest 1 or 2 sites lying outside of the cortical gray matter. Neural spikes were detected online for monitoring purposes, although all reported results are based on spikes that were identified off-line, as described in Data Analysis.

At each recording probe location, the characteristic frequencies (CFs) of neurons were estimated with pure tones. Cortical area A1 was distinguished from neighboring auditory areas by brisk short-latency responses to noise bursts (latencies ∼10–15 ms), V-shaped frequency tuning curves, and a caudal-to-rostral increase in CFs (see, e.g., Polley et al. 2007; Sally and Kelly 1988). The borders of A1 were defined by reversals in tonotopy and increases in latencies (Doron et al. 2002; Rutkowski et al. 2003). After a probe was positioned in A1 at a desired position in the tonotopic map, the cortex was covered with warmed 2% agarose in Ringer solution. The agarose cooled to form a gel that reduced brain pulsations and kept the cortical surface moist. Frequency response areas (FRAs) were measured with pure tones presented at a rate of 1/s from the loudspeaker at −40°. The tones varied in frequency in 1/6-octave steps from 1 to 40 kHz and in level in 10-dB steps, typically from 0 to 60 or 70 dB SPL, 10 repetitions at each combination of frequency and level. Off-line, the CF of each unit was defined by the frequency that evoked a reliable response that was significantly greater than spontaneous activity at the lowest sound level.

The spatial sensitivity of each unit was measured with a stimulus set that consisted of 80-ms noise bursts presented at a 1/s repetition rate from 18 locations in the horizontal plane (−180° to 160°, in 20° increments), varying in 10-dB level steps, typically from 0 to 60 or 70 dB SPL, with 15–40 repetitions per level. A silent condition also was included for the purpose of measuring spontaneous activity. Sounds at every combination of location and level were presented once in a random order during each repetition. Collection of the data reported here was accomplished in ∼2.5 h at each recording probe placement. Experiments yielded data from one to five probe placements per animal.

Data Analysis

Spike sorting.

Neural action potentials were discriminated on the basis of waveform shapes with off-line spike-sorting procedures (Kirby and Middlebrooks 2010; Middlebrooks 2008). Of the 168 units studied, 18 (11%) were classified as well-isolated single units and 150 (89%) consisted of unresolved spikes from two or more neurons. We did not observe differences between tuning properties calculated from the single units or multiunits across any measure of spatial sensitivity at any suprathreshold level (K = 0.14–0.33, P = 0.11–0.95, 2-sample Kolmogorov-Smirnov test) and therefore use the term “unit” to refer to both. The unit count did not include the small number of units that were excluded from the analysis because they responded with less than an average of one spike per trial to their most effective stimulus or with a maximum spike rate less than 2 standard deviations above their spontaneous rates. Spike times were stored as latencies relative to the estimated time of arrival of sound at the animal's head, i.e., stimulus onset was taken as the time of onset of sound at the loudspeaker plus the 3.5-ms acoustic travel time from each loudspeaker to the location of the center of the rat's head. Most responses to noise bursts consisted of bursts of spikes restricted to a range of >10 to ∼40 ms after stimulus onset. Spikes were counted in the 10- to 80-ms interval after the onset of each stimulus.

Discrimination of sound source locations with a linear discriminator model.

We used procedures based on signal detection theory (Green and Swets 1966; Macmillan and Creelman 2005) to estimate excitation thresholds and thresholds for discrimination between pairs of stimulus locations. In both cases, we accumulated spike counts for all repetitions of each of two stimuli. An empirical receiver operating characteristic (ROC) curve was formed from those two distributions. The area under the ROC curve gave the proportion of trials in which a particular stimulus elicited more spikes than the other stimulus. That proportion was expressed as a z score, and the z score was multiplied by √2 to yield the discrimination index, d′ (Green and Swets 1966; Macmillan and Creelman 2005; Middlebrooks and Snyder 2007). When the area under the ROC curve was 1.0 (and the corresponding z score was undefined), d′ was written as 2.77, corresponding to 97.5% correct discrimination. Magnitudes of d′, therefore, could range between 0 (chance-level discrimination) and 2.77. A d′ value of 1 indicates a one-standard deviation separation of the means of the two distributions and is conventionally taken as the criterion for significant discrimination of two stimuli.

Excitation thresholds were estimated by computing d′ for successive increasing pairs of noise burst levels, plotting d′ versus sound level, and taking as threshold the interpolated sound level at which d′ = 1. Spatial discrimination thresholds were estimated by specifying a reference sound source location, computing d′ for successively increasing sound source separations, and interpolating with 1° resolution to find the separation at which d′ = 1. The minimum discriminable angle (MDA) was the minimum discrimination threshold for each unit observed across all reference locations. We also report the maximum d′ for each unit across all pairs of locations. The maximum d′ provides an indicator of the overall spatial sensitivity of a unit and has the advantage of incorporating both the stimulus-dependent mean and the trial-by-trial variance in maximum and minimum spike counts. A closely related measure is “modulation depth,” which is 100 × (Spk_max − Spk_min)/Spk_max for maximum and minimum spike counts Spk_max and Spk_min. We report modulation depth in addition to maximum d′ because modulation depth can be compared with a similar metric used in previous reports and because modulation depth provides a somewhat more intuitive measure of spatial sensitivity than maximum d′.

Locations of centroids and steepest slopes.

The preferred stimulus location of each unit was characterized by its spatial centroid (Middlebrooks et al. 1998), which was computed as follows. First, the peak of the rate-azimuth function (RAF) was identified by finding the range of one or more contiguous locations at which responses exceeded a criterion spike rate of 0.75 times the maximum spike rate. Then, the spike rate-weighted vector sum was computed from these peak locations plus the two flanking below-criterion locations (i.e., from a total of 3 or more locations). The angle of the resultant vector gave the spatial centroid. Units showing no more than 50% modulation of their spike rates throughout all tested locations were classified as having no centroid (NC).

The location of the steepest slope for each unit was determined by smoothing its RAF (circular convolution with a 40° boxcar). Slopes were given by the first spatial derivative of the smoothed RAF. We identified the location at which the slope magnitude was maximal.

Equivalent rectangular receptive field.

The spatial tuning of each unit was represented by the width of its equivalent rectangular receptive field (ERRF). The ERRF was computed by integrating the area under the RAF and reshaping it to form a rectangle of equivalent peak rate and area (see Supplementary Fig. 1 in Lee and Middlebrooks 2011). The ERRF width was favored over more conventional measures of tuning width because it reflects both the breadth of tuning and the depth of location-dependent spike rate modulation. Also, ERRFs are computed from responses to all stimulus locations. For that reason, they are less sensitive to trial-by-trial response variability than metrics that are based on particular criteria on RAFs (e.g., tuning width at half-maximal response).

Fig. 1.

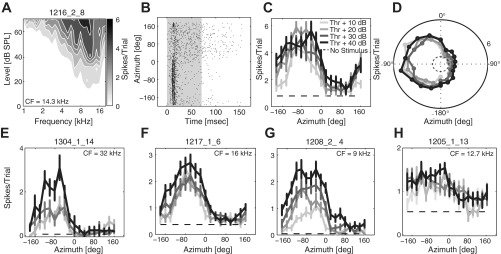
Examples of neural responses in rat A1. A–D: 1 example unit. A: contour plot of the frequency response area (FRA) plotted as the average spike count per trial in response to pure-tone stimulation varying in frequency (x-axis) and sound level (y-axis). Dark shades of gray indicate high spike rate. B: dot rasters of spike times (x-axis) elicited by noise stimuli at 40 dB above the unit's threshold, varying in azimuth (y-axis). Each dot in the plot represents 1 spike. Gray shading represents the stimulus duration. C: rate-azimuth functions (RAFs) of mean spike count per trial plotted against stimulus azimuth locations at levels 10, 20, 30, and 40 dB above threshold. D: the same responses from C, replotted in polar coordinates. E–H: RAFs from 4 additional units that represent the range of spatial tuning among cortical units with sharp spatial tuning (E) to slightly broad spatial tuning (H). Darker shades of gray represent higher stimulus levels above threshold. Dashed black lines represent spontaneous rate. Error bars indicate SE. Characteristic frequencies (CFs) are indicated for each example unit.

Tests of statistical hypotheses.

Data analysis employed custom MATLAB scripts (The MathWorks), incorporating the MATLAB Statistics Toolbox when appropriate. Multiple comparisons used the Bonferroni correction. Data sets for most measures were not normally distributed across units. For those measures, median and interquartile values were reported and nonparametric statistical tests were used for comparison across/between conditions. Distributions of ERRF widths were normally distributed, however, permitting characterization by means ± SE and parametric statistical tests.

To test for statistically significant correlations between the spatial sensitivity measures with CF, we performed a Spearman rank correlation analysis on the data set with 10,000 bootstrapped replications. For each replication we randomly drew with replacement 10 units per 1-oct CF bin from the sampled population. From these distributions of Spearman rank correlation coefficients (ρ), empirical two-tailed 98.75% confidence intervals (CIs) were calculated. A statistically significant relationship between CF and the tested metric at P < 0.05 (Bonferroni corrected for tests at 4 sound levels) was determined if zero fell outside the 98.75% CI.

RESULTS

Data were obtained from 168 units recorded from 22 probe placement sites in 15 animals. Across the sample, CFs ranged from 1 to >40 kHz (median = 14.3 kHz, interquartile range = 8.5–32 kHz); 10th and 90th percentiles were 4 and >40 kHz. The 15% of units that showed minimum thresholds at 40 kHz, the highest frequency that was tested, were designated as having CFs “>40 kHz” because we assume that a higher CF would have been seen had we tested at a higher frequency. The FRA of one unit with a CF of 14.3 kHz is shown in Fig. 1A. The response pattern of this unit to noise bursts presented at 40 dB above threshold and varying in azimuth is represented by a dot raster plot in Fig. 1B. This unit was representative of the entire sample in that it responded phasically to the onset of a noise burst and most strongly and with shortest latencies to sounds in the contralateral hemifield. Across the population of units, first-spike latencies for the most effective stimuli ranged from 10 to 15 ms (median = 12.5 ms).

Characteristics of Spatial Tuning

Spatial tuning is summarized in Fig. 1, C and D, for the unit represented in Fig. 1, A and B. At the highest sound level that was tested (40 dB above threshold), this unit had a centroid of −74°, steepest slope at −1°, an ERRF width of 200°, a modulation depth of 75%, and a maximum d′ of 2.66. Those values were comparable with the median or mean values across the population at 40 dB above threshold (centroid median: −69.8°, steepest slope location median: −1°, ERRF width mean: 195.9°, modulation depth median: 83%, maximum d′ median: 1.57).

The overall range of sharpness of spatial tuning is well represented by the RAFs of four units shown in Fig. 1, E–H. These examples are ranked from the unit showing the narrowest ERRF width (102°; Fig. 1E) to the unit having the broadest ERRF width (289.5°; Fig. 1H). The three units shown in Fig. 1, E–G, all possessed steepest slopes located around the frontal midline, and all showed maximum d′ values > 2. The most broadly tuned unit of the sample (Fig. 1H), in contrast, had maximum d′ values < 1 at all tested sound levels and a modulation depth < 50% at the highest tested sound level (40 dB above threshold). Although this unit did not possess a spatial centroid at this level, it showed the same general RAF shape as those of the other units. The other example units had centroids located in the contralateral field, toward the lateral pole. The similarity among the five example units in Fig. 1 and the entire population of sampled units indicates that the distribution of spatial tuning among units in rat area A1 was remarkably homogeneous, with RAFs consistently centered near the contralateral pole of the sound field, encompassing the contralateral hemifield, and steepest slope locations near the midline. Consistent with previous reports (e.g., Middlebrooks and Pettigrew 1981), we refer to this as “contralateral-hemifield” tuning.

The distributions of preferred azimuth locations (“centroids”) and steepest slope locations are depicted in Fig. 2. Large majorities of units (100%, 99%, 97%, and 94% at 10, 20, 30, and 40 dB above threshold, respectively) had modulation depths ≥ 50%, and therefore had measurable centroids. The <6% of units that had modulation depths < 50% responded with more than half of their maximum spike rates to sound sources throughout 360° of azimuth—those units are indicated as “NC” (for “no centroid”) in Fig. 2. Every unit preferred contralateral locations, toward the contralateral pole, regardless of stimulus level (Fig. 2, A–D: centroid medians: −75.4°, −75.1°, −76.3°, and −69.8°; interquartile ranges: −91.2° to −56.5°, −96.6° to −57.4°, −100.5° to −58.3°, and −95.2° to −55.9° at 10, 20, 30, and 40 dB above threshold, respectively), whereas the borders of the receptive fields, represented by steepest slope locations, were clustered around the frontal midline (Fig. 2, E–H: steepest slope medians: −1°, −1°, −1°, and −1°; interquartile ranges: −41° to 1°, −21° to 14°, −21° to 13°, and −21° to 9° at 10, 20, 30, and 40 dB above threshold, respectively). The distributions of centroids and steepest slope locations showed no significant differences across sound levels of 10, 20, 30, and 40 dB above threshold [centroids: χ_(3,651)² = 2.01, P = 0.57, Kruskal-Wallis; steepest slope locations: χ_(3,668)² = 4.97, P = 0.17, Kruskal-Wallis], indicating that the sampled population of units maintained their basic tuning properties across a 30-dB range of levels.

Fig. 2.

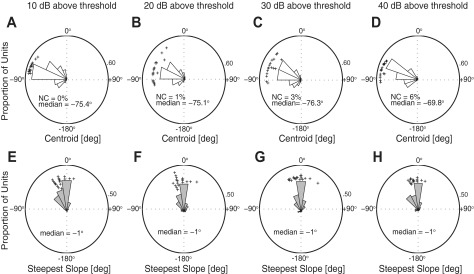
Distributions of azimuth centroids (A–D) and steepest slope locations (E–H) for noise burst stimuli presented at the stated sound levels. The area of each sector gives the proportion of units per 20° bin for centroids and steepest slope locations. Crosses represent data from well-isolated single units; radial distances of crosses are varied to improve readability. Plots are shown from an overhead perspective with 0° directly in front of the animal (frontal midline), −180° directly behind the animal, and −90° (+90°) on the left (right) of the animal. Percentage of units with no centroid (NC) and median values are given in the appropriate panels.

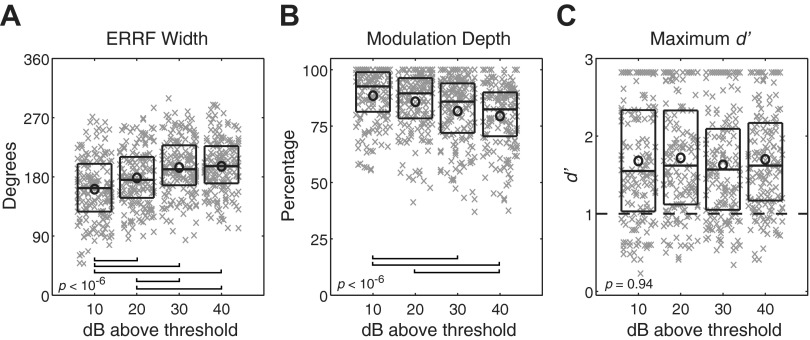
The breadth of spatial tuning of each unit was represented by the width of its ERRF (see materials and methods). The distributions of ERRF widths from the sampled population of units and across suprathreshold levels are shown in Fig. 3A. ERRF width means (±SE) at 10, 20, 30, and 40 dB above thresholds were 161.3° (±3.7°), 178.5° (±3.3°), 194.3° (±3.3°), and 195.9° (±3.2°), respectively. The spatial tuning broadened slightly with increasing sound level [F_(3,668) = 22.73, P < 10⁻⁶, ANOVA], with Bonferroni-corrected pairwise comparisons indicating significant broadening from 10 to 20, 30, and 40 dB above threshold as well as 20 to 30 and 40 dB above threshold (P < 0.05), as indicated in Fig. 3A. The only nonsignificant difference in ERRF width was between 30 and 40 dB above threshold.

Fig. 3.

Distributions of equivalent rectangular receptive field (ERRF) width (A), modulation depth (B), and maximum discrimination index d′ (C). For each box plot, horizontal lines forming the boxes indicate the 25th, 50th, and 75th percentiles. × Symbols indicate data from individual units, and circles represent the means. A random horizontal offset was added to each symbol to minimize overlap. P values shown in each panel indicate results of analysis of variance (A) or Kruskal-Wallis (B and C) tests. Horizontal bars at bottom of A and B indicate pairs of levels showing significant differences at the Bonferroni-corrected P < 0.05 level. In C, the horizontal dashed line indicates discrimination threshold of d′ = 1.

The magnitude of spatial sensitivity was represented by the depth of modulation of spike rate by azimuth (see materials and methods) and by the maximum d′ across all location pairs for each unit. Figure 3B displays the distribution of modulation depths at 10, 20, 30, and 40 dB above threshold, with medians of 93%, 90%, 86%, and 83% (interquartile ranges: 81–99%, 78–96%, 72–94%, and 71–90%), respectively. Modulation depth showed a small, but significant, decrease with increasing stimulus level [χ_(3,668)² = 29.88, P < 10⁻⁶, Kruskal-Wallis]. Bonferroni-corrected pairwise comparisons indicated significant differences between 10 and 30 dB above threshold, 10 and 40 dB above threshold, and 20 and 40 dB above threshold (P < 0.05), as indicated in Fig. 3B. Maximum d′ values were level invariant [χ_(3,668)² = 0.40, P = 0.94, Kruskal-Wallis], with medians of 1.55, 1.62, 1.57, and 1.62 (interquartile ranges: 1.03–2.34, 1.12–2.33, 1.05–2.10, and 1.17–2.17) at 10, 20, 30, and 40 dB above threshold, respectively (Fig. 3C). Maximum d′ was ≥1 for 75%, 80%, 75%, and 82% of units at 10, 20, 30, and 40 dB above threshold, respectively. Overall, the great majority of units in the sample showed robust, level-invariant, contralateral-hemifield spatial tuning.

Discrimination Between Azimuth Locations by Spike Count

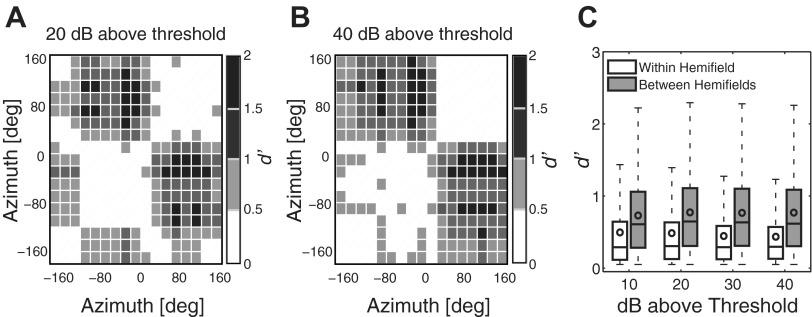
We tested the accuracy with which a linear discriminator could distinguish between azimuth locations on the basis of trial-by-trial distributions of spike counts (as described in materials and methods). The matrices in Fig. 4, A and B, show, for one unit, d′ for discrimination of every pair of locations at levels of 20 dB (Fig. 4A) and 40 dB (Fig. 4B) above threshold. Values of d′ ≥ 1 indicate significant discrimination between the compared spatial locations. Significant discriminations generally were high for comparisons between lateral hemifields (i.e., upper left and lower right quadrants in Fig. 4, A and B). In contrast, discriminations were relatively poor, as reflected by low d′ values, for comparisons within a hemifield (i.e, upper right and lower left quadrants in Fig. 4, A and B). The differences among within- and between-hemifield location discriminations are summarized in Fig. 4C across all units by the white and gray boxes, respectively. For all suprathreshold levels, pairwise comparisons between left and right hemifields yielded significantly higher d′ values than for comparisons within hemifields (Z = 39.3, 45.2, 51.7, and 51.8, P < 10⁻⁶, Wilcoxon rank sum at all suprathreshold levels). Note that while population median and mean values for between-hemifield comparisons were below d′ = 1, many location pairs for individual units exhibited values well above 1.

Fig. 4.

A and B: pairwise d′ matrices for corresponding pairs of stimulus locations for 1 example unit at 20 dB (A) and 40 dB (B) above threshold. Stimulus locations were separated by 20°. Darker shades of gray signify higher d′ values. Pairwise location comparisons with d′ values ≥ 1 indicate successful discrimination. C: distribution of all pairwise location comparison d′ values from all sampled units. Each box plot displays the distribution of d′ values for within- and between-hemifield location comparisons across suprathreshold levels, as indicated. Horizontal lines indicate the 25th, 50th, and 75th percentiles. Whiskers represent 1.5 times the interquartile range. Circles within the boxes indicate the means.

We estimated the spatial acuity of all units by finding the threshold sound source separation at which d′ was ≥1. Figure 5, A–D, display the distribution of threshold separations as a function of each reference location in the frontal field. In this plot, each data point represents the smaller of the threshold spatial separations to the left and right of the reference location. For each suprathreshold level, separation thresholds varied significantly across reference locations [χ_(8,857)² = 199.5, χ_(8,911)² = 201.7, χ_(8,857)² = 164.9, χ_(8,895)² = 178.7, P < 10⁻⁶, Kruskal-Wallis], with near-midline locations (0° and ±20°) showing significantly lower separation thresholds than locations within either lateral field (±40°, ±60°, and ±80°) (post hoc multiple comparison, Bonferroni corrected: P < 0.05). For each unit, the MDA was given by the narrowest threshold separation observed across all reference source locations. Distributions of MDA, across all units, are shown in Fig. 5, E–H, at each indicated suprathreshold level. Median MDAs at all suprathreshold levels were within the range of 35–40° (interquartile range: 20–67°), with no significant difference across sound levels [χ_(3,511)² = 1.72, P = 0.63, Kruskal-Wallis]. As an indication of the acuity of the most sensitive units, the 10th and 25th percentiles of MDAs ranged from 15° to 16° and from 20° to 25°, respectively, across all levels and CFs sampled.

Fig. 5.

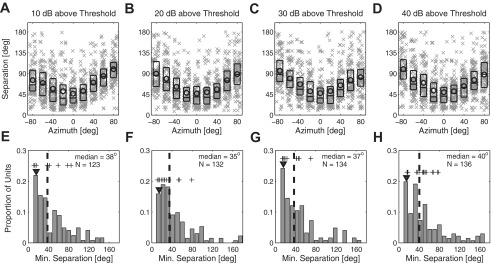
A–D: distribution of minimum separation thresholds (y-axis) as a function of a reference azimuth location in the frontal field (x-axis) across suprathreshold levels. Each × symbol represents a data point from 1 unit. Details regarding plot format are as described in Fig. 3. E–H: distribution of minimum discriminable angle (MDA) values across all units. Values on the y-axis give the total proportion of units per 10° bin. Vertical dashed lines indicate the medians. Downward arrowheads indicate the 10th percentiles. Crosses represent data from well-isolated single units. Median values and total number of units (N) are indicated in the appropriate panels. Each column represents a specific level above threshold, as indicated.

Spatial Sensitivity of First-Spike Latencies

Rat area A1 units exhibited spatial sensitivity of their first-spike latencies. Figure 6, A–D, plot the grand means of first-spike latency corresponding to all sound source locations for all sampled units at the indicated suprathreshold level. Generally, first-spike latencies were shorter for sound source locations in the contralateral field, with the steepest location-dependent increases in latency occurring across the frontal midline. This is inversely related to the higher spike rate responses to contralateral sounds (normalized grand means, Fig. 6, E–H). This inverse relationship was quantified by computing the Spearman ρ between normalized spike rate and first-spike latencies for each unit across all tested sound locations. The distributions of those coefficients are shown in Fig. 6, I–L. At each suprathreshold level, units demonstrated a strong negative correlation of first-spike latency and spike count (median ρ = −0.62, −0.63, −0.67, and −0.67; interquartile ranges: −0.79 to −0.38, −0.81 to −0.22, −0.82 to −0.44, and −0.83 to −0.47 for 10, 20, 30, and 40 dB above threshold, respectively).

Fig. 6.

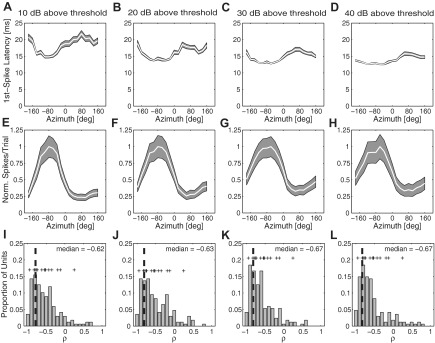
A–D: grand mean first-spike latencies as a function of azimuth sound location across suprathreshold levels, as indicated. E–H: grand mean spike rates (normalized spikes per trial) as a function of azimuth sound location across suprathreshold levels. White curves and shading in A–H indicate means and SE, respectively. I–L: distributions of Spearman rank correlation coefficients (ρ) between first-spike latency and spike count from all sampled units across suprathreshold levels. Values on the y-axis give the total number of units per bin of 0.10 on the x-axis. Vertical dashed line indicates the median. Crosses represent data from well-isolated single units.

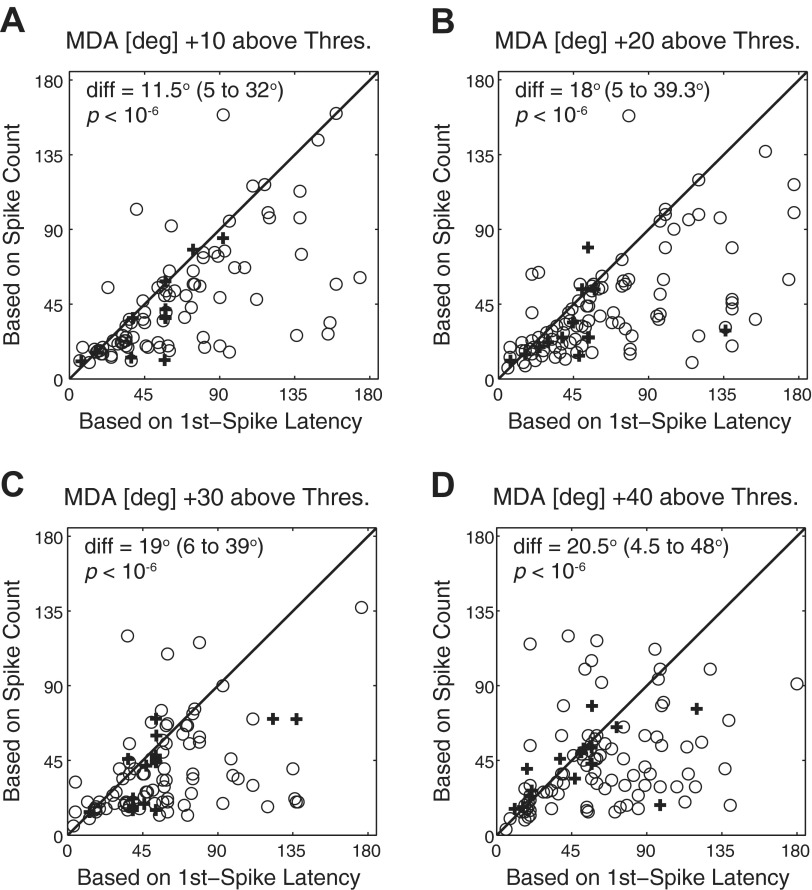
The strong correlations between first-spike latency and spike count suggest that the information conveyed by response latency is redundant with, or supportive of, the information conveyed by the modulation and distribution of spike counts. We further tested this notion by comparing the accuracy with which units could discriminate between azimuth locations on the basis of first-spike latency to spike count-based discriminations. Direct comparisons of MDAs for each unit on the basis of spike count versus first-spike latency are shown in Fig. 7, A–D, at 10, 20, 30, and 40 dB above threshold. Depending on the sound level, MDAs based on spike counts were 11.5–20.5° (medians) narrower than those based on latency; the difference was significant at all sound levels after Bonferroni correction (Z = −5.98, −6.60, −5.12, and −4.89, P < 10⁻⁶, Wilcoxon rank sum), as indicated in Fig. 7. Although this indicates that azimuth discrimination based on first-spike latencies was not as acute as that seen on the basis of spike count (Fig. 4), we note that spike counts and first-spike latencies shared the property that discrimination acuity was finer between hemifields than within a hemifield.

Fig. 7.

A–D: comparison of MDAs based on spike count (y-axis) vs. those based on first-spike latency (x-axis) for each unit at various levels above threshold, as indicated. The solid diagonal line indicates equal MDA derived from both measures. Median and interquartile range of the differences and P values for pairwise comparisons are indicated within each panel. Crosses and circles represent data points from well-isolated single units and multiunits, respectively.

Frequency Independence of Spatial Tuning Properties

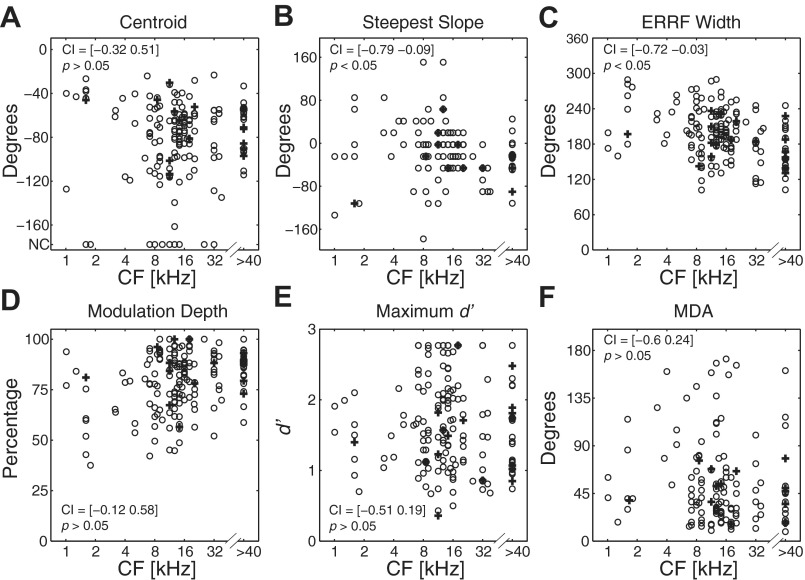
Our sample of unit CFs ranged from 1 to >40 kHz (>5 octaves), with half of the sample between 8.5 and 32 kHz; the upper boundary of the sample was determined by the calibrated frequency range of our speakers. For reference, the rat's behavioral audiogram shows greatest sensitivity from 8 to 40 kHz, thresholds within a ∼25-dB range from 1 to 40 kHz, and thresholds increasing sharply at frequencies <1 kHz and >40 kHz (Heffner et al. 1994; Heffner and Heffner 2007; Kelly and Masterton 1977). Scatterplots of spatial tuning metrics at 40 dB above threshold as a function of corresponding unit CF are shown in Fig. 8. As described in materials and methods, we performed a Spearman rank correlation analysis with 10,000 bootstrapped replications in order to test for statistically significant correlations between spatial tuning metrics and CF. Across all tested levels, only the data at 40 dB above threshold showed slight but significant correlations of more contralateral steepest slope location and narrower ERRF width with increasing CF (steepest slope locations: CI = [−0.79 −0.09], P < 0.05; ERRF widths: CI = [−0.72 −0.03], P < 0.05; Spearman rank correlation; Bonferroni-corrected for tests at 4 sound levels). No significant correlation existed for steepest slope location and ERRF width at 10-, 20-, or 30-dB levels or for any other spatial tuning metric at any tested level (P > 0.05; Spearman rank correlation; Bonferroni-corrected for tests at 4 sound levels). This indicates that the spatial tuning properties of neurons in rat area A1 are largely frequency independent across the rat's audible range.

Fig. 8.

Spatial tuning metrics as a function of units' CF (kHz). Each panel displays a scatterplot of a spatial tuning metric (centroid, A; steepest slope, B; ERRF width, C; modulation depth, D; maximum d′, E; MDA, F) at 40 dB above threshold on the y-axis as a function of corresponding unit CF on the x-axis. Crosses and circles represent data points from single units and multiunits, respectively. Empirical 2-tailed 98.75% confidence intervals (CIs) from the bootstrapped distribution of Spearman rank correlation coefficients and corresponding P values are indicated within each panel.

DISCUSSION

Spatial Representation in Rat Primary Auditory Cortex

The present results demonstrate that neurons in rat area A1 display contralateral-hemifield tuning across a 30-dB range of suprathreshold sound levels. The distribution of spatial tuning is homogeneous, showing little systematic variation across the sample of units within area A1. A linear discriminator based on either spike count or first-spike latency demonstrated that cortical units discriminate best between pairs of locations from opposing hemifields and show little or no discrimination among pairs of locations that were both within a lateral hemifield. Spatial acuity is greatest for pairs of locations that straddled the frontal midline.

The present study of the spatial sensitivity of neural spikes complements a recent study by Chadderton and colleagues (2009) that focused on the spatial sensitivity of excitatory postsynaptic potentials (EPSPs) in urethane-anesthetized rats. In that study, neural EPSPs tended to respond to sounds presented throughout the range of ±78.75° of azimuth that was tested. The majority of units showed maximum EPSP amplitudes in response to contralateral sound sources, but a minority of units showed maximum EPSP amplitudes in response to central or ipsilateral locations. The EPSPs of all studied units, however, showed fastest EPSP rise times for contralateral sounds. In a small subset of neurons for which spatial tuning was measured for both EPSPs and spiking, spike latencies and variability of latencies tended to decrease with increasing EPSP rise times, meaning that, for those neurons, contralateral sound sources elicited the most reliable responses.

We are aware of no other detailed studies of spatial sensitivity of spiking activity of cortical neurons in the rat. There have been, however, studies of cortical representation of interaural differences in sound pressure level (ILD), which probably are the principal acoustic cue for horizontal sound location in the rat; we note that rats apparently cannot distinguish the locations of low-frequency tones, for which interaural time differences would be the principal cue (Wesolek et al. 2010). Kelly and Sally (1988) mapped the topographic distribution in rat area A1 of units showing various patterns of sensitivity to ILD. Some 42.2% of units showed suppression of responses by ipsilateral stimulation at all contralateral levels, and 18.5% showed “mixed” responses that included ipsilateral suppression at moderate levels. Both of those unit classes, totaling 60.7%, responded best to ranges of ILD that would be produced by contralateral free-field sound sources. It is more difficult to predict the spatial preference of the 35.3% of units that showed summation of contra- and ipsilateral inputs. Higgins and colleagues (2010) studied the ILD sensitivity of multiple-unit clusters in rat area A1 and reported that all recordings showed preference for ILDs favoring the contralateral side. The finding that the majority (or all) of units in the rat prefer contralateral-favoring ILDs contrasts with results of similar studies in the cat (Imig and Adrian 1977; Middlebrooks et al. 1980), in which only about one-third of the samples of area A1 showed suppressive responses. The lower incidence of ipsilateral suppression in the cat is reflected in a lower incidence of neurons showing contralateral spatial receptive fields. In one study in the cat, for instance (Middlebrooks and Pettigrew 1981), only 48% of units showed contralateral (“hemifield” and “axial”) spatial tuning, and 52% showed “omnidirectional” tuning, which likely would have been scored as “no centroid” in the present study.

Koka and colleagues (2008) measured the horizontal location dependence of ILD in the rat. Consistent with the small size of the rat's head, ILDs were small at frequencies < 5 kHz. Maximum ILDs, and the rate of change of ILD with sound source distance from the midline, increased systematically with frequency up to ∼20 kHz, beyond which the patterns became more complicated. On the basis of those results, one might have expected the sharpness of spatial sensitivity of rat cortical units to increase with CF increasing between at least 5 and 20 kHz. The present results do not support that expectation. Although we found statistically significant negative correlations between steepest slope location and ERRF width with CF for stimuli 40 dB above threshold, we found no such correlation for any other spatial sensitivity metric or for steepest slope location or ERRF width at lower levels. We note that the analysis by Koka and colleagues (2008) computed ILDs within 0.12-oct bandwidths, which were substantially narrower than the FRAs of rat A1 units (e.g., Fig. 1A). The broader physiological bandwidths might have blunted the frequency dependence seen in the acoustical measurements. Also, it might be the case that the ILD cues that are available to the rat around 5 kHz are sufficient to support the contralateral-hemifield spatial tuning that we have observed. Any additional sharpening of spatial tuning resulting from sharper spatial ILD dependence might have been obscured by the overall between-neuron variance in spatial tuning. The present auditory cortex data suggest that the rat should be able to use a broad range of frequencies equally well for localization and discrimination across the midline.

Species Differences in Cortical Representation of Acoustic Space

The homogeneity and level invariance of spatial tuning seen in rat area A1 contrast with the diversity of spatial tuning that has been described in area A1 of carnivores and primates, in both anesthetized conditions (cat: Brugge et al. 1996; Harrington et al. 2008; Imig et al. 1990; Middlebrooks and Bremen 2013; Middlebrooks and Pettigrew 1981; Rajan et al. 1990; Stecker et al. 2003, 2005a; ferret: Mrsic-Flogel et al. 2003, 2005; Nelken et al. 2005) and unanesthetized conditions (cat: Lee and Middlebrooks 2011, 2013; Mickey and Middlebrooks 2003; nonhuman primate: Recanzone et al. 2000, 2011; Werner-Reiss and Groh 2008; Woods et al. 2006; Zhou and Wang 2012). Generally, the primary auditory areas in primates and carnivores show large populations of “omnidirectional” neurons that respond with at least half of their maximum firing rates to stimuli from all tested locations. Among the remainder of units showing greater spatial sensitivity, the majority favor contralateral locations, but sizable populations of neurons display a preference for ipsilateral or midline locations. In contrast, nearly all units encountered in the present study of rat area A1 displayed sharp hemifield tuning comparable to the most common class of spatially selective neurons seen in carnivores and primates (i.e., the contralateral-hemifield units).

Although carnivores and primates exhibit greater diversity of spatial tuning than the rat, those species share with the rat the property that neural spatial acuity is greatest for near-midline locations. In cat area A1, for instance (Stecker et al. 2005b), spatial acuity is sharpest around 0° azimuth, and the distribution of discrimination thresholds (i.e., MDAs) has a median of 40°, which is close to the medians of 35–40°, depending on sound level, that we observed in the rat.

Many neurons studied in anesthetized carnivores display a broadening of spatial tuning associated with increased sound level. Neurons in awake carnivore and primate preparations, in contrast, tend to be more level tolerant (Mickey and Middlebrooks 2003; Miller and Recanzone 2009; Zhou and Wang 2012). Spatial sensitivity in the present urethane-anesthetized rat preparation was largely level invariant, more like that in awake animals than in previous anesthetized preparations. The difference in level sensitivity might reflect a true species difference. Alternatively, it might be the case that the urethane anesthesia that was used here produced less disruption of the balance of contra- and ipsilateral excitation and inhibition than ketamine, barbiturate, and α-chloralose that have been used in previous studies.

Anesthesia was used in the present study to facilitate comparison with the majority of studies of cortical spatial sensitivity in other species and for ease of data collection. Our research group previously has studied spatial sensitivity in area A1 of cats under anesthetized conditions (e.g., Middlebrooks and Pettigrew 1981; Stecker et al. 2003) and, in other cats, awake conditions (Mickey and Middlebrooks 2003) and awake/behaving conditions (Lee and Middlebrooks 2011, 2013). Across those studies, we observed prominent differences in the temporal firing patterns of spikes and some differences in spatial sensitivity. Nevertheless, all of those conditions showed similar distributions of omnidirectional and spatially sensitive units, with the spatially sensitive units most often favoring contralateral locations. Given the general stability of distributions of spatial sensitivity across a wide range of experimental conditions in cats, we think it is unlikely that the use of anesthesia in the present study would have masked basic characteristics of spatial tuning in the rat.

Species Differences in Spatial Representation Correlate with Spatial Acuity

Rats can discriminate locations of sound sources on either side of the frontal midline with acuity comparable to that of other rodents, carnivores, and primates. Reported psychophysical thresholds around the midline are 11–14° for rats (Heffner and Heffner 1985; Ito et al. 1996; Kavanagh and Kelly 1986), compared with 7–23° for gerbils (Carney et al. 2011; Heffner and Heffner 1988b; Lesica et al. 2010; Maier and Klump 2006), 15–19° for ferrets (Kavanagh and Kelly 1987), 3–4° for cats (Heffner and Heffner 1988a; Martin and Webster 1987; Moore et al. 2008), 2–10° for monkeys (Recanzone and Beckerman 2004), and around 3° for humans (Middlebrooks and Onsan 2012; Recanzone et al. 1998). Discrimination of near-midline locations by the most sensitive single- and multiple-unit cortical recordings in the present rat experiment was comparable in scale with psychophysical thresholds. That is, the 10th percentile of spatial acuity for sources near the midline was ∼16° across a 30-dB range of sound levels.

Psychophysical discrimination of sound sources within a hemifield (e.g., pairs of sources centered on 60°) is strikingly worse in rat than in carnivores and primates. Carnivores and primates can successfully discriminate lateral sounds, with discrimination thresholds that average 28.8° for ferrets (Kavanagh and Kelly 1987), range from 3° to 10° for monkeys (Heffner and Heffner 1990; Populin 2006; Recanzone and Beckerman 2004), and range from 2° to 4° for humans (Middlebrooks and Onsan 2012; Recanzone et al. 1998); also, cats can correctly localize sounds from among loudspeakers separated by 15° (Malhotra et al. 2004). The psychophysical ability to discriminate or localize lateral sounds is matched by cortical spatial sensitivity, such that spike rates of single neurons in cats (Stecker and Middlebrooks 2003) and of populations of neurons in monkeys (Miller and Recanzone 2009) can identify a lateral sound source with considerable accuracy. In contrast to carnivores and primates, rats are essentially unable to discriminate source locations within a hemifield. Rats could not reach criterion psychophysical discrimination of sources separated by 60° when the pair of sources was centered on 60° (Kavanagh and Kelly 1986). Consistent with rats' poor psychophysical discrimination of lateral sounds, the present cortical recordings in rats showed substantially worse discrimination of lateral sources than of near-midline sources. For instance, median discrimination thresholds were >53° for pairs of sources located >40° from the midline.

We note that the parallels between spatial sensitivity of rat cortical neurons and localization/discrimination psychophysics do not demonstrate that psychophysical acuity is necessarily a product of the cortical activity. Indeed, contrary to such a claim of causality, bilateral lesions of rat auditory cortex have little or no impact on midline sound location discrimination (Kelly 1980; Kelly and Glazier 1978; Kelly and Kavanagh 1986). In carnivores and primates, bilateral auditory cortex lesions or inactivation results in profound sound localization deficits (Heffner and Heffner 1990; Jenkins and Masterton 1982; Jenkins and Merzenich 1984; Kavanagh and Kelly 1987; Malhotra and Lomber 2007; Thompson and Cortez 1983). Even in carnivores and primates, however, discrimination between sound hemifields is largely preserved after bilateral lesion or inactivation. In that sense, the main difference between rats and other studied species is that auditory cortex lesions in carnivores and primates disrupt discrimination of lateral sources whereas rats cannot discriminate lateral sources even with the auditory cortex intact. Although it is difficult to attribute rat auditory psychophysics to cortical function, we can say with some confidence that spike activity of A1 cortical neurons appears to follow the same principles of spatial sensitivity as rat sound localization psychophysics.

Several recent studies have raised the possibility that sound locations are represented by the relative activity of as few as two “opponent” neural populations (McAlpine and Grothe 2003; Phillips 2008; Salminen et al. 2009; Stecker et al. 2005b). Nevertheless, unilateral cortical lesions in carnivores and nonhuman primates result in strictly contralesional sound localization deficits (see, e.g., Jenkins and Masterton 1982; Thompson and Cortez 1983). For that reason, our group has argued that an opponent model of cortical representation must include both contra- and ipsilaterally tuned neurons within the same cortical hemisphere (Stecker et al. 2005b). Our present results in rats demonstrate the requisite hemifield spatial sensitivity of neurons but fail the requirement for contra- and ipsilateral tuning within the same cortical hemisphere. The absence of diverse patterns of contra- and ipsilateral spatial tuning in the rat's auditory cortex, and presumably elsewhere in its auditory pathway, might leave the rat without a mechanism for discrimination of lateral sound sources. A failure to discriminate such sources, however, is exactly what is seen in the rat's psychophysics. In light of the present cortical results, with consideration of previous rat psychophysical studies, we are inclined to think about sound location coding in the rat auditory cortex simply in terms of strong activity in one cortical hemisphere or the other, depending on the left or right location of the sound source, which might be sufficient to permit the rat to turn toward the sound of a desired target or turn away from a possible predator. Thus, while the absence of frontal-tuned, ipsilateral-tuned, and omnidirectional sensitive neurons in the rat is striking, we have found that the rat's single class of contralateral-tuned neurons represents a physiological counterpart to its sound localization psychophysics and, seemingly, to its ecological niche.

Concluding Remarks

Cortical neurons in area A1 in the rat lack the diversity of spatial sensitivity that is seen in carnivores and primates and lack the ability to code nonmidline sound source locations with great acuity. This might make the rat seem uninteresting for future study of spatial representation. On the other hand, the homogeneity of spatial sensitivity in the rat auditory cortex lends itself to future studies regarding the cortical mechanisms of hemifield spatial tuning, which is the most common pattern of spatial sensitivity seen in more sophisticated auditory cortices. That is, in studies employing in vitro, pharmacological, or optogenetic procedures, one could be assured that any neuron encountered in cortical area A1 would show contralateral-hemifield spatial tuning, even in situations in which that tuning could not be confirmed with in vivo recording with calibrated free-field stimulation. We hope to take advantage of this characteristic in future experiments.

GRANTS

This work was supported by National Institute on Deafness and Other Communication Disorders Grants R01-DC-000420 and T32-DC-010775.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).

AUTHOR CONTRIBUTIONS

Author contributions: J.D.Y., P.B., and J.C.M. conception and design of research; J.D.Y. and P.B. performed experiments; J.D.Y. and P.B. analyzed data; J.D.Y., P.B., and J.C.M. interpreted results of experiments; J.D.Y. prepared figures; J.D.Y. drafted manuscript; J.D.Y., P.B., and J.C.M. edited and revised manuscript; J.D.Y., P.B., and J.C.M. approved final version of manuscript.