Quantification of regional differences in aortic stiffness in the aging human

Abstract

There has been a growing awareness over the past decade that stiffening of the aorta, and its attendant effects on hemodynamics, is both an indicator and initiator of diverse cardiovascular, neurovascular, and renovascular diseases. Although different clinical metrics of arterial stiffness have been proposed and found useful in particular situations, there remains a need to understand better the complex interactions between evolving aortic stiffness and the hemodynamics. Computational fluid–solid-interaction (FSI) models are amongst the most promising means to understand such interactions for one can parametrically examine effects of regional variations in material properties and arterial geometry on local and systemic blood pressure and flow. Such models will not only increase our understanding, they will also serve as important steps towards the development of fluid–solid-growth (FSG) models that can further examine interactions between the evolving wall mechanics and hemodynamics that lead to arterial adaptations or disease progression over long periods. In this paper, we present a consistent quantification and comparison of regional nonlinear biaxial mechanical properties of the human aorta based on 19 data sets available in the literature and we calculate associated values of linearized stiffness over the cardiac cycle that are useful for initial large-scale FSI and FSG simulations. It is shown, however, that there is considerable variability amongst the available data and consequently that there is a pressing need for more standardized biaxial testing of the human aorta to collect data as a function of both location and age, particularly for young healthy individuals who serve as essential controls.

1. Introduction

A healthy aorta augments left ventricular function by distending during systole and recoiling elastically during diastole. That is, a distensible aorta reduces systolic pressure, and thus workload on the heart, and it enhances diastolic pressure, and thus coronary perfusion (e.g., O’Rourke and Hashimoto, 2007; Boutouyrie et al., 2008). In contrast, a stiffened aorta propagates the pulse pressure wave faster and farther, which adversely affects the heart, because reflected waves return earlier in the cardiac cycle and increase central artery pulse pressure, and likewise the brain and kidneys, because of increased pulsatility within the cerebral and renalmicrovasculatures (e.g., Adji et al., 2010). Given the importance of quantifying aortic stiffness and its attendant effects on the hemodynamics, it should not be surprising that diverse clinically inferable quantities have been identified, including the pressure–strain modulus (E_p), distensibility (D), central pulse pressure (cPP), augmentation index (AI_x), pulse wave velocity (PWV), and the amplitude of the backward traveling pressure wave (P_b)—see, for example, Agabiti-Rosei et al. (2007), Najjar et al. (2008), Avolio et al. (2009), Adji et al. (2010), McEniery et al. (2007), Redheuil et al. (2010), and Wang et al. (2010).

Notwithstanding arguments that particular metrics are better than others, especially for certain age groups (cf. Barodka et al., 2011), the carotid-to-femoral pulse wave velocity (CF-PWV) has tended to find the most favor clinically; indeed, it is sometimes referred to as the “gold standard” for measurement of arterial stiffness (Lacolley et al., 2009; Boutouyrie et al., 2010). Although CF-PWV is simply an empirical metric, the Moens–Korteweg equation $(c=\sqrt{Eh/2\rho \alpha ,}$ where c is wave speed, E the Young’s modulus of isotropic linear elasticity, ρ the mass density of the blood, and a and h the inner radius and thickness of the wall) is often cited to appropriately emphasize the fundamental importance of both arterial geometry (radius and thickness) and intrinsic physical properties (material stiffness and density) on wave propagation. Nevertheless, this simple equation is based on many assumptions that do not apply over the aorta and iliac artery that span the distance from the carotid to the femoral arteries. Namely, one cannot assume a uniform radius and wall thickness or a uniform, isotropic, linear material behavior under small strains. There is, therefore, a pressing need to understand more rigorously the roles of spatial and temporal changes in arterial geometry and material properties on pulse wave propagation as well as other postulated clinical metrics of arterial stiffening. Because of the associated geometric and material complexities, one must resort to computational models for such understanding and use appropriate methods from nonlinear mechanics.

Fortunately, advances in medical imaging and computational mechanics now enable patient-specific anatomical models for simulating the hemodynamics within large segments of a deformable vasculature tree (cf. Coogan et al., 2012; Xiao et al., 2013). These models remain limited, however, due to the continuing lack of information on potential regional variations in anisotropic wall properties and changes therein due to genetic mutations, exercise, aging, disease, and so forth. The goals of this paper, therefore, are twofold: first, to mine and compare information from the literature on the material properties of non-atherosclerotic human aorta as a function of location and age, and second, to present a consistent representation of these data via an appropriate linearization of a single nonlinear, anisotropic constitutive descriptor of the aortic wall. Finally, we also calculate the associated distensibility for comparison to data that have been reported based on clinical measurements. We conclude that, although considerable information is available, much more consistently and rigorously collected biaxial data are needed, particularly for young, healthy aortas that serve as important controls in most modeling efforts.

2. Methods

2.1. Constitutive relation

The aortic wall exhibits a nonlinear mechanical behavior over finite strains, hence one must employ an appropriate theoretical framework (Humphrey, 2002). Amongst the many constitutive relations that have been proposed to describe the passive mechanical properties of the aorta, we employed a “four-fiber family” model that has been shown to describe well an extensive set of biaxial data for both human abdominal aortic aneurysms and aging of the human abdominal aorta (Ferruzzi et al., 2011a). Moreover, this four-fiber family model motivates relations that have been found useful in simulations of aneurysmal development from an initial non-aneurysmal abdominal aorta (cf. Wilson et al., 2012). This particular functional form is motivated by the assumption that the primary constituents that bear load under tension are an elastin-dominated amorphous matrix and multiple embedded families of locally parallel collagen fibers. Notwithstanding increasingly better data on site-specific collagen fiber orientations (Schriefl et al., 2012), the four-fiber family model can phenomenologically capture stress–stretch data that may be influenced by yet unquantified lateral cross-links, physical entanglements, and even passive smooth muscle contributions. It can be written in terms of a (pseudo) strain energy function W of the form

$$W=\frac{c}{2}(I_c-3)+\sum _{k=1}^4\frac{c_1^k}{4c_2^k}(\text{exp}[c_2^k{({({\lambda }^k)}^2-1)}^2]-1),$$ (1)

where c,$c_1^k$, and $c_2^k$ are material parameters, I_c is the first invariant of the right Cauchy–Green tensor C (i.e., trC), and λ^k is the stretch experienced by the kth fiber family, which is oriented in direction ${\mathbf{M}}^k=[0,\text{sin}{\alpha }_0^k,\text{cos}{\alpha }_0^k]$ in an appropriate reference configuration (i.e., ${\lambda }^k=\sqrt{{\mathbf{M}}^k·\mathbf{C}{\mathbf{M}}^k}$). We let ${\alpha }_0^1=0^{°}$ (axial family), ${\alpha }_0^2={90}^{°}$ (circumferential family), and ${\alpha }_0^{3,4}=\pm {\alpha }_0$ (symmetric diagonal families), the last of which is thus a free parameter. It should be noted that families 3 and 4 are typically assumed to be mechanically equivalent, which in combination with the assumption of their symmetric orientations about the axial direction disallows twisting of the vessel due to pressurization.

2.2. Simulated biaxial data

Best-fit values of the eight model parameters $(c,c_1^1,c_2^1,c_1^2,c_2^2,c_1^{3,4},c_2^{3,4},{\alpha }_0)$ within Eq. (1) can be estimated using nonlinear regression, and such estimates are best found from data obtained via multiple biaxial stretching protocols (Humphrey, 2002). Moreover, when comparing results for different vessels or ages thereof, it is best to use data from the same protocols. Because data in the literature have been collected using different types of tests (e.g., uniaxial, equibiaxial, and non-equibiaxial stretching tests on excised strips or slabs of aorta as well as extension–distension tests on cylindrical specimens), we re-analyzed results from diverse studies wherein a nonlinear constitutive relation was reported with associated best-fit values of the material parameters. Specifically, based on the reported results, we “created” consistent sets of biaxial data (i.e., Cauchy stress–stretch data, σ_θ–λ_θ and σ_z–λ_z, where σ_θ and σ_z are mean circumferential and axial stresses and λ_θ and λ_z are mean circumferential and axial stretch ratios) that resulted from the same five simulated in-plane biaxial loading protocols: stress-controlled tests wherein σ_θ: σ_z=0.5:1, 0.75:1, 1:1, 1:0.75, and 1:0.5, with maximum values of stress allowed to reach ~120 kPa. Given the common assumption of incompressibility, the point-wise Cauchy stress t= −pI + 2F (∂W/∂C)F^T, where p is a Lagrange multiplier that enforces incompressibility (i.e., det F = 1), C=F^T F, and the deformation gradient tensor in a standard in-plane biaxial test is given by F=diag [λ_r, λ_θ, λ_z], with these stretch ratios computed relative to an unloaded reference configuration. Mean values of the Cauchy stress (i.e., transmural averages) result directly from simulated biaxial tests with homogeneous deformations.

We then used nonlinear regression (Levenberg–Marquardt) to determine best-fit values of the eight model parameters by minimizing the following objective function,

$$e=\sum _{i=1}^n[{({\sigma }_{\theta \theta }^{th}-{\sigma }_{\theta \theta }^{\text{exp}})}_i^2+{({\sigma }_{zz}^{th}-{\sigma }_{zz}^{\text{exp}})}_i^2]$$ (2)

where n is the total number of data pairs contained within the five simulated protocols for each set of biaxial data, with n~600 per set. The superscripts “th” and “exp” denote theoretically calculated (based on the four-fiber family model) and experimentally measured (based on the data generated from the results in the literature), respectively. In this way, we used a consistent means to compare results regardless of the original testing protocols or constitutive relations.

2.3. In vivo stress analysis

Possible inertial effects due to pulsatile hemodynamics are often negligible in arterial mechanics (Humphrey, 2002); hence, we assumed quasi-static motions in the absence of body forces. The governing equation of motion thus reduces to divt=0. For simplicity, we then considered idealized short sections of aorta to be straight, circular tubes of uniform thickness subjected to cyclic distensions while maintained at a fixed axial extension. The reduced equilibrium equation is thus:

$$\frac{\partial t_{rr}}{\partial r}+\frac{1}{r}(t_{rr}-t_{\theta \theta })=0,$$ (3)

which can be solved easily via numerical integration to compute the transmural distribution of stress. Moreover, assuming boundary conditions t_rr (r_i)=−P and t_rr (r_a) = 0, where r_i and r_a denote the intimal (inner) and adventitial (outer) radii, this equilibrium equation also allows one to compute the distending pressure

$$P={\int }_{r_i}^{r_a}\left(\frac{t_{\theta \theta }-t_{rr}}{r}\right)dr,$$ (4)

which is useful for relating computational results back to the in vivo setting. For example, computing the distending pressure at systole and diastole allows one to estimate the Distensibility (with units of kPa⁻¹, where 7.5 mmHg=1 kPa), often defined as

$$D=\frac{d_{\mathit{\text{sys}}}-d_{\mathit{\text{dias}}}}{(P_{\mathit{\text{sys}}}-P_{\mathit{\text{dias}}})d_{\mathit{\text{dias}}}},$$ (5)

where d denotes luminal diameter.

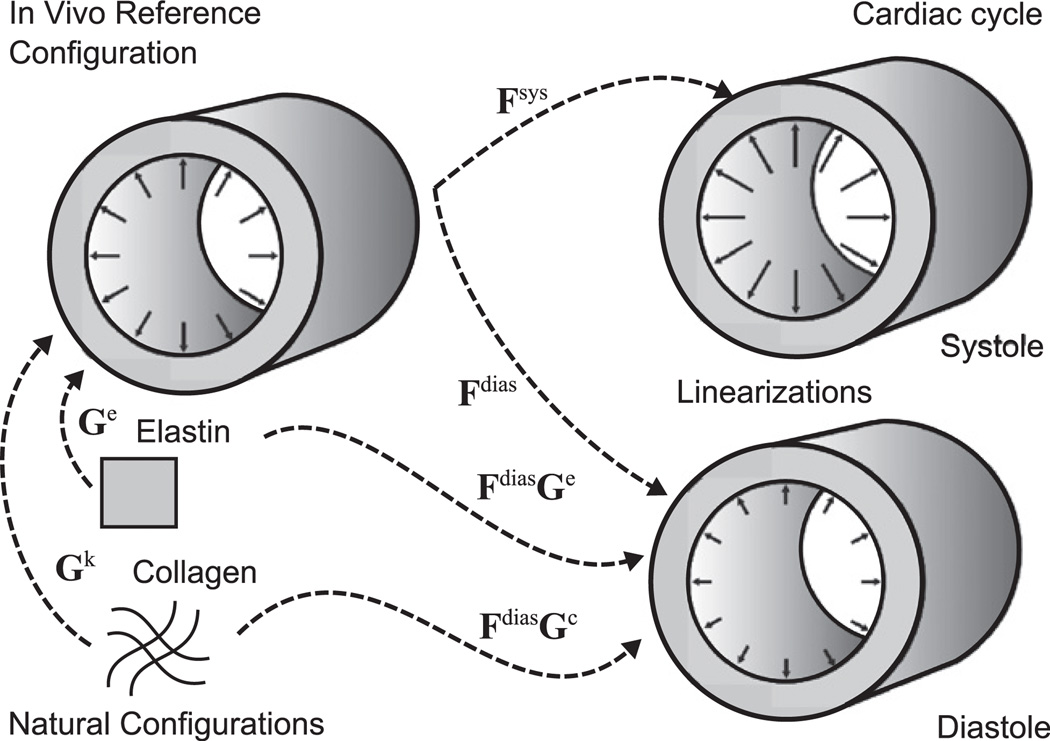
In contrast to classical approaches in arterial wall mechanics wherein the reference configuration is taken to be an excised, radially-cut, nearly stress-free configuration (cf. Fung, 1993; Humphrey, 2002), we solved Eq. (4) by following Cardamone et al. (2009) and defining the reference configuration to be an in vivo configuration near mean arterial pressure (MAP=P_dia + (P_sys–P_dia)/3) and at the in vivo axial stretch ${\lambda }_z^{iv}$ Advantages of this approach are many, including the ability to estimate residual stresses naturally rather than needing to prescribe an opening angle that is tractable theoretically only for axisymmetric vessels; more-over, the opening angle cannot be inferred in vivo and it has not been consistently reported for the human aorta as a function of location or age.

Hence, albeit consistent with Eq. (1), to compute in vivo stresses we further assumed that the different structural constituents within the aortic wall constitute a constrained mixture, whereby the different constituents can exhibit different material properties and possess different natural (stress-free) configurations despite deforming with the vessel as a whole. Specifically, we computed the assumed neo-Hookean response of the elastin-dominated matrix in terms of its constituent-specific deformation, namely trC^e, where

$${\mathbf{C}}^e={({\mathbf{F}}^e)}^T{\mathbf{F}}^e,{\mathbf{F}}^e=\mathbf{F}{\mathbf{G}}^e,$$ (6)

and the tensor G^e describes the in vivo pre-stretch of the elastin that results from both its deposition stretch during development and its stretch due to somatic growth (Valentín et al., 2009). Conversely, F accounts for deformations from the in vivo reference configuration to all other configurations, including those at diastole or systole. Notice, therefore, that F=I in the in vivo reference configuration, whereby F^e = G^e as desired. Similarly, the behavior of each family of collagen fibers was described by a Fung-type exponential relation (cf. Eq. (1)) wherein the stretch in each family of fibers was computed as

$${\lambda }^k=G^k\sqrt{{({\lambda }_z\text{cos}{\alpha }_0^k)}^2+{({\lambda }_{\theta }\text{sin}{\alpha }_0^k)}^2,}$$ (7)

where G^k represents the deposition stretch of the k=1, 2, 3, 4 families of collagen fibers, that is, the stretch in the in vivo reference configuration relative to the family-specific natural (stress-free) configuration. For purposes herein, we let the tensor G^e=1.2I for elastin and the scalar G^k=1.08 for each family of collagen fibers; there is clearly a need for more experimental data to prescribe such values according to location and age. Using this approach, residual stresses, which tend to homogenize the transmural distribution of wall stress under normal conditions (Fung, 1993; Humphrey, 2002) results naturally without prescribing a measured opening angle (cf. Cardamone et al., 2009). We assumed but a single homogenized representation of the wall, however, due to the lack of related information. That is, although we know that the aortic wall consists of three layers – the intima, media and adventitia – data are particularly scarce regarding the layer-specific composition and material behaviors as a function of location and age and it will be difficult to estimate layer-specific properties based on in vivo data. Again, there is a pressing need for more data.

2.4. Consistent linearization

Notwithstanding the need to use geometrically and materially nonlinear constitutive relations to describe the mechanical behavior of the aorta and then compute associated stresses within the aortic wall, the deformations experienced by these vessels tend to be modest over a cardiac cycle, particularly in aging and diseases wherein the vessel stiffens (e.g., hypertension or Marfan syndrome). Hence, we used the concept of “small deformations superimposed on large” to find appropriately linearized material properties (Baek et al., 2007) that are suitable for use in many fluid–solid-interaction codes (cf. Figueroa et al., 2009). Briefly, one first assumes that the deformation is finite from a suitable reference configuration (e.g., either an excised, traction-free configuration in a classical formulation or a constituent-specific natural configuration in a constrained mixture formulation) to a configuration during the cardiac cycle (e.g., near mean arterial pressure); one then assumes an additional multiplicative deformation to any configuration during the cardiac cycle, as, for example, at diastole or systole (Fig. 1). One can then construct a stress–strain relation that depends on both the initial finite deformation and the superimposed small deformation, thus resulting in a stiffness tensor (matrix) that includes information on the “initial stress” and subsequent material behavior. In particular, as shown by Baek et al. (2007), the Cauchy stress can be written as

$$t_{ij}=-p{\delta }_{ij}+t_{ij}^0+C_{ijkl}{\epsilon }_{kl}+D_{ijkl}{\Omega }_{kl},$$ (8)

where the superscript o denotes an “original” value and the linearized part is described by 𝒞_ijklε_kl + 𝒟_ijklΩ_kl, with the first (second) term taking into account the symmetric (anti-symmetric) part of the small deformation. In our kinematic description, the anti-symmetric part of the deformation (i.e., rotation) is zero, hence we focus on the following linearized measure of stiffness:

$$C_{ijkl}=2{\delta }_{ik}{F}_{lA}^o{F}_{jB}^o\frac{\partial W}{\partial C_{AB}}+2{\delta }_{jk}{F}_{iA}^o{F}_{lB}^o\frac{\partial W}{\partial C_{AB}}+4F_{iA}^o{F}_{jB}^o{F}_{kP}^o{F}_{lQ}^o{\frac{{\partial }^{2}W}{\partial C_{AB}\partial C_{PQ}}|}_{C^o}$$ (9)

Fig. 1.

Schema showing the three in vivo configurations used in our calculation of blood pressure, mean wall stresses, linearized stiffness, and distensibility: an in vivo reference configuration defined near mean arterial pressure and at the in vivo axial stretch as well as configurations defined at end diastole and end systole, also at the in vivo axial stretch. Note, therefore, that the linearization is about an intermediate configuration during the cardiac cycle (cf. Baek et al., 2007). Also shown are constituent-specific natural (stress-free) configurations and the associated deposition stretches that place stressed constituents into the in vivo reference configuration, which allows it to be a useful stressed reference (Cardamone et al., 2009).

Using this relation, one can easily compute stiffness given the finite deformation about which the linearization is performed and the nonlinear strain energy functionW, which in general represents anisotropic behavior whether in terms of a constrained mixture or not.

3. Results

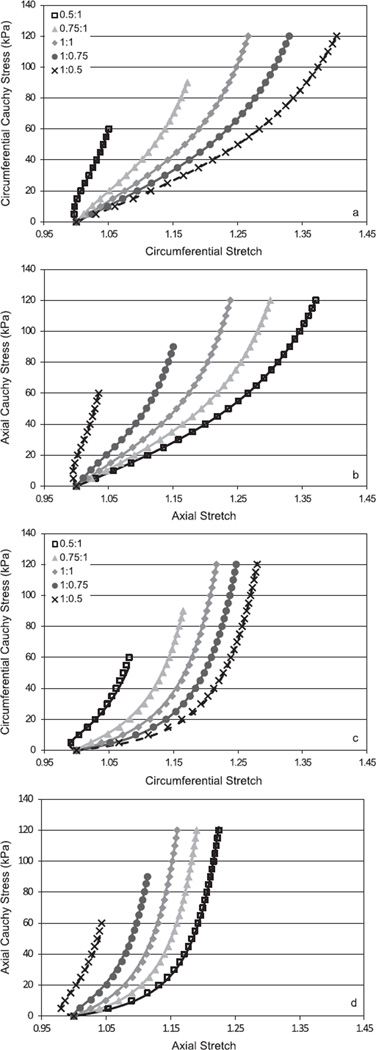
Amongst the data available in the literature on the mechanical behavior of the human aorta, results were recreated for 19 cases (i.e., different aortic locations and ages) from findings reported in six studies that provide best-fit values of material parameters within a specified nonlinear constitutive relation: Vorp et al. (2003), Vande Geest et al. (2004), Labrosse et al. (2009), Haskett et al. (2010), García-Herrera et al. (2012), and Martin et al. (2011). Fig. 2 shows representative results for both our simulation of five different stress-controlled biaxial testing protocols for the descending thoracic aorta based on findings from two of the six papers (i.e., the 20–35 year old group reported by García-Herrera et al. (2012) and the 57–71 year old age group reported by Labrosse et al. (2009)) and the ability of the four-fiber family constitutive model to fit (solid lines) the simulated data (symbols). Similarly excellent results were found for each of the parameter estimations, which likely resulted in large part because comparable constitutive functions were typically used to generate the data (e.g., García-Herrera et al. (2012) used a two-fiber family model to describe their data). For a visual comparison with actual data obtained during such biaxial tests, see Vande Geest et al. (2004) or Martin et al. (2011). Although anisotropy can only be assessed visually via equibiaxial stretching protocols, not stress-controlled protocols (Humphrey, 2002), the two sets of results in Fig. 2 reveal an expected decrease in extensibility due to aging.

Fig. 2.

Representative biaxial Cauchy stress–stretch data recreated for five different stress-controlled loading protocols (different paired symbols) and the associated best-fit (solid lines) by the four-fiber family constitutive model. These results were obtained by first generating data using previously reported nonlinear constitutive relations and associated best-fit parameters regardless of the type of experiment (e.g., uniaxial or biaxial) or constitutive relation used in the original paper. The upper two panels ((a) and (b)) show results for the 20–35 year old age group reported by García-Herrera et al. (2012) whereas the lower two panels ((c) and (d)) show results for the 57–71 year old age group reported by Labrosse et al. (2009), both for the descending thoracic aorta. The predicted loss of extensibility with aging was expected. The excellent fit by the four-fiber family model likely resulted, in part, because the data were generated from reported exponential-type constitutive relations.

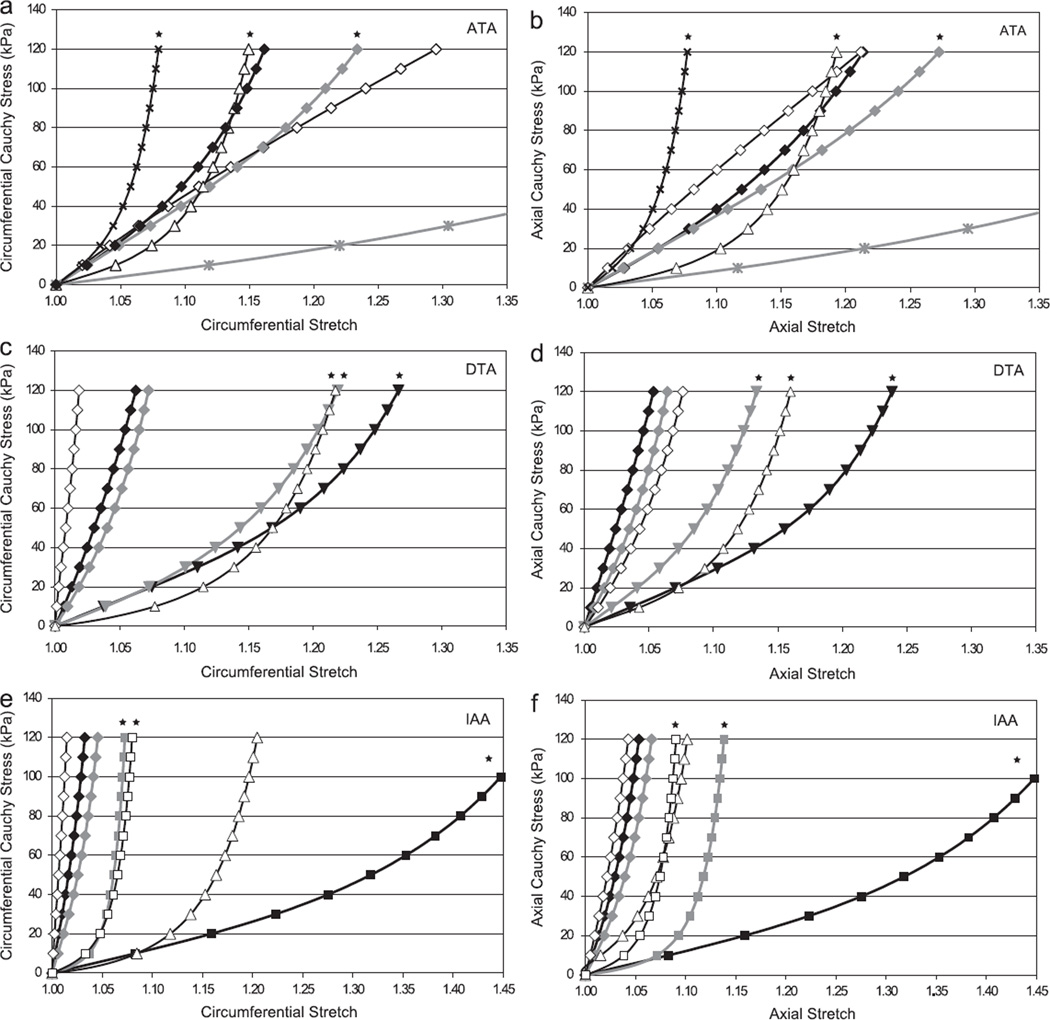
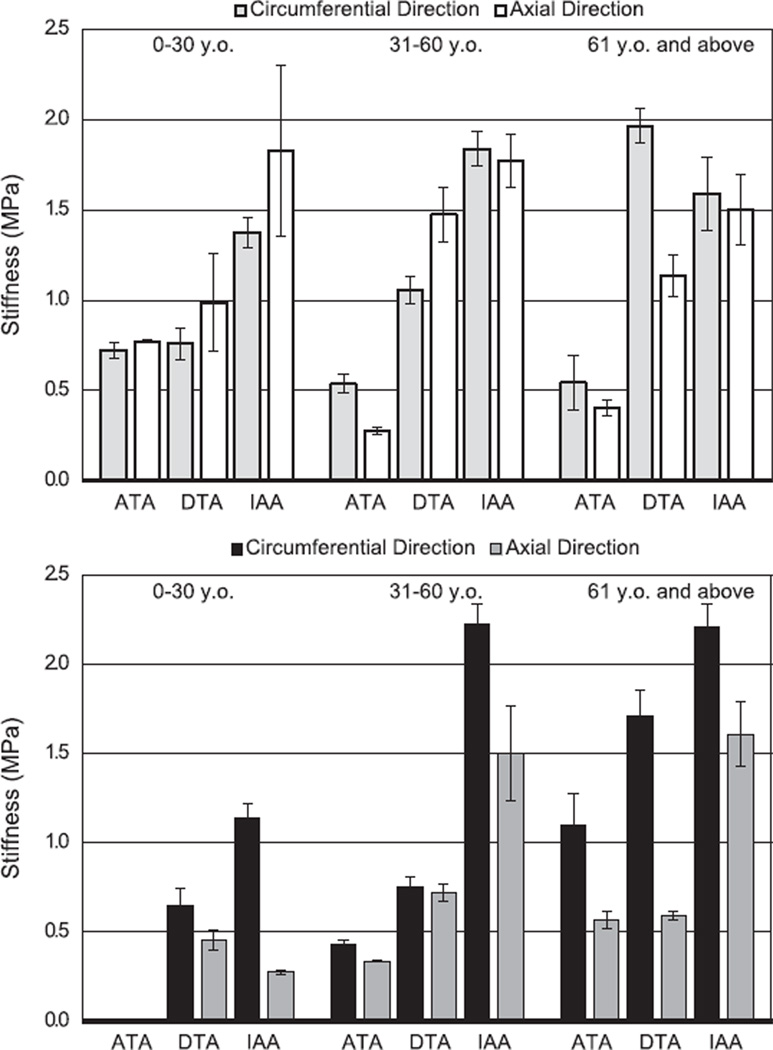
Fig. 3 compares circumferential and axial Cauchy stress–stretch responses in equibiaxial stress protocols (i.e., σ_θ:σ_z = 1:1) for each of the three aortic locations studied (ascending thoracic aorta—ATA, descending thoracic aorta—DTA, and infrarenal abdominal aorta—IAA) and the three primary age groups (denoted by black-filled symbols for the young group, gray-filled symbols for the middle aged group, and open symbols for the older age group, which includes the × and asterisk), which yielded 19 basic groups for comparison. Note, in particular, that the infrarenal abdominal aorta changed dramatically from the younger to the older group, generally becoming the least distensible (circumferential) and extensible (axial response) of the three locations. Associated best-fit values of the model parameters are listed in Table 1 for the 19 different groups (separated by aortic location, age group, and investigative team that generated the original findings); whereas it is difficult to compare directly the eight best-fit values of the model parameters for the many different groups, it is easier to compare values of linearized stiffness that are computed directly from an appropriate strain energy function W (cf. Ferruzzi et al., 2013). Fig. 4a shows overall mean results for the two primary tensional components of the linearized stiffness matrix 𝒞_ijkl for all 19 groups based on all data, separated by location (ATA, DTA, and IAA) and age-group (young, <30 y.o., middle age, >31 y.o. and <60 y.o., and older, >61 y.o.). The associated values are listed in Table 2 for all four primary components. As discussed in detail below, however, our assessment of the findings obtained from the aforementioned six studies suggested that certain results were more reasonable than others. Hence, Fig. 4b shows only those values of linearized stiffness that appear to be reliable and thus appropriate for use in fluid–solid-interaction (FSI) and fluid–solid-growth (FSG) simulations. Note that the associated studies and parameter values that we feel are most reasonable are bold face in Table 2.

Fig. 3.

Cauchy stress–stretch responses during simulated equibiaxial stress-controlled loading protocols for the 19 different cases (i.e., aortic locations and age groups) studied herein (cf. Table 1). Left and right panels represent circumferential and axial behaviors, respectively, for the ascending thoracic aorta (ATA), descending thoracic aorta (DTA), and infrarenal abdominal aorta (IAA). Results were based on findings reported in the following six papers: Garcia-Herrera et al. (inverted triangle), Haskett et al. (diamond), Labrosse et al. (triangle), Martin et al. (×), Vande Geest et al. (square), and Vorp et al. (asterisk). With the exception of the single data sets from Martin et al. and Vorp et al. (shown by the × and asterisk), results for young groups are denoted by filled black symbols, results for middle aged groups by filled gray symbols, and results for older groups by open symbols. Of particular note is the biaxial stiffening of the DTA with aging that is revealed by the Garcíla-Herrera et al. (2012) data and also the excellent correspondence between the García-Herrera et al. (2012) and Labrosse et al. (2009) data for the middle aged DTA group despite the use of different experimental methods and constitutive models by these investigators. Results of Vande Geest et al. (2004) for the aging abdominal aorta similarly reveal a stiffening effect with aging as expected. Finally, note that a small black star at the top of a curve denotes those data sets that appear to be most reliable overall, consistent with those values that are found bold face in Tables 1 and 2.

Table 1.

Best-fit values of the eight model parameters for the four-fiber family constitutive model.

	c (kPa)	$c_1^1$ (kPa)	$c_2^1$	$c_1^2$ (kPa)	$c_2^2$	$c_1^{3,4}$ (kPa)	$c_2^{3,4}$	a0 (deg)
Ascending aorta
Haskettb (0–30)	22.41	58.37	0.60	60.16	3.24	59.85	2.99	48.10
Haskettb (31–60)	47.43	35.23	7.65E−06	40.84	0.10	15.21	2.58	48.98
Vorpf (51)	8.30	16.22	0.07	15.74	1.46E−06	1.53E−05	0.07	2.54
Haskettb (61 and above)	88.82	28.38	1.40E−06	0.15	1.94E−06	7.31	1.18E−07	45.00
Labrossec (66–71)	4.18E−07	10.27	6.31	8.29	11.06	58.17	9.41	47.18
Martind (80–98)	1.56E−08	113.18	17.38	110.27	16.86	121.58	50.17	44.82
Descending aorta
Garcia Herreraa (20–35)	37.20	4.68E−06	2.97E−07	2.90E−05	1.68E−05	28.16	3.48	43.88
Haskettb (0–30)	26.77	43.33	1.52	26.73	1.53	743.35	4.97	44.87
Garcia Herreraa (45–60)	24.66	1.01E−05	4.22E−05	4.81E−05	1.92E−05	90.10	5.33	42.19
Haskettb (31–60)	8.41E−08	74.50	2.21	67.82	1.68	487.27	15.95	44.71
Haskettb (61 and above)	7.48E−11	98.34	1.11E−08	162.73	13.72	803.36	35.64	48.12
Labrossec (57–71)	2.46E−07	3.87	10.72	6.61	5.02	61.18	6.83	42.47
Abdominal aorta
Haskettb (0–30)	1.46E−09	92.08	1.43	108.68	4.66	869.40	38.47	46.03
Vande Geeste (19–26)	13.98	2.50	0.02	2.50	0.02	16.07	0.51	45.00
Haskettb (31–60)	3.88E−09	68.10	2.47	76.82	5.08	550.95	34.79	45.93
Vande Geeste (35–50)	1.20E−08	15.81	13.10	28.49	55.12	29.03	54.26	46.96
Haskettb (61 and above)	24.29	152.52	0.00	205.02	9.81	1483.32	55.73	47.08
Labrossec (57–71)	2.35E−14	2.05	23.98	5.60	6.08	81.68	12.04	41.05
Vande Geeste (61–75)	3.21E−08	47.43	30.28	54.18	38.08	45.94	70.79	45.53

Estimates were determined via nonlinear regression of data recreated for five biaxial stress-controlled loading protocols based on findings from six papers wherein a nonlinear constitutive relation was reported with associated best-fit values of the material parameters. The first column notes the paper where the constitutive information was found and the age range for the aortic samples:

The bold face represents the most reliable material parameters based on calculated stress–stretch responses and distensibility.

^aGarcía-Herrera et al. (2012).

^bHaskett et al. (2010).

^cLabrosse et al. (2009).

^dMartin et al. (2011).

^eVande Geest et al. (2004).

^fVorp et al. (2003).

Fig. 4.

Calculated linearized stiffness as a function of location along the aortic tree (ATA, DTA, and IAA) and age (cf. Table 2). Top: light gray and white bars represent, respectively, the mean values of circumferential and axial stiffness (in MPa) based on all 19 results considered. Bottom: Black and dark gray bars represent values of circumferential and axial stiffness (in MPa) that appear to be most reliable based on relative comparisons of the stress–stretch results from which they were obtained (cf. Fig. 3) and their correspondence with associated calculations of distensibility (cf. Fig. 6).

Table 2.

Values of the linearized elasticity tensor (cf. Eq. 9) for the four-fiber family constitutive model and best-fit model parameters listed in Table 1.

	Age (years)	Elasticity tensor (MPa)
		𝒞θθθθ	𝒞zzzz	𝒞θθzz	𝒞θzθz
Ascending aorta
Haskettb (0–30)	21	0.72	0.77	0.24	0.33
Haskettb (31–60)	42	0.44	0.34	0.04	0.13
Vorpf (51)	55	0.84	0.09	6.04E−10	0.11
Haskettb (61 and above)	68	0.26	0.33	3.84E−17	0.11
Labrossec (66–71)	68	1.10	0.57	0.51	0.56
Martind (80–98)	68	1.55	4.42	1.37	1.47
Descending aorta
Garcia Herreraa (20–35)	30	0.65	0.46	0.35	0.45
Haskettb (0–30)	25	0.99	2.05	1.05	1.05
Garcia Herreraa (45–60)	51	0.75	0.72	0.54	0.64
Haskettb (31–60)	44	1.22	1.89	1.12	1.21
Haskettb (61 and above)	69	2.22	1.68	1.47	1.55
Labrossec (57–71)	69	1.71	0.59	0.56	0.63
Abdominal aorta
Haskettb (0–30)	22	1.61	3.38	1.82	1.93
Vande Geeste (19–26)	22	1.14	0.28	0.30	0.43
Haskettb (31–60)	49	1.45	2.04	1.36	1.44
Vande Geeste (35–50)	49	2.22	1.51	0.97	1.03
Haskettb (61 and above)	67	2.60	2.76	2.08	2.18
Labrossec (57–71)	64	0.61	0.69	0.50	0.55
Vande Geeste (61–75)	67	2.21	1.61	1.00	1.05

The first column cites the reference wherein the original constitutive information was found plus the reported age range for the aortic samples.

The second column (age) reveals the particular age associated with information on geometry and pressure from tables in the Appendix.

Finally, bold face represent the most reliable values consistent with Table 1.

^aGarcía-Herrera et al. (2012).

^bHaskett et al. (2010).

^cLabrosse et al. (2009).

^dMartin et al. (2011).

^eVande Geest et al. (2004).

^fVorp et al. (2003).

In particular, for purposes of comparison with in vivo metrics, we calculated the distensibility for each of the 19 individual sets of data that were generated from the six different studies. Because distensibility depends upon both geometry and material properties over the range of distending pressures of interest, first note data in Fig. 5 that were found or computed for the three aortic locations as a function of age based on information provided in 16 additional studies in the literature as well as some of our own unpublished measurements (see the Appendix for tabulated values). These data reflect the generally expected increase in inner radius and pressure with aging, but show that the ratio of radius to wall thickness does not change dramatically or consistently at the three locations. Using information from Fig. 5 (i.e., the tables in the Appendix) and the best-fit material parameters (Table 1), distensibility was computed for the 19 data sets using our four-fiber family model and compared directly with values found in the literature (Fig. 6). The computed values are denoted by open symbols, an ×, or an asterisk whereas the measured values are denoted by filled circles; the solid regression lines are based on the reported measured values alone and the gray region denotes the associated 95% confidence range for the measured values. As it can be seen, distensibility decreases with increased age at all three locations as expected. In addition, however, note that values computed based on data from some of the six papers matched the measured values much better than did others.

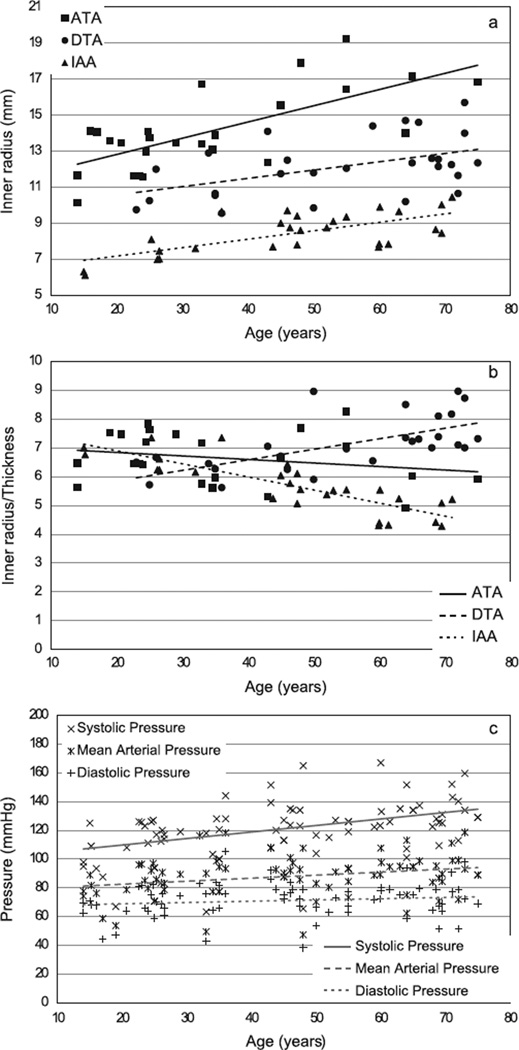
Fig. 5.

In vivo values of inner radius, ratio of inner radius to wall thickness, and blood pressure plotted as a function of age (cf. Table 3). Geometric data correspond to mean arterial pressure and are shown as closed black symbols: squares for the ascending thoracic aorta (ATA), circles for the proximal descending thoracic aorta (DTA), and triangles for the infrarenal abdominal aorta (IAA). Values for pressure are shown at systole, mean arterial pressure, and diastole. The lines show linear regressions of each data set. As expected, the data suggest an increase in caliber and pressure with age, but not a strong trend across the three aortic locations regarding the inner radius:wall thickness (a/h), a term that appears in both the Laplace equation for mean circumferential wall stress and the Moens–Korteweg formula for pulse wave velocity.

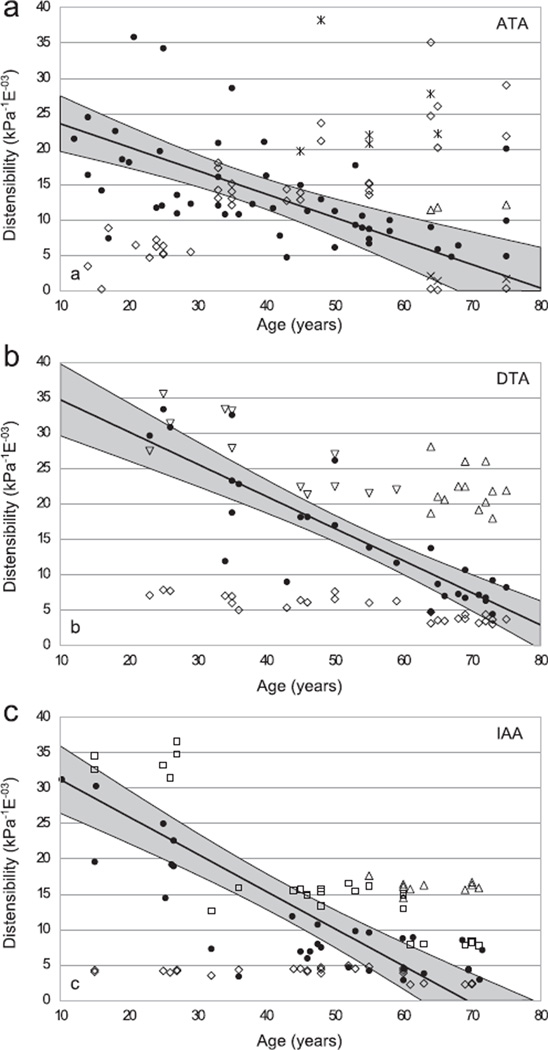
Fig. 6.

Distensibility plotted as a function of age for the ascending thoracic aorta (top), descending thoracic aorta (middle), and the infrarenal abdominal aorta (bottom). Measured values mined from the literature are denoted by closed circles, with the solid line showing the associated linear regression of the data and the grey region the 95% confidence intervals. Calculated values based on the nonlinear constitutive model are denoted as follows: Garcia-Herrera et al. (open inverted triangle), Haskett et al. (open diamond), Labrosse et al. (open triangle), Martin et al. (×), Vande Geest et al. (open square), and Vorp et al. (asterisk). Note, in particular, the unexpected near constancy of predictions based on the Haskett et al. data, particularly for the DTA and IAA, which similar to observations based on the predicted stress–stretch responses (Fig. 3) suggests that these results must be considered suspect.

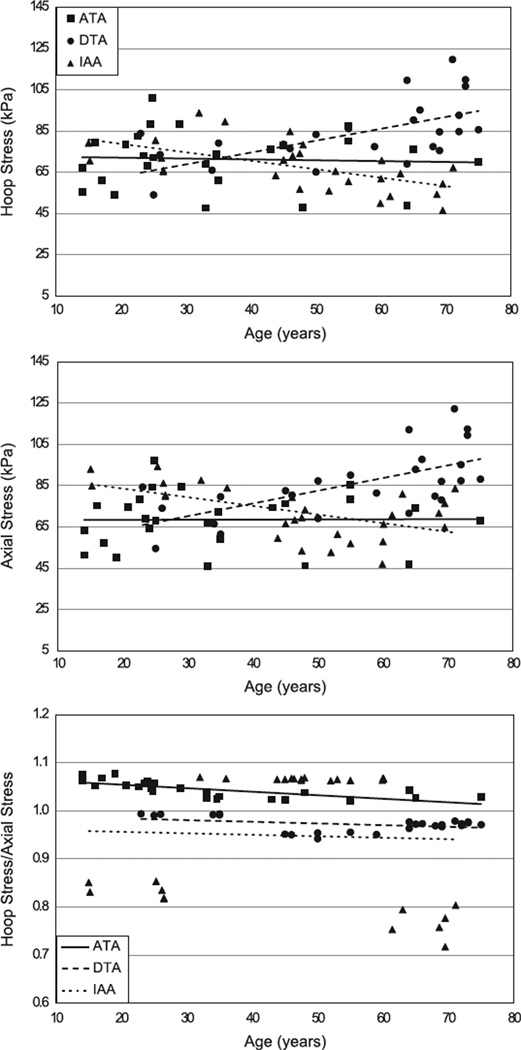
Finally, Fig. 7 shows mean values of the in vivo circumferential and axial wall stress (i.e., spatially averaged through the wall) as well as the ratio of the two as a function of aortic location and age. All calculations were performed at the mean arterial pressure and the in vivo axial stretch based on all results considered. Although there are different trends for the different locations, it is interesting that the spatially averaged mean wall stresses tended not to change, on average, with increasing age, consistent with early suggestions by Clark and Glagov (1985). Moreover, it appears that the stresses tended to remain nearly equibiaxial, as revealed by the nearly constant ratios of circumferential to axial stress.

Fig. 7.

Values of the mean (i.e., transmural average) circumferential (i.e., hoop) and axial Cauchy stresses calculated at mean arterial pressure (MAP) and the in vivo axial stretch shown as a function of location (ascending thoracic aorta, ATA; descending thoracic aorta, DTA; infrarenal abdominal Aorta, IAA) and age. Also shown is the associated ratio of these two components of stress. All results were determined using data in Table 1 and A1–A3

4. Discussion

The vast majority of prior hemodynamic models have been built upon the assumption that the vasculature is rigid (cf. Taylor and Figueroa, 2009). Although this assumption may allow reasonable estimates of wall shear stress or the formation of thrombus under some conditions, it does not allow computation of pulse wave velocity or the associated pulse pressure (e.g., the pulse wave velocity is infinite in a rigid tube, consistent with the Moens–Korteweg equation). There is, therefore, a pressing need to understand better the complex interactions between the hemodynamics and wall mechanics, each of which evolve under many circumstances. Indeed, one of the most common risk factors for many diseases of the heart, brain, and kidney is stiffening of central arteries due to aging, both normal and accelerated (Greenwald, 2007; O’Rourke and Hashimoto, 2007; Safar, 2010; Barodka et al., 2011). Whereas normal aging of the arterial wall typically includes a loss of elastic fibers, increased apoptosis and/or loss of contractile function of smooth muscle cells, an increase in fibrillar collagen and its cross-linking, and possibly an accumulation of glycosaminoglycans (Sawabe, 2010), it has been suggested that other arterial disorders are characterized by similar changes. That is, many now consider arterial disorders resulting from hypertension, diabetes, and heritable disorders such as Mar-fan syndrome to represent a type of pre-mature or accelerated aging (e.g., Agabiti-Rosei et al., 2007; Barodka et al., 2011). Consequently, there is a pressing need to understand both the causes and consequences of aging-related stiffening of central arteries, particularly the associated changes in local and systemic hemodynamics that ultimately govern organ function.

Notwithstanding the important correlations that have been reported between changes in clinical metrics such as PWV, cPP, AI_x, or P_b and the arterial stiffening that associates with aging or any of the aforementioned disorders, there is also a need to correlate the underlying changes in cell function and matrix structure with the evolving nonlinear material behavior. In particular, endothelial cells, smooth muscle cells, and fibroblasts respond to changes in hemodynamic loads (which can be quantified in terms of correlations with stresses or strains induced by blood pressure and flow) via changes in gene expression that, in turn, affect cellular function and matrix composition and organization. In other words, we must understand the interactions between wall mechanics and hemodynamics if we are to exploit our increasing understanding of vascular mechanobiology (cf. Humphrey, 2008). For example, mounting evidence suggests that pulse pressure is a particularly important local stimulus of mechanobiological responses by the wall (cf. Eberth et al., 2009). Rigid wall models of hemodynamics have no role in such studies.

This paper represents the first attempt to collect and then compare diverse results from the literature on the passive biaxial nonlinear mechanical behavior of human aorta as a function of location and aging within the context of a single theoretical framework. Our basic findings (Figs. 3 and 4 and Table 2) are generally consistent with the longstanding thought that the abdominal aorta is materially stiffer than the thoracic aorta and that aging increases aortic stiffness (cf. Figure 4.10 in Nichols and O’Rourke, 1990). Indeed, our computed values of linearized stiffness (Table 2) were of the same order of magnitude as those reported by others based on different methods, including those that often assume isotropy and thus a single modulus (cf. values from ~0.7 to 1.3 MPa in Nichols and O’Rourke). We submit, however, that one should quantify potential changes in anisotropy given the importance of axial wall mechanics, particularly in compensatory adaptations by arteries (Humphrey et al., 2009).

Although the present findings represent the first consistent comparison of biaxial results across multiple studies in terms of an appropriate nonlinear multiaxial constitutive relation and linearization thereof, many calculations of the associated values of distensibility were concerning. That is, Fig. 6 revealed that calculated values (open symbols or an × or asterisk) were often dramatically different from measured values (filled circles, solid regression line, and gray confidence interval). Although in vivo measures of distensibility are subject to experimental errors, this metric represents the state-of-the art in clinical inference (cf. Boutouyrie et al., 2010) and must be considered as useful for comparison. We similarly acknowledge that values of distensibility computed herein (via Eqs. (1) and (4) and the related assumptions) are subject to uncertainty, including consequences of the assumption of the lack of perivascular support (which should result in an overestimation of the actual distensibility) as well as a circular geometry defined by uncertain input values of luminal diameter (cf. Fig. 5 and the table in the Appendix). Hence, one should not expect complete agreement. Nevertheless, results for distensibility for those data sets that appeared most reasonable during parameter estimation (cf. Fig. 3), such as those by García-Herrera et al. (2012) for the descending thoracic aorta, agreed well with the experimental values of distensibility. Conversely, results for data sets that appeared suspect during parameter estimation (cf. Fig. 3), such as many of those from Haskett et al. (2010) and those of Vorp et al. (2003), did not agree well with the measured values of distensibility. For example, results from Haskett et al. (2010) for the ascending aorta suggested a softening with aging, which is not expected, and those for the descending thoracic aorta and abdominal aorta were much stiffer (and nearly linear) than the other data examined for those locations. These unexpected findings for stress–stretch behavior based on the Haskett et al. (2010) data were borne out by the distensibilty calculations, which suggested, for example, a nearly constant value regardless of age for both the descending thoracic aorta and the infrarenal abdominal aorta (cf. open diamonds in Fig. 6). Although our analysis cannot isolate reasons for such examples of unexpected results, one might question the determination of the reference configuration in the actual tests given the reported limited extensibility in the data, particularly for samples from younger subjects. Conversely, data from Haskett et al. (2010) appeared to be too compliant at older ages in the ascending aorta, similar to results from Vorp et al. (2003) that were obtained via uniaxial tests. It is known that uniaxial tests often underrepresent arterial stiffness relative to that under biaxial loads such as those that are experienced in vivo. Regardless of possible reasons, based on our assessments of the biaxial Cauchy stress–stretch behavior and computed distensibility as well as observed consistency across reports, we submit that those values that are bold face in Tables 1 and 2 are most reliable for FSI or FSG calculations. Moreover, we suggest that until multiple biaxial studies from different laboratories can be used to check for consistency in results at particular locations along the aorta, or aging related effects thereof, estimations of distensibility can provide a quick check of reasonableness.

Specifically, consistent with our calculations of distensibility, we suggest that the data of Martin et al. (2011) provide particularly good information on the ascending aorta in extreme old age, the data of García-Herrera et al. (2012) provide particularly good information on the behavior of the descending thoracic aorta in younger and middle ages, and the data of Vande Geest et al. (2004) provide very good data on the infrarenal aorta across all three age groups. Moreover, the data of Haskett et al. (2010) and Labrosse et al. (2009) provide very good results for the ascending aorta in middle and older ages, respectively, and the data of Labrosse et al. (2009) provide very good results for the descending thoracic aorta in old age. Note, too, that the stress–stretch results of García-Herrera et al. (2012) and Labrosse et al. (2009) showed good agreement for the descending aorta in middle age (cf. Fig. 3), hence providing further confidence in both of these data sets. It is thus interesting to note that best-fit values of the model parameters for the data of García-Herrera et al. (2012) suggested that the symmetric diagonal families of collagen dominated the stress–stretch behavior (cf. Table 1); this suggestion is also consistent with experimental measurements of the primary collagen fiber directions in the descending aorta (Schriefl et al., 2012), again providing more confidence in the results. It is also noteworthy that the value of c, which is meant to capture effects of the elastin-dominated matrix, tended to be very small for the oldest data sets at each location (Table 1), consistent with the expectation of a progressive loss of elastic fiber integrity with aging (cf. Ferruzzi et al., 2011b). Finally, it should be noted that Ferruzzi et al. (2011a) previously reported best-fit model parameters for the four-fiber family model based directly on the actual data reported by Vande Geest et al. (2004). Comparison of those values with the present values (Table 1) reveals notable differences that are likely due to our recreating the data herein based on the constitutive relations and material parameters reported by Vande Geest et al. (2004). In particular, they used different constitutive relations to fit their data depending on the age of the specimen, including a polynomial rather than exponential form for data from the youngest aorta. Clearly, it is best to fit constitutive relations to actual data when possible, but because we did not have access to all of the original data for all six of the studies considered herein, we recreated the data consistently for all groups to facilitate comparisons.

Finally, based on the findings that appeared to be more reliable, the present results (Fig. 4b and Table 2) suggest that the ascending and descending thoracic aorta are similar in behavior whereas the infrarenal abdominal aorta is stiffer at most ages. Moreover, with the exception of the ascending aorta in extreme old age, the circumferential direction tended to stiffen more with aging than did the axial direction (based on assumed, but clearly limited information on in vivo values of axial stretch). There is clearly a need for much more data, however, particularly for the ascending aorta at younger ages and more information on the associated in vivo axial stretches, relative mass fractions of elastin and collagen, and their prestretches, as well as changes in cross-link densities and roles of glycosaminoglycans. The values assumed herein for constituent pre-stretches are consistent with results in Wilson et al. (2012) for the older infrarenal abdominal aorta, but results are lacking for other locations and ages.

In closing, we note that despite the complexity of the four-fiber family model (8 parameters), it is possible to estimate values of these parameters from limited clinical data (cf. Masson et al., 2008). That is, provided that the functional form of a constitutive relation is well validated using extensive in vitro data and that reasonable ranges of many of the parameters are known a priori, it should be possible to determine patient-specific material properties from in vivo data, which in turn would allow fluid–solid interaction models to be truly patient-specific (geometry, wall properties, and hemodynamic boundary conditions based on ultrasound, phase-contrast MRI, or other imaging modalities). Indeed, others have similarly suggested that material parameters in comparable nonlinear constitutive relations can be well estimated from in vivo data (Stålhand et al., 2004; Åstrand et al., 2011), hence this must be our goal. As we show herein, once the nonlinear constitutive equation is known, one can check the result by evaluating the distensibility and then compute appropriately linearized values of stiffness as needed in FSI models. Because of the very different time-scales during the cardiac cycle and in arterial growth and remodeling, FSI simulations represent a vital part of a fluid–solid-growth model (Figueroa et al., 2009).

Nevertheless, we also emphasize that, like similar structurally-motivated models (cf. Holzapfel et al., 2000; Zulliger and Stergiopulos, 2007; Wan et al., 2012), our four-fiber family model is an advance over purely phenomenological models (cf. Fung, 1993), but it is phenomenological nonetheless. For example, whereas we have shown that the value of the parameter c (which is motivated by contributions of elastin to overall wall properties) decreases in cases wherein there is a loss of elastic fiber integrity (Ferruzzi et al., 2011a,2011b; Eberth et al., 2011), there is yet a need to model better the underlying reasons for such changes in load carrying capability. For example, although we can interpret c as φ^e (1–ξ^e) c^e where φ^e, ξ^e and c^e are, respectively, a mass fraction, damage function, and intrinsic modulus for elastin, there is also a need to model structural interactions between elastin and other components of the extracellular matrix as well as intramural cells. Clearly, the lack of combined histological and mechanical data as a function of location and age also impeded the present study. As a result, we did not compute distending pressure based on a multilayered model due to the lack of information on the percentage of the wall that was intima, media, and adventitia in each of the aforementioned studies and the associated lack of layer-specific histology or biaxial mechanical data. An important step in that direction is the work by Weisbecker et al. (2012), though they focused on uniaxial tests and the investigation of preconditioning related effects and damage.

The general framework presented herein can incorporate additional histopathological information as it becomes available, but advances in linking genetics to arterial stiffness (cf. Yasmin and O’shaughnessy, 2008; Lacolley et al., 2009) will necessitate the development of improved, structurally-based constitutive relations. Such relations will need to account not only for the elastic fibers and fibrillar collagen, but also the many different associated proteins and glycoproteins (e.g., collagen V or fibrillin-1) that play important roles in determining arterial stiffness and structural integrity. Although human data will ultimately be needed in this regard (cf. de Wit et al. 2012), genetically modified mouse models may well prove essential for the initial studies (cf. Ferruzzi et al., 2013).

In summary, arterial stiffening can result from changes in the composition, organization, and interactions of diverse extracellular matrix proteins, glycoproteins, and proteoglycans that constitute the wall. Given that stiffening of the aorta and its attendant effects on hemodynamics serve both as an indicator and an initiator of diverse cardiovascular diseases (see, e.g., Blacher and Safar, 2005; O’Rourke and Hashimoto, 2007; Lakatta et al., 2009; Barodka et al., 2011), there remains a pressing need for well performed biaxial tests, better correlations of mechanical behaviors with histological information, and appropriate quantification in terms of nonlinear constitutive relations, which in turn can be linearized appropriately to obtain values of stiffness needed in fluid–solid-interaction and thus fluid–solid-growth models. The present work sought to summarize current data and to present a theoretical framework sufficient for quantification. Based on the findings presented, we hope that this work stimulates additional studies that seek to collect the much needed experimental data, particularly for human arteries but for mouse models as well. Only in this way will we be able to understand fluid–solid-interactions that impact many aspects of cardiovascular, neurovascular, and renovascular health.

Table A1.

Ascending aorta
Age (years)	Inner radius (mm)			Thickness (mm)			λz	Pressure (mmHg)			Mean hoop stress (kPa)			Mean axial stress (kPa)
	Dias	Mean	Syst	Dias	Mean	Syst		Dias	Mean	Syst	Dias	Mean	Syst	Dias	Mean	Syst
Haskett(2) (0–30)
14c	10.12	10.12c	10.29	1.98	1.80	1.63	1.20	63c	74c	98c	47.48	55.29	73.85	17.02	51.36	105.68
17c	13.84	14.05c	14.55	2.01	1.80	1.59	1.20	44c	59c	88c	45.25	61.18	93.90	19.47	57.27	117.77
21l	13.36	13.47l	13.87	2.00	1.80	1.60	1.20	64l	79l	108l	63.59	78.59	109.79	30.03	74.66	141.54
23l	11.59	11.63l	11.91	1.99	1.80	1.61	1.20	81l	96l	126l	69.87	82.45	109.99	32.58	78.53	146.08
24l	11.47	11.64l	12.09	2.01	1.80	1.59	1.20	66l	85l	123l	56.37	73.06	108.91	26.20	69.12	135.17
24c	11.45	11.56c	11.89	2.00	1.80	1.61	1.20	64c	80c	111c	54.56	68.29	96.70	23.90	64.34	126.50
25l	12.85	12.97l	13.41	2.00	1.80	1.60	1.20	75l	92l	126l	71.70	88.13	123.85	35.41	84.21	156.08
25l	14.05	14.10l	14.49	1.99	1.80	1.61	1.20	82l	97l	127l	85.60	101.02	135.02	43.49	97.10	173.50
25j	13.70	13.75j	14.03	1.99	1.80	1.62	1.20	59j	71j	94j	60.05	72.05	96.74	26.70	68.14	130.61
29b	13.41	13.46b	13.84	1.99	1.80	1.60	1.20	75b	89b	119b	74.79	88.42	120.77	36.20	84.51	155.58
Haskett(2) (31–60)
33c	16.53	16.71c	17.31	2.60	2.33	2.06	1.15	43c	50c	63c	40.82	47.62	61.71	19.16	45.86	80.28
33f	13.16	13.40f	14.17	2.61	2.33	2.03	1.15	76f	90f	118f	57.64	68.78	94.41	30.67	67.00	111.97
35l	12.86	13.08l	13.80	2.60	2.33	2.04	1.15	84l	99l	128l	62.23	73.85	99.75	33.53	72.07	119.27
35j	13.71	13.90j	14.61	2.60	2.33	2.04	1.15	66j	77j	100j	52.08	61.02	82.54	26.52	59.25	100.39
43c	11.99	12.37c	13.41	2.63	2.33	1.99	1.15	86c	108c	152c	59.53	76.19	114.89	33.93	74.41	124.16
45j	15.32	15.55j	16.36	2.60	2.33	2.04	1.15	75j	88j	113j	66.10	78.03	104.52	36.26	76.26	125.11
48c	17.54	17.90c	18.95	2.62	2.33	2.02	1.15	38c	47c	65c	38.27	47.95	69.66	18.99	46.20	81.69
55c	19.05	19.25c	20.17	2.60	2.33	2.04	1.15	63c	73c	93c	68.92	80.13	106.23	37.97	78.38	127.85
55j	16.11	16.45j	17.62	2.62	2.33	2.00	1.15	77j	93j	126j	71.39	87.24	125.48	41.10	85.48	139.65
Labrosse(3) (66–71)
64g	13.61	14.01g	14.60	3.00	2.85	2.68	1.08	59g	75g	107g	37.63	48.98	72.45	35.22	46.97	66.71
65j	16.52	17.15j	18.05	3.03	2.85	2.65	1.08	75j	95j	134j	58.07	75.98	112.19	57.00	73.97	101.44
75j	16.20	16.85j	17.77	3.03	2.85	2.65	1.08	69j	89j	129j	52.39	69.93	106.33	51.69	67.92	95.01

Table A2.

Descending aorta
Age (years)	Inner radius (mm)			Thickness (mm)			lz	Pressure (mmHg)			Mean hoop stress (kPa)			Mean axial stress (kPa)
	Dias	Mean	Syst	Dias	Mean	Syst		Dias	Mean	Syst	Dias	Mean	Syst	Dias	Mean	Syst
Garcia Herrera(1) (20–35)
23h	9.25	9.75h	10.73	1.57	1.50h	1.38	1.14	82	97	126	67.42	83.78	119.20	79.13	84.30	94.75
25j	9.69	10.25j	11.29	1.88	1.79	1.65	1.14	59j	71j	94j	42.60	54.00	78.30	50.47	54.51	62.76
26h	11.34	12.00h	13.37	1.89	1.80h	1.64	1.14	69	83	112	57.96	73.51	109.89	68.92	74.03	85.27
34h	12.19	12.90h	14.30	2.10	2.00h	1.83	1.12	64	77	103	52.03	65.96	97.30	61.79	66.49	76.51
35j	10.06	10.55j	11.56	1.84	1.77	1.63	1.12	66j	77j	100j	50.00	60.96	86.31	57.74	61.48	69.74
35h	10.16	10.65h	11.59	1.77	1.70h	1.58	1.12	82	95	120	65.34	79.09	108.21	75.23	79.60	88.33
Garcia Herrera(1) (45–60)
45j	11.28	11.75j	12.55	1.81	1.75	1.65	1.10	75j	88j	113j	64.39	78.51	107.31	75.08	82.51	97.85
46h	11.90	12.50h	13.52	2.09	2.00h	1.87	1.10	76	92	124	60.30	76.41	110.90	71.87	80.41	98.96
50h	11.15	11.80h	12.85	2.10	2.00h	1.86	1.09	66	83	117	49.12	65.07	99.38	59.99	69.06	88.76
50h	9.24	9.85h	10.90	1.16	1.10h	1.00	1.09	54	70	104	60.48	83.28	136.43	75.36	87.29	115.76
55j	11.47	12.05j	13.08	1.81	1.73	1.61	1.08	77j	93j	126j	68.07	86.08	126.04	80.96	90.08	110.71
59h	13.64	14.40h	15.64	2.30	2.20h	2.05	1.08	72	89	122	59.55	77.39	114.74	71.96	81.40	101.48
Labrosse(3) (57–71)
64h	13.95	14.68h	15.97	2.09	2.00h	1.86	1.07	94	113	152	86.76	109.54	159.93	103.31	112.12	131.45
64h	9.34	10.17h	11.37	1.30	1.20h	1.09	1.07	43	62	101	43.90	68.97	125.57	59.95	71.58	96.97
65j	11.59	12.33j	13.51	1.81	1.71	1.58	1.06	75j	95j	134j	67.09	90.31	139.40	83.27	92.87	112.97
66h	13.73	14.57h	15.91	2.11	2.00h	1.85	1.06	79	99	137	71.62	95.12	143.44	88.17	97.72	117.16
68h	11.79	12.58h	13.83	1.91	1.80h	1.66	1.06	65	84	123	56.15	77.38	124.21	70.59	79.86	100.00
69h	11.19	12.12h	13.44	1.61	1.50h	1.37	1.06	51	71	109	50.08	75.48	128.27	66.70	78.05	101.11
69h	11.72	12.53h	13.75	1.81	1.70h	1.57	1.06	67	87	125	60.93	84.54	133.08	77.03	87.06	107.42
71h	11.58	12.23h	13.38	1.58	1.50h	1.39	1.05	91	111	152	92.97	119.61	178.61	112.11	122.22	144.36
72h	10.69	11.62h	12.98	1.40	1.30h	1.18	1.05	51	72	113	55.15	84.67	148.37	74.57	87.33	114.22
72h	10.02	10.63h	11.67	1.58	1.50h	1.38	1.05	79	99	140	69.74	92.59	143.46	85.79	95.13	115.75
73h	13.25	13.98h	15.21	2.10	2.00h	1.86	1.05	98	119	160	85.87	109.82	160.27	103.21	112.42	131.67
73h	14.70	15.67h	17.31	1.91	1.80h	1.65	1.05	73	93	134	78.75	106.70	169.71	98.34	109.42	134.10
75j	11.55	12.33j	13.57	1.79	1.69	1.55	1.05	69j	89j	129j	62.25	85.60	136.29	78.27	88.13	109.27

Table A3.

Abdominal aorta
Age (years)	Inner radius (mm)			Thickness (mm)			lz	Pressure (mmHg)			Mean hoop stress (kPa)			Mean axial stress (kPa)
	Dias	Mean	Syst	Dias	Mean	Syst		Dias	Mean	Syst	Dias	Mean	Syst	Dias	Mean	Syst
Vande Geest(5) (19–26)
15i	5.87	6.30i	7.25	0.96	0.90	0.79	1.16	71i	89i	125i	61.84	82.80	132.85	77.11	82.84	93.47
15k	5.76	6.11k	6.84	0.95	0.90	0.81	1.16	68k	82k	109k	58.05	73.98	109.49	69.68	74.02	81.92
25i	7.60	8.10i	9.18	1.16	1.10	0.98	1.14	70i	86i	117i	64.48	84.14	128.89	78.84	84.20	93.92
26k	6.59	6.98k	7.81	1.18	1.12	1.02	1.14	76k	91k	120k	59.68	75.41	110.46	71.24	75.46	83.16
27a	6.89	7.45	8.66	1.21	1.13	0.99	1.14	61a	79a	114a	49.65	69.19	115.23	63.77	69.25	79.13
27a	6.54	7.02	8.09	1.20	1.13	1.00	1.14	66a	83a	117a	51.02	68.56	110.39	63.77	68.61	77.64
Vande Geest(5) (35–50)
32e	7.02	7.52e	8.19	1.32	1.24	1.16	1.13	83e	116e	183e	62.77	93.70	160.76	77.72	87.58	106.04
36e	9.16	9.55e	10.16	1.37	1.32	1.25	1.12	76e	93e	128e	70.11	89.49	130.99	77.62	83.88	96.01
44k	7.35	7.60k	7.98	1.53	1.49	1.43	1.11	79k	93k	120k	52.22	63.41	85.86	55.98	59.52	66.21
45e	8.51	8.90e	9.48	1.56	1.51	1.43	1.11	72e	90e	127e	54.31	70.92	106.52	61.20	66.57	77.03
46e	9.23	9.59e	10.16	1.58	1.52	1.45	1.10	84e	101e	135e	67.90	84.69	119.79	74.04	79.34	89.57
46i	8.30	8.65i	9.20	1.59	1.54	1.46	1.10	79i	97i	134i	56.97	72.87	106.91	63.25	68.32	78.26
48a	8.83	9.29	9.94	1.62	1.56	1.47	1.10	72a	93a	134a	54.55	74.02	114.03	63.17	69.46	81.12
48a	7.34	7.70	8.20	1.62	1.56	1.48	1.10	67a	86a	123a	42.17	56.73	86.21	48.61	53.33	62.02
48e	7.98	8.50e	9.20	1.65	1.57	1.47	1.10	79e	108e	165e	53.82	78.32	129.11	65.43	73.28	87.55
52e	8.26	8.64e	9.20	1.71	1.65	1.57	1.09	63e	80e	115e	42.08	55.90	85.46	48.09	52.62	61.44
53e	8.61	8.99e	9.56	1.73	1.67	1.59	1.09	73e	91e	127e	50.30	65.46	96.92	56.56	61.45	70.68
55e	8.84	9.24e	9.83	1.77	1.71	1.62	1.09	67e	84e	119e	46.25	60.48	91.14	52.28	56.89	66.01
60d	7.27	7.57	8.02	1.86	1.80	1.72	1.08	72d	89d	123d	38.82	49.92	72.98	43.40	46.93	53.73
60e	7.27	7.75e	8.38	1.90	1.81	1.70	1.08	78e	108e	167e	41.95	61.80	102.92	51.57	57.85	69.32
60i	9.39	9.78i	10.37	1.87	1.81	1.72	1.08	80i	98i	133i	55.46	70.68	101.66	61.45	66.28	75.36
Vande Geest(5) (61–75)
61k	7.52	7.68k	7.89	1.87	1.84	1.80	1.08	79k	95k	126k	43.38	53.26	72.63	65.66	70.68	80.48
63e	9.22	9.48e	9.81	1.92	1.88	1.83	1.07	75e	95e	135e	49.39	64.31	94.59	73.36	80.95	96.15
69k	8.30	8.48k	8.72	2.03	1.99	1.95	1.06	79k	95k	128k	44.19	54.27	75.32	66.50	71.62	82.26
70a	9.55	9.84	10.19	2.05	2.00	1.95	1.06	69a	90a	131a	44.10	59.35	89.60	68.58	76.38	91.65
70a	8.03	8.27	8.56	2.05	2.01	1.95	1.06	64a	84a	125a	34.38	46.50	71.75	58.59	64.83	77.67
71i	9.97	10.27i	10.64	2.08	2.03	1.97	1.06	77i	99i	143i	50.69	67.19	100.52	75.22	83.58	100.23

Appendix A

Tables A1–A3. Information used to calculate values of aortic distensibility shown in Fig. 6 and linearized stiffness in Fig. 4 and Table 2. Specifically, data on geometry (inner radius and thickness at mean arterial pressure), in vivo axial stretch, and blood pressure (systolic, diastolic and mean arterial pressures) were mined from 11 papers in the literature, each denoted by a superscript letter associated with each value:^aÅstrand et al. (2011),^bFattori et al. (2000),^cGreenfield and Patel (1962),^dHirai et al. (1989),^eImura et al. (1986),^fIsnard et al. (1989),^gKoullias et al. (2005),^hLang et al. (1994),ⁱLänne et al. (1992),^jRedheuil et al. (2010),^kSonesson et al. (1993), and^lTellides (unpublished). These data were combined with constitutive parameters listed in Table 1, which were determined based on data from 6 additional papers:⁽¹⁾García-Herrera et al. (2012),⁽²⁾Haskett et al. (2010),⁽³⁾Labrosse et al. (2009),⁽⁴⁾Martin et al. (2011),⁽⁵⁾Vande Geest et al. (2004), and⁽⁶⁾Vorp et al. (2003). Finally, note that values denoted by boldface were used as an input; the other values were evaluated using our model and model parameters from Table 1.