Using the Concept of Transient Complex for Affinity Predictions in CAPRI Rounds 20–27 and Beyond

Abstract

Predictions of protein-protein binders and binding affinities have traditionally focused on features pertaining to the native complexes. In developing a computational method for predicting protein-protein association rate constants, we introduced the concept of transient complex after mapping the interaction energy surface. The transient complex is located at the outer boundary of the bound-state energy well, having near-native separation and relative orientation between the subunits but not yet formed most of the short-range native interactions. We found that the width of the binding funnel and the electrostatic interaction energy of the transient complex are among the features predictive of binders and binding affinities. These ideas were very promising for the five affinity-related targets (T43–45, 55, and 56) of CAPRI rounds 20–27. For T43, we ranked the single crystallographic complex as number 1 and were one of only two groups that clearly identified that complex as a true binder; for T44, we ranked the only design with measurable binding affinity as number 4. For the nine docking targets, continuing on our success in previous CAPRI rounds, we produced 10 medium-quality models for T47 and acceptable models for T48 and T49. We conclude that the interaction energy landscape and the transient complex in particular will complement existing features in leading to better prediction of binding affinities.

INTRODUCTION

The predictions of binders and binding affinities are important themes in the study of protein-protein interactions. Recent years have seen significant progress in the prediction of binders^1,2 and growing efforts in the prediction of binding affinities.^3–6 These predictions have mostly been based on structural and energetic features pertaining to the native complexes. Potentially the full interaction energy surface of the two subunits encodes information for predicting binders and binding affinities. Here we explore this potential and report our findings for affinity-related targets in CAPRI rounds 20–27.

The inter-protein interaction energy surface is not directly observable but it determines the observable entities such as the structure of the native complex, whether the two subunits have measurable binding affinity (i.e., classification as either binders or non-binders), and if so the magnitude of the binding affinity and the association and dissociation rate constants. The potential value of the full interaction energy surface for predicting such observable entities has been demonstrated in previous studies. Shen et al.⁷ used semi-definite underestimation to search for local minima on the interaction energy surface and to locate the native complex (corresponding to the global minimum). They suggested that this search process mimics the diffusional approach of the subunits in forming the native complex.

The association rate constant is certainly dependent on the full interaction energy surface. In developing a theory for the association rate constant, we mapped the interaction energy surface to introduce the concept of transient complex.^8,9 This is an intermediate on the association pathway, located at the outer boundary of the native-complex energy well (Fig. 1). It separates the “near” region, where the two subunits have significant native interactions but their relative translation and rotation are restricted, and the “far” region, where the two subunits have few specific interactions but have nearly unrestricted translational and rotational freedom. The two subunits reach the transient complex by translational and rotational diffusion. Subsequently they can undergo further conformational rearrangements and tightening of the binding interface to reach the native complex. When this forward step is fast (relative to the breakup of the transient complex by diffusion in the reverse direction), the overall association rate constant is well approximated by the rate constant for reaching the transient complex by diffusion. We have developed an automated method called TransComp (http://pipe.sc.fsu.edu/transcomp/) for predicting the association rate constant in this diffusion-limited regime.¹⁰

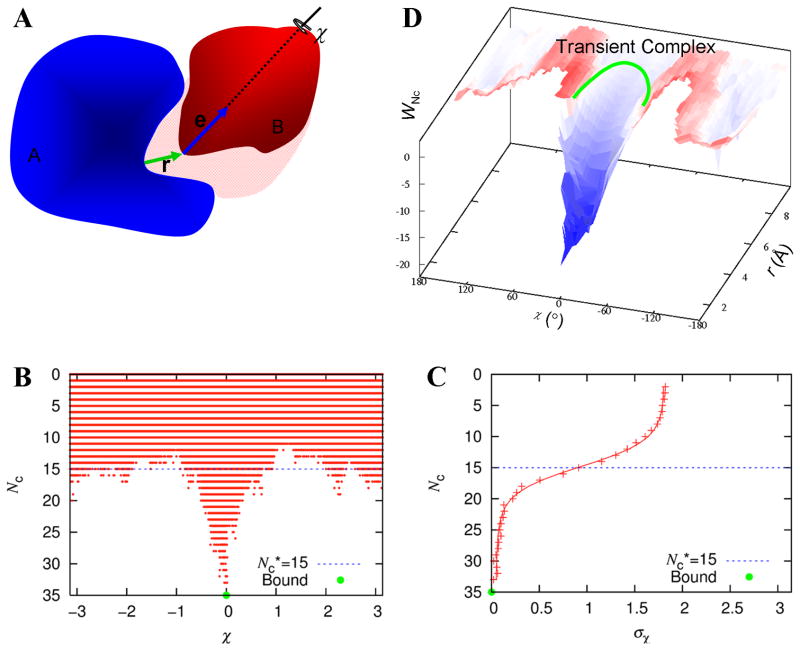
Figure 1.

Identification of the transient complex of two proteins, A and B. (A) The three translational coordinates, as defined by the relative displacement r between the centers of the binding sites on the two subunits; and the three rotational coordinates, as defined by the unit vector e attached to subunit B and the rotation angle χ around this unit vector. (B) Scatter plot of contact number (N_c) versus χ. Only clash-free poses are present in the scatter plot. (C) Specification of the transient complex, by fitting the standard deviation of χ values of clash-free poses at a given N_c to a function modeling two-state protein denaturation. The set of poses with the N_c value (designated as N_c^*) at the midpoint of the transition constitutes the transient complex. The N_c^* value is highlighted in both (B) and (C) by a blue dashed line. (D) The interaction free energy surface in the r-χ space. The location of the transient complex is sketched. Adapted from Alsallaq and Zhou⁸ and Qin et al.¹⁰

Here we report the use of the interaction energy landscape and the transient complex in particular for the five affinity-related targets (T43–45, 55, and 56) of CAPRI rounds 20–27. We found that the width of the binding funnel and the electrostatic interaction energy of the transient complex are among the features predictive of binders and binding affinities. For the nine docking targets, continuing on our success in previous CAPRI rounds,^11,12 we produced 10 medium-quality models for T47 and acceptable models for T48 and T49.

METHODS

Mapping of interaction energy surface and generation of transient complex

The procedure for mapping the interaction energy surface and identifying the transient complex was published previously.^8–10 Briefly, the mapping involved sampling in the 6-dimensional space of relative translation and relative rotation between the subunits (Fig. 1A). The sampling covered the native-complex basin and the surrounding region. Each subunit was treated as rigid and adopted the native conformation. The 3 translational coordinates were specified by the displacement vector r between the centers of the binding sites on the two subunits. The 3 rotational coordinates were specified by a unit vector e attached to subunit B and the rotation angle χ around this unit vector. In the native complex, this unit vector is perpendicular to the least-squares plane of the interface atoms and points from subunit A to subunit B. Poses in this 6-dimensional space was randomly generated, with the restriction that the magnitude of r (i.e., r) was below a cutoff r_cut.

Of all the randomly generated poses, the clash-free ones were saved. For each of these, the number of contacts, N_c, between interaction locus atoms was calculated (Fig. 1B). The interaction locus atoms were selected from interface atoms and came in cognate pairs. In each clash-free pose, contacts formed between cognate atoms were denoted as native and between non-cognate atoms as nonnative. Both were counted in calculating N_c. For poses at a given N_c, the standard deviation, σ_χ, of χ was calculated (Fig. 1C). The dependence of σ_χ on N_c was used to identify the transient complex. An earlier scheme relied on how σ_χ grew with decreasing N_c;⁹ in the subsequent, automated implementation, the dependence of σ_χ on N_c was fitted to a function for modeling protein denaturation data (Fig. 1C).¹⁰ The midpoint of the transition from the native-complex basin (with high N_c and low σ_χ) to the far region (with low N_c but high σ_χ) was identified as the transient complex. That is, all the poses with the midpoint N_c (designated as N_c^*) constituted the transient complex.

The width of the binding funnel (see Fig. 1D) can be measured in different ways. We used this parameter for targets T55 and T56, adopting a very simple measure. This was the fraction f_cf, of clash-free poses among all the randomly generated poses with r_cut = 6 Å.

Calculation of electrostatic interaction energy

Except for targets T55 and T56, the electrostatic interaction free energy was calculated by solving the nonlinear Poisson-Boltzmann equation. We used the APBS solver,¹³ following a protocol described previously.¹⁰ For the native complex, the electrostatic interaction free energy is

$$\mathrm{\Delta }{G}_{\text{el}}=G_{\text{el}}(\text{C})-G_{\text{el}}(\text{A})-G_{\text{el}}(\text{B})$$ (1)

where G_el(C), G_el(A), and G_el(B) are the electrostatic free energies of the complex and their two subunits. The electrostatic interaction free energy of the transient complex, ΔG_el^*, was calculated similarly for each pose within the transient-complex ensemble, and then averaged over 100 or 10 representative poses.

For target T55 and T56, because the large amounts of calculations needed to deal with the ~1000 mutants, we used the simple Debye-Hückel potential:

$$\mathrm{\Delta }{G}_{\text{el}}=332\sum _{i,j}\frac{q_i{q}_j{e}^{-\kappa r_{ij}}}{\epsilon r_{ij}}$$ (2)

where q_i and q_j are the atomic partial charges of subunits A and B, respectively, r_ij are the distances between atoms, ε = 78.5 is the dielectric constant of water, and κ is the Debye-Hückel screening parameter (at ionic strength 0.15 M).

Method for docking targets

Model generation and selection largely followed our previous work.^11,12 For targets where only a homologous template of a subunit was provided, the structure of the subunit was built by using MODELLER 8v2.¹⁴ Except for T47 and T57, all docking poses were generated by ZDOCK 2.3.¹⁵ The docking poses were then selected according to biochemical information if available. The poses were clustered and representatives of clusters were manually inspected. The final selected ten models were subjected to energy minimization by the AMBER program (including 50 steps of steepest descent). Models were generated by homology modeling and HADDOCK¹⁶ for T47 and by Autodock Vina¹⁷ for T57.

RESULTS AND DISCUSSION

CAPRI rounds 20–27 had five affinity-related targets: T43–45, 55, and 56; and nine docking targets: T46-T51, T53, T54, and T58. Below we briefly describe our performance and what we have learned from these exercises.

Native complexes generally have favorable electrostatic interactions

Before going into CAPRI rounds 20–27, we knew that electrostatic interactions between subunits in native complexes are generally favorable (i.e., ΔG_el < 0). While testing the robustness of our automated TransComp method for predicting association rate constants, we ran this method on the 176 complexes in benchmark 4.0 of Hwang et al.,¹⁸ and successfully completed these runs for 132 cases (Supplemental Table S1 of Qin et al.¹⁰). The distribution of the electrostatic interaction free energies (ΔG_el^*) in the transient complexes peaks at −0.5 kcal/mol (Fig. 2A). The favorable electrostatic interactions are even more significant in the native complexes (Fig. 2B), with the distribution peaking at −2.5 kcal/mol. However, native complexes sometimes can contain unphysically close contacts (due to low resolution of the structure or poor quality of modeling), which may lead to spurious results for ΔG_el. One such case actually occurred among the 132 complexes (the resulting spurious ΔG_el was not included in Fig. 2B). Because ΔG_el^* and ΔG_el show reasonable correlation (R² = 0.48; Fig. 2C) and the subunits in the transient complex are usually separated by a layer of solvent such that there is less chance for unphysically close contacts, whenever possible we chose to use ΔG_el^* for the affinity-related CAPRI targets.

Figure 2.

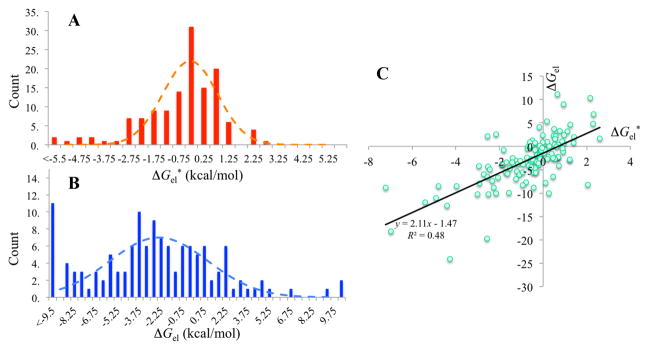
Generally favorable electrostatic interaction free energies in native complexes and in transient complexes. (A) Histogram of ΔG_el^* values for 132 protein-protein complexes in benchmark 4.0 of Hwang et al.¹⁸ (B) Histogram of ΔG_el values. (C) Correlation of ΔG_el and ΔG_el^*. Results were calculated by solving the nonlinear Poisson-Boltzmann equation at a temperature of 298 K (with ε = 78.5) and an ionic strength of 0.15 M.

Of course van der Waals interactions should also be favorable in native complexes and may even dominate over electrostatic interactions. However, given their strong dependence on interatomic distances, we reasoned that they might not be particularly useful for discriminating between binders and non-binders among designed complexes. In particular, the effects of subunit conformations, poor contacts, and the neglect of water molecules on van der Waals interaction energies would be very unpredictable. Indeed, while many groups found electrostatic interactions to be useful for the affinity-related targets,^19,20 the same cannot be said about van der Waals interactions.

The finding of generally favorable electrostatic interactions between the subunits is in contrast to the previous conclusion of Sheinerman et al.²¹ that “the total effect of electrostatics is generally net destabilizing” for protein-protein complexes. We have noticed that the calculated electrostatic free energy from solving the Poisson-Boltzmann equation is very sensitive to the choice of the boundary between the protein low dielectric and the solvent high dielectric.^22,23 The popular choice of using the molecular surface as the dielectric boundary indeed generally produces unfavorable electrostatic contributions to protein folding and binding. However, the alternative choice of using the van der Waals surface typically reverses the sign of ΔG_el, thus predicting a stabilizing effect on binding stability for electrostatic interactions,^24–26 consistent with the results shown in Fig. 2B.

Our systematic assessment of calculated effects of charge mutations on protein folding and binding stability led us to conclude that the use of the van der Waals surface as the dielectric boundary produces better agreement with experimental results.^22–27 Moreover, significant electrostatic enhancements of rate constants observed for many protein complexes can only be produced by the use of the van der Waals surface.^9,28 The Poisson-Boltzmann equation-based electrostatic calculations carried out here followed this protocol.

Target T43

For T43 we were given 20 models generated by Rosetta along with a blinded crystal structure (also based on Rosetta design). We generated transient complexes for these models and calculated the electrostatic interaction free energies of the transient complexes. The results, sorted according to ΔG_el^*, are listed in Table I. The top-ranked Model 10 has a significantly more favorable ΔG_el^* value (at −7.02 kcal/mol) than the other 20 models (closest ΔG_el^* at −4.95 kcal/mol, for Model 9).

Table I.

Ranking of models for T43 and T44 according to ΔG_el^* (in kcal/mol).

T43		T44
Model	ΔGel*	Model	ΔGel*
10a	−7.02	10	−0.88
9	−4.95	19	−0.73
11	−2.31	17	−0.57
8	−1.23	2b	−0.56
2	−0.59	16	−0.34
6	−0.48	3	−0.29
20	−0.21	1	−0.19
14	0.14	8	−0.05
7	0.17	15	0.05
3	0.22	11	0.14
16	0.30	20	0.41
15	0.34	14	0.43
19	0.41	5	0.52
12	0.56	6	0.63
21	0.63	18	0.64
17	0.75	4	0.69
18	0.84	9	0.74
4	1.02	21	0.93
5	1.11	12	0.95
13	1.32	7	1.01

^aThis top-ranked model corresponds to crystal structure 3Q9N.

^bThis fourth-ranked model was shown to have measurable binding affinity.

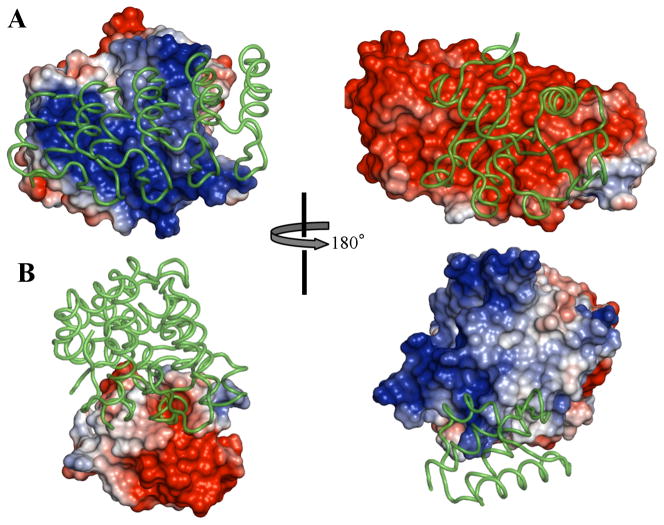
Model 10 turned out to be the crystal structure (Protein Data Bank ID 3Q9N).²⁹ (Only one other group clearly identified Model 10 as a true binder.) The two subunits feature very strong electrostatic complementarity at the interface (Fig. 3A), thus explaining the strong favorable ΔG_el*. Our TransComp web server predicted an association rate constant of 4.6 × 10⁸ M⁻¹s⁻¹, with over three orders of magnitude electrostatic rate enhancement. Karanicolas et al.²⁹ reported a rate constant of (7–9) × 10⁵ M⁻¹s⁻¹ for a precursor of 3Q9N (before affinity maturation) using surface plasmon resonance (SPR). However, this experimental technique is limited by mass transport, precluding accurate determination of rate constants higher than about 10⁶ M⁻¹s⁻¹.²⁸ The affinity maturation may have further improved the association rate constant, as Karanicolas et al. noted large contribution of charged residue mutations during the affinity maturation. They also noted high salt sensitivity of the binding free energy. These observations all point to a significant role of electrostatic interactions, consistent with our calculations.

Figure 3.

T43 and T44 models. (A) Crystal structure 3Q9N, corresponding to Model 10 of T43. (B) Rosetta-generated structure for Model 2 of T44. Each model is presented in two views, rotated 180° from each other. In each view, one subunit is represented by the electrostatic surface and the other as ribbon; the representations are then swapped in the other view.

Target T44

There were also 21 Rosetta-generated models for T44. We again ranked the models according to ΔG_el^* (Table I). This time the ΔG_el^* values were all moderate; the top-ranked model had ΔG_el^* = −0.88 kcal/mol. After the ranking of the models was submitted, the CAPRI participants were informed by the Baker group that Model 2 had measurable binding affinity. We ranked this model as 4th.

Examining of the electrostatic surfaces of the subunits in Model 2 shows that one features a strong positive patch and the other features a strong negative patch (Fig. 3B). However, in the model of the complex generated by Rosetta, these strong complementary patches are not placed within the interface. Rather the interface is positioned at the peripheries of both patches, explaining the moderate ΔG_el^* for this model (at −0.56 kcal/mol). It is possible that in the complex actually formed the complementary electrostatic patches on the two subunits are placed in the interface.

Target T45

The goal for this target was to discriminate between Rosetta-designed interfaces from natural complexes. The 87 designed interfaces had favorable computed binding energies but did not show measurable binding affinities; the 120 natural complexes were from benchmark 3.0 of Hwang et al.³⁰ Again we used ΔG_el^* as the role parameter for ranking, with modest success. Our AUC value, 0.69, falls in the lower mid-range among the 28 participating groups (full AUC range is between 0.55 and 0.86).¹⁹

Our retrospect comparison shows that the designs and natural complexes do show distinct distributions in ΔG_el^*, with a significant overall shift toward higher ΔG_el^* for the designs. However, the two distributions also have significant overlap over the range of ΔG_el^* from −2 to 3 kcal/mol. This suggests that, while electrostatic calculations are useful for characterizing natural complexes (e.g., in the regulation of binding affinity and association rate constant), they have limited ability in discriminating decoy interfaces from natural ones.

Targets T55 and T56

The goal of these two targets was to test the ability of predicting how single mutations affect the binding affinities of two designed protein inhibitors of Influenza hemagglutinin, HB36.4 and HB80.3. The experimental data were provided by the enrichment of mutant sequences in a selection for hemagglutinin binding;³¹ the enrichment data were used as the proxy for mutational effects on binding affinity in lieu of direct affinity measurements.

To predict the effect of each mutation, we used an energy function with the combination

$$\mathrm{\Delta }G=\mathrm{\Delta }{G}_{\text{el}}+ln{f}_{\text{cf}}$$ (3)

where ΔG_el is the electrostatic energy calculated according to the Debye-Hückel potential [Eq (2)], and f_cf is the fraction of clash-free poses in generating the transient complex. The latter quantity was expected to capture the influence on the binding affinity by the width of the binding funnel. Our performance on T55 and T56 was reasonably successful. Evaluated according to Kendall’s tau-b coefficient, among 22 participating groups, we ranked 7th for T55 and 6th for T56.²⁰

We carried out retrospective analysis to assess the relative contributions of the two terms of Eq (3) (Table II). The terms appear to be synergistic in their impact on prediction accuracy; Kendall’s tau-b coefficient for the combined energy function is much higher than that for either term. Interestingly, the contribution of f_cf seems more significant for T55 whereas that of ΔG_el seems more significant for T56.

Table II.

Retrospective analysis on the contributions of the two terms of our energy function for T55 and T56.

	T55		T56
Factor	Kendall	p-value	Kendall	p-value
ΔGel	0.0386	0.06	0.0737	9.6E-4
fcf	0.102	1.3E-6	0.0210	0.36
Both	0.145a	1.8E-12	0.131b	4.21E-9

^aThe corresponding value from the official evaluation is 0.165.

^bThe corresponding value from the official evaluation is 0.147.

Docking targets

We submitted 10 medium-quality models for T47, 3 acceptable models for T48 and 1 acceptable model for T49. T47 is the complex of DNase E2 with immunity protein Im2;³² the CAPRI participants were told that interface water was to be the focus of prediction. We generated docking poses by HADDOCK, using as input 11 homology models of E2 based on the structure of E9 in 2WPT (for the E9-Im2 complex) and 60 models of Im2 in the NMR structure 2NO8 along with the structure of Im2 in 2WPT. In two independent HADDOCK runs, residues K83, F86, and R98 on E2 and D33, R38, E41, and R42 on IM2 were defined as active restraints, based on mutational studies of Li et al.³³ 10 models were selected based on clustering and manual inspection, with all water molecules were stripped. To each of these models, we added 10 interface water molecules conserved between the structures of the E9-Im9 complex (1EMV) and the E9-Im2 complex (2WPT). The final models were subject to 200 steps of energy minimization before submission.

T48 and T49 are the complex of T4moH and T4moC, components of the toluene 4-monooxygenase holoenzyme. T4moH was taken from 3DHH for T48 and was an unpublished unbound structure for T49. The active site in T4moH is buried, with three tunnels leading to the exterior.³⁴ In identifying a possible binding site for T4moC, we focused on the largest channel of the three. For convenience, we used a residue, S187, near the center of this channel as a representative. We chose models in which the iron-sulfur cluster of T4moC is close to S187. Specifically, the final 10 models all have < 10 Å distances between T4moH S187 and T4moC H47 or H67, which coordinate the iron-sulfur cluster.

T58 serves as an example for the docking targets for which we failed to submit at least an acceptable model. This is the complex of the SalG lysozyme with the inhibitor PliG.³⁵ Mutation studies of Leysen et al.³⁶ suggested that mutations on PliG Y47 and R119 significantly reduced inhibitory activity; these authors also noted that these residues are located in an area predicted by our meta-PPISP web server.³⁷ Our model selection thus placed SalG lysozyme active-site residues E73, D86, and D97 and PliG Y47 and R119 in the interface, assuming that the inhibitor completely blocked the substrate-binding site. It turned out that in the actual complex (4G9S)³⁵ the inhibitor blocks only half of the substrate-binding site, from a sideway direction. In retrospect our assumption is untenable, since the substrate-binding site is too shallow to hold the inhibitor from a “head-on” direction, so we had to pull the inhibitor away to avoid clash, leading to a physically unreasonable interface.

Additional work with affinity prediction

Partly due to the encouraging results on targets T55 and T56, we attempted to develop a predictor for protein-protein binding affinities, based on linear regression analysis of features defining the full protein-protein interaction surface. For a subset of 33 complexes from an affinity benchmark³ that have relatively small differences between bound and unbound structures (I-RMSD < 1 Å), we found a linear combination of parameters, akin to Eq (3), that strongly correlates with the binding free energies (R² = 0.64). The parameters included the number of nonnative contacts (part of N_c defined above) in the native complex, the curvature of the binding funnel, the largest gap in N_c in the configurational sampling to generate the transient complex, and I-RMSD. We conclude that the interaction energy landscape and the transient complex in particular will complement existing features^3–6 in leading to better prediction of binding affinities.

Figure 4.

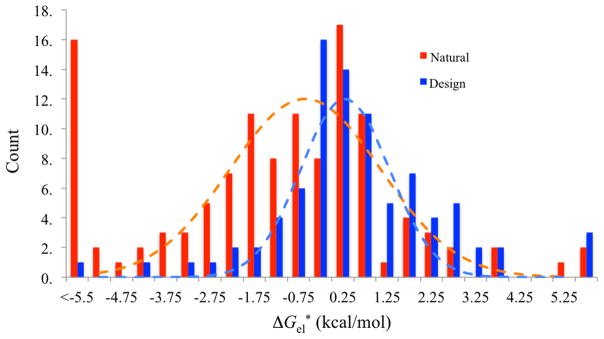
Distributions of ΔG_el^* for 120 natural complexes and 87 designs.