Recoding of Sensory Information across the Retinothalamic Synapse

Abstract

The neural code that represents the world is transformed at each stage of a sensory pathway. These transformations enable downstream neurons to recode information they receive from earlier stages. Using the retinothalamic synapse as a model system, we developed a theoretical framework to identify stimulus features that are inherited, gained, or lost across stages. Specifically, we observed that thalamic spikes encode novel, emergent, temporal features not conveyed by single retinal spikes. Furthermore, we found that thalamic spikes are not only more informative than retinal ones, as expected, but also more independent. Next, we asked how thalamic spikes gain sensitivity to the emergent features. Explicitly, we found that the emergent features are encoded by retinal spike pairs and then recoded into independent thalamic spikes. Finally, we built a model of synaptic transmission that reproduced our observations. Thus, our results established a link between synaptic mechanisms and the recoding of sensory information.

Introduction

The world we see is represented time and again in the hierarchical stages of visual system (Van Essen et al., 1992). Each of these representations is defined by the activities of neuronal populations. How neurons encode sensory information and the ways in which neural strategies for coding change across synapses are central problems in systems neuroscience.

We addressed these questions using the connection between the retina and lateral geniculate nucleus (LGN) of the thalamus as a model system for several reasons. First, it is the earliest site in the visual pathway where sensory information is transmitted across a synapse between spiking neurons. Second, the synapse is experimentally accessible; spike trains of connected retinal [retinal ganglion cells (RGCs)] and thalamic cells can be recorded simultaneously with extracellular (Bishop et al., 1958; Hubel and Wiesel, 1961; Cleland et al., 1971; Kaplan and Shapley, 1984; Mastronarde, 1987; Sincich et al., 2007) or intracellular techniques (Wang et al., 2007; Koepsell et al., 2009). Third, neural responses in the early visual pathway are somewhat simple and can be well characterized with standard models (Carandini et al., 2005).

Our approach combined experiment with theory. We recorded from connected retinal and thalamic neurons using cell-attached or whole-cell patch recordings and used information theory to compare presynaptic and postsynaptic spike trains. Just as information theory has been used to analyze the communication of messages in telephone lines, it can be used to understand how neurons encode sensory information at single stages in the visual system (Rieke et al., 1997; Borst and Theunissen, 1999).

To learn how information is communicated from one stage in the hierarchy to the next, we identified differences between the features that presynaptic and postsynaptic spikes encoded. For this purpose, we developed a novel “joint encoding model” that subsumed stimulus features encoded by the presynaptic and postsynaptic neurons. Using the model, we separated thalamic features that were merely inherited from retinal spikes from those that emerged, or were “gained” by thalamic spikes as a result of synaptic transmission.

Our results revealed different strategies of neural coding in retina and thalamus and gave insight into underlying synaptic mechanisms. Previous work had shown that information can be conveyed by correlations (or patterns) in spike trains, in addition to single independent spikes (Brenner et al., 2000). By estimating the amount of information encoded in retina, we found that pairs conveyed significantly more information than independent spikes. Each thalamic spike not only encoded more information than a retinal spike (Sincich et al., 2009) but, critically, encoded information more independently. Furthermore, the joint encoding model allowed us to identify specific features that were encoded by pairwise correlations in the retinal spike train and then recoded into independent spikes in the thalamus. Finally, we built a mechanistic model [using time-dependent changes in the efficacy of retinal inputs (Usrey et al., 1998; Carandini et al., 2007; Casti et al., 2008)] that explained our experimental observations.

In sum, our work demonstrates how a correlation code between spike pairs in an early stage of a sensory pathway can be transformed into a more efficient (i.e., independent-spike code) in the next stage by means of a simple synaptic mechanism.

Materials and Methods

Recording.

In vivo patch recordings, in cell-attached or whole-cell mode, were made from adult cats anesthetized with propofol and sufenta (Hirsch et al., 1998; Martinez et al., 2005; Wang et al., 2007) and were digitized at 10 or 25 kHz.

Stimulation.

Visual stimuli were displayed on a cathode ray tube monitor with a monochrome phosphor (x′ = 0.42, y′ = 0.53; CIE 1931) placed at 915 mm from the eyes; the luminance ranged from 0 to 110 cd/m² and the video refresh rate was 144 Hz. The stimuli were Gaussian white noise with a mean and SD of 55 and 18.33 cd/m²; luminance values outside the dynamic range were truncated. The stimulus update rate was 72 or 48 Hz and typical sequences lasted ∼10 min. For some cases, 50 or 60 repetitions of a different stimulus sequence (10–20 s in duration) that had the same statistics as the original sequence was used for cross-validation of models. The spatial arrangement of the stimulus was either a checkerboard or a target pattern of concentric rings centered on the receptive field (see Fig. 2A); both stimuli yielded receptive fields with the same temporal structure (see supplement H, available at www.jneurosci.org as supplemental material). In addition, we often used alternating sinusoidal gratings (Hochstein and Shapley, 1976) to classify neurons as X or Y.

Figure 2.

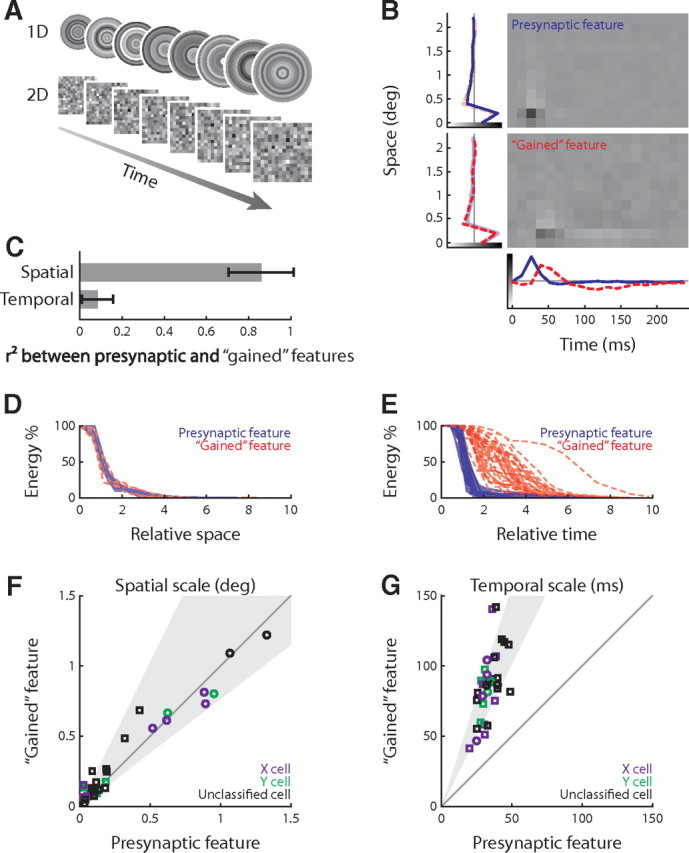
Spatiotemporal analysis of the joint retinothalamic feature space. A, Two types of Gaussian white noise used in this study, checkerboards (2D) and concentric rings (1D). B, The presynaptic and gained stimulus features (receptive fields) for an X-cell; side and bottom plots show the factorized spatial and temporal profiles. C, Comparison of spatial and temporal components of the presynaptic and gained features. Error bars indicate SD. D, E, Cumulative energy of the presynaptic and gained features over space and time; the spatial and temporal scales of the presynaptic features are normalized to 1. F, G, Population comparison (26 RGC–LGN pairs) of the spatial and temporal scales of presynaptic and gained features; the shaded zone shows the mean and SD of the logarithm of gained to presynaptic ratio. The circle and squares indicate data obtained using the one-dimensional and two-dimensional stimuli, respectively.

Joint relevant subspace.

We used spike-triggered average and covariance (STA/STC) (Schwartz et al., 2006) as well as information-theoretic STA and STC (iSTAC) analysis (Pillow and Simoncelli, 2006) to identify the “relevant subspace” (or feature space) that drives neural responses (for details, see supplement B, available at www.jneurosci.org as supplemental material). Note that we use the term “feature” in reference to the stimulus subspace rather than properties of the neural response. We chose a 250 ms temporal window for the spike-triggered analyses and used appropriate spatial windows for each case.

The relevant subspaces for the retinal and thalamic neurons were essentially one-dimensional; STA analysis could be used to recover the relevant feature space efficiently (see supplement G, available at www.jneurosci.org as supplemental material). The features we obtained from these analyses were normalized to unity modulus. Thus, the projection of the stimuli (which were Gaussian distributed and had unity covariance) onto the feature subspace were Gaussian distributed with unity covariance.

To extend the relevant subspace of a single neuron to the “joint relevant subspace” of a synaptically connected pair, we used the following procedure. First, we identified the relevant subspace of the presynaptic neuron and then added the relevant filters for the postsynaptic neuron that were orthogonalized to the presynaptic subspace. Note that we executed the analysis in a nested, sequential manner (Pillow and Simoncelli, 2006) instead of separately (Sincich et al., 2009) for the presynaptic and postsynaptic neurons. Using this scheme, we were able to assess the significance of the features we identified by bootstrap resampling.

Spatiotemporal feature analysis.

The spatial and temporal components of the relevant filters were obtained by least-squared difference factorization. The spatial and temporal extents of visual features were computed as the average radii weighted by filter power. Specifically, the temporal extent is as follows:

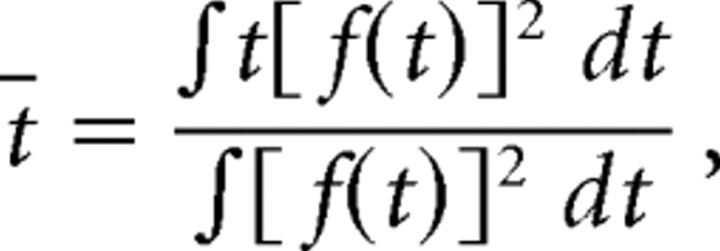where f(t) is the temporal filter. And likewise, the one-dimensional spatial extent is as follows:

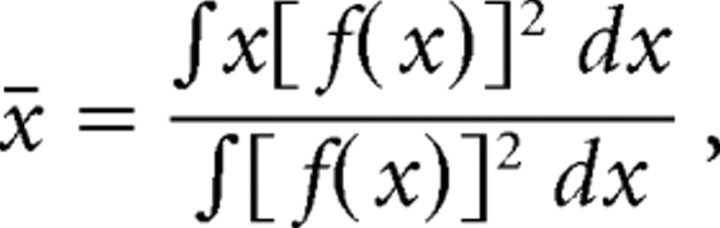where f(x) is the spatial filter. For the two-dimensional checkerboard stimulus, the spatial extent is as follows:

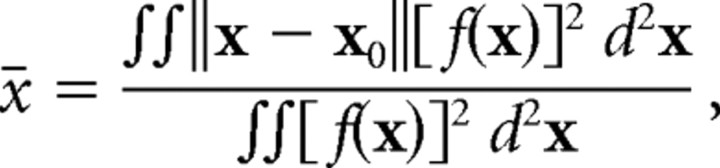where

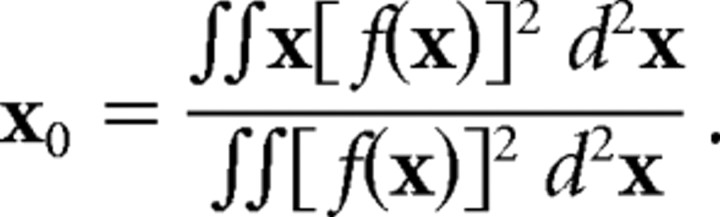Information-theoretic analysis.

Information about the stimulus s conveyed by single spikes can be estimated using the following formula (Brenner et al., 2000):

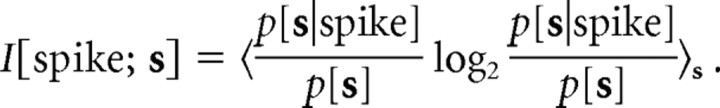To quantify information about particular stimulus features that single spikes covey, we used the following formula:

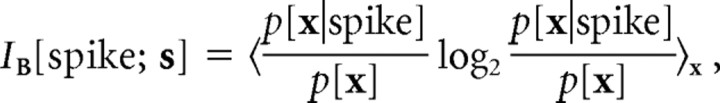where x(t) = s(t) · B is the stimulus projection on a stimulus subspace B.

The prior p[x] was Gaussian distributed because the stimulus was Gaussian white noise. In practice, we approximated the posterior p[x|spike] as a Gaussian whose mean was the STA and whose covariance was the STC. Under such approximations, the formula is simplified to the following:

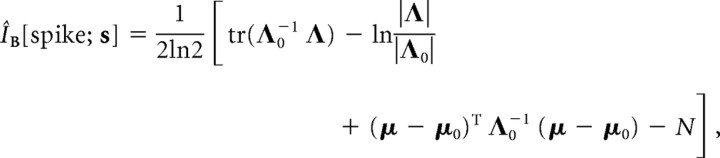where (μ₀, Λ₀) and (μ, Λ) are the mean and covariance of the prior and posterior, and N is the dimensionality of the relevant subspace B. The Gaussian posterior approximation fit the RGC–LGN data well (we will illustrate both the nonparametric estimations of distributions and the Gaussian approximations throughout this paper). Note that, in our case, Î_B[spike; s] is a lower bound for the single-spike information I[spike; s] as follows:

The first inequality holds if the prior is Gaussian (as for our experiments) and the terms are equal when the posterior is also Gaussian. The second relationship always holds because B is a subspace of the stimulus space. We assessed the tightness of the lower bound using methods described in supplement E (available at www.jneurosci.org as supplemental material).

Of course, the accuracy of the estimates was limited by the amount of data available (i.e., how densely the distributions were sampled). We evaluated the variance of the estimation as follows. First, we assessed accuracy by comparing estimates made with progressively smaller datasets. Next, we computed the SD based on the inverse-square-root law of the deviation as a function of the amount of data (Brenner et al., 2000).

We estimated the information conveyed by spike pairs by treating these as compound events. The event “pair(τ) at t” is equivalent to the coincidence of a “spike at t” and another “spike at t + τ.” The spike pair information with respect to a certain subspace B was estimated as follows:

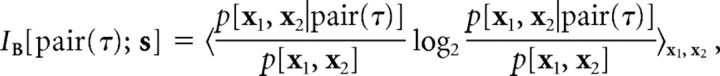where x₁(t) = s(t) · B and x₂(t) = s(t + τ) · B were arguments of two-dimensional probability distributions. Gaussian approximations were also used to estimate efficiently the spike pair information. We then used the concept of “synergy” (Brenner et al., 2000) to assess the role of pairwise correlations in encoding the feature space B as follows:

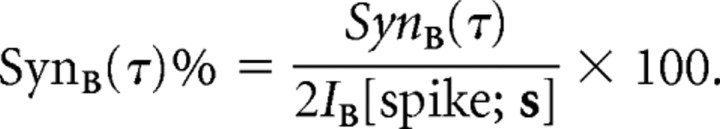Positive synergy indicates that a spike pair conveys more information than is encoded independently by the two component spikes. Conversely, negative synergy indicates that correlations between spikes introduce redundancy in the neural code. Finally, zero synergy indicates that all information is conveyed by independent spikes (higher order correlations among spikes excluded). These analyses were performed at the temporal resolution set by the stimulus update rate (for assessments of information rates made for fine timescales, see supplement E, available at www.jneurosci.org as supplemental material).

Model of retinothalamic transmission.

One can describe retinothalamic transmission of spike trains as a binary parsing process (each spike either relayed or not) by making two biologically realistic assumptions. The first assumption is that each thalamic spike is causally associated with a single retinal spike, and the second is that the latency between the two spikes is negligible (typically shorter than 0.5 ms by our measures). Control studies that we performed suggested that both of these assumptions are reasonable (see supplement C, available at www.jneurosci.org as supplemental material). Thus, we built models of retinothalamic transmission as “binary parsing” processes (see Fig. 6A), as follows. Let the retinal spike train be denoted {t_i}, and the binary “relayed” state {μ_i}. The resulting simplified model of retinothalamic spike transmission is then a map of {t_i} to {μ_i}. With the additional assumption that μ_i does not depend on its own history {μ_i, μ_{i − 1}, …}, the output of the model {μ_i} is then an instance of a stochastic variable with the binary-transfer probability distribution as follows:

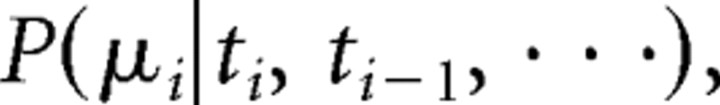which forms the deterministic component of the model. Note that the relayed probability P(μ_i = 1|t_i, t_i−1, …) averaged over the subindex i is also known as the efficacy, which is defined as the probability that a given presynaptic spike pattern {t_i, t_i−1, …} elicits a postsynaptic spike (Usrey et al., 1998). The transfer probability distribution can be written as conditioned on interspike intervals P(μ_i|t_i−t_i−1, t_i−1 − t_{i −2}, …).

Figure 6.

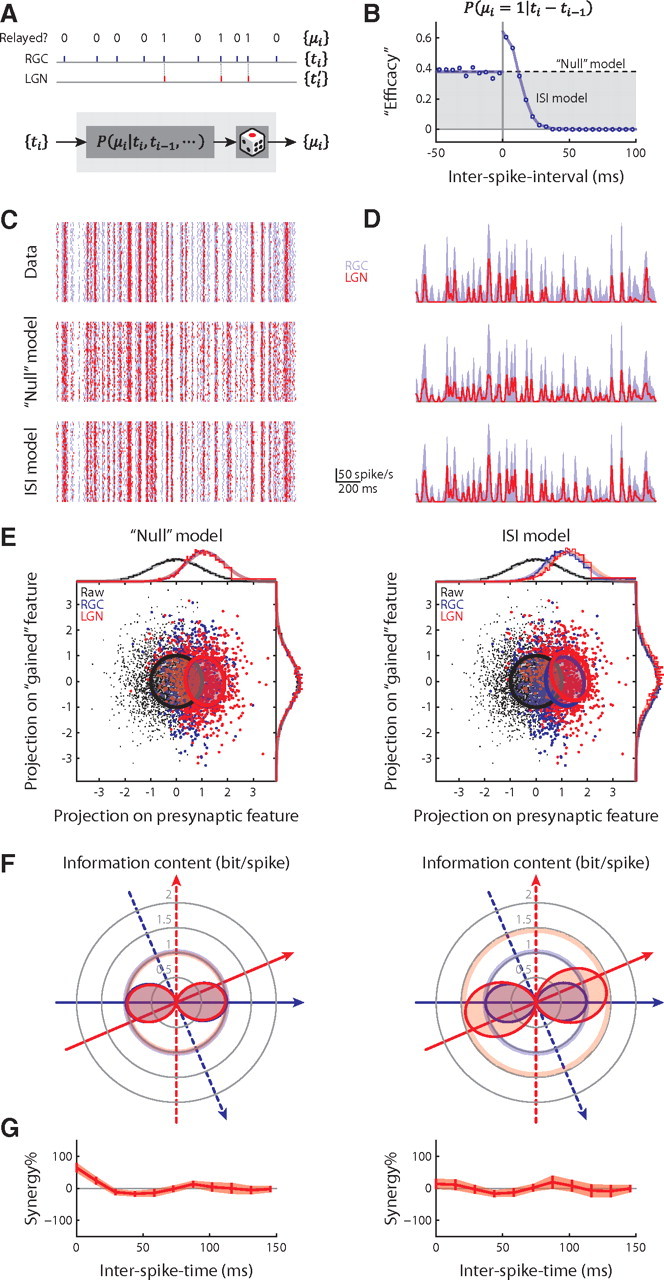
“Paired-spike enhancement” as a model of the retinothalamic transmission. A, Retinothalamic transmission illustrated as binary “editing” of the retinal spike train shown above a model of the process. B, Efficacy plotted as a function of interspike interval for the example X-cell pair. C, Rasters of 50 trials of the actual RGC spike train superimposed on the actual and modeled LGN spike trains. D, Instant firing rates of the RGC and the actual and modeled LGN cells. A Gaussian window of 5 ms was used to estimate the firing rates. E, Reconstructions of Figure 1F for the “null” and interspike interval models. F, Reconstructions of Figure 3C for the two models. G, Reconstructions of Figure 4A, bottom, for the two models.

We constructed two versions of the model. The first, the “null” model, contained a transfer-probability distribution that did not depend on spike history: P(μ_i = 1)= $\frac{{\overline{r}}_{\text{LGN}}}{{\overline{r}}_{\text{RGC}}}$ and P(μ_i = 0) = 1 − $\frac{{\overline{r}}_{\text{LGN}}}{{\overline{r}}_{\text{RGC}}}$ (r̄_RGC and r̄_LGN being the average firing rates of the presynaptic and postsynaptic neurons); this essentially rescales retinal firing rate to match the postsynaptic firing rate. The second, the interspike interval model, used a transfer-probability distribution conditioned only on the interspike interval that immediately preceded the retinal spike, P(μ_i|t_i − t_i−1); this was empirically estimated as the efficacy of the preceding interspike interval (see Fig. 6B). We also evaluated second-order interspike interval models P(μ_i|t_i − t_i−1, t_i−1 − t_i−2) for a control study (results not shown). Both models were cross-validated.

Results

Our sample includes 26 retinal and thalamic neuronal pairs in 12 adult cats; all records were obtained by using patch recordings in cell-attached or whole-cell mode (Wang et al., 2007). Figure 1A shows an example of a cell-attached recording from an X-cell in the LGN. The trace includes two classes of stereotyped events, action potentials and “S-potentials,” extracellularly recorded retinogeniculate EPSPs (Hubel and Wiesel, 1961; Bishop et al., 1962; Kaplan and Shapley, 1984). By using a custom method to sort these events (Wang et al., 2007), we were able to recover the spike trains of the thalamic relay cell and the presynaptic RGC (Fig. 1B).

Figure 1.

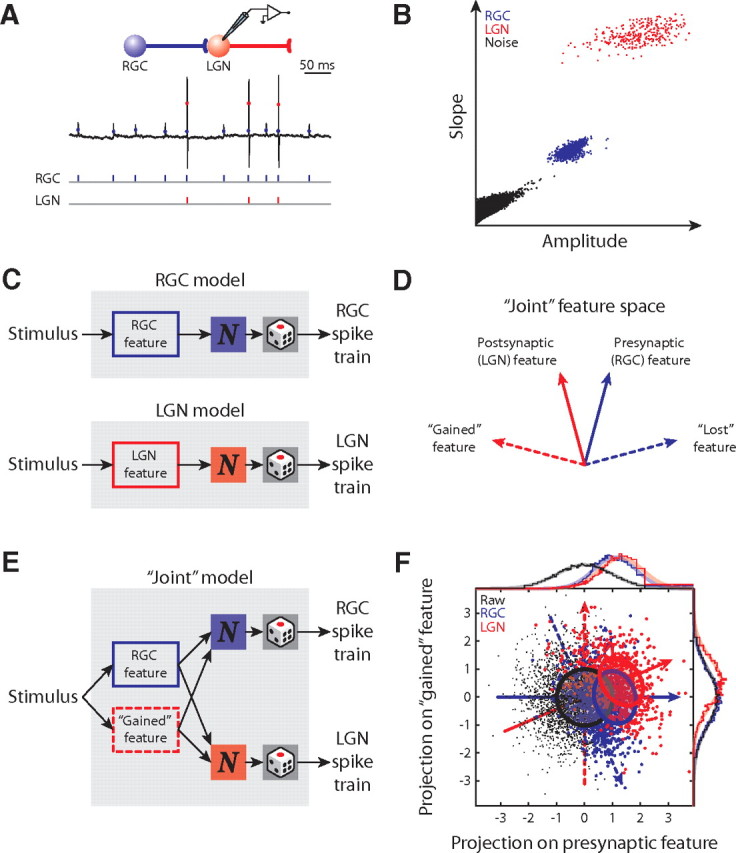
Identification of the joint relevant subspace across the retinothalamic synapse. A, “Cell-attached” recording from the LGN and the detected retinal (blue) and thalamic (red) spike trains. B, Clusters of sorted retinal and thalamic spikes are discrete from each other and noise. C, Schematic diagrams of separate linear-nonlinear-Poisson encoding models for RGC and LGN neurons. D, A diagram of the joint feature space of the retinal and thalamic neurons with presynaptic (solid blue), postsynaptic (solid red), gained (dashed red), and lost (dashed blue) features represented as vectors. E, A schematic diagram of the joint encoding model and its use of the joint relevant subspace of both RGC and LGN neurons. F, Joint feature space for an X-cell pair; the presynaptic and postsynaptic relevant subspaces are both one-dimensional. The raw (black), RGC-spike-triggered (blue), and LGN-spike-triggered (red) stimulus ensembles are illustrated as scatterplots and marginal histograms (above and right); the ovals and smooth lines represent the Gaussian approximations of the distributions. The luminance values are dimensionless, unity Gaussian distributions. Conventions here apply to all remaining figures.

The joint encoding model

Variations of the linear-nonlinear (LN) model (Carandini et al., 2005) are often used to characterize the encoding of sensory information in the early visual pathway. The linear components of the model are filters that map the high-dimensional spatiotemporal stimulus onto the low-dimensional subspace to which a neuron is sensitive (in essence, the receptive field). This subspace is usually referred to as the “feature space” or the “relevant subspace” (Agüera y Arcas and Fairhall, 2003; Sharpee et al., 2004; Bialek and de Ruyter van Steveninck, 2005). Furthermore, the nonlinear components of the model determine how neural responses are generated from the output of the filters.

If one wanted to explore neural coding across a retinothalamic synapse, it would seem straightforward to compare individual models for the presynaptic (RGC) and the postsynaptic (LGN) neurons (Fig. 1C). However, each single model treats the presynaptic and postsynaptic feature space separately. Thus, this strategy fails to describe how features are transformed across the synapse. Rather, it is necessary to use a common feature space to explore how neurons on both sides of the synapse process specific features. Therefore, we developed a novel joint encoding model whose linear filters subsume the feature spaces of the presynaptic and postsynaptic neuron. We schematize the presynaptic and postsynaptic feature spaces as vectors (solid blue and solid red, respectively) in Figure 1D. The joint relevant subspace is the plane spanned by the presynaptic and postsynaptic subspaces (Fig. 1D); it has higher dimensions than either the presynaptic or the postsynaptic feature spaces unless they are identical. Moreover, the orthogonal complements of the presynaptic and postsynaptic subspaces (Fig. 1D, dashed lines) identify the features that emerge, or are “gained,” and those that vanish, or are “lost,” across the synapse.

The joint model can be built with any set of linear filters that form a basis of the joint relevant subspace. In practice, we used the presynaptic and the gained feature (Fig. 1E). We obtained these filters from the simultaneously recorded retinal and thalamic spike trains by using conventional spike-triggered average/covariance (Schwartz et al., 2006) in addition to information-theoretic approaches (Pillow and Simoncelli, 2006) (for details, see supplement B, available at www.jneurosci.org as supplemental material). In our case, the presynaptic and postsynaptic feature spaces were basically one-dimensional and were not identical; thus, they formed a two-dimensional joint feature space. Figure 1F depicts the distributions of the presynaptic and postsynaptic spike-triggered stimulus ensembles in the joint-encoding model for an X-cell pair. The arrows mark the presynaptic, postsynaptic, gained, and lost features of the subspace. Note that the distributions of the presynaptic and postsynaptic spike-triggered stimulus ensembles are significantly different from each other (blue vs red), suggesting that the feature sensitivity within the joint relevant subspace is altered across the retinothalamic synapse.

Temporal, but not spatial, features emerge across the retinothalamic synapse

Next, we quantified the difference between the visual features encoded by retinal versus thalamic spikes. We used two types of spatiotemporal Gaussian noise patterns as stimuli (Fig. 2A); these were the commonly used checkerboard or a target pattern that was centered on the receptive field (see Materials and Methods). The presynaptic and gained features of the X-cell pair in Figure 1A are illustrated in Figure 2B (the stimulus was the target pattern). As for all retinothalamic cell pairs, both the presynaptic and the gained features were mostly space–time separable (Jones and Palmer, 1987; Wolfe and Palmer, 1998); the separated spatial and temporal components (lines plotted in Fig. 2B) accounted for 89 ± 7% (for the presynaptic) and 72 ± 14% (for the gained) of total variance (n = 26). [The residual variance might be accounted for, in part, by the modest space–time inseparable component of the receptive field (e.g., the slight delay of the surround relative to the center) and noise.]

The main differences between the retinal and thalamic features were temporal rather than spatial, as follows. Qualitatively, the presynaptic and the gained features resembled each other in space but not time (Fig. 2B). Quantitatively, the spatial features were very similar, whereas the temporal ones were nearly orthogonal, as measured by Pearson's r² (Fig. 2C). The features differed not only in shape but also in size, or extent [Fig. 2D,E, shows data for the population (n = 26)]. The spatial and temporal extents (see Materials and Methods) of the presynaptic and gained features are depicted as plots of cumulative energy over time, scaled so that the extents for the presynaptic features equaled 1. There was little change in the spatial extents of the two features, across the synapse (Fig. 2D); by contrast, the temporal extents changed significantly (Fig. 2E). Importantly, the cumulative energy stretched farther back in time for the gained than for the presynaptic features, which suggests that thalamic spikes are more sensitive to the history of the stimulus than are retinal ones. In addition, the variance in temporal extent was much higher for the gained than for the presynaptic feature (Fig. 2G). These results held for both the X and Y pathways. Thus, the retinothalamic synapse seems to create temporal diversity in the thalamus.

Specific stimulus features can be conveyed by thalamic and retinal spikes with more or with less efficiency

So far, we have described the differences between visual features that are represented on either side of the retinothalamic synapse. Next, we asked how much information each retinal or thalamic spike encoded about particular stimulus features: the larger the amount of information that a single spike conveys about a given feature, the greater the efficiency of the code for that feature.

By using an LN encoding model fitted to the data, we established a lower bound on the amount of information conveyed by single spikes (see Materials and Methods). Then, using the joint-encoding model, we estimated the total information about the entire relevant subspace that single spikes encoded; this analysis was done for all RGC–LGN pairs (Fig. 3A). Consistent with a recent study (Sincich et al., 2009; Uglesich et al., 2009), single spikes in the thalamus were more informative than those in the retina.

Figure 3.

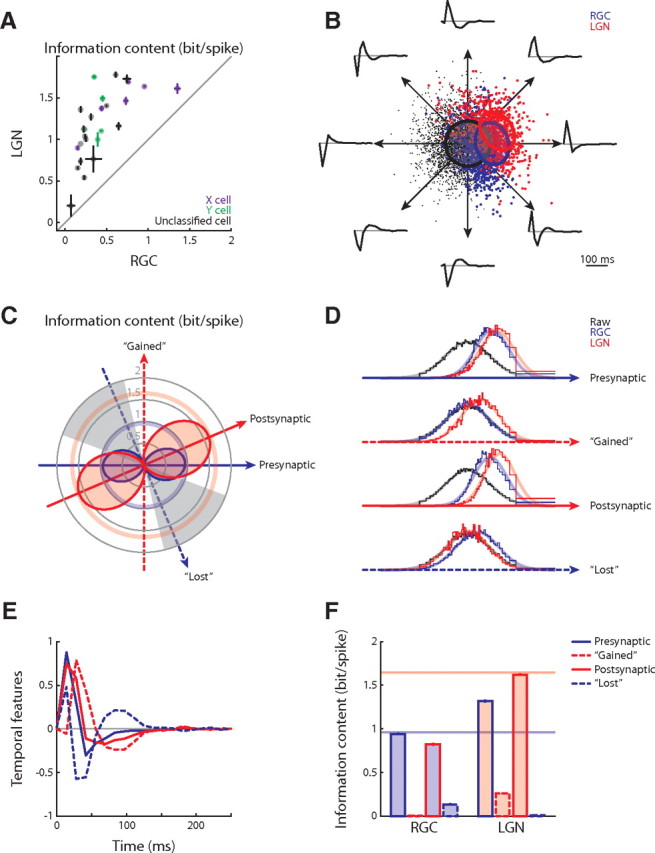
Change of single-spike code across the retinothalamic synapse. A, Single-spike information across the retinothalamic synapse for the population (n = 26); error bars show SDs. B, The RGC–LGN joint feature space for the example X-cell pair in Figure 1F; each direction within the plane represents a distinct feature. Only temporal components (8 examples) are illustrated because spatial components are nearly unaltered. C, Information content about the joint feature space illustrated as polar plots. The angular coordinate corresponds to different features and the radial coordinate represents information in single spikes; the solid arrows mark the presynaptic and postsynaptic features, and the dashed arrows indicate the gained and lost features, according to the conventions in Figure 1. The information about particular features falls on the filled, dumbbell-shaped curves and is limited by the pale pink and blue circles, which mark the single-spike information about the total joint feature space. Last, the gray sectors indicate the subset of features about which a thalamic spike conveyed less information that a retinal one. D, Marginal distributions of the raw, RGC-spike-triggered and LGN-spike-triggered stimulus ensembles along the presynaptic, gained, postsynaptic, and lost features. E, The presynaptic, gained, postsynaptic, and lost temporal features. F, The presynaptic and postsynaptic single-spike information about the presynaptic, gained, postsynaptic, and lost features; the horizontal lines mark the information for the joint feature space.

We then compared the amounts of information that retinal and thalamic spikes conveyed about specific features in the joint relevant subspace. We illustrate the result of the analysis with an RGC–LGN X-cell pair that we will continue to use as an example in the remaining figures. The two-dimensional joint subspace for the example pair is depicted in Figure 3B (same as in Fig. 1F). Here, each direction represents a distinct stimulus feature, as illustrated by eight example features (only the temporal components are plotted since the spatial were nearly identical). The efficiency with which the presynaptic and the postsynaptic spikes encoded these stimulus features is displayed in Figure 3C as a polar plot of the amount of information each spike conveyed. Although, on average, each thalamic spike was more informative about the whole subspace than a retinal spike (thick circles in pale blue and red), the relative information about specific features differed (blue and red dumbbell-shaped curves). For some features (Fig. 3C, unshaded sectors), the postsynaptic spike was more informative, whereas for other features (Fig. 3C, gray sectors), the presynaptic spike was more informative. Finally, we compared the amount of information encoded by retinal and thalamic spikes for four characteristic features: presynaptic, postsynaptic, gained, and lost (Fig. 3E). Marginal distributions of the raw, presynaptic, and postsynaptic spike-triggered stimulus ensembles along these features are plotted in Figure 3D; the more the spike-triggered distributions (colored) differ from the raw stimulus distribution (black), the more information is conveyed by spike rate. The information that the presynaptic and postsynaptic spikes convey about each of these four features is quantified in Figure 3F. The average thalamic action potential was more informative about the presynaptic feature than the average retinal spike, suggesting a thalamic refinement of the retinal code. In addition, the thalamic spike encoded information about the gained feature, whereas the retinal spike did not, revealing a marked change in feature selectivity across the synapse.

Even though our analysis suggests that single spikes in the thalamus convey more information than those in the retina, this improved efficiency did not necessarily hold for all encoded features. Rather, some features were encoded more efficiently in the thalamus than in the retina and others less. We next explore the mechanisms by which the thalamic spikes become more informative about certain features, such as the gained feature.

Thalamic spikes encode information more independently than retinal spikes

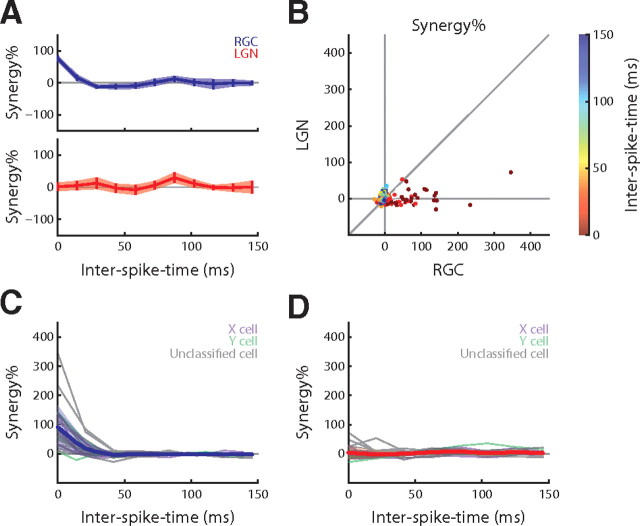
Thus far, we have described the efficiency with which individual spikes on either side of the retinothalamic synapse encode visual information. We now move forward to quantify information that is encoded in temporal patterns of spikes (Brenner et al., 2000). Correlated activity, such as spike pairs, can convey stimulus information that is not encoded by single spikes. To explore the possibility of a correlation code in the retina or the LGN, we estimated the specific information about the joint relevant subspace transmitted by pairs of spikes with various interspike times. We also quantified the corresponding synergy (see Materials and Methods), a metric that addresses how independently each spike in a pair encodes information. For this type of analysis, a spike pair is defined as two spikes with a specific temporal offset, regardless of other spikes occurring before, after, or in between (Brenner et al., 2000). This temporal offset is named interspike time in contrast to the term interspike interval, a term often to name the delay between two adjacent successive spikes.

Synergy is zero if the spikes encode information independently, whereas positive and negative synergy indicates cooperativity or redundancy of the pair code, respectively. The percentage of synergy as a function of interspike time for the sample cell pair is shown in Figure 4A. Presynaptic spikes with short interspike times showed significantly positive synergy, whereas the postsynaptic synergy did not depart from zero. This suggests that the thalamic spikes encode information about the joint feature space independently, whereas the retinal ones are cooperative.

Figure 4.

Change of pairwise correlation code across the retinothalamic synapse. A, Percentage of pairwise synergy computed over the joint feature space for the X-cell pair. B, The synergy in LGN plotted against synergy in RGCs for all spike pairs (n = 26); interspike time is color coded. C, D, Plots of synergy as a function of interspike time for all individual RGCs (left) and relay cells (right) (gray lines); the population mean (thick colored line) and SD (shade) overlie the curves for individual cells; Gaussian approximations are shaded for clarity.

To compare presynaptic versus postsynaptic synergy directly for all cell pairs, we plotted the thalamic against the retinal synergy at different (color-coded) interspike times (Fig. 4B). If the synergy had been the same for the retinal and thalamic spike trains, the points would have fallen along the diagonal. However, many points clustered near or along the horizontal axis, indicating that the postsynaptic synergy was essentially zero, that is, thalamic spikes were independent. By contrast, the presynaptic synergy was often positive, that is, the retinal spikes were synergistic. We also display the presynaptic and postsynaptic synergy as a function of interspike time separately, for every RGC and relay cell (Fig. 4C,D, gray lines, respectively), with the means and SDs overlaid as a thick blue (for RGC) or red (for LGN) line. Like the example depicted in Figure 4A, nearly all retinal spike trains had positive synergy for short interspike times; thalamic spike trains, however, had synergy near zero. In aggregate, these results suggest that spikes in the thalamus encode the joint relevant subspace more independently than do those in the retina.

The retinothalamic synapse transforms a correlation code to a single-spike code

The previous analysis showed that synergistic encoding of information by correlation between spikes is more prominent in retinal than in thalamic spike trains. This observation suggests that there is a channel through which information about the gained feature is transmitted across the retinothalamic synapse. Specifically, we tested the hypothesis that the thalamus is able to extract information about the gained feature from correlations between retinal spikes, even though such information is not conveyed by single retinal spikes (Fig. 3C).

To test this hypothesis, we estimated how much information pairwise correlations between retinal spikes encoded about specific features (Fig. 5A). For most of the cell pairs, we found significant positive synergy for both the presynaptic and the gained feature. In particular, the synergy for the gained feature was positive at particular interspike times (Fig. 5A, middle). The synergy for a control, “irrelevant” feature was not significant (Fig. 5A, right); this feature was randomly generated and forced to be orthogonal to the relevant subspace (Fig. 5B, inset, right). Furthermore, plots of the amount of information conveyed by single (gray lines) and paired (blue, red and orange lines) retinal spikes (Fig. 5B) show that pairs with short interspike times convey significant amounts of information about the gained feature, whereas single spikes convey none.

Figure 5.

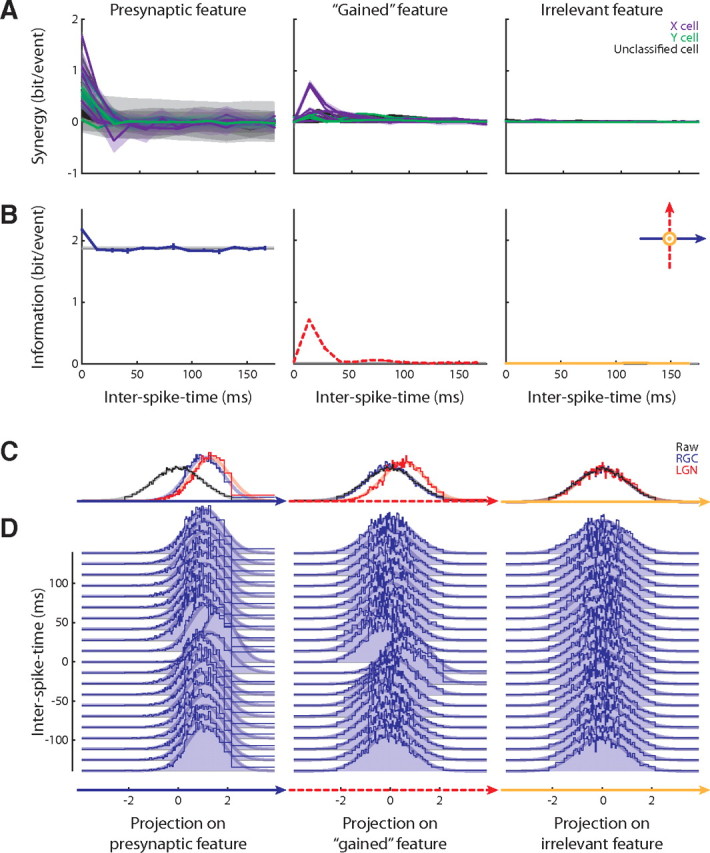
Transformation of retinal correlation code into thalamic single-spike code explains the changes in coding efficiency across the retinothalamic synapse. A, The pairwise synergy for three different features: presynaptic (left), gained (middle), and irrelevant, or control (right) for the population (n = 26); the shaded band represents the SD. B, Information conveyed by single spikes and spike pairs for the example X-cell pair. The horizontal gray lines mark twice the amount of information conveyed by a single spike (these cannot be seen in the middle and right panels because they coincide with the horizontal axes). The colored lines plot the information conveyed by spike pairs. The inset illustrates that the irrelevant feature is orthogonal to the relevant subspace. C, Marginal distributions of the raw, RGC-spike-triggered and LGN-spike-triggered stimulus ensembles along the three features for the example X-cell pair. D, Marginal distributions of the RGC-spike-pair-triggered stimulus ensembles along the three features, families of distributions shown according to the intervals between RGC spikes in a pair.

This finding is also reflected by the marginal distributions of the raw, retinal and thalamic spike-triggered stimulus ensembles and the retinal spike pair-triggered ensembles, illustrated in Figure 5C (similar to Figs. 1F, 3D) and Figure 5D, respectively. The distributions of the retinal (single) spike-triggered ensemble and the raw stimulus ensemble were identical with each other when projected onto the gained feature (Fig. 5C, middle). However, the distribution of the retinal spike pair-triggered ensemble (for interspike times between 0 and 50 ms) differed significantly from that of the raw ensemble when projected on the gained feature (Fig. 5D, middle). Thus, retinal ganglion cells indeed encode information about the gained feature, but in pairwise correlations rather than single, independent spikes.

Paired-spike enhancement as a mechanism for retinothalamic recoding

What synaptic processes could explain how information available in pairwise correlations between retinal spikes might be read out and recoded as single spikes in the thalamus? Past work points to the mechanism of “paired-spike enhancement” (Usrey et al., 1998). This term describes the experimental observation that short interspike intervals in the presynaptic spike train increase the efficacy of synaptic transmission (Usrey et al., 1998), presumably as the result of temporal summation of retinogeniculate EPSPs (Carandini et al., 2007; Casti et al., 2008). The efficacy is defined as the fraction of presynaptic spikes that are relayed by the postsynaptic neuron.

We built mechanistic models to determine whether paired-spike enhancement could account for recoding at the retinothalamic synapse. To build the models, we assumed that transmission across the retinothalamic synapse falls into three conceptual categories (Levine and Cleland, 2001): (1) retinal spikes that fail to be relayed, (2) retinal spikes that are successfully relayed, and (3) anonymous thalamic spikes without a retinal trigger. We disregarded the third case (see controls in supplement C, available at www.jneurosci.org as supplemental material) because there are very few anonymous spikes (Sincich et al., 2007); typically, these are produced during bursts (Wang et al., 2007), which occur reliably but rarely during vision (Guido and Weyand, 1995; Usrey et al., 1999) and are better driven by naturalistic stimuli than by noise (Lesica and Stanley, 2004; Denning and Reinagel, 2005). Thus, we were able to model transmission as a binary selection (i.e., relayed or not) of the retinal spike train (Fig. 6A) (for details, see Materials and Methods).

We used two models to simulate synaptic transmission, the “null” model and the interspike interval model. In the null model, the relayed retinal spikes are randomly selected based on the efficacy of single spikes. By contrast, the interspike interval model used the efficacy of the interval between preceding spikes, as illustrated the sample cell pair in Figure 6B (see Materials and Methods).

As expected, the interspike interval model matched the actual instantaneous firing rate better than the null model did (example in Fig. 6C,D). Surprisingly, this model, despite its simplicity, was also able to reproduce three of our major observations. By contrast, the null model predicted none. The observations are as follows: (1) the thalamic spike became more selective to the presynaptic feature than the retinal spike and developed selectivity to the gained feature (compare Fig. 6E,F with Figs. 1F, 3C); (2) thalamic spikes were more informative than the retinal impulses (compare Fig. 6F with Fig. 3C); (3) thalamic spikes with short interspike times encoded information more independently than retinal action potentials (compare Fig. 6G with Fig. 5A, bottom).

The observation that the interspike interval model alone was able to describe the experimental findings held for our dataset. Only this model was able to reproduce the increase in the information content of each postsynaptic spike (Fig. 7A) [albeit the increase in information the model achieved was smaller than that observed empirically (Fig. 7B)]. The interspike interval model also predicted the enhanced selectivity to the presynaptic feature precisely (Fig. 7C) and captured the emergent selectivity to the gained feature in large measure (Fig. 7D) (for reasons that might explain the quantitative disparity between modeled and real results, see Discussion). Last, the interspike interval model correctly predicted that the synergy of thalamic spike pairs is near zero for all interspike times, whereas the null model did not (Fig. 7E,F). Thus, our results suggest that paired-spike enhancement can explain recoding across the retinothalamic synapse.

Figure 7.

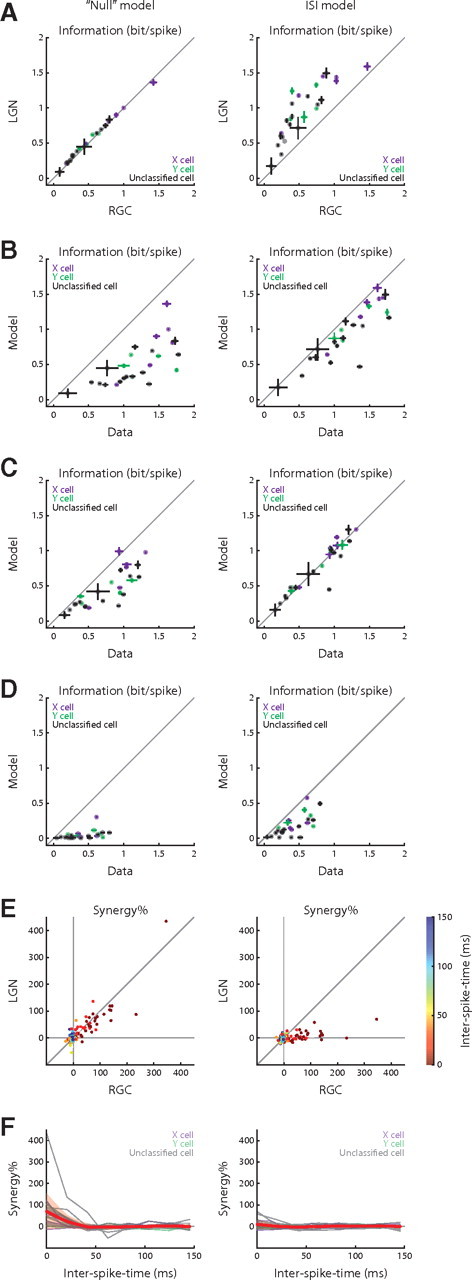
Performance of the models of retinothalamic transmission. A, Reconstructions of Figure 3A for the “null” and interspike interval models. B–D, Model–data comparison of the LGN single-spike information content for the two models; the information contents are estimated with regard to the joint feature space (B), the presynaptic feature (C), and the gained feature (D). E, Reconstructions of Figure 4B for the “null” and interspike interval models. F, Reconstructions of Figure 4D for the two models.

Discussion

Here, we addressed the basic question of how the representation of a stimulus changes across a synapse by recording from connected retinal and thalamic neurons during vision. First, we used a novel computational approach that permitted identification of visual features that thalamic spikes detect but that presynaptic retinal spikes do not. We then asked how the thalamus gained selectivity to these emergent features by assessing information encoded by temporal correlations of retinal spikes rather than single action potentials. This analysis revealed that the gained or emergent features were conveyed by pairwise correlations within retinal spike trains. Finally, we used computational models to show how the mechanism of paired-spike facilitation (or enhancement) could explain the transformation from a pairwise to a single spike code. Our work provides a first biological example of the transformation of a correlation code into an independent code across a synapse through which sensory information flows from the periphery to the brain.

Resolving visual features encoded by synaptically connected neurons

Classical linear-nonlinear models provide a means to identify the particular features of the stimulus that a single neuron encodes (Carandini et al., 2005). Two linear-nonlinear models can be used to describe separately the features encoded by two different neurons (Sincich et al., 2009). However, if one wants to understand how information about various features propagates from one cell to the next—which features are inherited, gained, or lost—a single model that encompasses the responses of both neurons is needed. Thus, we built a linear-nonlinear joint encoding model that subsumes the features (relevant subspaces) that the presynaptic and postsynaptic spikes encode (see Materials and Methods). This framework revealed that thalamic neurons inherited selectivity for the spatial features encoded by their retinal inputs, but gained sensitivity to different temporal features, consistent with recent work (Sincich et al., 2009).

Comparing the efficiency with which spikes encode information in the retina and thalamus

We compared how efficiently thalamic and retinal spikes encoded visual information in general as well as with respect to specific features. For the general case, we estimated the mutual information between single or paired spikes and the stimulus (Brenner et al., 2000). The results showed that relay cells encode visual information more efficiently and more independently than do their retinal inputs. That is, each thalamic action potential transmitted more information about the stimulus than each retinal impulse, consistent with previous work (Sincich et al., 2009; Uglesich et al., 2009). Moreover, in thalamus, each spike in a pair encoded information independently, whereas in retina spike pairs encoded more information than two separate spikes.

Critically, our joint encoding model allowed us to use information theory to explore differences in the efficiency of the neural code with respect to individual features across the synapse. The most dramatic difference in efficiency was for the gained features that emerged in the geniculate. Specifically, thalamic neurons transmitted a substantial amount of information about these features, whereas their retinal inputs conveyed almost none. Otherwise, remaining features were encoded either with greater or lesser efficiency in thalamus than retina.

From a pairwise correlation code to an independent spike code

How do retinal firing patterns transmit information about the emergent (gained) features that single thalamic spikes convey? Since retinal spikes encoded the relevant features synergistically, we hypothesized that information about the gained feature might be embedded in the structure of presynaptic firing patterns. As predicted, we found that information about the emergent thalamic features was encoded by pairwise correlations between retinal impulses.

These results have bearing on the theoretical limit that the “data processing inequality” (Cover and Thomas, 1991) imposes on the amount of information per unit time that can be transmitted across a synapse. It had been suggested that this limit is set by the total amount of information the presynaptic neuron transmits using single spikes (Sincich et al., 2009). However, if information in correlations within the presynaptic spike train were recoded postsynaptically as independent spikes, then the rate of information transmitted by those postsynaptic impulses could exceed that coded solely by independent presynaptic spikes without violating the data processing inequality (see supplements D, F, available at www.jneurosci.org as supplemental material).

Experimental caveats

Three main techniques are used to record simultaneously from synaptically coupled neurons in retina and thalamus, each with advantages and disadvantages. One approach involves cross-correlation analysis of spikes recorded with separate electrodes for retina and thalamus (Usrey et al., 1998). We adopted the remaining methods; these use a single electrode to record retinal inputs and thalamic spikes. One, an extracellular technique, detects retinogeniculate EPSPs (“S-potentials”) large enough to be sensed near the surface of the relay cell (Bishop et al., 1958, 1962; Hubel and Wiesel, 1961; Kaplan and Shapley, 1984; Sincich et al., 2007, 2009). The other method, intracellular recording (Wang et al., 2007), reveals additional inputs too small to generate “S-potentials.” Unlike dual electrode recording, the single electrode methods permit selection of the dominant retinal input and do not rely on statistical inference to determine connectivity. However, single electrode recordings share a disadvantage. Since all events are mixed in one signal, spikes might occlude the triggering EPSPs and seem to arise from an anonymous source. To ask whether masked EPSPs could influence our result, we compared results using the retinal train we detected to one in which an EPSP was added for each anonymous spike (see supplement A, available at www.jneurosci.org as supplemental material). Both sets of results were the same.

Mechanistic models of retinothalamic processing

Past work used computational models to show how physiological processes, such as postsynaptic depression (Goldman et al., 2002), can remove temporal correlations from the neural code. To explore how a correlation code might be transformed to a single spike code, we built a simple model based on a mechanism that is important for relaying spikes across the synapse (Usrey et al., 1998; Carandini et al., 2007; Casti et al., 2008). The mechanism is paired-spike enhancement (as the interval between two inputs shortens, the probability of evoking a postsynaptic spike increases). The model reproduced our main results. Specifically, the model captured the conversion of a correlation code in retina to an independent code in thalamus for the gained feature, preserved the features that thalamus inherited from retina, and accounted for the increase in the efficiency of thalamic spikes. Thus, a simple mechanism was able to account for our main results. Still, the amount of information about the gained feature the model predicted was less than the actual, even if higher order statistics of retinal spike trains were taken into account. The performance of the model might be improved by including additional biological components like cortical feedback, additional retinal inputs, or local inhibition. The first two options seem the least plausible of the three. Current evidence does not support a strong role for cortical feedback; ablating visual cortex does not seem to influence size of thalamic receptive fields (Cudeiro and Sillito, 1996), although it does affect spike timing (Wörgötter et al., 1998). Also, the gained feature is temporal not spatial, so undetected retinal inputs probably cannot explain the difference between the simulated and actual results, as follows. If the sensitivity to the gained feature did not result from retinothalamic processing per se, but reflected input from additional retinal inputs that were not detected, then spatial features should be transformed in thalamus. This is because the receptive fields of neighboring ganglion cells are displaced (Wässle et al., 1981; Peichl and Wässle, 1983) (a case in which we identified spike trains from two ganglion cells supports this assumption; see supplement A, available at www.jneurosci.org as supplemental material). By contrast, previous theoretical studies support a role for local inhibition; these suggest that intrathalamic inhibition influences the temporal precision of thalamic responses (Butts et al., 2007) and helps encode visual information (Babadi et al., 2007).

Functional roles for emergent temporal features in the thalamus

Numerous studies have shown that thalamic responses vary widely and often outlast retinal responses by long times (Mastronarde, 1987; Wolfe and Palmer, 1998). This widespread distribution of spike latency with respect to the stimulus is thought to serve different functional roles. For example, a leading model of direction selectivity in cortex depends on convergent input from relay cells with staggered timings (Wolfe and Palmer, 1998). Our results suggest that the recoding of visual features by means of paired-spike enhancement at the retinogeniculate synapse might contribute to temporal diversity in thalamus.

Recoding of sensory representations

The representation of sensory information is continuously transformed by neural circuits. Past studies of the somatosensory system (Ahissar and Arieli, 2001; Arabzadeh et al., 2006) had suggested that temporal patterns of firing in the periphery might be transformed to rate codes at later stages of processing. To our knowledge, our work provides the first biological example of how information about a sensory feature is encoded by temporal correlations in the presynaptic spike train and then recoded (with enhanced efficiency) by independent postsynaptic spikes. This transition from correlation to rate coding might be iterated downstream in the cortex, continuing to increase the efficiency and independence of the neural code. We hope that our approach of using a model that combines presynaptic and postsynaptic encoding will be useful for exploring diverse regions of the brain.