Model of Tryptophan Metabolism, Readily Scalable Using Tissue-specific Gene Expression Data

Background: Changes in tryptophan metabolism are associated with various diseases.

Results: A comprehensive model of human tryptophan metabolism was constructed and verified with existing experimental data.

Conclusion: The subtle balance of tryptophan derivatives required for proper brain function is sensitive to alterations in peripheral tissues.

Significance: The model is applicable as a diagnostic tool to study disease related changes in tryptophan metabolism.

Abstract

Tryptophan is utilized in various metabolic routes including protein synthesis, serotonin, and melatonin synthesis and the kynurenine pathway. Perturbations in these pathways have been associated with neurodegenerative diseases and cancer. Here we present a comprehensive kinetic model of the complex network of human tryptophan metabolism based upon existing kinetic data for all enzymatic conversions and transporters. By integrating tissue-specific expression data, modeling tryptophan metabolism in liver and brain returned intermediate metabolite concentrations in the physiological range. Sensitivity and metabolic control analyses identified expected key enzymes to govern fluxes in the branches of the network. Combining tissue-specific models revealed a considerable impact of the kynurenine pathway in liver on the concentrations of neuroactive derivatives in the brain. Moreover, using expression data from a cancer study predicted metabolite changes that resembled the experimental observations. We conclude that the combination of the kinetic model with expression data represents a powerful diagnostic tool to predict alterations in tryptophan metabolism. The model is readily scalable to include more tissues, thereby enabling assessment of organismal tryptophan metabolism in health and disease.

Introduction

Tryptophan metabolism plays a number of important roles in human physiology. It participates in the regulation of growth, moods, sleep-wake cycles, and immune responses. In addition to being an essential amino acid, tryptophan is the precursor of important molecules such as serotonin, melatonin, and NAD and is converted into several neuroactive compounds on its route to these products. Imbalances in tryptophan metabolism have been associated with neurological diseases such as Parkinson (1), Alzheimer (2), and Huntington (3) as well as gastrointestinal disorders (4). It has also been shown that some types of cancers exhibit alterations of tryptophan utilization that enable them to evade the immune responses of the host (5–8).

After carrier-mediated uptake into cells, tryptophan can be used as a substrate for six different reactions, thereby entering the individual branches of tryptophan metabolism see (see Fig. 1). The kynurenine and serotonin pathways are the two most important branches with regard to the formation of bioactive intermediates. The fate of tryptophan utilization is tissue-specific. Most dietary tryptophan is metabolized in the liver, and most of the serotonin is synthesized in the gut, whereas many of the intermediate compounds are important in the brain (9, 10). Given the rather complex network of reactions and the tissue specificity of tryptophan metabolism, pathological shifts of tryptophan metabolite concentrations (i.e. in blood plasma) do not readily indicate the underlying alterations in enzyme expressions or activities. Therefore, a comprehensive mathematical model could provide a predictive tool that would facilitate the identification of potential pathological changes in tryptophan metabolism.

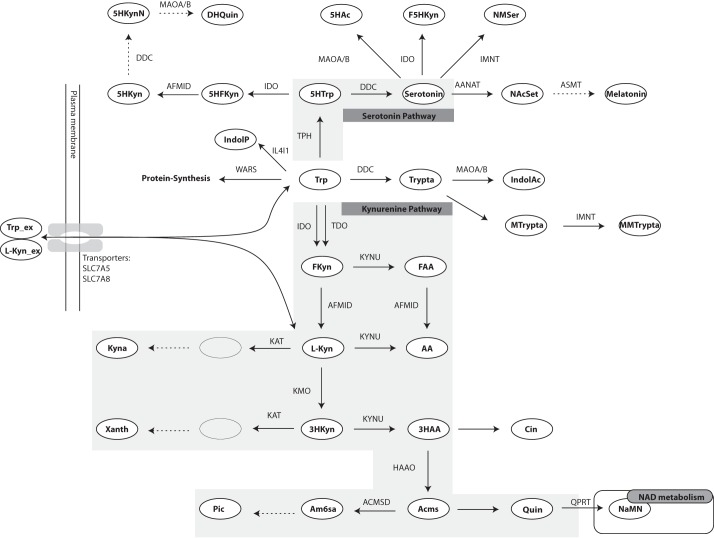
FIGURE 1.

Overview of the tryptophan metabolic pathway. The two most important branches of this pathway are the serotonin pathway and the kynurenine pathway. These have been marked by gray backgrounds. Metabolites are shown in ellipses, and directions of reactions are shown by arrows with the enzyme names next to them. Enzyme names are written in uppercase letters. Arrows without enzyme names are non-enzymatic reactions. Dotted arrows are reactions for which kinetic data were missing. The double vertical lines on the left hand side depict plasma membrane, and the bi-directional arrows crossing it show the transport of tryptophan and l-kynurenine. The names of the transporters are written next to the arrows. Fkyn, formyl-kynurenine; FAA, formyl-AA; Xanth, xanthurenic acid; Acms, 2-amino-3-carboxymuconate semialdehyde; Am6sa, 2-aminomuconate semialdehyde; Pic, picolinic acid; Cin, cinnabarinic acid; 5HTrp, 5-hydroxy-tryptophan; Trypta, tryptamine; MTrypta, methyl-tryptamine; MMTrypta, dimethyl-tryptamine; IndolAc, indole-3-acetaldoxime; 5HFKyn, 5-hydroxy-N-formylkynurenine; 5HKyn, 5-hydroxy-kynurenine; 5HKynN, 5-hydroxykynuramine; DHQuin, 4,6-dihydroxy-quinoline; 5HAc, 5-hydroxy-indoleacetaldehyde; F5Hkyn, formyl-5-hydroxykynurenamine; NMSer, N-methyl-serotonin; NAcSet, N-acetyl-serotonin; IndolP, indole-pyruvate. The abbreviations of the enyzmes are as follows: AFMID, arylformamidase; KYNU, kynureninase; ACMSD, 2-amino-3-carboxymuconate semialdehyde-decarboxylase; QPRT, quinolinic acid phosphoribosyltransferase; IL4I1, interleukin 4 induced 1; AANAT, arylalkylamine N-acetyltransferase; ASMT, acetylserotonin N-methyltransferase; MAOA/B, monoamine oxidase A/B; IMNT, tryptamine N-methyltransferase; WARS, tryptophanyl-aminoacyl-tRNA synthetase. The abbreviations of the transporters are: SLC7A5, large neutral amino acids transporter small subunit 1; SLC7A8, large neutral amino acids transporter small subunit 2.

One particular complication that needs to be taken into account when building a kinetic model of tryptophan metabolism is that several enzymes in the network have rather low substrate selectivity and, therefore, catalyze reactions in more than one branch. That is, various metabolites arising in different branches of the network compete for the active site of the same enzyme. For example, indoleamine-pyrrole 2,3-dioxygenase (IDO)³ uses l-tryptophan (Trp), 5-hydroxy-tryptophan, 5-hydroxytryptamine (serotonin), and N-acetyl-5-methoxytryptamine (melatonin) as substrates (cf. Fig. 1). Other enzymes that use multiple substrates in the pathway include aromatic l-amino acid decarboxylase (DDC), arylformamidase, kynureninase, and kynurenine aminotransferase (KAT). Similarly, l-kynurenine (l-Kyn), an intermediate product of the kynurenine pathway, is a large neutral amino acid that can be transported across the cell membrane using the same transporters as tryptophan (11). Because uptake of tryptophan has been suggested to be rate-limiting for its cellular metabolism (12), competition between l-kynurenine and tryptophan for membrane transport could also have significant impact on the metabolic outcome. These complex interactions are difficult to assess biochemically and constitute another important motivation for using a modeling approach to study the pathway dynamics in health and disease.

Metabolic control analysis (13–15) has proved to be a powerful mathematical approach to assess pathway dynamics. Metabolic control analysis calculates the distribution of control among the enzymes in a pathway (13–16) based on the assumption that the flux control is shared by all enzymes in the pathway. Flux control coefficients (FCCs) always sum up to unity, implying that concentration (activity) changes of one enzyme always affects the control exerted by other enzymes. Importantly, within biochemical pathways some enzymes may have particularly high control (i.e. a high FCC) over the flux through the entire pathway. Given their decisive role for the “throughput” of the pathway, these enzymes are generally considered to be promising drug targets. Indeed, Metabolic control analysis has been successfully used in pharmacology to identify drug targets but also in biotechnology to optimize the production of desired metabolites (17, 18).

An often limiting prerequisite for building a kinetic model is the availability of the relevant kinetic data for all enzymes in the pathway or network. Although the exact kinetic mechanisms are not known for many enzymes, Michaelis-Menten kinetics is considered to be a good approximation for most enzymes and is commonly used to describe reaction rates. The parameters required for Michaelis-Menten kinetics are the specific half-saturation constant or Michaelis-Menten constant (K_m) and the maximal velocity (V_max). V_max can either be measured directly as tissue-specific activity or calculated from the turnover number (k_cat) and the enzyme concentration (E_T). These kinetic parameters, except E_T, can be found in kinetics databases or in the literature. Due to the extensive work that has been done to characterize tryptophan metabolism, kinetic data for the mammalian enzymes are available for most of the enzymes. In fact, kinetic models of the kynurenine pathway of tryptophan metabolism, limited to the branch synthesizing quinolinic acid (Quin), have been reported (12, 19). However, these simple one-branch models do not capture the complex dynamics of the multi-branched tryptophan metabolic network (20, 21).

Besides the kinetic data, generation of a suitable kinetic model for specific organs or an entire organism has another prerequisite; that of specific enzyme activities. Fluxes and their control in metabolic pathways vary between tissues because of differential expression of the corresponding genes as well as co- and posttranslational modifications. Therefore, the introduction of scaling factors to adjust the activity of each individual enzyme according to the actual expression level within a given tissue would be required. Such a factor would essentially provide a measure for E_T. Thus, simulation of the dynamics of tryptophan metabolism in diseases or upon drug treatment would necessitate establishing tissue-specific flux controls. As several intermediates of tryptophan metabolism are known to be transported into the blood (22, 23), it is reasonable to expect that metabolites generated in one tissue can affect tryptophan metabolism in another. To explore such interdependences would additionally necessitate connecting the mathematical models established for individual tissues assuming blood as “metabolite carrier.”

In this article we report the construction of a comprehensive kinetic model of mammalian tryptophan metabolism that includes kinetic data for the enzymes in all known branches of the network (see Fig. 1). The kinetic model was integrated with gene expression data from human liver and brain, thereby establishing tissue-specific models, and analyzed for control in the system using metabolic control analysis. The simulations returned expected steady state flux distributions for these tissues validating the applicability of the modeling approach in combination with gene expression data. We demonstrate the flexibility and scalability of the model by combining the brain and liver models into a multi-tissue model. Finally, the usability of the model for the study of diseases is illustrated by applying gene expression data from Tuberculosis meningitis patients and from a cancer study that resulted in the prediction of metabolic changes that coincided with those measured in the patients. Thus, our model provides a valuable diagnostic tool to predict pathological changes of tryptophan metabolism based on a limited number of clinical measurements.

MATERIALS AND METHODS

A Dynamic Model of Mammalian Tryptophan Metabolism

The set of reactions involved in tryptophan metabolism was obtained from KEGG (24). When available, enzyme kinetic data were originally retrieved from Brenda (25), and transporter substrate affinities were retrieved from Uniprot 26). The original literature cited in the databases was reviewed to verify the kinetic values and to make sure that measuring conditions were appropriate. A few reactions could not be included in the model due to lack of kinetic data. Fortunately, these reactions are at the end of branches, and excluding them does not affect the model. Michaelis-Menten kinetics or modified versions thereof were used for all enzymatic and transport reactions, whereas non-enzymatic reactions were modeled using mass action kinetics.

Establishment of a comprehensive model of tryptophan metabolism was found to be still limited by incomplete experimental data, especially with regard to tissue-specific enzyme activities (i.e. protein levels), metabolite, and cofactor concentrations as well as enzyme mechanisms. Therefore, we needed to include a few simplifications and assumptions as outlined below.

Except for the transport processes, all reactions were modeled as irreversible for two reasons. First, reactions involving oxygenation, acetylation, ring forming, and ring breaking are unlikely to be reversed due to their chemical nature. Second, potentially reversible reactions in the network are all followed by fast non-enzymatic reactions, which drive the preceding enzymatic reaction in the forward direction.

Some of the enzymatic reactions are inhibited by up- or downstream metabolites such as picolinic acid, Quin, anthranilic acid (AA), and kynurenic acid (Kyna) in vitro. However, in all cases the half-maximal inhibitory concentrations are >1000-fold above reported physiological concentrations. That is, there is no known feedback inhibition of physiological relevance, and such events were, consequently, not included in the model.

We limited the model by setting all co-substrates, including 5-phospho-α-d-ribose 1-diphosphat, NADPH, acetyl-CoA, and oxygen as external metabolites. Their concentrations were set to 1 mm (except NADPH = 0.03 mm) to not limit the flux. In turn, this also implied that kinetic rate laws could be modeled as monomolecular reactions. A full list of rate laws used is shown in supplemental Table 1. The external tryptophan concentration was set to 5 μm unless otherwise stated.

Tissue-specific Models of Tryptophan Metabolism

Two different approaches were used to generate tissue-specific models. One was based on reported enzyme activities measured in tissue homogenates, and the other combined measured activities of purified enzymes with tissue-specific gene expression data.

Tissue activities can be used as a measure for the maximum reaction rate V_max in the Michaelis-Menten equation,

where v is the reaction rate, K_m is the Michaelis-Menten (half-saturation) constant, and S is the substrate concentration. If enzyme activities were lacking for liver, as was the case for monoamine oxidase A/B, TPH1/2, interleukin 4 induced 1 (IL4I1), and protein synthesis, measurements from another tissue were scaled to liver levels using gene expression data.

In the alternative approach purified enzyme activities can be used to calculate the enzymatic turnover number k_cat, which when multiplied with the total enzyme concentration E_T, gives V_max,

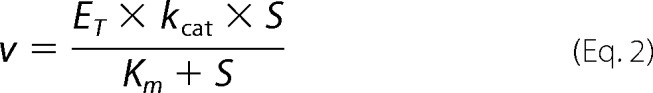In most cases, however, tissue-specific enzyme concentrations are not available. In contrast, gene expression data are available for many tissues, and mRNA levels can be used as a crude estimate for enzyme concentration,

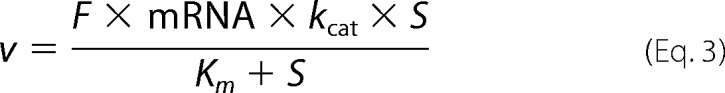where mRNA is the measured microarray signal (unit-less) from gene expression experiments, and F is a factor (unit mm) used to convert microarray signals to enzyme concentrations. In our model F is a global factor, as our model assumes that the microarray signals are in a linear range and that the mRNA levels correspond linearly to enzyme concentrations. To calculate meaningful absolute fluxes and metabolite steady state concentrations for substrates and products of non-enzymatic reactions, F must be determined. In contrast, relative fluxes and steady state concentrations of substrates and products of enzymatic reactions are independent of F. If not stated otherwise, F was arbitrarily set to 1 mm, with the implication that the simulations returned arbitrary absolute fluxes and arbitrary concentrations for substrates and products of non-enzymatic reactions.

Gene expression data sets were obtained from Array Express or Gene Expression Omnibus (GEO) (www.ncbi.nlm.nih.gov). For the tissue simulations, replicate arrays were combined using the biweight function implemented in the gene expression analysis software J-Express Pro to obtain one signal value representing the expression for each enzyme for a tissue. For the glioblastoma and tuberculosis datasets, separate simulations were done for each replicate array, and average concentrations and standard deviations were calculated afterward. The signal values were used directly without further processing. If a gene was represented by multiple probes on the array, the probe with the highest signal was chosen. The various data sets are referenced in the results section and listed in supplemental Table 4. The sbml-file of the model generated for human liver tryptophan metabolism is available in the BioModels database accession number MODEL1310160000.

Enzyme Competition

The Michaelis-Menten rate law for competitive inhibition of irreversible reactions was used for the enzymatic reactions when enzymes catalyze more than one reaction,

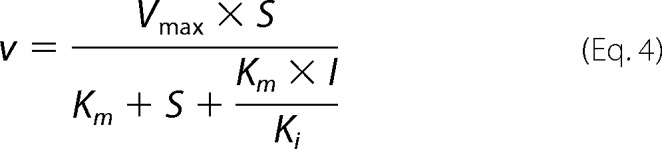where I is the concentration of the competing substrate, and K_i is the Michaelis-Menten constant of the competing substrate. Equation 4 can be extended to any finite number of competitors as shown mathematically by Chou and Talaly (27). For the reversible transport of tryptophan and l-kynurenine we used a rate law for two competing substrates based on steady state assumptions (28).

For the approach using purified enzyme activities and gene expression data, V_max in Equation 4 was substituted with F × mRNA × k_cat as in Equation 3.

Sensitivity Analysis

Global sensitivity analysis was performed with respect to enzyme specific K_m values and the gene expression data. To be able to do global sensitivity analysis within a reasonable amount of time and with moderate computational power, we used the method described by Sahle et al. (29). This method is based on optimization of an objective function. Two different optimization algorithms were applied (evolutionary programming and particle swarm) to make sure that the result was independent of the method used. For the optimization based on evolutionary programming, we used a population size of 40 and 500 generations. The particle swarm algorithm was applied with the default settings (iteration limit 2000 and swarm size 50).

Sensitivity to changes in the K_m values were assessed by searching the parameter space for values that would maximize or minimize flux control coefficients for 3-hydroxyanthranilic (3HAA) oxygenase (HAAO) in the kynurenine pathway and DDC in the serotonin pathway. Combining the search with an optimization algorithm allows searching the parameter space for sets of K_m values that leads to optimal conditions for the objective function. To limit the search space, minimum and maximum values were set for each K_m parameter. If diverging K_m parameter values had been found in the literature or in BRENDA, the lowest and highest values recorded were used as limits. If the available data were consistent or only single measurements were found, we set ±90% of the model values as parameter range.

Similarly, the sensitivity to changes in gene expression values was assessed by searching the parameter space for expression values that would result in maximum or minimum flux through HAAO or DDC. The parameter space for each enzyme was limited by the minimum and maximum expression value measured for the respective genes on the microarrays across all tissues of the data set by Dezso et al. (30) (GEO accession number GDS3113). The parameter search space for expression values was huge, and there could be several optimal parameter combinations that would result in similar maximum and minimum fluxes through HAAO and DDC. Each optimization was, therefore, repeated 20 times to get an estimate for the variability of optimized expression values. Enzymes with small variations of expression values across the 20 runs would then be important for obtaining the optimized fluxes.

Software Used for Analysis and Visualizations

Expression data were formatted using J-Express Pro 2012 (31, 32). All calculations of fluxes and intermediate concentrations were performed with the steady state task of COPASI 4.10 (33). The sensitivity analysis was performed using the metabolic control analysis task and the command line version of the software.

RESULTS

Kinetic Model of Tryptophan Metabolism Predicts Expected Flux Distribution Patterns and Metabolite Concentrations in Rat Liver

To simulate flux distributions and metabolite concentrations in the mammalian tryptophan pathway, we constructed a tissue-specific kinetic model (Fig. 1). Kinetic data for 29 enzymatic reactions and two transporters in the network were retrieved from databases (KEGG and Brenda) and cross-validated with the original literature. Some of the reactions are catalyzed by different isoenzymes, e.g. KAT1–3 and TPH1–2. Separate reactions were added to the model for each isoenzyme, and isoenzyme-specific kinetic constants were used if available. Each of the two transport reactions for tryptophan and l-kynurenine can be carried out by two different transporters. Hence, the model consists of 35 enzyme-catalyzed reactions (set irreversible) and 4 reversible transport reactions. For those enzymes that catalyze more than one reaction in the network, we included competition between these reactions. Because the different substrates compete for the same active sites of these enzymes, one substrate can be seen as competitive inhibitor of the others. Therefore, the kinetic model included competitive inhibition where appropriate (cf. Fig. 1). We recently demonstrated that such competition can affect both steady state concentrations and the dynamic behavior of metabolic systems (28). Initial simulations with the tryptophan metabolic model confirmed that the calculated fluxes were affected by the inhibition as expected. Tryptophan and l-kynurenine were allowed to be exchanged with the environment. Because both use the same transporters, competition also had to be considered for the exchange reactions.

To adjust the model according to liver-specific enzyme activities, we first tried to make use of published studies in which activities were measured in rat liver homogenates. Indeed, liver-specific activities were available for most of the reactions. For the remaining reactions, activities measured in total extracts from other tissues were used in combination with gene expression data to scale the specific activities to liver levels (33). The predicted flux toward protein synthesis was 98.9% relative to tryptophan import, suggesting that almost all of tryptophan is used for protein synthesis. This prediction is in stark contrast to the actual situation in which little dietary tryptophan is used for protein synthesis (10). To assess the effect of excluding protein synthesis, simulations were performed with a variant of the model that excluded tryptophan tRNA ligase (tryptophanyl-aminoacyl-tRNA synthetase). This resulted in increased relative fluxes through the kynurenine pathway (tryptophan 2,3-dioxygenase (TDO, 21%), serotonin pathway (TPH, 29.3%), and interleukin 4-induced 1 (47.8%). However, this is still far from physiological conditions, where up to 99% of tryptophan has been reported to be degraded through the kynurenine pathway in liver (9, 10). Furthermore, the calculations predicted metabolite concentrations far outside the physiological range (e.g. l-Kyn, 0.053 μm; 3-hydroxy-kynurenine (3HKyn), 2.2 nm; serotonin, 0.7 μm; for comparison, see Table 1). The discrepancy between the observed and calculated fluxes may be due to problems inherent to determining specific enzyme activities in tissue homogenates. Most likely such determinations are affected by enzyme instability (for example, TDO has a half-life of only about 2 h (10)). Moreover, they can only to a limited extent account for competition between pathways or product utilization in subsequent reactions. Given this result, we did not continue building models based on enzyme activities measured directly in tissues.

TABLE 1.

Comparison between calculated and experimentally measured concentrations of tryptophan pathway metabolites in rat

The rat liver and cortex models were built using averaged tissue-specific gene expression data to scale enzyme specific activities. The calculated concentration ranges were obtained by varying the amount of tryptophan used as input for models. For liver, the tryptophan range was based on human blood values, as rat blood concentrations are of limited availability. They do, however, appear to be in the same range (36, 46). The concentration of free tryptophan available for uptake in liver corresponds to 10–20% of the total tryptophan measured (39.7–91 μm (35, 37)), and hence the input range was set to 4–16 μm. For the rat cortex model a tryptophan range of 0.9–2.6 μm, resembling human CSF concentrations (37), was used directly.

Metabolite	Units	Calculated		Measured		References
		Rat Liver	Rat cortex	Rat blood plasma	Rat cerebrospinal fluid
Seretonin	nm	4.1–10.8	6.0–16.2
l-Kyn	μm	1.0–3.0	0.035–0.11	1.4–3.8	0.032–0.047	23, 36, 46
3HKyn	nm	19.8–58.3	0.9–5.0	39.5–63.3		36, 46
3HAA	nm	0.2–0.7	0.02–0.06

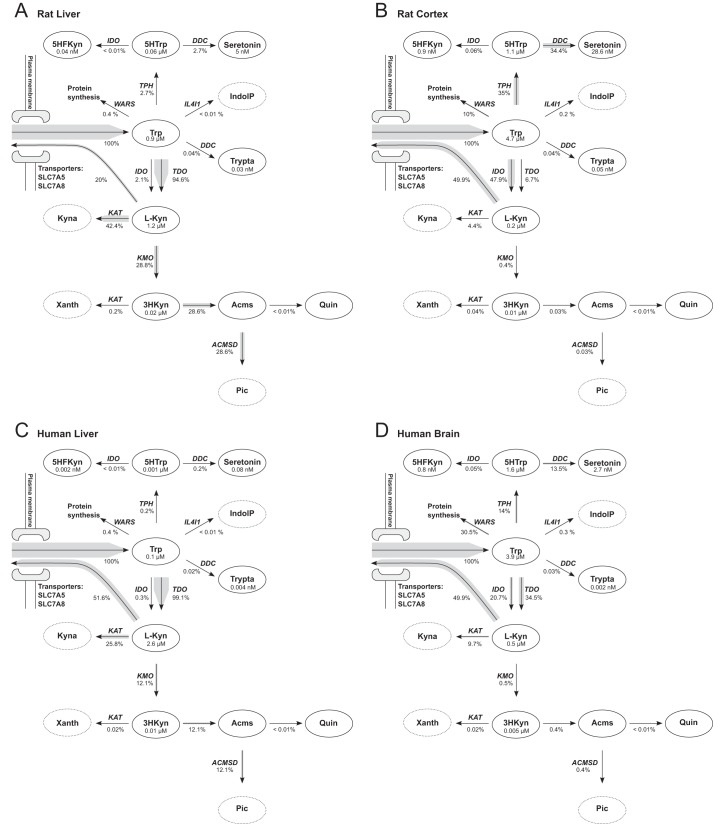
As an alternative approach, we used specific activities measured for purified enzymes that were available for most enzymes. From these activities we calculated the enzymatic turnover number, k_cat. To estimate the total enzyme concentrations, E_T, gene expression data (34; ArrayExpress accession E-BASE-4) were used as described under “Materials and Methods.” Fig. 2A shows the result (for rat liver) of steady state calculations with this model in a simplified figure of the tryptophan metabolic pathway. For visualization purposes (here and in subsequent figures) only the main branch points of the kynurenine and serotonin pathways are shown, whereas the simulations are based on the full model. Simulations suggested that 94.6% of tryptophan are metabolized by TDO in the kynurenine pathway and then split between KAT and kynurenine 3-monooxygenase (KMO). These predictions resemble known flux distributions for rat liver (9, 10). In addition, as can be inferred from Table 1, the calculated intermediate concentrations for l-Kyn (1.2 μm) and 3HKyn (0.02 μm) are close to the values measured in rat plasma. Consequently, kinetic modeling using turnover numbers in conjunction with measured mRNA abundance of the corresponding genes to adjust for gene expression appeared to reflect the actual physiological situation rather accurately. Importantly, this approach does not rely on tissue-specific activities and, therefore, can be readily used to generate models for other tissues. The same turnover numbers will apply, and E_T values are adjusted by tissue-specific expression data.

FIGURE 2.

Predicted flux distribution in brain and liver. For simplicity, only the main metabolic compounds and reactions of the serotonin and kynurenine pathways are shown. The width of the arrow shades represents the predicted flux relative to tryptophan inflow. Relative fluxes and metabolite concentrations are indicated. A tryptophan concentration of 5 μm was used for all simulations presented in this figure to allow tissue comparison. See the names of the transporters are written next to the arrows. Xanth, xanthurenic acid; Acms, 2-amino-3-carboxymuconate semialdehyde; Pic, picolinic acid; 5HTrp, 5-hydroxy-tryptophan; Trypta, tryptamine; 5HFKyn, 5-hydroxy-N-formylkynurenine; IndolP, indole-pyruvate; ACMSD, 2-amino-3-carboxymuconate semialdehyde-decarboxylase; IL4I1, interleukin 4 induced 1; WARS, tryptophanyl-aminoacyl-tRNA synthetase; SLC7A5, large neutral amino acids transporter small subunit 1; SLC7A8, large neutral amino acids transporter small subunit 2. A, rat liver. B, rat cortex. C, human liver. D, human brain.

Tissue-specific Flux Distributions Are Similar in Human and Rat

To compare predicted metabolite concentrations and relative fluxes in different tissues of different species, we created additional models for rat cortex, human liver, and human brain. E_T in the different tissues were estimated using gene expression datasets from rat (Ref. 34; ArrayExpress accession E-BASE-4) and human (30; GEO accession GDS3113). The calculated concentrations and fluxes are shown in Fig. 2. Interestingly, the models predict that fluxes in rat and human liver are similar but different from fluxes in rat cortex and human brain. Moreover, rat cortex fluxes are comparable to those of the human brain. In cortex and brain, the flux is shifted from the kynurenine pathway (IDO/TDO) toward the serotonin pathway (TPH). This results in higher concentrations of serotonin in the brain tissues and lower concentrations of the potentially neurotoxic metabolites 3HKyn and 3HAA. The latter is also reflected in the flux ratios between KAT and KMO, which is 1.5–2.1 in liver and 11–19.4 in brain. The relative flux toward protein synthesis (tryptophanyl-aminoacyl-tRNA synthetase) is predicted to be 10 and 30.5% in rat cortex and human brain, respectively, which is higher than expected.

To assess the validity of the predicted metabolite concentrations, we performed simulations using a range of tryptophan concentrations. The total tryptophan concentration in blood has been reported to be in the range from 39.7–91 μm (12, 35–37) but with only 10–18% freely available to the cells (10, 37, 38). Hence, the range for the fixed concentration of tryptophan used in the simulations of liver metabolism was 4–16 μm. The tryptophan concentration reported for cerebrospinal fluid and used for simulations of brain metabolism in Table 1 was somewhat lower (1.3–2.6 μm (37)). Calculated metabolite concentrations for human liver and brain along with measured concentrations from blood plasma and cerebrospinal fluid are shown in Table 2.

TABLE 2.

Comparison between calculated and experimentally measured concentrations of tryptophan pathway metabolites in human

The human liver and brain models were built using averaged tissue-specific gene expression data to scale enzyme specific activities. The calculated concentration ranges were obtained by varying the amount of tryptophan used as input to the models. For the liver model, the tryptophan range was set to 4–16 μm (see Table I legend), and for the brain model the reported concentration range of 0.9–2.6 μm measurements in CSF (37) was used. The human metabolome database (36) and the review by Chen and Guillemin (37) each summarize several independent studies reporting metabolite measurements. The total number of original articles is indicated in parentheses. The most comprehensive dataset comprises measurements from 94 healthy persons, and the range reported represents the 5th and 95th percentile (35).

Metabolite	Units	Calculated		Measured		References
		Human liver	Human brain	Human blood plasma	Human cerebrospinal fluid
Seretonin	nm	0.1–0.2	0.6–6.4		0.6–12 (5)	36
l-Kyn	μm	2.2–6.9	0.08–0.23	0.7–4.32 (19)	0.027–0.061 (9)	35–37
3HKyn	nm	9.8–30.4	0.9–2.6	12.5–383 (2)		35, 37
3HAA	nm	2.7–8.3	0.06–0.2	7.9–209 (3)		35, 37

To assess to what extent the results from model simulations depended on the accuracy of the kinetic values, sensitivity analysis was performed. This was done by varying the K_m values (supplemental Tables 2 and 3) and the expression data (supplemental Fig. 1); see “Materials and Methods” for details. The results from the sensitivity analysis showed that some K_m values could be varied considerably without noticeably affecting simulation outcomes, whereas changing K_m values for other enzymes significantly affected the outcome. Similar observations were made when the numbers for the expression data were varied. Generally, variation in the values for enzymes at branch points resulted in greater variation of simulation results. Therefore, it appears particularly important to accurately determine the kinetic constants and protein concentrations for the enzymes at branch points.

Pathway Control Is Distributed Differently in Brain and Liver

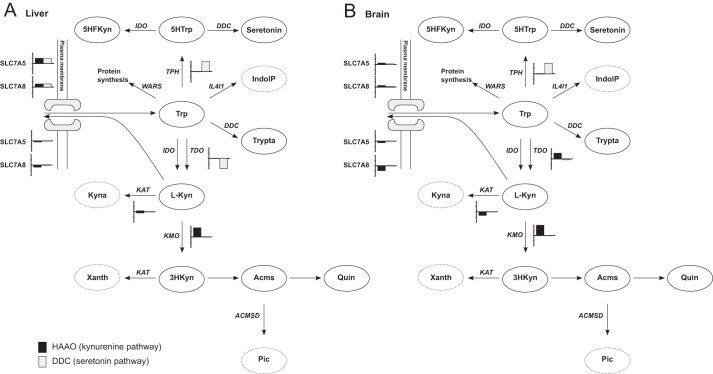
Metabolic control analysis was used to analyze the distribution of control in tryptophan metabolism in human liver and brain (Fig. 3). The control of flux through the reaction converting 5-hydroxytryptophan into serotonin, catalyzed by DDC, was used as a measure for the control of the serotonin pathway. Similarly, the control of the flux through the reaction converting 3HAA into 2-amino-3-carboxymuconate semialdehyde, catalyzed by HAAO was used as a measure for the control of the kynurenine pathway. In liver, the flux control for the serotonin pathway seems to be shared between TPH, TDO, and the transport of tryptophan with FCC of 0.99, −0.96, and 0.91, respectively. Sensitivity analysis showed that these control coefficients were rather robust as they varied little when changing kinetic or expression values. In brain, TPH was the major control point for serotonin synthesis with an FCC of 0.98. In the kynurenine pathway, KMO was a major control point in both liver (0.88) and brain (0.99). Transport of tryptophan also had control in liver (0.93), whereas TDO, IDO, transport of tryptophan, and transport of l-kynurenine had control in brain with FCCs of 0.55, 0.33, 0.22, and −0.82, respectively. Additionally, KATs exert some control in the brain (−0.35). In summary, the analyses showed that the flux control was distributed differently in brain and liver. The flux through the kynurenine pathway in liver is chiefly controlled by KMO, whereas in brain flux control is shared among several enzymes.

FIGURE 3.

Predicted flux control is different between liver and brain. Flux through DDC in the serotonin pathway and HAAO were used as measures of fluxes in the serotonin pathway and kynurenine pathway, respectively. A bar plot is added next to the reactions that have a control coefficient of more than +0.1 or less than −0.1. The bar is black for control of flux through HAAO (kynurenine pathway) and gray for control of flux through DDC (serotonin pathway). The interval between the tics on the y axis is 0.5. The distribution of flux control is different between human liver (A) and human brain (B). Xanth, xanthurenic acid; Acms, 2-amino-3-carboxymuconate semialdehyde; Pic, picolinic acid; 5HTrp, 5-hydroxy-tryptophan; Trypta, tryptamine; 5HFKyn, 5-hydroxy-N-formylkynurenine; IndolP, indole-pyruvate; ACMSD, 2-amino-3-carboxymuconate semialdehyde-decarboxylase; IL4I1, interleukin 4 induced 1; WARS, tryptophanyl-aminoacyl-tRNA synthetase; SLC7A5, large neutral amino acids transporter small subunit 1; SLC7A8, large neutral amino acids transporter small subunit 2.

Building a Multi-tissue Model

Simulations of tryptophan metabolism in individual tissues have great value, for example, to predict or understand pathological alterations. However, several intermediates of tryptophan metabolism undergo exchange between tissues and blood. Therefore, it is important to consider the possibility that tryptophan metabolism in one tissue can influence that in other tissues.

Our modeling approach permitted us to combine the simulations for human liver and brain and to connect them via a “blood compartment” mediating the exchange of metabolites between these tissues (Fig. 4). We assumed tissue volumes to be 1.5 and 1.35 liters for liver and brain, respectively, and 6 liters for blood. Tryptophan and l-kynurenine were the only metabolites that were allowed to be exchanged between these tissues and blood. Other intermediates are known to be transported into the blood (22, 23), but it is uncertain whether they can cross the blood brain barrier in significant amounts.

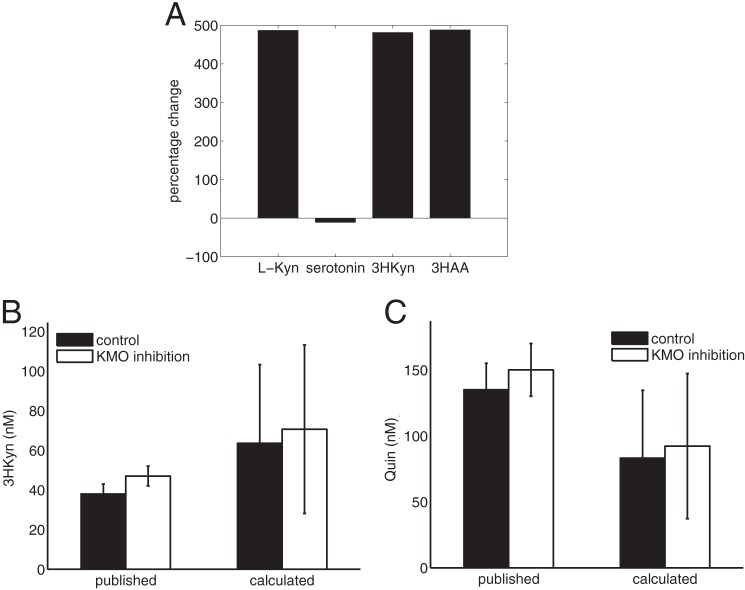
FIGURE 4.

Simulation of the influence of liver metabolism on brain kynurenine metabolites. A, percentage change of selected metabolite concentrations calculated in the combined brain-liver model relative to the isolated brain model. Shown are changes in brain l-Kyn concentrations (B) and changes in Quin concentrations (C) upon reduction of liver KMO activity to 10%. The simulation results are presented as a range of concentrations because the reported range of free tryptophan (4–16 μm, see Table 2) was used as input for the model. The calculated values are compared with measurements reported by Zwilling et al. (39).

The most notable change in calculated brain metabolite concentrations, as a result of connecting the two tissues, was elevated levels of kynurenine pathway metabolites (Figs. 4A). This is caused by a decrease in the net outflow of l-kynurenine from the brain, as liver maintains a high blood concentration of l-kynurenine. These simulations thus indicate that liver tryptophan metabolism contributes to the generation of both neuroprotective and neurotoxic intermediates in the brain. Interestingly, Zwilling et al. (39) showed that pharmacological inhibition of KMO in peripheral tissues with the pro-drug JM6 provided protection against neurodegeneration in mouse models of Huntington and Alzheimer disease even though JM6 cannot cross the blood-brain barrier. Although not statistically significant, they also reported a small increase in 3HKyn and Quin. We used our multi-tissue model to simulate these experiments by limiting the activity of KMO in liver to 10% of its original value. To allow calculation of meaningful metabolite steady state concentrations for substrates and products of non-enzymatic reactions, including Quin, the model was scaled using the F factor. The reported KMO activity measurements for control mice (39) was used to calculate F and was found to be 7.29e-10 mm. Using this scaled model we can reproduce the slight increase in 3HKyn and Quin concentrations observed in the experiments, see Fig. 4, B and C. The largest change in treated mice, however, was observed with Kyna. Unfortunately, our model is unable to calculate steady state concentrations for Kyna, as it is an external metabolite due to lacking information about transport and excretion of Kyna. However, our simulations showed a 14% increase in the Kyna production rate (KAT flux), which qualitatively agrees with the experimental data. In conclusion, our simulations resembled to a large extent the experimental results reported by Zwilling et al. (39).

Simulation of Pathological Alterations of Tryptophan Metabolism

Several cancers are known to up-regulate TDO or IDO leading to elevated l-kynurenine and decreased Trp concentrations. Opitz et al. (7) showed that l-kynurenine binds to the aryl hydrocarbon receptor that suppresses anti-tumor immune responses and promotes cancer survival. We simulated a 2-fold up-regulation of TDO in our isolate brain model, and our calculations showed an increase of l-kynurenine of 49.9%. Next, we used microarray data from a brain cancer study (Ref. 40; GEO accession GSE15824) to adjust the concentrations of enzymes in the same brain model. The results are displayed in Fig. 5 and show a decrease in steady state concentration of Trp and an increased of l-Kyn in secondary glioblastoma compared with primary glioblastoma and healthy brain samples. The great variation within each group reflects the variations in gene expression data. Nevertheless, there was a clear correlation between the calculated concentration of l-kynurenine and the gene expression levels of IDO and TDO (correlation coefficients were 0.74 and 0.96, respectively) across all healthy and cancer samples in the data set, confirming the observations by Opitz et al. (7).

FIGURE 5.

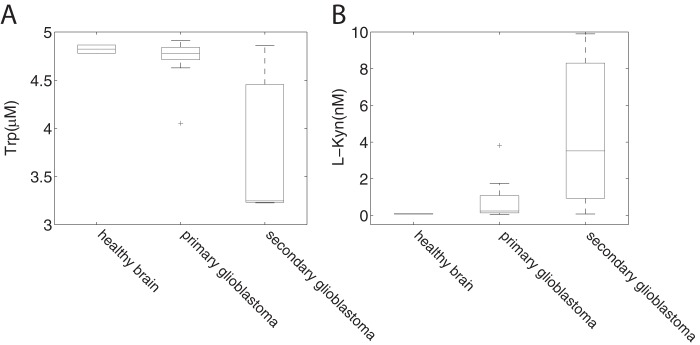
Simulation of changes in the tryptophan pathway in brain cancer. Using expression data from a brain cancer study by Grzmil et al. (40) we simulated intermediate concentrations of tryptophan (A) and l-Kyn (B) for healthy brain, primary glioblastoma, and secondary glioblastoma. For each patient a separate model was generated resulting in individual intermediate concentrations. The tryptophan concentration used as input for the model was 5 μm. To show the variance between the samples, distribution of the concentrations was plotted. The central mark is the median, and the edges of the box are the 25th and 75th percentiles. Thus, whiskers extend to the most extreme data points not considered to be outliers; outliers are plotted individually.

Finally, we integrated gene expression data from a T. meningitis profiling study of human brains (GEO accession GSE23074) with the isolate brain model and calculated steady state concentrations of the metabolic intermediates for brains of both infected individuals (n = 5) and normal controls (n = 4). Our model simulations predicted a slight decrease in serotonin concentrations as well as a slight increase in the intermediate concentrations of the kynurenine pathway for infected individuals (Table 3). Moreover, our simulations predict that the ratio of mean fluxes through KAT/KMO decreased by 28.1% in T. meningitis patients. O'Connor et al. (41) showed that induction of IDO by Bacille Calmette-Guerin (a pathogen widely used as a vaccine against tuberculosis) is responsible for a depressive-like behavior in mice. They proposed that a shift to a less favorable ratio of neuroprotective and neurotoxic kynurenine derivatives could contribute to a depressive phenotype. Our analyses lend support to such a metabolic shift as a diminished KAT/KMO ratio would, for example, lead to higher concentrations of neurotoxic quinolinic acid while diminishing protective kynurenate concentrations.

TABLE 3.

Calculation of tryptophan pathway metabolite concentrations in T. meningitis patients

The model for healthy individuals and T. meningitis (TBM) patients was constructed using expression data (GEO accession GSE23074) to scale enzyme specific activities. For each sample a separate model was generated, and the concentrations were calculated with a fixed tryptophan concentration of 1.75 μm as input. This concentration resembles the medium concentration for human CSF found in the literature (37).

Metabolite	Units	Normal	TBM
Seretonin	nm	21 ± 11	19 ± 6
l-Kyn	μm	0.13 ± 0.08	0.19 ± 0.05
3HKyn	nm	3.4 ± 2.4	4.8 ± 3.2
3HAA	nm	0.22 ± 0.11	0.31 ± 0.14
KAT/KMO		5.7 ± 2.6	4.1 ± 2.0

DISCUSSION

The present study provides the most comprehensive kinetic model of tryptophan metabolism to date. It includes all branches of this complex network, thereby enabling the detection of interdependencies between the individual pathways. Moreover, inclusion of nearly all reactions of the network into the calculations makes it possible for the first time to generate realistic predictions for intermediate metabolite concentrations and flux distributions of tryptophan metabolism in different tissues. This possibility has arisen from the successful adjustment of individual enzyme activities according to tissue-specific expression of the corresponding genes.

Intuitively, it would appear that using specific enzyme activities measured in tissue extracts would provide the most accurate values. However, our results indicate that, at least in liver, the application of these data to the generic model returns flux distributions that do not reflect the physiological situation. Inaccuracies of measurements (for example, due to enzyme instabilities), even if only for a few enzymes, are likely to affect the outcome of the simulations for such a complex metabolic network. Indeed, our sensitivity analyses revealed that this would be the case, particularly when it concerns enzymes at branch points, such as TDO.

Even though we are well aware that gene expression (mRNA levels) does not necessarily correlate with the amount of the corresponding protein, we used such data to scale our kinetic model to tissue-specific enzyme activities. Using this approach, the calculations of tryptophan metabolism for both liver and brain returned flux distributions and metabolite concentrations that closely resemble physiological values (35–37). Our mathematical approach also produced results for diseased tissues, such as cancers or infections, that predict changes similar to those reported (7, 39). According to these results, the possibility exists that the ratio between corresponding mRNA and protein levels, at least for the key enzymes, is similar within the network of tryptophan metabolism. Unfortunately, there are no quantitative proteomics data available to verify this notion. In fact, this is the reason why we needed to resort to gene expression data in the first place rather than using tissue protein levels.

Another interesting observation is the correspondence of our predictions with measured values despite the absence of any regulatory components, such as allosteric regulation and product inhibition, in our model. Indeed, the concentrations required to achieve known inhibitory effects of metabolites on enzymes of tryptophan metabolism are far beyond physiological values. Nevertheless, we cannot exclude the existence of hitherto undiscovered regulatory mechanisms within this network. However, expression of the genes encoding TPH1/2, TDO, IDO, and IL4I1 are known to be regulated by melatonin and Trp/l-Kyn and upon inflammation, respectively. Thus, it appears as though tryptophan metabolism could be primarily regulated through enzyme abundance rather than by allosteric mechanisms or product inhibition. Thus, the inclusion of gene expression data into our model has the further advantage that it would account for this type of regulation.

As for any metabolic model, an unequivocal verification would, however, only be achieved if simultaneously metabolomics quantitative proteomics, and expression analyses were conducted in several organs from the same organism. Therefore, it is important to note that comparison of values obtained from the model with those from the literature has limitations because measurements have been made in different samples including blood, serum, or cell culture and may vary considerably depending on the experimental conditions (37).

Integration of expression data with a kinetic model has been successfully done for a model of the citric acid cycle in Escherichia coli and Mycobacterium tuberculosis (33). In this case, -fold change values were calculated from gene expression data and used to scale the V_max values obtained from published literature to simulate different conditions. To our knowledge, our approach to use turnover numbers and expression values has so far not been used for kinetic modeling.

Gene expression data are also regularly used in flux balance calculations to adjust the flux capacity of a reaction (see e.g. Ref. 42). In contrast to flux balance analysis, we apply additional constraints that are the steady state requirement and the measured metabolite affinities. One problem of using gene expression data directly, as we have done in most of our models, is that the calculated absolute flux values are arbitrary, and only relative fluxes can be meaningfully compared with experimental data. However, as we have shown in simulations of KMO inhibition experiments in mice, the model can be scaled to produce absolute flux values provided that experimentally measured enzyme activities are available from a reference tissue. In addition to absolute fluxes, such a scaled model also permits the calculation of steady state concentrations for substrates and products of non-enzymatic reactions, such as quinolinic acid.

The metabolic control analyses we conducted suggested that TPH and KMO are major control points in both liver and brain, along with TDO or IDO, depending on the tissue. This was not surprising. Indeed, all these enzymes have emerged as promising drug targets based on biochemical studies of tryptophan metabolism. TPH is targeted for irritable bowel syndrome (43), and KMO is targeted for Huntington disease and may be a promising target for several neurodegenerative diseases (44). TDO inhibition is regarded as a strategy for cancer suppression (45). Our analyses further demonstrated that the metabolite transporters also have significant control over tryptophan metabolism. Targeting the transporters, however, is likely to have adverse effects because they are also required for the transport of other amino acids (11). All in all, the control analyses showed that there are several control points in tryptophan metabolism, particularly in the brain. Therefore, mutations that affect the activity of these enzymes to a small extent when measured in isolation may still have considerable effects on the network as a whole. That is, there could be seemingly harmless variations in individual enzyme structures that could account for tryptophan metabolism being involved in many different diseases.

Another important outcome of the present study is the demonstrated potential to scale the kinetic models of individual organs into a comprehensive multi-tissue model. We have tested this possibility by combining the models generated for liver and brain and connecting them via blood as a metabolite carrier for tryptophan and l-kynurenine. Even though this model was based on relatively simple assumptions for tissue volumes and constrained to only two permeable metabolites, the calculations indicated that the tissues interact metabolically as indicated by modified fluxes (Fig. 4). This notion became especially apparent when simulating liver KMO inhibition by JM6, which was experimentally investigated recently (39). The inhibitor was administered orally and showed positive effects in Huntington disease despite the fact that the inhibitor is unable to cross the blood-brain barrier. The protection was ascribed to increased levels of kynurenate in the brain. Our simulations showed elevated levels of l-kynurenine and increased kynurenate production rates, in line with the experimental results. Moreover, the simulations also reproduced the experimentally measured slight increased levels of the neurotoxic compounds 3HKyn and Quin. Despite the promising results of our simulations, the development of an adequate multi-tissue model would require inclusion of more peripheral tissues, more precise estimation of tissue volumes, and availability of data regarding the presence and kinetics of transporters for other metabolites of the network.

The flexibility and scalability of our approach opens up wide-ranging possibilities for studying the dynamics of tryptophan metabolism in different diseases. For example, increased levels of l-kynurenine have been observed in cancers and may be part of the mechanism by which tumors evade immune responses (7). As a case study we integrated gene expression data from brain cancers with our kinetic model. The results indicated great variability in the levels of this metabolite, which actually fits well with measurements in glioblastomas (7). In our simulations, the l-kynurenine concentration correlated with the expression level of TDO, as would have been expected from the experimental data.

In conclusion, a comprehensive and robust kinetic model of mammalian tryptophan metabolism has emerged from the present study. Based on comparison with reported biochemical measurements, we conclude that the model provides unprecedented accuracy in describing the actual state of tryptophan metabolism in tissues. Because it can be easily adjusted to essentially any tissue using readily available gene expression data, the model has the potential to become widely used as a predictive and diagnostic tool, considering that tryptophan metabolism is affected in a broad range of diseases. We envision the possibility that, once it can be scaled to a reliable multi-organ model, metabolite measurements in blood may provide sufficient information to deduce organ-specific alterations in tryptophan metabolites. Moreover, the principal approach of integrating a kinetic model with mRNA levels of the corresponding genes can be readily adopted for other metabolic pathways as long as the kinetic data are available.