Abstract
Most of the myofibers in long muscles of vertebrates terminate within fascicles without reaching either end of the tendon, thus force generated in myofibers has to be transmitted laterally through the extracellular matrix (ECM) to adjacent fibers; which is defined as the lateral transmission of force in skeletal muscles. The goal of this study was to determine the mechanisms of lateral transmission of force between the myofiber and ECM. In this study, a 2D finite element model of single muscle fiber was developed to study the effects of mechanical properties of the endomysium and the tapered ends of myofiber on lateral transmission of force. Results showed that most of the force generated is transmitted near the end of the myofiber through shear to the endomysium, and the force transmitted to the end of the model increases with increased stiffness of ECM. This study also demonstrated that the tapered angle of the myofiber ends can reduce the stress concentration near the myofiber end while laterally transmitting force efficiently.
Keywords: Lateral transmission, Finite element modeling, Tapered end, Myofiber model, Myofiber, Endomysium
1. Introduction
Skeletal muscles have a complex hierarchical structure which is mainly composed of myofibers and the extracellular matrix (ECM) surrounding them. There are three different structural levels of the ECM: endomysium that surrounds every single myofiber; perimysium that binds the muscle fascicles; and epimysium that encompasses the entire skeletal muscle. ECM not only provides structural support to ensure integrity of the whole muscle, but more importantly, interactions between the ECM and myofibers determine the mechanical behaviors of skeletal muscles. The unique structural, biochemical and biophysical properties of the ECM make it an important structure in passing mechanical signals into the cell to produce a signaling cascade through molecules that connect the ECM to muscle cells (Lieber, 2002). Changes in the ECM will cause altered mechanical environments around the cell through this interactions, and therefore initiate the mechanotransduction process in muscle (Kjaer, 2004; Purslow, 2002), which affects the muscle adaptation to aging, injury, disease, and the outcomes of corresponding treatments.
The mechanical interactions between the muscle cell and ECM mainly occur through the force transmission between them. It has been shown that for many muscles, across species, muscle fiber commonly ends within the fascicles without reaching the myotendinous junction (Gaunt and Gans, 1992; Trotter, 1993, 2002; Trotter and Purslow, 1992). This suggests that the force generated in these muscle fibers must be transmitted laterally via the endomysium. Such pathway of force transmission was defined as lateral transmission of force (Huijing, 1999; Monti et al., 1999). Although the existence and the necessity of lateral transmission of force have been demonstrated experimentally between single muscle fibers and fascicles, and even different muscles (Balice-Gordon and Thompson, 1988; Huijing et al., 1998; Street and Ramsey, 1965; Street, 1983), the mechanical mechanism of this transmission is not well understood.
Skeletal muscle has a complicated microstructure, and therefore it is difficult to experimentally determine the mechanisms of lateral transmission of force. Mathematical models have the advantages in manipulating variables which is otherwise difficult to do experimentally. The most commonly used mathematical models to describe forces generated in myofibers are the Hill model and the Huxley model. The Hill (1938) model is a phenomenological model in which microstructures of muscles are not incorporated; therefore, it is not able to provide structural mechanisms of muscle contractions (Herzog, 2000). In contrast, the Huxley model is a model including structures that affect the force generation, in which force generated in myofibers is described as a function of attachments of cross-bridges (Huxley, 1957). Zahalak further developed the Huxley model by incorporating chemical changes during muscle contractions and introducing a distribution-moment (DM) method to save computing expense (Zahalak, 1981; Zahalak and Ma, 1990). However, the Zahalak model is a model of sarcomeres based on the cross-bridge theory, and it is focused only on myofibers without the surrounding endomysium. Therefore it cannot be directly used to study the interactions between myofibers and the ECM.
Most previous mathematical models considered skeletal muscles as one tissue without separating the structures of myofibers and the ECM, therefore, no information about force transmission between them can be determined from those models (Blemker et al., 2005; Chen and Zeltzer, 1992; Johansson et al., 2000; Kojic et al., 1998; Van der Helm, 1994). Yucesoy et al., (2002, 2003) developed a FE model, in which two single layers of mesh, the muscle fiber layer and the ECM layer, were linked elastically. However, the geometry of that model could not represent the physiological structure of long muscles, in which the muscle fibers terminate intrafascicularly.
The objective of this study was to determine the mechanisms of lateral transmission of force between myofibers and the ECM. We developed a 2D FE model of single muscle fiber with two separate tissues, myofiber and endomysium. The Zahalak model was incorporated in the FE model to describe the active force generated in the myofiber during contractions. Stress distributions along the myofiber and the interface between myofiber and endomysium were analyzed. Parametric studies were performed to determine effects of mechanical properties of the endomysium and tapered end of myofiber on the lateral transmission of force between the myofiber and endomysium.
2. Methods and models
A fiber-reinforced composite is a material that is composed of two different components with discontinuous and strong fibers being embedded in a relatively compliant matrix. Muscle is functionally a fiber-reinforced composite consisting of an ECM with reinforcement by myofibers (Huijing, 1999). The basic structural unit of the muscle is composed of one myofiber and the surrounding endomysium. In this study, the force transmission between the myofiber and the endomysium within such one structural unit, i.e., one single muscle fiber was studied.
2.1. Model description
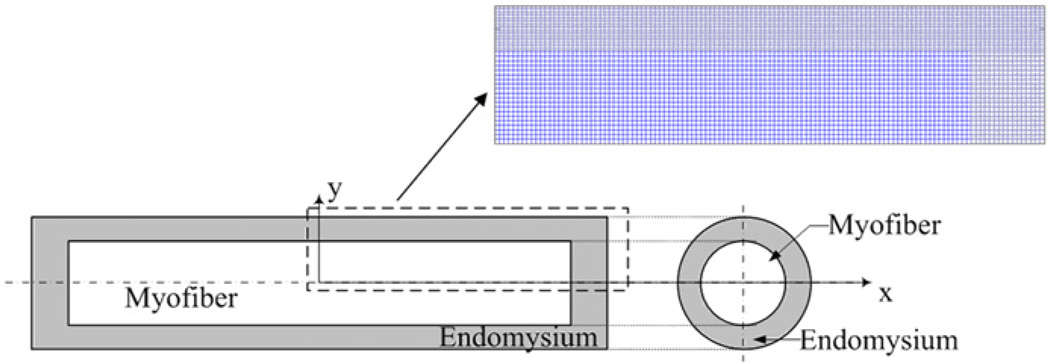
The geometry of a simplified single muscle fiber, or one structural unit, is shown in Fig. 1, in which the myofiber is surrounded by the endomysium. The interface between the myofiber and the endomysium was modeled as perfectly bonded. For 2D problems, both myofiber and endomysium were modeled to be of rectangular shape. Both ends of the single fiber model were fixed to simulate isometric contraction, by which no injury will be induced. To reduce computational time, only the upper right quarter of the model, which is in the dashed line in Fig. 1, was calculated due to the geometric symmetry of this model. Symmetric boundary conditions were applied on symmetry axes.
Fig. 1.
Schematic diagram of 2D single muscle fiber model. The single muscle fiber is composed of myofiber and the surrounding endomysium.
Physiological structures of the tapered end of single muscle fiber have been well observed in previous studies (Barrett, 1962; Eldred et al., 1993; Gaunt and Gans, 1990; Trotter, 1990). For the purpose of geometric simplification, a trapezoid shape and a constant angle of fiber end were chosen for tapered ends. Based on the previous observation on the ratio of cross-section area to the taper length (Eldred et al., 1993), effects of tapered end on force transmission were determined by changing the rectangular ends to the ends with 5° and 15° tapered angles (Fig. 2). Although the angles may not reflect the physiological geometry, the purpose of this study is to determine the sensitivity of lateral transmission of force between the myofiber and endomysium to the taper angle.
Fig. 2.
End of myofiber with θ=5° and θ=15° tapered angels.
A 2 s, 100 Hz stimulation signal was applied to myofibers to induce a tetanic contraction. Total force transmitted was calculated as the reaction force at the right end of single muscle fiber, and stress distributions of the interfacial shear stress, τ, and the tensile stress in the myofiber, σ were calculated (Fig. 3). The role of ECM on force transmission was then determined by changing the stiffness of the endomysium.
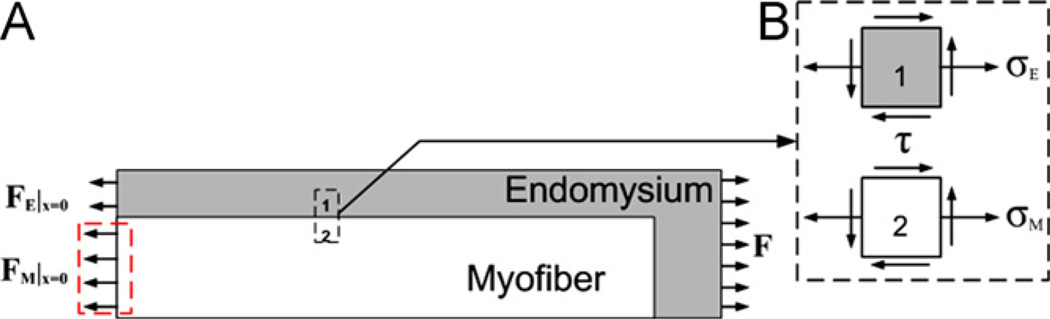
Fig. 3.
(A). Free body diagram of the single muscle cell, or the structural unit, during muscle contraction. F is the total force transmitted to the end of the single fiber and is calculated as reaction force at the right end of the single muscle fiber. FM represents the tensile load in the myofiber, and FM|x = 0 represents the force in myofiber at x = 0. FE represents the tensile load in the endomysium, and FM|x = 0 represents the force in the endomysium at x = 0. Equilibrium in force requires that FM + FE = F at any transversal cross section along x. The force in myofiber is FM = Fa + Fp, in which Fa and Fp are the active force and the passive force in the myofiber, respectively. (B). Stress state of elements in the endomysium and the myofiber.
2.2. Modeling active stress of myofibers
Active stress in myofiber during contraction is calculated using Zahalak’s model (Zahalak and Ma, 1990) in which distribution of bonded cross-bridge density n(x,t) is determined by net attachment and detachment rates of bonded cross-bridge, f(x) and g(x), and the relative shortening velocity ν(t) between actin and myosin:
| (1) |
where r([Ca]) is a function of sarcoplasmic free calcium concentration defined as
| (2) |
In Eq. (2), [Ca] is the concentration of free Ca2+ ions in the sarcoplasm; k1 and k−1 are binding and release rates of calcium, respectively, which can be determined by stimulation signals and initial calcium concentrations. The distribution-moment method developed by Zahalak, (1981) is then used to calculate force generation. For a more detailed method for calculating the active stress in the myofibers, please refer to Appendix A or previous study by Zahalak, (1981).
2.3. FEM implementation of the model
To reduce the complexity of muscle contraction, the contraction process was modeled as small discretized time steps in this study. Within each step, the muscle contraction was modeled as a quasi-static problem, and viscoelastic behaviors of the model were neglected. The principle of virtual work was applied to solve for nodal displacements at each time step. The Total Lagrange (TL) formulation, in which all quantities are measured with respect to the original configuration at t0, is used to describe the deformation. The principle of virtual work at the time t + Δt is described as
| (3) |
where:
| (4) |
| (5) |
in which 0S and 0E are the incremental growth of the stress and strain tensors, respectively, from time t to time t + Δt. and are the second PK stress tensor and the Green strain tensor, respectively, at the end of time t related to the original configuration at the time t0.
The stress tensor S is calculated as a summation of active stress induced by contraction and passive stress due to contraction induced deformation:
| (6) |
The active stress component in myofiber is calculated by Zahalak’s model, and is zero in the endomysium. Both the ECM and the passive behavior of myofiber were modeled as nearly incompressible Mooney–Rivlin materials.
Nonlinear terms in Eq. (3) were then linearized, and the Newton–Raphson method was applied to solve the nodal displacement within this step. The final matrix form of the problem can be written as
| (7) |
where the incremental nodal displacement vector û is the quantity needed to be solved in each iteration, and BL, BNL are matrices of the linear and nonlinear part of strain from nodal displacements, respectively (Bathe, 1996). Nodal displacements calculated at the end of the current iteration were then used to calculate new , and matrices for the next iteration step. The final displacement at time t + Δt was determined only when both displacement and out-of-balance load convergence criteria were satisfied in the model. The entire model was implemented in MATLAB R2011a (MathWorks, Inc. Natick, MA).
2.4. Parameters
The values for each parameter we used for the myofiber and the endomysium are listed in Table 1.
Table 1.
Values for each parameters used in the model.
| Model parameters of active force modela | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| f1 | g1 | g2 | f0 | f′1 | τ1 | τ2 | km | b | ρ | τ | ||
| 30 [s−1] | 8[s−1] | 170 [s−1] | 20 [s−1] | 20 [s−1] | 0.005 [s] | 0.001 [s] | 0.006 [−] | 0.7 [−] | 2 [−] | 0.25 [s] | ||
| Model parameters of passive properties of myofiber and endomysium model | |||
|---|---|---|---|
| C1 (kPa) | C2 (kPa) | K (kPa) | |
| Endomysium (control)b | 0.3 | 0.15 | 10 |
| Endomysium (high stiffness)c | 0.6 | 0.3 | 20 |
| Myofiberd | 3 | 1.5 | 100 |
Taken from Zahalak and Ma (1990).
Determined from Sharafi and Blemker (2011).
Determined from Gao (2008) and Sharafi and Blemker (2011).
Determined from Sharafi and Blemker (2011).
3. Results
3.1. Forces transmitted to the end of the model
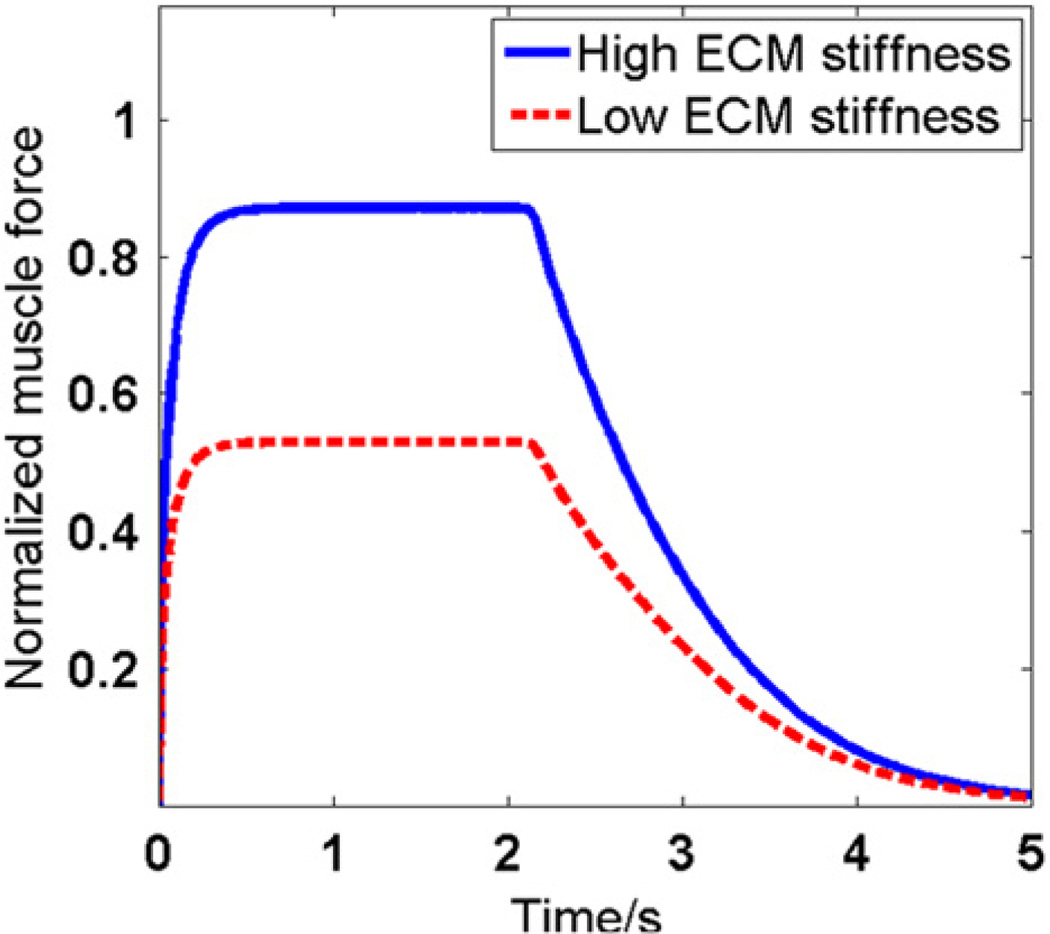
Total force transmitted to the end of the model as a function of time and ECM stiffness is shown in Fig. 4. The total force transmitted is normalized by maximum active force generated in the myofibers during contraction. The model with low and high ECM stiffness transmitted 52.9% and 87.1% of the total force generated in myofiber, respectively. Therefore, increasing the ECM stiffness without changing myofiber properties resulted in larger force transmitted to the end of muscle fiber.
Fig. 4.
Force transmitted to the end of fiber, i.e., F, with different ECM stiffnesses. In this figure, all forces were normalized by the active force generated in the myofiber, i.e., Fa as defined in Fig. 3.
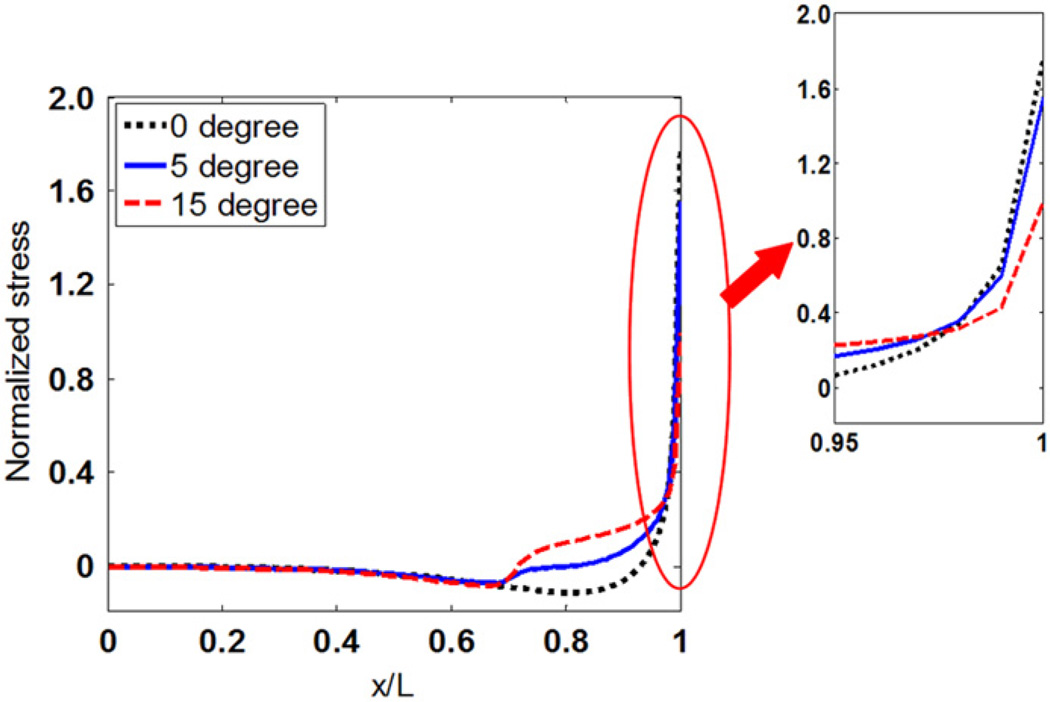
3.2. Stress distribution along myofiber–ECM interface
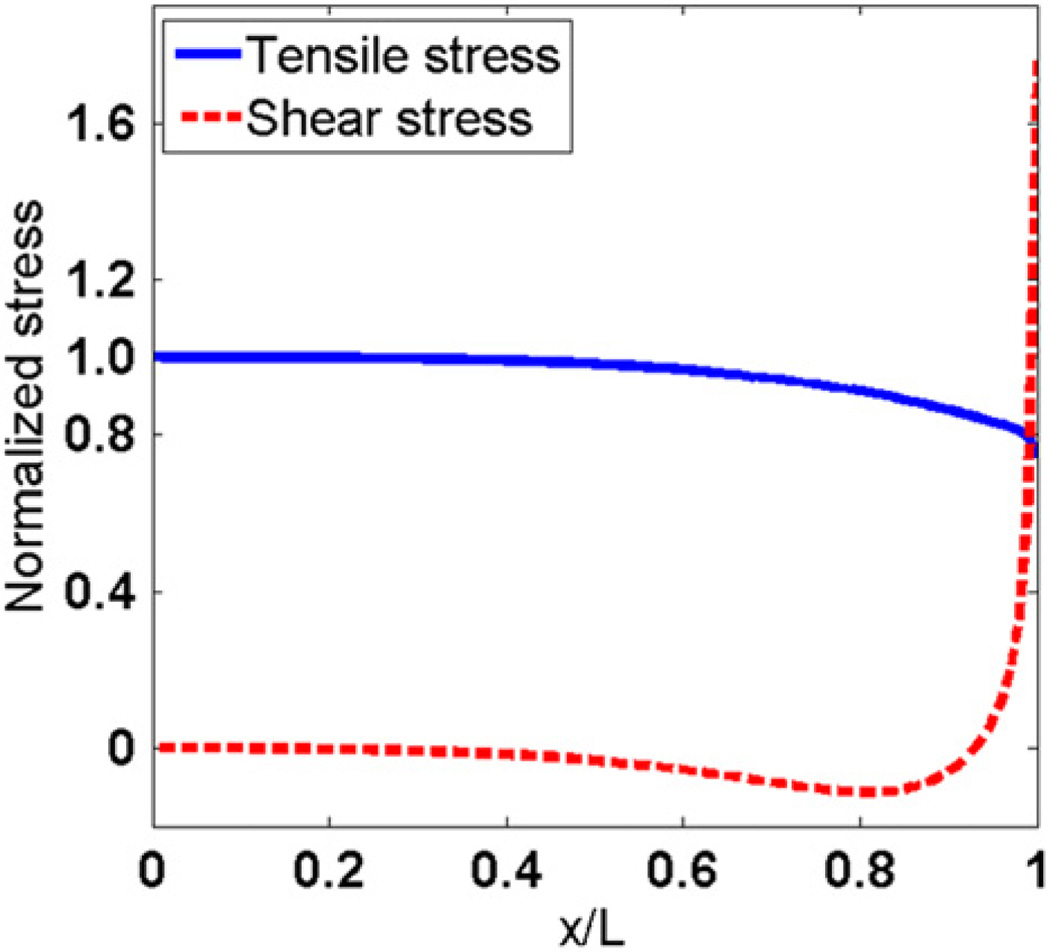
Tensile stress and shear stress distributions along the myofiber of the model are shown in Fig. 5. In the rest of the paper, unless otherwise mentioned, the x coordinates are normalized by the myofiber length, L, and the y coordinates are normalized by the average tensile stress on the middle cross-section of myofiber. The tensile stress is maximal in the middle of the fiber, and decreases to minimum at the end of myofiber. The shear stress has a minimum value in the middle of myofiber, and reaches a maximum value at the end.
Fig. 5.
Tensile stress (σ) and interfacial shear stress (τ) along the longitudinal direction of myofiber.
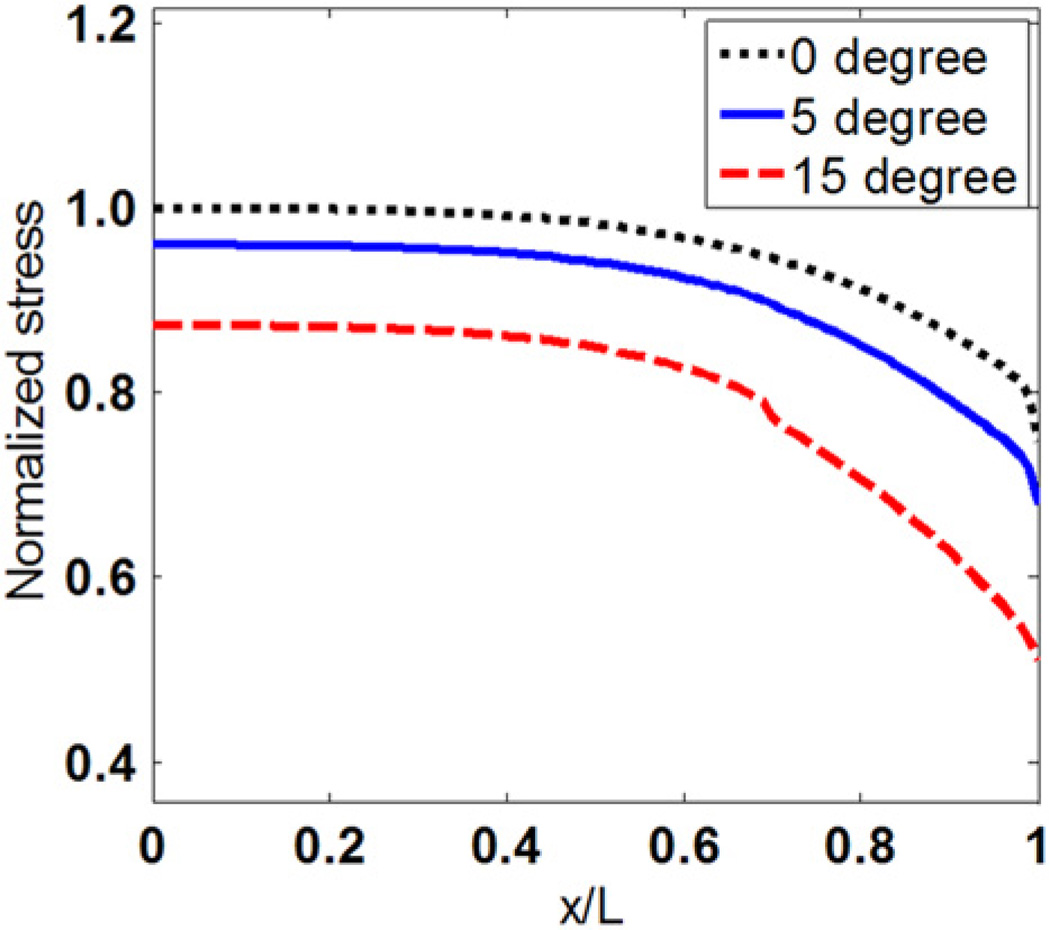
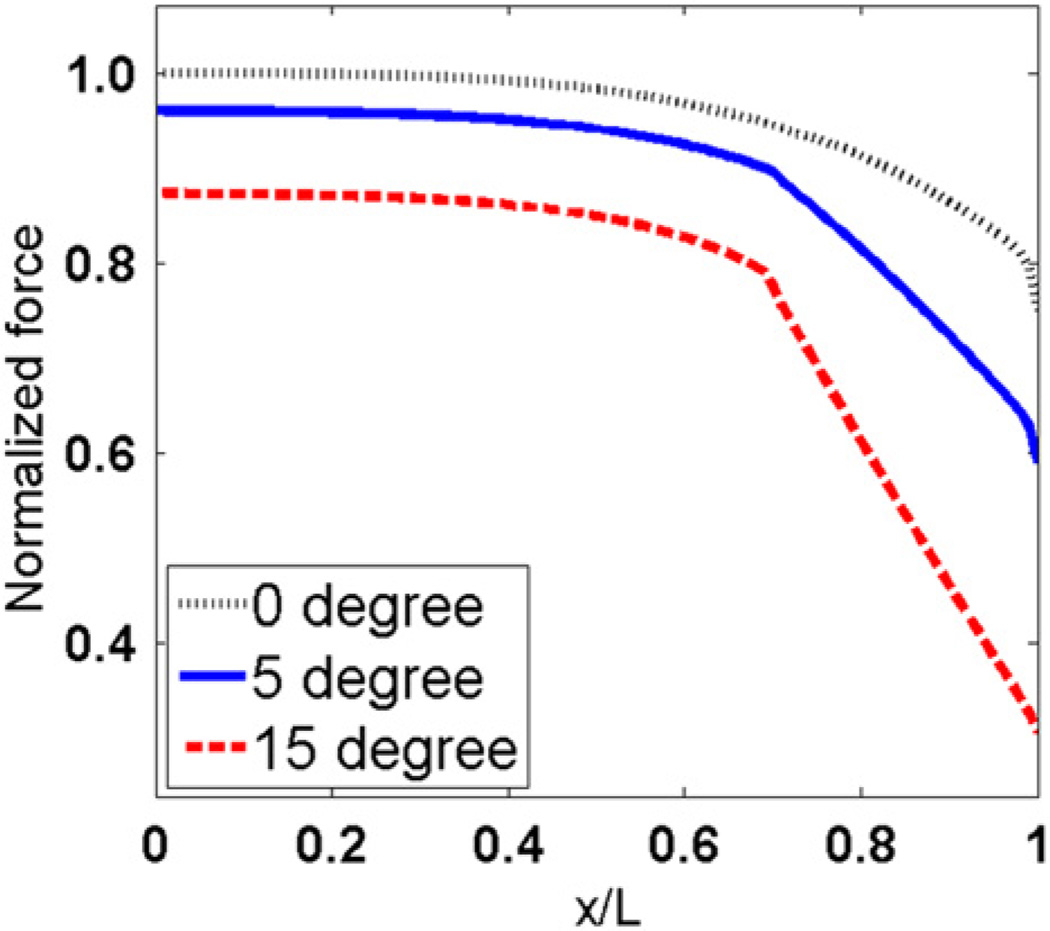
3.3. Stress distributions in myofibers with tapered ends
Figs. 6 and 7 show the effect of tapered angle on distributions of tensile stress and interfacial shear stress. Both tensile stress and the maximum shear stress at the end of myofibers decrease as the tapered angle increases. Forces that are transmitted through tensile stress in myofibers with different tapered angles are compared in Fig. 8. The y coordinates are normalized to force in the middle of myofiber without tapered end. Fig. 8 shows that force transmitted along the myofiber decreases with increased tapered angle. The myofiber without tapered end has the highest force distribution along the whole myofiber. The tensile forces at the end of the myofiber in the 5° and 15° tapered end models were 79.06% and 40.96% of that in the one without tapering, respectively.
Fig. 6.
Tensile stress distributions along myofibers with different tapered angles.
Fig. 7.
Interfacial shear stress distributions along the myofiber with different tapered angles.
Fig. 8.
Normalized tensile force distribution along the longitudinal direction of myofiber with different tapered angles.
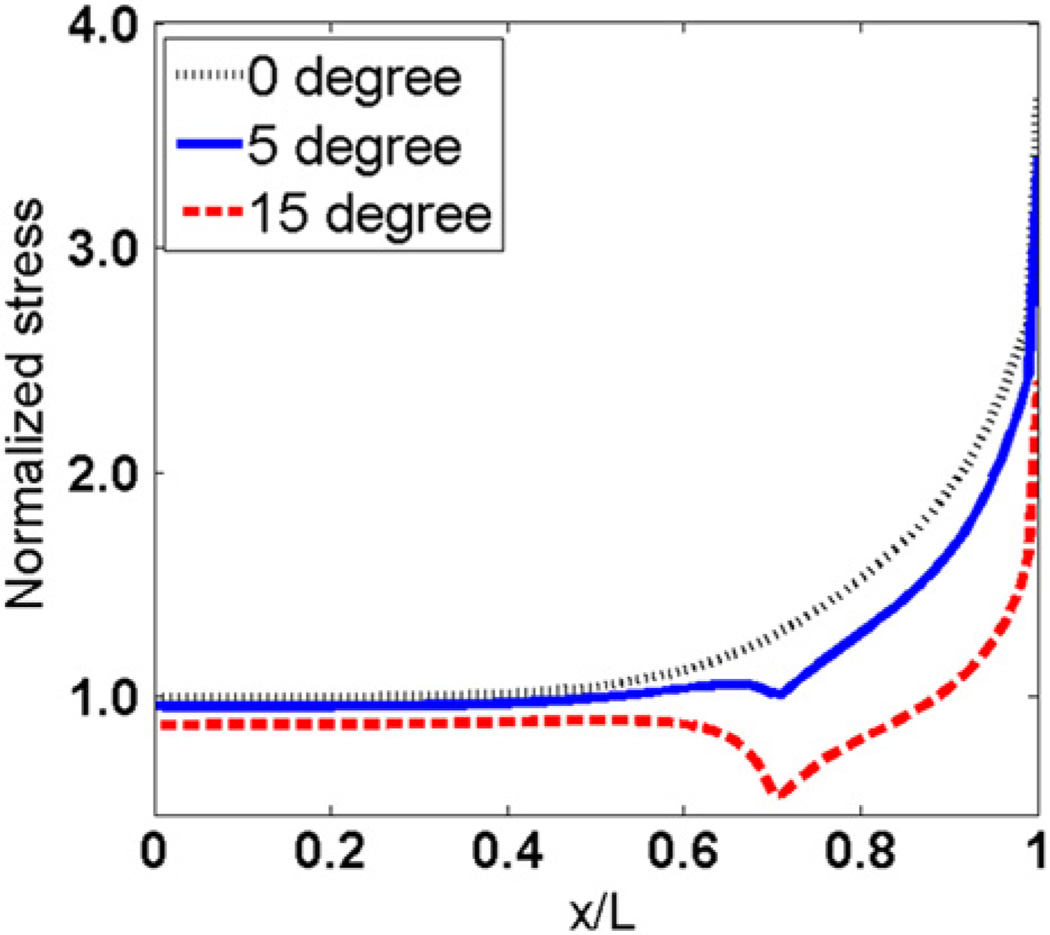
3.4. Von Mises stress distributions along myofiber–ECM interfaces
Von Mises stress distributions along the myofiber–ECM interface in models with different tapered angles are shown in Fig. 9. Von Mises stresses are constant near the middle of myofiber, and reach maximum values at the ends of the myofibers. The myofiber without tapering end has the largest von Mises stress at the end, and the one with a 15° tapered angle has the lowest value there. The sharp changes in 5° and 15° curves locate at the starting points of the tapered ends of myofibers.
Fig. 9.
Von Mises stress distributions along myofibers with different tapered angles.
4. Discussion
We present an FE model of a single muscle fiber that is composed of the myofiber and surrounding endomysium. The Zahalak model was applied to simulate active force generated by the myofiber. Compared to previous studies, the present model has several advantages. First of all, unlike most previous models which considered myofibers and ECM as one material (e.g. Blemker et al., 2005; Johansson et al., 2000; Oomens et al., 2003; Van der Linden et al., 1998), the present model modeled the single muscle fiber as a fiber-reinforced composite, namely, the myofiber is embedded in the endomysium, which made it possible to analyze the force transmission between the myofiber and endomysium. Secondly, although some previous FE studies also incorporated two separate materials (e.g. Yucesoy et al., 2002; Sharafi and Blemker, 2011), the myofiber and the ECM, geometrical limitations of these models restricted the force generated to be transmitted to the ECM only through shear stress, which is not consistent with experimental studies (Purslow, 2002). The geometry of our model represented a microstructure which allowed transmissions of force through both the tensile stress and the shear stress on the myofiber–endomysium interface simultaneously, by which contributions from both tensile and shear stress to the force transmission can be determined. Additionally, most of the previous FEM models (Blemker et al., 2005; Chen and Zeltzer, 1992; Chi et al., 2010; Johansson et al., 2000; Sharafi and Blemker, 2011; Van der Helm, 1994; Yucesoy et al., 2002; Zajac, 1989) used the Hill model to describe the muscle force generation, therefore, providing no information of structural mechanism of muscle contraction. Our model combined an active force model based on biophysical and biochemical behaviors within sarcomeres during the contraction to describe the constitutive relationship of the myofiber. Injury, aging and diseases in muscle will result in changes in structures, and therefore it is desirable to develop models that include structures that affect the force generations. The active force model incorporated in the present study provided us with more control of parameters related to the fiber structure and the ECM environment, and therefore allowed us to further study the effects of injury, disease and aging on structure–function relationship of skeletal muscle in the future.
Two stress distributions along the longitudinal direction were determined in this study: tensile stress distribution in the myofiber and the interfacial shear stress between the myofiber and the endomysium. The distributions suggested that the force generated by myofiber contractions is transmitted to the endomysium by shear mainly at the end of the myofiber. Our results showed that very small interfacial shear between myofiber and the endomysium is observed in the middle of the myofibers, indicating that little or no force transmission between myofiber and the endomysium happens in this region. The tensile stress dropped at the end of the myofiber and the interfacial shear stress increased simultaneously, suggesting that the tensile force is transmitted to the endomysium by shear as the endomysium is too compliant to transmit the high tensile stress. Therefore, as shown in Fig. 5, except at the very end of the myofibers, the tensile stress is much larger than the interfacial shear stress.
Stress distributions predicted from our model are consistent with analytical analysis of 1D shear lag model (Cox, 1952), a model commonly used to analyze the stress transfer between fiber and matrix in fiber-reinforced composites. According to the shear-lag model, tensile stress is maximal in the middle of fiber and drops to zero towards the end. Shear stress in the matrix increases from zero in the middle of fibers to the maximal value at the end of fibers. In addition, our result that increasing the stiffness of the ECM would enhance the force that can be transmitted to the end of the single fiber is also consistent with the analytical analysis from the shear lag model. This result is also consistent with a recent study (Sharafi and Blemker, 2011), indicating that the total force transmitted increased with increasing ECM stiffness.
In this study, tapered ends resulted in a gradual change of geometry at myofiber ends. Smaller shear stress and von-Mises stress were observed in myofibers with larger taper angle at the end of myofiber, which suggested that the gradual changes in geometry have advantages in reducing the stress concentrations. Tidball et al., (1993) demonstrated that at the muscle level, the failure of skeletal muscles during contraction mostly took place around the myotendinous junction, and it was suggested that this failure is related to the stress concentration there (Gao et al., 2008). In addition to gradual change of geometry, previous study demonstrated that there were increased folding interfaces near the tapered end of myofibers, with which the circumferential surface area of the fiber towards the end is significantly increased (Trotter, 1991; Trotter et al., 1995), which will further decrease the stress concentration at the end of myofibers.
While reducing the stress concentration at the end of the myofiber, tapered end also has an advantage in increasing the efficiency of the force transmission between the myofiber and the endomysium. In myofibers with tapered ends, the number of sarcomeres in parallel decreases along the myofiber towards the end due to reduced cross-sectional area, which in turn results in a decrease in the tensile force along the fiber (Fig. 8). However, the loss of contractile force induced by the cross-sectional area change is compensated by transmitting the force to the endomysium laterally, and therefore, the total force transmitted to the end of the muscle fiber (the structural unit) does not decrease as much as that at the end of the myofiber. To better explain this effect, efficiency of lateral transmission of force, ηL, was introduced and defined as the ratio of the reaction force at the end to the tensile force at the end of myofiber, i.e., ηL = F/FM|x = l, where FM|x = l is the force in myofiber at x = l (Fig. 3). Values of ηL of single muscle fiber with 0°, 5° and 15° of tapered angle are 1.43, 1.53 and 1.87, respectively, all of which reach 90% of corresponding value FM|x = 0. This observation is supported by Trotter and Purslow (1995), in which the authors stated that the tapered ends in the fiber significantly increased the efficiency of force transmission through shear at the myofiber–ECM interface.
In the present study, we proved that most of the force generated is transmitted near the end of the myofiber through shear stress to the ECM, and the force transmitted to the end of the model increases with increased stiffness of the ECM. The present work also demonstrates that the tapered angle of the myofiber end has an effect of reducing the stress concentration near the myofiber end which might lead to injury within skeletal muscles. We showed that the mechanical mechanisms of force transmission are affected only by mechanical and geometrical properties of myofibers and the endomysium, and therefore, no differences are expected with lengthening and/or shortening contraction with no injuries occurring during the contractions. However, lengthening contractions and shortening contractions could lead to injuries in myofibers (Lieber, 2002), the endomysium and their interface, and such injuries will in turn cause changes in force transmission (Gao et al., 2008). Therefore, only the isometric contraction was studied in this present study. Effects of injury on force transmission and, on the other hand, how force transmission affects injury should both be studied in the future. To accomplish it, the myofiber–endomysium will be modeled as a non-perfect bonding surface. Additionally, in the future, lateral transmission of force between muscle fibers will be studied by incorporating the present model to a three-fiber system by modifying a previously developed simplified analytical model (Gao et al., 2007). Effect of nonlinearity and time dependent properties of the ECM will then be considered in the model as studied previously (Gao et al., 2009).
Supplementary Material
Acknowledgment
This study was supported by NIH grant 5R03AR59225-2.
Footnotes
Conflict of interest
None declared
Appendix A. Supporting information
Supplementary data associated with this article can be found in the online version at http://dx.doi.org/10.1016/j.jbiomech.2012.04.026.
References
- Balice-Gordon RJ, Thompson WJ. The organization and development of compartmentalized innervation in rat extensor digitorum longus muscle. Journal of Physiology. 1988;398:211–231. doi: 10.1113/jphysiol.1988.sp017039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barrett B. The length and mode of termination of individual muscle fibers in the human Sartorius and posterior femoral muscles. Acta Anatomica. 1962;48:242–257. doi: 10.1159/000141843. [DOI] [PubMed] [Google Scholar]
- Bathe KJ. Finite Element Procedures. Englewood Cliffs, NJ: Prentice-Hall; 1996. pp. 485–765. [Google Scholar]
- Blemker SS, Pinsky PM, Delp SL. A 3D model of muscle reveals the causes of nonuniform strains in the biceps brachii. Journal of Biomechanics. 2005;38:657–665. doi: 10.1016/j.jbiomech.2004.04.009. [DOI] [PubMed] [Google Scholar]
- Chen DT, Zeltzer D. Pump it up: computer animation of a biomechanically based model of the muscle using the finite element method. Computer Graphics. 1992;26:89–98. [Google Scholar]
- Chi SW, Hodgson J, Chen JS, Edgerton VR, Shin DD, Roiz RA, Sinha S. Finite element modeling reveals complex strain mechanics in the aponeuroses of contracting skeletal muscle. Journal of Biomechanics. 2010;43:1243–1250. doi: 10.1016/j.jbiomech.2010.01.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cox HL. The elasticity and strength of paper and other fibrous materials. British Journal of Applied Physics. 1952;3:72–79. [Google Scholar]
- Eldred E, Ounjian M, Roy RR, Edgerton VR. Tapering of the intrafascicular endings of muscle fibers and its implications to relay of force. The Anatomical Record. 1993;236:390–398. doi: 10.1002/ar.1092360213. [DOI] [PubMed] [Google Scholar]
- Gao Y, Waas AM, Wineman AS. Mechanics of injury to muscle fibers. Journal of Mechanics in Medicine and Biology. 2007;7(4):381–394. [Google Scholar]
- Gao Y, Wineman AS, Waas AM. Mechanics of muscle injury induced by lengthening contraction. Annals of Biomedical Engineering. 2008;36(10):1615–1623. doi: 10.1007/s10439-008-9547-3. [DOI] [PubMed] [Google Scholar]
- Gao Y, Waas AM, Wineman AS. Time dependent lateral transmission of force in skeletal muscle. Proceedings of the Royal Society of London, Series A. 2009;12(2009):1–20. [Google Scholar]
- Gaunt AS, Gans C. Architecture of chicken muscles: short-fiber patterns and their ontogeny. Proceedings of the Royal Society of London, Series B Biological Sciences. 1990;240:351–362. doi: 10.1098/rspb.1990.0041. [DOI] [PubMed] [Google Scholar]
- Gaunt AS, Gans C. Serially arranged myofibers: an unappreciated variant in muscle architecture. Experientia. 1992;48:864–868. [Google Scholar]
- Herzog W. Considerations on the theoretical modelling of skeletal muscle contraction. In: Herzog W, editor. Skeletal Muscle Mechanics: From Mechanisms to Function. Chichester: Wiley; 2000. pp. 89–90. [Google Scholar]
- Hill AV. The heat of shortening and the dynamic constants of muscle. Proceedings of the Royal Society of London, Series B. 1938;126:136–195. doi: 10.1098/rspb.1949.0019. [DOI] [PubMed] [Google Scholar]
- Huijing PA, Baan G, Rebel G. Non-myotendinous force transmission in rat extensor digitorum longus muscle. Journal of Experimental Biology. 1998;201:683–691. [PubMed] [Google Scholar]
- Huijing PA. Muscle as a collagen fiber reinforced composite: a review of force transmission in muscle and whole limb. Journal of Biomechanics. 1999;32:329–345. doi: 10.1016/s0021-9290(98)00186-9. [DOI] [PubMed] [Google Scholar]
- Huxley AF. Muscle structure and theories of contraction. Progress in Biophysics and Biophysical Chemistry. 1957;7:255–318. [PubMed] [Google Scholar]
- Johansson T, Meier P, Blickhan R. A finite-element model for the mechanical analysis of skeletal muscles. Journal of Theoretical Biology. 2000;206:131–149. doi: 10.1006/jtbi.2000.2109. [DOI] [PubMed] [Google Scholar]
- Kjaer M. Role of extracellular matrix in adaptation of tendon and skeletal muscle to mechanical loading. Physiological Reviews. 2004;84:649–698. doi: 10.1152/physrev.00031.2003. [DOI] [PubMed] [Google Scholar]
- Kojic M, Mijailovic S, Zdravkovic N. Modeling of muscle behavior by the finite element method using Hill’s three-element model. International Journal for Numerical Methods in Engineering. 1998;43:941–953. [Google Scholar]
- Lieber RL. Skeletal Muscle Structure, Function and Plasticity: The Physiological Basis of Rehabilitation. Philadelphia, PA: Lippincott, Williams and Wilkins; 2002. [Google Scholar]
- Monti RJ, Roy RR, Hodgson JA, Edgerton VR. Transmission of forces within mammalian skeletal muscles. Journal of Biomechanics. 1999;32(4):371–380. doi: 10.1016/s0021-9290(98)00189-4. [DOI] [PubMed] [Google Scholar]
- Oomens CW, Maenhout M, van Oijen CH, Drost MR, Baaijens FP. Finite element modelling of contracting skeletal muscle. Philosophical Transactions of the Royal Society of London, Series B. 2003;358:1453–1460. doi: 10.1098/rstb.2003.1345. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Purslow PP. The structure and functional significance of variations in the connective tissue within muscle. Comparative Biochemistry and Physiology Part A. 2002;133:947–966. doi: 10.1016/s1095-6433(02)00141-1. [DOI] [PubMed] [Google Scholar]
- Sharafi B, Blemker SS. A mathematical model of force transmission from intrafascicularly terminating muscle fibers. Journal of Biomechanics. 2011;44:2031–2039. doi: 10.1016/j.jbiomech.2011.04.038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Street SF. Lateral transmission of tension in frog myofibers: a myofibrillar network and transverse cytoskeletal connections are possible transmitters. Journal of Cellular Physiology. 1983;114:346–364. doi: 10.1002/jcp.1041140314. [DOI] [PubMed] [Google Scholar]
- Street SF, Ramsey RW. Sarcolemma transmitter of active tension in frog skeletal muscle. Science. 1965;149:1379–1380. doi: 10.1126/science.149.3690.1379. [DOI] [PubMed] [Google Scholar]
- Tidball JG, Salem G, Zernicke R. Site and mechanical conditions for failure of skeletal muscle in experimental strain injuries. Journal of Applied Physiology. 1993;3:1280–1286. doi: 10.1152/jappl.1993.74.3.1280. [DOI] [PubMed] [Google Scholar]
- Trotter JA. Interfiber tension transmission in series-fibered muscles of the cat hindlimb. Journal of Morphology. 1990;206:351–361. doi: 10.1002/jmor.1052060312. [DOI] [PubMed] [Google Scholar]
- Trotter JA. Dynamic shape of tapered skeletal muscle fibers. Journal of Morphology. 1991;207:211–223. doi: 10.1002/jmor.1052070212. [DOI] [PubMed] [Google Scholar]
- Trotter JA. Functional morphology of force transmission in skeletal muscle. A brief review. Acta Anatomica (Basel) 1993;146(4):205–222. doi: 10.1159/000147459. [DOI] [PubMed] [Google Scholar]
- Trotter JA. Structure–function considerations of muscle-tendon junctions. Comparative Biochemistry and Physiology Part A: Molecular and Integrative Physiology. 2002;133(4):1127–1133. doi: 10.1016/s1095-6433(02)00213-1. [DOI] [PubMed] [Google Scholar]
- Trotter JA, Purslow PP. Functional morphology of the endomysium in series fibered muscles. Journal of Morphology. 1992;212(2):109–122. doi: 10.1002/jmor.1052120203. [DOI] [PubMed] [Google Scholar]
- Trotter JA, Richmond FJR, Purslow PP. Functional morphology and motor control of series-fibered muscles. Exercise and Sport Sciences Reviews. 1995;23:167–214. [PubMed] [Google Scholar]
- Van der Helm FCT. A finite element musculoskeletal model of the shoulder mechanism. Journal of Biomechanics. 1994;27(5):551–553. 555–569. doi: 10.1016/0021-9290(94)90065-5. [DOI] [PubMed] [Google Scholar]
- Van der Linden BJJJ, Koopman HFJM, Grootenboer HJ, Huijing PA. Modelling functional effects of muscle geometry. Journal of Electromyography and Kinesiology. 1998;8:101–109. doi: 10.1016/s1050-6411(97)00026-6. [DOI] [PubMed] [Google Scholar]
- Yucesoy CA, Koopman BH, Huijing PA, Grootenboer HJ. Three--dimensional finite element modeling of skeletal muscle using a two-domain approach: linked fiber–matrix mesh model. Journal of Biomechanics. 2002;35:1253–1262. doi: 10.1016/s0021-9290(02)00069-6. [DOI] [PubMed] [Google Scholar]
- Yucesoy CA, Koopman BH, Baan GC, Huijing PA, Grootenboer HJ. Effects of inter- and extramuscular myofascial force transmission on adjacent synergistic muscles: assessment by experiments and finite-element modeling. Journal of Biomechanics. 2003;36:1797–1811. doi: 10.1016/s0021-9290(03)00230-6. [DOI] [PubMed] [Google Scholar]
- Zahalak GI. A distribution-moment approximation for kinetic theories of muscular contraction. Mathematical Biosciences. 1981;55:89–114. doi: 10.1016/j.mbs.2020.108455. [DOI] [PubMed] [Google Scholar]
- Zahalak GI, Ma SP. Muscle activation and contraction: constitutive relations based directly on cross-bridge kinetics. Journal of Biomechanical Engineering. 1990;112:52–62. doi: 10.1115/1.2891126. [DOI] [PubMed] [Google Scholar]
- Zajac FE. Muscle and tendon: properties, models, scaling, and application to biomechanics and motor control. Critical Reviews in Biomedical Engineering. 1989;17:359–411. [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.