Analyzing Propensity Matched Zero-Inflated Count Outcomes in Observational Studies

Abstract

Determining the effectiveness of different treatments from observational data, which are characterized by imbalance between groups due to lack of randomization, is challenging. Propensity matching is often used to rectify imbalances among prognostic variables. However, there are no guidelines on how appropriately to analyze group matched data when the outcome is a zero inflated count. In addition, there is debate over whether to account for correlation of responses induced by matching, and/or whether to adjust for variables used in generating the propensity score in the final analysis. The aim of this research is to compare covariate unadjusted and adjusted zero-inflated Poisson models that do and do not account for the correlation. A simulation study is conducted, demonstrating that it is necessary to adjust for potential residual confounding, but that accounting for correlation is less important. The methods are applied to a biomedical research data set.

1. Introduction

Investigators are often met with the challenge of determining the relative effectiveness of different treatments from observational data, which are characterized by imbalance between groups due to a lack of random assignment of the treatments. Propensity matching on the treatment of interest may be used in order to rectify the imbalance [21, 24, 28]. Briefly, the propensity score is defined as a subject's probability of receiving a specific treatment conditional on the observed covariates. Conditioning on the propensity score allows one to replicate some of the characteristics of a randomized controlled trial (RCT)[2]. Several analytic strategies have been applied for determining the association between a treatment and count outcomes in propensity matched observational studies [12, 16] but there is no uniformly accepted approach, especially when zero inflation is present. Even though the majority of studies in the biomedical literature actually ignore correlation induced by matching [2], researchers have demonstrated the need to account for correlation [3, 15]. For example, Li [15] suggested that an unmatched analysis of propensity matched count data results in conservative statistical inferences on the rate ratios. However, others do not recommend matched approaches in all cases [8, 32]; for example, Hill [8] commented that accounting for correlation is not always warranted since correlation in the predictor does not necessarily result in correlated outcomes. Although failure to address dependence induced by matching can result in overly conservative standard errors, it is possible that (post matching) covariate adjustment can alleviate some of this in theory. These two issues of addressing correlation and adjusting for residual confounding in propensity matched data are relatively unexplored in the setting of counts with excess zeros.

Models for correlated counts with excess zeros have been well characterized and are briefly reviewed here. They are often addressed via the use of the blue zero inflated Poisson (ZIP) model of Lambert [13], which is derived from a mixture of a binary distribution degenerated at zero and a Poisson distribution, which enables the inclusion of covariates in both the binary and Poisson part. Researchers have accommodated both zero inflation and correlated/clustered data by incorporating random effects into the Poisson part of the model [7], or into the two distinct Poisson and binary components of the model [10, 14, 33]. For example, Hur et al [10] presented a random effects zero inflated Poisson model and accompanying software for analyzing predictors of the number of postoperative complications after partial colectomy, where patients were clustered into hospitals.

The statistical issues in the current setting are two-fold. Firstly, propensity matching within a small caliper of the propensity score may induce correlation in count outcomes. A “matched pair,” in generalized linear mixed model (GLMM) terminology, [12] would be called a “cluster,” since patients within the cluster are expected to be correlated. Secondly, commonly used models for zero inflated data may prohibit the adjustment for a large number of variables (with random effects, an adjusted model is often overparameterized). Thus, while the above-described ZIP models may be applicable in the current setting, it is unknown whether correlation in the treatment variable induced by propensity matching necessarily induces correlation in the outcome [8], and if it does, whether modeling procedures for correlated data will be identifiable. As a consequence, it is of interest to assess and apply methods for correlated, zero inflated count data to determine the optimal approach in the current setting.

To achieve this end, unconditional (assuming outcomes are uncorrelated) and conditional (assuming outcomes are correlated using random effects) models, both unadjusted and adjusted for the covariates used in estimating the propensity score are assessed via simulation and practice. The remainder of the paper is organized as follows. Section 2, presents the approaches for analyzing correlated zero inflated count outcomes. Section 3, presents a simulation study assessing the bias and efficiency of these approaches in the propensity matched setting. Section 4 presents a study of the effect of a pharmacological treatment on blood product utilization after open heart surgery [5]. Section 5 is a Discussion.

2. Methods

2.1 Statistical Models for Count Outcomes

In a ZIP model, the total set of zeros in the data is considered a mixture of ‘sampling zeros,’ those generated from the underlying Poisson process, and ‘structural zeros,’ the remaining zeros that do not originate from any process. The distinction relies on the result of a Bernoulli trial to dichotomize the study population into two populations. In general terms, the 0/1 process is modeled separately from the Poisson process when the observed zero is determined not to have arisen from a Poisson process (i.e., when the observed zero is a structural zero). Assuming independence, the discrete count response variable, Y_i, where i = 1,…, N total patients in the study follows the following distribution:

$$P(Y_i=0|Z_i)={\varphi }_i+(1-{\varphi }_i)e^{-{\mathrm{\lambda }}_i}$$

$$P(Y_i=y_i|X_i)=(1-{\varphi }_i)\frac{{\mathrm{\lambda }}^{y_i}{e}^{-{\mathrm{\lambda }}_i}}{y_i!}$$ (1)

where 0 < ϕ < 1 so that the model incorporates more zeros than permitted under the Poisson assumption (i.e., where ϕ = 0). In this setup observations are independent between and within matched pairs. The probability of zero inflation and the Poisson mean are modeled as a function of predictors,

$$\mathit{log}\left[\frac{{\varphi }_i}{1-{\varphi }_i}\right]=Z_i\gamma$$ (2)

$$\mathit{log}\left({\mathrm{\lambda }}_i\right)=X_i\beta$$ (3)

where N × p and N × q matrices of covariates Z and X appearing in the logistic and Poisson components, respectively, may or may not overlap, and γ and β are the corresponding p × 1 and q × 1 vectors of regression coefficients.

Since zero inflation and lack of independence may be simultaneously present in the current setting, the within matched pair correlation explicitly can be modeled. Let Y_ij be the count outcome where i = 1, …, M matched pairs and j = 1, 2 members of the pair and rewrite the discrete count distribution from equation 3,

$$P(Y_{ij}=0|Z_{ij},w_i)={\varphi }_{ij}+(1-{\varphi }_{ij})e^{-{\mathrm{\lambda }}_{ij}}$$

$$P(Y_{ij}=y_{ij}|X_{ij},u_i)=(1-{\varphi }_{ij})\frac{{\mathrm{\lambda }}_{ij}^{y_{ij}}{e}^{-{\mathrm{\lambda }}_{ij}}}{y_{ij}!}$$ (4)

where observations are now independent between matches but correlation within a match is accounted for by explicitly modeling random effects attached to the linear predictor, i.e.,

$$\mathit{log}\left[\frac{{\varphi }_{ij}}{1-{\varphi }_{ij}}\right]=Z_{ij}\gamma +w_i$$ (5)

$$\mathit{log}\left({\mathrm{\lambda }}_{ij}\right)=X_{ij}\beta +u_i$$ (6)

In this representation, w_i and u_i denote match-specific random effects. Typically, the random effects are assumed to be independent and normally distributed with mean zero and variance equal to ${\sigma }_w^2$ and ${\sigma }_u^2$ respectively Alternatives are to model w_i, u_i as a bivariate normal distribution in order to induce correlation between the zero and Poisson process, or to simplify equations 5 and 6 by using a shared random effect at the match level, i.e., w_i=u_i. After considering these alternatives along with the models in Equation 5 and Equation 6, simulation and practice indicate a single parameter sufficiently accounts for correlation in the current setting while decreasing the number of parameters.

When random effects are included in the model to account for correlation in the outcome, the interpretation of regression coefficients is conditional on the random effects. As pointed out by Hur, et al. [10], the differences in the parameters γ and β for the same covariate may be of interest. The interpretation of these parameters is the same as that for logistic and Poisson regression models, respectively. The parameter, γ, is interpreted as the log odds ratio of a structural zero in the outcome and β is interpreted as the log relative risk of the outcome for the covariate comparison of interest. The ZIP model with and without random effects is fitted in SAS Version 9.3 proc NLMIXED by inputting the zero-inflated log likelihood for the models presented in equations 1 or 4 [29]. The iterative estimation procedure is initialized by fitting logistic and Poisson regression models respectively, and by setting parameter estimates resulting from those models as initial values. The initial value of ${\sigma }_w^2$ is set to 1.

The particularities of model identifiability for the propensity matched data setting are important. First, if in the matched data set significant unbalance remains in covariate distributions across treatment groups, it may be necessary to fit an adjusted ZIP model. However, as the number of covariates in equations 5 and 6 increases, the identifiability of the model becomes an issue; in general, the mixture model does not handle a large number of variables predicting zero inflation even for moderate sample size. Thus it is sensible to propose a sparse number of covariates for the logistic regression component. Accordingly, for both simulation and application, Z_ij only consists of an intercept and a treatment indicator, while X_ij contains treatment and the most important set of variables used to predict the propensity score. However, it is necessary to determine in both simulation and practice, if this approach provides a sufficiently well-fitting model in the propensity matched setting.

For the rest of the paper, the term “conditional” refers to the ZIP random effect model in Equations 4-6 (since inference is conditional on random effects). The term “unconditional” refers to the ZIP model without random effects, presented in Equations 1-3 (since inference is marginal). The terms “adjusted” and “unadjusted” refer to covariate adjusted and unadjusted models, respectively.

3. Simulation Study

A simulation study is used to explore the need to account for the correlation induced by matching when estimating treatment effects from propensity matched data, and the need to account for adjustment. Austin [2] and Li [15] performed similar simulation studies for count outcomes in the context of propensity matching. For each of the four possibilities (conditional and unconditional, both adjusted and unadjusted), bias and efficiency are compared. Efficiency, in part, depends on whether matching is able to create sufficient balance in the first place [8]. The average estimated treatment effects, the average estimated standard error (SE) of the treatment effects, the standard deviation of the empirical distribution (Emp SD) of treatment effects, and the coverage probability of the 95% confidence interval across the 500 simulated datasets are reported. The ratio of the SE to Emp SD is also reported.

A sample of 856 patients corresponding to 428 matched pairs is simulated with the same covariate structure observed in the 1:1 matched application data set. The benefit of this is that the true correlation structure of the data is preserved in simulations, thereby enhancing the findings' applicability to the data set of interest. Zero inflated count outcomes, Y_i assuming eight confounders with treatment effect, are generated as follows,

$$\mathit{log}\left({\mathrm{\lambda }}_i\right)=-1.15+{\beta }_1{\text{TRT}}_i+0.009X_{2i}-0.006X_{3i}+0.097X_{4i}-0.057X_{4i}-0.057X_{5i}-0.021X_{6i}+0.175X_{7i}+0.107X_{8i}+0.0693X_{9i}$$

Where

$$\begin{array}{c}{T}_i~\mathit{\text{Poiss}}\left({\mathrm{\lambda }}_i\right)\\ \mathit{\text{logit}}\left({\varphi }_i\right)=-0.50+{\gamma }_1{\text{TRT}}_i\\ U_i~\mathit{\text{uniform}}(0,1)\\ \text{if}{U}_i\le {\varphi }_i\text{then}{Y}_i=0\text{else}{Y}_i=T_i\end{array}$$

and vary (β₁, γ₁) covering three clinically meaningful log RR and log OR scenarios: (β₁, γ₁) = (0.30, -0.70), (0, -0.70), and (-0.50, -0.70). With regard to the application data set, these parameters reflect the fact that lysine analogues increase the risk of bleeding and decrease the odds of a zero count, that lysine analogues have no effect on the risk of bleeding but decrease the odds of a zero count, and that lysine analogues decrease the risk of bleeding but also decrease the odds of a zero count, respectively. These three conditions are labeled conditions 1, 2, and 3 in Tables 1 and 2. The effect sizes translate to the following modest relative risk and odds ratios (RR, OR): (1.35, 0.50), (1.0, 0.50), and (0.61, 0.50). The parameters (β₂, …, β₉) for covariates X₂, …, X₉ reflect reasonable effect sizes for covariates predicting blood product use observed in the data. The intercept, γ₀ = - 0.50, reflects 55% zero counts in the baseline treatment group, which reflects the percentage of patients who did not receive blood products in the data set.

Table 1.

Average treatment effect estimate (Est), average of estimated standard error (SE), and standard deviation of the empirical distribution of treatment effects (Emp SD) for data simulated under the 3 conditions. ZI = zero inflation parameter.

	Unconditional/Unadjusted			Unconditional/Adjusted			Conditional/Unadjusted			Conditional/Adjusted
	Est	SE	Emp SD	Est	SE	Emp SD	Est	SE	Emp SD	Est	SE	Emp SD
Condition 1
Poisson (β1=.030)	0.201	0.081	0.095	0.275	0.082	0.084	0.280	0.095	0.086	0.280	0.095	0.086
ZI (γ1 =-.070)	-0.500	0.163	0.172	-0.631	0.180	0.187	-0.679	0.230	0.235	-0.685	0.201	0.207
Condition 2
Poisson (β1=0)	-0.069	0.092	0.110	-0.011	0.093	0.099	-0.086	0.135	0.122	-0.020	0.106	0.103
ZI (71 =-.070)	-0.560	0.172	0.179	-0.664	0.190	0.195	-0.686	0.253	0.247	-0.692	0.212	0.207
Condition 3
Poisson (β1 =-.50)	-0.530	0.123	0.138	-0.496	0.123	0.126	-0.598	0.171	0.157	-0.529	0.139	0.134
ZI (γ1 =-.070)	-0.619	0.204	0.207	-0.681	0.225	0.225	-0.632	0.320	0.302	-0.669	0.257	0.244

Table 2.

Ratio of the average of estimated standard error to the standard deviation of the empirical distribution of treatment effects, and coverage probability of the 95% confidence interval for data simulated under the 3 conditions. ZI = zero inflation parameter.

	Unconditional/Unadjusted		Unconditional/Adjusted		Conditional/Unadjusted		Unconditional/Adjusted
	Ratio	% Coverage	Ratio	% Coverage	Ratio	% Coverage	Ratio	% Coverage
Condition 1
Poisson	0.853	0.864	0.976	0.917	1.105	0.676	1.105	0.864
ZI	0.948	0.858	0.963	0.936	0.979	0.858	0.971	0.930
Condition 2
Poisson	0.836	–	0.939	–	1.107	–	1.030	–
ZI	0.961	0.898	0.974	0.930	1.024	0.812	1.024	0.914
Condition 3
Poisson	0.891	0.994	0.976	0.990	1.089	0.968	1.037	0.978
ZI	0.986	0.840	1.000	0.848	1.060	0.542	1.053	0.784

Table 1 indicates that for the unadjusted analysis, the conditional model fitted to simulated data results in less biased parameter estimates for both the Poisson part of the model (i.e., β̂₁) and the zero inflated part of the model (i.e., γ̂ 1). This implies that when residual confounding is not adjusted for, there is bias in the estimated treatment effect when one does not account for matching. This is true for both the non null and null condition (Conditions 1 and 2) and when (β₁, γ₁) provide conflicting evidence (Condition 3) and in general, is consistent with observations made by Austin (2008) [2]. In unadjusted analysis, the average SD of the estimated treatment effects is larger for the conditional model. That is, the standard error estimates from the unconditional (unmatched) analysis tends to under-estimate the empirical error, while estimates from conditional (matched) analysis tends to over-estimate the empirical error. The magnitude of the ratios presented in Table 2 indicate that for the covariate unadjusted fits, the underestimation observed in the unmatched analysis is greater than the overestimation observed in the matched analysis.

Comparing the unconditional covariate unadjusted simulation results to the unconditional covariate adjusted simulation results, it is evident that bias in both the Poisson and zero inflated treatment effects decreases substantially in the adjusted analysis. The adjusted analysis more accurately reflects the true estimates, and standard errors appear to be similar. It is known in regression settings that covariate adjustment can increase precision of treatment effects, which is reflected by the smaller standard errors and larger coverage probability seen in Tables 1 and 2. Additionally, the ratios of the standard error estimates to the empirical SDs are also nearer to 1.0 in the adjusted analysis. The overall resultant improvement in bias, precision, coverage, and ratio may reflect the fact that there is some residual confounding left over despite best attempts at propensity matching that when accounted for, decreases bias and more accurately reflects the standard error.

Finally, standard error estimates are consistently smaller and coverage probabilities larger in the unconditional, covariate adjusted analysis versus the conditional, covariate adjusted analysis. The bias of parameter estimates differ depending on the condition considered but the unconditional model is uniformly preferable with regard to (SE, ratio, and coverage probability). The simulations indicate that for this covariate structure, post-matching covariate adjustment in the ZIP model is important for obtaining unbiased and precise estimates, and that one may not need to account for matching in the ZIP model after one has already adjusted for residual confounding. For ZIP models, the correlation induced by matching may not be strong enough to necessitate the application of models for correlated data; this is an especially useful observation in the current context since some of the conditional adjusted ZIP models are overparameterized.

4. Application

4.1 Data

The data arise from a retrospective study of 787 patients undergoing coronary artery bypass graft surgery (CABG), valve replacement, or transplant requiring CPB at the Medical University of South Carolina [5]. Outcomes of interest are the number of units of red blood cells (RBC), fresh frozen plasma (FFP), cryoprecipitate (CRYO), and platelet (PLTS) administered either intra or post operatively, and the number of doses of recombinant factor VIIa (FVIIa) used peri-operatively. The treatments are aprotinin and lysine analogues; the former has recently been withdrawn from the market while the latter has not been approved as a pharmacological approach to address post-cardiac surgery-related bleeding. It is unknown to what degree blood product utilization is effected by these treatments once the myriad confounding variables are taken into consideration [17]. A difference in findings in the effect of treatment on bleeding has immediate implications for both the patient health, and cost of treatment.

To generate the propensity score, 27 variables are considered, several of which previously were shown to be confounders of the effect of treatment on cardiac surgery outcomes [17]. These include demographic variables such as patient age, gender, body surface area, and smoking status, comorbidities and prognostic factors such as diabetes, hypertension, coagulation disorders, re-operation, chronic renal/liver disease, pre-operative medication profiles, and Euro score, and intra operative variables such as procedure type, cardiopulmonary bypass time, cross-clamp time, perfusion time, and total operative time. To estimate the propensity score, the confounders are included as predictors in a multiple logistic regression model with treatment as the outcome. In the model building process clinically relevant interactions as well as functional forms of covariates, such as age are also considered. After arriving at the propensity model an optimal matching algorithm is employed to match nearest aprotinin/lysine analogue pairs within a specified maximum caliper of 0.1 [23, 28] resulting in 214 matched pairs. Each outcome is dichotomized into clinically relevant groups - blood products utilized in the first 24 hours and blood products utilized 24 hours after the initial procedure and until discharge. The range of zeros in the outcomes is [52%, 95%].

4.2 Propensity Matching and Balance Diagnostics

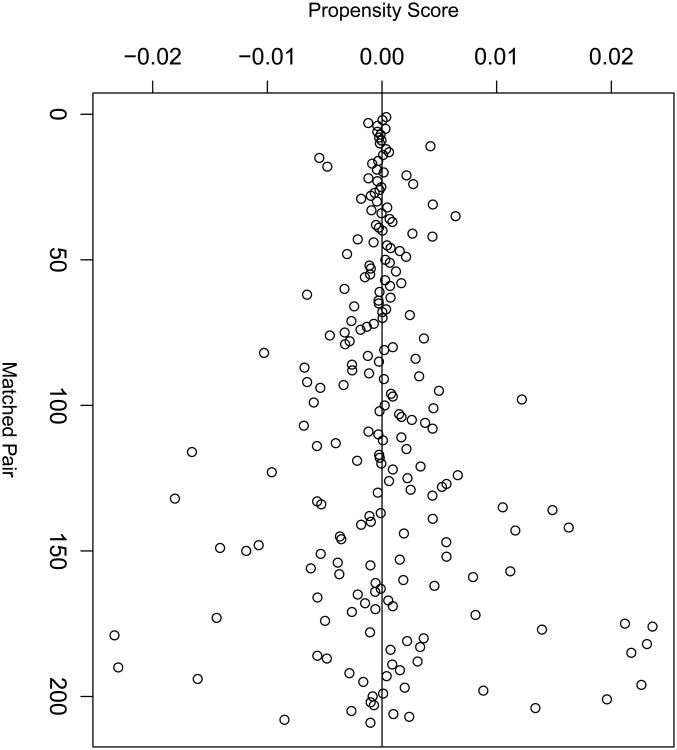
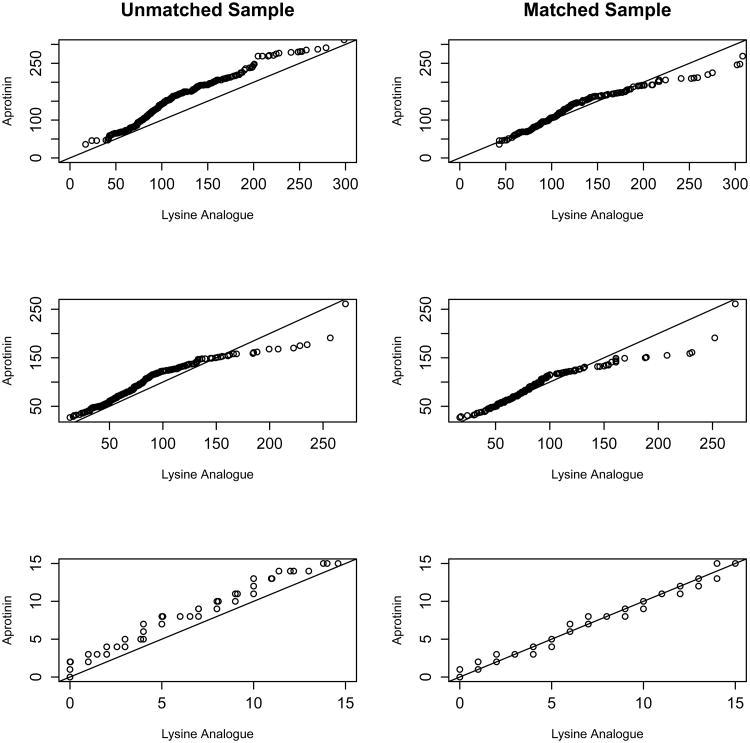
Since it has become standard practice in the biomedical literature to assess the resulting covariate balance in any matched dataset, balance statistics are reported here. Figure 1 demonstrates the quality of the matches in terms of distance between propensity scores for each matched pair (x-axis). The majority of matched pairs are closely matched, within a caliper of 0.01. Close matching typically decreases bias at the expense of variance in observational study [28]. There is much literature on this topic for both continuous and categorical covariates; here, the methods described by [4, 9, 11, 22] are presented in Tables 3 and 4 for continuous and categorical covariates respectively. They display means and higher order moments (in terms of a variance ratio) in matched and unmatched samples, and nonparametric assessments of distributional balance. Since the three continuous covariates used for estimating the propensity score are right skewed, it is sensible also to report medians and interquartile range (IQR) in order to demonstrate the quality of the match (Table 3). In addition, following the recommendations of Sekhon (2011) and Austin (2009) respectively, results of Kolmogorov-Smirnov tests for the equality of distributions and Q-Q plots to compare empirical distributions for both the matched and unmatched samples are presented (Figure 2) [2, 31]. Of note, [11] recommend balancing treatment groups on covariates, “without limit,” and, since hypothesis tests are sample size dependent, researchers should not fully rely only on P-values to assess covariate balance. Finally, to test balance for categorical covariates, Table 4 presents frequencies by treatment group.

Figure 1.

Quality of the matched sample as indicated by the caliper within which matching is possible.

Table 3.

Assessment of match balance for continuous covariates. This includes a comparison of summary statistics by group for unmatched and matched samples. The Kolmogorov Smirnov (KS) test compares covariate distributions across treatment group.

	Cross Clamp Time		Perfusion Time		Euro Score
Statistics	LA	Aprotinin	LA	Aprotinin	LA	Aprotinin
Unmatched Sample
Mean	79.7	92.1	111.4	144.6	5.3	7.0
Median	72	84	98	139	5	7
25th Percentile	54	65	75	96	3	4
75th Percentile	94	118	133	177	7	9
Variance Ratio		0.78		1.33		1.11
KS p-value		0.001		0.001		0.001
Matched Sample
Mean	83.8	85.6	123.0	124.4	6.3	6.3
Median	76	80	109	120	6	6
25th Percentile	60	62	84	84	4	4
75th Percentile	95	108	145	162	8	8
Variance Ratio		0.69		0.68		1.06
KS p-value		0.16		0.10		0.99

Table 4. Assessment of match balance for categorical covariates. In the penultimate row, the “Other” category includes valve replacements and transplant recipients.

	Unmatched Sample		Matched Sample
Outcome	LA	Aprotinin	LA	Aprotinin
Diabetes	44.7	24.9	31.0	27.0
Preop Aspirin	27.4	47.5	40.2	44.5
Preop Diuretics	6.5	19.0	11.0	11.0
Preop ACE Inhibitors	16.2	40.7	27.3	32.5
Surgery Type (Transplant/Other)	7.0	16.9	8.6	8.1
Surgery Type (CABG)	65.8	41.2	49.8	61.2

Figure 2.

Q–Q plots assessing the quality of matching for the three continuous covariates: cross-clamp time, perfusion time and Euro score, respectively.

Tables 3 and 4 and Figure 2 show that before matching, the covariate distributions for continuous covariates are highly disparate by treatment group, as demonstrated by means, medians, IQR, highly significant KS tests, and Q-Q plots that deviate from the line through the origin with slope equal to 1. In the matched sample, the means, medians, and IQR are much closer, the KS tests are all insignificant, and Q-Q plots are generally improved. As demonstrated by the Q-Q plots for the matched sample, the right tail of the distribution of intra operative variables is still heavier for the aprotinin group, although the lower end of the distributions are very similar. The most significant confounder of treatment is Euro Score and accordingly, Figure 2 shows that adequate balance on this variable is obtained in the matched sample. Table 4 similarly shows improved balance among most of the categorical covariates with the exception of surgery type.

It can be concluded that there is improved similarity between the matched samples for both categorical and continuous variables over the unmatched sample but that adjustment for some remaining covariate imbalance might be necessary in the analysis stage. It is not surprising that some covariates are difficult to balance in a closely matched sample; matching is not expected to balance individual covariates as patients are matched on an overall distance measure calculated in our case as the observed propensity score. Further, Imai et al. (2008) demonstrate that matching contains no threshold below which the level of imbalance is always acceptable; these authors recommend parametric adjustment to account for any remaining differences [11].

4.3 Results

Tables 5 and 6 show estimates of treatment effects, standard errors of treatment effects, and p-values. Table 7 presents Akaike Information Criteria (AIC) and Bayesian Information Criteria (BIC) for each model considered. Adjustment is made for important covariates, i.e., those that are strong predictors in the original propensity score model or those that still exhibit imbalance in the matched sample. These covariates include Euro score, cross clamp time, perfusion time, and surgery type. The reason that all of the covariates used to generate the propensity score are not included is that in our experience, sparsity should be encouraged when fitting the ZIP model to medium sample sizes since convergence problems occur. Indeed in the current case, several conditional models are not identifiable even when attempting to adjust for these four covariates, as presented below.

Table 5.

Covariate unadjusted zero inflated Poisson model fit to the observed data. The γ is the log odds of a structural zero in lysine analogue versus aprotinin group. The β is the log relative risk of blood product usage in the lysine analogue versus aprotinin group. RBC= red blood cells, FFP = fresh frozen plasma, CRYO = cryoprecipitate, PLTS = platelets. NE indicates the model is not estimable.

	Unconditional						Conditional
	Poisson			ZI			Poisson			ZI
Outcome	β	se(β)	p-val	γ	se(γ)	p-val	β	se(β)	p-val	γ	se(γ)	p-val
Intra RBC	0.289	0.095	0.002	0.007	0.211	0.974	0.295	0.113	0.009	0.033	0.222	0.882
Intra FFP	0.447	0.154	0.004	-0.656	0.279	0.019	0.452	0.203	0.027	-0.630	0.284	0.027
Intra CRYO	NE			NE			NE			NE
Intra PLTS	0.019	0.077	0.803	-0.479	0.240	0.046	-0.157	0.294	0.594	-0.516	0.251	0.04
Post RBC	0.025	0.077	0.748	-0.458	0.200	0.023	0.295	0.182	0.982	-0.609	0.308	0.048
Post FFP	0.033	0.112	0.770	0.092	0.244	0.707	0.031	0.290	0.914	0.083	0.284	0.769
Post CRYO	-0.443	0.842	0.599	-0.170	0.985	0.863	-0.447	0.863	0.604	-0.180	1.032	0.862
Post PLTS	0.461	0.194	0.018	0.192	0.282	0.496	0.522	0.426	0.221	0.395	0.477	0.409
FVIIa	0.098	0.165	0.554	-1.566	0.505	0.002	0.084	0.231	0.715	-1.567	0.505	0.002

Table 6.

Covariate adjusted zero inflated Poisson model fit to the observed data. Model is adjusted for cross clamp time, perfusion time, Euro score, and surgery type. The γ is the log odds of a structural zero in lysine analogue versus aprotinin group. The β is the log relative risk of blood product usage in the lysine analogue versus aprotinin group. RBC= red blood cells, FFP = fresh frozen plasma, CRYO = cryoprecipitate, PLTS = platelets. NE indicates the model is not estimable.

	Unconditional						Conditional
	Poisson			ZI			Poisson			ZI
Outcome	β	se(β)	p-val	γ	se(γ)	p-val	β	se(β)	p-val	γ	se(γ)	p-val
Intra RBC	0.243	0.096	0.012	0.006	0.221	0.977	0.247	0.112	0.028	0.022	0.236	0.927
Intra FFP	0.403	0.165	0.015	-0.631	0.284	0.027	0.398	0.352	0.259	-0.675	0.429	0.117
Intra CRYO	2.803	1.165	0.122	-1.050	1.056	0.320	1.611	1.645	0.272	-1.324	1.254	0.292
Intra PLTS	-0.026	0.081	0.749	-0.481	0.240	0.046	NE			NE
Post RBC	-0.048	0.080	0.551	-0.542	0.216	0.013	-0.124	0.176	0.981	-0.966	0.398	0.016
Post FFP	0.043	0.123	0.726	0.099	0.247	0.688	0.104	0.296	0.728	0.050	0.302	0.868
Post CRYO	0.345	0.832	0.678	0.773	1.105	0.485	0.333	0.803	0.679	0.860	0.994	0.368
Post PLTS	0.434	0.245	0.077	0.256	0.327	0.434	NE			NE
FVIIa	0.288	0.190	0.130	-1.564	0.506	0.002	0.286	0.208	0.169	-1.564	0.506	0.002

Table 7.

AIC and BIC for different model fits. RBC= red blood cells, FFP = fresh frozen plasma, CRYO = cryoprecipitate, PLTS = platelets. NE indicates the model is not estimable.

	Unadjusted				Adjusted
	Unconditional		Conditional		Unconditional		Conditional
Outcome	AIC	BIC	AIC	BIC	AIC	BIC	AIC	BIC
Intra RBC	1297.1	1313.4	1289.1	1309.4	1273.5	1310.0	1269.0	1309.5
Intra FFP	668.4	684.6	656.5	676.8	663.4	699.9	647.5	688.0
Intra CRYO	NE	NE	NE	NE	229.4	265.9	225.5	266.0
Intra PLTS	1369.2	1385.5	993.2	1013.4	1343.0	1379.5	NE	NE
Post RBC	1838.1	1854.3	1456.7	1476.9	1717.6	1754.1	1423.5	1464.0
Post FFP	970.1	986.2	808.3	828.5	933.8	970.4	799.3	839.8
Post CRYO	240.1	256.3	242.2	261.5	232.2	268.7	235.5	276.0
Post PLTS	674.1	690.4	625.9	646.2	645.7	682.2	NE	NE
FVIIa	358.2	374.4	351.9	372.1	348.9	385.5	350.4	390.9

The parameter estimate, γ̂, represents the log odds of a structural zero in the lysine analogue versus aprotinin group while the estimate β̂ represents the log relative risk of blood product utilization in the lysine analogue versus aprotinin group. Therefore, a positive γ̂ value is in favor of lysine analogues while a negative value is in favor of aprotinin; the opposite is true for the log relative risk, β̂.

Tables 5 and 6 show that accounting for matching in the adjusted setting compromises estimability, which is what prompted the current exploration. The tables also show that accounting for the matching decreases precision in both the zero and Poisson part of the model, resulting in a lower power to detect treatment differences in both the odds and risk of blood product utilization. On the other hand, covariate adjustment increases precision of the parameter estimates for both the zero inflation and Poisson parameter; this is likely dependent on the amount of residual confounding present for that particular outcome. These observations are consistent with the simulation results presented in Section 3.

All models fit indicate that the odds of a structural zero in post operative RBCs is significantly lower in the lysine analogue versus the aprotinin group and the odds of a structural zero in FVIIa is significantly lower in the lysine analogue versus the aprotinin group; these two findings are highly significant for all four of the models considered.

Referring to Table 6, for the unconditional model, the risk of intraoperative FFP administration is significantly higher (p-value=0.015) while the odds of a structural zero is significantly lower (p-value=0.027) in the lysine analogue versus aprotinin group. Neither of these effects are detectable from the conditional ZIP model, which for most outcomes, suffers from lower precision than any other model.

Conditional adjusted ZIP models for intra and post operative platelets are not estimable (NE) likely due to the large number of excess zeros; however, the unconditional adjusted models provide a reasonable fit, and demonstrate significance and borderline significance in the zero and Poisson part of the model, respectively (Table 6). Specifically, the odds of a structural zero in intra operative platelets is significantly lower in the lysine analogue group versus the aprotinin group (p-value=0.046) and the risk of post operative platelets is higher in the lysine analogue group versus the aprotinin group (this last effect approaches, but does not meet, statistical significance (p-value = 0.077). These effects would not be detectable if the clustered data model had been employed.

It is notable that adjustment is necessary to fit adequately the zero inflated Poisson model to the intra operative cryoprecipitate data. Unadjusted analyses in Table 5 reflect unstable parameter estimates and standard errors for this outcome. However, both (conditional and unconditional) covariate adjusted analyses (Table 6) show reliable estimates in the direction of an increased risk of intra operative cryoprecipitate use in the lysine analogue versus aprotinin group. In general, it makes sense that adjustment improves the precision of treatment estimates in light of residual confounding since the variables perfusion time, cross clamp time, and surgery type are slightly imbalanced with respect to treatment group in the matched sample. The findings show that adjusting for residual confounding may be sufficient in the zero inflated setting. This is important in light of the fact that several conditional models are not estimable.

Finally, although information criteria is not ideal for selecting among different classes of models (e.g., unconditional versus conditional), it is useful for selecting whether adjustment is needed within a class of model (along with likelihood ratio tests, which are not presented). Smaller AIC and BIC indicate that for most outcomes, adjustment in the regression model improves the fit.

5. Discussion

The current research has ramifications across many fields since zero inflated count outcomes are ubiquitous in statistical research. For example, health services outcomes, post operative complications, the number of claims to an insurance company, environmental, and ecological outcomes are frequently reported and analyzed as counts. As a result, it is important to provide some guidelines on how to analyze 1:1 propensity matched zero inflated count data. There is no consensus in the literature as to whether the correlation induced as a result of propensity matching should be accounted for, or whether adjustment for covariates used to estimate the propensity score is necessary, and this question remains even less explored when outcomes are counts that are subject to zero inflation. However, this is an important question to address for the following reason. Fitting a 2-part mixture model with many covariates in addition to random effects to accommodate clustering may result in model identifiability issues, especially regarding estimability of covariate effects in the zero inflation regression. Since simultaneous incorporation of random effects and covariate adjustment makes it difficult to obtain reliable parameter estimates, then the applicability of this model for matched zero inflated data is compromised.

The importance of covariate adjustment when analyzing outcomes of other metrics has been underscored in the literature on propensity analysis [2, 3, 25–27]. We demonstrate that covariate adjustment decreases bias, and results in similar or better precision of parameter estimates in both parts of the mixture model than the unadjusted approach. This finding implies that, even after matching and in spite of much improved balance diagnostics, there may still be residual confounding of the effect of treatment on outcome. However, when residual confounding is accounted for, it might not be necessary to account further for matching. In fact in both simulations and practice, the conditional ZIP model that accounts for the matched nature of the data results in lower precision, lower coverage probabilities, and therefore a small loss of power over the unconditional ZIP model. This observation aligns well with the general observations made by other researchers [8, 11, 32] who show that matched pairs analysis can result in a loss of power and suggest consideration of alternatives, such as covariate adjustment. Specifically, methods that explicitly adjust for pairwise dependence are not always the best choice (even if, algorithmically, the dependence was created by forming matched pairs) [8].

One of the most important findings of this study is specific to computational issues in mixture modeling. In the data example, some of the zero inflated Poisson models for correlated data do not converge when all of the confounding variables are included in the Poisson part of the model. This limitation is even more profound when these covariates are added to the binary part of the model. Thus, in the current setting, there may be a conflict between properly accounting for induced dependence and model identifiability. Allowing two different random effects in the Poisson and zero inflated portion of the model can be computationally difficult using commercial software[14]. Min & Agresti (2005) [18] showed that this simpler form of either a single shared random effect, or one random effect for zero inflated count data, is often adequate in practice. These authors demonstrated this on a clinical trial data set where the outcome was number of side effects in response to two treatments. Findings from the current research are consistent with this observation; it appears that the match-specific random effect induces a sufficient correlation structure for the outcome, Y.

The current research has particular ramifications for the interpretation of odds ratios in the ZIP model. In an I × J × K contingency table representing the joint distribution of 3 discrete variables (call these treatment X, outcome Y, and con-founder Z), a measure of association between X and Y is considered collapsible across strata (subtables) of Z if it is both constant across strata, and if this constant value is equal to the marginal value [6]. However, odds ratios as an effect measure are subject to the peculiar property of noncollapsibility even without confounding. So even if Z does not meet the definition of a confounder, crude and adjusted ORs disagree [6]. Thus in the case where there are no confounders, one must be careful not to misinterpret unadjusted ORs as “biased” since this does not represent a true statistical bias. This has obvious implications for the ZIP model if one were to include variables with direct modes of action into the zero inflated part of the model.

In addition to methodological implications, the current study has implications related to the primary clinical question: whether the use of lysine analogues versus aprotinin increases the risk bleeding after heart surgery involving CPB. These implications along with a detailed analysis of this data set are published in [5]. The current findings indicate that in a propensity matched sample, aproptinin reduces the amount of blood product administered both intra-operatively and post-operatively. However, limitations of the data example must be discussed. The matching algorithm was able to match 214/314 aprotinin patients indicating some aprotinin patients had a baseline profile with an unobservable counterpart in lysine analogue patients. To assess this limitation in the form of a sensitivity analysis, stratification by estimated propensity score (which retains all patients for analysis) was also implemented and the directionality of the findings for blood product usage was similar, supporting findings from the matched sample. The current analysis also did not consider the fact that blood product outcomes are likely correlated. By fitting repeated univariate analyses to these outcomes, the presented hypothesis tests are probably subject to a larger than 0.05 type I error rate. Future research should accommodate the additional level of clustering on blood product outcomes. This could be achieved by modeling Y_ijt, where t indicates blood product type, and incorporating an additional random effect, s_ij into the ZIP model, representing pair within outcome type. Further exploration would be needed to determine where this random effect should enter the ZIP model.