Abstract
The Potts model has enjoyed much success as a prior model for image segmentation. Given the individual classes in the model, the data are typically modeled as Gaussian random variates or as random variates from some other parametric distribution. In this manuscript we present a non-parametric Potts model and apply it to an FMRI study for the pre-surgical assessment of peritumoral brain activation. In our model we assume that the Z-score image from a patient can be segmented into activated, deactivated and null classes, or states. Conditional on the class, or state, the Z-scores are assumed to come from some generic distribution which we model non-parametrically using a mixture of Dirichlet process priors within the Bayesian framework. The posterior distribution of the model parameters is estimated with a Markov chain Monte Carlo algorithm and Bayesian decision theory is used to make the final classifications. Our Potts prior model includes two parameters, the standard spatial regularization parameter and a parameter that can be interpreted as the a priori probability that each voxel belong to the null, or background state, conditional on the lack of spatial regularization. We assume that both of these parameters are unknown, and jointly estimate them along with other model parameters. We show through simulation studies that our model performs on par, in terms of posterior expected loss, with parametric Potts models when the parametric model is correctly specified, and outperforms parametric models when the parametric model in misspecified.
Keywords: Decision Theory, Dirichlet process, FMRI, hidden Markov random field, Non-parametric Bayes, Potts model
1 Introduction
Functional magnetic resonance imaging (FMRI) has found widespread use in the cognitive neurosciences due to its ability to non-invasively detect changes in brain activity induced by an experimental stimulus (1). The blood-oxygen-level dependent (BOLD) signal is the MRI contrast of blood deoxyhemoglobin and is a surrogate for neural activity. More recently, there has been a growing interest in using FMRI to assist in the pre-surgical planning of resection of brain tumors or epileptic foci (2). In these applications, the experimental paradigm used in the FMRI acquisition is carefully planned to detect changes in the BOLD signal near, around and within the tumor in an effort to assist the surgeon in excising the tumor while preserving brain tissue regions involved in common tasks, such as speaking, as determined by the FMRI data.
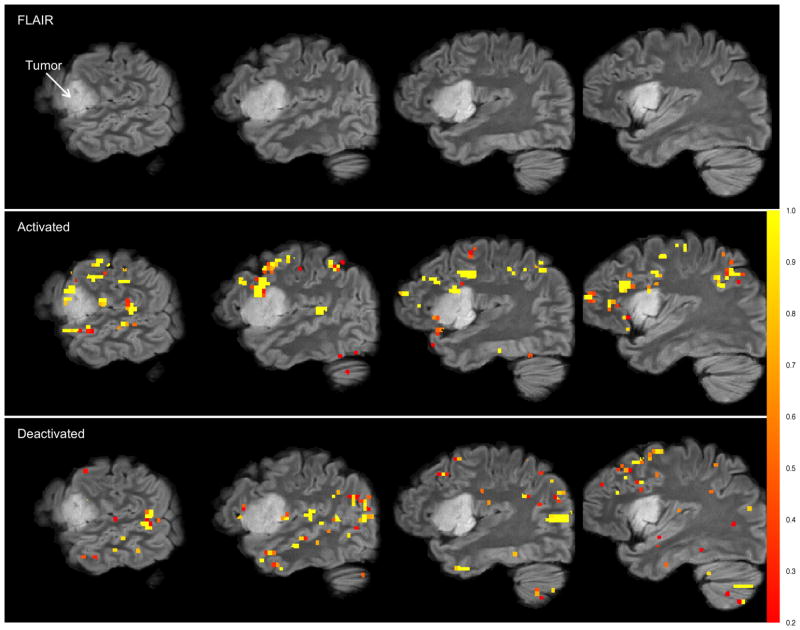
Our motivating data set comes from such a study. After a seizure with a speech arrest, a 32 year old female patient presented with a WHO grade II oligodendroglioma, a particular type of a primary brain tumor derived from oligodendrocytes, in the left inferior frontal and insular lobe. Pre-surgery, the patient underwent an FMRI exam to determine vital peritumoral regions of the brain responsible for executive language functions and expressive speech. The patient was asked to recite tongue-twisters followed by periods of rest because she exhibited slight impairments in the repetition of phonemically challenging phrases while other speech and language functions were not disturbed. A high-resolution FLAIR (fluid attenuated inversion recovery) (3) sagittal image of the left hemisphere is displayed in the top row of Figure 1 where the tumor is clearly visible.
Figure 1.
Results from the NP-Potts model. Top row: Four sagittal slices of the high resolution FLAIR image in the left hemisphere. Second row: FLAIR image with activation overlay. Bottom row: FLAIR image with deactivation overlay. The gray-scale bar (color bar in electronic version) represents the posterior probability of both activation (for the second row) and deactivation (for the bottom row). The overlays are highly pixelated as the analysis is performed in the functional MRI space which has a much lower resolution than the high resolution FLAIR image. The hyperprior distribution on pi0 is pi0 ~ (Beta(0.95(0.2N), 0.05(0.2N)). Loss function is (12) with c1 = c2 = 4.
In a standard FMRI analysis a mass-univariate model is fit (e.g. with SPM (4) or FSL (5; 6)), where a regression model is fit independently at every volume element, or voxel. The resulting image of statistics is thresholded such that the risk of false positives over the brain is controlled at a specified level. The most common approach is to use a threshold that controls the familywise error rate using random field theory (RFT) (7). However, RFT rests on the assumption that the data arise as a realization of a smooth Gaussian random field. With no smoothing, FMRI data violate this assumption (8; 9) and thus the data are convolved with an isotropic Gaussian kernel prior to analysis to make this assumption hold, at least approximately. The result of this smoothing is that the activation (large, positive BOLD signal) and deactivation (large, negative BOLD signal) are spatially smeared out. Spatial diffusion of the signal is tolerable for the cognitive neurosciences as it increases the signal-to-noise ratio and gives results that may be typical for a population of subjects. In pre-surgical planning, however, spatial precision of the signal is paramount. According to electrical stimulation mapping (ESM), the size of speech-eloquent areas is known to vary between a few millimeters to a few centimeters. Thus, smoothing by a single uniform Gaussian kernel will inevitably smear out some activations and shrink or even extinguish others below the detection level. Both scenarios are highly undesirable for pre-surgical planning. Thus, we develop an image segmentation model that does not rely on such random field assumptions.
The Potts model (10) was originally developed as a generalization of the Ising model (11; 12) in the field of statistical mechanics. However, it has also been very successful as a prior model for image segmentation (12; 13; 14; 15). A crucial feature of the Potts model is that it does not smooth over abrupt changes in image intensity (12) as does the convolution of the image with an isotropic Gaussian kernel.
Several authors have proposed nonparametric hidden Markov random field models (such as the Potts model) (16; 17; 18; 19, e.g.). These authors all assume that the number of states in the hidden Markov random field is unknown and is to be estimated. To this end, they all use the Dirichlet process (20) which naturally clusters the data. These clusters become the states of the hidden Markov random field. Once the number of states is known, the image intensity at every voxel in a given state has the same (parametric) distribution. In our application, we know a priori that the BOLD activation data consists of exactly three states: activated, null and deactivated. Thus our model is different in that we assume that the number of states is known and model the image intensities of the voxels within each state non-parametrically. This is the key difference in our model from those previously proposed. Using one of the previously proposed models in our application would more than likely result in a model with more than three states and would be useless in identifying the activated, null and deactivated voxels.
This paper brings together several advanced statistical ideas including the Potts model, path sampling, mixture of Dirichlet process priors, slice sampling (via the Swendsen-Wang algorithm) and decision theory to estimate which voxels are deactivated, activated or null. Our simulation studies show that, in terms of minimizing the posterior expected loss, our model performs equivalently to parametric Potts models when the parametric model is correctly specified and outperforms parametric models when the parametric model is misspecified.
The remainder of the paper is laid out as follows. In Section 2 we introduce notation and the Potts model along with our generalization to the Bayesian non-parametric Potts model (NP-Potts). Some of the key algorithmic details are outlined in Section 3. The motivating example is analyzed with our model in Section 4, where we contrast it to a standard Potts model, and present results from our simulation studies. We finish the paper with a discussion in Section 5.
2 Model
2.1 The Potts Model
Let Y denote a digitized image of intensity values. Let
 denote the set of voxels (volume elements) if Y is a three dimensional image or pixels (picture elements) if Y is a two dimensional image. The cardinality of
denote the set of voxels (volume elements) if Y is a three dimensional image or pixels (picture elements) if Y is a two dimensional image. The cardinality of
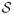 is N. The Potts model (10) relies on a neighborhood system and its associated cliques (13). Throughout we will assume a first-order neighborhood system. In the first-order neighborhood system, two pixels are neighbors if they share a common edge and two voxels are neighbors if they share a common face. Thus, each voxel in the interior of Y has six neighbors. Henceforth, we refer only to voxels and reference them by a single index, say i. The correspondence between voxels and pixels should be obvious. We denote the fact that two voxels i, i′ ∈
is N. The Potts model (10) relies on a neighborhood system and its associated cliques (13). Throughout we will assume a first-order neighborhood system. In the first-order neighborhood system, two pixels are neighbors if they share a common edge and two voxels are neighbors if they share a common face. Thus, each voxel in the interior of Y has six neighbors. Henceforth, we refer only to voxels and reference them by a single index, say i. The correspondence between voxels and pixels should be obvious. We denote the fact that two voxels i, i′ ∈
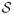 are neighbors by i ~ i′. The set of neighbors of voxel i ∈
are neighbors by i ~ i′. The set of neighbors of voxel i ∈
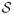 is
is
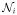 = {i′ : i′ ~ i, i′ ∈ S}. For the first-order neighborhood system, the cliques are the singletons {i} and all sets of pairs of neighbors {i, i′}. The image intensity, a random variable, at voxel i is Yi with Y = (Y1, …, YN)T. (We denote random variables by upper case letters and realized values by lower case letters).
= {i′ : i′ ~ i, i′ ∈ S}. For the first-order neighborhood system, the cliques are the singletons {i} and all sets of pairs of neighbors {i, i′}. The image intensity, a random variable, at voxel i is Yi with Y = (Y1, …, YN)T. (We denote random variables by upper case letters and realized values by lower case letters).
Assume there exists a finite hidden Markov random field (21), Z = (Z1, …, ZN)T on a finite state space
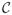 with C states. It is easy to see that this random field forms a partition of the set of voxels
with C states. It is easy to see that this random field forms a partition of the set of voxels
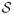 with C equivalence classes (15). That is, voxels i and i′ are equivalent if Zi = Zi′. For fMRI images we partition voxels into three equivalence classes denoted as deactivated, null and activated and will label these classes −1, 0, and 1 respectively:
with C equivalence classes (15). That is, voxels i and i′ are equivalent if Zi = Zi′. For fMRI images we partition voxels into three equivalence classes denoted as deactivated, null and activated and will label these classes −1, 0, and 1 respectively:
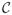 = {−1, 0, 1}. We will use the words ‘state’ and ‘class’ interchangeably. We denote the class to which voxel i belongs by c(i). We consider the joint distribution of Y and Z given two sets of parameters: ϕ and θ:
= {−1, 0, 1}. We will use the words ‘state’ and ‘class’ interchangeably. We denote the class to which voxel i belongs by c(i). We consider the joint distribution of Y and Z given two sets of parameters: ϕ and θ:
where A ⊂ ℝN is a measurable set. We assume Z follows a Potts distribution, a special case of a Gibbs distribution, see reference (13), given by
| (1) |
where
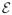 (z; θ) is the energy function,
(z; θ) is the energy function,
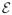 :
:
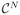 → ℝ ∪{∞}. The energy function is typically written as a sum of Gibbs potential functions indexed by cliques Q: VQ(z; θ) where VQ ≡ 0 if Q is not a clique and for all z, z′ ∈
→ ℝ ∪{∞}. The energy function is typically written as a sum of Gibbs potential functions indexed by cliques Q: VQ(z; θ) where VQ ≡ 0 if Q is not a clique and for all z, z′ ∈
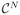 and for cliques Q ⊂
and for cliques Q ⊂
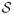 , we have z(Q) = z′(Q) ⇒ VQ(z; θ) = VQ(z′; θ) where for a set A ⊆
, we have z(Q) = z′(Q) ⇒ VQ(z; θ) = VQ(z′; θ) where for a set A ⊆
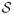 , z(A) = {zi : i ∈ A} (see (13) for details).
, z(A) = {zi : i ∈ A} (see (13) for details).
In what follows, we let θ = {β0, β1}. Our Potts distribution is
| (2) |
where the first summation is taken over all neighboring pairs and δk(A) is the Dirac measure:
that is, δj[c(i)] = 1 if and only if zi = zj and zero otherwise. β0 ≥ 0 is called the spatial regularization parameter and controls the strength of association between neighboring voxels. When β0 = 0, class membership of a voxel is independent of its neighbors and all configurations, z, are equally probable. For β0 > 0, the Potts distribution favors configurations where neighboring voxels are members of the same equivalence class. The larger β0, the stronger the association between neighbors. When β0 = 0 the second summation in equation (2) has a nice interpretation: Pr(Z = z | β0 = 0, β1) = Πi∈
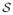 Pr(Zi = zi | β0 = 0, β1) ∝ Πi∈
Pr(Zi = zi | β0 = 0, β1) ∝ Πi∈
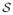 exp(−β1|zi|). Thus, for zi ∈ {−1, 0, 1}, Pr(Zi = zi | β0 = 0, β1) ∝ exp(−β1|zi|). In particular, Pr(Zi = −1 | β0 = 0, β1) = Pr(Zi = 1 | β0 = 0, β1) = exp(−β1)/(1 + 2 exp(−β1)) and Pr(Zi = 0 | β0 = 0, β1) = (1 + 2 exp(−β1))−1. That is, the prior probability of a voxel belonging to the null state given β0 = 0 and β1 is (1 + 2 exp(−β1))−1 and the prior probability of a voxel belonging to either the deactivated or activated state is exp(−β1)/(1 + 2 exp(−β1)). Note that β1 ∈ ℝ.
exp(−β1|zi|). Thus, for zi ∈ {−1, 0, 1}, Pr(Zi = zi | β0 = 0, β1) ∝ exp(−β1|zi|). In particular, Pr(Zi = −1 | β0 = 0, β1) = Pr(Zi = 1 | β0 = 0, β1) = exp(−β1)/(1 + 2 exp(−β1)) and Pr(Zi = 0 | β0 = 0, β1) = (1 + 2 exp(−β1))−1. That is, the prior probability of a voxel belonging to the null state given β0 = 0 and β1 is (1 + 2 exp(−β1))−1 and the prior probability of a voxel belonging to either the deactivated or activated state is exp(−β1)/(1 + 2 exp(−β1)). Note that β1 ∈ ℝ.
The normalizing constant in equation (2) is given by
| (3) |
where the outer sum is over all possible configurations:
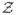 = {z : zi ∈
= {z : zi ∈
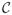 , i ∈
, i ∈
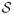 }. This normalizing constant is computationally intractable, even for moderate sized images and classes. For example a small 4 × 4 × 4 image and 3 equivalence classes results in
}. This normalizing constant is computationally intractable, even for moderate sized images and classes. For example a small 4 × 4 × 4 image and 3 equivalence classes results in
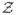 = 364 ≈ 3.4 × 1030 possible configurations. This fact complicates Bayesian computation unless one assumes β0 and β1 are known, a priori. However, it is possible to estimate β0 and β1 along with all other parameters (see Section 3.2).
= 364 ≈ 3.4 × 1030 possible configurations. This fact complicates Bayesian computation unless one assumes β0 and β1 are known, a priori. However, it is possible to estimate β0 and β1 along with all other parameters (see Section 3.2).
We assume that conditional on Z, the Yi are independent:
where Ai ⊂ ℝ and A1 × A2 × ··· × AN = A. Furthermore, the conditional distribution of each Yi is independent and identically distributed (iid)
| (4) |
where ϕj ∈ ϕ and the Fj(ϕj) and G(ψj) are parametric distributions.
2.2 The Bayesian Non-Parametric Potts Model
The G(ψj) given in equation (4) is a parametric distribution. To relax this assumption we will use a mixture of Dirichlet process (MDP) priors (22; 23; 24). The model defined in equation (4) is replaced by
| (5) |
In what follows, Fj is Gaussian and where μi is the mean and is the variance of Yi given Zi = j. There are two important differences to point out between the models in equations (4) and (5). First, in equation (5), each Yi is only conditionally independent and not independent and identically distributed as in equation (4). This is reflected in the fact that each Yi has its own parameter set ϕi. Second, the distribution of each ϕi is specified as a random measure Gj that follows a Dirichlet process (DP) with base measure Gj0 and concentration parameter αj. The concentration parameter αj determines how concentrated Gj is about Gj0 with E(Gj) = Gj0. Furthermore, in our work, the base measure Gj0 is Gaussian, parametrized by its mean, μj0, and variance, . We note that the conditional prior of Z is given in equation (2). In order to finish specifying our model, we assign prior distributions to αj, β0, β1, μj0 and :
T specify a prior on β1, we first place a prior on Pr(Zi = 0 | β0 = 0, β1) ≡ pi0 = (1 + 2 exp(−β1))−1. Let pi0 ~ Beta(pa, pb). This induces a prior on β1 with density
For the mean of the base measure for the deactivated and activated states we assume that the mean must be negative, respectively, positive. This aids in identifying the model, yet still allows, for example, an activated voxel to have a negative intensity (of course its neighbors will more than likely be large positive numbers). The hyperprior parameters a, b, c, d, f, g, h, pa, pb are assumed known and will be identified below in the application section. Now each class in the Potts model is modeled non-parametrically as opposed to having a parametric structure. Note we place a hyperprior distribution on the inverse scale parameter, βσzi, of the gamma prior for . The number of components of the MDP is sensitive to both the precision parameter αzi and to the variance of the base measure. By placing priors on the βσj and on the αj, we allow the data to inform on the amount of precision in the Dirichlet process, the variance of the base measure, Gj0 and, hence, the number of components needed to fit the distribution of each class in the Potts model. We note here that our interest is not in the number of components that make up each class, rather it is in minimizing the posterior expected loss defined in Section 3.4. Simulation studies confirm that the posterior expected loss is insensitive to the prior distributions on αj and . The model specified in equation (5) is non-parametric in the sense that the number of parameters is not fixed. The number of parameters goes to infinity as the number of voxels goes to infinity (which can happen as the size of the voxel is reduced). It is a mixture model in that if we marginalize over the θi the distribution of Yi is a mixture of sampling distributions Fj(ϕi) with mixing measure Gj:
Thus, our model allows much more flexibility in modeling the three classes of voxels.
3 Algorithmic details
In this section we highlight some of the algorithmic details of the MCMC sampling scheme. In particular, in Section 3.1 we discuss the Swendsen-Wang algorithm (25) that we use to efficiently update the hidden Markov random field, Z; in Section 3.2 we discuss the path sampling algorithm (26) we use to estimate the ratio of normalizing constants we need in updating the parameters in the Potts model; in Section 3.3 we discuss the algorithm we use to update the mixture of Dirichlet process priors parameters (27); and in Section 3.4 we discuss the loss function we adopt in making our final assignment of voxels to classes using a Bayesian decision theoretic approach.
3.1 Swendsen-Wang algorithm
The Swendsen-Wang algorithm is a particular case of the slice sampler (28) that we now present. First, the full conditional posterior of Z is
| (6) |
Now define “bond variables”, Wij, for each neighbor pair i ~ j, where Wij is a real, non-negative random variable, as follows. Let W = {Wij : i ~ j} and define the conditional distribution of each Wij, given Z to be uniform and independent with density
| (7) |
Hence,
| (8) |
Furthermore,
| (9) |
To sample from the joint posterior of Z and W, we iteratively sample between equations (8) and (9). Integrating this joint distribution with respect to W results in the full conditional of Z given in equation (6). Sampling W | Z is straightforward: sample each Wij | Z from equation (7). To sample a new Z | W we note the following:
That is to say, if Wij > exp(−β0) then zi and zj are constrained to be equal and this occurs with probability 1 − exp(−β0) (see equation (7)). In other words, neighbors in the same equivalence class are “bonded” with probability 1 − exp(−β0). Thus, W partitions
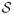 into clusters of voxels that share the same activation state. We can think of this new partition as a refinement of the partition of equivalence classes where each new equivalence class is a cluster of voxels that share the same activation state. For more details consult (15). For any particular cluster K,
into clusters of voxels that share the same activation state. We can think of this new partition as a refinement of the partition of equivalence classes where each new equivalence class is a cluster of voxels that share the same activation state. For more details consult (15). For any particular cluster K,
where ZK = j is shorthand notation for Zi = j for all i ∈ K. Hence, each cluster can be updated independently according to its conditional distribution. For a nice discussion on the Swendsen-Wang algorithm see Higdon (14).
We alternate between Swendsen-Wang updates of the state space map Z and single voxel Gibbs updates, adopting the strategy recommended by Higdon (14) who found that this aids in mixing of the posterior of Z, to ensure movement in large patches.
3.2 Estimation of the potential energy parameters, β0, β1
The full conditionals for β0 and β1 are, respectively,
and
where c(β0, β1) is given in equation (3). These full conditionals do not have a closed form from which we can easily sample and so we turn to the Metropolis-Hastings algorithm (29). The issue with this algorithm and the full conditionals is that we must compute the ratio of these normalizing constants when attempting to update either β0 or β1. However, as mentioned previously, these constants are analytically and computationally intractable for any reasonably sized image.
Gelman and Meng (26) demonstrate how log ratios of normalizing constants can be efficiently estimated using path sampling. This is feasible as long as one can efficiently sample from the Potts prior (i.e. the prior distribution of Z | β0, β1). The Swendsen-Wang algorithm can be used for this purpose by replacing the full conditional of Z with its prior in the previous section.
Here we outline the general procedure given in Gelman and Meng (26) for our particular application. We first consider the ratio of normalizing constants when updating β0 for fixed β1.
Let λβ1 (a, b) ≡ ln[c(b, β1)/c(a, β1)]. Then,
| (10) |
Likewise, if λβ0 (a, b) ≡ ln[c(β0, b)/c(β0, a)], then
| (11) |
For both λβ1 (a, b) and λβ0 (a, b) we have two integrals to evaluate. We approximate the inner integrals, or expectations, using MCMC and are precomputed and saved prior to sampling from the posterior. We draw from Pr(Z = z | β0, β1) via the Swendsen-Wang algorithm (see Section 3.1) replacing the full conditional of Z with its prior and approximating the expectations on a grid of values for β0 and β1. We let β0 vary on [0, 2] in increments of 0.01. We determine the grid points for β1 by varying pi0 on [0.01, 0.99] in increments of 0.01 and setting β1 = −ln[(1 − pi0)/2pi0]. The outer integrals are evaluated numerically using the trapezoidal rule. For values of a and b not on the grid for which the expectations are evaluated, we linearly interpolate.
3.3 Posterior estimate of the MDP parameters
Over the past ten to fifteen years, there has been an explosion of Bayesian nonparametric papers stemming from the seminal works by Ferguson (20) and Antoniak and Ferguson (22) on Dirichlet processes. The first algorithm developed to sample from a Dirichlet process was the Polya urn scheme by Blackwell (30). Since then, several algorithms have been developed including the stick-breaking algorithm (31) and the Chinese restaurant process (32). Neal (27) compared six existing algorithms and presented two new algorithms that sample from the posterior of a Dirichlet process mixture model with non-conjugate priors. We adopt algorithm 8 from his publication to update and βσ and refer the interested reader to his paper.
The precision parameters, αj, are updated by the method given in Escobar and West (23). In particular for each j, define a latent random variable ηj ∈ [0, 1] by
where kj is the number of components in class j and Nj is the number of voxels in class j. Then,
where πηj = (a + kj − 1)/(a + kj − 1 + Nj(b − ln ηj)). See Escobar and West (23) for full details.
3.4 Loss function
The goal of using fMRI as a pre-surgical tool is to accurately determine which voxels belong to which class. That is, to determine the equivalence classes. We will make such assignments using a Bayesian decision theoretic approach. The surgeon wants to avoid removing or cutting through regions of the brain that are responsible for vital tasks such as speech, for example. Hence, a loss function that asymmetrically treats the various types of losses that can occur may be advantageous. In our example, there are three types of losses. Misclassification of a null voxel, misclassification of a deactivated voxel and misclassification of an activated voxel. It may be more important to correctly classify voxels and regions of the brain that are activated during a speech related task, for example, than correctly classifying those regions that are not responsible for speech as null.
Let wi ∈ {−1, 0, 1} denote the true state of voxel i. Let di ∈ {−1, 0, 1} denote our decision about the state of voxel i. That is, wi = −1 if voxel i is truly deactivated, wi = 0 if voxel i has no true BOLD signal change from resting state and wi = 1 if voxel i is truly activated. Let c1 and c2 be positive weights and define w = (w1, …, wN) and d = (d1, …, dN). Let δij denote the Kronecker delta function which is equal to one if i = j and zero otherwise. Our loss function is
When c1 = c2 = 1, the loss is simply the number of incorrectly classified voxels. When the weights are less than one, more weight is given to incorrectly classified null voxels. When c1 > 1 more weight is given to incorrectly classified deactivated voxels and when c2 > 1 more weight is given to incorrectly classified activated voxels, relative to null voxels.
Now, let
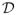 denote the set of all possible decisions:
denote the set of all possible decisions:
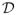 = {d :
di ∈ {−1, 0, 1}, ∀ i ∈
= {d :
di ∈ {−1, 0, 1}, ∀ i ∈
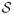 }. From the Bayesian perspective, the optimal decision, d*, minimizes the posterior expected loss:
}. From the Bayesian perspective, the optimal decision, d*, minimizes the posterior expected loss:
That is
Define qji = Pr(Zi = j | Y) for j ∈ {−1, 0, 1}. Suppose we draw T samples from the posterior with z(t) denoting the value of Z from draw t. Then the posterior estimate of qji is and an estimator of posterior expected loss is
| (12) |
which achieves its minimum by setting di = −1 if , di = 0 if , and di = 1 if . Typically, one sets c1 = c2, but this is not necessary.
4 Data Analysis and Simulation Studies
In this section we present results of a data analysis from a patient with a low-grade primary brain tumor in the left inferior frontal and insular lobe. We also present results from simulation studies, demonstrating the robustness of our model.
4.1 Data Analysis
As a clinical tool, the goal of pre-surgical FMRI is to assist the neurosurgeon in the planning and intra-operative navigation of resections or biopsies of intra-axial lesions, e.g. primary brain tumors, while avoiding damage to critical cerebral regions such as those responsible for motor, speech and language, visual or memory functions. Figure 1, top row, shows four sagittal slices of the FLAIR image of our example of a 32 year-old right-handed female patient suffering from a histologically proven oligodendroglioma of the left inferior frontal and insular lobe. The tumor is clearly visible in Figure 1. The paradigm to evoke executive speech- and language-related FMRI activations in the patient’s brain was designed as a simple box-car of alternating on/off-episodes lasting 30 seconds each. During the on-episodes, the patient was asked to silently repeat auditorily presented tongue-twisters. The task was chosen because the only slight speech- and language-related deficit of the patient consisted of a slightly impaired tongue-twister repetition. During the off-episodes, the patient was asked to silently repeat “tock-tock-tock” without interruption, i.e. an unchallenging word train. Standard preprocessing and analysis was applied using FSL 4.1 (5; 33). The resulting z-statistic image is our data and we fitted the data with our NP-Potts model. Note that the z-statistic image is not smoothed (convolved with an isotropic Gaussian kernel) as is typically performed prior to analyses via random field theory. Smoothing is incorporated in the model via the Potts prior. However, as mentioned in the introduction the model also respects boundaries in the image; i.e. performs segmentation) (12, Ch. 2).
We now finish the definition of our model by specifying the particular prior and hyperprior parameter values. For the Dirichlet process concentration parameters, αj, j = −1, 0, 1, we assign a gamma distribution with shape 3 and rate 2: αj ~ Gamma(3, 2). The hyperprior distributions for the base measures means are defined in Section 2.2 and the precisions, with βσj ~ Gamma(1, 1), for j ∈ {−1, 0, 1}. For the spatial regularization parameter we assume β0 ~ Gamma(0.001, 0.001)—a rather uninformative prior. For β1 we place an informative prior on pi0, which induces a prior on β1. FMRI experiments are designed to find activation in very focal, specific regions of the brain. Thus, in virtually all FMRI experiments, a great majority of the voxels are not activated and the BOLD signal change evoked by the paradigm is expected to be zero in these areas. Thus, a priori, we believe that each voxel has a probability of 0.95 of belonging to the background, or null region. Thus, pi0 ~ Beta(0.95 * (0.2N), 0.05 * (0.2N)), where the beta distribution parameters have a ‘prior sample size’ interpretation. Specifically, in our specification we are assuming a prior sample size of 20% of the number of voxels, N, with 95% of the prior sample size belonging to the null class (background) and 5% belonging to either the deactivated or activated state.
We fit our model to the three-dimensional 64 × 64 × 40 (pixel size: 3.0mm × 3.0mm × 3.45mm) z-statistic image and use Bayesian decision theory to decide which voxels are activated, deactivated and null. Our collaborators want to ensure that truly activated or truly deactivated voxels are not misclassified and so we agreed on setting c1 = c2 = 4 in the posterior expected loss function found in equation (12), expressing the belief that false negatives are 4-times as costly as false positives. Thus, we classify any voxel, i, with posterior probability of activation greater than as activated and with posterior probability of deactivation greater than as deactivated. The results are shown in the last two rows of Figure 1 where we display the FLAIR images with gray-scale overlay (color overlay in electronic version) depicting the probability of activated voxels (second row) and deactivated voxels (third row).
Clinicians are mainly interested in detecting functional activations. However, deactivations are also depicted because i) the baseline condition comprised a low-level rhythmic fluency task for comparison and ii) brain tumors can cause paradoxical blood oxygenation changes (34). Therefore, bidirectional statistical assessments and classifications are mandatory for clinical decision-making by pre-surgical FMRI (35). In the case presented here, strong frontal and peritumoral activations relevant for resection planning and neuronavigation were delineated (Figure 1, second row).
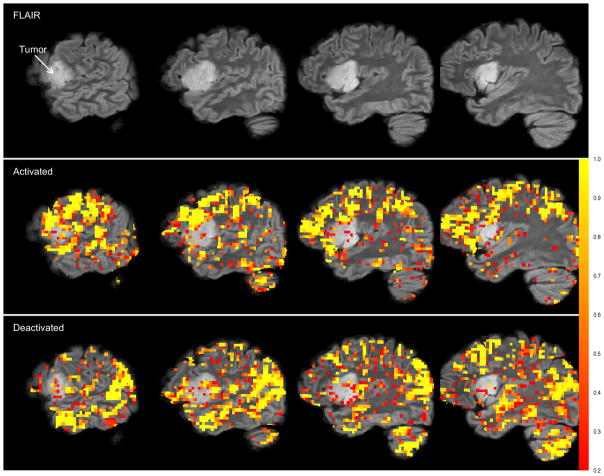
As a comparison, in Figure 2 we show results of a “standard” Potts model: compare equation (2) with
Figure 2.
Results from the normal-gamma model. Top row: Four sagittal slices of the high resolution FLAIR image in the left hemisphere. Second row: FLAIR image with activation overlay. Bottom row: FLAIR image with deactivation overlay. The gray-scale bar (color bar in electronic version) represents the posterior probability of both activation (for the second row) and deactivation (for the bottom row). The overlays are highly pixelated as the analysis is performed in the functional MRI space which has a much lower resolution than the high resolution FLAIR image. The prior on pi0 is fixed: pi0 = 1/3. Loss function is (12) with c1 = c2 = 4.
| (13) |
where β0 is a random quantity to be estimated along with all other parameters. Our “standard” Potts model is parametrically defined by
We will refer to this model as the normal-gamma Potts model. In the normal-gamma Potts model, only voxels with negative intensities are allowed to belong to the deactivated state and only voxels with positive intensities are allowed to belong to the activated state. Gamma* is the “reflected” gamma distribution defined for non-positive random variables as follows: if Y ∈ (−∞, 0], then π(y | r−1, s−1) ∝ |y|r−1−1 exp(−s−1|y|). One last restriction is put on the gamma and reflected gamma distributions: there must exist a mode greater than 0. This restriction was suggested by Woolrich, et al. (36) as it results in a sensible “belief about the expected shape of the activation and deactivation distributions with respect to the non-activation.” This implies that r1 > 1 and r−1 > 1. This model is a slight modification from that published in (36), which is currently implemented in FSL. For the normal-gamma Potts model, we adopt improper and uninformative priors: π(μ) ∝ 1, π(σ2) ∝ 1/σ2, [rℓ] ~ Gamma(0.0001, 0.0001) and [sℓ] ~ Gamma(0.0001, 0.0001) for ℓ = −1, 1. The same loss function as with the NP-Potts model was used to determine activated, deactivated and null voxels.
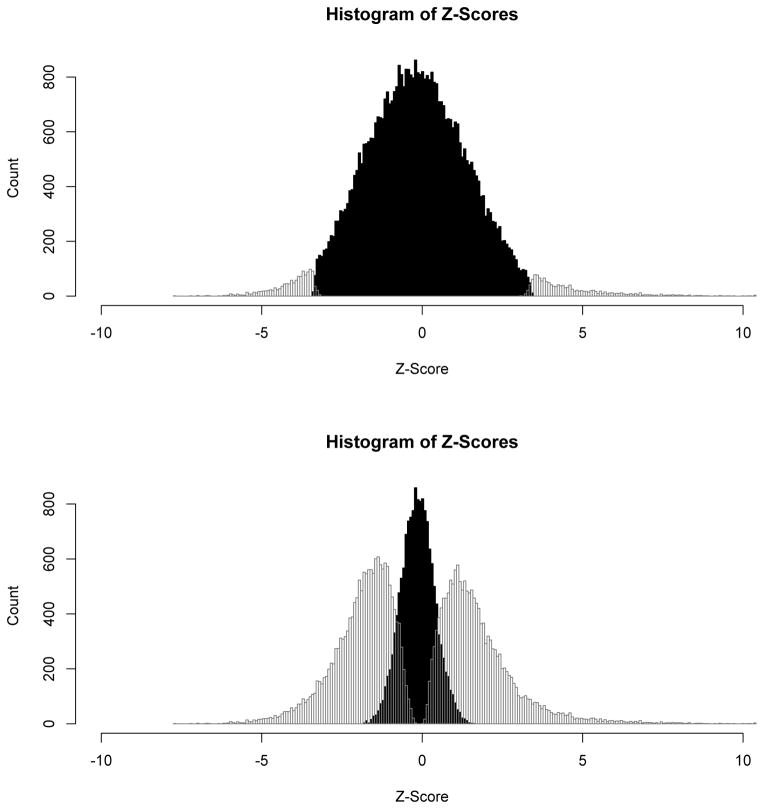
There exists dramatic differences between the results of our NP-Potts model and the normal-gamma Potts model. The simple experimental task of covert tongue-twister repetitions, when contrasted to a lower-level rhythm/fluency condition, is not expected to be supported by vast portions of the brain like those depicted in Figure 2. Intra-operative mapping during awake craniotomy confirmed that these extensive activations were over-inclusive and contained a large proportion of false-positive voxels. The differences are largely attributable to the fact that the standard Potts model implicitly assumes that the a priori probability of belonging to any one class is 1/C conditional on β0 = 0—or, in our case, 1/3. In our NP-Potts model we place a hyperprior distribution on the probability of belonging to background and this has a significant impact on the number of voxels that are classified into each of the three states. Histograms, for comparison, of the three states for both the NP-Potts and the normal-gamma Potts model are shown in Figure 3.
Figure 3.
Histograms of the Z-scores from the final classifications into deactivated, null and activated states. The top histogram is from the DP-Potts model and the bottom histogram is from the normal-gamma model. The black histogram corresponds to the null classified voxels and their Z-scores, The outlined histograms to the left of the null histogram correspond to the deactivated voxels and those to the right, the activated voxels.
In the next section, we present results from simulation studies that demonstrate the robustness of our model compared to several parametric Potts models.
4.2 Simulation Studies
We conducted a comprehensive simulation study and present the results in this section. We note here that all comparisons use the Gibbs distribution found in equation (2) and not that in equation (13). Our main goals in the simulation study are a) to demonstrate the robustness of our model to model misspecification and b) to demonstrate that we can accurately estimate the Potts model parameters β0 and β1. To demonstrate the robustness of our model we compare our model to several parametric Potts models and show that the NP-Potts model performs as well or better in terms of smaller posterior expected loss. To demonstrate that we can accurately estimate β0 and β1 we consider the root mean squared error, relative bias and coverage of the 95% credible intervals.
Model robustness
We simulate the hidden Markov random field, Z, using the Swendsen-Wang algorithm at all combinations of β0 ∈ {0, 0.15, 0.25, 0.5, 0.75, 1} and β1 ∈ {ln(4), ln(2), ln(1)} (corresponding to a marginal a priori probability of a voxel belonging to the background of 1/3, 1/2 and 2/3, respectively, assuming a three class state space). For Z at each combination of β0 and β1, we create an image Y by populating each voxel i as determined by zi from one of three distributions. For each voxel belonging to the null, or background, we draw independently from a N(0, 1) distribution. For voxels belonging to the deactivated or activated states, we draw independently from one of four distributions: a mixture of normals, a normal, a gamma and a log-normal. The specific distributions are given in Table 1 and were chosen such that segmentation is a difficult task (e.g. the resulting mixture distribution is unimodal). Each of these 4 models, which we call the normal-mixture (NM), the normal-normal (NN), the normal-gamma (NG) and the normal-log-normal (NL), generates data with a parametric structure. We then fit our model and three parametric Potts models to all simulated data sets and run each algorithm for 35000 iterations discarding the first 10000 iterations as burn-in. The three parametric Potts models we use to fit the data are the normal-gamma (background voxels fitted with a normal distribution, the activated voxels fitted with a gamma distribution and the deactivated voxels fitted with a reflected gamma), the normal-normal model (all three states fitted with normal distributions) and the normal-log-normal model (background fitted with a normal distribution, activated voxels fitted with a log-normal distribution and deactivated voxels fitted with a reflected log-normal distribution). We then compare the posterior expected loss (with c1 = c2 = 1) between all models on all data sets. Figure 4 shows a bar plot of the posterior expected loss for all four models fitted to the four data sets generated from the four parametric Potts models. In this example β0 = 0.25 and β1 = ln(2). From this figure we see that the NP-Potts model performs as well (in terms of posterior expected loss) as the parametric models when the parametric model is correctly specified. When the parametric model is misspecified, the NP-Potts model outperforms (has smaller posterior expected loss) the parametric models. This trend is consistent for all simulation settings (results not shown) except when β0 = 0. In Table 3 we present the proportion of correctly classified voxels from this simulation study for all three states as well as the total proportion of correctly classified voxels.
Table 1.
The four parametric models used in the simulation studies. Gamma* and ln N* represent the reflected gamma and log-normal distributions.
| State
|
|||
|---|---|---|---|
| Deactivated
|
Null
|
Activated
|
|
| Normal-mixture (NM) | 0.75N(−2, 1) + 0.25N(−5, 1) | N(0, 1) | 0.75N(2, 1) + 0.25N(5, 1) |
| Normal-normal (NN) | N(−2, 1) | N(0, 1) | N(2, 1) |
| Normal-gamma (NG) | Gamma*(5, 2) | N(0, 1) | Gamma(5, 2) |
| Normal-log-normal (NL) | ln N*(0.75, 0.25) | N(0, 1) | ln N(0.75, 0.25) |
Figure 4.
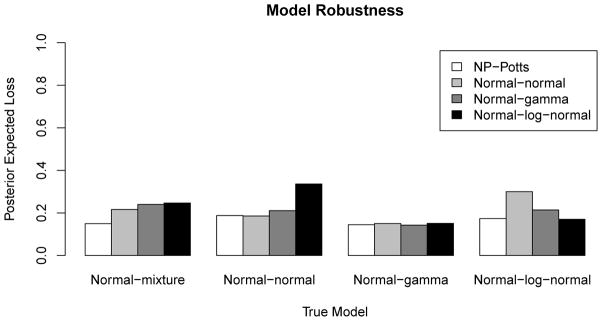
Robustness of the NP-Potts model. The NP-Potts model performs on par with the correctly specified model and performs better than misspecified models. β0 = 0.25, β1 = ln(2) (marginal prior probability = 0.5). The gray scale bars represent the posterior expected loss from the model used to fit the data (see legend) generated from the true model.
Table 3.
Proportion of correctly classified voxels from the simulation study. The results show that the NP-Potts perform equally to the correctly specified parametric model and outperforms the misspecified parametric models.
| True Model | Fitted Model | Deactivated | Null | Activated | Overall |
|---|---|---|---|---|---|
| Normal-mixture | NP-Potts | 0.680 | 0.931 | 0.680 | 0.845 |
| Normal-normal | 0.346 | 0.997 | 0.343 | 0.774 | |
| Normal-gamma | 0.284 | 0.999 | 0.281 | 0.754 | |
| Normal-log-normal | 0.261 | 1.000 | 0.261 | 0.747 | |
|
| |||||
| Normal-normal | NP-Potts | 0.652 | 0.896 | 0.657 | 0.813 |
| Normal-normal | 0.662 | 0.892 | 0.663 | 0.813 | |
| NG | 0.456 | 0.968 | 0.456 | 0.793 | |
| NL | 0.000 | 1.000 | 0.000 | 0.657 | |
|
| |||||
| Normal-gamma | NP-Potts | 0.734 | 0.914 | 0.757 | 0.857 |
| Normal-normal | 0.667 | 0.936 | 0.710 | 0.851 | |
| Normal-gamma | 0.739 | 0.914 | 0.755 | 0.857 | |
| Normal-log-normal | 0.703 | 0.932 | 0.717 | 0.856 | |
|
| |||||
| Normal-log-normal | NP-Potts | 0.728 | 0.885 | 0.732 | 0.832 |
| Normal-normal | 0.840 | 0.001 | 0.813 | 0.284 | |
| Normal-gamma | 0.381 | 0.986 | 0.371 | 0.777 | |
| Normal-log-normal | 0.746 | 0.879 | 0.734 | 0.831 | |
When β0 = 0 there is no spatial correlation between voxels in the data. In this case, the analysis reduces to fitting a univariate distribution of image intensities with a mixture of distributions (one can think of modeling a univariate histogram with a mixture density). Obviously, in this case, a single mixture of Dirichlet process priors model suffices in fitting the distribution. The NP-Potts model breaks down as there is no information in the data or in the prior to inform how to fit the data with three non-parametric distributions and results are inconsistent when fitting the same data set multiple times. For our particular application (or for that matter, for any image analysis) this is not alarming to us as we expect spatial correlation between neighboring voxels. This raises the question of how much spatial regularization is necessary in the image data in order for our NP-Potts model to perform effectively. We found, through simulation studies, that a value of β0 ≥ 0.15, a rather small amount of spatial information, results in our NP-Potts model consistently performing as well or better than the parametric Potts models in terms of posterior expected loss.
Estimation of β0 and β1
We consider the case when the true values are β0 = 0.5 and β1 = ln(2). We simulate 500 data sets using the NG model and 500 data set using the NM model (see above and Table 1). For all 1000 data sets we fit our NP-Potts model by drawing from the posterior 25000 times after a burn-in of 10000 draws. We consider the coverage of the 95% equal tail area credible intervals, the root mean squared error (RMSE) and the relative bias (rBias) of the posterior expected mean of β0 and β1 over the 1000 simulations. Results are given in Table 2. The coverage of the 95% credible intervals are near the nominal levels of 0.95. β0 has a slight positive bias (relative bias 0.014) while the relative bias for β1 is a bit larger in the negative direction (−0.074). However, in terms of pi0, which is arguably more interpretable, the relative bias is −0.026, or about an average pi0 of 0.487 over the simulations as opposed to the truth of 0.5. Overall, our model performs well and we can accurately estimate the Potts prior parameters. At the end of Section 2.2 we stated that the posterior expected loss is insensitive to the priors on the αj and the . For one randomly selected simulated data set from the normal-mixture model with true β0 = 0.5 and β1 = ln(2) we fit our model with different priors. For the αj we consider the proposed prior, G(3, 2), and three other priors: G(1, 1), G(2, 4) and G(5, 1). The resulting posterior expected losses are 0.1515, 0.1521, 0.1518 and 0.1512, respectively. For we consider the proposed prior, G(3, βσj) with βσj ~ G(1, 1) and two other priors: G(6, βσj) and G(1, βσj). The resulting posterior expected losses are, respectively, 0.1515, 0.1526 and 0.1527.
Table 2.
Estimation of β0 and β1 in the simulation study.
| Parameter
|
||
|---|---|---|
|
β0 (truth: 0.5)
|
β1 (truth: ln(2))
|
|
| RMSE | 0.0167 | 0.067 |
| rBias | 0.014 | −0.074 |
| Coverage | 0.964 | 0.957 |
5 Discussion
We have presented a non-parametric Potts model and combined several ideas from the literature, including mixture of Dirichlet process priors, advanced sampling methods (path sampling and slice sampling using the Swendsen-Wang algorithm) and decision theory to adapt loss to the pre-surgical planning context. Our simulation studies show that, in terms of the posterior expected loss, our model performs on par with parametric Potts models when the parametric model is correctly specified, and that it outperforms parametric models when the parametric model is incorrectly specified. Hence, we argue for the use of the NP-Potts model as one never knows the true distribution of the data. We have also shown that we can accurately estimate the Potts prior parameters β0 and β1.
Computationally, 125,000 iterations of the MCMC algorithm takes about 3 hours of CPU time on a MacBook Pro with 8 GB of memory and a 3.06 GHz Intel Core 2 Duo processor. This is for the 64 × 64 × 40 image in our data example. In this example, the number of voxels within the brain is 46999. Larger images will take more computation time.
In Section 3.2 we show how the Potts prior parameters, β0 and β1, can be estimated using the idea of path sampling (26). The expectations in equations (10) and (11) have to be precomputed via MCMC simulation and the computation of these expectations is expensive. Furthermore, these expectations need to be computed for every patient since the size and shape of brains differ from patient to patient, making this implementation of the algorithm arduous and not very appealing. To circumvent this bottleneck, one could require that the Z-score maps of every patient be mapped onto a common atlas, compute the expectations once, off-line, on the atlas. The expectations could then be used for all patients. The down-side of this is that the data are interpolated and this induces some smoothness in the interpolated image, which may not be desirable. It would be interesting to investigate the effects of this smoothing on parameter estimates and the posterior expected loss. Another possible alternative would be to approximate the likelihood with the pseudolikelihood (37). However use of the pseudolikelihood results in overestimation of the smoothing parameter and tends to oversmooth the data (38)—which is not a desirable outcome for presurgical planning, as argued earlier.
We feel it is imperative to always include the spatial regularization parameter β0 in equation (2). For without it, one is assuming that all voxels are independent of one another and this assumption is almost never satisfied in medical imaging. On the other hand, β1 plays a big role in determining the number of voxels that are classified as active or deactive, as is evident in our data analysis.
Acknowledgments
Dr. Johnson is partially funded by the U.S. National Institutes of Health [P01-CA87634].
References
- 1.Huettel SA, Song AW, McCarthy G, editors. Functional Magnetic Resonance Imaging. 2. Sinauer Associates; 2008. [Google Scholar]
- 2.Yeo DTB, Meyer CR, MPJ, Minecan DN, Sagher O, Kluin KJ, et al. Formulation of current density weighted indices for correspondence between functional MRI and electrocortical stimulation maps. Journal of Clinical Neurophysiology. 2008;119:2887–2897. doi: 10.1016/j.clinph.2008.07.275. [DOI] [PubMed] [Google Scholar]
- 3.Bakshi R, Ariyaratana S, Benedict RH, Jacobs L. Fluid-attenuated inversion recovery magnetic resonance imaging detects cortical and juxtacortical multiple sclerosis lesions. Archives of Neurology. 2001;58(5):742–748. doi: 10.1001/archneur.58.5.742. [DOI] [PubMed] [Google Scholar]
- 4.Friston KJ, Jezzard P, Turner R. Analysis of functional MRI time-series. Human Brain Mapping. 1994;1:153–171. [Google Scholar]
- 5.Smith SM, Jenkinson M, Woolrich CF, Behren TEJ, Johansen-Berg H, Bannister PR, et al. Advances in functional and structural MR image analysis and implementation as FSL. NeuroImage. 2004;23(S1):208–219. doi: 10.1016/j.neuroimage.2004.07.051. [DOI] [PubMed] [Google Scholar]
- 6.Smith SM, Beckmann CF, Ramnani N, Woolrich MW, Bannister PR, Jenkinson M, et al. Variability in FMRI: A re-examination of intersession differences. Human Brain Mapping. 2005;24:248–257. doi: 10.1002/hbm.20080. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Worsley KJ, Marrett S, Neelin P, Vandal AC, Friston KJ, Evans AC. A unified statistical approach for determining significant voxels in images of cerebral activation. Human Brain Mapping. 1996;4:48–73. doi: 10.1002/(SICI)1097-0193(1996)4:1<58::AID-HBM4>3.0.CO;2-O. [DOI] [PubMed] [Google Scholar]
- 8.Petersson KM, Nichols TE, Poline JB, Holmes AP. Statistical limitations in functional neuroimaging II. Signal detection and statistical inference. Philosophical Transactions of the Royal Society B: Biological Sciences. 1999;354(354):1261–1281. doi: 10.1098/rstb.1999.0478. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Nichols TE, Hayasaka S. Controlling the familywise error rate in functional neuroimaging: a comparative review. Statistical Methods in Medical Research. 2003;12(5):419–446. doi: 10.1191/0962280203sm341ra. [DOI] [PubMed] [Google Scholar]
- 10.Potts RB. Some generalized order-disorder transformations. Proceedings of the Cambridge Philosophic Society. 1952;48:106–109. [Google Scholar]
- 11.Ising E. Beitrag zur Theorie des Ferromagnetismus. Zeitschrift für Physik. 1925;31(1):253–258. [Google Scholar]
- 12.Winkler G. Image Analysis, Random Fields and Markov Chain Monte Carlo Methods. Springer; Berlin: 2003. [Google Scholar]
- 13.Brémaud P. Markov Chains, Gibbs Fields, Monte Carlo Simulation, and Queues. Springer; New York: 1999. [Google Scholar]
- 14.Higdon DM. Auxiliary variable methods for Markov chain Monte Carlo with applications. Journal of the American Statistical Association. 1998;93(442):585–595. [Google Scholar]
- 15.Johnson TD, Piert M. A Bayesian analysis of dual autoradiographic images. Computational Statistics and Data Analysis. 2009;53:4570–4583. [Google Scholar]
- 16.da Silva ARS. A Dirichlet process mixture model for brain MRI tissue classification. Medical Image Analysis. 2007;2:169–182. doi: 10.1016/j.media.2006.12.002. [DOI] [PubMed] [Google Scholar]
- 17.Orbanz P, Buhmann J. Nonparametric Bayes image segmentation. International Journal of Computer Vision. 2008;77:25–45. [Google Scholar]
- 18.Du L, Ren L, Dunson D, Carin L. A Bayesian model for simultaneous image clustering, annotation and object segmentation. In: Bengio Y, Schuurmans D, Lafferty J, Williams CKI, Culotta A, editors. Advances in Neural Information Processing Systems. Vol. 22. MIT Press; 2009. pp. 486–494. [PMC free article] [PubMed] [Google Scholar]
- 19.Chatzis SP, Tsechpenakis G. The infinite hidden Markov random field model. IEEE Transactions on Medical Imaging. 2010;21(6):1004–1014. doi: 10.1109/TNN.2010.2046910. [DOI] [PubMed] [Google Scholar]
- 20.Ferguson TS. A Bayesian analysis of some nonparametric problems. The Annals of Statistics. 1973;1(2):209–230. [Google Scholar]
- 21.Besag J. Spatial Interaction and the Statistical Analysis of Lattice Systems. Journal of the Royal Statistical Society Series B. 1974;6:192–236. [Google Scholar]
- 22.Antoniak CE. Mixtures of Dirichlet processes with applications to Bayesian nonparametric problems. The Annals of Statistics. 1974;2(6):1152–1174. [Google Scholar]
- 23.Escobar MD, West M. Bayesian density estimation and inference using mixtures. Journal of the American Statistical Association. 1995;90(430):577–588. [Google Scholar]
- 24.Müller P, Quintana FA. Nonparametric Bayesian data analysis. Statistical Science. 2004;19(1):95–110. [Google Scholar]
- 25.Swendsen RH, Wang JS. Nonuniversal critical dynamics in Monte Carlo simulations. Physical Review Letters. 1987;58:86–88. doi: 10.1103/PhysRevLett.58.86. [DOI] [PubMed] [Google Scholar]
- 26.Gelman A, Meng X. Simulating normalizing constants: from importance sampling to bridge sampling to path sampling. Statistical Science. 1998;13(2):163–185. [Google Scholar]
- 27.Neal R. Markov Chain Sampling Methods for Dirichlet Process Mixture Models. Journal of Computational and Graphical Statistics. 2000 Jun;9(2):249–265. [Google Scholar]
- 28.Robert CP, Casella G. Monte Carlo Statistical Methods. Springer; New York: 2005. [Google Scholar]
- 29.Hastings WK. Monte Carlo sampling methods using Markov chains and their applications. Biometrika. 1970;57(1):97–109. [Google Scholar]
- 30.Blackwell D, MacQueen JB. Ferguson disributions via Polya urn schemes. The Annals of Statistics. 1973;1(2):353–355. [Google Scholar]
- 31.Ishwaran H, James LF. Gibbs Sampling for Stick-Breaking Priors. JASA. 2001;96:161–173. [Google Scholar]
- 32.Pitman J. Exchangeable and Partially Exchangeable Random Partitions. Probability Theory and Related Fields. 1995;102(2):145–158. [Google Scholar]
- 33.Woolrich MW, Jbabdi SBP, Chappell MSM, Behrens T, et al. Bayesian analysis of neuroimaging data in FSL. NeuroImage. 2009;45:173–186. doi: 10.1016/j.neuroimage.2008.10.055. [DOI] [PubMed] [Google Scholar]
- 34.Fujiwara N, Sakatani K, Katayama Y, Murata Y, Hoshino T, Fukaya C, et al. Evoked-cerebral blood oxygenation changes in false-negative activations in BOLD contrast functional MRI of patients with brain tumors. NeuroImage. 2004;21(4):1464–1471. doi: 10.1016/j.neuroimage.2003.10.042. [DOI] [PubMed] [Google Scholar]
- 35.Bartsch AJ, Homola G, Biller A, Solymosi L, Bendszus M. Diagnostic functional MRI: illustrated clinical applications and decision-making. Journal of Magnetic Resonance Imaging. 2006;23(6):921–932. doi: 10.1002/jmri.20579. [DOI] [PubMed] [Google Scholar]
- 36.Woolrich MW, Behrens TEJ, Beckmann CF, Smith SM. Mixture Models With Adaptive Spatial Regularization for Segmentation With an Application to FMRI Data. IEEE Transactions on Medical Imaging. 2005;24(1):1–11. doi: 10.1109/tmi.2004.836545. [DOI] [PubMed] [Google Scholar]
- 37.Besag J. Statistical Analysis of Non-Lattice Data. The Statistician. 1975;24(3):179–195. [Google Scholar]
- 38.Melas DE, Wilson SP. Double Markov random fields and Bayesian image segmentation. IEEE Transactions on Signal Processing. 2002;50:357–365. [Google Scholar]