Conformational dynamics is more important than helical propensity for the folding of the all α-helical protein Im7

Abstract

Im7 folds via an on-pathway intermediate that contains three of the four native α-helices. The missing helix, helix III, is the shortest and its failure to be formed until late in the pathway is related to frustration in the structure. Im7H3M3, a 94-residue variant of the 87-residue Im7 in which helix III is the longest of the four native helices, also folds via an intermediate. To investigate the structural basis for this we calculated the frustration in the structure of Im7H3M3 and used NMR to investigate its dynamics. We found that the native state of Im7H3M3 is highly frustrated and in equilibrium with an intermediate state that lacks helix III, similar to Im7. Model-free analysis identified residues with chemical exchange contributions to their relaxation that aligned with the residues predicted to have highly frustrated interactions, also like Im7. Finally, we determined properties of urea-denatured Im7H3M3 and identified four clusters of interacting residues that corresponded to the α-helices of the native protein. In Im7 the cluster sizes were related to the lengths of the α-helices with cluster III being the smallest but in Im7H3M3 cluster III was also the smallest, despite this region forming the longest helix in the native state. These results suggest that the conformational properties of the urea-denatured states promote formation of a three-helix intermediate in which the residues that form helix III remain non-helical. Thus it appears that features of the native structure are formed early in folding linked to collapse of the unfolded state.

INTRODUCTION

The influence of α-helical propensity on how proteins fold has been well explored.^1–5 In some cases it appears that the unfolded state of the protein contains nascent helical structure that favours folding by the diffusion-collision mechanism,⁶ in which marginally stable elements of secondary structure dock together aiding their stabilization and promoting formation of the native state. Other helical proteins fold via a hydrophobic collapse mechanism⁷ in which collapse of the chain precedes helix formation,⁸ thus again linking the propensity of an amino acid sequence to form secondary structure with its mechanism of folding. Daggett and Fersht⁹ view the hydrophobic collapse and diffusion-collision models as extremes of the nucleation-condensation mechanism in which secondary and tertiary structure form concomitantly and note that the position a protein occupies along the continuum is determined by the conformational preferences of the residues in the amino acid sequence.

The groundwork that led to current understanding of protein folding mechanisms has involved kinetic, thermodynamic and computational studies of many small proteins. Amongst these the colicin immunity proteins,^10,11 which are inhibitors of DNase bacteriocins and provide immunity to the producing cells,¹² have played an important part. The family of immunity proteins are highly homologous, with Im7 and Im9 having 57% sequence identity and sharing a common distorted four α-helical structure.^13,14 Despite their high structural similarity, Im9 folds via a two-state mechanism from its urea-denatured state,¹⁰ while Im7 folds in a three-state manner [Fig. 1(A)] via an on-pathway kinetic intermediate.¹⁵ Φ-analysis,¹⁶ NMR spectroscopy,^17–19 and MD simulations^11,20 have revealed this intermediate to be a compact structure that contains helices I, II, and IV of the native state, arranged in a manner that allows both native and non-native inter-helical contacts. Building on these observations, Sutto et al.²¹ showed that Im7 has a native structure that is not minimally frustrated and hence has an energy landscape that is rough^22,23 and gives rise to a low-lying excited state close to the native state which is populated during folding and is manifested as the intermediate. Even in the absence of chaotropes this excited state is populated at equilibrium which has allowed it to be probed by equilibrium NH exchange¹⁷ and relaxation-dispersion NMR.¹⁹

Figure 1.

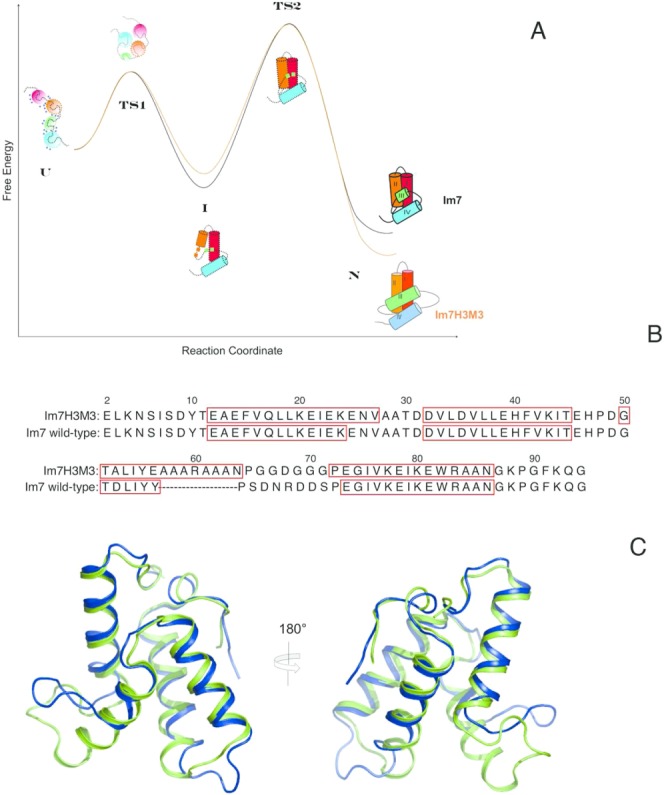
(A) Schematic comparison of the energetics of folding of Im7 and Im7H3M3 based on the thermodynamic and kinetic parameters reported by Knowling et al.²⁴ for Im7H3M3. Except for the cartoon of the native structure of folded Im7H3M3 all other structure cartoons represent Im7 along the folding path. The first is the urea-unfolded state of Im7 which is extended, contains four independent clusters of residues with each cluster containing interacting hydrophobic side chains and has urea molecules (blue circles) associated with it. In the absence of urea the unfolded state (U) rapidly collapses towards the native state (N), traversing transition state 1 (TS1), which lies between the extended (U) and intermediate (I) states, and transition state 2 (TS2) which lies between I and N. (TS1) is almost devoid of secondary structure and lacks a stable hydrophobic core whilst TS2 is a three-helix bundle. The four helices of the native structures are coloured differently, with the important helix III coloured green. Even though helix III has been elongated in Im7H3M3 this protein folds via an on-pathway intermediate²⁴ similarly to wild-type Im7 demonstrating that the formation of an intermediate is an integral feature of the folding mechanism of Im7 that does not result from the short length and low helical propensity of the native helix III. Overall, the elongation of helix III of Im7 to create Im7H3M3 has marginally destabilized the intermediate state by less than 2.5 kJ mol⁻¹ and stabilized the native state by the same amount.²⁴ (B) The Im7 and Im7H3M3 amino acid sequences. The redesigned helix III in Im7H3M3 is longer than its counterpart in Im7. Residues in boxes correspond to α-helices in the native structures. (C) Overlay of the most representative conformer (closest to the average model judged by global RMSDs) from the NMR solution structure ensemble of Im7H3M3 (green)²⁴ and the X-ray crystal structure of Im7 (blue).¹⁴ The NMR ensemble of 30 conformers of Im7H3M3 was superimposed onto the crystal structure of Im7 using the SuperPose web server²⁵ global RMSDs over all residues 1.3 Å, heavy atoms 1.1 Å, and backbone atoms 0.8 Å, respectively. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

A significant feature of the Im7 folding pathway is that the final step in folding is the formation of helix III of the native state [Fig. 1(A)]. This is the smallest of the four helices of Im7 and comprises only six residues in the native structure compared with the 13 or 14 residues of the other helices I, II, and IV. Helix III exhibits the lowest helical propensity of all the helices and this led to considerations of whether it is the last helical element to form because it has the lowest helix propensity, or because there are specific features of the amino acid sequence that promote formation of the three helix intermediate. To explore this question Knowling et al.²⁴ engineered Im7 to create a variant in which helix III was lengthened via insertion of a polyalanine helix, designed to extend into the original residues of helix III and be stabilized via an internal solvent exposed salt bridge. Upon redesign helix III had the highest predicted helical propensity. Knowling et al.²⁴ showed that the resulting variant, Im7H3M3 [Fig. 1(B,C)], had a three-dimensional structure little altered from that of native Im7 in the common areas despite the increased length of helix III, and also that this variant folds via the same on-pathway intermediate as the wild-type protein. Thus, it appears that folding of Im7 via a three-helical intermediate is independent of the helical propensity of helix III. This leads on to the question addressed by this paper: what are the specific features of the amino acid sequence that promote formation of the three-helix intermediate?

NMR studies of both urea-denatured Im7²⁶ and a triple-variant of Im7 that is unfolded under nondenaturing conditions²⁷ have revealed that the unfolded states of these proteins contain four noninteracting hydrophobic clusters that align with the helices of the native state. To explore whether urea-denatured Im7H3M3 has similar clusters and to determine whether there is frustration in the structure of Im7H3M3 similar to that of native Im7, we here report NMR studies of the folded and urea-denatured states of Im7H3M3. Our results confirm that the presence of the on-pathway folding intermediate is connected with the presence of frustration in the structure of Im7H3M3, and show that the conformational properties of the denatured protein play a key role in determining the details of the folding landscape and the topology of the native state.

RESULTS AND DISCUSSION

Frustration in the structure of Im7H3M3

The structure of Im7H3M3 was determined by NMR as described in Knowling et al.²⁴ The core region of Im7H3M3 that has the same amino acid sequence as Im7 [Fig. 1(B)], residues 2 to 55 and 72 to 93, has an identical fold to Im7 [Fig. 1(C)], as revealed by backbone RMSDs of 0.8 Å, and, importantly, the long helix III of Im7H3M3 overlays well with the shorter helix III of native Im7, as shown by the backbone RMSDs for the common residues, 50 to 55, of 0.4 Å. Having demonstrated that the structures of Im7 and Im7H3M3 are strikingly similar we carried out an analysis of frustration in the structure of Im7H3M3 using the approach of Sutto et al.²¹ with the protein Frustratometer Server (http://www.frustratometer.tk/),²⁸ an algorithm that spatially localises and quantifies the energetics of frustration present in a protein structure. Energy landscape theory states that sites of minimal frustration are associated with stable folding cores of proteins and that these minimal frustrations result when inter-residue interactions in a polypeptide chain are not in conflict with each other and cooperatively lead to a low-energy conformation.²³ In such cases the protein's statistical energy landscape may have a roughness reflecting the occurrence of favourable non-native interactions during the folding process but the consequences of this are not likely to be significant to the folding pathway. However, where the landscape is more rugged due to considerable roughness a relatively long-lived non-native state may arise that acts as a kinetic folding intermediate, as with Im7. Since analysis of frustration in protein structures highlights apparently unfavourable inter-atomic contacts, which might also come about through errors in the structure coordinates, in what follows it is pertinent to note that the structures of Im7 and Im7H3M3 were determined entirely independently, the former by X-ray crystallography¹⁴ and the latter by NMR spectroscopy.²⁴

As Sutto et al. reported for Im7²¹ we found that frustration is considerable and not randomly scattered across the Im7H3M3 primary sequence [Fig. 2(A)]. However, residues with minimal frustration are found within all four of the α-helices, generally located in inter-helix contacts so that the core of Im7H3M3 itself is largely minimally frustrated [Fig. 2(B)]. Importantly, residues 51 to 55 of Im7H3M3, which are equivalent to the same residues of Im7 and contribute to helix III in both proteins, show the same degree of frustration. Overall, the engineered helix III has the same number of minimally frustrated sites as helix III of Im7. However, despite the similarity between Im7 and Im7H3M3, the engineered protein has an increased number of highly frustrated interactions, particularly at the C-terminus of helix III and the adjacent loop [red lines in Fig. 2(B)].

Figure 2.

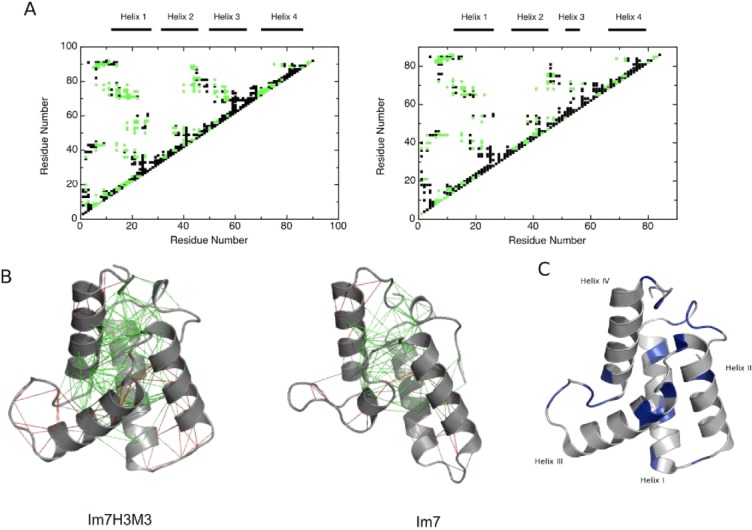
(A) Frustration contact maps of Im7H3M3 (left) and wild-type Im7 (right), with highly frustrated contacts coloured black and minimally frustrated coloured green. The frustration index (F_ij)²¹ gives the energetic fitness for a given set of residues to interact. An interaction is minimally frustrated when F_ij > 0.78 and highly frustrated when F_ij < −1. (B) Configurational frustration network interactions represented on atomic structures of Im7H3M3 (PDB code: 2K0D) and wild-type Im7 (PDB code: 1AYI). A cluster of minimally frustrated contacts (green) defines the core of the protein, which involves all the α-helices, with highly frustrated contacts shown in red. (C) Backbone fold of Im7H3M3 with the residues exhibiting R_ex terms derived from model-free analyses (see below) shown in blue. Residues without R_ex terms are coloured grey. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

NMR relaxation studies of Im7 and Im7H3M3

Backbone NH groups of ¹⁵N-labeled proteins act as isolated IS spin systems with the relaxation of the ¹⁵N nuclei dominated by dipole-dipole interaction with their attached ¹H and the chemical shift anisotropy, both of which are modulated by changes in orientation of the NH bond vector with time, making them good probes of protein dynamics.^29,30 Detailed relaxation analyses have been reported previously for Im7 and its His-tagged variant, Im7*, leading to the identification of residues undergoing chemical exchange on a time scale that impacts the measured R₂ rates.¹⁸ Whittaker et al.¹⁹ reported a direct correlation between residues involved in this conformational exchange and those that Sutto et al.²¹ reported as experiencing frustration, and showed that the correlation resulted from exchange between the native state of Im7 and a low-lying excited state that is populated as a consequence of frustration. To explore whether a similar excited state is present for Im7H3M3 we undertook ¹⁵N relaxation analyses (Table I). Data for 86 of the 94 residues of Im7H3M3 expected to have a detectable ¹H-¹⁵N HSQC resonance (i.e. excluding the N-terminal and Pro residues) were obtained (Supporting Information Fig. S1), with residues for which relaxation data are not reported excluded because their resonances were too overlapped with others for accurate determination of signal intensities. Surprisingly, the average relaxation parameters for Im7H3M3 suggest the protein is behaving as if it were smaller than Im7* (Table I) despite its additional seven residues. Consistent with this, the hydrodynamic radii of Im7*¹⁸ and Im7H3M3, determined as described in Materials and Methods, 19.3 ± 0.4 Å and 17.8 ± 0.3 Å, respectively, indicates that Im7H3M3 is more compact than Im7*. This must largely be caused by a difference in the properties of the His-tags, with Im7H3M3 having a more restricted His-tag than Im7*.

Table I.

Parameters Describing Global Dynamics of Im7* and Im7H3M3 from ¹⁵N Relaxation Analyses at 600 MHz

	Im7* (Whittaker et al.18)	Im7H3M3 (this work)
Average 15N R1 (s−1)	1.71 ± 0.03	1.89± 0.04
Average 15N R2 (s−1)	10.18 ± 0.13	8.59 ± 0.08
Average {1H}-15N NOE	0.68 ± 0.09	0.71 ± 0.02
τm (ns)	5.27	5.98
D||/D⊥	0.784	1.22
Average S2	0.87 ± 0.09	0.88 ± 0.02

The sequence variations of ¹⁵N R₁, ¹⁵N R₂, and {¹H}-¹⁵N NOE values (Supporting Information Fig. S1) are consistent with Im7H3M3 being a well-structured globular protein. With the exception of the residues close to the termini and the inter-helix loop regions, particularly the Gly-rich linker between helices III and IV the profiles are largely featureless. The sequence variation of the R₂/R₁ ratios for the backbone ¹⁵N resonances (Fig. 3) highlights those residues, which have relaxation properties significantly different from the majority of residues. The same plot for Im7 (Fig. 4 of Ref. 19 also identifies the corresponding residues to have heightened R₂/R₁ ratios, suggestive of similar motions in both proteins.

Figure 3.

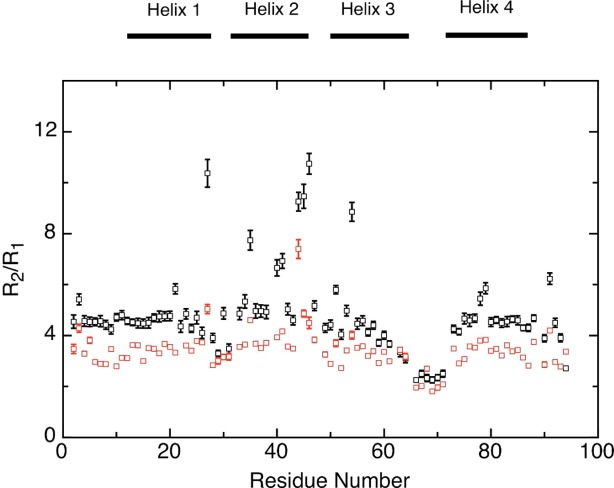
The sequence dependence of the ¹⁵N R₂/R₁ ratios of Im7H3M3 at 25°C, in 50 mM phosphate buffer, pH 7, 10% ²H₂O, at a ¹H frequency of 600 MHz (black) and 400 MHz (red). Horizontal bars at the top of the figure represent the secondary structure elements. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

Figure 4.

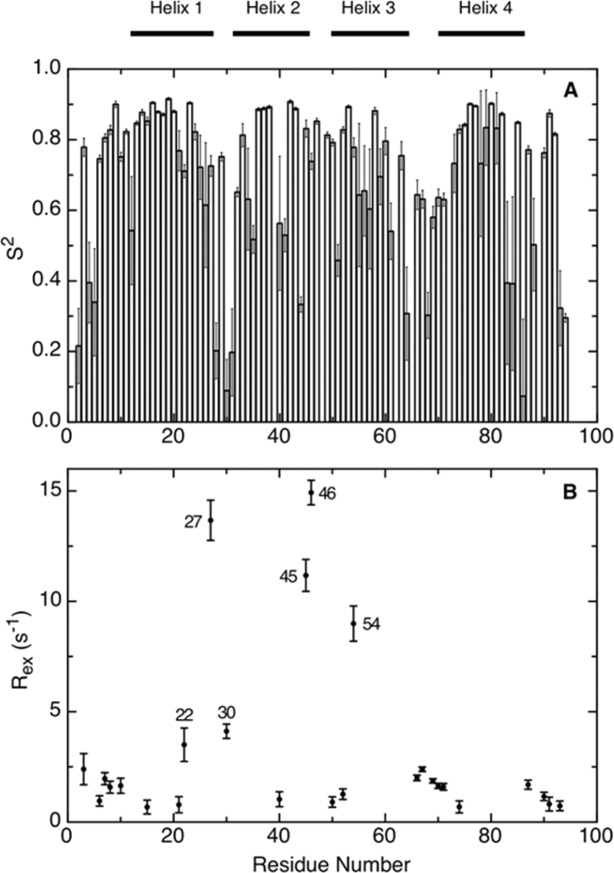
Model-free relaxation analysis of Im7H3M3 at 25°C using data measured at 400 and 600 MHz. The generalized order parameter S² (A) provides a measure of atomic flexibility of the ¹H-¹⁵N bond vector on the ps-ns time scale. The chemical exchange terms R_ex at 600 MHz (B) describe residues affected by motions occurring on the μs-ms time scale. Residues with R_ex values > 3 s⁻¹ are identified. The horizontal bars at the top of the figure indicate secondary structure elements.

In order to proceed with a model-free analysis^31–33 of the Im7H3M3 relaxation data the diffusion tensor was determined. This was performed by calculating the relative lengths of the principal axes of the inertia tensor using the program pdbinertia.³⁴ These were 1.00:0.82:0.70, which indicates that the rotational diffusion tensor is either axially symmetric, as it is for Im7, or fully anisotropic. When the ¹⁵N R₂/R₁ ratio is independent of the rapid internal motions and magnitude of the chemical shift anisotropy, it can be used to derive the rotational diffusion tensor. Excluding relaxation parameters for residues Val 27, Asp 35, His 40, Phe 41, Ile 44, Thr 45, Glu 46, and Ile 54, which have ¹⁵N R₂/R₁ ratios indicating significant contributions from internal motions, the data gave an estimate of the correlation time (τ_c) of 5.98 ns calculated with Modelfree 4.2.^29,35 This value is consistent with the 6.06 ns calculated from the structure coordinates with HYDRONMR.³⁶ Since the fully anisotropic model does not provide an improvement relative to the axially symmetric model (Table S1 in Supporting Information), the axially symmetric diffusion tensor model was chosen to best represent the motion of Im7H3M3 in solution, which we assign to be rotation as a prolate ellipsoid. The description of the rotational diffusion tensor of Im7H3M3 as a prolate ellipsoid is consistent with the distribution of R₂/R₁ ratios according to the method developed by Clore³⁷ (Supporting Information Fig. S2).

The backbone model-free parameters, S² and R_ex (Fig. 4), were determined from the relaxation data (Supporting Information Fig. S1) using the axially symmetric diffusion parameters as described in Materials and Methods; a full listing of the model-free parameters are given in Table S2 in Supporting Information. High values are seen for the average S² giving a picture of a largely rigid protein, except for the termini and Gly-rich linker between helices III and IV. Of most significance in terms of the concept of frustration, the analysis reveals a considerable number of residues that exhibit sizable R_ex terms, which align with the residues predicted to have highly frustrated interactions [Fig. 2(B,C)].

Equilibrium peptide N¹H/N²H exchange rates of Im7 and Im7H3M3

Peptide hydrogen exchange experiments are routinely used to investigate conformational dynamics of proteins,³⁸ including determining structural features of transiently populated intermediates³⁹ such as that formed in Im7.¹⁷ Provided that hydrogen exchange occurs by an EX2 mechanism, free energies of exchange can be extracted from the observed rates of exchange and it is these free energies, which provide the key structural insights. Experimental exchange rates, k_ex and free energies of exchange, ΔG_HX for Im7M3H3 are summarized in Table II (with the sequence dependence of ΔG_HX given in Fig. 5) and compared with similar data obtained previously for Im7.¹⁷

Table II.

Amide Hydrogen Exchange Stabilities for Im7H3M3 Measured at 10°C

Residue	Position in the native structure	kex (s−1)	ΔGHX (kJ mol−1)
Ser 6	N-terminus	2.42 × 10−3	18.80
Asp 9	N-terminus	1.85 × 10−4	21.12
Tyr 10	N-terminus	3.60 × 10−5	22.54
Thr 11	N-terminus	3.97 × 10−5	24.64
Phe 15	Helix I	1.33 × 10−5	25.21
Val 16	Helix I	8.26 × 10−6	24.97
Gln 17	Helix I	1.58 × 10−5	26.48
Leu 18	Helix I	2.25 × 10−5	24.01
Leu 19	Helix I	7.86 × 10−6	24.27
Lys 20	Helix I	1.91 × 10−5	25.11
Glu 21	Helix I	9.47 × 10−5	20.59
Ile 22	Helix I	4.69 × 10−5	19.58
Glu 23	Helix I	4.38 × 10−4	15.08
Val 33	Helix II	3.97 × 10−4	14.55
Leu 37	Helix II	4.03 × 10−4	15.38
Leu 38	Helix II	1.22 × 10−4	17.81
Phe 41	Helix II	2.20 × 10−3	15.43
Val 42	Helix II	9.02 × 10−4	13.92
Lys 43	Helix II	2.39 × 10−3	14.11
Leu 53	Helix III	2.27 × 10−3	12.07
Ile 54	Helix III	3.43 × 10−4	14.57
Tyr 55	Helix III	4.84 × 10−4	16.14
Glu 56	Helix III	4.52 × 10−3	11.10
Ile 75	Helix IV	5.42 × 10−3	10.13
Val 76	Helix IV	1.76 × 10−4	16.19
Lys 77	Helix IV	2.82 × 10−4	19.14
Glu 78	Helix IV	2.59 × 10−4	18.21
Ile 79	Helix IV	3.79 × 10−5	20.09
Lys 80	Helix IV	1.10 × 10−4	20.87
Glu 81	Helix IV	1.30 × 10−4	19.85
Trp 82	Helix IV	8.39 × 10−5	19.94
Arg 83	Helix IV	1.12 × 10−4	22.13
Ala 84	Helix IV	1.98 × 10−4	22.14
Ala 85	Helix IV	4.78 × 10−4	18.88
Lys 88	C-terminus	1.78 × 10−4	21.91
Lys 92	C-terminus	5.43 × 10−4	18.69

Figure 5.

Gibbs free energy of exchange (ΔG_HX) for residues of wild type Im7 (grey) and Im7H3M3 (blue) measured at 10°C, in 50 mM phosphate buffer, pH 7, and 0.4M Na₂SO₄. The dashed lines represent the ΔG⁰_UI (14.8 kJ/mol for Im7H3M3 and 12.4 kJ/mol for Im7) and the dotted lines represent the ΔG⁰_UN (23.3 kJ/mol for Im7H3M3 and 25.6 kJ/mol for Im7).²⁴ Secondary structure elements are illustrated at the top of the figure, with the extended helix III on the mutant Im7H3M3 displayed in red. The ΔG_HX values for Im7 were taken from Gorski et al.¹⁷ [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

The ΔG_HX values obtained for Im7H3M3 are remarkably similar to those of Im7. Thus, residues in unstructured regions have NH exchange rates that are too fast for their ΔG_HX values to be measured. Residues in helices I and IV have ΔG_HX values similar to the corresponding ΔG°_UN, indicating that their exchange requires global unfolding, while residues in helix II have ΔG_HX values that are similar to ΔG°_UI determined previously²⁴ using Φ-value analysis. For helix III ΔG_HX < ΔG°_UI for both Im7 and Im7M3H3 indicating that helix III is not formed in the intermediate ensemble.

NMR characterization of urea-unfolded Im7H3M3

Having characterized the conformational dynamics of the native state of Im7H3M3 and probed the conformation of the intermediate state that is in equilibrium with the native state, we next turned our attention to urea-denatured Im7H3M3. The limited chemical shift dispersion of the ¹H-¹⁵N HSQC spectrum of Im7H3M3 denatured in 6M urea (Supporting Information Fig. S3), particularly in the ¹H dimension, shows the protein to be unfolded, as expected from the fluorescence and CD studies of Knowling et al.²⁴ Despite the poor dispersion almost complete assignments (88 peptide NH groups; 94% completeness excluding Met 1 and the three Pro residues) were obtained from standard triple resonance experiments (CBCANH, CBCA(CO)NH, HNCO) supplemented by a three-dimensional HNN spectrum.

Since the unfolded states of proteins are highly dynamic, the observed NMR parameters are a population-weighted average over all structures in the conformational ensemble. Nevertheless, deviations of chemical shifts from their expected random coil values, secondary chemical shifts (Δδ = δ_obs - δ_rc, where the chemical shift δ is referenced to a random coil shift δ_rc), are a useful measure of transient secondary structure.⁴⁰ However, determination of secondary chemical shifts is dependent on an appropriate choice of random coil chemical shifts. We have used the latest random coil values reported in the literature,^41,42 which take into account a set of sequence corrections to the random coil values for all nuclei (for pH, temperature, and neighbouring residues), following the approach of Schwarzinger et al.⁴³ The widely used method for identification of protein secondary structure elements uses ¹³C chemical shift data,⁴⁰ which reflect the relative population of backbone dihedral angles in the α and β regions of conformational space.⁴⁴ The secondary chemical shifts incorporating sequence corrections (Fig. 6) suggest that though the protein is largely unfolded in 6M urea there are regions that may be involved in transient secondary structure. This is suggested by the predominantly positive secondary shifts for ¹³Cα and ¹³CO, particularly for regions of the protein corresponding to native helices, since positive values are indicative of α-helices.⁴⁵ Though ¹³Cβ chemical shifts are less sensitive to the presence of α-helices,⁴⁶ Δδ¹³Cα − Δδ¹³Cβ values are a useful tool to reveal secondary structure propensities. For Im7H3M3 in 6M urea, Δδ¹³Cα − Δδ¹³Cβ values [Fig. 6(D)] suggest that residues forming helices I, III, and IV of native Im7H3M3 have a preference for φ/Ψ angles close to those required for α-helices, because they are positive. In contrast, the negative Δδ¹³Cα − Δδ¹³Cβ values [Fig. 6(D)] for residues that form helix II in native Im7H3M3 indicate that these residues have a preference for φ/Ψ angles in the β region. As Pashley et al.²⁷ note in their NMR study of a Im7 variant that is unfolded in the absence of chaotrophs, though positive ¹³Cα chemical shift changes indicate formation of helices the magnitude of the shifts are less than the ∼2.6 ppm change observed in folded proteins⁴⁵ which means that the tendency for some residues in unfolded proteins, and here we include Im7H3M3, to adopt helical structure is weak. Pashley et al.²⁷ found that residues in their unfolded Im7 variant that form the four helices in native Im7 had helical character, with those from the native helices I and IV having most. Given that their sample was unfolded in the absence of urea and had 0.2M Na₂SO₄ present our findings for Im7H3M3 in the presence of urea and absence of Na₂SO₄ are in reasonable agreement.

Figure 6.

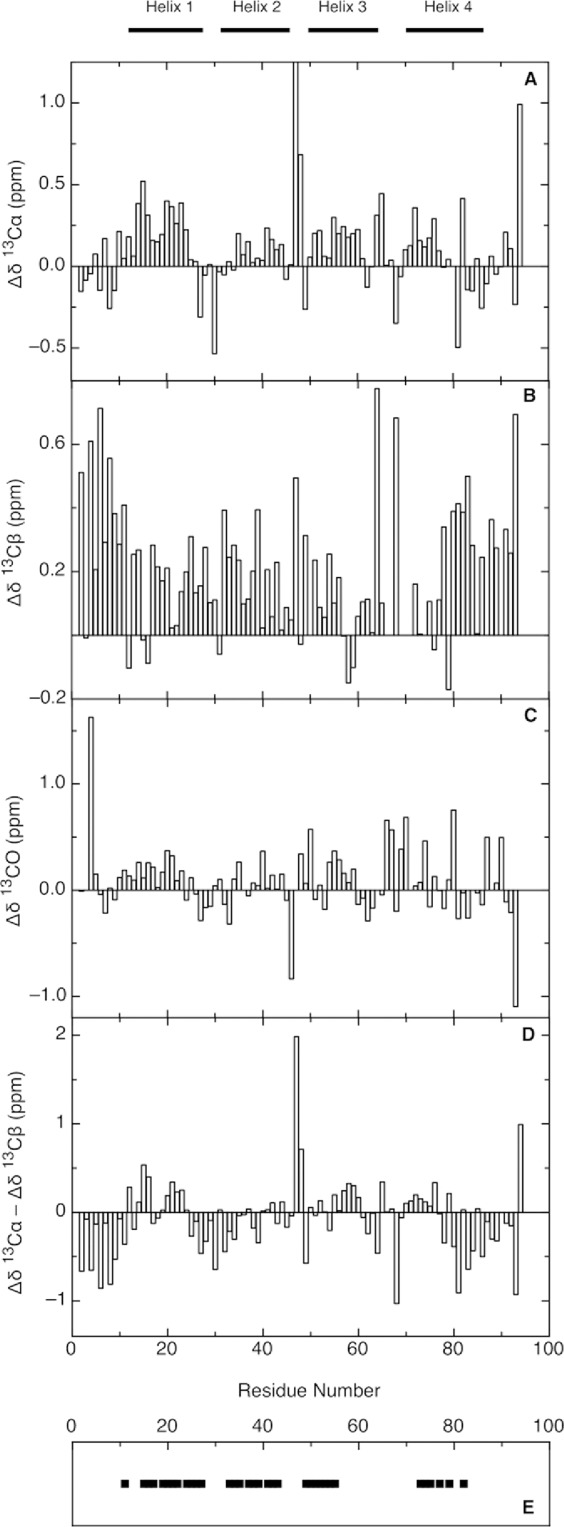
Chemical shift deviations of Im7H3M3 in the urea-unfolded state (6M urea) for ¹³Cα (A), ¹³Cβ (B), and ¹³CO (C), in 50 mM phosphate buffer, pH 7 at 25°C. Intrinsic random coil chemical shifts were used according to reference.^41,42 Secondary chemical shift differences Δδ¹³Cα − Δδ¹³Cβ (D) provide a valuable probe of secondary structure propensities; positive values indicate α-structure propensity and negative values indicate β-structure propensity. His 47 show a large ¹³Cα deviation ∼2.5 ppm (A), nevertheless a linear analysis of chemical shifts (LACS) was performed validating all Im7H3M3 chemical shifts. Summary of the assigned cross-peaks in the ¹H-¹H-¹⁵N NOESY-HSQC spectrum of Im7H3M3 (E) showing NOEs between the HN of residue i and the HN of residue i + 1 (black squares). Though some NOE connectivities between NH resonances could be observed in the three-dimensional NOESY-HSQC spectrum, the severe overlap of the amide resonances limited the number of NOE peaks that could be assigned. The horizontal bars on the top of the figure indicate the secondary structure elements present in the native state.

Even with disordered proteins NOEs can provide valuable structural information though they are not readily interpreted quantitatively because of the conformational averaging. However, as Yao et al.⁴⁷ showed, d_{NN(i,i + 1)} NOEs measured at long mixing times are good indicators of helical content in disordered proteins. For Im7H3M3 in 6M urea d_NN(i,i+1) NOEs were observed [Fig. 6(E)] for regions that are helices in the folded structure, correlating well with the regions suggested by the chemical shift analyses to have transient helical content. Long range NOEs indicative of the presence of preferred topologies, were not observed for Im7H3M3 in 6M urea.

Polypeptide chain dynamics of urea-unfolded Im7H3M3

Backbone dynamics of urea-unfolded Im7H3M3 were investigated with ¹⁵N R₁, ¹⁵N R₂, and {¹H}-¹⁵N heteronuclear NOE data recorded at ¹H frequencies of 600 and 800 MHz at 10°C. Relaxation parameters were determined for 80 of the 94 backbone amides (Supporting Information Fig. S4) as described in Materials and Methods. For residues 2 to 94, the average R₂ values at 600 MHz and 800 MHz are 4.46 (± 0.08) s⁻¹ and 5.03 (± 0.13) s⁻¹, respectively, while the average R₁ values at 600 and 800 MHz are 1.76 (± 0.04) s⁻¹ and 1.54 (± 0.04) s⁻¹, respectively. The {¹H}-¹⁵N NOE values alone indicate considerable flexibility throughout the urea-unfolded Im7H3M3 sequence, below the average value of +0.78 expected for backbone amides of a rigid globular protein tumbling isotropically.⁴⁸

The slight increase in the R₂ values for Im7H3M3 compared with those of urea-unfolded Im7 suggests that a change in the conformational ensemble has occurred. To explore this we determined the hydrodynamic radius (R_h) of Im7H3M3 from NMR diffusion experiments (see Materials and Methods). At 25°C and 10°C, respectively, it was 29.7 ± 0.4 Å and 25.5 ± 0.6 Å compared with the theoretical maximum value of 30.7 Å, calculated as described by Wilkins et al.,⁴⁹ and the R_h of urea-unfolded Im7* at 10°C, 29.8 ± 1.6 Å.²⁶ Thus, as with the native folded proteins, Im7H3M3 appears to be more compact than Im7* in their urea-unfolded states. Im7H3M3 in 6M urea shows a similar degree of compaction as the Im7 mutant L18A-L19A-L37A unfolded in the absence of urea since the hydrodynamic radius of the latter at 10°C is 26.1 ± 0.6 Å.

Dynamics of a polypeptide chain can be deduced from the backbone NH relaxation parameters R₁, R₂, and {¹H}-¹⁵N NOE through the use of the reduced spectral density functions J(0), J(ω_N), and J(0.87ω_H).^50–52 The magnitudes of the spectral density functions are sensitive to motions at the corresponding frequencies, zero, ω_N and 0.87ω_H. Thus, J(0) reflects slow internal motions on the millisecond to microsecond time scale as well as slow global rotational diffusion while J(0.87ω_H) reports on the presence of fast internal motions, on the picosecond timescale.^50–52 In the case of urea-unfolded Im7H3M3, J(0) is most informative as it shows that many residues involved in secondary structure elements in the native state have restricted mobility, with J(0) values above the average [Fig. 7(A)]. However, those residues comprising helix III of the native state of Im7H3M3 fall into two distinct groups: the N-terminal segment from residues Gly 50 to Glu 56, whose J(0) values [Fig. 7(A)] indicate restricted motion, and the C-terminal segment from residues Ala 57 to Asn 64 which appears to have largely random fast motions on the picosecond timescale unrestricted by whatever perturbs the motions of the N-terminal segment. Comparing the J(0) values between the urea-unfolded states of Im7H3M3 and wild-type Im7 [compare Fig. 7(A) with Fig. 6 of Ref. 26], both measured at 600 MHz, gives further insight into the motional variations due to the elongation of helix III. While residues forming helices I and II of native Im7 have similar J(0) values for urea-unfolded Im7H3M3 and wild-type Im7, smaller J(0) values were observed for the residues forming the C-terminal region of helix III in native Im7H3M3 and the adjacent loop, indicating that these residues are more flexible than those forming the loop between helices III and IV of native Im7 in urea-unfolded Im7.

Figure 7.

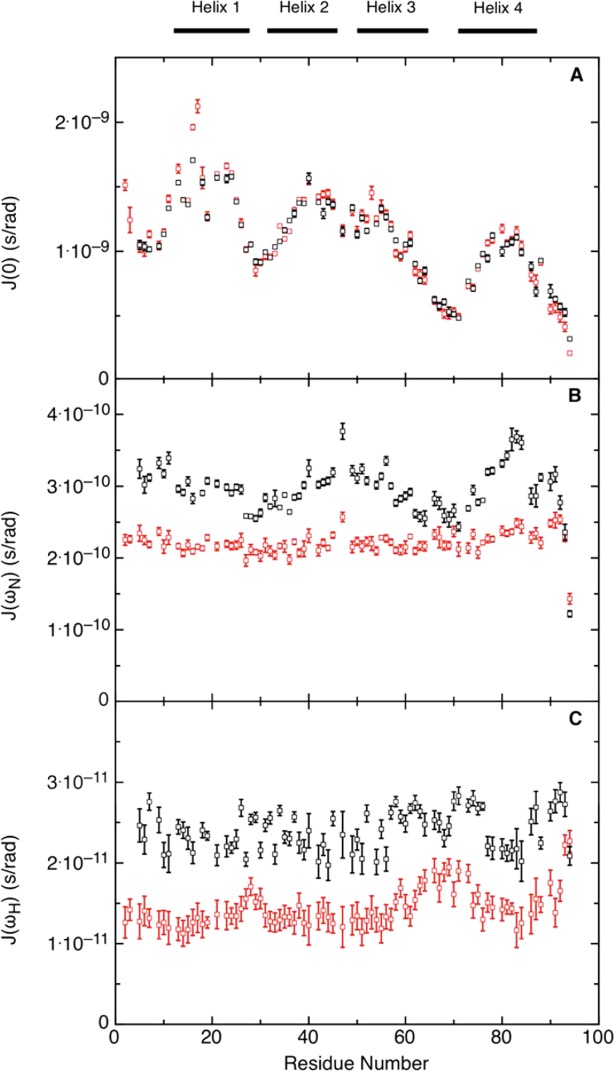
Reduced spectral density mapping of urea-unfolded Im7H3M3. Data recorded at 600 MHz (black) and 800 MHz (red), at pH 7 and 10°C; (A) J(0), (B) J(ω_N), and (C) J(ω_H) calculated as described in Materials and Methods. The black bars at the top of the figure indicate the location of the α-helices in the native protein. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

As reported for urea-unfolded Im7,²⁶ and shown here to facilitate comparison [Fig. 8(A,C)], the maxima in the sequence profile of J(0) [Fig. 7(A)], indicating motional restrictions on the backbone NH groups, can be accounted for by clusters of side chains coming together to restrict the motions of the polypeptide backbone (Fig. 8). The correlation between the clusters and the average area buried upon folding (AABUF),⁵³ which is proportional to the hydrophobic contribution of a residue to the conformational free energy of a protein, and not the helix propensity as determined by AGADIR⁵⁴ [Fig. 8(B,D)], confirms that it is the hydrophobicity of the amino acid sequence and not the helix propensity that is the driving force for cluster formation. Nevertheless, as was observed previously with Im7 the clusters are associated with residues forming α-helices in the native structure, which is a consequence of many of the residues that promote cluster formation also promoting helix formation. This is also shown by the correspondence between the location of the α-helices of the native state and hydrophobic clusters identified by HCADraw.⁵⁵

Figure 8.

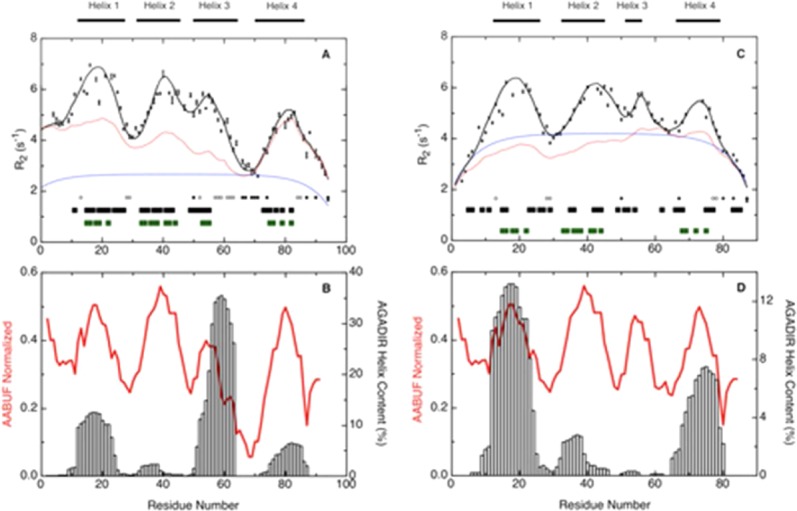
R₂ relaxation rates for (A) Im7H3M3 in 6M urea and (C) Im7 in 6M urea, pH 7 and at 10°C, and the average area buried upon folding (AABUF)⁵³ and helix propensity (AGADIR)⁵⁴ for (B) Im7H3M3 and (D) Im7, plotted as a function of residue number. Measured R₂ rates are shown as black squares with error bars; red lines in (A) and (C) shows the R₂ values calculated according to the volume-dependent model⁵⁸ incorporating only the side chain radius of gyration and with persistence length λ₀ = 7 except for Gly and Ala for which the value of λ₀ was set to 2, and a Gaussian term incorporating four clusters centered at residues Leu 18, Val 42, Gly 56, and Lys 80 (Im7H3M3). The blue lines in (A) and (C) show the R₂ values described by the segmental motion model.^56,57 Black bars at the bottom of graphs (A) and (C) represent d_NN (i, i + 1) NOEs found in the urea-unfolded states; green bars, show hydrophobic clusters predicted by HCA_Draw;⁵⁵ and the positions of glycine residues (filled circles) and alanine residues (open circles) in the sequence of each protein is indicated. Open vertical bars in (B) and (D), AGADIR⁵⁴ prediction of helix propensity; the average area buried upon folding (red line) was normalized from 0 to 1 with a window size of seven residues. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

Characteristics of the clusters can be obtained from fitting the observed R₂ rates to models for polypeptide motion. We have used the segmental motion model^56,57 and the volume dependent model,⁵⁸ as described in Materials and Methods, because there is not clear agreement in the literature on which is most applicable. However, the key features extracted about the clusters (Table III) were the same for both models: clusters I, II, and IV of urea-unfolded Im7H3M3 are the same size as the corresponding clusters of wild-type Im7, which is not surprising since the engineered insert into Im7H3M3 is not in these sequence regions and the clusters are largely non-interacting. Cluster III, the smallest in Im7 is still one of the smallest in Im7H3M3. We return to this observation below.

Table III.

Clusters in Urea-Unfolded Im7H3M3 and Urea-Unfolded Wild-Type Im7 Determined from Fits of ¹⁵N R₂ Relaxation Data to Models for Polypeptide Motion

	Helical residuesa	Cluster centre	Cluster width
	12-27 (Helix I)	Leu 18	9
	32-45 (Helix II)	Val 42	9
Im7H3M3	50-64 (Helix III)	Glu 56	3
	72-86 (Helix IV)	Lys 80	6
	12-24 (Helix I)	Leu 18	9
	32-45 (Helix II)	Val 42	9
Im7b	51-56 (Helix III)	Tyr 56	3
	66-79 (Helix IV)	Lys 73	6

^aFrom the corresponding native structure: Im7H3M3 (2K0D.pdb) and wild-type Im7 (1AYI.pdb), respectively.

^bFrom Ref.25.

Implication for the folding mechanism of Im7

In the previous study of Knowling et al.²⁴ the notion that helix III in Im7 is the last to fold because it has the lowest helical propensity was dispelled by engineering the helix to contain an extended poly-Ala sequence in Im7M3H3. Remarkably, the extended helix III contributes to an enhanced network of highly frustrated contacts without hindering formation of the minimally frustrated contacts and without perturbing the folding pathway. The data reported here allow us to see why the extended helix III does not perturb the folding pathway by demonstrating that it is the properties of the unfolded ensemble that favour the folding of Im7 via a three helical intermediate. The observation that the clusters in the urea-denatured state of Im7H3M3 mirror those of urea-denatured Im7 (Table III), as well as Im7 denatured in the absence of chaotrope²⁷ are the critical findings that underpin this conclusion. However, cluster III of Im7H3M3 is the smallest of the four clusters, as it is in Im7 despite this region having the highest helix propensity (Fig. 8). The reason is clear; the high helix propensity has been achieved largely by inserting a polyalanine helix, and because Ala is small it has a low AABUF⁵³ (Fig. 8) and thus does not give rise to a large cluster. Thus, hydrophobic collapse involving the interaction of the largest clusters early in folding creates the three helical intermediate that is common to the folding pathways of both Im7 and Im7H3M3 in which their largest clusters, I, II, and IV, interact. Since such an interaction promotes these clusters adopting their preferred helical conformations the similarity of the collapsed states leads to similar three-helical intermediate states. Furthermore, it is clear that such cluster interactions can be correlated with the network of minimally frustrated contacts observed in the native state. It is noteworthy that the elongation of the sequence with the insert to create Im7H3M3 inevitably means that there is a greater separation in sequence-space between residues in clusters I, II, and IV, however, this greater separation in sequence-space does not materially affect the folding pathway (Fig. 1), consistent with it being the inter-cluster interactions that drive the early stages of folding.

General implication for protein folding

Numerous studies of many small proteins have contributed to the current view that the rates of folding for proteins that do not involve kinetic intermediates are determined by the topology of the native state.⁵⁹ Following the initial analyses of Baker and his colleagues,^60–63 who showed there was a direct correlation between the rate at which such a protein folds and the average sequence separation between contacting residues expressed as an absolute value or relative to the sequence length, which they called the contact order, there have been other analyses confirming that the long-range order of the native state is an important determinant of folding rate.^5,64–67 Grantcharova et al.⁶² discussed some of the implications of the correlation of the folding rate with contact order and pointed out that this correlation implies that the contact order of the native state is correlated with the contact order of the transition state ensemble. The work presented here adds to this view, suggesting that the conformational properties of the folding intermediate of Im7 are determined by the nature of hydrophobic clusters in the denatured state and the network of highly frustrated interactions in the native state. Consistent with this view of the significance of structure in the unfolded state, Nishimura et al.⁶⁸ and Felitsky et al.⁶⁹ used NMR measurements to show that transient long-range contacts in unfolded apomyoglobin, some of which are non-native but some native-like, are important for folding, suggesting that the contact order of the native state does indeed start to appear early on the folding pathway. Calculations also support the idea that native-like contacts are formed early in protein folding linked to hydrophobic collapse.⁷⁰ Overall, therefore, the detailed analyses of Im7H3M3 presented here, combined with previous NMR analyses of wild-type Im7,^18,19 urea denatured Im7,²⁶ Im7 denatured in the absence of chaotrope²⁷ and Im9¹⁹ all point to the collapsed status of the denatured protein playing a role in determining the details of the folding landscape and the topology of the native state. Since sequence determines both collapse in the denatured state and its inherent secondary structure propensity, the correlation of structure in the denatured state, the ruggedness of the folding energy landscape, and the rate of folding to the native state is perhaps not surprising. Finally, our study reveals the importance of considering minimal frustration for protein design, where rational engineering of frustrated regions may provide clues about folded states.

Materials and Methods

Sample preparation

¹⁵N labeled and ¹³C/¹⁵N double-labeled samples of Im7H3M3 were produced and purified as described previously.⁷¹ For NMR experiments lyophilized samples were resuspended in 50 mM phosphate buffer, pH 7, 10% ²H₂O/90% H₂O at a concentration of ∼0.5 to 1 mM. For urea-unfolded studies the lyophilized protein was dissolved in 50 mM phosphate buffer, 10% ²H₂O/90% H₂O containing 6M urea, pH 7.0. The urea concentration was determined using a refractometer, as described by Pace.⁷²

Frustration analysis of Im7 and Im7H3M3

The Im7 crystal structure (1AYI.pdb) and the Im7H3M3 NMR solution structure (2K0D.pdb) were used in the calculation of the residue-based configurational frustration using the web server at http://www.frustratometer.tk/. The algorithm quantifies the degree of frustration manifested in spatially local interatomic interactions.²⁸

NMR spectroscopy

All NMR experiments were performed at 25°C (unless otherwise specified) and acquired with Bruker Avance III 800 MHz, Avance II+ 600 and Avance II+ 400 spectrometers or with Varian Unity Inova spectrometers operating at 500 and 600 MHz proton Larmor frequencies. The Avance II+ 600 MHz spectrometer at Lisbon was additionally equipped with a cryogenic probe. Proton chemical shifts were referenced against external DSS while nitrogen and carbon chemical shifts were referenced indirectly to DSS using absolute frequency ratios. All NMR data were processed using NMRPipe⁷³ or Bruker TopSpin 2.1 software and analyzed with CCPNMR⁷⁴ or NMRView.⁷⁵

¹⁵N relaxation measurements of native Im7H3M3

¹⁵N R₁ and R₂ relaxation rates and {¹H}-¹⁵N heteronuclear NOE values for native Im7H3M3 were measured at a ¹H frequency of 600 MHz and 400 MHz at 25°C by standard procedures.^76,77 The R₁ measurements included a recycle delay between scans of 4.0 s and an array of ten different relaxation delays: 0.01 (in duplicate), 0.05, 0.08, 0.2 (in duplicate), 0.5, 0.75, 1, 2 s. The R₂ relaxation delays were: 0.01 (in duplicate), 0.03, 0.05 (in duplicate), 0.07, 0.11, 0.15 (in duplicate), 0.25 s. A 3 s saturation delay was applied during d1 in all {¹H}-¹⁵N steady-state NOE experiments with a total recycle delay of 5 s to allow the longitudinal magnetization to relax back to equilibrium. For both R₁ and R₂ data, monoexponential two-parameter decay functions were fit to peak intensity versus measured relaxation delay profiles using the CURVEFIT program freely available from Arthur G. Palmer, III.⁷⁸ Uncertainties in the derived R₁ and R₂ values were estimated using Monte-Carlo simulations with 1000 random Gaussian noise iterations, taking into account the root mean square noise in the spectra.²⁹ Heteronuclear NOE values were calculated as the ratio of peak volumes in spectra recorded with and without saturation. In the experiment without saturation, a total recycle delay, d1, of 5 s was used in place of the saturation delay to ensure the same recycle delay between scans for both experiments. Errors in the NOE values were calculated from the uncertainties in the peak volume measurements estimated by the root mean square noise in each of the two spectra.

For model-free analysis, an initial estimate of the rotational diffusion tensor was obtained from the R₂/R₁ ratios of the individual residues and the PDB coordinates of the solution structure of Im7H3M3 (2K0D.pdb) using the programs pdbinertia, r2r1[lowem]diffusion and quadric[lowem]diffusion distributed by Arthur G. Palmer, III.³⁴ After exclusion of residues with hetNOE values lower than 0.65, or with R₁ or R₂ values exceeding one standard deviation from the mean, according to the criteria proposed by Tjandra,^{79 15}N transverse relaxation data were analyzed by the extended model free approach using FAST-Modelfree⁸⁰ and automated version of Modelfree 4.2.²⁹ Fitting of the R₂/R₁ ratios was performed using the combined magnetic field data for different rotational diffusion tensors: isotropic, axial and fully anisotropic with the model selection criteria based on the methods proposed by Palmer,²⁹ including the use of the F-test to judge the statistical significance of invoking any additional parameter. A ¹⁵N magnetogyric ratio of −2.71, a CSA of the ¹⁵N atom −160 ppm and a NH bond distance of 1.02 Å were used. The following five models were used to describe the spin relaxation data: the first model (model 1) was based simply on fitting the generalized order parameter S² alone (τ_f = τ_s = 0) used to fit the amplitude of internal motions on the picosecond to nanosecond timescale; model 2, incorporated the presence of fast internal motions (τ_f < 100–200 ps) by fitting both S² and τ_e (the effective correlation time for internal motions); models 3 and 4 added an R_ex term to the model-free formalism to take into account the loss of transverse magnetization due to chemical and/or conformational exchange for microsecond to millisecond motions and provided fits to S² and R_ex (model 3) and S², τ_e, and R_ex (model 4), respectively. Finally, the last model (model 5) considered the presence of internal motions slower than τ_f but faster than the overall rotational correlation time of the protein by fitting S², τ_e, and S²_f (model 5). Residues were individually fitted to the five dynamic models by hierarchical fitting²⁹ to subsets of the parameters in the extended Lipari-Szabo expression³³ for the spectral density. The exchange terms were scaled quadratically with respect to the different magnetic fields. A grid search was used to obtain initial estimates for the values of the remaining model parameters by minimising the χ² function defined within the program documentation.^29,80 Statistical properties of the model-free parameters were obtained from Monte Carlo simulations using 600 randomly distributed synthetic data sets.³⁵ The quality of the fit between the experimental data and theoretical model was assessed for each spin by comparing the optimal value of Γ_i with the α = 0.05 critical value of the distribution of Γ_i obtained from the Monte Carlo simulations. Model selection was conducted according to the protocol outlined by Palmer et al.²⁹ and implemented in FAST-Modelfree.⁸⁰ For comparison purposes with experimental data rotational diffusion tensor was also predicted using HYDRONMR,³⁶ using an atomic element radius of 3.3 Å.

N¹H/N²H exchange

¹⁵N-labeled samples were used to analyze the decay of amide proton signal intensities due to hydrogen exchange with ²H₂O. A ¹⁵N sample lyophilized from water was dissolved into 100% ²H₂O buffer, 50 mM phosphate buffer, with 0.4M Na₂SO₄ and containing 0.01% sodium azide, pH* 6.96, (*indicating direct meter reading uncorrected for any isotope effects). Spectra were acquired at a sample temperature of 10°C. To reduce the time required for the sample to reach temperature the buffer solution was pre-equilibrated at 10°C for 40 min before dissolution of the lyophilized protein. The dissolved protein was then immediately placed in the NMR tube and inserted into the NMR spectrometer, previously tuned and shimmed using a sample with the same buffer characteristics. The dead time elapsed between dissolving the sample in ²H₂O and recording the first spectrum was approximately 2 min. Consecutive ¹H-¹⁵N HSQC spectra were recorded on a Varian Unity Inova spectrometer operating at ¹H frequency 600 MHz with successive increase in the number of scans, in order to get an acceptable signal/noise ratio maintained along the experiment as peak intensities decreased with amide hydrogen exchange for deuterium. After approximately 6 h the majority of amide protons had exchanged completely. Cross-peak volumes were obtained using NMRPipe⁷³ and normalized over the number of scans of each ¹H-¹⁵N HSQC spectrum. To calculate the exchange rates, the normalized peak volumes corresponding to each amide peak acquired as a function of the exchange time (defined as the period from the suspension of the lyophilized sample in ²H₂O to the successive two-dimensional ¹H-¹⁵N HSQC spectra) were fitted to the following three-parameter single-exponential decay function using Origin (OriginLab, Northampton, MA).

where C is the baseline noise offset, I₀ is the amplitude of the exchange curve at zero time, t is the time in minutes and k_ex is the exchange rate. Intrinsic exchange rates, k_int, were obtained by using the web program SPHERE⁸¹ with default activation energies: E_acid = 15 kcal/mol, E_base = 2.6 kcal/mol. In the transiently open condition, a kinetic competition between exchange and reclosing ensues. If reclosing is faster k_cl >> k_int, the structural opening reaction appears as a preequilibrium step prior to the rate-limiting chemical exchange, and the observed rate constant (k_ex) is k_ex = K_op k_int where K_op is the equilibrium constant for structural opening (K_op = k_op/k_cl) – EX2 mechanism. From the Boltzmann relationship (ΔG_HX = -RT ln K_op) one can then calculate the free energy change for the structural opening reaction that exposes the hydrogen to exchange. To guarantee the same exchange mechanism (EX2) as previously reported for wild-type Im7¹⁷ the same conditions were used (ionic strength, pH, and temperature) to monitor the amide hydrogen exchange for Im7H3M3.

Urea-unfolded Im7H3M3

¹³C/¹⁵N labeled and ¹⁵N labeled samples of Im7H3M3 in 6M urea were used for backbone resonance assignment and for relaxation studies, respectively. All NMR measurements were done with freshly prepared samples that were allowed to reach equilibrium before NMR acquisition over a period of 5 h. Standard triple resonance experiments for backbone assignment (CBCANH, CBCA(CO)NH, HNCO, and HNN) were measured at 25°C on Bruker Avance III 800 MHz and Varian INOVA 500 MHz spectrometers, equipped with room temperature triple resonance probes. The spectral widths for the three-dimensional NMR experiments recorded at 500 MHz (CBCA(CO)NH, HNCO, and HNN) were 5629 Hz for ¹H, 1320 Hz for ¹⁵N, 7535 Hz for ¹³Cαβ, and 1294 Hz for ¹³CO; at 800 MHz spectral widths were 11,161 Hz for ¹H, 1953 Hz for ¹⁵N, and 12,500 Hz for ¹³Cαβ (CBCANH).

To probe the existence of inter- and/or intra-residue NOEs in urea-unfolded Im7H3M3, a three-dimensional ¹H-¹H-¹⁵N NOESY-HSQC experiment was recorded at 800 MHz with a mixing time of 200 ms. The buffer conditions were the same as used for the backbone assignment but the temperature was lowered to 10°C. To monitor for temperature dependence of the chemical shifts, two-dimensional ¹H-¹⁵N HSQC spectra were recorded from 10 to 25°C, which allowed us to follow completely the full backbone assignment of the protein.

Residue-specific backbone amide ¹⁵N longitudinal (R₁) and transverse (R₂) relaxation rates and steady-state heteronuclear {¹H}-¹⁵N NOE were collected on uniformly ¹⁵N-enriched Im7H3M3 in 6M urea at two static magnetic fields strengths, 600 and 800 MHz, respectively, and at 10°C using standard procedures described in the literature.^{76,77 15}N R₁ data were acquired with the following relaxation delay times: 10 (duplicate, 2×), 50, 80, 200 (2×), 500 (2×), 750, 1000, and 2000 ms. Similarly, ¹⁵N R₂ values were obtained from a series of 20 experiments recorded in an interleaved manner with (randomly distributed) relaxation delays of 16 (2×), 32 (2×), 48, 64 (2×), 80, 96, 112, 128 (2×), 144, 160 (2×), 192, 208, 240, 320, 400 ms. The interpulse delay for the 180° ¹⁵N pulse in the CPMG experiment was 625 μs. The rates were fit with the program CURVEFIT,⁷⁸ as for the relaxation studies in the native state. Steady-state {¹H}-¹⁵N NOE values were obtained by recording spectra with and without ¹H saturation. {¹H}-¹⁵N NOE values were calculated as the ratio of peak volumes from spectra recorded with and without saturation. Three repeats of the NOE measurement were performed and the results were averaged together. The errors in the NOE values were calculated from the uncertainties in the peak volume measurements estimated by the root mean square noise in each spectrum.

Following the procedure in Le Duff et al.,²⁶ R₂ relaxation rate profiles were fitted to a segmental motion model^56,57 and to a segmental motion model incorporating a residue volume dependence.⁵⁸ The first model predicts a bell-shaped profile distribution for the dynamics of a linear peptide, with increased flexibility at the termini, as shown by the first term of equation:

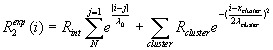It assumes that the influence of the neighbouring residues in a polypeptide chain is independent of side chain volume or hydrophobicity, and decays exponentially as the distance from a given residue increases; R_int is the intrinsic relaxation rate, which depends on temperature and viscosity, λ₀ is the persistence length of the polypeptide chain (in terms of number of residues) and N is the total chain length. The second term of the equation accounts for the residue volume dependence. This Gaussian term is characterized by the position of the cluster in the protein (residue number) x_cluster, the cluster width λ_cluster, and a distinct relaxation rate for each cluster, R_cluster. Overall, the first term of the equation characterises the baseline, whereas the second term fits clusters yielding the deviation from the baseline relaxation profile.

The spectral density at zero frequency, J(0), was calculated as described by Lefevre⁵¹ using the reduced spectral density. From the relaxation parameters ¹⁵N R₁, R₂, and {¹H}-¹⁵N NOE, reduced spectral densities were calculated using the jw[lowem]mapping.py python script incorporated in the relax program.⁸² The spectral density functions were obtained assuming that at higher frequencies J(ω_H) ≍ J(ω_H + ω_N) ≍ J(ω_H − ω_N) ≍ J(<ω_H>)⁵¹ and that J(<ω_H>) is equivalent to J(0.87ω_H) or J(ω_H + ω_N), where ω_H + ω_N < ω_H since the Larmor frequencies of proton and nitrogen have opposite sign. Thus, J(0) is represented as follows:

where,

The constants c² and d² are approximately equal to 1.25 × 10⁹ (rad/s)² and 1.35 × 10⁹ (rad/s)², respectively, at 14.1 T (ω_H = 600 MHz), and 2.25 × 10⁹ (rad/s)² and 1.35 × 10⁹ (rad/s)² at 18.8 T (ω_H = 800 MHz). ¹⁵N chemical shift anisotropy was considered to be −160 ppm and the NH bond length 1.02 Å. Uncertainties in the spectral density values were estimated from 500 Monte Carlo simulations using the relax program.⁸²

NMR diffusion experiments

Pulsed-field gradient diffusion NMR experiments were carried out with lyophilized Im7H3M3 dissolved in 100% D₂O and with 20 μL 1,4-dioxane added as internal molecular radius standard. The PG-SLED pulse sequence⁴⁹ was used to collect pulsed-field-gradient diffusion experiments on a Bruker Avance III 800MHz at 10°C, respectively. Fifteen gradient experiments were acquired for each data set, with the gradient strengths augmented linearly through the acquisition from 0 to 30 G/cm and all other delays and pulses held constant. Gradient pulses (δ) were applied for 6.3 ms with a recovery time of 0.7 ms, and diffusion delay (Δ) of 100 ms. This was found to be adequate to give a total decay of more than 90%. Thirty-two transients were acquired per gradient experiment. Data were analyzed using the variable gradient fitting routines in Bruker TopSpin 2.1 software and in all cases protein resonances were fit with a single exponential decay function using peak intensities. Theoretical hydrodynamic radii (R_h) values were calculated from the empirical equation for folded and denatured proteins.⁴⁹ Experimental R_h values for Im7H3M3 were determined as follows: (D_ref/D_protein) × R_h(ref), where D_ref and D_protein are the measured diffusion coefficients of dioxane and the protein, respectively, and R_h(ref) is the effective hydrodynamic radius of dioxane, taken to be 2.12 Å.⁴⁹

Hydrophobic analysis

The per-residue average area buried upon folding (AABUF) was calculated using the method described by Rose et al.⁵³ using the ExPaSy tool ProtScale (http://us.expasy.org/tools/protscale.html), with a window size of seven residues and normalized from 0 to 1. Hydrophobic cluster analysis was performed using the program HCADraw⁵⁵ on the ExPaSy tool web server (http://mobyle.rpbs.univ-paris-diderot.fr/cgi-bin/portal.py?form=HCA).

Glossary

AABUF

average area buried upon folding

DSS

2,2-(dimethylsilyl)propanesulfonic acid

fid

free induction decay

HSQC

heteronuclear single quantum coherence

Im7

the immunity protein for colicin E7

Im7*

His-tagged Im7

Im7H3M3

Im7 variant containing an engineered helix III

MD

molecular dynamics

NOE

nuclear Overhauser enhancement

ppm

parts per million

Supplementary material

Additional Supporting Information may be found in the online version of this article.