Metal cation controls myosin and actomyosin kinetics

Abstract

We have perturbed myosin nucleotide binding site with magnesium-, manganese-, or calcium-nucleotide complexes, using metal cation as a probe to examine the pathways of myosin ATPase in the presence of actin. We have used transient time-resolved FRET, myosin intrinsic fluorescence, fluorescence of pyrene labeled actin, combined with the steady state myosin ATPase activity measurements of previously characterized D.discoideum myosin construct A639C:K498C. We found that actin activation of myosin ATPase does not depend on metal cation, regardless of the cation-specific kinetics of nucleotide binding and dissociation. The rate limiting step of myosin ATPase depends on the metal cation. The rate of the recovery stroke and the reverse recovery stroke is directly proportional to the ionic radius of the cation. The rate of nucleotide release from myosin and actomyosin, and ATP binding to actomyosin depends on the cation coordination number.

Introduction

Myosin is a muscle's molecular motor, consecutively interacting with two ligands, ATP and actin. Myosin changes conformation upon ligand binding, producing the recovery stroke (interaction with ATP) and then the power stroke, upon interaction with actin. It was shown previously that the cross-bridge kinetics can be directly modulated by altering a nucleoside triphosphate,^1–4 which apparently affects position of the triphosphate within myosin active site. Metal cation, coordinating β and γ phosphates of a nucleotide at the active site, should modulate myosin-nucleotide interaction in even larger extent, affecting kinetic steps of myosin ATPase. The goal of this work was to determine if the kinetics of myosin and actomyosin ATPase cycle can be modulated using different metal cations, complexed with ATP. Direct modulation of myosin and actomyosin kinetics is an attractive approach in myopathies treatment. Fine tuning of myosin kinetics may increase muscle performance and muscle power output in a diseased muscle.

It is known that calcium and manganese support myosin and cross-bridge ATPase activity,^5–8 as well as natural ligand Mg.ATP, and the rate of basal myosin ATPase depends on metal cation, complexed with ATP. Intrinsic fluorescence of myosin, rapidly mixed with Mn.ATP, exhibits apparent rapid destabilization of the post-recovery stroke state (M** state),⁹ suggesting increased rate of the reverse recovery stroke and phosphate release, which therefore can be responsible for observed increased rate of myosin ATPase activity. All these data suggest that myosin is not a specific enzyme and interacts with nucleotide, complexed with different divalent metal cations. This allows systematic study of myosin kinetic response on different metal cations, placed right in the center of the hydrolysis reaction. In this work we provide detailed study and rational clarification of the effect of metal cation on myosin and actomyosin ATPase activity.

We have studied myosin and actomyosin kinetics, using Mg, Mn, and Ca complexed with ATP as a ligand. All three cations have different ionic radii for octahedral coordination, 0.072 nm (magnesium), 0.083 nm (manganese), and 0.1 nm (calcium). Both magnesium and manganese cations maintain octahedral ligand coordination geometry. Calcium belongs to the same group in the periodic table as magnesium, but its larger size makes it maintaining irregular coordination geometry with the coordination number seven. Therefore, in this work we studied the effect of the ionic radius and the coordination number of the metal cation in the metal.ATP complex on myosin and actomyosin kinetics. We used previously characterized double-Cys D. discoideum myosin construct (A639C:K498C),¹⁰ labeled with IAEDANS:Dabcyl FRET pair (Fig. 1). We thoroughly studied myosin and actomyosin steady state ATPase activities. We employed the collection of transient spectroscopic techniques, based on the transient time resolved FRET (TR²FRET), myosin intrinsic fluorescence, and the fluorescence of pyrene labeled actin. We measured rates of myosin conformational changes upon interaction with metal.ATP, and actomyosin association and dissociation in the presence of the nucleotide, according to Scheme 1.¹¹ In the result we conclude that the rate of myosin conformational changes, the recovery and the reverse recovery strokes, are proportional to the cation ionic radius. The cation coordination number affects the rate of the nucleotide binding to and release from myosin and actomyosin. We found that actin activation of myosin ATPase is constant and does not depend on metal cation, suggesting that the mechanism of actin activation is different from the mechanism of myosin ATPase modulation by different metal cations. TR²FRET was a critical resource for the quantitative conclusions in this study, due to the resolution of TR²FRET technique to the mole fractions of myosin conformational states M* and M** during interaction with the nucleotide.

Figure 1.

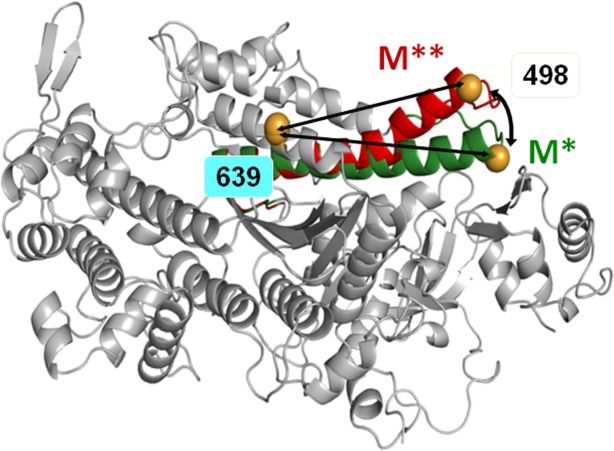
D.discoideum myosin head structural change during the recovery stroke. Overlay of crystal structures 1FMV (M*) and 1VOM (M**), showing bending of the relay helix. Spheres: engineered labeling sites, showing predicted shortening of distance between A639C and K498C (arrows) during the recovery stroke. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

Results

Myosin maintains the same pre- and post- recovery stroke conformations (M* and M**) upon interaction with magnesium-, manganese-, or calcium ATP complexes

Two FRET probes were attached to the designed labeling sites within myosin force generation region (Fig. 1). The FRET effect between the probes, allowing the interprobe distance measurement and therefore reflecting myosin structure in the force generation region, was virtually the same when myosin was rapidly mixed with Mg-, Mn-, or Ca.ATP. Measured interprobe distance was 4.1 ± 0.94 nm in the M* state and 3.1 ± 0.66 nm in the M** state.

Myosin intrinsic fluorescence reflects conformation of the force generation region

Change of myosin intrinsic fluorescence during its interaction with ATP reflects myosin conformational change.¹² Myosin head has several tryptophan residues, contributing to intrinsic fluorescence and potentially responsible for the change in the intrinsic fluorescence upon myosin interaction with ATP. The spectral response of these tryptophan residues is similar, so the information on the location of myosin conformational change is missing in the intrinsic fluorescence experiment.¹³ Single tryptophan studies^14–16 concluded that the main contribution to myosin fluorescence change comes from W501 (D. discoideum sequence), although single tryptophan W501 mutant showed unexpected initial decrease of intrinsic fluorescence.¹⁴ We have found that kinetics of myosin recovery stroke, measured with TR²FRET, agrees well with the kinetics of the intrinsic fluorescence (Supporting Information Fig. S1). This result directly confirms that intrinsic fluorescence reflects kinetics of myosin force generation region during the recovery stroke. The distinct advantage of TR²FRET is that it provides quantitative data on the mole fractions of the pre- and post-recovery stroke states M* and M**, in contrast to intrinsic fluorescence, measuring just changes in fluorescence intensity.

Metal cation controls the rate limiting step of myosin ATPase

Transients of myosin conformational change upon interaction with metal are shown in Figure 2. All metal cations support myosin ATPase activity, showing increase of M** population upon interaction with metal, and then decrease of M** population in the cases of Mn.ATP and Ca.ATP. Figure 2 shows that myosin reaches the steady state M** when mixed with Mg.ATP, reflecting that the reaction limiting step is the reverse recovery stroke and the phosphate release. In the presence of manganese the steady state M* is reached, showing that the reaction rate limiting step is the step after the reverse recovery stroke and the phosphate release. This could be the myosin—ADP isomerization or the ADP release, according to Scheme 1. Ca.ATP produces fast reached steady state of myosin at the level of ∼20% M**, indicating that Ca.ATPase cycle is fast and there is no distinct reaction rate limiting step, myosin spends 20% of the cycle time in the M** structural state. Transients, obtained at different ATP concentrations, were fitted to Scheme 1 with the set of differential equations [Eqs. (1,2)]. In the experiment we observe changes of myosin intrinsic fluorescence, or the change in the FRET effect (TR²FRET technique), therefore the direct information on the first two steps of myosin cycle in Scheme 1 is missing. Obtained transients (myosin-Mg.ATP, and initial parts of myosin-Mn.ATP and myosin-Ca.ATP transients) can be fitted to the single exponential function, showing that they reflect a single step reaction. We conclude that the first two steps of Scheme 1 (K₁K₂) are fast and cannot be resolved due to the dead time of our stopped flow units (2.4 ms and 2.6 ms). The fit of myosin-Mg.ATP transient with Eq. (1) (assuming step 4 the reaction limiting step), and subsequent fit of observed rate constants k_obs to the hyperbola to find maximum rate (see Materials and Methods) gives k_max = 20.2 ± 2.6 s⁻¹. This corresponds well to the maximal rate of fluorescence changes of another D.discoideum myosin construct,¹⁷ and associated with the rate of ATP cleavage k₊₃. We found that the backward rate is k₋₃ = 4.8 ± 3.9 s⁻¹. The fit of the same transients to the single exponential function and subsequent fit of the rates to the hyperbola produced V_max = 31.7 ± 3.9 s⁻¹, in good agreement with the fit to Eq. (1). Transients of myosin mixed with Mn.ATP and Ca.ATP require more reaction steps to be accounted for. According to the previous studies, the step 4 is practically irreversible,^11,18 the step 5 is fast¹¹ and irreversible, therefore the rate constant k₊₄ determines the rate of the reverse recovery stroke and the phosphate release. The rate constant k₋₆ and k₊₇ are fast,¹¹ therefore the state M.D is not populated. Assuming that the rate of ADP binding to myosin is the same as the rate of ATP binding,¹¹ and considering significant difference in ATP and ADP concentrations in the reaction, we do not expect M.D state be populated due to myosin-ADP association. Therefore, the transients of myosin mixed with Mn.ATP or Ca.ATP were fitted to Eq. (2), and the results are shown in Table I.

Figure 2.

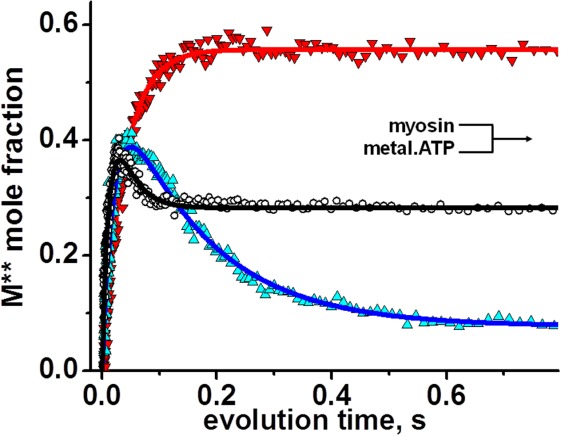
Kinetics of the post-recovery stroke M** structural state formation upon rapid mixing of myosin and metal.ATP. Magnesium, upturned triangles, manganese, triangles, calcium, circles, lines, fit. Mg.ATP shifts equilibrium towards M** state, Mn.ATP – towards M* state, indicating that Mn.ADP release is the rate limiting step. Myosin – Ca.ATP interaction produces fast equilibrium of M* and M**, depending on the forward and reverse rate constants. Concentrations after mixing, [ATP]=300 µM, [metal cation] = 3 mM, [myosin] = 0.4 µM. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

Table I.

The Rates of Kinetic Steps of Myosin ATPase Cycle (Scheme 1) With Metal.Nucleotide as a Ligand

Cation	Ionic radius, Angstroms	Coordination number	k+3, s−1 recovery stroke, forward rate	k−3, s−1 recovery stroke, backward rate	k+4, s−1 reverse recovery and Pi release	k+6, s−1 myosin.ADP isomerization and ADP release
Mg2+	0.72	6	20.2±2.6	4.8±3.9	0.25±0.03*	0.65±0.08**
Mn2+	0.83	6	58.3±11.6	4.7±5.0	8.6±0.7	0.85±0.17
Ca2+	1.0	7	67.6±15.8	22.0±7.3	22.4±2.6	16.9±4.1

^*The rate of basal ATPase, in assumption that the reverse recovery stroke and the phosphate release is the rate limiting step.

^**Data from ATP chase experiment.

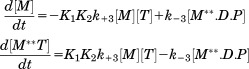(1)

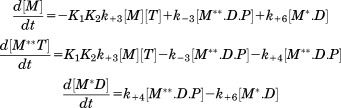(2)

The rate of Mg.ADP release from myosin was measured with the ATP chase experiment, when myosin pre-mixed with Mg.ADP was rapidly mixed with Mg.ATP, and the recovery stroke was observed. The rate constant k₊₆, reflecting Mg.ADP dissociation from myosin, is shown in Table I. The rates of Mn.ADP and Ca.ADP dissociation from myosin were determined from the fit of myosin-ATP transients. Omitting the step of ADP dissociation in the fit significantly decreases the fit quality.

ATP binding and ADP release from actomyosin depend on metal cation coordination number

The rates of metal.nucleotide binding to actomyosin were determined with the pyrene-labeled actomyosin, rapidly mixed with metal.ATP. Pyrene fluorescence was monitored to measure ATP-induced actomyosin dissociation (Fig. 3, left). Transients of pyrene fluorescence were fitted to the double exponential function. Fast exponential reflects ATP binding, and slow exponential reflects conformational change at the nucleotide binding site of myosin and subsequent actomyosin dissociation.¹⁹ Obtained rates of the fast component at small ATP concentrations were fitted to the straight line (Fig. 3, right). The second order reaction rate, determined from the slope of the line, shows virtually the same rate of Mg- and Mn.ATP binding to actomyosin (1.6 µM⁻¹ s⁻¹) and approximately four times lower rate for Ca.ATP binding (0.35 µM⁻¹ s⁻¹, Table II), indicating that ATP binding to actomyosin depends on the cation coordination number.

Figure 3.

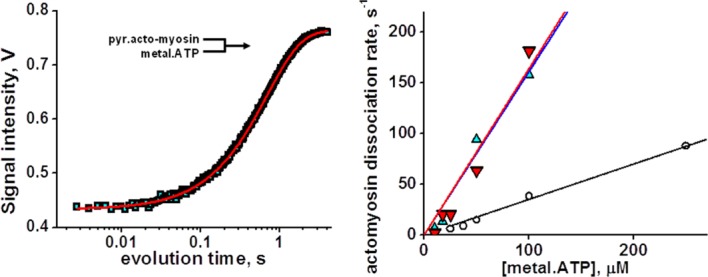
ATP-induced actomyosin dissociation. Left, pyrene fluorescence transient after rapid mixing of 50 µM ATP and 0.15 µM pyrene.acto-myosin, fitted with two exponents. Right, dependence of observed rate constants of actomyosin dissociation (fast exponential component) on ATP concentration. Magnesium, upturned triangles, manganese, triangles, calcium, circles, lines, linear fit. The second order reaction rate constant of actomyosin dissociation is determined from the slope of the line, 1.6 µM⁻¹s⁻¹ (magnesium and manganese), and 0.35 µM⁻¹ s⁻¹ (calcium). Slow exponential component represents [ATP] independent myosin isomerization, probably nucleotide pocket opening.²⁷ [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

Table II.

The Rates of Kinetic Steps of Actomyosin ATPase Cycle With Metal.Nucleotide as a Ligand

Cation	Ionic radius, Angstroms	Coordination number	Actin binding to myosin.ADP, µM−1 s−1	ATP induced actomyosin.ADP dissociation, µM	ATP induced actomyosin dissociation, µM−1 s−1
Mg2+	0.72	6	1.69 ± 0.13	16.7 ± 1.9	1.64 ± 0.16
Mn2+	0.83	6	1.29 ± 0.39	11.2 ± 1.6	1.71 ± 0.29
Ca2+	1.0	7	1.61 ± 0.26	34.1 ± 3.7	0.35 ± 0.01

ATP binding to pyrene-labeled actomyosin premixed with ADP reflects the affinity of ADP to actomyosin. Figure 4 shows normalized rates of ATP-induced actomyosin dissociation in the presence of different ADP concentrations and the fit to determine the rate of ADP dissociation from actomyosin, k'₊₆K'₇.²⁰ The asterisk indicates actin presence, and the scheme of the reaction is the same as Scheme 5, but with actin, bound to myosin. Figure 4 shows that affinity of Ca.ADP to actomyosin is 2–3 times weaker than affinities of Mg.ADP and Mn.ADP (Table II), indicating the dependence of ADP dissociation from actomyosin on the cation coordination number.

Figure 4.

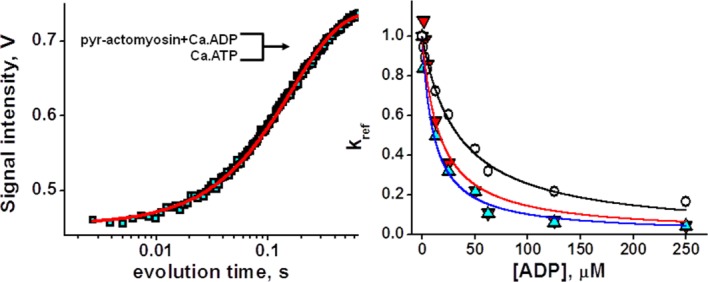
ATP induced actomyosin dissociation in the presence of ADP. Left, pyrene fluorescence transient after rapid mixing of 50 µM Ca.ATP and 0.15 µM pyrene-actomyosin, premixed, and incubated with 50 µM Ca.ADP. Fit with one exponent. Right, normalized rates of ATP induced actomyosin dissociation in the presence of ADP. Magnesium, upturned triangles, manganese, triangles, calcium, circles, lines, fit. Ca.ADP has weaker affinity to actomyosin, compared with Mg.ADP and Mn.ADP. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

Figure 5.

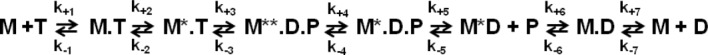
Myosin ATPase cycle. M - myosin; T - ATP; D - ADP; P - phosphate; M* - myosin in the pre-recovery stroke structural state; M** - myosin in the post-recovery stroke structural state.

Actin binding to myosin

ADP is not affected by metal cation. The rates of actin binding are similar and the dependence of the rates on ADP concentration are the same for magnesium-, manganese- and calcium-ADP complexes (Table II).

Actin activation of myosin metal ATPase

The rates of actin activated and basal myosin ATPase in the presence of magnesium, manganese, or calcium cations are shown in Table III and Figure 6. We were not able to obtain a good fit of actin activated Ca.ATPase rates with the standard Briggs-Haldane equation²¹ (see Materials and Methods). Addition of a constant term to the Briggs-Haldane equation significantly increased the fit quality (Supporting Information Figs. S4, S5). This constant term is interpreted as an admixture of the basal Ca.ATPase activity to the actin activated myosin ATPase activity. Both actin activated and basal ATPase rates depend linearly on metal cation radius, with virtually the same slopes, showing that actin activation does not depend on the size of metal cation, complexed with ATP. Apparently, actin directly affects myosin structural transition M** → M*, forcing myosin power stroke. The independence of actin activation on metal cation indicates that the mechanism of actin activation is different from the effect of metal cation (Mn and Ca), destabilizing myosin active site and thus inducing the reverse recovery stroke in myosin.

Table III.

The Rates of Myosin Basal and Actin Activated ATPase Activity With Metal.ATP as a Ligand

			Experimental data
Cation	Ionic radius, Angstroms	Coordination number	Basal ATPase, s−1	Actin activated ATPase, s−1	Actin activation, s−1	Km, Michaelis constant
Mg2+	0.72	6	0.25 ± 0.04	3.73 ± 0.36	3.48 ± 0.36	39.8 ± 7.3
Mn2+	0.83	6	1.19 ± 0.20	5.66 ± 0.20	4.46 ± 0.04	49.5 ± 13.1
Ca2+	1.0	7	3.86 ± 0.71	7.92 ± 0.75	4.06 ± 0.23	50.0 ± 33.0

Figure 6.

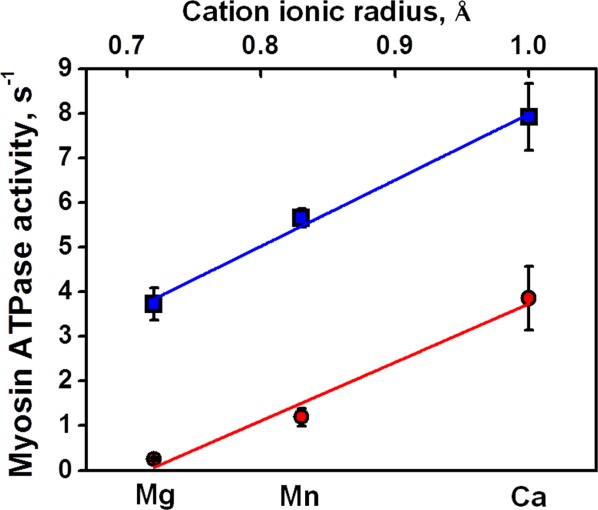
The rates of myosin metal.ATPases, basal, circles, and actin activated, squares. Fitting lines have the same slope, showing that the actin activation is the constant value and does not depend on metal cation. [Color figure can be viewed in the online issue, which is available at http://wileyonlinelibrary.com.]

Discussion

TR²FRET has two distinct advantages in transient kinetic measurements. First, the mole fraction of protein conformations is determined in the TR²FRET experiment. FRET effect is reciprocally proportional to the distance between donor and acceptor probes attached to the protein, and protein conformations are discriminated by the interprobe distance. FRET effect is proportional to the number of FRET donor-acceptor pairs (protein molecules), which allows determination of the mole fraction of each protein conformation. Second, TR²FRET allows localization of the transient conformational change within the molecule, due to known position of FRET donor-acceptor pair. These make TR²FRET a structural kinetics technique, in which determination of interprobe distance provides quantitative measure of molecular structure in transient experiment with millisecond time resolution.

Magnesium, manganese, and calcium, complexed with ATP, support myosin ATPase activity, showing that myosin is a nonspecific enzyme, binding, and hydrolyzing different metal.ATP complexes. The timing of myosin and actomyosin kinetics changes with different metal.ATP complexes, confirming that myosin and cross-bridge kinetics can be modulated. This opens up a possibility to modify myosin function directly, introducing changes in myosin's natural ligand, the metal nucleotide complex.

We found that the rate of myosin conformational change depends on the cation size. We suggest that the bigger cation at the active site destabilizes the salt bridge R238:E459 (D.discoideum sequence) between Switch I and Switch II loops,²² promoting faster phosphate release and thus increasing the rate of myosin conformational changes.

Kinetic rates of myosin ATPase cycle and the rate of basal ATPase activity

The rate of basal Mg.ATPase activity is slower than measured rates of Mg.ATP binding and the recovery stroke, and slower than the rate of Mg.ADP release, which allows assigning the rate of basal Mg.ATPase as the rate of the reverse recovery stroke and the phosphate release. The rate of myosin.Mn.ADP isomerization and Mn.ADP release corresponds well with the rate of basal Mn.ATPase, allowing assignment of Mn.ADP release as a rate limiting step. For calcium, all measured rates of myosin ATPase cycle are faster than the measured rate of basal ATPase. The rate of myosin basal Ca.ATPase is determined in the assumption that all myosin molecules perform ATPase cycle. To correlate our transient data and the steady state myosin Ca.ATPase results, we propose that not all myosin molecules participate in Ca.ATPase cycle. Then, the slowest kinetic step should limit myosin Ca.ATPase activity (myosin.ADP isomerization and ADP release, K₆K₇ = 17 s⁻¹). Normalization of the basal Ca.ATPase rate to the slowest kinetic step rate gives 20% myosin molecules, participating in the Ca.ATPase activity. This number corresponds well to the kinetic trace of Figure 2, showing reached equilibrium of Ca.ATPase at the level of ∼20% M**, indicating that in the any moment no more than 20% of myosin molecules are in M** structural state and the rest of them are in M* state.

Actin activation of myosin ATPase does not depend on metal cation, complexed with ATP

This indicates that the mechanism of actin activation has different nature than the mechanism of myosin ATPase rate modulation by metal cation. We propose that the bigger metal cation destabilizes myosin active site, which follows by faster release of products of hydrolysis and then initiating faster myosin conformational change. We propose that actin binding destabilizes myosin's pre-power stroke conformation and initiates the power stroke, followed by faster release of products of hydrolysis.

Our data suggest independence of actin activation and the modulation of myosin ATPase activity by metal cation. To account for this independence we modified the steady state Briggs-Haldane equation,²¹ similarly to the standard analysis of solute uptake for two independently operating uptake systems, where the solute concentration is the independent variable, and the measured uptake rate is the dependent variable. This approach allowed us fitting all ATPase activity experimental data within one model, assuming simultaneous basal and actomyosin ATPase activities. The independence of mechanisms of myosin ATPase activation allows estimation of the probability of actomyosin futile cycle as the ratio of V_basal and V_total (V_total = V_basal + V_max, where V_max is the maximum rate of actin activated myosin ATPase). Then, for Mg.ATP it is V_basal/V_total = 5.9%, Mn.ATP – 22.9%, and Ca.ATP – 49.1%. Manganese and calcium ATP complexes increase the rate of actomyosin ATPase cycle, but make it less efficient in terms of the force production.

Conclusions

We have found that metal cation controls the rate limiting step of myosin ATPase. It is the reverse recovery stroke and the phosphate release for magnesium, myosin.ADP isomerization and ADP release for manganese and the absence of well defined reaction limiting step for calcium. Actin binding to myosin.ADP and actin activation of myosin ATPase do not depend on metal cation complexed with ATP. The rate of myosin conformational changes upon interaction with nucleotide depends on the ionic radius of metal cation. The rate of nucleotide binding to and dissociation from myosin and actomyosin depends on metal cation coordination number.

Materials and Methods

Myosin preparation and labeling

A639C:K498C mutant of D. discoideum myosin motor domain (Fig. 1) was constructed and purified as described previously.^10,23 For FRET measurements protein was labeled in two steps. First, 50 µM myosin was incubated with 25 µM donor (IAEDANS) for 12 h on ice, then protein was diluted to 25 µM and incubated with 100 µM acceptor (DABCYL). After final labeling step, unreacted label was removed with Zeba size-exclusion spin columns (Pierce) and labeled myosin was centrifuged at 100,000g for 40 min to remove possible aggregates. Concentration of unlabeled myosin was determined spectrophotometrically assuming extinction coefficient A280nm = 0.69 (mg/mL)⁻¹cm⁻¹.²⁴ Concentration of labeled myosin was determined with Bradford assay (BioRad). The experimental buffer contained 20 mM MOPS pH 7.5, 50 mM KCl, 0.2 mM EDTA, 0.2 mM EGTA.

Actin preparation and labeling

Actin was prepared from rabbit back and leg muscles as described previously²⁵ in G-buffer (5 mM MOPS pH 7.5, 0.2 mM CaCl₂, 0.5 mM ATP), polymerized with 2 mM MgCl₂ for 30 min at room temperature, labeled with pyrene (8:1 label:actin molar ratio) overnight at T = 4^°C. Then labeled actin was centrifuged one hour at 200,000g at T = 4^oC, the pellet was homogenized in G-buffer, and the solution was centrifuged 1 h at 200,000g at T = 4^oC. Then collected G-actin was polymerized with 2 mM MgCl₂, and centrifuged 1 h at 200,000g at T = 4^oC. The pellet was resuspended in F-buffer (5 mM MOPS pH 7.5, 2 mM MgCl₂, 0.2 mM ATP), phalloidin was added in molar ratio 1.1:1 phalloidin:actin, and the solution was dialyzed overnight at T = 4^oC against experimental buffer. Concentration of unlabeled actin was determined spectrophotometrically assuming extinction coefficient A290 nm = 0.63 (mg/mL)⁻¹cm⁻¹.²⁶ Concentration of labeled actin was determined with the Bradford assay (BioRad).

ATPase assays

Myosin ATPase activity was measured at T = 25°C in the experimental buffer with 5 mM ATP and 5 mM metal cation (MgCl₂, or MnCl₂, or CaCl₂) in the presence and absence of actin, by the liberation of inorganic phosphate.²⁷ Myosin or actomyosin were mixed with metal.ATP and aliquots were collected in equal time intervals and analyzed for phosphate by adding ammonium molybdate–malachite green solution and quenching the reaction with sodium citrate. All added solutions contained 1N HCl for stable color formation. The absorption of the resulting mix at 620 nm is proportional to phosphate concentration. To quantify phosphate production in the hydrolysis reaction, the obtained myosin and actomyosin data were compared with the data of the same reaction, performed with the phosphate standard of known concentration. To determine the maximum velocity of the actomyosin ATPase, the data were fitted to the modified Briggs-Haldane equation v = V_basal + V_max[actin]/(K_m +[actin]), where v is the rate of the ATPase in the presence of actin, V_basal is the rate of myosin ATPase without actin, V_max is the rate of myosin ATPase at infinite actin concentration, and K_m is the Michaelis constant. The modification of the Brigg-Haldane equation accounts for possible basal ATPase activity of myosin in the presence of actin. Determined basal and actin activated myosin Mg.ATPase rates were comparable to values reported for other D. discoideum myosin constructs.^18,28–31

Transient time resolved FRET was measured with the home built transient fluorimeter, based on Applied Photophysics SX-18 stopped flow unit, equipped with passively Q-switched microchip YAG laser (SNV-20F-100, Teem Photonics, 355 nm, 20 kHz), photomultiplier (H6779-20, Hamamatsu), and fast digitizer (Acqiris DC252, Agilent). Dead time of the mixing unit is 2.6 ms. All experiments were done at T = 20^oC. FRET pair labeled myosin was rapidly mixed with metal.ATP solution, and donor fluorescence was acquired after each laser pulse with the picosecond resolution. Multiple traces were usually acquired and averaged to increase signal to noise ratio. The analysis of transient time-resolved luminescence data was performed using software package FargoFit, designed by I. Negrashov, executing global least-square fitting of multiple time-resolved luminescence waveforms using different models with ability to link fitting parameters between waveforms. The analysis of the donor lifetime in terms of myosin structural conformations M* and M**, pre- and post-recovery stroke states, is described in the Supporting Information Material.

Transient myosin intrinsic fluorescence and pyrene actin fluorescence was measured with Bio-Logic SFM-300 stopped flow transient fluorimeter, equipped with FC-15 cuvette. The mixing unit dead time is 2.4 ms. All experiments were done at T = 20^oC. Two or three syringes (one or two mixers) were used depending on the experiment. Myosin intrinsic fluorescence was excited by mercury-xenon lamp at 302 nm, and detected using 320 nm cutoff filter. Pyrene fluorescence was excited at 365 nm and detected using 420 nm cutoff filter. Multiple traces were usually acquired and averaged to improve signal to noise ratio. Maximum number of points was acquired in all experiments (8000 points) and then experimental points were selected according to the logarithmic scale to reduce fitting time.

Analysis of transients

Transients of myosin conformational change were measured by rapid mixing of myosin (0.8 µM in intrinsic fluorescence, and 10 µM in TR²FRET, syringe concentrations) and ATP of variable concentrations. TR²FRET transients were fitted to the set of differential equations [Eqs. (1), (2)] according to Scheme 1. In the result, the rate constants K₁K₂k₊₃ (K₁K₂k₊₃ ·[ATP]=k₊₃) and k₋₃ for myosin-Mg.ATP transients, and k₊₃, k₋₃, k₊₄, k₊₆K₇ for myosin-Mn.ATP and myosin-Ca.ATP transients were determined. Kinetics of myosin intrinsic fluorescence transients and pyrene-actin transients were fitted to the single S(t) = S_o+A·exp(-k_obs·t), or double exponential function S(t) = S_o+A₁·exp(-k_obs1·t) + A₂·exp(-k_obs2·t), where S(t) is the observed signal at time t, S_o is the final intensity of a signal, A is the signal amplitude, and k_obs is the observed rate constant. The dependence of observed rates (v) on the nucleotide concentration was fitted to the hyperbola v = V_max[ATP]/(K_m +[ATP]), according to the steady state approach,²¹ allowing determination of V_max, maximum kinetic rate, and Michaelis constant K_m.

The rate of ATP-induced myosin.ADP dissociation was determined from the experiments where 0.8 µM myosin was initially incubated with ADP of variable concentrations and then rapidly mixed with 600 µM ATP (syringe concentrations). Myosin intrinsic fluorescence transients (Supporting Information Fig. S3) were measured, their intensities were normalized to TR²FRET data to determine M** fraction, and then fitted to the Scheme 1. Reaction rates k₊₆, obtained for different ADP concentrations were averaged.

Competitive inhibition of ATP-induced actomyosin dissociation by ADP was measured with pyrene-actin, complexed with myosin, and incubated with ADP of variable concentrations. This solution was rapidly mixed with ATP (50 µM, syringe concentration) and the transient of pyrene-actin, dissociated from myosin was measured. Transients were fitted to the single exponential function. The observed reaction rates were normalized to the value of the observed rate in the absence of ADP, k_res = k_obs/k_{obs, [ADP]=0} and fitted to the equation k_res = 1/(1+[ADP]/ (k'₊₆K'₇)),^19,20,32 assuming that ATP binding to actomyosin is fast. Here k'₊₆K'₇ is the rate of ADP dissociation from actomyosin. The asterisk indicates actin presence, and the scheme of the reaction is the same as Scheme 1, but with actin, bound to myosin (A.M*.D↔A.M.D↔AM+D).

Differential equations were solved numerically and the solution was fitted to the transients using the Differential Evolution algorithm, realized in Wolfram Mathematica software suite. We used 10,000 search points, scaling factor 2, and cross probability 0.8. Each transient was fitted several times, starting with different initial conditions to be sure that global minimum is found during the fit.

Glossary

TR²FRET

transient time-resolved FRET

Supplementary material

Additional Supporting Information may be found in the online version of this article.

Supplementary information