Abstract
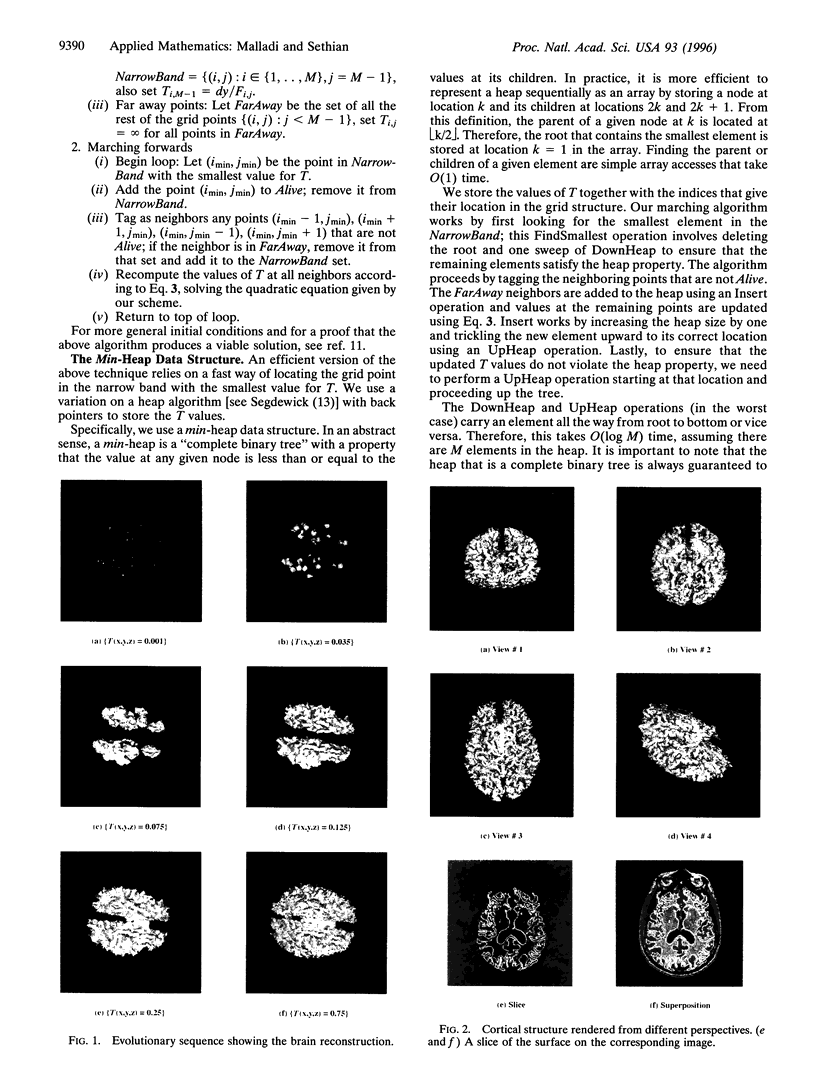
We present a shape-recovery technique in two dimensions and three dimensions with specific applications in modeling anatomical shapes from medical images. This algorithm models extremely corrugated structures like the brain, is topologically adaptable, and runs in O(N log N) time, where N is the total number of points in the domain. Our technique is based on a level set shape-recovery scheme recently introduced by the authors and the fast marching method for computing solutions to static Hamilton-Jacobi equations.
Full text
PDF


Images in this article
Selected References
These references are in PubMed. This may not be the complete list of references from this article.
- Malladi R., Sethian J. A. Image processing via level set curvature flow. Proc Natl Acad Sci U S A. 1995 Jul 18;92(15):7046–7050. doi: 10.1073/pnas.92.15.7046. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sethian J. A. A fast marching level set method for monotonically advancing fronts. Proc Natl Acad Sci U S A. 1996 Feb 20;93(4):1591–1595. doi: 10.1073/pnas.93.4.1591. [DOI] [PMC free article] [PubMed] [Google Scholar]