Repopulation of interacting tumor cells during fractionated radiotherapy: Stochastic modeling of the tumor control probability

Abstract

Purpose: Optimal treatment planning for fractionated external beam radiation therapy requires inputs from radiobiology based on recent thinking about the “five Rs” (repopulation, radiosensitivity, reoxygenation, redistribution, and repair). The need is especially acute for the newer, often individualized, protocols made feasible by progress in image guided radiation therapy and dose conformity. Current stochastic tumor control probability (TCP) models incorporating tumor repopulation effects consider “stem-like cancer cells” (SLCC) to be independent, but the authors here propose that SLCC-SLCC interactions may be significant. The authors present a new stochastic TCP model for repopulating SLCC interacting within microenvironmental niches. Our approach is meant mainly for comparing similar protocols. It aims at practical generalizations of previous mathematical models.

Methods: The authors consider protocols with complete sublethal damage repair between fractions. The authors use customized open-source software and recent mathematical approaches from stochastic process theory for calculating the time-dependent SLCC number and thereby estimating SLCC eradication probabilities. As specific numerical examples, the authors consider predicted TCP results for a 2 Gy per fraction, 60 Gy protocol compared to 64 Gy protocols involving early or late boosts in a limited volume to some fractions.

Results: In sample calculations with linear quadratic parameters α = 0.3 per Gy, α/β = 10 Gy, boosting is predicted to raise TCP from a dismal 14.5% observed in some older protocols for advanced NSCLC to above 70%. This prediction is robust as regards: (a) the assumed values of parameters other than α and (b) the choice of models for intraniche SLCC-SLCC interactions. However, α = 0.03 per Gy leads to a prediction of almost no improvement when boosting.

Conclusions: The predicted efficacy of moderate boosts depends sensitively on α. Presumably, the larger values of α are the ones appropriate for individualized treatment protocols, with the smaller values relevant only to protocols for a heterogeneous patient population. On that assumption, boosting is predicted to be highly effective. Front boosting, apart from practical advantages and a possible advantage as regards iatrogenic second cancers, also probably gives a slightly higher TCP than back boosting. If the total number of SLCC at the start of treatment can be measured even roughly, it will provide a highly sensitive way of discriminating between various models and parameter choices. Updated mathematical methods for calculating repopulation allow credible generalizations of earlier results.

INTRODUCTION

Current treatment planning

Modern technological developments for fractionated external beam radiotherapy include IMRT (intensity modulated radiation therapy), IGRT (image guided radiation therapy), and SBRT (stereotactic body radiation therapy).¹ Such techniques allow planning and efficient delivery of very conformal treatments as well as escalated doses to appropriate volumes, and therefore offer new versatility in treatment strategies. Nonhomogeneous dose distributions and nonuniform dose fractionations are becoming more common. Due to the wide spectrum of emerging protocols and to the substantial time-lag between treatment and the availability of data on outcomes, radiotherapy treatment planning needs ongoing new inputs from radiobiology. Inputs on tumor control probability (TCP) are based on modern versions (reviewed in Ref. 2) of the “five Rs” of radiobiology, including repopulation.

TCP and stochastic tumor repopulation during radiotherapy

It has been known since the seminal research of Tucker and co-workers^{3, 4, 5} that tumor repopulation during treatment must often be considered in quantitative estimates of TCP, may have to be estimated stochastically, and should then take into account non-Poisson statistics of malignant cell numbers. Stochastic estimates can take eradication of cells into account more systematically than can deterministic ones. Prospective estimates of repopulation are especially important for novel protocols. Reviews of the mathematical, computational, and translational aspects of stochastic and deterministic TCP estimates taking into account repopulation include.^{6, 7, 8} Repopulation models indirectly incorporate some aspects of reoxygenation (reviewed in Ref. 9).

Stochastic estimates involve a mathematical/computational approach to repopulation that uses “stochastic processes” (also known as “random processes”); roughly speaking a stochastic process is a time-dependent variable that is subject to random fluctuations;¹⁰ in stochastic TCP analyses it can be specified by a time-dependent probability distribution function for malignant cell number. A stochastic-exponential process applicable to proliferating, noninteracting cells (the Feller-Arley birth-death process with time dependent, state-independent per-cell rates, as characterized, e.g., in Ref. 11, Example 4.1) has been studied for more than 70 years.¹² It has been applied, as an extension of the previously standard deterministic-exponential equation, to TCP estimates.^{3, 6} It leads to a front-loading theorem:¹³ other things being equal, giving dose earlier increases the TCP.

Interactions of stem-like cancer cells (SLCC)

For TCP estimates the relevant repopulating tumor cells in a heterogeneous tumor are those that can individually regrow the entire tumor population when in the appropriate microenvironment. Such cells are sometimes called stem-like cancer cells;¹⁴ we use SLCC for short in what follows. However, in this context no additional “stem” properties are implied¹⁵ and various other terms have been used (e.g., “clonogens”^{8, 16}).

Previous stochastic TCP models have assumed independent, i.e., noninteracting, SLCC. However, cell-cell interactions are ubiquitous in vivo,¹⁷ and there is increasing evidence that tumors include microenvironmental niches within which important SLCC-SLCC interactions occur.¹⁸ A niche can be an actual biological structure, such as a crypt in the case of colon cancer;¹⁹ or be a locale for radio-resistant clones;²⁰ or it may merely approximate low cell mobility with dominant cell-cell interactions localized.

Preview

This paper develops a new radiobiologically based formalism for analyzing repopulation of interacting SLCC. The formalism emphasizes subpopulations of SLCC, each within its own niche,²¹ rather than individual SLCC. The niches are visualized as comparatively distant from each other. Generalizing the stochastic-exponential model described above and its deterministic counterpart, all kinds of LSCC-LSCC interactions are allowed, though only among SLCC within the same niche (Fig. 1).

Figure 1.

Niches and intercellular interactions. SLCC are shown as small red ellipses separated into two different niches (yellow circles).

Interactions within one niche are comparatively easy to model because the number of SLCC per niche is comparatively small. Interactions among SLCC in different niches are assumed negligible.

The following ten comments preview motivations, characteristic aspects, and limitations of our approach.

• 1.The niche model is here illustrated with mathematical examples motivated by our recent and prospective SBRT dose boosts to the gross tumor volume in standard NSCLC (non-small-cell lung cancer) treatments. Such boosts were found to be feasible, in agreement with Ref. 22.
• 2.The main example of the new formalism is summarized in Table 1. It tracks intraniche SLCC proliferation between dose-fractions using a stochastic-logistic process, as defined and motivated in example 4.1 of Ref. 11.
• 3.This process is a probabilistic version of the deterministic-logistic equation. As reviewed, e.g., in Ref. 23 the deterministic-logistic equation: (a) incorporates intercellular interactions such as competition for limited microenvironmental resources by assuming that per-cell net birth rate decreases with increasing cell number; (b) implies sigmoid (“S-shaped”) repopulation curves that approach a maximum value (the “carrying capacity”) at large times; (c) has simple explicit solutions; and (d) is very widely applicable. Equation S1 of the supplementary material reviews this and two other relevant deterministic equations using a notation corresponding to that in our main example.⁴⁴
• 4.For reasons argued in Refs. ²⁴ and ²⁵ and to facilitate comparisons with standard results in the literature, the linear-quadratic (LQ) equation is used for average SLCC survival at each dose fraction. Generalizations are discussed in Sec. S2 of the supplemental material.⁴⁴
• 5.The main example uses specific parameter values, given in Table 1 and motivated below that table. To check robustness of the resulting conclusions 14 auxiliary examples were considered. Ten of these merely alter the parameters of the main example, e.g., use α = 0.03 Gy⁻¹ instead of α = 0.3 Gy⁻¹, while four relate to robustness relative to change in model. Twelve are stochastic and two are deterministic.
• 6.The number of SLCC within one niche is not assumed to follow a Poisson distribution, but the number of SLCC-occupied niches per patient just before treatment starts is. A corresponding mathematical technique is called “poissonization” (reviewed in Ref. 26) and has become common in probability theory because it simplifies many calculations and/or adds to the realism. The Poisson assumption on initial niches per patient is at least as reasonable as an alternative assumption, often made (explicitly or implicitly) that, after stratifying for age, gender, nationality, and cancer stage, all grouped patients have exactly the same number of SLCC before treatment starts.
• 7.Niche time evolution obeys “IID” (independent, identically distributed) assumptions. For example, it is assumed that the probability distribution function for the number of SLCC per niche just before radiation starts is the same for all niches. The IID assumption does not imply that all the SLCC niches initially have the same number of SLCC, just the same probabilities. Also, two niches that happen to have the same number of SLCC at some given time need not always continue to have the same number, but the SLCC in both niches have the same birth and death rates at that particular time. The IID assumption for niches is more general than the corresponding assumption usually made for individual SLCC because SLCC within a niche need not be independent.
• 8.When giving illustrative numerical results, we will, as is often done, take TCP as the probability that all SLCC have been eradicated (due to either radiation or stochastic fluctuations) at a specified time; generalizations are mentioned in item 10. For our stochastic niche models we will take the time as 23 days (a weekend plus 3 weeks) after the end of therapy. Here the specific number 23 days is chosen for three main reasons: (a) it is short enough that long-term processes^{8, 27} such as microscopic tumor dormancy^{28, 29} have not yet had time to set in; (b) it is long enough that for our stochastic sigmoid niche calculations it gives the same numerical TCP (to within less than 0.1%) as does artificially extending the calculations to periods too long to be within their domain of validity; and (c) it corresponds roughly to an actual recovery period observed clinically.
• 9.Our approach is meant mainly for comparing similar but somewhat different protocols.
• 10.It uses a number of intentional oversimplifications and has a number of limitations, though not, we would argue, more than similar approaches. Examples of limitations include the following: (a) the TCP criterion just described above glosses over various possibilities, e.g., complete remission without SLCC eradication, and it circumvents modeling of long-term processes; (b) we do not here attempt to give novel mathematical results on the other four Rs, on early or late deterministic normal tissue complications, or on iatrogenic second cancers. These aspects will be briefly discussed, but without quantifications.

Table 1.

Notation, descriptions, default values, and pointers to definitions or explanations.

Symbol	Descriptive phrase	Default value	More details
dk,D	Dose in the kth fraction, total dose D = Σkdk	dk = 2 Gy, D = 60 Gy	Eqs. 1, 2
K	Number of dose fractions	30	Fig. 2
Tk	Time t of the kth fraction, with T1 = 0.	30 weekdays	Fig. 2
t = 0−	Time just before the first fraction	Slightly less than 0	Fig. 2
t = TK+	Time just after the last fraction	39 days	Fig. 2
t = TK+1	End of recovery period	62 days	Fig. 2
α	Linear quadratic (LQ) parameters	0.3 Gy−1	Eqs. 1, 2
β		α/(10 Gy)	Eqs. 1, 2
S(k)	Average clonogenic cell survival for the kth fraction	Calculated with LQ	Eqs. 1, 2
J(t)	Number of SLCC per niche at time t, a stochastic process with non-negative integer values	Stochastic-logistic with default parameters	Eq. 3
J(0−)	J(t) just before treatment starts	Binomially distributed	Eq. 4
J	Average of J(0−)	10 SLCC per niche	Below Eq. 4
N(t)	Number of nonempty SLCC niches, a stochastic process	Calculated	Above Eq. 5
N	Average of N(t) just before treatment starts	Calculated	Eq. 5 and below
n0	Average initial SLCC number: n0 = NJ	Calculated	Below Eq. 5
C	Carrying capacity (maximum number of SLCC per niche)	20 SLCC
b(j)	Birth rate when a niche contains j SLCC	Calculated from m, σ, and C	Preliminary comments above,
d(j)	“Endogenous” death rate1 when a niche contains j SLCC		Subsection 1E,
m	b1-d1 “Malthusian” rate	ln(2)/(3 days)
σ	d/b ratio	0.5	Eq. 4

¹Applies between fractions, and also after the last fraction before recovery ends.

Explanations of and motivations for the default parameter values in Table 1

The 60 Gy protocol is one that was used^{30, 31} in NSCLC treatments that gave a (dismal) TCP of 14.5%. The LQ parameters are consensus values for an individual patient (e.g., Ref. 32). Smaller values of α are used in calculations intended to model the shape of the TCP vs dose curve near TCP₅₀ for a heterogeneous patient population³³ so two of our auxiliary examples will use α = 0.03 per Gy instead. The default value of the (one-cell) Malthusian rate m corresponds to a commonly adopted minimum doubling time of 3 days (e.g., Ref. 34). The binomial distribution for J(t) before treatment starts, the value J = 10, and the value C = 20 of the carrying capacity are merely illustrative; several auxiliary models will be used to estimate the sensitivity of the conclusions to varying these values. Finally, the biological motivation for assuming a substantial default endogenous death rate (σ = 0.5) is the observed high cell loss in pulmonary tumors (e.g., Refs. ³⁵ and ³⁶).

The parameter σ is a quantity with no real analogue in deterministic models. It can be interpreted as follows:³⁷ if net endogenous birth rate b-d is fixed, σ = 1 corresponds to a highly stochastic situation such as neutral drift for SLCC population number between fractions, while σ = 0 usually gives results much closer to a corresponding deterministic model with b-d as growth rate. Four of our auxiliary examples will explore the effects of changing σ compared to its default value 0.5.

METHODS

Fractionated radiotherapy

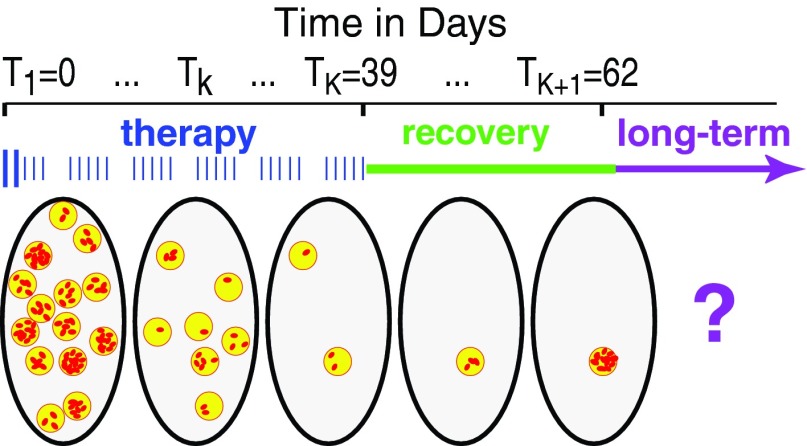
We consider throughout a multiweek protocol of K dose fractions, administered at times T₁ = 0, T₂, …, T_K so far apart that complete sublethal damage repair occurs between fractions. The respective doses, which can be different for different fractions, are denoted by d_k and the total dose is denoted by $D={\sum }_{k=1}^K{d}_k$. For example, Fig. 2 shows a protocol with front boosting of dose.

Figure 2.

Therapy timing. Schematic figure shows developments in one patient's tumor volume (large ellipses, five different snapshots shown). Before therapy starts there are many SLCC (red dots), grouped into niches (yellow circles). Shown is a protocol where 30 weekday fractions are given: two boosted fractions followed by 28 normal ones.

During therapy, SLCC are killed by radiation but also repopulate. On average the SLCC number per niche decreases markedly, as indicated. Most SLCC niches will be cleared of SLCC during treatment, indicated here by omitting such “eradicated” niches. If all niches are eradicated, the tumor is controlled. Otherwise, remaining SLCC niches may die out accidentally after therapy during a recovery period. During recovery there could also be an increase in the number of SLCC per niche, as shown. If some SLCC remain, the outcome during the following months and years (indicated as “long term”) could be recurrence, but could also be different, e.g., formation of tumors that are dormant, microscopic, and thus asymptomatic.^{28, 29} Long-term processes are not analyzed in this paper.

We define S(k) as the LQ cell survival probability for the kth fraction:

$$S\left(k\right)=\exp \left[-\alpha d_k-\beta d_k^2\right],\alpha >0,\beta \ge 0.$$ (1)

If there are j SLCC present just before the kth fraction the probability of having i SLCC present just after is thus

$$\begin{array}{ccc}& & \mathrm{Binomial}[j,i,S\left(k\right)]=\frac{j!{\left[S\left(k\right)\right]}^i{\left[1-S\left(k\right)\right]}^{j-i}}{i!(j-i)!},\hfill \\ & & (i,j=0,1,...,C).\hfill \end{array}$$ (2)

We can and shall regard this expression as a square matrix with rows labeled by i and columns labeled by j. It is a “stochastic” and “triangular” matrix (i.e., each row sum is 1 and the (i,j) entry is 0 if i > j).

Customized computer programs

Subsection 2C describes calculations for our main example. Those for the 14 auxiliary examples were similar. Computer calculations used the R language. Section S1 of the supplementary material gives open source R scripts which can be used to reproduce the main calculations.⁴⁴

Time evolution of SLCC

For repopulation between fractions or after treatment stops, the assumptions stated and motivated in the Introduction imply the following for the main example, i.e., for the stochastic-logistic process with the default parameter values in Table 1.

• (a)
  When j SLCC are present in a niche, the endogenous birth b and death d rates are

  $$\begin{array}{c}\hfill b\left(j\right)=\frac{m(C-j)j}{(1-\sigma )(C-1)}\mathrm{and}d\left(j\right)=\sigma b\left(j\right).\end{array}$$ (3)
• (b)
  The probability distribution of SLCC number in one niche just before treatment starts is

  $$\begin{array}{ccc}& & p\left(j\right)=\mathrm{Binomial}(C,j,0.5)=\frac{C!{\left(0.5\right)}^C}{(C-j)!j!}\hfill \\ & & \mathrm{so}\mathrm{that}J\equiv {\sum }_1^{C}jp\left(j\right)=C/2.\hfill \end{array}$$ (4)
• (c)The specific numerical values are C = 20, m = ln(2)/3 per day, and σ = 0.5.

Using Eqs. 3, 4 we integrated 20 ordinary differential equations (ODE) numerically 20 times to construct a 21 × 21 repopulation matrix, which in the jth row gives the probability distribution for ending one interfraction day with i SLCC (i = 0, 1, …, 20) given that the day started with j SLCC. We then used this repopulation matrix, the survival matrix given by Eq. 2, and a day-by-day iteration to find the probability P[J(62) = 0] that a niche has no SLCC at the end of the recovery period (Fig. 2). This matrix approach was spot-checked with Monte Carlo simulations.

These calculations and poissonization allowed calculation of (a) the average initial number of SLCC per patient (n₀ in Table 1) from data on the default protocol and (b) the TCP for boosted protocols, given this calculated n₀.

RESULTS

Results on examples

Recall the following: (a) our “default” protocol is 30 weekday doses of 2 Gy each and by adjusting parameters is assigned the 14.5% TCP found in some NSCLC studies;^{30, 31} (b) our “illustrative TCP criterion” is that there are no SLCC at day 62 (Fig. 2); and (c) our “main” example of niche dynamics during periods of no radiation is a stochastic-logistic process with the default parameters in Table 1.

In our main example, the basic Poisson color theorem,¹⁰ that a random thinning of a Poisson process is a Poisson process, implied that under our assumptions the number of nonempty malignant niches N(t) per patient remains Poisson distributed at all times, in contrast to the number of SLCC per niche. The mean of N(t) is the initial mean N times the probability that J(t) ≠0. Using our criterion that TCP is given by the Poisson zero class thus gave

$$\mathrm{TCP}=\exp [-Nq],$$ (5)

where q is the probability that a niche has at least 1 SLCC at time T_K+1.

Equation 5 applied to the default protocol gave N ∼ 5.2 × 10⁵. Using this N in 64 Gy front or back loaded protocols gave row 1 in Table 2, where Front2 and Back2 denote two fractions each boosted from 2 to 4 Gy at the very start or very end, respectively.

Table 2.

Calculated TCP and calculated initial SLCC number n₀.

		Protocol or number
	Model	Default	Front2	Back2	n0/1000
1	Main: default parameter values in Table 1; stochastic-logistic	14.5%	72.8%	70.7%	52071
2	Deterministic-exponential2	14.5	75.3	75.3	566
3	Main but σ = 0.9	14.5	73.3	72.0	194 500
4	Main but σ = 0	14.5	72.7	70.3	1650
5	Main but σ state dependent: d(j)/b(j) = 0.5 ± 0.05× (j − 10)	14.5	71.2	70.6	2990
6		14.5	76.6	74.9	8 331 052
7	Main but deterministic	14.5	72.2	75.3	681
8	Main but C = 200, J = 100	14.5	72.3	69.6	2170
9	Main but J = 20	14.5	70.8	70.7	1475
10	Main but delayed repopulation	14.5	75.3	70.7	18 461
11	Main but m = ln(2)/(10 days)	14.5	74.7	74.0	687 739
12	Main but α = 0.03, β = α	14.5	15.2	14.9	0.034
13	Main but α = 0.03, β = α/10	14.5	15.2	14.8	0.020
14	Stochastic-exponential2	14.5	75.3	69.4	1500
15	Stochastic-Gompertz2	14.5	71.3	71.7	20 600

¹That is, n₀ = JN = 10N ∼ 5 207 000.

²Default parameters used.

Calculations for 14 auxiliary examples were similar. The results are shown in rows 2–15 of Table 2. For all sigmoid stochastic examples, (i.e., all rows except 2, 7, and 14):

• (a)the extinction probability at day 62, here used to calculate TCP, was not substantially different from the nominal large-time limit;
• (b)a majority of the nonempty niches were completely full after the 23 day recovery period.

Section S1 of the supplementary material gives open-source R scripts for, and intuitive interpretations of, Table 2.⁴⁴

More detailed results on time dependence

In all 13 stochastic examples, the probability distribution of SLCC per niche differed strongly from a binomial or Poisson distribution even after <10 dose fractions—for example, the surviving fraction was much smaller than for a Poisson distribution of the same mean.

It was found that the niche model can give fully detailed time-dependent results. As one specific example, consider the following procedure for estimating with any of the stochastic examples the probability that, say, a patient has exactly M niches that contain exactly j SLCC at a particular time <62 days. By the Poisson color theorem this probability is

$${\left(Np\right)}^M\exp (-Np)/\mathrm{M}!.$$ (6)

Here p is the probability that a niche has exactly j SLCC at the given time, calculated from the niche dynamics as described in Sec. 2.

It was also found that the special case where each niche starts out with exactly one cell and the niche-dynamics is stochastic-exponential gives stochastic-exponential dynamics, corresponding to noninteracting SLCC, for the SLCC population as whole. Section S3 of the supplementary materials analyzes some previously known TCP results^{3, 6, 13} obtained assuming such dynamics, thereby supplying some additional mathematical and intuitive explanations of the results shown in Table 2.

DISCUSSION

Review

We argued that biologically based prospective TCP estimates, though difficult, are needed. A mathematical niche model was given for estimating TCP. The calculations emphasized: (a) intercellular interactions during tumor repopulation, (b) stochastic effects, (c) comparing similar individualized protocols, and (d) illustrative numerical examples.

Effectiveness of moderate boosting

For α = 0.3 per Gy, Table 2 shows that modest boosts are predicted to be very effective, with an extra 4 Gy improving TCP from 14.5% to >70% irrespective of the particular model or the other parameters. We suggest that the contrary result predicted by assuming α = 0.03 per Gy (rows 12 and 13 in Table 2) is not applicable to individually designed protocols for two reasons. First, these small values of α are estimated not from the average of heterogeneous patient α values but as a formal consequence of the effect of heterogeneity in flattening the observed TCP₅₀ slope.³³ Second, the small values of initial SLCC number predicted, 20 for row 12 and 34 for row 13, are not plausible. For example, if, as has been suggested,³⁸ >1% of all NSCLC cells are SLCC, then the initial number of SLCC must be >1 000 000, rather than 34.

Additional comments on Table 2

Table 2 shows that if n₀ can be estimated from separate, biological data it becomes a highly sensitive way to select preferred models and/or appropriate parameters; for example, when the assumed value of α is decreased by one log as above, the resulting estimate of initial SLCC number decreases by more than five logs. In the present context, n₀ in Table 2 serves as an indicator of how effectively SLCC are eradicated: higher effectiveness means more initial SLCC must be present to lead to 14.5% survival for the default protocol. Proliferation is predicted to have a marked effect on loss of control, as exemplified, e.g., by the greater n₀ in row 11 vs row 1. Thus unplanned interruptions are, as usual, deprecated.

Front boosting is slightly favored over back boosting in most models. A different consideration that favors front boosting is that often treatment is preceded by a positron emission tomography scan and the location of the gross tumor volume is more accurately known at the start of the treatment than during later fractions.

Parsimony

Equations 1, 3, 4, 5 imply that our main model uses the following adjustable parameters: α, β, m, σ, C, and n₀ = JN. For comparison, the only previously used stochastic model, the stochastic-exponential (Feller-Arley) model, uses all of these except C. The deterministic-exponential equation for the time evolution of the average SLCC number, which has long been the mainstay of TCP estimates, uses all but C and σ. Thus this paper introduces one new parameter, C, to take intercellular interactions into account, and, as in previous stochastic calculations, uses σ. In some cases, such as colon cancer,^{39, 40} niches are identifiable and independent estimates for C are then available; σ is observable, e.g., by observing net endogenous birth rate and cell death. In Table 2 the TCP estimates change by ∼5% or less when σ or C are varied, in contrast to the more sensitive dependence of TCP on α and n₀.

The insensitivity of our conclusion about boost effectiveness to many parameter alterations (Table 2, rows 3–6 and 8–11) means that for this purpose the niche model is no less parsimonious than the earlier models that assume no SLCC-SLCC interactions. In one way it may actually be more parsimonious. The calculations that showed almost all surviving niches in the sigmoid models have been filled up to the carrying capacity by the end of a 23 day recovery period indicate that perhaps long-term primarily the TCP and the carrying capacity are relevant, not additional details on the SLCC per niche probabilities.

Some further limitations of the present approach

Results on TCP must always be considered in the context of other relevant factors, such as the probability of late normal tissue complications and the influence of other “Rs.” In this paper this broader context was not quantified. For example, redistribution, radiosensitivity, and especially reoxygenation might be modified by radiation and therefore affect TCP dependence on front vs back boosting. Such factors can depend in a complex manner on dose timing, tumor type, and stage. Scenarios increasing TCP and scenarios decreasing TCP can both be envisaged.

In the related problem of radiogenic second cancers,²⁷ increasing attention is now being paid to the long-term tumor dynamics.^{21, 41} For TCP the corresponding question concerns events during the years after treatment (Fig. 2), which determine whether surviving SLCC, if any, lead to recurrence or remain controlled at sub-clinical levels, and also determine the timing of any recurrences that do recur.⁸ The assumption made here (and in most other TCP analyses) that every SLCC must be eradicated by the end of the recovery period for control to occur is an oversimplification;^{8, 21, 41} this particular assumption tends to underestimate TCP. We did not attempt postrecovery period analyses here because finding parsimonious, well-motivated models for the long-time behavior is, in our opinion, a difficult, separate task.²⁷ For example, some long-term processes increase niche number²¹ and then the basic Poisson color theorem cannot be used in corresponding long-term calculations.

Another complication is that, apart from deterministic late normal tissue effects, early boosts might modify the probability of radiation-induced, independent secondary cancers, where malignant or premalignant cell repopulation during treatment can be important.^{27, 42} Stochastic calculations suggest that early boosts are less dangerous in this respect than late boosts.^{21, 43} The intuitive reason is that new malignant clones initiated by early boosts can be eradicated by later fractions, whereas those initiated by late boosts are more likely to survive the entire treatment.

Finally, we here considered only individualized protocols, not protocols designed for a cohort, where interpatient variations in basic radiobiological parameters are known to be important to the TCP. For the latter the predictions of drastically improved TCP for moderate boosts are overoptimistic, as discussed above.

CONCLUSIONS

The application of our results to full treatment planning protocols, which attempt to consider all relevant major effects, thus remains problematical. But we would argue:

• Prospective, biologically motivated calculations that produce numerical TCP estimates are important, especially for designing model-assisted, physician controlled, individualized protocols.

• The niche model can give such estimates using a more general, at least equally practical, and at least equally credible approach compared to older models.