An RF dosimeter for independent SAR measurement in MRI scanners

Abstract

Purpose: The monitoring and management of radio frequency (RF) exposure is critical for ensuring magnetic resonance imaging (MRI) safety. Commercial MRI scanners can overestimate specific absorption rates (SAR) and improperly restrict clinical MRI scans or the application of new MRI sequences, while underestimation of SAR can lead to tissue heating and thermal injury. Accurate scanner-independent RF dosimetry is essential for measuring actual exposure when SAR is critical for ensuring regulatory compliance and MRI safety, for establishing RF exposure while evaluating interventional leads and devices, and for routine MRI quality assessment by medical physicists. However, at present there are no scanner-independent SAR dosimeters.

Methods: An SAR dosimeter with an RF transducer comprises two orthogonal, rectangular copper loops and a spherical MRI phantom. The transducer is placed in the magnet bore and calibrated to approximate the resistive loading of the scanner's whole-body birdcage RF coil for human subjects in Philips, GE and Siemens 3 tesla (3T) MRI scanners. The transducer loop reactances are adjusted to minimize interference with the transmit RF field (B₁) at the MRI frequency. Power from the RF transducer is sampled with a high dynamic range power monitor and recorded on a computer. The deposited power is calibrated and tested on eight different MRI scanners. Whole-body absorbed power vs weight and body mass index (BMI) is measured directly on 26 subjects.

Results: A single linear calibration curve sufficed for RF dosimetry at 127.8 MHz on three different Philips and three GE 3T MRI scanners. An RF dosimeter operating at 123.2 MHz on two Siemens 3T scanners required a separate transducer and a slightly different calibration curve. Measurement accuracy was ∼3%. With the torso landmarked at the xiphoid, human adult whole‑body absorbed power varied approximately linearly with patient weight and BMI. This indicates that whole-body torso SAR is on average independent of the imaging subject, albeit with fluctuations.

Conclusions: Our 3T RF dosimeter and transducers accurately measure RF exposure in body-equivalent loads and provide scanner-independent assessments of whole-body RF power deposition for establishing safety compliance useful for MRI sequence and device testing.

INTRODUCTION

As magnetic resonance imaging (MRI) trends towards higher static magnetic field strengths for increased signal-to-noise ratios (SNR) and improved image quality,^{1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11} radio frequency (RF) heating becomes an increasing safety concern,^{4, 12, 13} since RF power deposition increases approximately quadratically with field strength if flip angle, pulse length, and duty-cycle are left unchanged.^{14, 15, 16} RF heating results mainly from eddy currents induced in the body's electrically conducting tissues during MRI. This heating can be worsened by the presence of conductive implanted or interventional devices.^{17, 18, 19, 20, 21, 22, 23, 24} Although rare, RF heating-related injuries do occur each year, and many do not involve confounding factors such as the presence of additional conducting leads, surface coils or implanted devices (Examples of burns during MRI scans can be found in the USFDA MAUDE database. Use a simple search with search term “magnetic resonance,” then screen individual entries for RF burn injuries.)²⁵ Thus the monitoring and proper management of RF exposure levels is crucial for evaluating instances of injury and ensuring MRI safety.

Regulatory agencies such as the US Food and Drug Administration (FDA) and the UK Medicines and Healthcare products Regulatory Agency specify guidelines^{26, 27} for MRI RF exposure in terms of both the average whole body specific absorption rate (SAR), and the peak local SAR. SAR measures the RF power absorbed by body mass in W/kg. Local SAR can be estimated from average body SAR via numerical simulation.^{15, 28, 29, 30, 31, 32, 33, 34} Accordingly, clinical scanners monitor both the average body and local SAR for routine MRI, based on proprietary calculations that typically involve patient data entries and assumed or factory-determined properties of the transmit coils, scaled by estimates of the delivered RF power.^{35, 36} However, as our recent study of power deposition showed, clinical scanners often overestimate the deposited RF power and average adult human torso whole-body SAR by as much as 2.2-fold.³⁵ Because regulatory limits on both whole-body average and peak local SAR are simultaneously applicable, and because the determination of both depends on estimating or measuring the total power deposited in the subject, it is critically important to get the total power deposited right.

Incorrect estimation by the MRI scanner's SAR monitoring system can inappropriately restrict MRI scans^{35, 36} and create unnecessary hurdles for clinical scanning and pulse sequence development.^{36, 37, 38} In particular, when implementing power-intensive MRI sequences such as fast spin-echo at higher fields, erroneous SAR limits can impose tradeoffs in image acquisition rates and spatial resolution that result in suboptimal imaging performance and unnecessary compromises that may affect diagnostic utility.⁴ Incorrectly set scanner SAR limits can also constrain RF pulse design by necessitating flip-angle reductions or prolonged sequence repetition times (TR) that compromise SNR and increase total scan time.^{39, 40} Whole body SAR must be properly evaluated in order to facilitate the development of new MRI protocols or conducting devices and leads in the magnet.

SAR can be estimated using computer calculations or measured with experimental calorimetry or direct power measurements.^{35, 41, 42} However, numerical analysis is highly subject dependent because of the complexities and variability of human anatomy and cannot be used for individual clinical exams.⁴² Importantly, any computer simulation still requires an empirical measure of at least one proxy for the power actually delivered by the scanner to the subject in order to scale the calculations to reality. Calorimetric SAR measurements require extended periods of exposure—large, if not massive phantoms that approximate human dimensions—and detailed knowledge of the body's heat capacity.⁴² Direct scanner power measurements involves connecting electronics to the scanner's RF power transmission hardware, generally requiring considerable electronics expertise and the agreement of a manufacturer's service technician to avoid scanner warranty violations.^{31, 35, 41, 42, 43} In order for the MRI scanner's RF power level to be set for any MRI study, the scanner must be loaded with a body-equivalent phantom or a human subject. The latter would not be appropriate for investigating the cause of scanner-induced thermal injuries or evaluating implanted devices.

In summary, these approaches are cumbersome, require advanced technical or engineering knowledge to perform successfully, and are generally unusable in routine clinical settings. Presently there is no easy or practical method of independently establishing reliable SAR exposure levels for assessing device safety or routine MRI quality assessment by medical physicists.

This paper attempts to address this deficiency with a scanner-independent RF dosimeter that works as follows.⁴⁴ (i) A body-equivalent load^{43, 44}—an RF transducer—is used in lieu of an adult human subject positioned with torso in the scanner bore to absorb RF power for a given MRI sequence. (ii) The MRI pulse sequence is applied, and the total absorbed power (P_A) in the transducer is monitored in real time using a true root‑mean‑square (rms) power meter. In practice, P_A can be obtained from power sampled across a resistor in a transducer loop^{43, 44} (P_sample) multiplied by a calibration factor. (iii) The adult human torso average whole-body SAR is derived using P_A divided by the equivalent weight represented by the RF transducer.

The general idea of using loops to simulate a body load had been used previously for measuring SNR (Ref. ⁴³) and the concept was tested in bench experiments with a 1.5 tesla (T) head coil.⁴⁴ However, currents induced in the transducer's loading loops can produce fields in the imaging volume that affect the net applied RF magnetic field B₁. These can cause the scanner to incorrectly set the RF power levels for the pulses being prescribed by the MRI pulse sequence and compromise the accuracy of P_A measurements for a given sample load. This problem is overcome by changing the loop reactance so that the net field (transmitter + loop) has the same magnitude as the original intended transmit field.

The present study reports the development and reduction to practice of the first independent RF dosimeter for measuring adult human whole-body torso average SAR with validation in GE, Philips, and Siemens 3T clinical MRI scanners. The RF dosimeter comprises: first, a two-loop RF transducer that mimics an average human body torso load with minimized B₁-field interference; second, a small MRI phantom which the scanner uses to adjust the MRI sequence RF power level; and third, associated electronics that measures the absorbed power P_sample in each loop. P_A is then determined from a calibration factor that compares P_sample to a direct power measurement of P_A using a high-dynamic range power monitoring system developed previously.³⁵ The RF dosimeter was calibrated and tested in eight different 3T MRI scanners from three leading manufacturers with different body RF coils.

MATERIALS AND METHODS

RF dosimeter

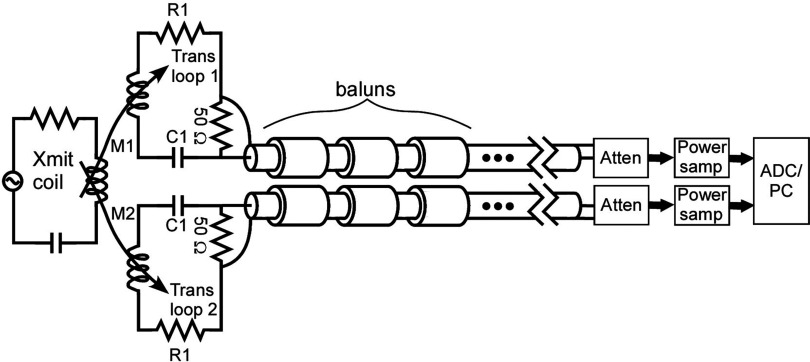
An RF transducer that mimics an average body load inside the body coil was constructed to dissipate RF power (Fig. 1). The transducer consists of two orthogonal rectangular metal loops containing lumped element resistors and capacitors to accommodate the MRI body coil's quadrature excitation. As explained below, loop sizes of 50 × 35 cm—comparable to average adult human torso dimensions—were chosen after consideration of the RF field interactions between the loops and the scanner's transmit coil. The loops were constructed using 12.5 mm wide copper strips fixed on a polycarbonate frame. Each loop was tuned by 16 sets of capacitors (ATC Ceramics, Huntington Station, NY) distributed evenly around the loop. The sample loading was provided by 10 sets of high power RF resistors (Bourns Inc, Riverside, CA) in series, also uniformly distributed around each loop. To elicit an MRI signal for the scanner to set the pulse power, a spherical phantom (diameter 10 cm) filled with negligible-loss mineral oil (Marcol 52, ExxonMobil, Irvine, TX) was placed at the center of the transducer loops.

Figure 1.

3T RF dosimeter setup. The cables connect to a real time MRI RF power monitor.

Figure 2 shows the dosimeter electronic schematic.

Figure 2.

Dosimeter electronic schematic. The transducer loops are magnetically coupled to the transmit coil. The transducer loops are tuned such that the net B1 field magnitude (B_net = transmitter field (B_appl) + transducer induced fields (B_induc)) is the same as the magnitude of the applied B1 field at the NMR sample (see Sec. 2C). The baluns prevent unwanted common mode currents. The power sampling modules and ADC/PC setup are described in Ref. 35.

The RF power absorbed in the transducer was detected by sampling a 50 Ω resistor on each loop and transmitting that signal through two sets of leads, each containing seven serially serially connected baluns (Fig. 1). Each balun, on average, provided 38 dB surface current attenuation. The coaxial connections to the two loops were closely positioned to minimize unbalanced surface currents arising from any RF magnetic flux between the coaxial lines. Following the baluns, the signals continued along ordinary 50 Ω coaxial cables to two remotely located 50 dB attenuating directional couplers (Werlatone Inc., Patterson, NY) at the inputs of our remotely located, 90 dB dynamic range RF power monitoring system capable of measuring pulsed RF power with a 90 dB dynamic range.³⁵ The accuracy of the RF power monitor over the 70 dB dynamic range of signals measured in this work (−10 to 60 dBm), was about 0.14 dB or 3.3%, as determined by the mean absolute deviation from linearity. For each power determination, the rms power was averaged over ten TR intervals.

Two separate 3T RF dosimeters were built. One was used for Philips and GE 3T MRI systems, which both operate at 127.8 MHz. The other unit was for Siemens 3T systems, which operate at a lower MRI frequency of 123.2 MHz.

Loop design

In order to minimize the disturbance of the scanner's B₁ field produced by current in the loop, it is desirable to make the loading loops as large as possible. We can see this from the following argument.

The power P_A dissipated in a loop of a given geometry must be proportional to the square of the excitation field B₁. So assuming the applied B₁ = B_appl to be approximately homogeneous,

$$P_A=\alpha ·B_{\mathrm{appl}}^2,$$ (1)

where α is a proportionality constant. The voltage induced on each loop is proportional to the changing B₁ flux through the loop, V_induc = β · B_appll², where β is another proportionality constant and l is a scale dimension of the loop. Neglecting for now loop reactance, $P_A\approx V_{\mathrm{induc}}^2/R,$ and

$$P_A\approx {\beta }^2·B_{\mathrm{appl}}^2{l}^4/R.$$ (2)

Setting Eqs. 1, 2 equal and solving for R we get

$$R\approx {\beta }^2·l^4/\alpha .$$ (3)

Finally, the field induced at the center of the loop B_induc is given by

$$B_{\mathrm{induc}}\approx \frac{\lambda ·I}{l}=\frac{\lambda }{l}·\frac{V_{\mathrm{induc}}}{R}=\left[\frac{\lambda \alpha }{\beta }\right]·\frac{B_{\mathrm{appl}}}{l^3},$$ (4)

where λ is another proportionality constant.

From Eq. 4 we see that the field induced at the loop center is inversely proportional to the cube of the loop dimension. Thus, to decrease the effect of B_induc on $B_{\mathrm{appl}}$, the sampling loop should be made as large as possible while staying within the homogeneous B₁ region of the MRI scanner's body transmit coil. With these considerations in mind, we made rectangular sampling loops 50 cm long × 35 cm wide—comparable to average adult human torso dimensions, but contained within the reasonably homogeneous static magnetic field region of a typical clinical MRI scanner.

Adjusting loop reactance to minimize B₁-field interference

We first tuned the transducer loops to the scanner resonance frequency using added series capacitors to make the net loop impedance a pure resistance. However, we found that the RF field induced in the loop disturbed the B₁-field inside the scanner bore during RF transmission, causing the scanner's pulse-setting algorithm to reduce the RF power, B_appl, required to produce the prescribed flip-angle over the range of loop resistances that produced body-equivalent loading. This prevented proper calibration of the transducer for a given body load.

The field disturbing effect on the scanner's flip angle adjustment can be understood as follows. The current induced on the transducer loops generates a B_induc field that adds vectorially to the transmit coil's applied B₁-field B_appl. Both amplitude and phase of the two signals must be taken into account. Scanners typically use an iterative “prescan” B₁ field (flip angle) determination to adjust the RF power amplifier output to generate a desired flip angle. If the resultant |B_net| is larger than the desired (applied) |B_appl|, the scanner incorrectly reduces the RF amplifier's power output below what is required for a given load. If the resultant |B_net| is lower than expected for the desired (applied) |B_appl|, the RF amplifier power is incorrectly increased. To remedy the problem, the magnitude and phase of the induced field B_induc must be adjusted so that the net field magnitude |B_net| is the same as the scanner's applied field magnitude |B_appl|. We found that this can be achieved by readjusting the reactance of the RF transducer loop.

The current induced in a transducer loop is

$$I_{\mathrm{induc}}=\frac{-j\omega B_{\mathrm{appl}}A}{R+jX}.$$ (5)

The EMF induced in each conductive loop is calculated in the numerator by Faraday's law,⁴⁵ where ω is the angular MRI frequency and A is the area of the transducer loop. In the denominator, R and X are the resistance and reactance of the dosimeter loop impedance. For a rectangular wire loop, the induced B₁ field B_induc perpendicular to the plane at the center of the loop is⁴⁶

$$B_{\mathrm{induc}}=\frac{{\mu }_0{I}_{\mathrm{induc}}}{\pi }·\frac{\sqrt{a^2+b^2}}{ab},$$ (6)

where μ₀ = 4π × 10⁻⁷ H/m and a and b are, respectively, half the length and height of the rectangular loop. The resultant net B₁ field ${\vec{B}}_{net}$ is

$$|{\vec{B}}_{\mathrm{net}}|=|{\vec{B}}_{\mathrm{appl}}+{\vec{B}}_{\mathrm{induc}}|.$$ (7)

There are two important considerations to note about Eq. 7. First, ${\vec{B}}_{\mathrm{net}}$ is the complex sum of ${\vec{B}}_{\mathrm{appl}}$ and ${\vec{B}}_{\mathrm{induc}}$, which are generally out of phase. Second, the vectors ${\vec{B}}_{\mathrm{appl}}$ and ${\vec{B}}_{\mathrm{induc}}$ might not be aligned in physical space. So ${\vec{B}}_{\mathrm{net}}$ is a vector sum in both phase and physical space. Here we calculate the scalar $B_{\mathrm{net}}=\left|{\vec{B}}_{\mathrm{net}}\right|$ at the center of a loop, where the applied and loop fields are aligned and perpendicular to the loop plane, and where the NMR test sample is located.

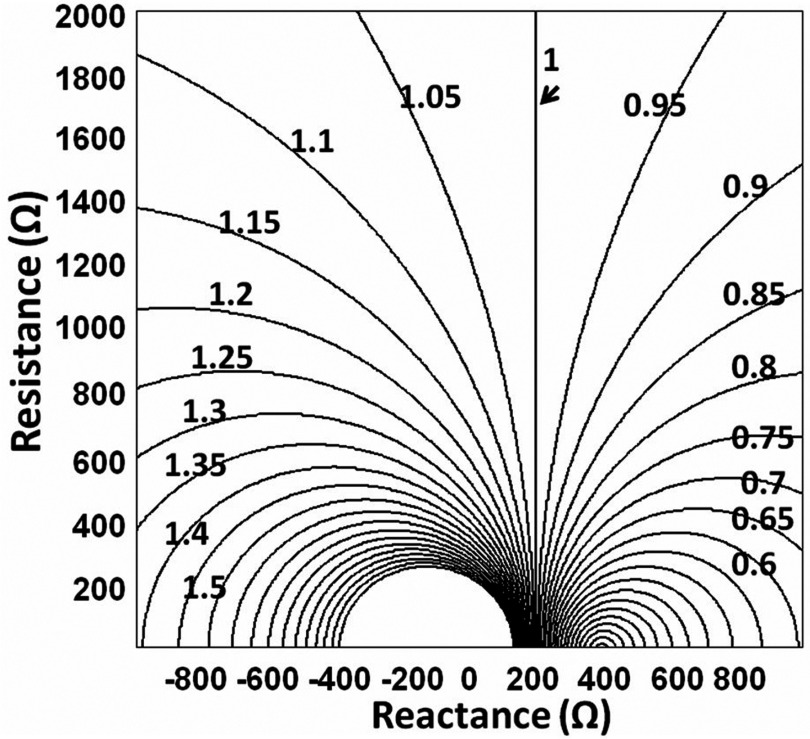
The magnitude of B_net for RF transducers at operating frequencies of 127.8 MHz for Philips/GE 3T systems, and 123.2 MHz for the Siemens 3T system were calculated and normalized to the scanner $|{\vec{B}}_{\mathrm{appl}}|$. The results are shown in Fig. 3 as a contour plot (5% steps) of normalized $B_{\mathrm{norm}}=|{\vec{B}}_{\mathrm{net}}|/|{\vec{B}}_{\mathrm{appl}}|$ as a function of loop reactance and resistance at 127.8 MHz. When the loops are tuned to the MRI resonance (net X = 0 Ω), B_norm varies from 3.04 (+ 204%) at R = 100 Ω to 1.074 (+7.4%) at R = 1000 Ω. We originally approximated the vertical B_norm = 1 contour using X = 211 Ω. An exact algebraic solution for X that defines the unity contour and thus minimizes the B₁ field distortion is derived in the Appendix. Although X = 211 Ω was slightly higher than the exact answer of X = +189 Ω at 123.2 MHz, the value of B_norm for X = 211 Ω only differs from B_norm = 1by about 3%.

Figure 3.

Contour plot of normalized B₁ field magnitude $B_{\mathrm{norm}}=|{\vec{B}}_{\mathrm{net}}|/|{\vec{B}}_{\mathrm{appl}}|$ as a function of loop reactance and resistance at 127.8 MHz. The unity contour indicated by the arrow is where $|{\vec{B}}_{\mathrm{net}}|=|{\stackrel{\rightharpoonup }{B}}_{\mathrm{appl}}|$ for a particular value of X and the full range of R. The contour interval is 5%.

Once the reactance of each loop is offset to this value, the verticality of the B_norm = 1 contour means it is possible to change the coil resistance to represent different sample/body loads (and consequent losses) and be confident that ${\vec{B}}_{\mathrm{net}}$ will be close to $|{\stackrel{\rightharpoonup }{B}}_{\mathrm{appl}}|$, independent of the load.

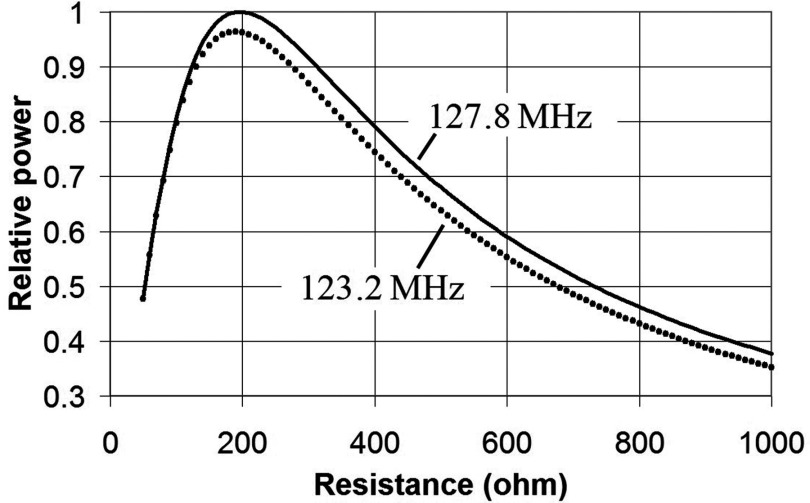
It is instructive to look at the power absorbed as a function of resistance for the B_norm = 1 contour. This can be done by substituting the algebraic solution X into the formula for the loop current (Eq. 5) and then calculating $I_{\mathrm{induc}}^2\times R$. Figure 4 shows a normalized plot for this quantity for the two operating frequencies (127.8, 123.2 MHz). Note that at low resistance (<200 Ω), the relative power decreases because the resistance R gets smaller than the reactance X, so the reactance determines the current. We used a resistance of just under 400 Ω for both frequencies to yield a power deposition in the range of that for our sampled subjects. Above 200 Ω, Fig. 4 shows that R must be decreased in order to emulate the increasing RF power demands of larger and/or heavier subjects. However, at 200 Ω, the maximum power absorbed by the transducer is reached, and the loading of subjects that absorb greater power than this cannot be simulated by further reductions in R. Thus there is an upper limit to subject loading that this kind of transducer can simulate.

Figure 4.

Relative power absorption of transducer loop as a function of loop resistance when loop reactance X is adjusted to give unity contour as shown in Fig. 3.

Calibrating the transducer as a body-equivalent load

The RF transducer loop resistance was adjusted to make its absorbed rms power P_A fall within the range of P_As delivered to our xiphoid-landmarked subjects. Transducer loading was measured³⁵ on a Philips 3T Achieva XMR scanner using a gradient echo (GRE) MRI sequence with TR = 50 ms, flip angle = 90°.

We obtained P_A for the transducer loop using a direct rms power measurement by connecting RF power monitors to the body coil quadrature hybrid output ports.^{35, 41} The total power P_total incident on the body coil was measured at the quadrature hybrid output ports of the body coil, with the coil loaded by the transducer. The coil loss P_coil was also measured at the hybrid ports with the body coil loaded with a negligible loss sample, a 1 L bottle filled with mineral oil.³⁵ Both P_total and P_coil were computed as the difference between forward and reflected power.³⁵ Then P_A = P_total − P_coil.

Calibrating power sampled in the transducer

To calibrate the power (and subsequently the SAR) deposited in the dosimeter in the MRI scanner, we compared the power sampled from the dosimeter P_sampled to P_A measured from direct electrical connections to the MRI system.

We measured the power dissipated in the dosimeter by sampling the RF power across a 50 Ω resistor on each of the two loops with our RF power monitoring system.³⁵ The 127.8 MHz dosimeter was calibrated in three Philips 3T scanners (two Achieva dual-channel systems operated in quadrature mode, one quadrature transmit Intera system) and three GE 3T scanners (two HDx systems and one MR750 system). The 123.2 MHz dosimeter was calibrated on two Siemens 3T Trio scanners. To obtain a calibration curve relating P_A and P_sampled, the power output of the RF amplifier was changed over a range consistent with routine MRI pulse sequences and patient size by varying the following scan parameters: TR, RF amplifier scale and maximum B₁ on Philips scanners; TR and transmit gain TG on GE scanners; and TR and pulse amplitude on Siemens scanners. The calibration factor was taken from the slope of the linearly fitted P_A vs P_sampled data plots.

Converting power to SAR

With the calibration factors determined above, we used the dosimeter to measure the average power deposited by the same GRE sequence described in Sec. 2D. To determine the body torso average SAR, the P_A measured by the dosimeter must be divided by the weight of the subject m in accordance with its regulatory definition.⁴⁷ Peak local spatial SAR can then be derived from the average body SAR using numerical factors obtained through numerical electromagnetic simulations for the sample model.^{15, 28, 29, 30, 32, 33, 34}

Dosimetry for subjects with different weight or body mass index (BMI)

Here we investigate how power measurements from a transducer calibrated for a fixed load can be rescaled to represent different-sized subjects. Clinical MRI often requires entry of the body weight as a metric of body size, so the use of subject weight alone may be convenient, or BMI, if available. The measured P_A can be rescaled based on P_A vs weight or P_A vs BMI, as both are approximately linear.^{16, 35}

For P_A vs weight m and for P_A vs BMI, we assume

$$P_A=a_1·m,$$ (8)

$$P_A=a_2·\mathrm{BMI},$$ (9)

with slopes a₁ and a₂. Determination of the constants a₁ and a₂ in principle enables extension of dosimetry from a single individual represented by the dosimeter to other subjects of different size and/or weight.

In practice, predicted power absorption values depend on how well the straight lines of Eqs. 8, 9 characterize the net power absorption for different sized subjects. To test these relationships and obtain the linear parameters, we determined P_A by direct power measurements³⁵ in 26 healthy volunteers (21 males and 5 females, landmarked at the xiphoid) on the Philips Achieva 3T scanner as a function of m and BMI. All human studies were approved by the Johns Hopkins Institutional Review Board after subjects provided written informed consent.

Balun efficiency

The studies above utilized seven baluns attached to each loop (see Fig. 1) to provide a nominal 266 dB of total attenuation to the common mode current on the surface of the coaxial cable carrying the analog power signal to the power meter. We subsequently investigated whether the number of baluns could be reduced to simplify the dosimeter setup. For this study, the power calibration procedure was repeated using one, two, three, four, and seven sets of baluns on each transducer loop with the dosimeter in the Philips 3T XMR Achieva scanner. P_sampled vs P_A was measured with the same GRE sequence at six TR values. The difference in line attenuation was factored in for each configuration when determining P_sampled.

RESULTS

Loop reactance adjustment to maintain correct B₁

With the desired reactance value X determined as shown in Fig. 3, we calculated the inductance for a 0.5 m × 0.35 m rectangular conducting loop⁴⁸ and estimated the change in reactance and consequent off‑resonance frequency needed to achieve$|{\vec{B}}_{1\mathrm{net}}|\approx |{\vec{B}}_1|$_. We then adjusted the loop capacitance to achieve that tuning. The total inductance of the loop, fabricated from the 13 mm wide copper strip, was calculated to be 1.43 μH. The capacitance needed to achieve X = 211 Ω at 127.8 MHz (Philips/GE) was calculated to be 1.32 pF and the new tuning frequency of the loop with this capacitance was 115.7 MHz. For the 123.2 MHz Siemens systems, the capacitance needed to achieve X = 189 Ω was 1.41 pF, and the resulting tuning frequency was 112.2 MHz. Both loops were empirically tuned using a network analyzer while varying the capacitance.

Correct operation of the transducer loops containing adjusted reactances was verified on the Philips 3T XMR Achieva scanner by running the GRE sequence of Sec. 2D and looking at the flip angles recorded during the prescan power-optimization stage in the scanner's log file. The Philips scanner first estimates the B₁ field amplitude for the desired pulse using B₁ pickup loops located near the whole‑body RF transmitter coil. It then uses the MRI signal to optimize the power to achieve the desired flip angle. The scanner log file records a value for the initial flip angle estimate corresponding to the initial B₁ field amplitude established by the pickup loops. Normally (without the transducer) the initial flip angle is close to the final desired flip angle. Only the Philips scanner provided this initial flip angle, which was extremely useful in correctly setting up our transducer.

When the 127.8 MHz transducer was tuned exactly to the MRI resonant frequency and inserted into the Philips Achieva scanner, the initial flip angles, measured for the prescribed 90° flip angle, were above 110° for all load resistances less than 1900 Ω. This caused the scanner to incorrectly reduce the RF power output regardless of loop resistance (<1900 Ω). When the loops were tuned to 115.7 MHz (X = 211 Ω), Table 1 shows that the measured initial flip angles were all close to 90°, consistent with minimal B₁-field interference. A similar loop resistance (382 Ω) was used for the Siemens Trio 3T RF transducer. Table 2 shows the power absorbed in the final transducers, averaging 27.5 W in the Philips scanners and 17.1 W for the Siemens scanners. Note that the pulse sequences and parameters differ between the two scanners, thus the absorbed power difference.

Table 1.

Philips 3T Achieva initial flip angle and absorbed power P_A in an RF transducer prototype with reactance X = 211 Ω for various loop resistances (R). The results for a particular human subject (89 kg) are also included. All scans are performed using the same pulse sequence.

	Initial flip angle (deg)
Loop R (Ω)	determined in Achieva	PA(W)
1000	90.3	9.8
700	90.9	14.3
375	87.9	25.1
Human subject	90.2	24.5

Table 2.

Test pulse sequences absorbed power P_A in the final RF transducers for the Philips and Siemens 3T scanners studied.

	Loop impedance
Scanner	R + jX (Ω)	PA(W)
Philips Achieva XMR		26.6
Philips Achieva	375 + j211	28.6
Philips Intera		27.3
Siemens Trio (I)		17
	382 + j189
Siemens Trio (II)		17.1

Table 3 shows that the power calibration curves relating P_sampled and P_A are highly linear. The calibration factors (line slopes) obtained for the six 127.8 MHz and two 123.2 MHz MRI scanners are essentially equivalent for both RF dosimeters.

Table 3.

Calibration curve linearity and slope data for the final RF dosimeters on 127.8 and 123.2 MHz systems. In brackets is the software version running on each scanner.

	No. of data	Slope
	points	(calibration line)	R2
3T MRI systems, 127.8 MHz
Philips Achieva XMR Dual-Channel, quadrature mode [R3.2.1]	29	30.02 (0.07 SD)	0.9999
Philips Achieva Dual-Channel, quadrature mode [R3.2.1]	29	29.96 (0.09)	0.9996
Philips Intera [R3.2.2]	29	29.06 (0.04)	0.9998
GE MR750 [22M4]	10	29.82 (0.12)	0.9998
GE HdX (I) [15M4]	11	29.10 (0.13)	0.9999
GE HdX (II) [15M4]	10	28.30 (0.14)	0.9998
All 127.8 MHz combined data	118	29.32 (0.07)	0.9994
3T MRI systems, 123.2 MHz
Siemens Trio (I) [VB17a]	14	27.11 (0.10)	0.9998
Siemens Trio (II) [VB17a]	14	26.82 (0.14)	0.9996

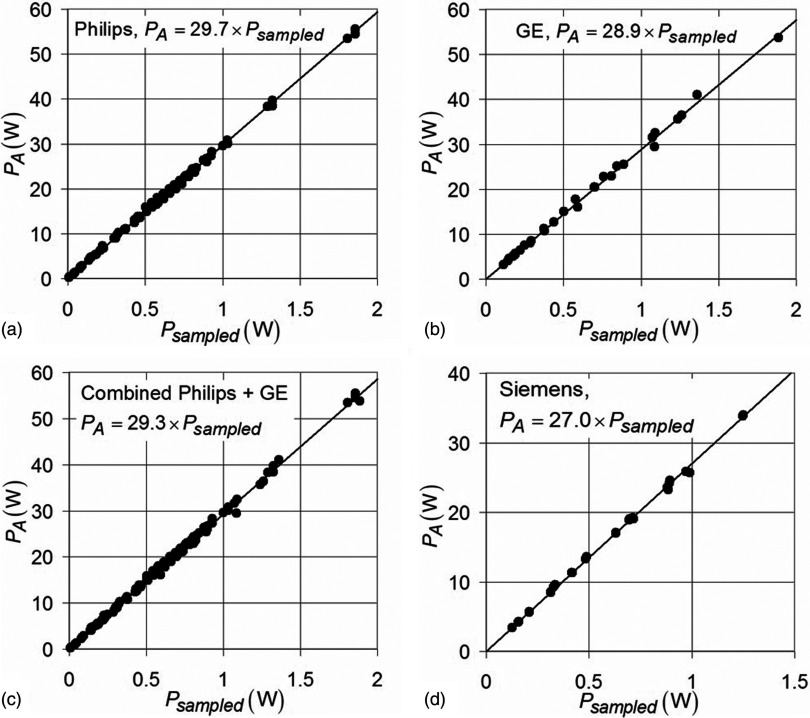
The 3T power measurement data from each manufacturer were combined on three separate plots and fitted by linear regression [Figs. 5a, 5b, 5d]. A separate plot was created by combining all of the 3T Philips and GE data, since they operate at the same scanner frequency [Fig. 5c]. The calibration factor for each 3T platform was: Philips = 29.6 (± 0.1 [SD]), GE = 28.7 (±0.2), Siemens = 26.7 (±0.2). The calibration factor for the combined GE and Philips data representing all 127.8 MHz systems was 29.0 (±0.1) and was very similar to the calibration curves of the individual GE or Philips systems.

Figure 5.

The P_A vs P_sampled measurement data fitted by linear regression for (a) 3T Philips scanners, (b) 3T GE scanners, (c) 127.8 MHz MRI systems (Philips + GE combined data), and (d) Siemens scanners (123.2 MHz). R² > 0.99 for all fits.

Dependence of adult whole body torso P_A on body mass and BMI

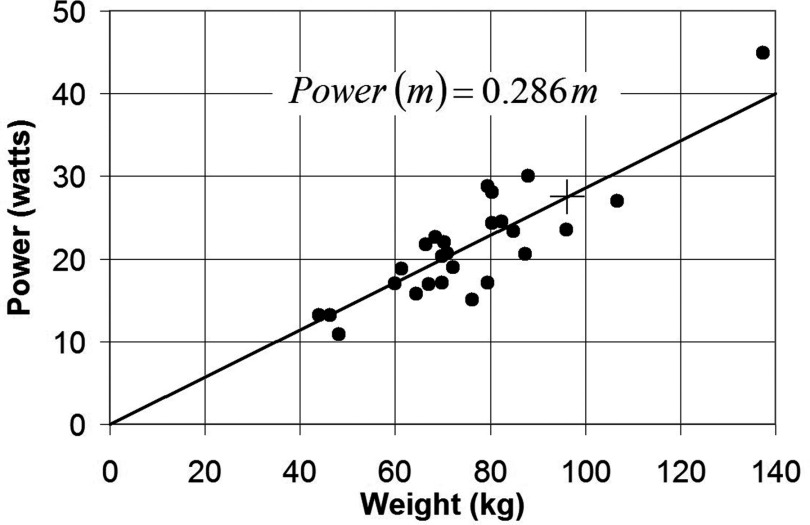
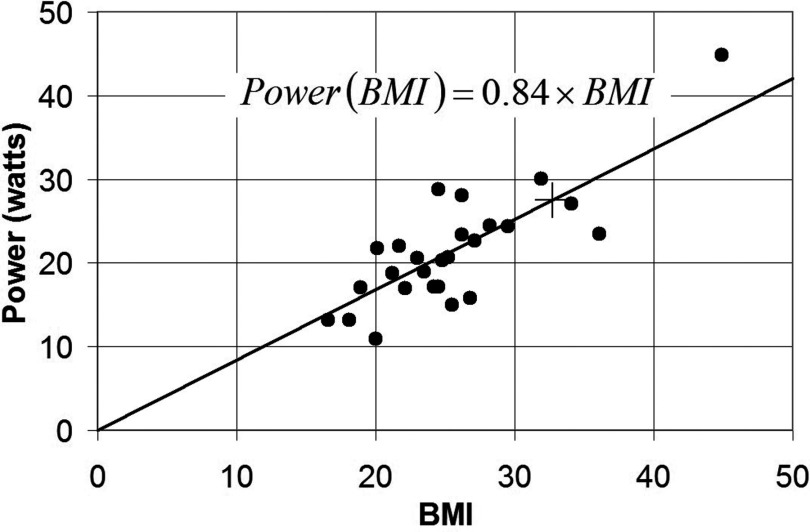
Plots of P_A vs m and P_A vs BMI are shown in Figs. 67 for 26 adult human volunteers landmarked at the xiphoid, with torso in the imaging region of the dual-channel Philips 3T XMR system using the GRE sequence described in 2D. Results are fitted to a straight line passing through the origin. The coefficients a₁ = 0.286 and a₂ = 0.84 enable extrapolation of deposited power and SAR measured by the dosimeter for the specified GRE sequence to subjects with a range of weights and BMIs.

Figure 6.

Plot of absorbed power P_A vs weight m for 26 xiphoid-landmarked research subjects measured in the Philips 3T XMR system, fitted by linear regression, R² = 0.98. The transducer power is shown as + and is equivalent to m = 96.2 kg.

Figure 7.

Plot of absorbed power P_A vs BMI for 26 xiphoid-landmarked research subjects measured in the Philips 3T XMR system, fitted by linear regression, R² = 0.97. The transducer power is shown as + and is equivalent to BMI = 32.7.

Using the linear relationships of Figs. 67 and the transducer power equivalent to weight m = 96.2 kg and BMI = 32.7, we can calculate the average adult human torso absorbed power $P_A^{*}$ for any pulse sequence on any scanner as approximately the dosimeter power divided by these figures and multiplied by the subject's mass (or BMI). Thus with the transducer equivalent to a weight m = 96.2 kg and a BMI = 32.7 we obtain:

$$P_A^{*}\left(m\right)\approx \left[\frac{P_A^{*}\left(\mathrm{dosimeter}\right)}{96.2}\right]\times m,$$ (10)

$$P_A^{*}\left(\mathrm{BMI}\right)\approx \left[\frac{P_A^{*}\left(\mathrm{dosimeter}\right)}{32.7}\right]\times \mathrm{BMI}.$$ (11)

Equations 10, 11, based on P_A vs m or BMI plots for an appropriate study population, can be applied to any scanner and any pulse sequence assuming that the RF fields within the dosimeter loops have approximately the same uniformity as the fields in the Philips scanner.

Note that a straight line fit of power vs weight [Eq. 10 and Fig. 6] says that any adult imaging subject torso (landmarked at the xiphoid) exposed to that pulse sequence has a whole‑body SAR ≈ 0.286W/kg, with scatter as shown.

If we take the individual power points shown in Fig. 6 and divide by the subjects’ weights, we get SAR = 0.283 ± 0.043 W/kg. The standard deviation is 15% with a maximum deviation within this dataset of −31% and +27%. Even the latter values are substantially less than the discrepancies between scanner SAR estimates and actual power measurements reported in our previous paper.³⁵

The Philips scanner console SAR numbers are independent of patient weight.³⁵ Although their rationale is proprietary, it would appear that Philips keep themselves “safe” by multiplying by an empirical factor (∼1.3) to ensure that their SAR estimate is higher than would be the case even for subjects whose SAR deviates positively from the average.

Balun efficiency

Table 4 shows that the average P_A vs P_sampled calibration factor using one set of baluns on each transmission line is ∼7% lower than the rest of the measurements. The results for two or more baluns show only a ∼2% variation. This suggests that using at least two baluns, corresponding to ≥76 dB of surface current attenuation, should suffice to protect the integrity of the analog signals for data transmission during MRI measurements.

Table 4.

P_A vs P_sampled calibration factors obtained from the RF dosimeter using different numbers of baluns on the transducer transmission line.

Number of 38 dB	Calibration factor
baluns on each line	(slope of PA vs Psampled)
1	27.4
2	29.6
3	28.7
4	30.0
7	29.5

DISCUSSION

The RF dosimeter is a scanner-independent SAR measurement tool that can quickly provide scanner SAR information to MRI users without any physical connections to or interference with the MRI scanner or its operation. This is particularly important in clinical settings requiring scanner-independent SAR evaluations by clinical technical staff or medical physicists while avoiding system down time. Deposited RF power determined from the dosimeter is based on direct empirical measurement, not mathematical estimation which can include undeclared safety factors or factory settings that may not reflect actual variations with time or loading.^{35, 36} The 3.3% nonlinearity of the power meter over the 70 dB operating range used here determines the accuracy of the measured power absorbed by a given transducer load.

Even though the transducer calibration is frequency-dependent because of the need for offsetting the tuning to minimize B₁ disturbance, the calibration is consistent between (i) 3T systems from the same scanner manufacturers including different models (GE, n = 3; Philips, n = 3; and Siemens, n = 2); and (ii) 3T systems from different scanner manufacturers operating at the same frequency (GE and Philips) but different RF body-coils. The ∼5 MHz variation in scanner center frequency for the Siemens units relative to GE/Philips did require a separate transducer. Separate RF transducers would thus be needed for RF dosimetry in scanners operating at other field strengths or significantly different center frequencies.

Scanner transmit coil dimensions may vary, but the consistency of the calibration curves suggests that differences in body coil and dosimeter loop interactions are not a confounding factor affecting the power dissipated in our transducers. We do not expect that the power dissipated in the transducers relative to the human subject's weight or BMI that it represents to be radically different for different scanners, certainly in comparison to the scatter for different imaging subjects.

While Figs. 67 present data from 26 subjects on the dependence of the power absorbed in the body as a function of BMI and m, it is evident that a study of significantly more subjects would be needed to better characterize these curves as representative of an MRI patient population when it is desirable to derive BMI- or weight-specific dosimetry using the approach described in Sec. 2G. An alternative wherein the dosimeter load is adjusted with variable resistors to match any desired body weight has also been considered. While this would simplify Eqs. 8, 9, 10, 11, it would still require calibrating body mass or BMI vs dosimeter power (P_sampled) as in Sec. 2G. Because changing the load is more complicated than holding it constant and providing a weight correction that is needed anyway, this alternative did not seem to afford much advantage.

Validation of the MRI dosimeters presented here are limited to whole-body transmitter coils in clinical 3T GE, Philips and Siemens scanners, but the dosimeter should work in other manufacturer's scanners operating at the same frequencies with similar excitation coils. The xiphoid landmark was chosen to coincide approximately with the center-of-mass of the torso.

Smaller transducer loops would be needed for limb- or head-coil dosimeters operating in RF head coils,⁴⁴ where the benefits of reactance adjustment for eliminating B₁-interference may also be important. Our measurements have been done on quadrature body coils commonly used on most clinical scanners (Table 3).⁵⁰ Transmit arrays using multiple independent surface coils are a different story, however.

As shown previously on several Philips and Siemens systems,³⁵ and supported here by data from even more scanners, the SAR reported by 3T MRI systems are typically overstated by substantial margins. Because SAR readings generally serve as a “gate-keeper” that prohibits clinical scanning at high RF exposures, 3T MRI clinical scanners almost invariably operate at true (average) SAR levels well below regulatory guidelines.

Our dosimeter data on adult torso SAR (landmarked at the xiphoid) have a ±30% range of scatter (Fig. 6) that covers all the subjects we studied. Philips scanners, which we have most extensively characterized, report SAR greater than or approximately equal to actual SAR for any subject. Thus dosimeter SAR measurements higher than Philips scanner reported SAR for a clinical MRI sequence might be reasonable grounds for safety concern and contacting scanner manufacturing service. However, as we have stated, our data needs to be supplemented by further measurements of larger patient samples on different systems in order to confidently set limits.

We reiterate that the dosimeter only provides measures of total power deposited and body average SAR, not local or peak SAR. Presently, local SAR is determined from experimentally validated models or experiments on phantoms,⁴⁷ which provide a numerical multiplier that is applied to the average SAR. For homogeneous cylinders and spheres, the peak 1-g average SAR is two to four times the average;²⁸ for heterogeneous models of the head, the multiplier is 4.5–6 between 63 and 175 MHz (Refs. ^{32, 33}, and ⁴⁹) and 10–16 for the torso at 1.5T and 3T.^{29, 34} Thus, once average SAR is measured with the dosimeter, a model-based peak local SAR can be obtained by multiplication based on the appropriate model.

CONCLUSIONS

We have constructed an RF dosimeter for MRI that minimally disturbs the scanner's applied B₁ field magnitude while providing a load comparable to that of an adult human subject torso. The dosimeter provides reproducible measurements of the deposited RF power in multiple 3T clinical MRI systems manufactured by Philips, GE, and Siemens. The RF power deposited in the dosimeter exhibits a highly linear relationship with the power sampled from the transducer loops. The calibration factors are consistent among all MRI systems operating at the same MRI frequency independent of manufacturer or model. These RF dosimeters are the first scanner-independent SAR measurement devices demonstrated on real clinical MRI scanners. The intent is to use them to independently verify average SAR exposure, to improve MRI safety for routine clinical MRI by providing a fast and independent quality assurance tool, and to facilitate development of new MRI technologies that may be limited by SAR.

APPENDIX: EXACT ALGEBRAIC SOLUTION FOR FIELD-PRESERVING LOOP REACTANCE

Here we derive an exact algebraic solution for obtaining the loop reactance, X, for which $|{\vec{B}}_{\mathrm{net}}|=|{\vec{B}}_{\mathrm{appl}}|$ independent of loop resistance.

First, we combine Eqs. 5, 6, add the initial B_appl and divide by B_appl to get the net, normalized field B_norm at the center of the rectangle:

$$B_{\mathrm{norm}}=\frac{4{\mu }_0}{\pi }·\left(\frac{-j\omega }{R+jX}\right)·\sqrt{a^2+b^2}+1.$$ (A1)

This can be separated into real and imaginary parts:

$$\begin{array}{ccc}& & B_{\mathrm{norm},\mathrm{real}}=1-\frac{4\omega {\mu }_{0}X\sqrt{a^2+b^2}}{\pi (R^2+X^2)},\hfill \\ & & B_{\mathrm{norm},\mathrm{imag}}=\frac{-4\omega {\mu }_{0}R\sqrt{a^2+b^2}}{\pi (R^2+X^2)}\hfill \end{array}$$ (A2)

The magnitude of this net field must equal unity, i.e., $B_{\mathrm{norm},\mathrm{real}}^2+B_{\mathrm{norm},\mathrm{imag}}^2=1$. Solving this for X finally yields:

$$X=\frac{2\omega {\mu }_0\sqrt{a^2+b^2}}{\pi }.$$ (A3)

Note that there is no dependence of X on R, which is consistent with the vertical line at the normalized field B_norm = 1 in Fig. 3. Substituting the loop dimensions, a = 0.35 m and b = 0.5 m, we get X = 196 Ω at 127.8 MHz and X = 189 Ω at 123.2 MHz.