Distance-preserving rigidity penalty on deformable image registration of multiple skeletal components in the neck

Abstract

Purpose: This study aims at developing and testing a novel rigidity penalty suitable for the deformable registration of tightly located skeletal components in the head and neck from planning computed tomography (CT) and daily cone-beam CT (CBCT) scans of patients undergoing radiotherapy.

Methods: The proposed rigidity penalty is designed to preserve intervoxel distances within each bony structure. This penalty was tested in the intensity-based B-spline deformable registration of five cervical vertebral bodies (C1–C5). The displacement vector fields (DVFs) from the registrations were compared to the DVFs generated by using rigid body motions of the cervical vertebrae, measured by the surface registration of vertebrae delineated on CT and CBCT images. Twenty five pairs of planning CT (reference) and treatment CBCTs (target) from five patients were aligned without and with the penalty. An existing penalty based on the orthonormality of the deformation gradient tensor was also tested and the effects of the penalties compared.

Results: The mean magnitude of the maximum registration error with the proposed distance-preserving penalty was (0.86, 1.12, 1.33) mm compared to (2.11, 2.49, 2.46) without penalty and (1.53, 1.64, 1.64) with the existing orthonormality-based penalty. The improvement in the accuracy of the deformable image registration was also verified by comparing the Procrustes distance between the DVFs. With the proposed penalty, the average distance was 0.11 (σ 0.03 mm) which is smaller than 0.53 (0.1 mm) without penalty and 0.28 (0.04 mm) with the orthonormality-based penalty.

Conclusions: The accuracy of aligning multiple bony elements was improved by using the proposed distance-preserving rigidity penalty. The voxel-based statistical analysis of the registration error shows that the proposed penalty improved the integrity of the DVFs within the vertebral bodies.

INTRODUCTION

Radiation therapy is an established method of treating head and neck cancer. Advanced radiotherapy techniques such as intensity-modulated radiation therapy (IMRT) (Ref. ¹) have enhanced treatment outcomes by delivering conformal radiation dose to tumors while sparing healthy surrounding tissues. Furthermore, the advent of in-room tomographic imaging suggests potentially convenient support of adaptive radiation therapy (ART) which aims to adapt treatment planning in response to patient variations. A typical procedure in ART includes (1) delineating contours of tumors and normal tissues and (2) adjusting the original treatment plan in response to the variations in the contours. However, it is extremely time consuming for physicians to manually delineate contours of tumor and normal organs at every treatment scan. In addition, it is not clinically feasible to re-optimize beam intensity maps in response to patient variations.

Deformable image registration, which computes a voxel-to-voxel map from a reference image to a target image, plays an important role in automating the procedures in ART such as contouring and dose accumulation. The contours delineated by the physician at initial planning can be propagated to target images from in-treatment scans by using deformation maps from deformable image registration.^{2, 3, 4} In a retrospective study,⁵ Lee et al. used a deformable registration method for automatic re-contouring and dose accumulation to calculate radiation dose delivered to the parotid gland. Several re-planning strategies were compared by accumulating radiation dose using deformable mappings.⁶ Peroni et al. reported an attempt to generate synthetic planning computed tomography (CT) images by performing deformable image registrations between the original planning CT and daily cone-beam CT (CBCT) images, which allows re-planning without additional acquisition of planning CT scans.⁷

While typical deformable image registration utilizes correlation of image intensities between reference and target images, this approach has the potential to result in physically implausible deformation maps. As reported in a recent study,⁸ image similarity measures such as root mean squares, normalized cross correlation, and normalized mutual information may not be reliable surrogates for image registration accuracy. Kirby et al. developed a two-dimensional deformable phantom to quantitatively verify B-spline deformable image registration algorithms. It was reported that the B-spline algorithms with four different intensity metrics (cross correlation, mutual information, sum of absolute differences, and sum of squared difference) resulted in at least 3 mm registration error for 24–25 of the 32 points at which the registration errors were estimated.⁹ For alignment of head and neck image volumes, average registration errors of 3.3 mm have been reported using B-splines and normalized mutual information.¹⁰

In order to prevent physically implausible deformation maps, there have been efforts to use mathematical or biomechanical penalties or constraints. Han et al. studied alignments in the head and neck, in which deformation of surface points was smoothed by minimizing the magnitude of displacement gradients.¹¹ Sorzano et al. developed a mathematical penalty term by using the divergence and curl of displacement vector field (DVF), represented as B-spline model, to enhance smoothness of the deformation field.¹² Sdika proposed constraints on the Jacobian of transformation and its derivatives in order to prevent noninvertible transformation.¹³ Rohlfing et al.¹⁴ developed a volume-preserving or incompressibility penalty defined as the integral of the absolute logarithm of the Jacobian so that local deviations of the Jacobian from unity were discouraged.

Rigidity penalties imposed on the subregions of the image volume which are anatomically rigid have been also developed for deformable image registrations.^{15, 16, 17} A rigidity penalty term proposed by Loeckx et al. was based on the orthonormality of the deformation gradient tensor and was defined as the summation of the Frobenius norm of the orthonormality condition.¹⁵ Staring et al.¹⁷ applied the orthonormality-preserving rigidity penalty combined with the affinity penalty which requires the second order derivatives of the displacement to be zero and the properness penalty which requires the determinant of the deformation gradient tensor to be one. They tested the method on the images of three dimensional thorax CT and digital subtraction angiography. However, this orthonormality-based rigidity penalty has a potential to fail to properly work with images that contain multiple rigid bodies in close proximity such as cervical vertebrae in the neck region as considered in this investigation; in fact, the “existing” orthonormality penalties do not work properly with these images. Since the existing penalty lacks the ability to separately preserve rigidity of multiple objects in a close proximity, imposing the penalty on regions containing interfaces between rigid bodies (which exhibit abrupt change in displacement field) would result in displacement fields that are either unrealistically smooth, and thus fail to accurately capture the motions between rigid vertebral bodies.

The purpose of this study is to develop a novel rigidity penalty suitable for the deformable registration of tightly located skeletal components in the head and neck in planning and daily treatment CT scans of patients undergoing radiotherapy. The proposed rigidity penalty is designed to preserve intervoxel distances within each rigid component. To calculate this distance-preserving rigidity penalty, the intervoxel distances are only calculated for the voxel pairs that belong to the same rigid object. By allowing rigidity of each bony object to be independently preserved while not penalizing relative orientation of disconnected objects, the proposed penalty decreases the possibility of local misalignments, which cannot otherwise be corrected by the existing rigidity penalty in regions containing multiple rigid bodies in close proximity. Furthermore, this penalty should not impact the intensity-driven deformation of soft tissue distal from the bony voxels.

METHODS

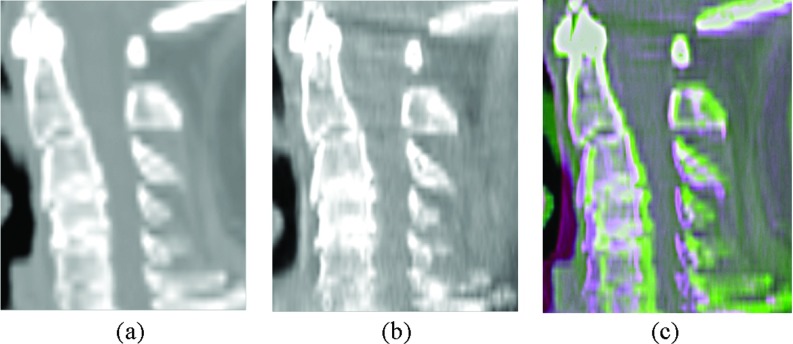
A new rigidity penalty was developed in order to improve the accuracy of deformable image registration of the cervical vertebrae in the neck, where the deformation occurs mainly due to neck articulation. Rigid alignment is clearly insufficient to describe daily variations, as illustrated in Fig. 1. Setup based on rigid alignment of the reference and target images at the C2 vertebra, while minimizing the likelihood of increased dose to the spinal cord for this particular treatment, results in significant variations of the locations of the remaining vertebra and the neck as a whole.

Figure 1.

Sagittal cuts of (a) a planning CT image and (b) a treatment CBCT image, and (c) the rigid alignment of the images at the C2 vertebra.

Deformable image registration

Deformable image registration computes a voxel-to-voxel transformation φ(x) of coordinates x of the reference image with intensity field I_R to the ones of the target image with intensity field I_T. Intensity-based image registration is, in general, formulated as an optimization problem to find the transformation that minimizes the intensity difference between the reference and target images. Mutual information (MI) is one of the most commonly used similarity metrics between images with different contrasts.^{18, 19}

Typically, the displacement u of the target image from the reference image is approximated as linear combination of B-spline basis function,²⁰

$$\phi ({\mathit{x}}_k;{\mathit{c}}_k)={\mathit{x}}_k+\mathit{u}({\mathit{x}}_k;{\mathit{c}}_k),$$ (1)

where x_k is the coordinates of the kth voxels in the reference image. The optimal B-spline coefficients c = (c₁, c₂, …, c_n) for each B-spline knot are iteratively determined as in Eq. 2 through numerical optimization:

$${\mathit{c}}^{*}=\arg \underset{\mathit{c}}{min}F\left(\mathit{c}\right),$$ (2)

where F(c) is the image dissimilarity metric.

Alternatively, the objective function can be a weighted sum of the image dissimilarity metric F(c) and penalty term P(c) as

$${\mathit{c}}^{*}=\arg \underset{\mathit{c}}{min}\left\{F\left(\mathit{c}\right)+w·P\left(\mathit{c}\right)\right\},$$ (3)

where w represents a weight factor.

In this study, intensity-based image registration with multi-resolution B-spline was implemented using Elastix, which is open source software for rigid and deformable registration of images (http://www.isi.uu.nl/Elastix).²¹ The deformable image registration begins with low resolution image which is down-sampled by a factor of 4 in the left-right (LR) and anterior-posterior (AP) directions. Then, the resolution of the reference and target images are doubled after each levels of registration are finished.

Existing orthonormality-based rigidity penalty

The orthonormality condition of the deformation gradient tensor F = ∂φ(x)/∂x is equivalent to the condition of zero strain tensor or zero right Cauchy-Green tensor, according to the finite strain theory.²² Typically, the orthonormality-preserving rigidity penalty term can be described as the sum of the squared Frobenius norm of F^TF − I over the rigid regions in reference images.¹⁵ Staring et al. improved this orthonormality-based rigidity penalty by supplementing with two other conditions (affinity and properness, as previously mentioned).¹⁷ For simplicity, this improved penalty will be referred to as the orthonormality-based rigidity penalty in this paper.

Proposed distance-preserving rigidity penalty

The proposed rigidity penalty term is based on fundamental geometric characteristic of rigid bodies: the distance between any two points in a rigid body should remain constant after deformation. Similarly, the distance between any two voxels, which belong to the same rigid object, is required to be constant before and after deformation. By imposing this constraint only on voxel pairs within the same rigid object, the proposed rigidity penalty has the advantage that rigidities enforced to multiple rigid objects can be uncoupled. On the other hand, the existing rigidity penalties enforced to different rigid regions may become interrelated in a close proximity since their values are simply determined by local deformation gradients at a voxel, not depending on which rigid region the voxel and neighboring voxels belong to.

The penalty term is defined as the normalized sum of the squared difference of squared intervoxel distance within each rigid body; for each voxel of a rigid component, the sum of the squared difference is normalized to the number of voxels that belong to both the same rigid object and its neighborhood, and the overall sum is normalized to the total number of voxels in rigid bodies:

$$\begin{array}{c}\hfill P\left(\mathit{c}\right)=\frac{\sum _{i\in \{1,...,N_R\}}\sum _{j\in R_i}\frac{1}{|R_i\cap P_j|}\sum _{k\in R_i\cap P_j}{\left[{\left\{d_{jk}^{\prime }\left(\mathit{c}\right)\right\}}^2-d_{jk}^2\right]}^2}{\sum _{i\in \{1,...,N_R\}}|R_i|},\end{array}$$ (4)

where N_R is the number of rigid bodies in the reference image, R_i ⊂ {1, 2,…, N} is a set of indices of voxels that belong to the ith rigid body, P_j ⊂ {1, 2, …, N} is a set of indices of voxels that belong to the neighborhood of the jth voxel (26-connected voxels are considered neighbors of a voxel), and

$$d_{jk}=\Vert {\mathit{x}}_j-{\mathit{x}}_k\Vert ,$$ (5)

$$\begin{array}{ccc}\hfill d_{jk}^{\prime }\left(\mathit{c}\right)& =& \Vert \phi ({\mathit{x}}_j;{\mathit{c}}_j)-\phi ({\mathit{x}}_k;{\mathit{c}}_k)\Vert \hfill \\ & =& \Vert {\mathit{x}}_j+\mathit{u}({\mathit{x}}_j;{\mathit{c}}_j)-{\mathit{x}}_k-\mathit{u}({\mathit{x}}_k;{\mathit{c}}_k)\Vert .\hfill \end{array}$$ (6)

Case study

Deformable image registrations were performed on 25 pairs of the CT and CBCT images from five patients and the corresponding ground-truth DVFs were generated by using the rigid transformations measured by surface registrations of the surface models of the cervical vertebrae.

Before performing deformable image registration, each pair of planning CT and daily treatment CT images were roughly aligned by rigid registration. For the deformable image registration, a multi-resolution strategy was utilized (three resolutions were applied in this study). After each level of registration, reference and target images were up-sampled by a factor of 2 only in the transverse plane so that the final resolution reached the resolution of the original images. For the three resolutions, the B-spline grid spacing was set to 32, 16, and 8 voxels in the transverse plane; at the final level of the registration with the highest resolution, the B-spline grid spacing was set to 1 voxel through the axial direction. The voxel sizes of the planning CT images ranged from (0.94, 0.94, 3.0) mm to (1.37, 1.37, 3.0) mm.

For fair comparisons, the existing orthonormality-based penalty developed by Staring et al. and the proposed distance-preserving rigidity penalty were both implemented on Elastix, which is open source software for deformable image registration. For both penalties, a gradient descent algorithm was utilized with 300, 300, and 500 iterations defined for the three resolutions.²³ The parameter a, which controls the gain factor in the optimization algorithm (see Spall et al.²³), was set to a = 10 000.0 for all experiments except with large weight parameters; with w = 0.2 for the existing rigidity penalty and w = 0.02 for the proposed rigidity, the parameter was halved to 5000.0 for convergence.

Generation of the computed DVFs

In order to generate the ground-truth DVFs for each image pair, the planning CT image and five daily treatment CBCT images for each of five patients were subject to segmentation and surface model generation. Voxels that belong to the five cervical vertebrae were automatically segmented by thresholding intensity values on both the reference and target images, and manual modifications were applied for separating each vertebral body from neighboring ones. The segmented voxel sets were then converted to the corresponding surface models.

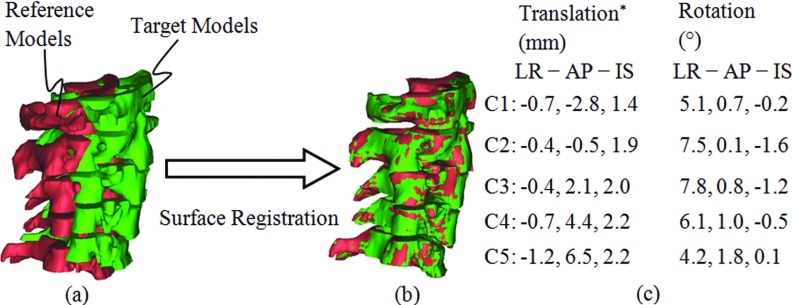
Rigid motions of the cervical vertebrae were measured by registering the surface models by minimizing the distances between them. The registration of each pair of the surface models results in a 4 × 4 transformation matrix from which a translation vector and rotation angles are calculated. The initial alignment in reference to the C2 vertebra was subtracted from the resultant translation vector. An example pair of the surface models before and after the registrations is shown in Figs. 2a, 2b, respectively, and an example of the resulting translations and rotations are summarized in Fig. 2c for the LR, AP, and inferior-superior (IS) axes, indicating that each bony element individually moved somewhat relative to the neighboring elements; the rotation centers were the average coordinates of voxels within each vertebra.

Figure 2.

Illustration of surface registration: reference and target models (a) before and (b) after registrations, and (c) an example of measured translations and rotations. (*) The shift from rigid registration in reference to the C2 vertebra was subtracted from the translation vectors.

Finally, the ground-truth DVFs were calculated by using the rigid transformations, which were measured by the surface registrations.

Evaluation of registration accuracy

Deformable registrations were performed on the 25 pairs of the planning CT images and the treatment CBCT images under three different conditions: (1) without rigidity penalty, (2) with the existing rigidity penalty, and (3) with the proposed rigidity penalty. Plotting the DVFs from registrations with the ground-truth DVFs allows qualitative evaluation of the registration accuracy. The registration accuracy was quantitatively evaluated by using three measures: registration error, transformation error, and the Procrustes distance. The registration error is defined as the difference between the ground-truth DVF (generated by using surface registration) and the DVF obtained by registration. The registration error was calculated at only the image voxels which belong to five cervical vertebral bodies. The transformation error was defined as the difference between the measured transformation of the vertebral body surfaces and the average transformation in DVF of points contained therein obtained by registration. The average transformation was obtained by solving the orthogonal Procrustes problem:²⁴ minimizing the distance between the original coordinates of each rigid body and its deformed coordinates. The transformation error was calculated for six degrees of freedom: three for translation and three for rotation. Translation was calculated as the distance between the geometric means of the original and deformed coordinates of voxels within vertebrae. The “Procrustes distance” was defined as the distance between the deformed coordinates from the DVF and the transformed coordinates by the average transformation. This analysis evaluates the effect of the penalties on preserving the shape of the voxel grid in each bony element, by quantifying the residual local deformation using the translation vector and rotation matrix obtained by the orthogonal Procrustes analysis.

RESULTS

The weight parameter w was experimentally determined in order to control the relative effect between the image metric and penalty term. Since the magnitude of the image discrepancy measure (negative of mutual information) is less than 1 and both the rigidity penalty terms are normalized to the number of voxels that belong to rigid regions, it can be expected that the magnitude of the weight parameter would not differ significantly from 1. The weight parameter was optimized by performing deformable image registrations with a few choices of weight parameters. The resulting optimal weights were 0.1 for the existing rigidity penalty and 0.01 for the proposed rigidity penalty. In addition, the relative weights of each terms related to affinity, orthonormality, and properness were chosen as 100.0, 1.0, and 2.0, respectively, in the existing orthonormality-based penalty, which were already optimally chosen for the alignment of CT images in Staring et al.¹⁷ It was also reported, in their study, that the registration results with the existing orthonormality-based rigidity penalty were not sensitive to the selection of the relative weights. All registrations with the proposed distance-preserving rigidity penalty were completed within 7 min on computers of a cluster which is comprised of AMD Opteron and Intel Nehalem processors.

Generation of the computed DVFs

Among the measured translations and rotations obtained by the surface registration, the translation in the AP direction and the rotation with respect to the LR axis were largest. The translation was largest for lower cervical vertebra in all directions (farthest from the setup point for the patients). However, there was no clear correlation between the translations and rotations.

The statistics of the measured translations and rotations are summarized in Tables 1, 2 where mean, standard deviation, and range of the motions were shown for three directions: LR, AP, and IS. The translation along the AP axis was most outstanding, being the smallest at the C2 vertebra (patient positioning point for treatment) and larger for lower cervical vertebra with a maximum displacement of 6.5 mm. The largest rotation (7.8°) was observed at the C3 vertebra about the LR axis. Furthermore, the largest rotation with respect to the IS axis was 6.6°, which was observed at the C1 vertebra.

Table 1.

Translation in the LR, AP, and IS directions of the five cervical vertebrae compared to the CBCT reference images taken at the first treatment fraction. Values are expressed as mean (SD) [range].

	Left-right (mm)	Anterior-posterior (mm)	Inferior-superior (mm)
C1	0.1 (0.7) [−1.6 to 1.5]	−0.6 (1.2) [−2.8 to 1.8]	−0.3 (0.8) [−2.2 to 1.4]
C2	0.0 (0.4) [−0.7 to 0.6]	−0.2 (0.4) [−0.9 to 0.8]	0.0 (0.8) [−1.5 to 1.9]
C3	0.1 (0.5) [−1.2 to 0.9]	0.4 (1.2) [−2.0 to 2.2]	0.3 (0.8) [−0.9 to 2.0]
C4	0.2 (1.1) [−2.1 to 2.3]	0.7 (2.2) [−3.5 to 4.4]	0.7 (0.9) [−0.9 to 2.2]
C5	0.1 (1.6) [−2.9 to 3.3]	0.9 (3.2) [−5.0 to 6.5]	0.8 (0.9) [−0.8 to 2.7]

Table 2.

Rotations about the LR, AP, and IS axes of the five cervical vertebrae compared to the CBCT reference images taken at the first treatment fraction. Values are expressed as mean (SD) [range].

	Left-right (deg)	Anterior-posterior (deg)	Inferior-superior (deg)
C1	0.4 (2.1) [−3.3 to 5.1]	0.2 (1.0) [−1.9 to 1.9]	−0.4 (2.6) [−3.4 to 6.6]
C2	2.2 (3.2) [−3.0 to 7.5]	0.1 (1.2) [−2.8 to 2.6]	0.2 (2.6) [−4.0 to 5.8]
C3	2.1 (3.6) [−4.7 to 7.8]	0.2 (1.2) [−1.9 to 2.9]	0.0 (2.5) [−4.4 to 4.7]
C4	1.5 (3.3) [−5.0 to 6.1]	−0.1 (1.6) [−2.5 to 3.2]	−0.1 (2.6) [−5.2 to 4.3]
C5	0.2 (2.8) [−3.8 to 5.4]	0.7 (1.3) [−1.3 to 3.2]	0.4 (2.2) [−4.1 to 3.9]

The mean of the displacement magnitude was largest at the lowest vertebra (C5) for all patients, and ranged from 0.9 mm to 4.0 mm across the patients. The maximum displacement was 8.8 mm at the C5 vertebra for patient.

Evaluation of registration accuracy

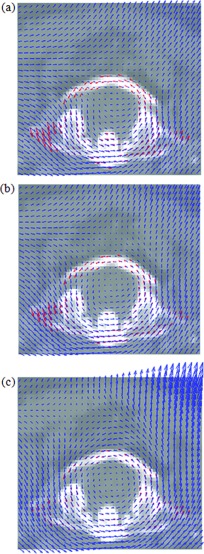
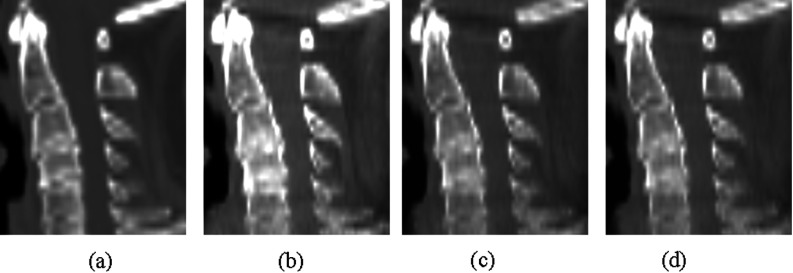
Figure 3 shows comparisons of the DVFs from registrations with the ground-truth DVF. Figure 4 shows the comparison of the planning CT image and the deformed treatment CBCT images generated by applying the DVFs from the registration. The DVFs without and with rigidity penalty (either existing or proposed) transformed bone voxels in the target image visibly close to those in the reference image, indicating that all image registrations performed reasonably well in terms of intensity matching. However, the detailed examination of the DVFs in Fig. 3 reveals that the unpenalized intensity-based deformable image registration resulted in the deformation maps that lacked biomechanical consistency in the skeletal elements, where considerable local deformation was observed in the vertebral bodies. The discrepancies of the DVFs compared to the ground-truth DVF, which can be seen from Figs. 3a, 3b, are due to relatively large rotation of C1 vertebra about the IS axis (6.6° in Fig. 3). This type of misalignment was well corrected by the proposed rigidity penalty while it can be still observed in the DVF with the existing rigidity penalty.

Figure 3.

Comparison of DVFs from registration (a) without penalty, (b) with the existing penalty, and (c) with the proposed penalty to the groundtruth DVF, which is plotted only at the bony regions.

Figure 4.

Sagittal cuts of (a) a planning CT image and treatment CBCT images deformed by DVFs from registration (b) without penalty, (c) with the existing penalty, and (d) with the proposed penalty, corresponding to the DVFs shown in Fig. 3.

The mean magnitudes and standard deviations of the registration errors are summarized in Table 3. Compared to the mean magnitude of (0.42, 0.32, 0.57) mm obtained by the intensity-based deformable image registration without rigidity penalty, the mean magnitude of registration error was reduced to (0.13, 0.16, 0.38) mm with the proposed distance-preserving penalty. Furthermore, the values were also smaller than (0.21, 0.20, 0.43) mm obtained with the existing orthonormality-based penalty. The mean magnitude of the maximum registration error was also reduced by the proposed distance-preserving rigidity penalty to (0.86, 1.12, 1.33) mm as compared to (2.11, 2.49, 2.46) mm without penalty and (1.53, 1.64, 1.64) mm with the existing orthonormality-based rigidity penalty.

Table 3.

Registration errors between the DVFs in the LR, AP, and IS directions of the five cervical vertebrae without and with the rigidity penalties.

	Intensity-based	Orthonormality-based	Distance-preserving
Registration error (mm)
Mean magnitude	(0.42, 0.32, 0.57)	(0.21, 0.20, 0.43)	(0.13, 0.16, 0.38)
Standard deviation	(0.38, 0.42, 0.61)	(0.23, 0.25, 0.34)	(0.11, 0.17, 0.26)
Mean magnitude of maximum error	(2.11, 2.49, 2.46)	(1.53, 1.64, 1.64)	(0.86, 1.12, 1.33)

The mean magnitudes and standard deviations of the transformation errors are summarized in Table 4. For both the translations and rotations of all vertebrae, the errors were reduced by the rigidity penalties. The transformation errors resulting from the deformable image registration with the rigidity penalty terms were similar to each other. The Procrustes distances are also summarized in Table 4. The Procrustes distances for the proposed distance-preserving penalty were less than those for no rigidity penalty and the existing orthonormality-based penalty: 0.11 mm (0.03 mm) versus 0.53 (0.11 mm) and 0.28 mm (0.04 mm).

Table 4.

Comparison of the transformation errors and Procrustes distance between the DVFs without penalty and with the rigidity penalties.

	Intensity-based	Orthonormality-based	Distance-preserving
Translation (mm)
Mean magnitude	(0.34, 0.13, 0.38)	(0.14, 0.11, 0.37)	(0.11, 0.11, 0.36)
Standard deviation	(0.41, 0.16, 0.32)	(0.16, 0.13, 0.25)	(0.13, 0.13, 0.25)
Rotation (deg)
Mean magnitude	(1.22, 0.50, 0.61)	(0.65, 0.32, 0.33)	(0.58, 0.34, 0.28)
Standard deviation	(1.32, 0.62, 0.84)	(0.69, 0.40, 0.42)	(0.70, 0.45, 0.35)
Procrustes distance (mm)	0.53 (0.11)	0.28 (0.04)	0.11 (0.03)

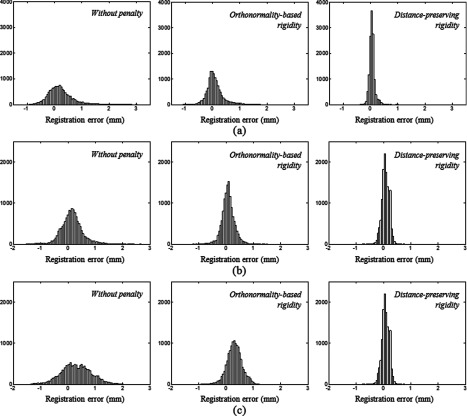
The difference of the effects of the penalty terms was further explored by plotting histograms of registration errors (Fig. 5). For the deformable image registration without penalty, the registration errors were distributed over a wide range in all directions while many of the errors were still close to zero. With the distance-preserving rigidity penalty, the distribution of registration errors was better concentrated around zero than those without penalty or with the existing orthonormality-based rigidity penalty, indicating that some large deviations were corrected by the proposed penalty.

Figure 5.

Histograms of the registration errors which resulted from the deformable image registrations between the planning CT scan and treatment CBCT scan at the 7th fraction of Patient 1 in (a) LR, (b) AP, and (c) IS directions.

The displacement components in the LR directions plotted in Fig. 6a show how the resultant DVFs with the existing and proposed penalties recovered the ground-truth DVF exhibiting abrupt changes across the vertebrae. Compared to the DVF obtained with the existing orthonormality-based penalty, the DVF obtained with the proposed distance-preserving penalty more accurately recovered the acute changes in the displacement, especially at regions within the C1 vertebra.

Figure 6.

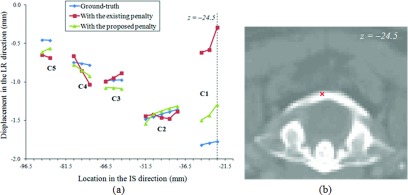
Plots of (a) the LR displacement component through an IS axis whose location is indicated in (b) an axial cut of the planning CT (Patient 1); the axial plane in (b), which is indicated as a dashed line in (a), coincides with the axial plane in Fig. 3.

In order to investigate the impact of the weight parameter on the registration accuracy with the rigidity penalties, deformable image registrations were additionally performed by varying the weight parameters. The weight parameter was increased or decreased by a factor of 2 from the optimal weight parameter, which is 0.1 for the existing orthonormality-based rigidity penalty and 0.01 for the proposed distance-preserving rigidity penalty. The resultant registration errors were summarized in Tables 5, 6. As the weight parameter was decreased from 0.01 to 0.0025 for the proposed distance-preserving rigidity penalty (from 0.1 to 0.025 for the existing orthonormality-based rigidity penalty), the registration errors were increased in all directions. Comparing the variations in the registration errors between the two rigidity penalties shows that the performance of the proposed distance-preserving rigidity penalty is less sensitive to the variation of the weight parameter than that of the existing orthonormality-based rigidity penalty.

Table 5.

Effect of the weight parameter on the registration errors with the existing orthonormality-based rigidity penalty.

	w = 0.025	w = 0.05	w = 0.1	w = 0.2
Registration error (mm)
Mean magnitude	(0.26, 0.25, 0.47)	(0.23, 0.22, 0.44)	(0.21, 0.20, 0.43)	(0.31, 0.22, 0.42)
Standard deviation	(0.30, 0.32, 0.41)	(0.26, 0.28, 0.37)	(0.23, 0.25, 0.34)	(0.25, 0.28, 0.34)
Mean magnitude of maximum error	(1.77, 2.15, 1.94)	(1.66, 1.91, 1.79)	(1.53, 1.64, 1.64)	(1.63, 1.56, 1.58)

Table 6.

Effect of the weight parameter on the registration errors with the proposed distance-preserving rigidity penalty.

	w = 0.0025	w = 0.005	w = 0.01	w = 0.02
Registration error (mm)
Mean magnitude	(0.14, 0.16, 0.40)	(0.13, 0.16, 0.39)	(0.13, 0.16, 0.38)	(0.31, 0.19, 0.38)
Standard deviation	(0.13, 0.18, 0.29)	(0.12, 0.17, 0.28)	(0.11, 0.17, 0.26)	(0.16, 0.22, 0.27)
Mean magnitude of maximum error	(1.02, 1.38, 1.55)	(0.94, 1.26, 1.44)	(0.86, 1.12, 1.33)	(1.17, 1.04, 1.16)

For the large weight parameters (w = 0.2 for the existing orthonormality-based rigidity penalty and w = 0.02 for the proposed distance-preserving rigidity penalty), the registration results shown in Tables 5, 6 were obtained with a = 5000. This is because the registrations converged to unreasonable solutions when the gain factor a was set to 10 000, possibly indicating a numerical instability of the optimization algorithm.

DISCUSSION

The proposed distance-preserving rigidity penalty improved the accuracy of deformable image registration of the five cervical vertebral bodies in the neck compared to B-spline intensity-based deformable image registration without rigidity penalty. All quantification measures utilized in this study showed the proposed distance-preserving rigidity penalty better aligned the five cervical vertebrae in CT-CBCT registrations than the existing orthonormality-based rigidity penalty. It is noteworthy to mention that, with the proposed penalty, deformable image registration of the cervical vertebrae achieved accuracies smaller than the sizes of image voxels in all directions. The mean magnitudes and standard deviations of the registration errors were (0.13, 0.16, 0.38) mm and (0.11, 0.17, 0.26) mm. Furthermore, the mean magnitudes of the maximum registration errors were comparable to the voxel dimensions: (0.86, 1.12, 1.33) mm with the proposed distance-preserving penalty. Although the voxel size in the axial direction was large, the achieved registration accuracy was much smaller than the slice thickness.

Since the registration errors were averaged over a large number of voxels belonging to the cervical vertebrae (ranging from 12 986 to 22 653), some improvements may not appear in the comparisons of the mean magnitudes of the registration errors. In other words, the statistics of the registration errors calculated at a large number of the voxels may not be considered as an equivalent concept to the target registration error calculated with a few number of landmark pairs as shown in other studies.^{9, 10} As shown in the histograms of the registration errors (Fig. 5), purely intensity-based deformable image registration failed to recover all rigid body motions of the five cervical vertebrae. Moreover, the discrepancies observed in the C1 vertebra were not corrected by the existing orthonormality-based rigidity penalty while these registration errors were prevented by applying the proposed distance-preserving rigidity penalty to deformable image registration.

The comparisons of the transformation errors and Procrustes distances between the DVFs showed the details of how the proposed penalty improved the DVFs compared to no penalty and the existing penalty. The difference in the Procrustes distance between the DVFs was relatively large while the transformation errors were comparable to each other. The relatively small difference in transformation error indicated that the DVFs with the existing penalty were, on average, shaped closely to the ground-truth rigid motions. However, the large values in the Procrustes distance for the DVFs with the existing penalty indicated that there exist some discrepancies in the resulting DVFs compared to the ground-truth DVFs, which cannot be captured by the transformation errors. These results suggest the proposed distance-preserving penalty is capable of reducing registration errors, which cannot be completely corrected by the existing orthonormality-based penalty in the deformable image registration of multiple rigid bodies in close proximity.

The comparison of the DVFs indicated that the intensity-based similarity metric may potentially mislead deformable image registration in articulated skeletal regions. As shown in Fig. 3, deformable image registration of head and neck images resulted in physically unreasonable DVFs without rigidity penalties. However, these substantial deviations in the DVF were not visible in the comparison of images in Fig. 4. This observation supports that comparing images is not a rigorous way of verifying registration results as well as that intensity-driven deformable image registration should be provided with additional guidance such as biomechanical penalties when the transformations are to be used for dose accumulation or functional mapping.

The use of the rigidity penalty term may have an impact on the accuracy of dose accumulation of surrounding tissues such as spinal cord. As can be seen in Fig. 3, both the orthonormality-based and distance-preserving rigidity penalties affected the deformation in the surrounding regions. A further investigation needs to be carried out to estimate the dosimetric impact of such residual uncertainty.

The rigid motions measured by the surface registration of individual vertebrae ranged from −5.0 to 6.5 mm for translation and from −4.7° to 7.8° for rotation as shown in Tables 1, 2. The results were comparable to those reported in Ahn et al.²⁵ For the magnitude of relative vertebral motions clinically observed from the five patients, the proposed penalty could successfully preserve rigidity of five cervical vertebral bodies during deformable alignment.

CONCLUSIONS

We proposed a new rigidity penalty designed to preserve intervoxel distance within each bony element and verified that it improved the integrity of deformable image registration of multiple skeletal components in the neck anatomy using 25 CT-CBCT image pairs from five patients. This distance-preserving penalty achieved subvoxel registration accuracy in all directions and outperformed the existing penalty designed to preserve the orthonormality of deformable gradient tensor, in terms of aligning multiple rigid elements in close proximity.