Abstract
Purpose: Performing lobe-based quantitative analysis of the lung in computed tomography (CT) scans can assist in efforts to better characterize complex diseases such as chronic obstructive pulmonary disease (COPD). While airways and vessels can help to indicate the location of lobe boundaries, segmentations of these structures are not always available, so methods to define the lobes in the absence of these structures are desirable.
Methods: The authors present a fully automatic lung lobe segmentation algorithm that is effective in volumetric inspiratory and expiratory computed tomography (CT) datasets. The authors rely on ridge surface image features indicating fissure locations and a novel approach to modeling shape variation in the surfaces defining the lobe boundaries. The authors employ a particle system that efficiently samples ridge surfaces in the image domain and provides a set of candidate fissure locations based on the Hessian matrix. Following this, lobe boundary shape models generated from principal component analysis (PCA) are fit to the particles data to discriminate between fissure and nonfissure candidates. The resulting set of particle points are used to fit thin plate spline (TPS) interpolating surfaces to form the final boundaries between the lung lobes.
Results: The authors tested algorithm performance on 50 inspiratory and 50 expiratory CT scans taken from the COPDGene study. Results indicate that the authors' algorithm performs comparably to pulmonologist-generated lung lobe segmentations and can produce good results in cases with accessory fissures, incomplete fissures, advanced emphysema, and low dose acquisition protocols. Dice scores indicate that only 29 out of 500 (5.85%) lobes showed Dice scores lower than 0.9. Two different approaches for evaluating lobe boundary surface discrepancies were applied and indicate that algorithm boundary identification is most accurate in the vicinity of fissures detectable on CT.
Conclusions: The proposed algorithm is effective for lung lobe segmentation in absence of auxiliary structures such as vessels and airways. The most challenging cases are those with mostly incomplete, absent, or near-absent fissures and in cases with poorly revealed fissures due to high image noise. However, the authors observe good performance even in the majority of these cases.
Keywords: lobes, pulmonary, segmentation, computed tomography (CT), fissures, lungs
INTRODUCTION
Anatomically, the lungs consist of distinct lobes: the left lung is divided into upper and lower lobes, while the right lung is divided into upper, middle, and lower lobes. Each lobe has airway, vascular, and lymphatic supplies that are more or less independent of those supplies to other lobes. Fissures (left oblique, right oblique, and right horizontal) define the most salient boundary cues between the lobes and present as 3D surfaces that have greater attenuation (i.e., are brighter) than the surrounding lung parenchyma in CT datasets. However, advanced emphysema and certain imaging protocols (low-dose, and acquisitions at relaxed exhalation) can make it difficult to detect fissures, and so-called incomplete fissures are not uncommon.1 In such instances, it is also possible to implicitly define lobe boundaries by considering surfaces maximally distant from the dedicated airway and vessel trees supplying each lobe.
Emphysema is a main component of chronic obstructive pulmonary disease (COPD), a disease with a worldwide prevalence of 10% in adults,2 and is characterized by the destruction of the lung parenchyma. There are ongoing efforts to produce clinically relevant disease subtypes for better diagnosis and patient management based on regional quantitative measures of emphysema and other radiographic phenotypes and clinical manifestations. Performing lobe-based quantitative analysis can assist such efforts, especially in the context of epidemiological and genetic studies.3 Lobe specific measurements can also help determine whether patients are good candidates for procedures such as lung volume reduction surgery based on the their emphysema distribution.4 These issues motivate the need for automatic and reliable lobe segmentation algorithms.
A variety of lung lobe segmentation approaches have been proposed that use auxiliary structures (airway and vessel trees) to assist with lobe boundary identification.5, 6, 7, 8, 9, 10 In Ref. 5, the authors address the issue of missing fissures. They use contextual information drawn from segmentations of the lung, fissure, and bronchial tree in conjunction with a multiatlas selection mechanism to segment datasets that exhibit incomplete fissures. They state that their algorithm can fail in cases with lobe boundaries not well represented in their atlases. We propose a lobe boundary modeling approach that we believe provides a more flexible alternative for capturing and using shape information. Furthermore, they report that their fissure segmentation routine has a typical run time of 90 min on a single core, 2.4 GHz processor. The method we will describe effectively samples the image space for fissure locations in about 4.5 min, and the complete run time is about 15 min on average.
The method proposed in Ref. 6 does not rely on the presence of fissures but instead relies on the absence of vessels in the vicinity of the fissures (leveraging the dedicated blood supplies to each lobe). This work was later extended to incorporate fissure image features for improved results11, 7 uses vascular and airway tree segmentations to provide contextual clues for fissure locations. They present results on normal subjects and subjects with mild to moderate emphysema (where the latter datasets were acquired at total lung capacity). Additionally, they report that manual interaction was needed to produce satisfactory results in 25% of the cases.10 combined vessel and airway tree segmentations with Voronoi analysis to identify the most likely location for lobar fissures.
Fissure detection and enhancement methods as well as lobe segmentation algorithms designed without recourse to auxiliary structures have also been proposed.12 present a 2D shape-based curve growing model for the purpose of fissure segmentation. Results were given on ten datasets for the oblique fissures only, and manual correction was needed on a small number of CT regions. In Ref. 13, the authors use Hessian and structure-tensor based filters to enhance the fissures14 and present a lung lobe segmentation method that only relies on the detection of fissures, but they only perform detection for the oblique fissures; the right horizontal fissure is not detected automatically. Also, results are reported for 22 datasets: 17 normals and 5 with conditions (peripheral nodules, mediastinal lymph nodes, and airway obstruction) unlikely to adversely affect the appearance of fissures in HRCT images. They suggest that deformable models are a natural extension to their work but state that the effectiveness of approaches based on such models are sensitive to initialization. However, we show that our lobe boundary (deformable) models are capable of attracting to and defining particles that indicate lobe boundaries. The method described in Ref. 15 involves fitting an average geometrical mesh model to a fissure feature image. Results are reported on a total of 23 scans, and total execution time was reported to be approximately 90 s on a 1.4 GHz Intel Pentium CPU. However, the authors do not describe how the labeled data to which they compare were created, nor do they describe the CT datasets on which they tested (in terms of fissure completeness, presence of disease, scanning protocol, etc.), so it is difficult to fully evaluate their proposed approach.
In our earlier work, we described the use of thin plate splines (TPS) to interpolate fissure surfaces given a sparse set of sample points.16 In a similar vein,17 use implicit radial basis functions to extend incomplete fissures to the lung boundaries. They demonstrated their approach on 65 datasets, with all images acquired from patients with relatively healthy or mildly diseased lungs. Results were evaluated by visual inspection using a five point scale, and about half of the datasets were rated as good or excellent. The authors use the fissure detection method described in Ref. 18 and state that large accessory fissures can lead to segmentation failures. The lobe boundary surface model that we propose is capable of distinguishing between accessory fissures and those that truly identify lobe boundaries.
We previously showed that a small set of points (approximately 10–20) along each of the three fissures is sufficient to accurately delineate the major lobes.16 However, the points in that study were manually selected. We build on this work and automatically identify fissure locations by fitting a shape model to fissure locations detected by means of a particle system for ridge surface sampling previously described by Ref. 19. Other fissure identification and enhancement schemes have been proposed, namely.18, 29 We choose the particle approach because it is a fast and flexible way in which to sample likely fissure locations from the image data without prior knowledge about the fissure location, and it fits seamlessly into the TPS surface fitting stage.
The particle system detects locally planar structures; these include fissures as well as supernumerary (accessory) fissures and nonfissure (noise) structures. In order to identify fissure particles, we apply a novel approach to incorporating lobe boundary shape information: by fitting these boundaries to particle data we are able to reliably identify image features representing true fissure surfaces.
In our earlier work, we describe a proof of concept study to investigate the efficacy of fitting thin plate spline surfaces to particles data using a maximum a posteriori (MAP) estimation formulation.20 In that approach, ten control points are used to describe each of the three lobe boundaries, and their values are optimized to achieve a fit to the particles data. After surface fitting, a postprocessing stage is performed to further remove nonfissure particles. We reported algorithm execution times of 30–45 min, with the most time consuming stage being the surface fitting. The lengthy surface fitting stage is a direct result of the size of search space (ten dimensional for each of the three lobe boundaries). Reducing the dimensionality would speed fitting, but by eliminating control points the ability to capture surface variation diminishes.
In this paper, we describe an alternative formulation in which we represent a population of training surfaces using principal component analysis (PCA) and fit surfaces by adjusting modes of variation, not individual control points. This also allows us to use many more than ten points to represent each of the three boundary surfaces. Note that in both our previous papers and the approach proposed here we use essentially the same ridge surface sampling scheme. Although here we describe a study justifying parameters used for ridge surface sampling, and we illustrate the effect of these parameters on the ability to detect features of interest (namely, pulmonary fissures).
As in Ref. 20, we apply a filtering stage after surface model fitting to further reduce the number of noise particles. Here we elaborate on a more sophisticated and principled approach using Fischer's linear discriminant to perform classification on the particles using the fit surfaces. We will show that performing postprocessing in this way yields a single parameter that can be set to generate good performance across a wide range of cases. The methodology described in Ref. 16 is then used to acquire the final lung lobe segmentation by fitting thin plate spine surfaces through the remaining particles.
The use of shape models to identify lobe boundaries in both inspiratory and expiratory scans based on ridge feature samples is the major contribution of this work. We show results in a validation set from the COPDGene study using 100 cases from both inspiratory and expiratory acquisitions that illustrate the utility of our approach. The paper is outlined as follows. In Sec. 2, we describe the steps in our approach: particles-based ridge surface sampling (Sec. 2A), lobe boundary model construction (Sec. 2B), boundary model fitting (Sec. 2C), particle classification (Sec. 2D), postprocessing and lobe voxel labeling (Sec. 2E). We provide the necessary mathematical detail for implementing our proposed approach. Our experimental design is given in Sec. 3 and includes a description of the test and training data used in our study, parameter selection schemes, and evaluation methods. Quantitative and qualitative results are presented in Sec. 4; Sec. 5 provides a discussion of our method and the reported results.
METHODS
In this section, we describe our approach to lobe boundary shape modeling, ridge surface sampling, and lobe segmentation. A brief overview of the algorithm is given, and we elaborate in Subsections 2A, 2B, 2C, 2D, 2E. At a very high level, the goal of our algorithm is to detect a set of points that lie on the three lobe boundaries of interest and to fit TPS surfaces through those points to define the lobe boundaries. We assume that a lung segmentation is available so that the search can be confined within the lung region. Lung segmentation algorithms have been described in Ref. 21, so we do not elaborate on this step here. However, we do note that lung segmentation can be a very challenging task in more general circumstances. The method we have adopted performs quite well on cases in the COPDGene cohort.
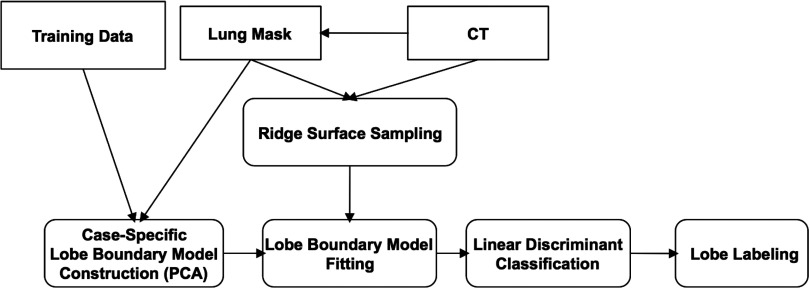
The main steps of our method are depicted in Fig. 1. The first step is ridge surface feature sampling and is an adaptation of the particle system described in Ref. 19. Particles easily identifiable as noise are removed using simple connected components filtering. Details are provided in Sec. 2A.
Figure 1.
Overview of the method steps for fissure detection and lobe segmentation.
Particles-based sampling can detect existing fissure regions in the CT image. However, nonfissure ridge features (hereafter denoted as noise) and accessory fissures are detected as well. The second step of our approach is shape model fitting and is needed to identify ridge surface particles that actually represent fissures. In Sec. 2B, we discuss the creation of the training data and the method used to build lobe boundary surface models using PCA. The PCA-based lobe boundary models are fit to the particles data by adjusting mode weights to minimize an objective function. This optimization procedure is described in detail in Sec. 2C. After optimizer convergence, we perform classification using Fisher's linear discriminant (described in Sec. 2D). This results in a set of particles highly likely to correspond to fissures. Finally, we segment the lung lobes using the approach described in Ref. 16, substituting the manually determined particle points with the particle points remaining after classification. The final lobe segmentation extraction is discussed in Sec. 2E.
Ridge surface sampling
We adopt a particle system for feature extraction described by Ref. 19. As the fissure surface between lung lobes has higher radio-opacity than the lobes themselves, the fissure can be isolated as a ridge surface, defined by Ref. 22 as the loci of points where the gradient of the image is orthogonal to the minor eigenvector of the Hessian. The particles sampling algorithm repositions points according to an image feature strength term, in our case defined as the third eigenvalue of the Hessian, and a potential energy that is a function of the distance between neighboring particles. Upon convergence, the system achieves a dense and uniform feature sampling in physical space.
The particle system results are affected by four key parameters: σgauss, λthresh, γthresh, and N. σgauss indicates the size of the Gaussian smoothing kernel used before sampling, and λthresh is a threshold on the ridge surface strength. γthresh is an upper threshold on the third standardized moment of the three Hessian eigenvalues (a perfect ridge surface might have Hessian eigenvalues {0, 0, −1}, with the third standardized moment being −1). Finally, N is the number of seed particles. We have conducted a study to determine the optimal set of parameters for the particle system, discussed in Appendix A1. For the remainder of the paper, we designate the number of particles after convergence as Np, the set of particles after convergence as P, and a single particle in P as ρ.
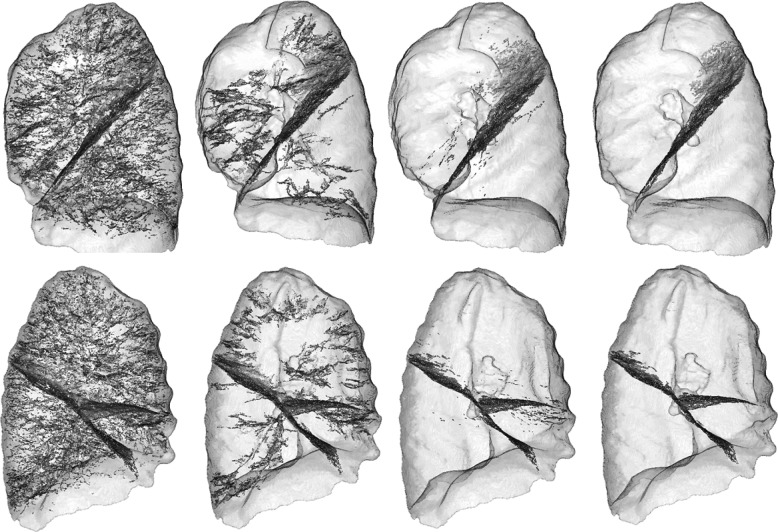
Although the particles sampling does a good job of identifying fissures, ridge surfaces that do not correspond to fissures are also sampled. However, the large majority of these false positives are easily eliminated with a simple connected-components filter as described in Ref. 20. Briefly, if two particles are sufficiently close to one another (specified with the threshold dthresh), and if the angles formed between each of their minor eigenvectors and the vector connecting the two particles are both greater than a specified angle threshold (θthresh), the particles are grouped into the same component. Intuitively, this operation will connect particles that are spatially close to each other and that lie on a surface that is approximately locally planar. After connected components are formed, we discard those that are not sufficiently large. Performance of the prefiltering operation on a typical case is illustrated by the first two columns of Fig. 3. The selection of θthresh, nthresh, and dthresh (indicating minimum component size) is described in detail in Appendix A2.
Figure 3.
Rendering of fissure particles resulting from each step of the proposed method. Particles are rendered with plate-like glyphs, and lungs are rendered semitransparently for context (sagittal view). From left to right: ridge particles sampling result and initial connected components (Subsection 2A), particles data after classification (Subsection 2D), and particles before lobe labeling (Subsection 2E). (Top) left lung; (bottom) right lung.
Lobe boundary model construction
Particles sampling tends to be sensitive but not specific: fissure regions are captured, but a great deal of other structures that are locally planar are also detected. A key component to our approach involves using lobe boundary models to identify ridge surface particles that are highly likely to represent fissures (lobe boundaries). In this section, we describe the boundary modeling process, which is based on PCA performed on a set of training data that are mapped to the input image's coordinate frame.
Definitions
Let us define as the index set of images constituting our training set. For each case in the training set, the lobe boundary is defined as the point collection
| (1) |
where s ∈ {l, h, o} letting l, h, o represent the left oblique, right horizontal, and right oblique, respectively. The ∧ symbol represents logical conjunction.
Let be the index set referring to the collection of test cases. Both and are described in Sec. 3A. Let indicate the input image, and note that the sets of cases to which and refer are disjoint.
Let represent the affine transform that results from registering each lung mask in the training set to a reference image's lung mask, , arbitrarily selected from . is used to map the manually selected fissure points from c's coordinate frame to cref's coordinate frame. This new collection of point sets is designated as
| (2) |
The reference image's lung mask in conjunction with the set | s ∈ {l, h, o} ∧ constitutes the data from which the PCA-based surface models are built. This process is described next.
Case-specific fissure model construction
We use PCA to model the surface variation across the training set for each fissure. PCA is performed in the coordinate system of the input image in the following manner.
The reference image's lung mask is registered to the input image's lung mask by means of an affine transformation . is applied to the points in in order to map them to the input image's coordinate frame. The resulting collection of point sets is then | s ∈ {l, h, o} ∧ , where | . Next, TPS surface representations are computed from these points for each of the three lobe boundaries across all 20 data sets. TPS interpolating surfaces are minimally curved surfaces that pass through all selected points. The TPS equation is given by
| (3) |
| (4) |
where U(r) = r2 log r is the radial basis function, and is the jth point in . The coefficient vector, and the weight vector, are determined from the Ns, c identified fissure points in such that the height function's bending energy is minimized.23
In order to create the PCA-based surface representation for a given fissure, s, we compute the TPS z-values for each of the 20 training data sets
| (5) |
where is the number of points in the set |, and is the jth point in . In other words, surface “height vectors” are created in the input image's coordinate system for each case in our training set, and the z-values (“heights”) are computed for the (x, y) location of every point that is mapped to the input image (for a given fissure). Constructing the height vectors in this way uses the same set of domain points for a given boundary model across all training datasets. PCA is performed on the training set of z-value vectors [Eq. 5] by computing the covariance matrix
| (6) |
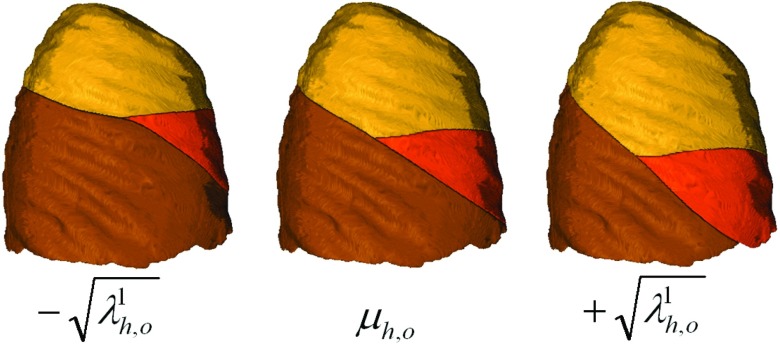
where and μs is the mean shape vector. The eigenvectors and eigenvalues of C are represented as , and , respectively. The projected z-value vector is then defined as . This follows the standard approach for applying PCA when the number of data instances is less than the dimensionality of the data space.24 The mean vector, the projected z-value vectors and the eigenvalues together with the (x, y) coordinates of the points in are saved for use in subsequent filtering stages. Note that the PCA modeling is performed independently for each of three boundary surfaces. Figure 2 illustrates the effect of adjusting the first mode of variation for the right horizontal and right oblique boundary surface models.
Figure 2.
Mean right horizontal (subscript h) and right oblique (subscript o) boundaries for a typical case (center rendering) together with changes in the first mode of variation.
The number of modes used in the PCA model is a parameter that has to be selected. We have conducted a study in Appendix A3 to find the optimal value based on the variability encountered in our shape space.
Lobe boundary model fitting
The model fitting stage that we introduce here is needed to isolate true fissure particles from large groups of nonfissure particles that can persist after the sampling stage described in Sec. 2A. Such particle groups can often be seen in scans of patients with bullae. After surface fitting, we perform classification to isolate likely fissure particles; this will be detailed in Sec. 2D.
Note that we can represent a general TPS fissure surface using the PCA representation described in Sec. 2B as ts(x, y), where the z-values used to construct the coefficient vector as and the weight vector ws are computed using
| (7) |
where Nm ⩽ Ntrain (the number of training cases in our study) is the number of modes selected to represent the variations in the training set population, and are the mode weights we adjust to achieve different fissure shapes.
Our task is to adjust the mode weights, mj, in order to find the fissure surface that best fits the particles data. We accomplish this using Nelder-Mead optimization. For each iteration of the optimization, we need to determine the nearest surface point and corresponding distance for every particle. For this we use a Newton optimizer. The details of these optimization schemes are presented in Secs. 2C1, 2C2.
Determining particle to TPS surface distance: Newton's method
In order to determine how well a given surface fits a collection of particles, it is necessary to compute the distance between a given particle and the surface. The objective function for this task is given by
| (8) |
where (xp, yp, zp) designates the particle coordinates, and ts(x, y) is the TPS surface representation for fissure, s. Note that this objective function is just the square of the distance between (xp, yp, zp) and (x, y, ts(x, y)); taking the square ensures that the objective function is differentiable for all points in the domain.
We use the Newton step, , at iteration k within a line search optimization scheme. Explicit expressions for the gradient and Hessian of the objection function are given in Appendix B. To ensure positive definiteness of the Hessian matrix, we examine the eigenvalues of ∇2fp, and if there are negative entries we reconstruct the Hessian as follows:
| (9) |
where Bk is the Hessian approximation at iteration k, and λj and qj are the jth Hessian eigenvalue and eigenvector, respectively.
Fitting TPS surface model to particles data: Nelder-Mead simplex-reflection method
The fissure surface model is fit to the particles data by optimizing the weights of the Nm modes, . The objective function that is minimized during this process is given by
| (10) |
where Np is the number of particles, ωj is the weight assigned to particle j (discussed below), dj(m) is the distance between the jth particle and the TPS surface, and θj(m) is the angle formed between the surface normal (n = [nx(x, y) ny(x, y) 1]) and the jth particle's Hessian minor eigenvector, e3. The angle between these vectors is then
| (11) |
The parameters σd and σθ are set by the user (we used values 7mm and 20° in our experiments). Note that both dj(m) and θj(m) are computed via the Newton method described in Sec. 2C1: dj(m) is determined directly as the square root of the optimal value of fp(x, y), and θj(m) is determined by computing the surface normal at the optimal parameter values, (x, y). In other words, for each of the Np particles in our dataset, Newton's method is used to determine the particle's contribution to the objective, fs, for a given choice of mode weights, m. The intuitive description of this objective function is that it penalizes particles that are far from the current surface and oriented perpendicular to it. Conversely, particles that are close to the surface and oriented parallel to the normal are rewarded.
The optimization of fs is carried out using the Nelder-Mead simplex-reflection method.25 The choice of this method is partially motivated from the intractability of closed form gradient and Hessian expressions. To initialize the simplex we used the mean of the surface model (all mode weights set to zero). The various vertices of the initial simplex were then constructed around this location in parameter space using a specified initial simplex edge length. For this quantity, we chose a value of 3 standard deviations from the mean along the shape parameter, which is large enough to capture significant variation around the mean, but not so large that the simplex takes too long to converge.
The fitting process for the left oblique fissure is carried out in a straightforward manner according to the description above, with particle weights [ωj in Eq. 10] all set to 1. The right oblique and right horizontal models are fit iteratively. Before either is fit, the particle weights, ωs, j, are computed separately according to
| (12) |
where and are as defined above for the jth particle and with respect to surface model s having mode weights ms. The mode weights are initially all set to 0 (i.e., the mean surface is used). Optimization then proceeds by fitting the right oblique model for 50 iterations, after which the particle weights are recomputed (with the updated mode weights for the right oblique). The right horizontal surface model is then fit for 50 iterations, after which the particle weights are again updated. This process repeats once more: 50 iterations for the right oblique, particle re-weighting, and then 50 iterations for the right horizontal. In this way, the particles more likely to represent a given fissure are given more weight; this prevents the right oblique model from latching on to the right horizontal particles and vice versa.
The use of PCA shape modeling provides a convenient way to detect severely distorted shape models during the fitting process. Namely, if the modes used during fitting are weighted too heavily, in indicates that the shape is being deformed in a highly irregular way. We exploit this fact to mitigate errors introduced by poor model fits to the right horizontal fissure, the most difficult of the three fissures to detect in general. We performed an experiment with the cases in our training set in which we eliminated the right horizontal particles from the particles dataset and then performed model fitting. With no right horizontal fissure particles to attract the right horizontal boundary model, it tended to gravitate to the particles defining the right oblique fissure. This leads to large right horizontal shape distortions, and we observed that in all cases one or more of the shape modes was weighted with a value of >2.0. On the other hand, when a sufficient number of right horizontal particles are present and the model is fit well, mode weights tended to be <2.0. Therefore, during the testing phase of our experiments (described below) we used the mean right horizontal boundary model in the final segmentation stage if we detected large right horizontal model distortions, as measured by mode weights exceeding 2.0. We do not apply the same approach to the other two boundary surfaces as it is rare that insufficient particles data exist for these fissures. Instead, we prefer to let the model deform in order to attract to the available signal.
Classification using Fisher's linear discriminant
After each of the three shape models has been fit to the particles data, we can use a given particle's relationship to the fit surface to further discriminate between fissure and noise. Intuitively, a particle that is close to the fit surface and has a minor eigenvector roughly parallel to the local surface normal is more likely to be a fissure particle. We can represent these two quantities for the ith particle with the feature vector xi = [di(m⋆), θi(m⋆)], where m⋆ represents the vector of mode weights at convergence of the Nelder-Mead simplex-reflection optimization, and θi(m⋆) and di(m⋆) are as defined above.
Fisher's linear discriminant provides a convenient way for projecting this two-dimensional feature vector onto a one-dimensional subspace such that the means of the two classes (noise particles and fissure particles) are well separated while also minimizing the variance of each of the classes in the projected one-dimensional space.24 Once in the projected one-dimensional space, we can use a single parameter to control the amount of noise filtering. The discriminant is given by the two-dimensional vector w,
| (13) |
where
| (14) |
and the means μs and μnoise are given by
| (15) |
| (16) |
where we have used the noise subscript to indicate noise particles and the s subscript to indicate the set of fissure particles.
Comparing columns two and three of Fig. 3 illustrate the benefit gained from this step. The selection of the discriminant, w, and the optimal threshold in the one-dimensional space that separate noise and fissure particles is described in Appendix A4.
Lobe labeling
The classification stage described above successfully eliminates most of noise particles while retaining the vast majority of the fissure particles. However, as can be seen in the third column of Fig. 3, some noise particles still persist. We perform a connected components final filtering step, as described in Ref. 20, to eliminate potential spurious particles given that the connected components formed by the particles remain largely intact after the classification stage, while the noise connected components tend to be “broken up” by classification. The final set of particles for a typical test case can be seen in the fourth column of Fig. 3.
The remaining particle points are then used to perform lung lobe voxel labeling according to the method described in Refs. 16 and 20. Briefly, this is accomplished by fitting TPS surfaces to each of the three particle sets that survive the noise reduction stages described above (recall that the classification stage assigns unique labels to each of the particles: left oblique, right oblique, or right horizontal). We do not enforce the TPS surfaces to pass directly through the particle points. Instead, we relax the interpolation with a regularization parameter value of 0.5.26 This mitigates the effect of spurious particles. The final voxel labeling is obtained by considering the original lung segmentation mask. For the left lung, all voxel locations falling below the TPS boundary surface are labeled as left lower lobe, while voxels above the boundary surface are labeled as left upper lobe. For the right lung, all voxels falling below the TPS boundary surface corresponding to the right oblique fissure are labeled as right lower lobe. All voxels beneath the TPS surface corresponding to the right horizontal fissure but above the right oblique boundary surface are labeled as right middle lobe. All remaining voxels in the right lung are labeled as right upper lobe.
MATERIALS AND EXPERIMENTAL DESIGN
In this section, we describe the test and training data and the evaluation methodology used in our study.
Testing data
We selected Ntest = 100 volumetric CT datasets from the COPDGene study,3 a multicenter investigation focused on examining the genetic and epidemiological basis of COPD and other smoking related lung diseases. Each subject enrolled in the study undergoes CT examination, with one scan acquired at full inspiration (INSP) and one scan acquired at relaxed exhalation (EXP). We randomly chose 50 inspiratory scans and 50 expiratory scans with the constraint that no inspiration-expiration pair could correspond to the same individual.
The CT examinations were performed either with GE scanners (LightSpeed 16 and LigthSpeed VCT) using the STANDARD reconstruction kernel or Siemens scanners (Sensation 64, Definition, DefinitionAS+, and Somaton) using the B31f reconstruction kernel. Slice thickness ranged from 0.625 mm to 1.25 mm. Tube current for the expiratory scans was either 100 mA or 110 mA, and for inspiratory scans it was either 400 mA or 440 mA. Tube voltage for all scans was 120 kV. In-plane pixel spacing ranged from 0.54 mm to 0.85 mm across all scans.
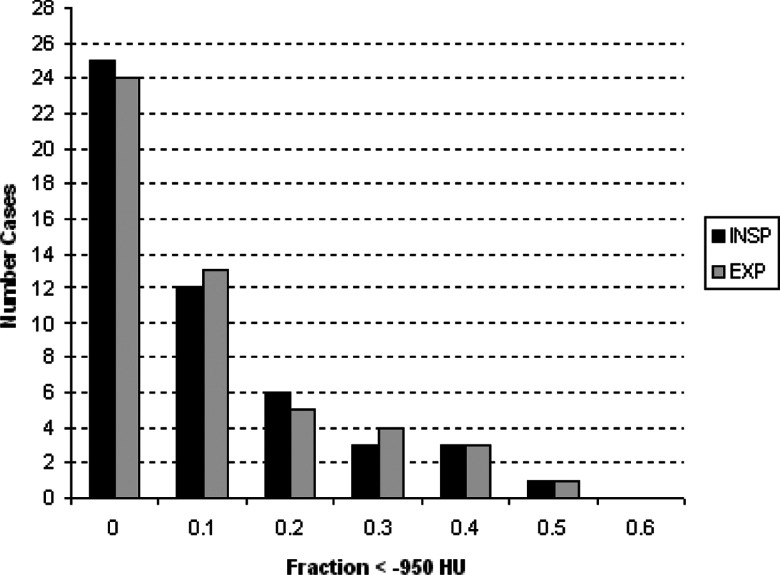
An experienced chest radiologist visually inspected all cases and detected a number of supernumerary fissures (13 in the right lower lobe, 13 in the left upper lobe, one in the left lower lobe, two in the right middle lobe, and one in the right upper lobe). Noticeable distortion due to emphysema was also observed for the right oblique (five cases), right horizontal (five cases), and left oblique (one case) fissures. The lower tube current prescribed for the expiratory protocol results in noisier images. This leads to more poorly defined fissures on these images (perceived as high attenuating regions near fissures on visual inspection). Other factors obscuring the visual clarity of the fissures (artifacts, blebs, nodules) were also observed in some cases. The amount of emphysema (as measured by the fraction of the lung region falling below the −950 HU threshold) for the cases used in this study is summarized in Fig. 4.
Figure 4.
Amount of emphysema as measured by the fraction of the lung region falling below the −950 HU threshold for the cases used in this study. Reported amounts for the expiratory cases were taken from the cases' corresponding inspiratory scans.
The chest radiologist was also asked to record the level of fissure completeness in each scan by ranking completeness on a five-point scale: complete/near complete (>87.5% complete), mostly complete (62.5%–87.5% complete), partially complete (37.5%–62.5% complete), mostly incomplete (12.5%–37.5% complete), absent/near absent (<12.5% complete). Fissure completeness for the cases used in this study is summarized in Table 1.
Table 1.
Fissure completeness breakdown for the left oblique (LO), right oblique (RO), and right horizontal (RH) fissures. Tallies are given for the inspiration (INSP) and expiration (EXP) cases. Descriptions of categories are provided in the text.
| Complete/near complete | Mostly complete | Partially complete | Mostly incomplete | Absent/near absent | |
|---|---|---|---|---|---|
| LO (INSP) | 32 | 13 | 3 | 2 | 0 |
| RO (INSP) | 23 | 22 | 5 | 0 | 0 |
| RH (INSP) | 13 | 12 | 9 | 11 | 5 |
| LO (EXP) | 33 | 14 | 3 | 0 | 0 |
| RO (EXP) | 24 | 23 | 3 | 0 | 0 |
| RH (EXP) | 10 | 11 | 16 | 8 | 5 |
We should mention that in 2011, there was a workshop held in conjunction with the Medical Image Computing and Computer Assisted Intervention (MICCAI) conference in 2011 that hosted a lobe segmentation challenge called Lobe and Lung Analysis (LOLA, www.lola11.org). Although the test dataset in this challenge covered various pathologies of the lungs, expiratory scans were not included. Because analysis of expiratory scans is an integral part of COPD analysis in general, we decided to build our own validation cohort.
Training datasets
We selected 20 datasets, Ntrain = 20, from the COPDGene cohort as our training set for fissure surface model construction. Eleven cases were acquired at relaxed exhalation, and nine cases were acquired at full inspiration (none of the cases in test set appear in the training set). The cases in the training set included normal subjects as well as those with a range of disease states (mild to severe emphysema and interstitial abnormalities). For each case in the training set, a pulmonologist used the interactive tool described in Ref. 16 to select points along each of the three main lobe boundaries until a satisfactory lobe segmentation was achieved. Note that with this tool, the user can place points both along the fissures and at locations where the user infers a boundary based on additional anatomical cues in locations where no fissure is visible. Those points defined the collection .
Registration
The transformations and were obtained by registering the lung masks to the corresponding target image using the Insight Toolkit27 with an affine transform, regular step gradient descent optimizer, and kappa statistic metric.
Evaluation
In this section, we describe the method we use for evaluating our algorithm's performance. We first note some of the evaluation approaches taken by other groups so that our results can be understood in the proper context. The gold standard used in Ref. 7 consists of manual tracings along visible fissures for every fifth CT slice; no manual tracings were drawn in incomplete fissure regions. To evaluate segmentation performance, in-plane distance measures were computed from each point along the manual tracing to the nearest point on the segmentation boundary. To address cases with incomplete fissures, the authors used a five-point, visual assessment scale. The authors in Ref. 5 used a similar system: comparison to manual tracings in visible fissure regions and a five point scale for visually evaluating cases with incomplete fissures. However, the scale used in Ref. 5 is more quantitative than that used in Ref. 7: the highest score (5) was assigned to results judged to be within 3 mm of the true boundary, a score of 4 was given results judged to be within 6 mm of the true boundary, etc. The authors in Ref. 17 used a five-point scale (ranging from “excellent” to “unacceptable”) to qualitatively evaluate whether the algorithm output was complete and suitable for lobe-based quantitative analysis, but no quantitative evaluation was performed.
In our study, we compute distance measures between the TPS surfaces determined by our algorithm and those produced by manual interaction. To produce the manual segmentations a pulmonologist used the interactive segmentation tool described in Ref. 16 to generate complete lung lobe segmentations for all datasets in our study. The tool enables users to select a sparse set of points along each of the three boundaries between the lung lobes. Once selected, TPS interpolation is used to fit surfaces through the points thus defining the boundaries between the lobes. After surface fitting, the user can inspect the result and add additional points in areas of misalignment. As reported in Ref. 16, this process only takes approximately 5−7 min of user time per case. The selected points for each lobe boundary are saved to file and subsequently used to produce TPS surfaces for quantitative evaluation, as described next.
In keeping with the evaluation methods described above, we also determine lobe boundary discrepancies specifically in regions with detectable fissures. We followed the same approach described in Ref. 5: a pulmonologist manually traced the visible fissures in every fourth coronal slice.
As discussed above authors have previously used visual scoring systems to evaluate algorithm accuracy in regions with missing fissure information. In these regions, human experts rely on other anatomical clues and their knowledge of fissure shape to infer the location of lobe boundaries. The extent to which lobe segmentation accuracy is affected by discrepancies in surface boundaries based on human inferences and TPS interpolation can also be gauged using the Dice coefficient
| (17) |
where A represents the set of voxels in the ground-truth segmentation and B represents the set of voxels in the algorithm's segmentation. This measure more directly indicates the suitability of our algorithm's segmentation output for the purpose of lobe-based disease quantification, the importance of which was discussed in the introduction. A Dice coefficient value of 1.0 indicates perfect overlap of the two sets, and value of 0.0 indicates no overlap.
RESULTS
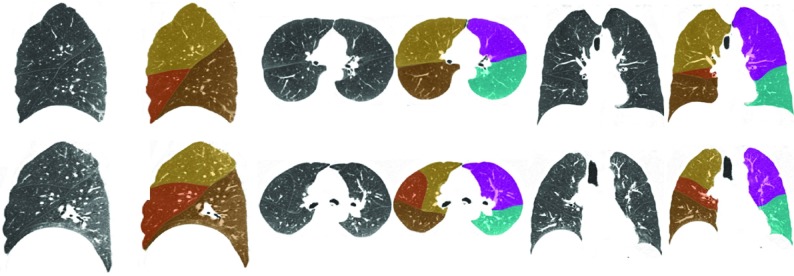
Qualitative segmentation results for typical inspiratory cases are given in Fig. 5, and results for expiratory cases are shown in Fig. 6. The algorithm performs well on these cases; as such, the boundaries indicated by the overlays accurately coincides with the reference standard boundaries. Tables 2, 3, 4 and Fig. 7 summarize the quantitative results for our study. Table 2 shows distance statistics computed with respect to algorithm output and the manually traced fissure regions. Table 3 shows total surface discrepancies computed with respect to algorithm output and the manual segmentations generated using the tool described in Ref. 16. Descriptions of several cases on which the segmentation algorithm performed poorly are elaborated on in Table 5.
Figure 5.
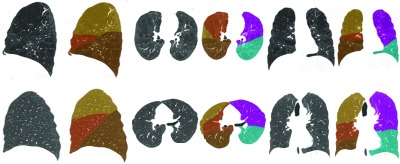
Sagittal, axial, and coronal views illustrating segmentation results for two INSP test set cases. Note the severe emphysema and the resulting fissure distortion in the topmost case.
Figure 6.
Sagittal, axial, and coronal views illustrating segmentation results for two EXP test set cases.
Table 2.
Mean, RMS, and max distances between manually traced fissure locations and automatically determined lobe boundaries for LO, RO, and RH fissures. Total results are reported for INSP and EXP datasets and are also given with respect to fissure completeness.
| Compete/ near complete | Mostly complete | Partially complete | Mostly incomplete | Absent/ near absent | Total | ||
|---|---|---|---|---|---|---|---|
| Mean (mm) | 0.92 ± 0.53 | 0.77 ± 0.18 | 0.91 ± 0.34 | 0.75 ± 0.12 | … | 0.87 ± 0.39 | |
| LO (INSP) | RMS (mm) | 1.64 ± 1.29 | 1.11 ± 0.39 | 1.38 ± 0.51 | 1.33 ± 0.19 | … | 1.45 ± 1.04 |
| Max (mm) | 10.28 ± 9.65 | 7.86 ± 6.54 | 6.72 ± 1.43 | 14.43 ± 6.87 | … | 10.09 ± 7.61 | |
| Mean (mm) | 1.08 ± 0.47 | 0.93 ± 0.83 | 0.76 ± 0.17 | … | … | 0.98 ± 0.67 | |
| RO (INSP) | RMS (mm) | 1.82 ± 1.00 | 1.57 ± 2.17 | 1.22 ± 0.35 | … | … | 1.60 ± 1.51 |
| Max (mm) | 11.47 ± 5.20 | 8.15 ± 8.18 | 7.58 ± 3.26 | … | … | 9.55 ± 7.00 | |
| Mean (mm) | 1.29 ± 0.13 | 0.54 ± 0.12 | 0.68 ± 0.12 | 1.83 ± 0.72 | 2.73 ± 2.11 | 1.90 ± 1.86 | |
| RH (INSP) | RMS (mm) | 2.99 ± 0.83 | 0.79 ± 0.21 | 0.92 ± 0.29 | 5.60 ± 3.12 | 4.32 ± 3.47 | 3.47 ± 2.06 |
| Max (mm) | 10.70 ± 2.69 | 3.68 ± 1.05 | 4.25 ± 0.88 | 14.37 ± 17.24 | 9.10 ± 6.88 | 9.84 ± 4.01 | |
| Mean (mm) | 2.52 ± 6.56 | 1.29 ± 0.73 | 1.37 ± 1.06 | … | … | 2.01 ± 5.10 | |
| LO (EXP) | RMS (mm) | 3.41 ± 6.88 | 1.97 ± 1.46 | 2.11 ± 1.46 | … | … | 2.88 ± 5.23 |
| Max (mm) | 10.93 ± 11.77 | 9.97 ± 6.12 | 10.90 ± 5.43 | … | … | 10.05 ± 9.34 | |
| Mean (mm) | 1.56 ± 2.32 | 1.03 ± 0.65 | 2.30 ± 2.64 | … | … | 1.39 ± 1.51 | |
| RO (EXP) | RMS (mm) | 2.63 ± 3.31 | 1.82 ± 1.06 | 3.46 ± 3.88 | … | … | 2.25 ± 2.85 |
| Max (mm) | 11.51 ± 8.70 | 9.28 ± 5.50 | 11.16 ± 11.68 | … | … | 10.64 ± 7.64 | |
| Mean (mm) | 1.16 ± 0.97 | 0.77 ± 0.17 | 1.21 ± 0.62 | 0.55 ± 0.03 | 10.90 ± 9.70 | 3.31 ± 12.89 | |
| RH (EXP) | RMS (mm) | 2.10 ± 1.95 | 1.31 ± 0.16 | 2.67 ± 1.11 | 0.81 ± 0.29 | 16.58 ± 9.50 | 5.29 ± 16.32 |
| Max (mm) | 7.89 ± 5.90 | 6.33 ± 1.19 | 12.72 ± 1.72 | 3.90 ± 3.04 | 23.63 ± 4.93 | 12.87 ± 24.77 |
Table 3.
Mean, RMS, and max distances between manually and automatically determined lobe boundaries for LO, RO, and RH fissures. Total results are reported for INSP and EXP datasets and are also given with respect to fissure completeness.
| Compete/near complete | Mostly complete | Partially complete | Mostly incomplete | Absent/near absent | Total | ||
|---|---|---|---|---|---|---|---|
| Mean (mm) | 5.67 ± 0.37 | 7.07 ± 1.84 | 10.05 ± 4.92 | 10.36 ± 5.02 | … | 9.89 ± 4.84 | |
| LO (INSP) | RMS (mm) | 6.39 ± 0.23 | 8.64 ± 1.96 | 11.79 ± 5.16 | 12.16 ± 5.53 | … | 11.62 ± 5.28 |
| Max (mm) | 11.42 ± 1.48 | 18.77 ± 5.04 | 22.84 ± 9.28 | 25.74 ± 11.66 | … | 23.99 ± 10.89 | |
| Mean (mm) | 5.44 ± 1.65 | 8.18 ± 4.24 | 8.13 ± 4.34 | … | … | 8.00 ± 4.18 | |
| RO (INSP) | RMS (mm) | 6.50 ± 1.49 | 9.65 ± 4.64 | 9.36 ± 4.58 | … | … | 9.32 ± 4.49 |
| Max (mm) | 14.11 ± 1.57 | 19.31 ± 8.24 | 19.49 ± 7.59 | … | … | 19.08 ± 7.70 | |
| Mean (mm) | 6.79 ± 3.63 | 7.93 ± 2.41 | 8.39 ± 7.04 | 9.68 ± 7.28 | 9.77 ± 8.70 | 8.85 ± 6.48 | |
| RH (INSP) | RMS (mm) | 7.36 ± 3.69 | 9.31 ± 2.73 | 9.16 ± 6.94 | 10.44 ± 7.20 | 10.60 ± 8.84 | 9.74 ± 6.49 |
| Max (mm) | 12.81 ± 5.47 | 19.10 ± 6.03 | 14.37 ± 8.81 | 16.32 ± 8.21 | 17.20 ± 12.21 | 16.41 ± 8.65 | |
| Mean (mm) | 8.50 ± 4.86 | 9.00 ± 3.04 | 10.25 ± 7.68 | … | … | 9.68 ± 6.77 | |
| LO (EXP) | RMS (mm) | 9.75 ± 5.04 | 10.57 ± 3.97 | 12.1111 ± 8.55 | … | … | 11.36 ± 7.50 |
| Max (mm) | 19.27 ± 7.90 | 21.63 ± 10.43 | 27.9511 ± 26.41 | … | … | 25.14 ± 22.19 | |
| Mean (mm) | 8.62 ± 3.97 | 9.28 ± 4.37 | 9.61 ± 2.37 | … | … | 9.02 ± 3.95 | |
| RO (EXP) | RMS (mm) | 10.05 ± 4.38 | 11.05 ± 4.94 | 11.61 ± 2.50 | … | … | 10.66 ± 4.42 |
| Max (mm) | 20.95 ± 7.58 | 23.79 ± 10.23 | 23.78 ± 5.12 | … | … | 22.48 ± 8.56 | |
| Mean (mm) | 10.37 ± 5.88 | 10.55 ± 4.82 | 11.29 ± 6.72 | 13.37 ± 10.92 | 13.89 ± 7.46 | 11.81 ± 7.32 | |
| RH (EXP) | RMS (mm) | 11.75 ± 5.73 | 11.93 ± 5.15 | 12.23 ± 6.45 | 14.16 ± 11.20 | 15.63 ± 9.10 | 13.08 ± 7.69 |
| Max (mm) | 22.17 ± 6.77 | 21.21 ± 8.29 | 18.96 ± 8.18 | 20.45 ± 14.97 | 25.52 ± 16.99 | 21.80 ± 11.36 |
Table 4.
Dice score statistics for the INSP and EXP cases evaluated in our study.
| LUL | LLL | RUL | RML | RLL | |
|---|---|---|---|---|---|
| Mean (INSP) | 0.99 ± 0.01 | 0.99 ± 0.01 | 0.97 ± 0.04 | 0.91 ± 0.13 | 0.98 ± 0.03 |
| Min (INSP) | 0.94 | 0.96 | 0.65 | 0.37 | 0.80 |
| Max (INSP) | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 |
| Median (INSP) | 0.99 | 0.99 | 0.98 | 0.95 | 0.99 |
| Mean (EXP) | 0.97 ± 0.08 | 0.97 ± 0.06 | 0.97 ± 0.03 | 0.91 ± 0.10 | 0.97 ± 0.04 |
| Min (EXP) | 0.78 | 0.81 | 0.75 | 0.31 | 0.79 |
| Max (EXP) | 0.99 | 0.99 | 0.99 | 0.98 | 0.99 |
| Median (EXP) | 0.99 | 0.98 | 0.98 | 0.94 | 0.98 |
Figure 7.
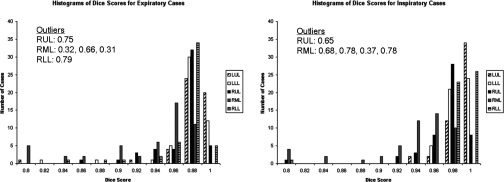
Dice scores for the left upper lobe (LUL), left lower lobe (LLL), right upper lobe (RUL), right middle lobe (RML), and right lower lobe (RLL) reported for the expiratory (top) and inspiratory (bottom) datasets. (No Dice scores equaling 1.0 were observed).
Table 5.
Elaboration on selected cases for which the segmentation algorithm performed poorly. Surface discrepancy measures are computed considering the total surface, not just in regions with clearly visible fissures.
| Quantitative results | Comments | |
|---|---|---|
| Case 1 (INSP) | RH Mean: 24.75 mm | RH absent/near absent |
| Case 2 (EXP) | RML Dice: 0.68 | RH mostly incomplete |
| Case 3 (INSP) | RH Mean: 43.44 mm, RUL Dice: 0.75, RML Dice: 0.66 | Mean RH surface used |
| Case 4 (EXP) | RH Mean: 20.92 mm | Mean RH surface used |
| Case 5 (INSP) | RML Dice: 0.31 | RH can not be evaluated due to RML atelectasis |
| Case 6 (EXP) | RO Mean: 17.31 mm; RO Max: 48.20 mm | Poor RO particles sampling |
| Case 7 (EXP) | – | LO failure; model fit heavily distorted |
| Case 8 (INSP) | RH Mean: 26.12 mm | RH mostly incomplete; Mean RH surface used |
| Case 9 (EXP) | RML Dice: 0.76 | RH absent/near absent; Mean RH surface used |
Because our algorithm uses particles detected at fissure locations, results tend to be most accurate in those regions. Table 2, which shows accuracies at user-defined fissure locations (tracings) reflects this. Table 3 indicates surface discrepancies across the entire lobe boundaries, even at locations where there are no discernible fissures. The difference between results reported in Tables 2, 3 reflects discrepancies in manually determined and algorithm-determined lobe boundaries in regions that tend not to show visible fissures. The algorithm uses interpolation through detected fissures to define lobe boundaries in these regions, while humans use additional anatomical cues. The differences in results reflect differences in these approaches in those regions.
For the results reported in Table 2, we performed Welch's t-test to evaluated the statistical significance between “Complete/Near Complete” results and “Mostly Complete” results for all six categories (INSP and EXP for LO, RO, and RH). Of these six categories no difference was statistically significant at the p = 0.05 confidence level except for the RH INSP group. While this particular result seems counter-intuitive, in the context of statistical results for the other five categories, it could be due to chance.
We did a similar analysis for the results reported in Table 3 and found a statistically significant decrease in performance from the “Complete/Near Complete” group to the “Mostly Complete” group for all three of the INSP categories (although no significant difference for the EXP categories). Taken together the statistics from Table 2 and the statistics from Table 3 tend to suggest that the algorithm's performance in the vicinity of fissure locations is independent of fissure completeness, whereas the performance in areas where no fissure is detectable does depend on fissure completeness, which agrees with intuition. Statistical comparisons between other groups begin to lose meaning given underpowered tests due to small sample sizes. It is therefore difficult to conclusively say that performance degrades with fissure completeness, although such a conclusion certainly makes sense and is suggested by the data.
We also see that the algorithm generally performs better on the inspiratory cases owing to the higher dose used for these scans, resulting in less noise and more clearly defined fissures.
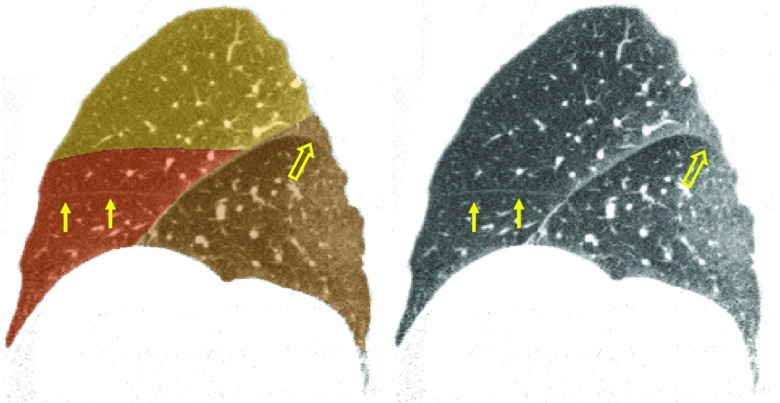
The ability of the algorithm to generate good results even in the presence of incomplete fissures (and in some cases in the presence of nearly absent fissures) indicates the ability of TPS interpolation to accurately define lobe boundaries across the lung region. However, interpolation fails to provide satisfactory results in some cases, as we highlight below. We also note that the ability of the surface model to completely capture the fissure typically decreases somewhat with greater boundary complexity. A poorer model fit in some areas leads to a portion of fissure particles being eliminated in the classification stage with a consequent poorer lobe boundary in the final segmentation in that region. The case shown in Fig. 9 illustrates this phenomenon (open arrows).
Figure 9.
Case for which the right horizontal fissure model was initialized too far from the true fissure location and became heavily distorted as it latched on to nonhorizontal fissure particles. The mean right horizontal fissure boundary was therefore used, but this still results in an unsatisfactory segmentation. Solid arrows indicate the true fissure location. Open arrows indicate a region of the right oblique that curls downward and was not properly captured with the automatic segmentation.
Dice scores shown in Table 4 indicate the suitability of the segmentation algorithm for tasks such as lobe-based disease quantification. Only 29 out of 500 (5.8%) lobes showed Dice scores lower than 0.9 (see Fig. 7), with the right upper and right middle lobes proving most problematic given the relative difficulty of defining the right horizontal boundary. We should emphasize that Dice scores reflect lobe boundary discrepancies only as we used the same lung segmentation mask as input to the automatic segmentation algorithm and the manual segmentation tool used to generate the reference standards.
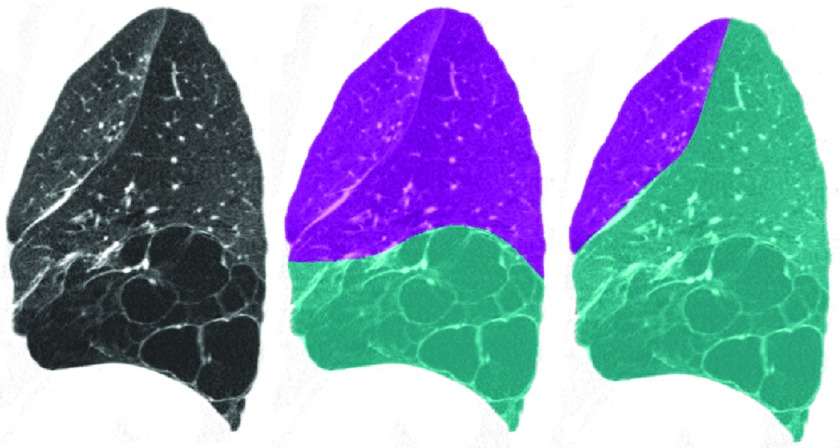
Figure 8 illustrates a segmentation failure in the left lung. The particles sampling stage adequately detected the left oblique fissure, but it also picked up the high attenuating boundaries of the emphysema regions in the lower lung. The relatively unusual fissure location in combination with the large number of particles in the emphysema region prevented the left oblique boundary model from fitting properly, as the shape model was initialized closer to the emphysema region than to the fissure particles. Therefore, subsequent classification and filtering stages failed as well. This was the only complete failure (no fissure particles were correctly identified) in the left lung. This case can be compared to the topmost case in Fig. 5, which also presents with advanced emphysema but for which the segmentation algorithm performs well.
Figure 8.
Left lung failure case (left: sagittal CT slice, middle: automatic segmentation result, right: reference standard). The severe lower lobe emphysema in combination with the relatively unusual fissure location caused the model fitting stage to fail. Therefore, subsequent classification, filtering, and segmentation stages failed as well.
For several of the test cases we noticed that the right horizontal shape model became heavily distorted given the relative lack of right horizontal fissure particles. The mean right horizontal boundary surface was used in the segmentation stage for these cases, mitigating the effect of the poorly fit surface. However, large errors can still occur with this approach as illustrated in Fig. 9. This case also demonstrates a scenario leading to a large maximum distance between the automatic and manually determined right oblique lobe boundary (open arrows). In this region the fissure “curls” downward, and the right oblique model did not deform to the fissure in this region. As a result, the subsequent classification stage did not designate particles in this region as fissure particles, so they were not used for fitting the final TPS surface used for segmentation.
Figure 10 shows a tough expiratory case on which the segmentation algorithm performs relatively poorly. The faint fissure and high degree of noise proved problematic for the particles sampling stage. Nevertheless, some fissure regions were correctly identified (arrows, left), and this is reflected in the automatic segmentation result (middle). Regions under-sampled by particles are indicated in the rightmost image, and the poor automatic segmentation in these areas is evident.
Figure 10.

A difficult expiratory case (left: sagittal CT slice, middle: automatic segmentation result, right: reference standard). The right horizontal fissure is mostly incomplete, and the particles sampling were not able to adequately capture the right oblique fissure. The final automatic segmentation reflects good lobe boundary detection near well-sampled areas (arrows, left), but the reference standard segmentation indicates poorly captured regions (arrows, right).
Table 6 provides timing results for the most intensive stages of the overall segmentation method (other stages contribute negligibly to the overall computational expense). The ridge surface sampling and shape model generation stages can be performed in parallel, resulting a total average time of 277 s for these two stages. Model fitting can be performed separately for the left lung and the right lung (the right oblique and right horizontal models must be fit together); this yields a total time of 366 s for this stage (2 × 183 for the right lung). Therefore, total average computation time for our lobe segmentation algorithm is approximately 15 min. The memory footprint for the cases that we were processing was less than 1 GB. The processing time is competitive with or superior to previously published timing results,5, 7, 17 although we acknowledge the inherent difficulty in directly comparing timing results given different experimental datasets, hardware platforms, etc.
Table 6.
Average execution time for each stage of the overall segmentation algorithm using a 2.4 GHz Intel Xeon CPU with 128 GBs RAM.
| Stage | Average time (s) |
|---|---|
| Particles sampling | 277 |
| Shape model generation | 185 |
| Model fitting (per fissure) | 183 |
| Voxel labeling | 272 |
DISCUSSION AND CONCLUSION
We have presented a fully automatic lung lobe segmentation algorithm that uses particles sampling and a novel fissure shape modeling scheme and have demonstrated the efficacy of our approach on challenging cases, including those with incomplete fissures and advanced emphysema. The most challenging cases we tested were those with mostly incomplete or near absent right horizontal fissures, consistent with what other groups have found. In our approach, we fit lobe boundary models to particle data and then use these models to discriminate between particles representing fissures and particles representing nonfissure structures or supernumerary fissures. If there are no particles defining one of the fissures or if the particle signal is extremely weak, our approach can fail, but we have observed good results even in cases with mostly incomplete and absent/near absent fissures, illustrating the ability of TPS interpolation to reliably define lobe boundaries even with a small number of points.
We tested our approach on CT datasets acquired with “smooth” CT reconstruction kernels. However, in our exploration of particles parameters we have seen that comparable sampling results can be achieved on CT datasets acquired with “sharp” kernels (provided that σgauss is lowered to a value of 1.0). Therefore, we expect similar segmentation performance for these scans, as the down-stream components (prefiltering, model fitting, classification, postfiltering, and lobe segmentation) depend only on the particles sampling.
The PCA-based surface model representation we propose provides a convenient way to capture variation across a population. We have observed good model fitting results despite our relatively small training set of 20 cases. The data storage requirements for our shape models are negligible: the information necessary to represent a case in the training set is stored in a file that is on the order of 20 KB. Also, our PCA approach could handle a very large number of training cases (hundreds or thousands) without appreciably affecting execution time (with the caveat being that as the number of training cases increases, the number of modes necessary to represent a very large percentage of the variance would likely also increase somewhat). In comparison, the atlas-based approach described in Ref. 5 incurs and additional “fast” registration stage (as described in their paper) as well as an additional image storage requirement with each new member of the training set. This could potentially become prohibitive with a very large atlas set.
We would like to emphasize that ridge feature samples could be derived in a number of ways. In the present work, our samples are derived from CT image features indicating lobe fissures. Another approach would be to sample ridge features computed from airway or vessel distance maps, leveraging those important anatomical clues for defining lobe boundaries. An example of such a ridge surface image can be seen in Ref. 11. Particles sampling can be applied to identify ridges in such images, and our shape model fitting could then be used to isolate those ridge features most likely to represent lobe boundaries. This is an area for further research.
ACKNOWLEDGMENTS
This work was partially funded by 1R01HL116931-01 and the COPDGene study NHLBI grants 2R01HL089897-06A1 and 2R01HL089856-06A1. Additional support provided by NIH grants K25 HL104085-04, K23HL089353-05, 1P50HL107192, R01HL116473, and R01HL107246.
APPENDIX A: PARAMETER SELECTION
Here we describe the parameter selection to define the optimal set of parameters for the particle sampling, the filtering stage that precedes the model fitting, the number of modes in the PCA model and the Fisher discriminant classification stage.
Particle system parameters
The particle system results are affected by four key parameters: σgauss, λthresh, γthresh, and N. A set of four images from our training set that showed complete fissures (two inspiratory and two expiratory scans each with “smooth” and “sharp” reconstructions) was selected. The goal of this study was to find a parameter setting making fissure detection very sensitive at the price of specificity. That is, we attempt to find a dense sampling of true fissure locations and permit nonfissure structures that locally behave like ridge surfaces to be detected. The number of true positive (TP) and false positive (FP) particles were computed after each run of the particle system for each parameter setting. TP and FP particles were determined by considering particle alignment and proximity to manually determined lobe boundary surfaces. Parameters were studied one at a time within a reasonable range of values. Optimal values were selected by considering both the number of TPs as well as the ratio TPs/FPs, which serves as a measure of signal to noise ratio (SNR). Parameter values were selected so as to maximize TPs but adjusted to minimize the TP/FP ratio for the maximized TP level.
The selected parameter set from this study were: σgauss = 1.2 mm, λthresh = −20, γthresh = −0.1, N = 6000. It is worth noting that the selected parameter set live in a very stable regime for both the inspiratory and the expiratory scans. The difference in reconstruction kernel only affected σgauss, with an optimal value for sharp reconstruction equal to 1 mm. A lower σgauss value for the sharp reconstruction kernel is expected given that it corresponds to a more narrow point spread function with respect to the smooth kernel. Initializing the particle system with more than 6000 did not appreciably improve the sampling of the fissure but increased the number of FPs, thus reducing the total system SNR. Due to the population control mechanism, the final number of particles ranges from 15 000 to 20 000 depending on the case.
Particle filtering parameters
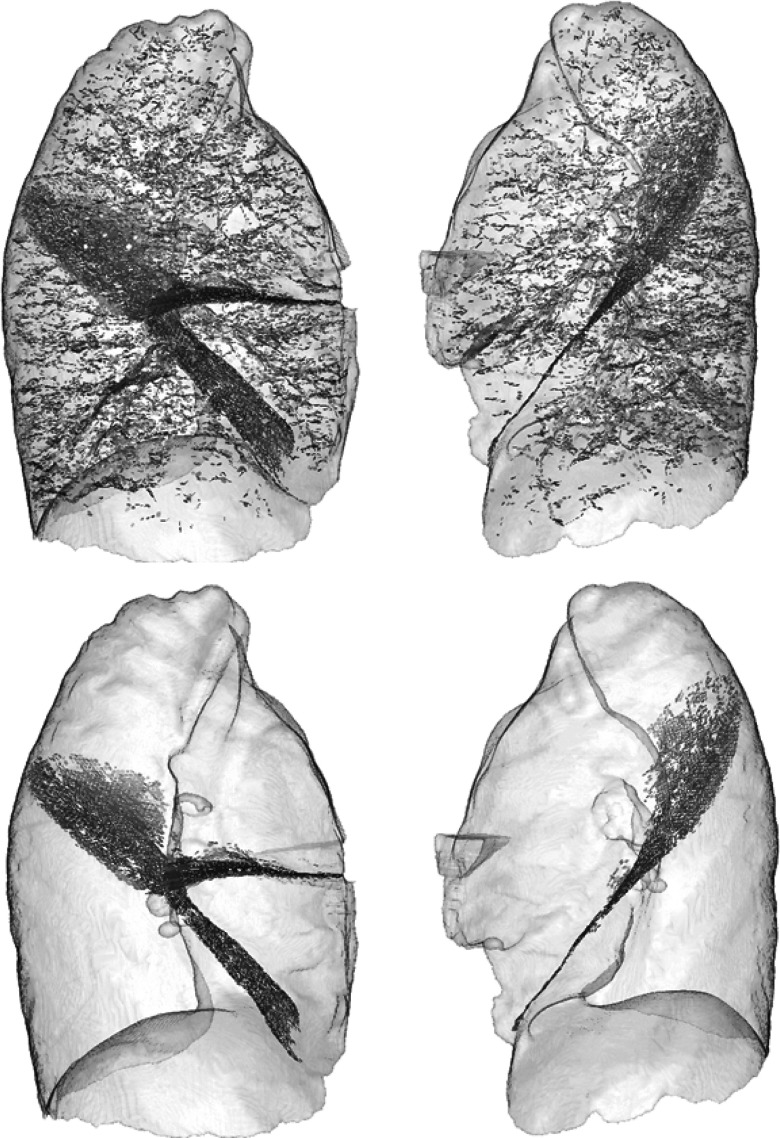
The particle filtering stage relies on three parameters: dthresh, θthresh, and nthresh (the minimum number of particles that must exist in a component to be considered for further processing). An optimal set of values for those parameters was defined using our training set (). First, we performed particles sampling on each training set case. dthresh was determined by measuring the spread of distances between nearby particles within training set cases. We observed that the mean distance was approximately 2.6 mm with a standard deviation of 0.16 mm. Therefore, we set dthresh to a value of 3 mm – two standard deviations from the mean – in order for 95% of a given particle's closest neighbors to be considered for connectedness on average. Given that we have user-defined lobe boundary surfaces for each of these cases, we next isolated the particles lying on those surfaces (identified by close spatial proximity and parallel orientation with respect to the local surface normals). This results in a set of ground-truth particles for each case, and the remaining particles are considered noise. Figure 11 illustrates particles sampling for one of the training set cases and the corresponding ground truth particles.
Figure 11.
(Top) Left and right lung particles sampling result for one of the training set cases (sagittal view). Particles are rendered with plate-like glyphs, and lungs are rendered semitransparently for context. (Bottom) corresponding ground truth particles.
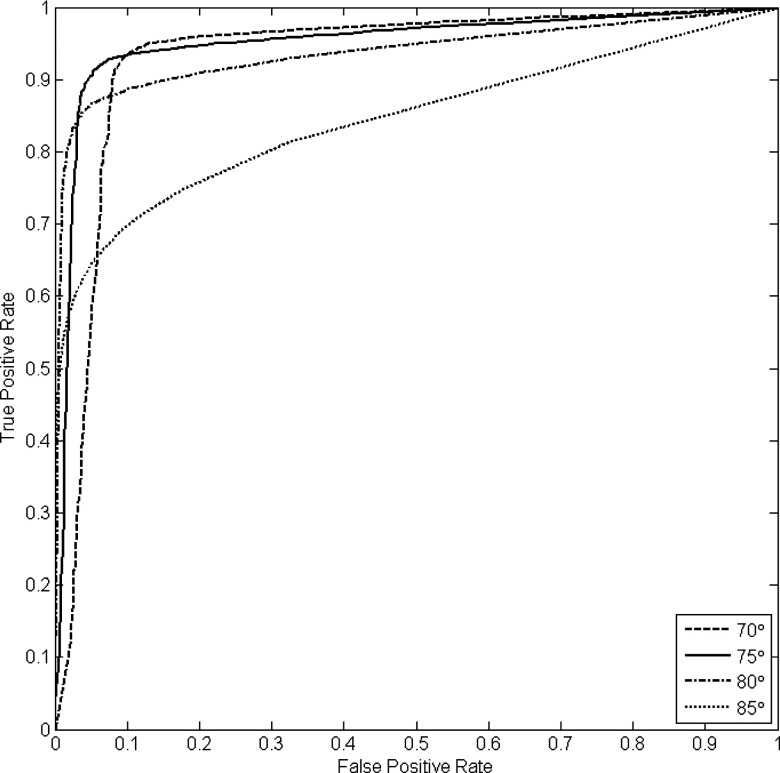
Given both noise and ground truth particles for each case, we then investigated the effect of various θthresh and nthresh settings by computing true positive and false positive rates across all training cases. We considered a wide range of size thresholds and four values for θthresh: 70°, 75°, 80°, and 85°. The results are summarized by the ROC curves shown in Fig. 12. Given this analysis we choose to operate the connected component filter at a 0.95 true positive rate along the 70° θthresh curve. This corresponds to a false positive rate of approximately 0.13 and a nthresh value of 110.
Figure 12.
ROC analysis of prefiltering parameter settings. Four θthresh values are considered (70°, 75°, 80°, and 85°) across a wide range of nthresh values.
Number of modes for PCA model
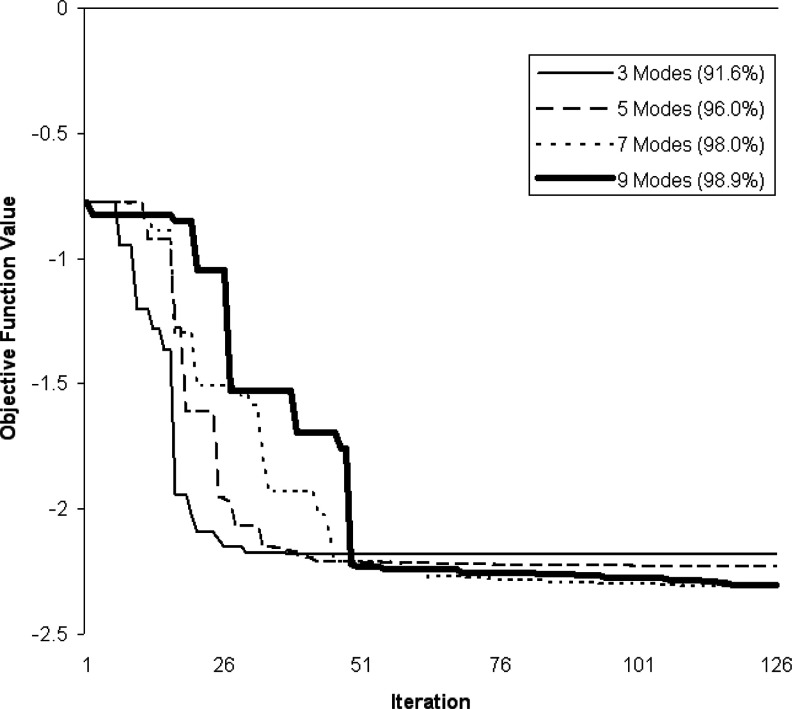
Typically in PCA-based methods, one selects a number of modes which describe most of the population variation (say 90%). However, the greater the number of modes, the larger the simplex for our application. On the other hand, incorporation of more modes potentially enables a better TPS surface fit to the particles. Figure 13 shows the convergence rate and metric values of the optimizer for different numbers of modes. As expected, the model fit to the particle data improves as a greater number of modes is used, and convergence is reached after approximately 100 iterations. In our experiments we choose to use 100 iterations for each of the three fitting operations, and we use enough modes to account for 99% of the variation. We observed in our test set that no more than 11 modes were ever used for a given fitting operation, and usually 99% of the variation could be explained by about five modes and sometimes as few as three.
Figure 13.
Convergence rate of model fitting to a typical fissure for various numbers of variation modes.
Fisher's discriminant parameters
The discriminant, w, and the threshold in the one-dimensional space that well separates noise and fissure particles was determined using the training cases, , for which we have established noise and ground truth particles. For each of the Ntrain = 20 training set cases, we fit surface models constructed from the remaining 19 cases. We then computed the two-dimensional feature vectors for both the noise and s classes. Collecting noise and s feature vectors computed across all 20 training set cases, we applied Eq. 13 to determine the vector w, which was found to be [−0.4677, −0.8839]. The histograms of the data in the projected one-dimensional space and the corresponding ROC curve are shown in Fig. 14. We choose to operate at a true positive rate of 0.95 which corresponds to a false positive rate of roughly 0.1 and a threshold value of −30.
Figure 14.
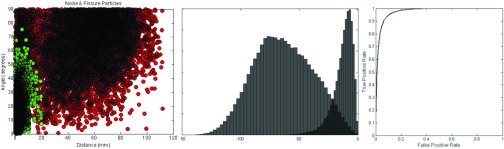
Left: Scatter plot of the 2D features space. The grouping in the lower left represents true fissure particles; the grouping towards the middle represents noise particles. (Middle) histograms of projected noise particles (left-most distribution), and fissure particles (right-most distribution). The x axis is unitless. (Right) corresponding ROC curve representing the distributions of the projected data.
Therefore, by computing feature vectors (x) after the fitting process, projecting into a one-dimensional space (wTx), and then thresholding, we can effectively leverage the shape information encoded in our fit surface and further eliminate noise. For the right lung, feature vectors are computed with respect to both the right horizontal and right oblique surface fits. If both feature vectors project above the threshold value, the one that is farthest from the threshold value gets the classification label. As we know whether particles fall within the left or right lung (given our starting lung segmentation mask), particles in the left lung with projected feature vector values falling above the threshold clearly get the left oblique fissure label. Note that this operation is performed on the prefiltered particles data.
APPENDIX B: NEWTON'S METHOD GRADIENT AND HESSIAN
Here we give expressions for the gradient and Hessian used in Newton's method described in Sec. 2C1.
The gradient of fp(x, y) (∇fp = [∂fp/∂x ∂fp/∂y]T) is given by
| (B1) |
| (B2) |
where the (non-normalized) components of the TPS surface normal are
| (B3) |
| (B4) |
and where r is analogous to Eq. 4. The components of the Hessian, ∇2fp (here using the notation convention for the Hessian common in optimization literature28), are
| (B5) |
| (B6) |
| (B7) |
where
| (B8) |
| (B9) |
| (B10) |
and
| (B11) |
| (B12) |
| (B13) |
References
- Aziz M., Ashizawa K., Nagaoki K., and Hayashi K., “High resolution CT anatomy of the pulmonary fissures,” J. Thorac. Imaging 19, 186–191 (2004). 10.1097/01.rti.0000131590.74658.24 [DOI] [PubMed] [Google Scholar]
- Halbert R. J., Natoli J. L., Gano A., Badamgarav E., Buist A. S., and Mannino D. M., “Global burden of COPD: Systematic review and meta-analysis,” Eur. Respir. J. 28, 523–532 (2006). 10.1183/09031936.06.00124605 [DOI] [PubMed] [Google Scholar]
- Regan E. A., Hokanson J. E., Murphy J. R., Make B., Lynch D. A., Beaty T. H., Curran-Everett D., Silverman E. K., and Crapo J. D., “Genetic epidemiology of COPD (COPDGene) study design,” COPD 7, 32–43 (2011). 10.3109/15412550903499522 [DOI] [PMC free article] [PubMed] [Google Scholar]
- N. E. T. T. R. Group, “A randomized trial comparing lung-volume reduction surgery with medical therapy for severe emphysema,” N. Engl. J. Med. 348, 2059–2073 (2003). 10.1056/NEJMoa030287 [DOI] [PubMed] [Google Scholar]
- van Rikxoort E. M., Prokop M., de Hoop B., Viergever M. A., Pluim J., and van Ginneken B., “Automatic segmentation of pulmonary lobes robust against incomplete fissures,” IEEE Trans. Med. Imaging 29, 1286–1296 (2010). 10.1109/TMI.2010.2044799 [DOI] [PubMed] [Google Scholar]
- Kuhnigk J. M., Dicken V., Zidowitz S., Bornemann L., Kuemmerlen B., Krass S., Peitgen H. O., Yuval S., Jend H. H., Rau W. S., and Achenbach T., “New tools for computer assistance in thoracic CT Part 1. Functional analysis of lungs, lung lobes, and bronchopulmonary segments,” Radiographics 25, 525–536 (2005). 10.1148/rg.252045070 [DOI] [PubMed] [Google Scholar]
- Ukil S. and Reinhardt J. M., “Anatomy-guided lung lobe segmentation in x-ray ct images,” IEEE Trans. Med. Imaging 28, 202–214 (2009). 10.1109/TMI.2008.929101 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Saita S., Yasutomo M., Kubo M., Kawata Y., Niki N., Eguchi K., Ohmatsu H., Kakinuma R., Kaneko M., Kusumoto M., Moriyama N., and Sasagawa M., “An extraction algorithm of pulmonary fissures from multislice CT image,” Proc. SPIE 5370, 1590–1597 (2004). 10.1117/12.534976 [DOI] [Google Scholar]
- Kuhnigk J. M., Hahn H., Hindennach M., Dicken V., Krass S., and Peitgen H. O., “Lung lobe segmentation by anatomy-guided 3D watershed transform,” Proc. SPIE 5032, 1482–1490 (2003). 10.1117/12.480321 [DOI] [Google Scholar]
- Zhou X., Hayashi T., Hara T., Fujita H., Yokoyama R., Kiryu T., and Hoshi H., “Automatic recognition of lung lobes and fissures from multislice CT images,” Proc. SPIE 5370, 1629–1633 (2004). 10.1117/12.534499 [DOI] [Google Scholar]
- Lassen B., van Rikxoort E. M., Schmidt M., Kerkstra S., van Ginneken B., and Kuhnigk J. M., “Automatic segmentation of the pulmonary lobes from chest CT scans based on fissures, vessels, and bronchi,” IEEE Trans. Med. Imaging 32, 210–222 (2013). 10.1109/TMI.2012.2219881 [DOI] [PubMed] [Google Scholar]
- Wang J., Betke M., and Ko J. P., “Pulmonary fissure segmentation on CT,” Med. Image Anal. 10, 530–547 (2006). 10.1016/j.media.2006.05.003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wiemker R., Blow T., and Blaffert T., “Unsupervised extraction of the pulmonary interlobar fissures from high resolution thoracic CT data,” Inter. Congr. Ser. 1281, 1121–1126 (2005). 10.1016/j.ics.2005.03.130 [DOI] [Google Scholar]
- Zhang L., Hoffman E. A., and Reinhardt J. M., “Atlas-driven lung lobe segmentation in volumetric x-ray CT images,” IEEE Trans. Med. Imaging 25, 1–16 (2006). 10.1109/TMI.2005.859209 [DOI] [PubMed] [Google Scholar]
- Blaffert T., Barschdorf H., von Berg J., Dries S., Franz A., Klinder T., Lorenz C., Renisch S., and Wiemker R., “Lung lobe modeling and segmentation with individualized surface meshes,” Proc. SPIE 6914, 69141I (2008). 10.1117/12.770099 [DOI] [Google Scholar]
- Ross J. C., Estepar R. San Jose, Diaz A., Westin C. F., Kikinis R., Silverman E. K., and Washko G. R., “Lung extraction, lobe segmentation and hierarchical region assessment for quantitative analysis on high resolution computed tomography images,” Med. Image Comput. Comput. Assist. Interv. 12, 690–698 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pu P., Zheng B., Leader J. K., Fuhrman C., Knollmann F., Klym A., and Gur D., “Pulmonary lobe segmentation in ct examinations using implicit surface fitting,” IEEE Trans. Med. Imaging 28, 1986–1996 (2009). 10.1109/TMI.2009.2027117 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pu J., Leader B., Zheng J. K., Knollmann F., Fuhrman C., Sciurba F. C., and Gur D., “A computational geometry approach to automated pulmonary fissure segmentation in CT examinations,” IEEE Trans. Med. Imaging 28, 710–719 (2009). 10.1109/TMI.2008.2010441 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kindlmann G. L., Estepar R. San Jose, Smith S. M., and Westin C. F., “Sampling and visualizing creases with scale-space particles,” IEEE Trans. Vis. Comput. Graph. 15, 1415–1424 (2009). 10.1109/TVCG.2009.177 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ross J. C., Estepar R. San Jose, Kindlmann G., Diaz A., Westin C. F., Silverman E. K., and Washko G. R., “Automatic lung lobe segmentation using particles, thin plate splines, and maximum a posteriori estimation,” Medical Image Computing and editor Computer-Assisted Intervention MICCAI 2010, Lecture Notes in Computer Science Vol. 6363 (Springer, New York, 2010), pp. 163–171. [DOI] [PMC free article] [PubMed]
- Hu S., Hoffman E. A., and Reinhardt J. M., “Automatic lung segmentation for accurate quantitation of volumetric x-ray CT images,” IEEE Trans. Med. Imaging 20, 490–498 (2001). 10.1109/42.929615 [DOI] [PubMed] [Google Scholar]
- Eberly D., Ridges in Image and Data Analysis (Kluwer Academic Publishers, 1996). [Google Scholar]
- Bookstein F. L., “Principal warps: Thin-plate splines and the decomposition of deformations,” IEEE Trans. Pattern Anal. Mach. Intell. 11, 567–585 (1989). 10.1109/34.24792 [DOI] [Google Scholar]
- Bishop C. M., Pattern Recognition and Machine Learning (Springer, New York, 2007). [Google Scholar]
- Nelder J. A. and Mead R., “A simplex method for function minimization,” Comput. J. 7, 308–313 (1965). 10.1093/comjnl/7.4.308 [DOI] [Google Scholar]
- Wahba G., Spline Models for Observational Data (SIAM, 1990). [Google Scholar]
- Ibanez L., Schroeder W., Ng L., and Cates J., The ITK Software Guide, 2nd ed. (Kitware, Inc., 2005), see http://www.itk.org/ItkSoftwareGuide.pdf. [Google Scholar]
- Nocedal J. and Wright S. J., Numerical Optimization (Springer, New York, 2006). [Google Scholar]
- van Rikxoort E. M., van Ginneken B., Klik M. A. J., and Prokop M., “Supervised enhancement filters: Application to fissure detection in chest CT scans,” IEEE Trans. Med. Imaging 27, 1–10 (2008). 10.1109/TMI.2007.900447 [DOI] [PubMed] [Google Scholar]