Patient-specific quantification of respiratory motion-induced dose uncertainty for step-and-shoot IMRT of lung cancer

Abstract

Purpose: The objective of this study was to quantify respiratory motion-induced dose uncertainty at the planning stage for step-and-shoot intensity-modulated radiation therapy (IMRT) using an analytical technique.

Methods: Ten patients with stage II/III lung cancer who had undergone a planning four-dimensional (4D) computed tomographic scan and step-and-shoot IMRT planning were selected with a mix of motion and tumor size for this retrospective study. A step-and-shoot IMRT plan was generated for each patient. The maximum and minimum doses with respiratory motion were calculated for each plan, and the mean deviation from the 4D dose was calculated, taking delivery time, fractionation, and patient breathing cycle into consideration.

Results: For all patients evaluated in this study, the mean deviation from the 4D dose in the planning target volume (PTV) was <2.5%, with a standard deviation <1.2%, and maximum point dose variation from the 4D dose was <6.2% in the PTV assuming delivery dose rate of 200 MU/min and patient breathing cycle of 8 s. The motion-induced dose uncertainty is a function of motion, fractionation, MU (plan modulation), dose rate, and patient breathing cycle.

Conclusions: Respiratory motion-induced dose uncertainty varies from patient to patient. Therefore, it is important to evaluate the dose uncertainty on a patient-specific basis, which could be useful for plan evaluation and treatment strategy determination for selected patients.

INTRODUCTION

One of the major challenges in radiation therapy of lung cancer is internal organ motion due to breathing. This motion during radiation treatment delivery might lead to dose distribution that differs drastically from the planned distribution. Tumor motion may be complex and usually is unpredictable.¹ In recent years, with the development of four-dimensional respiration-correlated computer tomography (4DCT),^{2, 3} it has become clinical routine to evaluate respiratory motion in planning radiotherapy for patients with lung or liver diseases. Various techniques, including respiratory gating and breath holding, have also been developed to manage respiratory motion.⁴ However, treatment plan evaluation of cases involving respiratory motion remains difficult as the dose distributions calculated on static image sets, which are still routinely used for plan evaluation, may not reflect the dose delivered to the patient.

The difference between dose to patient and the planned dose from internal organ motion consisted of two components:⁵ (1) a systematic component that could be eliminated by using 4D dose calculation with deformable registration, as reported in several publications,^{6, 7, 8, 9} instead of three-dimensional (3D) static dose calculation; and (2) a random component that is tied to the delivery process and often is referred to as motion-induced dose uncertainty or interplay effect.¹⁰ Both measurements and computer based simulation have been performed to evaluate random uncertainty in phantoms and selected patients for intensity-modulated radiation therapy (IMRT) and volumetric modulated arc therapy (VMAT).^{10, 11, 12, 13} However, although AAPM report TG 76 states that:⁴ “For individuals who still intend on using IMRT without any direct motion-correction strategy, it needs to be emphasized that the full extent of respiratory motion should be assessed and considered when assessing margins for the treatment plan,” assessment of motion-induced dose uncertainty for lung cancer patients receiving radiotherapy are not performed on an individual basis, partly because of the lack of an effective approach to determine the uncertainty. In this work, we used an analytical method to evaluate patient-specific respiratory motion-induced dose uncertainty for step-and-shoot IMRT. Since the purpose of this study was to estimate the dose uncertainty at the planning stage, it is assumed throughout the paper that there were only one set of 4DCT scan was available and that the 4DCT characterized the patient breathing pattern at the time of delivery.

METHODS AND MATERIALS

Patients and plans

Ten patients were selected with a mix of motion and tumor size for this retrospective study from stage II/III lung cancer patients treated at our center between March, 2010 and June, 2012. Since the problem of motion induced dose uncertainty is more relevant to patients with larger tumor motion,⁴ only patients with tumor motion ≥5 mm were included in this study. Each patient received a 4DCT simulation² on a GE Lightspeed 16-slice CT scanner (GE Medical Systems, Waukesha, WI), with breathing phases determined using an infrared reflecting maker and camera system (RPM system, Varian Medical Systems, Palo Alto, CA). The respiratory period was divided into ten equal phases, namely, T0–T90, with T0 defined as the full inhale and T50 as the full exhale phase. Each 4DCT data set therefore consisted of ten 3D image sets, each corresponding to a breathing phase, with average data set calculated from the ten phase image sets for treatment planning purposes.

The internal gross target volume (IGTV) for each patient was contoured on the 4DCT series by a radiation oncologist. The internal target volume (ITV) was then generated by expanding the IGTV by 8 mm, and the PTV by expanding ITV by 5 mm. A step-and-shoot IMRT plan was developed and reviewed by physicians for all patients. The IMRT plans were generated with the Pinnacle treatment planning system (Philips Radiation Oncology Systems, Fitchburg, WI) on the average CT. Between six and 11 coplanar beams were used for each plan, and the plan monitor units (MUs) ranged from 491 to 937. Each patient's tumor motion magnitude, defined as the distance between the centers of GTV at T0 and T50, and tumor volume, along with treatment parameters are summarized in Table 1.

Table 1.

Summary of patient specific parameters.

	Center of GTV	ITV	Tb	Fractions	Number of	Number of	Plan
Patient	motion (mm)	(cc)	at simulation (s)	(2 Gy)	beams	segments	MU
1	9	242.4	4	37	11	90	817
2	9	196.3	4	33	11	86	750
3	17	158.9	4	37	11	100	496
4	7	299.8	7	33	9	88	619
5	5	166.9	5	37	6	37	477
6	8	539.6	3	33	11	75	543
7	10	395.1	6	33	9	90	629
8	8	203.3	5	37	11	94	793
9	12	289.5	4	30	11	98	937
10	8	191.6	7	37	6	47	491

¹Note: T_b: Period of the patient breathing cycle.

Calculation of motion induced dose-uncertainty

For any given IMRT plan, the dose to a tissue element can be written as

$$D\left(\vec{x}\right)={\int }_0^{T_d}M(E\left(t\right),V\left(\vec{x}\right))dt,$$ (1)

where E denotes the fluence rate of the radiation beam, V is the volumetric CT of the patient, M is the dose function, and T_d is the beam on time required for delivery. With 4DCT simulation, the 4D dose can be calculated as

$$D_{4\mathrm{D}}\left(\vec{x}\right)=\frac{1}{N}\sum _{n=1}^N{\int }_0^{T_d}M(E\left(t\right),V(\vec{x},n))dt,$$ (2)

where n = 1 … N is the number of phases. To enable dose deformation and summation between different phases, a deformable registration technique is required. In this work, we used an accelerated “demons”-based technique.¹⁴M denotes the process of taking the radiation beam E and patient image V at phase n as input, and the calculated dose on phase n deformed to a reference phase (T50) as output. In this process, it can be observed that the maximum (and similarly, minimum) possible dose to the patient with respiratory motion could be calculated as follows:

$$D_{\max }\left(\vec{x}\right)={\int }_0^{T_d}\underset{j\in \{1...N\}}{max}(M\left(E\left(t\right)V(\vec{x},j)\right)dt,$$ (3)

where j denotes different phases.⁵ For step-and-shoot IMRT, Eq. 3 could be rewritten as

$$D_{\max }\left(\vec{x}\right)=\sum _{\mathit{cp}=1}^C\underset{j\in \{1...N\}}{max}(M(F_{\mathit{cp}},V(\vec{x},j)),$$ (4)

where cp = 1…C is the number of segments (control points), and F_cp is the incident beam fluence (MU) for segment cp. As can be observed from Eq. 4, for step-and-shoot IMRT, the upper bound of the expected dose to a patient with respiratory motion can be calculated from planning information only and without information on delivery.

Once the D_max and D_min are established, furthermore, the mean deviation of dose to patient from the calculated 4D dose over a course of treatment delivery, with knowledge of delivery parameters, can be written as a fraction of the maximum deviation for each segment⁵

$$\Delta D_{\mathit{cp}}^{+}/\Delta D_{\max ,\mathit{cp}}=\frac{N}{2(N-1)}\frac{T_b}{{\mathit{KT}}_{\mathit{cp}}}{\mathit{MAD}}_{\mathit{poisson}}\left(v\right),$$ (5)

where + denotes the positive variant from the 4D dose over the course of delivery, K is the number of fractions, T_cp is the delivery time needed for the segment, which is a function of plan MU and dose rate (T_cp = MU_cp/DR), T_b is the period of the patient breathing cycle, and^{5, 15}

$$v=\min \left(K\frac{T_{\mathit{cp}}\mathrm{mod}{T}_b}{T_b},K\left(1-\frac{T_{\mathit{cp}}\mathrm{mod}{T}_b}{T_b}\right)\right),$$ (6)

$${\mathit{MAD}}_{\mathit{poisson}}\left(\nu \right)=\frac{2e^{-v}{v}^{⌊v⌋+1}}{⌊v⌋!},$$ (7)

where v denotes the expected fractional deviation from a full breathing cycle, with a unit of time length of each phase (T_b/N), and MAD_poisson(v) is the mean absolute deviation (MAD) from v for a Poisson distributed process with mean v. $\Delta D_{\mathit{cp}}^{+}$ describes how the delivered segment dose deviates from the 4D dose with a given set of delivery and patient parameters. For example, if a segment was to be delivered in 4 s to a patient with T_b = 4 s, the 4D dose would perfectly predict the delivered dose, as each phase would receive equal beam on time. If the segment was to be delivered in 5 s, while the breathing pattern of the patient did not change, then the delivered dose would deviate from the 4D dose, as the beam on time as seen by each phase would be different. The dose effect of the fractionation, treatment delivery, and patient breathing were modeled by Eqs. 5, 6, 7 and discussed in more detail in Ref. 5.

Finally, the total mean deviation from the 4D dose, which was calculated from Eq. 2, and the total dose considering the motion-induced uncertainty for the given plan, could be written as

$$\begin{array}{ccc}& & \Delta D^{+}=\sum _{\mathit{cp}=1}^C\Delta D_{\mathit{cp}}^{+},\hfill \\ & & D^{+}=\sum _{\mathit{cp}=1}^C(D_{\mathit{cp}}^{\prime }+\Delta D_{\mathit{cp}}^{+}).\hfill \end{array}$$ (8)

ΔD⁻ and D⁻ can be similarly calculated. ΔD⁺ and ΔD⁻ then represent the motion-induced uncertainty for the given patient with the given treatment parameters and patient breathing cycle.

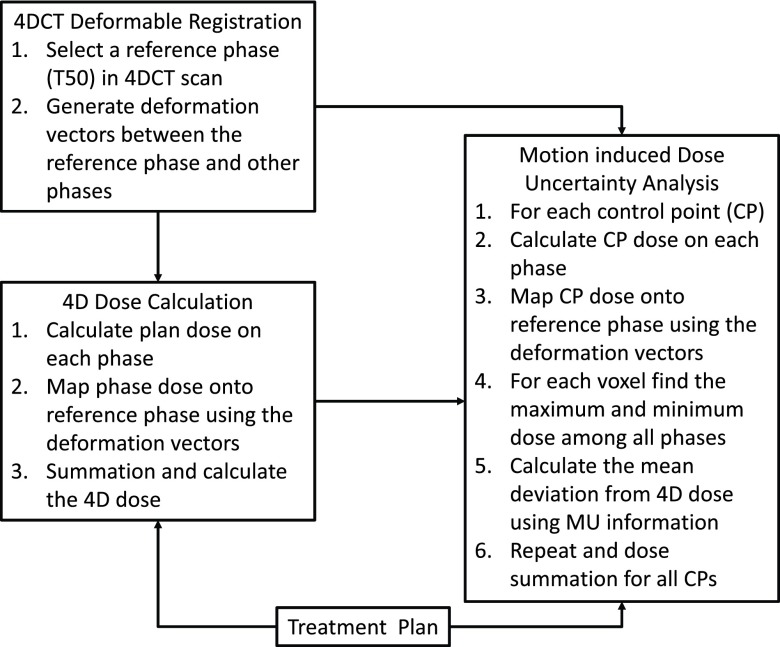
Thus, the process of determination of motion-induced dose uncertainty can be summarized as following: (1) The IMRT plan was calculated on every phase of the 4DCT, the dose was recorded per segment and then every dose distribution was deformed per segment and phase into the reference phase. So, for each segment there are N dose distributions on the reference CT, each corresponding to one of N breathing phases. (2) 4D dose (D_4D) is the average of the N dose distributions, sum over segments. (3) The extremes of the dynamic dose for each segment are defined by the maximum and minimum dose that every voxel gets over the breathing cycle. So, for each segment there are two extreme, unrealistic dose distributions, D_max,cp and D_min,cp, corresponding to the minimum and maximum dose per voxel over the N dose distributions. (4) For a single segment of step-and-shoot IMRT, the mean deviation of dose to patient from the 4D dose is derived as a fraction of maximum dose deviation (D_max−D_4D), and a function of residual time for all fractions (that follows a Poisson distribution), breathing cycles, and phases for all deliveries.⁵ The mean deviation of dose from the 4D dose was discussed and validated with measurement and simulation for a single segment of IMRT in Seco et al.¹⁰ and Li et al.⁵ (5) The total mean deviation from the 4D dose can be calculated by sum over segments. This process is also illustrated in Fig. 1.

Figure 1.

Flowchart of patient-specific motion-induced dose uncertainty analysis.

RESULTS

Figure 2 illustrates the process of dose calculation for this work. Figure 2a is a T50 axial image of a patient (patient #9) with GTV contour and a point of interest (POI) labeled. Figure 2b shows the beam-eye view (BEV) of a segment [segment #58, as indicated by the arrow in Fig. 2c] with multileaf collimator (MLC) leaves in place. The GTV is outlined with red; the trace of the POI is also marked on the BEV projection. At T50, the POI is colored magenta and T0 cyan, whereas other phases are colored blue. As can be observed from the figure, the MLC is blocking the POI at certain phases, which results in dose difference to the POI at the given segment for different phases. Figure 2c shows the dose to the POI at different segments at different phases. There are a number of segments giving minimum dose to the POI, some segments giving higher dose with minimum dose variance between phases, and some segments giving high dose with some degree of dose variance between phases.

Figure 2.

Dose calculation for a POI in a single patient (patient #9). (a) Axial image of the patient at T50 with gross total volume (GTV) outline and the POI labeled. (b) BEV of a segment [#58, as pointed out by the arrow in (c)], with GTV and the trace of the POI. T0 is cyan, T50 is magenta, and other phases are blue. (c) Total dose to the POI from different segments for different phases. (d) D_max,cp, D_max,cp, and 4D dose for the POI from different segments. (e) Total dose to the POI for different phases, 4D dose, D_max, D_min, along with D⁺ and D⁻ with T_b = 3, 4, 6, and 8 s (blue, green, red, and cyan, respectively).

Figure 2d shows the maximum and minimum phase doses (D_max,cp and D_min,cp), along with 4D dose (D_4D,cp), which is the average of the phase doses calculated by Eq. 2, for each segment. The plan has a total of 98 segments, giving a total dose of 64 Gy to the POI on the 4D dose distribution. Figure 2e shows the individual phase doses compared to the 4D dose (D_4D), which is the black line at the center, and D_max and D_min, which are calculated with Eq. 4 and displayed with black lines on top and bottom, respectively. D⁺ and D⁻, which are calculated with Eqs. 5, 6, 7, 8, are also shown at T_b = 3, 4, 6, and 8 s (blue, green, red, and cyan, respectively). For the calculation of D⁺ and D⁻, a dose rate of 200, 400, and 600 MU/min were used to calculate the delivery time needed for each segment, and number of fractions (K) varied as shown in Table 1.

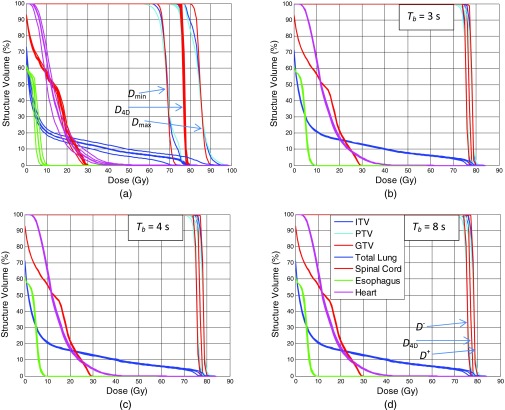
Figure 3 shows the result of dose calculation, in the form of DVHs for a single patient (patient #3). Figure 3a shows the DVHs for D_max, D_min, dose distribution calculated on individual phases, as well as the 4D dose. D_max and D_min are markedly different from the 4D dose and dose calculated on individual phases. Small difference is observed between the 4D dose and the dose on individual phases. Figures 3b, 3c, 3d show D⁺ and D⁻ at T_b = 3, 4, and 8 s, respectively. As the patient breathing cycle increases, the gap between the D⁺ and D⁻ is also increased.

Figure 3.

Dose-volume histograms (DVHs) of different organs for a single patient (patient #3). (a) DVHs for D_max, D_min, 4D dose, and individual phase doses. (b)–(d) DVHs for 4D dose, along with D⁺ and D⁻, with T_b = 3, 4, and 8 s, respectively. Dose rate is 400 MU/min.

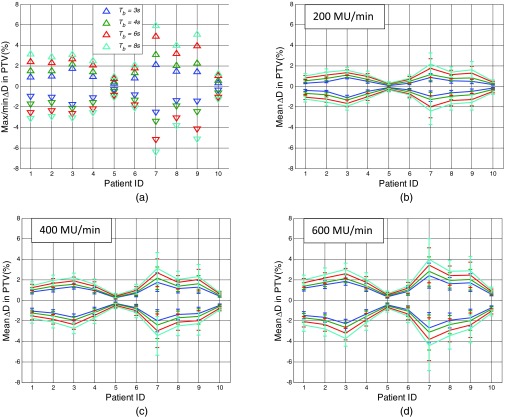
Figure 4a shows the maximum and minimum ΔD as calculated with Eq. 8 at T_b = 3, 4, 6, and 8 s for different patient PTVs, respectively, with DR = 200 MU/min. Figures 4b, 4c, 4d show the mean ΔD in PTVs for different patients with error bar being 2 standard deviations, for DR = 200, 400, and 600 MU/min, respectively.

Figure 4.

Maximum, minimum, and mean ΔD⁺ and ΔD⁻ in PTV for different patients with different dose rate. (a) Maximum/minimum ΔD⁺/ΔD⁻ for dose rate 200 MU/min in PTV for T_b = 3, 4, 6, and 8 s (blue, green, red, and cyan, respectively). (b)–(d) Mean ΔD⁺ and ΔD⁻ in PTV for different patients with different dose rate. Error bar is 2 standard deviation (SD). Dose rate: (a) 200, (b) 400, (c) 600 MU/min.

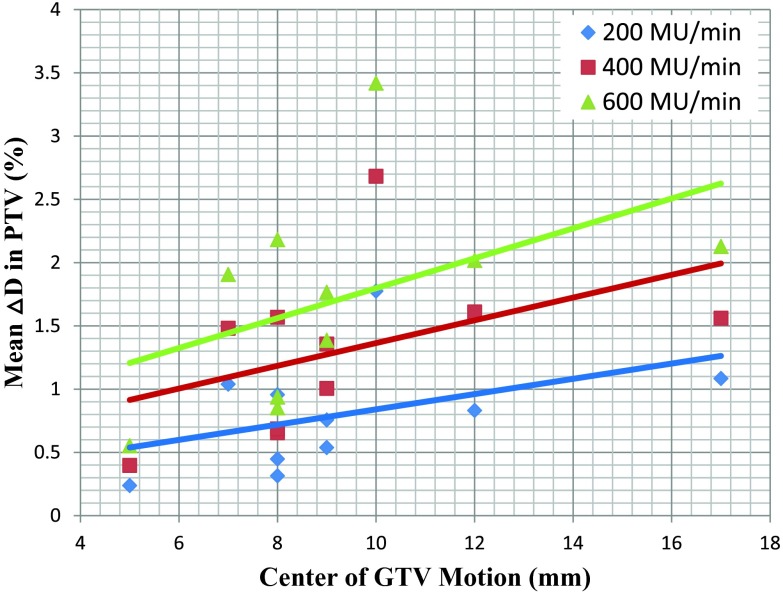
Figure 5 shows the mean ΔD⁺ in PTV plot against center of GTV motion for different patients with different dose rate, using T_b at the time of simulation, both of which are listed in Table 1. The R² of the linear fits, which are also shown for each dose rate, are < 0.20 for all three cases. Similar low correlations were found between mean ΔD⁺ in GTV and ITV, and center of GTV motion.

Figure 5.

Mean ΔD⁺ in PTV plot against center of GTV motion for different patients with different dose rate, using T_b at the time of simulation. Linear fits are also shown for each dose rate.

DISCUSSION

In this work, we demonstrated an analytical technique to determine the dose effect of respiratory motion for patients to be treated with step-and-shoot IMRT at the planning stage where only a single set of 4DCT were available. The motion-induced dose uncertainty of a single segment in IMRT was investigated by Seco et al.¹⁰ with measurement and simulation, and an analytical model was developed by Li et al.⁵ The proposed method, as an expansion of the above mentioned model, uses 4DCT and the treatment plan as input, and does not require repeated dose calculations or knowledge of the actual treatment delivery. The technique could easily be incorporated into the 4D dose calculation process and the planning system. As a follow up project, we will also evaluate the motion-induced dose uncertainties for other treatment modalities, such as VMAT or proton therapy, for the same group of patients, and compare the results between modalities.

For 3D conformal plan, dose uncertainty from motion could be minimized by using appropriate margins.¹⁶ However, for IMRT, as demonstrated in Fig. 2, increasing margin may not be useful for reducing the uncertainty as part of the uncertainty was generated inside the target. Unless the target was fully covered by each and every segment, which reduces the IMRT plan to a 3D plan, there will always be motion-induced dose uncertainty. As demonstrated in Figs. 23, D_max and D_min represent the extreme cases where all radiation doses are delivered in an instant to a certain breathing phase. For the ten patients evaluated in this study, the maximum dose difference from the 4D dose under such conditions could be >30%, which is consistent with the measurement results by Court et al.¹⁷ However, since in reality the treatment was delivered with fractionation, and at a specific dose rate, the mean dose uncertainty, taking the treatment parameters and patient breathing cycles into account, can be conservatively estimated using Eqs. 5, 6, 7, 8.

Among the ten patients evaluated in this study, the mean dose variation from the 4D dose could be up to 4%, with dose rate of 600 MU/min and breathing cycle of 8 s. However, the mean dose deviation could be reduced to <2.5%, with a standard deviation <1.2%, and maximum point dose variation from the 4D dose <6.2% in PTV even at the extreme situation of T_b = 8 s, when the delivery dose rate is decreased to 200 MU/min. The results with dose rate of 400/600 MU/min and patient breathing cycle of 4/5 s are in line with previous studies that used measurements or numerical simulations under similar conditions.^{8, 11, 12, 17} However, if dose rate of 600 MU/min were used, and patients’ breathing period did not change from the simulation, 4/10 patients had mean deviation from the 4D dose in PTV > 2%. With conservative estimation, where breathing period of 8 s was used instead of the breathing period as measured at the simulation, 4/10 patients had mean deviation from the 4D dose in PTV > 3%. For these patients, the motion induced dose uncertainty may not be negligible with delivery dose rate of 600 MU/min, and by lowering the dose rate, although the delivery time would be increased, the uncertainty could be reduced. These results indicate the benefit of evaluating motion-induced dose uncertainty on an individual basis for patients with larger tumor motion, which was not feasible prior to our work.

As shown in Figs. 2e, 3a, dose distribution calculated for an individual phase is very similar to the 4D dose with <1.5% maximum difference, partly because of the fact that the 4D dose is the average of the individual phase doses. These results, along with results shown in Fig. 5, indicate that individual phase dose and the center of GTV motion may not be good indicators for evaluation of motion-induced dose uncertainty, and again demonstrates the need for patient specific evaluation of the motion-induced dose uncertainty. Although motion-induced dose uncertainty is relatively small in magnitude overall, it is unique to moving tumors and is additional to the uncertainty from other sources such as setup and machine output. With the framework established in this work, the dose impact of the motion could be quantitatively calculated for any given step-and-shoot IMRT plan. This information could be used to evaluate the effectiveness of different 4D or robust optimization techniques;^{18, 19} and it could also be incorporated into optimization process as part of the object functions to further reduce or even eliminate the uncertainty.

As shown in Eqs. 5, 6, 7, 8, and Figs. 34, motion-induced dose uncertainty (ΔD⁺/ΔD⁻) is a function of D_max and D_min, delivery time (T_d, T_cp), patient breathing cycle (T_b), and number of fraction (K). D_max and D_min are associated with the modulation of the plan, as demonstrated in Fig. 1. Once the plan is finalized, K and MU/MU_cp would be fixed, but the delivery time T_d and T_cp could still be adjusted by changing the dose rate of the delivery. Increasing the delivery time (decreasing dose rate¹⁷), as well as decreased patient breathing cycle, would reduce the overall uncertainty. In practice, although patient breathing period (T_b) could vary from one breathing cycle to next, it is usually not a variable that can be controlled, and reduced dose rate could unnecessarily prolong the treatment time, as shown in Fig. 4.

This work did not consider the biological effect of physical dose variation between treatment fractions. Since the purpose of the study was to estimate the motion induced dose uncertainty at the planning stage, only a single set of 4DCT was used in this study. It was therefore assumed that the patient anatomy at any given time during treatment delivery could be represented by one of the phases at the time of simulation, and that the probabilities of each phase were equal. Variations of the patient breathing pattern are not expected to have a strong impact on the results, as the total treatment delivery time is much longer than the breathing cycle. However, if the patient breathing motion were monitored during the treatment, the dose to patient could be determined more accurately with the additional information using the established framework. This topic, along with the relationship between the magnitude of dose uncertainty and the magnitude of the respiratory motion will also be investigated in more details in a future study.

The accuracy of the 4D dose calculation depends on the quality of 4DCT and the accuracy of the deformable registration. Previous studies have established that the deformable registration algorithm used in this study has ∼2 mm of accuracy,^{14, 20} which is deemed acceptable for our purpose as the dose grid we used for the IMRT dose calculation is 3 mm. All patient image sets were visually inspected to ensure that all images were free of 4D artifacts at the levels of targets, and the deformation vectors were both visually inspected and validated for landmark points. With further improvement of 4DCT and deformable registration techniques, the accuracy of dose calculations may be expected to be further improved.

CONCLUSION

We presented an analytical technique that uses IMRT treatment plan information to determine the motion-induced dose uncertainty for a specific patient. Respiratory motion-induced dose uncertainty varies from patient to patient and may not be negligible in some patients under certain delivery conditions. For step-and-shoot IMRT, the uncertainty is a function of motion, modulation, delivery time, number of fractions, and patient breathing patterns. Patient-specific respiratory motion-induced dose uncertainty quantification, which was conventionally simulated by repeated dose calculations and thus not clinically feasible prior to our work, could be useful for treatment plan evaluation and treatment strategy determination for selected patients.