Respiratory effort correction strategies to improve the reproducibility of lung expansion measurements

Abstract

Purpose: Four-dimensional computed tomography (4DCT) can be used to make measurements of pulmonary function longitudinally. The sensitivity of such measurements to identify change depends on measurement uncertainty. Previously, intrasubject reproducibility of Jacobian-based measures of lung tissue expansion was studied in two repeat prior-RT 4DCT human acquisitions. Difference in respiratory effort such as breathing amplitude and frequency may affect longitudinal function assessment. In this study, the authors present normalization schemes that correct ventilation images for variations in respiratory effort and assess the reproducibility improvement after effort correction.

Methods: Repeat 4DCT image data acquired within a short time interval from 24 patients prior to radiation therapy (RT) were used for this analysis. Using a tissue volume preserving deformable image registration algorithm, Jacobian ventilation maps in two scanning sessions were computed and compared on the same coordinate for reproducibility analysis. In addition to computing the ventilation maps from end expiration to end inspiration, the authors investigated the effort normalization strategies using other intermediated inspiration phases upon the principles of equivalent tidal volume (ETV) and equivalent lung volume (ELV). Scatter plots and mean square error of the repeat ventilation maps and the Jacobian ratio map were generated for four conditions: no effort correction, global normalization, ETV, and ELV. In addition, gamma pass rate was calculated from a modified gamma index evaluation between two ventilation maps, using acceptance criterions of 2 mm distance-to-agreement and 5% ventilation difference.

Results: The pattern of regional pulmonary ventilation changes as lung volume changes. All effort correction strategies improved reproducibility when changes in respiratory effort were greater than 150 cc (p < 0.005 with regard to the gamma pass rate). Improvement of reproducibility was correlated with respiratory effort difference (R = 0.744 for ELV in the cohort with tidal volume difference greater than 100 cc). In general for all subjects, global normalization, ETV and ELV significantly improved reproducibility compared to no effort correction (p = 0.009, 0.002, 0.005 respectively). When tidal volume difference was small (less than 100 cc), none of the three effort correction strategies improved reproducibility significantly (p = 0.52, 0.46, 0.46 respectively). For the cohort (N = 13) with tidal volume difference greater than 100 cc, the average gamma pass rate improves from 57.3% before correction to 66.3% after global normalization, and 76.3% after ELV. ELV was found to be significantly better than global normalization (p = 0.04 for all subjects, and p = 0.003 for the cohort with tidal volume difference greater than 100 cc).

Conclusions: All effort correction strategies improve the reproducibility of the authors' pulmonary ventilation measures, and the improvement of reproducibility is highly correlated with the changes in respiratory effort. ELV gives better results as effort difference increase, followed by ETV, then global. However, based on the spatial and temporal heterogeneity in the lung expansion rate, a single scaling factor (e.g., global normalization) appears to be less accurate to correct the ventilation map when changes in respiratory effort are large.

INTRODUCTION

Regional pulmonary function, which measures the local lung volume change, can provide valuable physiological and pathological information about lung. One method to estimate regional pulmonary function has been developed using four-dimensional computed tomography (4DCT) and image registration. Since 4DCT has become a routine examination for lung cancer radiation therapy (RT) treatment planning, generating high resolution ventilation map adds no extra radiation dose to the patient. With image registration between CT images reconstructed at specific phases of the breathing cycle, the deformation field can be used to assess the regional pulmonary function. Several groups have developed this approach from different aspects. Reinhardt et al.¹ directly calculated the determinant of the deformation gradient tensor and used the Jacobian metric to analyze regional ventilation. Simon² and Guerrero et al.³ proposed density-based ventilation calculation with the deformation field and its relationship with air fraction change. Castillo et al.^{4, 5} demonstrated analytic and geometric Jacobian are mathematically equivalent, and studied the correlation between 4DCT-based ventilation and clinically acquired SPECT ventilation or perfusion. Longitudinal radiation-induced pulmonary function change throughout RT was investigated by several groups. Ding et al.⁶ compared regional ventilation before and after RT. Yaremko et al.⁷ and Yamamoto et al.⁸ identified high ventilated lung regions as avoidance structures in intensity modulated radiation therapy (IMRT) planning. Zhong et al.⁹ presented a 4DCT-based regional compliance method for evaluation of radiation-induced lung damage. Vinogradskiy et al.¹⁰ used ventilation maps calculated from weekly 4DCT data to study ventilation change throughout radiation therapy.

The variability in pulmonary function measurement must be accounted for when being used to identify underlying radiation-induced changes. Several groups have investigated the reproducibility of pulmonary function measurement. Mathew et al.¹¹ evaluated the reproducibility of 3-helium magnetic resonance imaging (MRI) ventilation measurements by comparing the ventilation defect volume (VDV), and reported reproducibility of VDV was higher at same-day rescan (R² = 0.941) compared to 7-day rescan (R² = 0.576) in 8 healthy volunteers and 16 COPD subjects. However, VDV reproducibility throws away most of the spatial correlations, and no voxel-by-voxel comparison was reported with the actual measurement. Nyeng et al.¹² studied local lung volume change in two thoracic 4DCT scans in five patients, however, the two scans were different—one scan with respiration restricted by an abdominal compression plate and the other under free breathing. To determine the real underlying radiation-induced pulmonary function changes using 4DCT and image registration, intrasubject variability needs to be established with voxel-by-voxel reproducibility study. In our previous work, we investigated the reproducibility of transformation-based¹³ (correlation coefficient 0.81 ± 0.10) and intensity-based¹⁴ (correlation coefficient 0.45 ± 0.14) measures of lung tissue expansion in two repeat prior-RT 4DCT acquisitions, and found the reproducibility of 4DCT ventilation imaging would be deteriorated by respiratory effort variation. Similarly, Yamamoto et al.¹⁵ investigated the reproducibility of lung ventilation over two different time frames and reported moderate voxel-based correlation between two ventilation images (Spearman rank correlation 0.50 ± 0.15). However, cross-scan respiratory effort variations were not compensated in previous reproducibility studies.

Uncertainty in pulmonary function measurement can be caused by many factors including the subject's breathing patterns and changes in tidal volume during spontaneous respiration, the imaging protocol, and the choice of the ventilation metric.^{13, 14, 15} Since the local lung expansion is dependent on the transformation from the EE (end of expiration) to the EI (end of inspiration) image, it will be affected by the lung volumes at which these two images are acquired. Therefore, the respiratory effort (e.g., amplitude, frequency, switching between abdominal and thoracic breathing, etc.) may play a critical role in reproducibility assessment. In our previous study,^{13, 14} all subjects are coached and trained to ensure steady, reproducible breathing patterns during the 4DCT, and audible respiratory timing cues are used to help guide the subject during image acquisition.¹⁶ However, even with the training and instrumentation, variations in breathing rate and tidal volume are likely to occur which may reduce the reproducibility of the pulmonary function measurements.

The effectiveness of pulmonary function measures increases as the uncertainty in the measurement is reduced. In this study we analyze a pair of 4DCT images obtained prior to RT, which should ideally yield identical pulmonary function maps. Variations in this measure will have an impact when being used for longitudinal study of pulmonary function (e.g., following RT, COPD, etc). Respiratory effort changes between scans may reduce reproducibility and therefore must be compensated for when used in longitudinal studies.

Several methods have been proposed to normalize respiratory effort differences. Guerrero et al.^{4, 7, 10, 17} converted ventilation images to percentile images as part of their normalization process to reduce the sensitivity to the maximum ventilation value on a particular image. However, the percentile image merely computes the rank of values rather than normalize the breathing effort difference. Vinogradskiy et al.¹⁰ used another normalizing method proposed by Seppenwoolde et al.¹⁸ They defined a normalization factor calculated from well-ventilated low-dose regions and applied it to the entire image. Similarly, Zhang et al.¹⁹ corrected SPECT scans for effort differences with a global scaling factor derived from a region of interest in the uninvolved lobe. Both Refs. ¹⁰ and ¹⁹ use a form of global normalization with a single scaling factor applied to the entire image. The global normalization approach is based on the assumption and/or approximation that the lung expansion rate is spatially uniform. If that assumption is not true, the global normalization method will overnormalize or undernormalize ventilation values in different regions.

One of the advantages of 4DCT data for this purpose is that it consists series of CT images resolved into different phases of the breathing cycle.^{20, 21} The 4D nature of the data implies that breathing effort difference can be corrected by choosing phase images with equivalent/similar lung volume or tidal volume, rather than merely registering EE and EI. In this paper we propose two strategies to select phase images, the equivalent tidal volume (ETV) method and the equivalent lung volume (ELV) method. These two approaches differ from other effort correction methods in that they select independent respiratory phases to compute pulmonary function, rather than modify the computed ventilation values directly. In this study we quantify impact of global normalization on 4DCT from subjects and compare and determine which method (if any) best improves the reproducibility of pulmonary function measurement.

MATERIALS AND METHODS

Patients selection

All the patients for this study were chosen from a protocol that was approved by the University of Iowa Institutional Review Board. Under the protocol, the patients underwent two 4DCT scans before radiation therapy for lung cancer. All scans were acquired in supine position on a Siemens Biograph 40-slice CT scanner operating in helical mode, using a pitch of 0.1, 120 kVp, 700 mAs, 1.2 mm beam collimator, 2 mm slice thickness, 0.5 mm slice increment, with a 500 ms tube rotation speed using 180° to reconstruct an image producing a temporal resolution of 250 ms.²² An Anzai AZ-773V system with a strain gauge belt as the pressure sensor was used to acquire the surrogate signal of respiratory motion. To maintain a constant breathing rate, prior to imaging, patients were trained by a biofeedback system (RESP@RATE, Intercure Ltd., Lod Israel). Audible respiratory timing cues were used to pace respiration during imaging.¹⁶

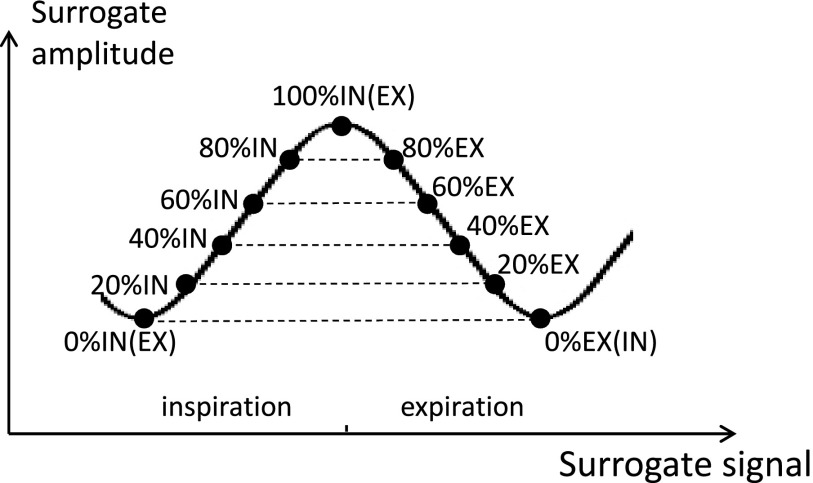
Two prior-RT 4DCT scans were acquired for each subject, with a short time between scans and the same imaging parameters.¹³ The subjects left the scanner table between scans. The 4DCT scanner used retrospective reconstruction to produce the 3DCT images at any user specified phase. As shown in Fig. 1, CT volumes were reconstructed using the retrospective respiratory gating technology from multiple breathing cycles according to the amplitude of respiratory trace, therefore in our study the term of 0%IN is equivalent to the term of 0%EX for the CT volume reconstructed for the subject during the beginning of inspiration, and the term of 100%IN is equivalent to the term of 100%EX when the subject is completing inspiration. Using the respiratory trace curve from the surrogate as reference, for each scan ten 3D CT images were produced, one at the end-expiration (EE, also denoted as 0%EX or 0%IN), four during inhalation in amplitude increments of 20% inspiration (20%IN, 40%IN, 60%IN, 80%IN), one at the end-inspiration (EI, also denoted as 100%IN or 100%EX), and four during exhalation in increments of 20% expiration (80%EX, 60%EX, 40%EX, 20%EX) in the scanner nomenclature.²³ Additional phases could be reconstructed at different amplitude if needed. The audio-coaching on patient respiration and the advantage of helical mode to allow manual selection of projection data could reduce and minimize the common artifacts in 4DCT.²³ Before image registration, all images were examined for evidence of severe breathing artifacts or other problems which may be caused during acquisition and reconstruction. In total 24 patients were used in this study.

Figure 1.

Retrospective reconstruction of 3D volumes based on the amplitude of respiratory surrogate.

Calculation of ventilation maps

The process of calculating ventilation maps with 4DCT and image registration was described in detail in our previous work.¹³ First, prior to image registration all images were resampled to proper size and resolution. The Pulmonary Workstation 2.0 software (VIDA Diagnostics, Inc., Iowa City, IA) helped delineating the lung and the lobes in CT images. All of the lung and lobar segmentations were examined and manually modified if necessary. The lung segmentation was used to limit the spatial domain of image registration, subsequent ventilation calculation, and statistics analysis. In addition, the lobe segmentations are used to characterize the heterogeneity of lung expansion on the lobar level. The lung volume was calculated by multiplying the number of voxels with the volume of each voxel.

Two separate 4DCT scans (denoted as scans 1 and 2) were acquired prior to RT with a short time interval for each subject. Ventilation maps were computed independently in the two studies and then compared in the same coordinate to determine the reproducibility of lung ventilation measurements.

A tissue volume preserving nonrigid algorithm was used for image registration.^{13, 24, 25} The algorithm uses a cubic B-spline transformation model and multi-resolution optimization procedure to minimize the sum of squared tissue difference (SSTVD), subject to a Laplacian regularization constraint. The SSTVD term in the cost function provides a lung-specific intensity similarity criterion that can compensate for the expected change in CT intensity as air is inspired or expired during the respiratory process. Subvoxel accuracy (<1 mm) of the image registration algorithm shown by landmark validation has been reported in previous work of Du et al.,^{13, 25, 26} Cao et al.,^{24, 27} and Murphy et al.²⁸

A displacement field that links corresponding lung voxels in two images is produced after image registration. The Jacobian determinant of the displacement field characterizes the local lung volume change and is used as the ventilation metric in this study. The Jacobian is given by Eq. 1, where (h₁(x), h₂(x), h₃(x)) represents vectors in three dimensions of the deformation field at location x. Encoded by colors, the Jacobian map will show regional ventilation throughout the lung. In the Lagrangian reference frame, Jacobian greater than one represents local tissue expansion, Jacobian less than one represents local tissue contraction, and Jacobian equals to one means no expansion or contraction.

$$J\left(\mathbf{h}\left(\mathbf{x}\right)\right)=\left|\begin{array}{ccc}\hfill \frac{\partial h_1\left(\mathbf{x}\right)}{\partial x_1}& \hfill \frac{\partial h_2\left(\mathbf{x}\right)}{\partial x_1}& \hfill \frac{\partial h_3\left(\mathbf{x}\right)}{\partial x_1}\\ \hfill \frac{\partial h_1\left(\mathbf{x}\right)}{\partial x_2}& \hfill \frac{\partial h_2\left(\mathbf{x}\right)}{\partial x_2}& \hfill \frac{\partial h_3\left(\mathbf{x}\right)}{\partial x_2}\\ \hfill \frac{\partial h_1\left(\mathbf{x}\right)}{\partial x_3}& \hfill \frac{\partial h_2\left(\mathbf{x}\right)}{\partial x_3}& \hfill \frac{\partial h_3\left(\mathbf{x}\right)}{\partial x_3}\end{array}\right|.$$ (1)

If we use T1 and T2 to denote the registration transformations in scans 1 and 2, the two scans would produce Jacobian maps JAC_T1 and JAC_T2. Additional transformation, T0, mapping scan 2 EE to scan 1 EE, is used to convert the ventilation maps into a common coordinate system for comparison. T0 transformation is computed using the same image registration algorithm as that used for T1 and T2. With the transformation T0, JAC_T2 is transformed to the same coordinate of JAC_T1, called JAC_T2○T0. The Jacobian ratio map JAC_RATIO, defined in the same coordinate system as JAC_T1, is a voxel-by-voxel ratio map of JAC_T1 and JAC_T2○T0 and can be used to assess reproducibility.

Respiratory effort correction strategies

When comparing measures of ventilation acquired from different studies, measured values may differ due to changes in respiratory effort. This section describes the most commonly used normalization strategy (global normalization) and two novel strategies proposed in this study.

Global normalization

By definition, the Jacobian reflects the ratio of volumes before and after deformation in a specified region. Since the average Jacobian is strongly correlated with the global volume change in the lung,¹³ the lung volumes can be used to calculate a global linear normalization factor to compensate for lung volume differences between scans 1 and 2.

Suppose I_a and I_b denote the fixed and moving image, respectively, in image registration. Jacobian map J₁ is calculated from the displacement field between two images I_1a and I_1b, and Jacobian map J₂ is calculated from the displacement field between two images I_2a and I_2b. We use V_i to denote the lung volume of image I_i. Then the Jacobian map J₂ can be globally normalized to match with the global inflation level of J₁.

$${\mathrm{J}}_2^{\mathrm{norm}}={\mathrm{J}}_2\times \frac{\frac{{\mathrm{V}}_{1\mathrm{b}}}{{\mathrm{V}}_{1\mathrm{a}}}}{\frac{{\mathrm{V}}_{2\mathrm{b}}}{{\mathrm{V}}_{2\mathrm{a}}}},$$ (2)

where ${\mathrm{J}}_2^{\mathrm{norm}}$ is J₂ after global normalization derived from the ratio of lung volumes in scan 1, normalized by the ratio of lung volumes in scan 2.

The global scaling normalization uses one factor applied to the entire image, commonly based on a ratio of ventilation or perfusion measures acquired from an identical region in the two scans that is assumed to be uninvolved. The global scaling approach is based on the assumption and/or approximation that the lung expansion rate is spatially uniform. These conditions will not be true if the expansion rate in the apex is not proportional to expansion in the base for all intermediate tidal volumes between EE and EI.

ETV and ELV

The basic approach used in global normalization is to compute ventilation from images with known differences in respiratory effort and to scale those values. We propose purposeful selection of the input data, rather than performing postprocessing corrections. This is accomplished by selecting CT images with similar lung volumes or tidal volumes, allowing calculation of the Jacobian under more similar conditions. This technique exploits one of the advantages of 4DCT images, which provides CT images with many different lung volumes. Other than EE and EI images, additional respiratory phases were selected to compute pulmonary function and evaluate reproducibility. This strategy was applied to repeat 4DCT scans of the 24 subjects as described below.

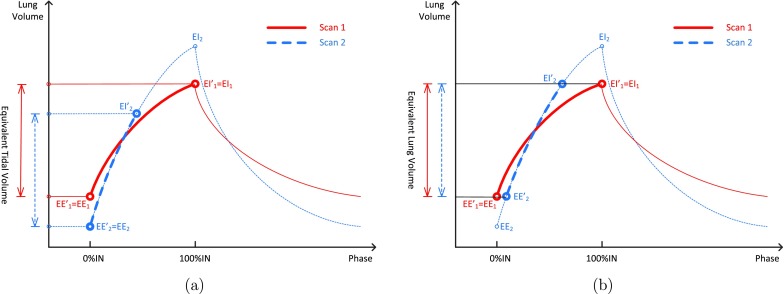
Figure 2 shows the schematic of two respiratory effort correction strategies. The red solid line is scan 1, while the blue dashed line is scan 2. In this example, scan 1, which has less respiration effort, is used as the baseline scan. The line segments in boldface show the process of phase selections based on equivalent tidal volume or equivalent lung volumes in two scans. EE₁, EI₁, EE₂, and EI₂ are original EE and EI phases before effort correction, ${\mathrm{EE}}_1^{\prime }$ and ${\mathrm{EE}}_2^{\prime }$ are reselected end-of-expiration phases, and ${\mathrm{EI}}_1^{\prime }$ and ${\mathrm{EI}}_2^{\prime }$ are reselected end-of-inspiration phases. Figure 2a is the ETV method that uses a pair of images selected from the followup 4DCT scan that produces a tidal volume equivalent to that of the baseline scan. The original EE₁, EE₂, and EI₁ phases do not change, and ${\mathrm{EI}}_2^{\prime }$ is selected to match the tidal volume of scan 1. Figure 2b is the ELV method. ELV uses a pair of 3DCT images selected from the followup scan that has corresponding images at the same lung volumes in the baseline 4DCT scan. Meanwhile, the volume difference between the pair of images should also be maximized. The original EE₁ and EI₁ phases for scan 1 do not change, but ${\mathrm{EE}}_2^{\prime }$ and ${\mathrm{EI}}_2^{\prime }$ for scan 2 have to be reselected to match the lung volumes of scan 1. We compared ETV and ELV with global normalization to determine which (if any) better improves reproducibility of pulmonary function measurement.

Figure 2.

Schematic of respiratory effort correction strategies. The red solid line is scan 1, while the blue dotted line is scan 2. (a) Equivalent tidal volume (ETV) and (b) equivalent lung volume (ELV).

Characterizing heterogeneity of lung expansion

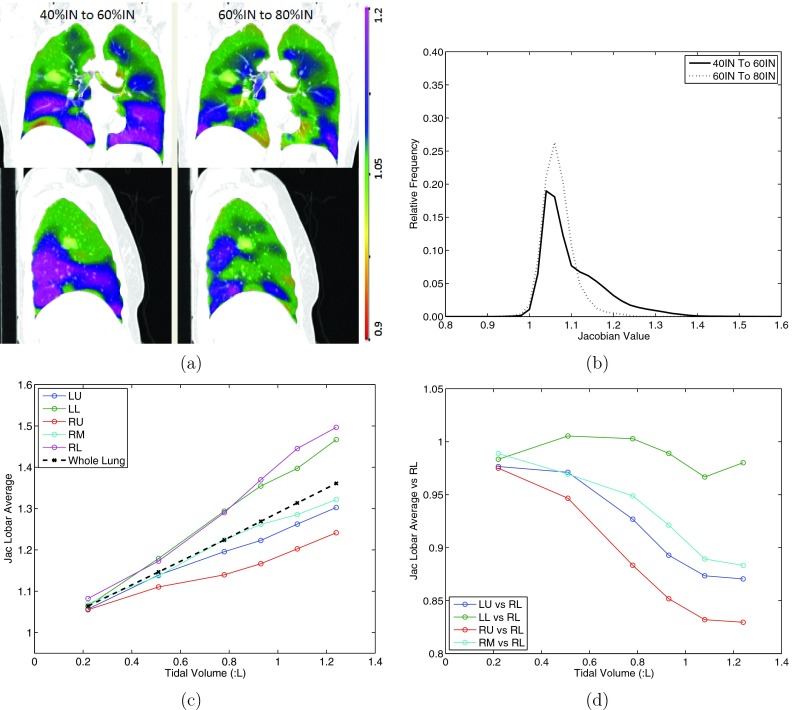
One 4DCT scan of subject H-8 was chosen to demonstrate the heterogeneity in lung expansion rate, as shown in Fig. 3. If the lung expansion rate is spatially uniform, the Jacobian map from 40%IN to 60%IN and the Jacobian map from 60%IN to 80%IN should be identical or be proportional to each other everywhere, and their histograms should have the same shape. The results for this experiment are shown in Figs. 3a, 3b.

Figure 3.

A 4DCT scan is used to show the heterogenous tissue expansion rate. (a) The coronal (top) and sagittal (bottom) views of Jacobian for registration pair 40%IN to 60%IN and 60%IN to 80%IN (left to right). The scales are both 0.9 to 1.2. (b) The corresponding histograms of the two Jacobian maps in (a). (c) The average tissue expansion from EE to each respiratory phase for each lobe and the whole lung. (d) The tissue expansion for lobes LU, LL, RU, RM, relative to lobe RL.

An additional experiment is performed to determine heterogenous spatial pattern of ventilation rate on the lobar level. The same scan as in Figs. 3a, 3b was used to plot how the mean Jacobian (calculated from EE to each inspiratory phase) in each lobe changes with different tidal volumes [results shown in Fig. 3c]. Referring to the right lower (RL) lobe, the relative expansion rate of the other four lobes were studied [result shown in Fig. 3d]. The hypothesis is if the lung expansion is spatially homogenous, the ventilation rate in RL should be proportional to the other lobes. Global normalization would be demonstrated to be less accurate if the ventilation rate in one lobe is not proportional to the other lobes when tidal volume is greater than certain number.

If calculated from registered EE and EI images, the Jacobian represents the accumulated volume expansion in the entire inspiration process. However, regional tissue expansion rate varies both spatially and temporally. Introducing intermediate inspiration phases brings several additional time sampling of lung expansion pattern. With the hypothesis of homogeneous lung expansion rate, which is the theoretical basis of global normalization, the only difference for each time sampling of the lung expansion should be the magnitude, i.e., the Jacobian maps will become identical to each other after scaling by certain constant. Hence, the heterogeneity of lung expansion can be quantified by comparing the global normalized Jacobian map from EE to each specific phase with the Jacobian maps from EE and EI.

Figure 4 shows a flowchart of the intrascan lung expansion heterogeneity analysis. Within a 4DCT scan, each Jacobian map from EE to a specific inspiration phase was scaled using global normalization to the same inflation level of Jacobian map from EE to EI, with a factor calculated from lung volumes. Equation 3 shows the process of the intrascan global normalization that normalizes Jacobian maps from EE to a inspiration phase to the Jacobian of full inspiration:

$$\begin{array}{ccc}\hfill J_{0\mathrm{IN}\to \mathrm{Phase}}^{\mathrm{norm}}& =& J_{0\mathrm{IN}\to \mathrm{Phase}}\times \mathrm{f}\left({\mathrm{V}}_{\mathrm{Phase}}\right)=J_{0\mathrm{IN}\to \mathrm{Phase}}\times \frac{\frac{V_{100\mathrm{IN}}}{V_{0\mathrm{IN}}}}{\frac{V_{\mathrm{Phase}}}{V_{0\mathrm{IN}}}}\hfill \\ & =& J_{0\mathrm{IN}\to \mathrm{Phase}}\times \frac{V_{100\mathrm{IN}}}{V_{\mathrm{Phase}}},\hfill \end{array}$$ (3)

where phase ∈ {20%IN, 40%IN, 60%IN, 80%IN}, f(V_Phase) is the global normalization factor, and V_0IN, V_Phase, and V_100IN are lung volumes. The mean absolute difference is calculated for all lung voxels between the Jacobian map from EE to EI and the global normalized Jacobian map from EE to each specific phase by Eq. 4:

$$\begin{array}{ccc}& & \mathrm{Mean}\mathrm{Absolute}\mathrm{Difference}\hfill \\ & & =\frac{\sum _{n=1}^N\left|J_{0\mathrm{IN}\to 100}\left(n\right)-J_{0\mathrm{IN}\to \mathrm{Phase}}^{\mathrm{norm}}\left(n\right)\right|}{N},\hfill \end{array}$$ (4)

where $J_{0\mathrm{IN}\to \mathrm{Phase}}^{\mathrm{norm}}$ is Jacobian map after intrascan global normalization, n represents each lung voxel, and N is the total number of lung voxels.

Figure 4.

Flowchart of the intrascan global normalization and intrascan lung expansion heterogeneity analysis. The Jacobian map from EE to each specific phase (phase ∈ {20%IN, 40%IN, 60%IN, 80%IN}) is globally normalized to the inflation level of full inspiration and then compared with the Jacobian map from EE to EI.

Both scans from all subjects were processed for the heterogeneity analysis. To study whether the heterogeneity increases with longer interval, we also investigate the relationship between heterogeneity and the inverse of the scaling factor, which represents the fraction of full inspiration for a specific intermediate phase compared to EI.

Outcome metrics and statistical analysis

Four outcome metrics were used to evaluate reproducibility: (1) mean of JAC_RATIO, which should be closer to one if reproducibility improves; (2) voxel-by-voxel coefficient of variation (CV) of JAC_RATIO, where smaller CV would suggest smaller regional difference between JAC_T1 and JAC_T2○T0 and thus indicate improved reproducibility. Since global normalization simply scales the whole ventilation map with a factor, there is no change in CV after global normalization; (3) mean square error (MSE) of JAC_T1 and JAC_T2○T0, as shown in Eq. 5, where JAC_T1 and JAC_T2○T0 are ventilation maps from scans 1 and 2, n represents each lung voxel, and N is the total number of lung voxels. Lower MSE indicates better reproducibility; and (4) gamma pass rate. We have proposed in previous work^{14, 26} a modified gamma index to compare two ventilation maps regionally and quantitatively. In addition to considering the ventilation difference, the gamma index adds a term to tolerate possible spacial misalignment. A voxel that passes gamma index evaluation implies that there is a matching voxel in the other ventilation map with less than the specified criterion for ventilation difference within a certain distance. In this study, we use acceptance criterions of 2 mm distance-to-agreement (DTA) and 5% ventilation difference. The pass rate is computed by counting all passed voxels and then dividing by total number of pulmonary parenchyma voxels:

$$\mathrm{MSE}=\frac{1}{N}\sum _{n=1}^N{({\mathrm{JAC}}_{\mathrm{T}1}\left(n\right)-{\mathrm{JAC}}_{\mathrm{T}2}\circ \mathrm{T}0\left(n\right))}^2.$$ (5)

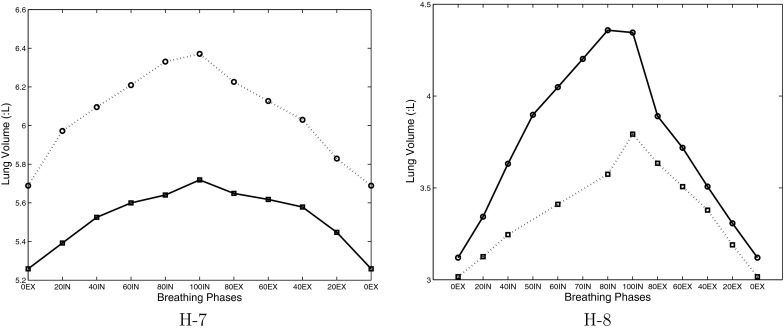
In this study 24 subjects were used. ETV can be applied to 18 subjects, and ELV can be applied to 21 subjects. ELV is not suitable for some subjects that had significant shift of breathing baseline. For example, for subject H-7 the EE lung volume of scan 2 is almost as high as the EI lung volume of scan 1 (Fig. 5). To the contrary, some subjects have intermediate phases applicable for ELV, but under ETV selection strategy no breathing phase is more optimal than the original EI phase before effort correction. The four reproducibility outcome metrics were calculated and analyzed using subject-specific tidal volume difference across scans. All three effort correction strategies were applied and assessed for their improvement of reproducibility, compared to making no correction for respiratory effort differences between scans. Comparisons were performed between global and ETV, between global and ELV, and between ETV and ELV on entire cohort and the cohort that have tidal volume difference greater than 100 cc.

Figure 5.

Lung volumes of 4DCT in two repeated scans for two sample subjects. Solid line is for scan 1, and dotted line is for scan 2. Note the scale is different for these two subjects.

Clinical application

In this study the effectiveness of effort correction schemes are assessed using repeated scans under the same conditions. Clinical longitudinal studies on pulmonary function can be evaluated by scan and rescan, and the improvement of measurement sensitivity by effective effort correction techniques can reduce the parameters during the longitudinal studies. Assessment of the post-RT scan can be considered as longitudinal function study with a larger time interval during which the time and treatments may have introduced more variables to the lung, compared to the prior-RT scan-rescan study. In this section, subject H-42 is used as an example case of pre- and post-RT ventilation to show the dose response is different when it is measured with effort correction compared to without effort correction. The subject was treated with an 11 field coplanar SBRT plan delivering 40 Gy in 4 fractions. During the post-RT scan the subject was breathing with a tidal volume of 0.7 L, while the pre-RT scan was acquired with a 0.25 L tidal volume. The gamma index evaluation was used to compare the pre-RT to post-RT ventilation in the entire lung region.

RESULTS

Results: Heterogeneity of lung expansion

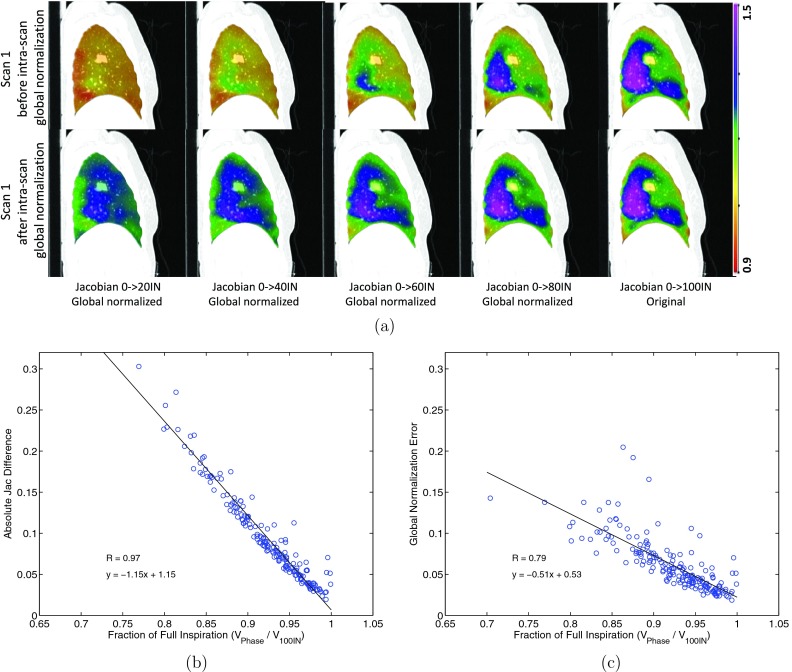
Figure 3 shows the heterogeneity in the spatiotemporal pattern of ventilation rate using scan 2 of subject H-8. Figure 3a shows the coronal and sagittal colored panel of Jacobian in registration pairs 40%IN to 60%IN (lung volume from 3.63 to 4.05 L) and 60%IN to 80%IN (lung volume from 4.05 to 4.36 L). The regions that are highly ventilated during 60%IN to 80%IN do not simply scale proportionally during 40%IN to 60%IN, i.e, the pattern of ventilation changes. Their corresponding Jacobian histograms also present different patterns as seen in Fig. 3b, where far fewer voxels expand with a Jacobian value >1.15 during the later stage of ventilation. Figures 3c, 3d show the heterogenous tissue expansion rate for different lobes from EE to each respiratory phase. Figure 3c shows the average Jacobian for the left upper (LU), left lower (LL), right upper (RU), right middle (RM), and right lower lobe (RL) along with the whole lung. As expected, greater ventilation is seen in the two lower lobes of the lung. Figure 3d shows the ventilation in each lobe when normalized to the ventilation in the right lower lobe, consistent with conventional respiratory effort correction strategies. With increasing lung expansion level, the other four lobes do not expand at the same rate as RL lobe, and even different expansion rates to each other. The lobar ventilation shows as high as 20% difference when the tidal volume is 0.8 L, and around 30% difference when the tidal volume is 1.2 L. These results demonstrates that the ventilation rate is not uniform throughout the lung, not even at the lobar level. The ventilation rate for the left lower lobe is similar to the right lower lobe, but the upper and middle lobes show more heterogeneous air filling rates.

Figure 6 shows results of the intrascan lung expansion heterogeneity analysis, which evaluates these differences at the voxel level. If ventilation is independent of spatiotemporal effects, ventilation patterns produced during the initial phases of inspiration could be scaled globally without deviation from the ventilation map determined at the end of inspiration. This intrascan study approach allows the end of inspiration map to be used as ground truth. Figure 6a shows the original and the globally normalized Jacobian maps computed for this intrascan experiment performed, for scan 1 of subject H-8. For this scan, all Jacobian maps were globally normalized to the inflation level of Jacobian from EE to EI. We can see after global normalization there are still differences between the ventilation maps from different inflation levels. The global normalization did not consider the regional difference of the lung expansion rate. For example, when the Jacobian from EE to 20%IN in scan 1 was normalized to the full inspiration level of scan 1, the magnitude of the ventilation changed but the distribution pattern did not change. For instance, some regions are going to expand with higher rates in next phases—they will be undernormalized by the global normalization, such as the dorsal lung; while some regions are going to expand with lower rates in next phases—they will be overnormalized by the global normalization, such as the ventral lung.

Figure 6.

Results of intrascan lung expansion heterogeneity analysis after global normalization. (a) Jacobian maps before and after intrascan global normalization for scan one of subject H-8. (b) Scatter plot made from all subjects shows how the ventilation difference changes with different fractions of full inspiration. (c) Scatter plot made from all subjects shows how the associated global normalization error changes with different fractions of full inspiration.

Another observation worth mentioning is that the ventilation map of EE to 80%IN, compared to that of EE to 20%IN, is more similar to the ventilation map for full inspiration. It suggests the global normalization may be adequate when tidal volume difference is small. Figures 6b, 6c show the scatter plots of how the ventilation difference and the associated global normalization error change with different fractions of full inspiration for all 24 subjects in this study. Possibly due to errors in the respiratory surrogate signal, seven phases were found from three subjects to have slightly bigger lung volumes than the full inspiration and were excluded from analysis. The horizontal axis $\frac{{\mathrm{V}}_{\mathrm{Phase}}}{{\mathrm{V}}_{100\mathrm{IN}}}$ enables a normalized measure of fraction of full inspiration across different subjects. Figure 6b shows the ventilation difference increases when the phase is further away from full inspiration (R = 0.97). In comparison, Fig. 6c shows quantitative heterogeneity results for scan 1 and scan 2 for all subjects, determined using Eq. 3. A linear correlation is found between global normalization error and the fraction of full inspiration (ratio of V_Phase and V_100IN, can be understood as a parameter for time interval). The vertical axis is the mean absolute difference in the globally normalized Jacobian maps. A linear relationship between lung expansion heterogeneity and the inflation level was observed with high correlation (R = 0.79). Figure 6c shows the limitations of global normalization to address the complexity of respiratory effort correction, which may require both a spatial and temporal component.

Results: All effort correction strategies

Figure 5 shows the lung volumes of two repeat scans for two sample subjects H-7 and H-8. The solid line represents scan 1, and the dotted line represents scan 2. While we can perform both ETV and ELV correction for subjects H-8, ELV cannot be applied on subject H-7 because the EE lung volume of scan 2 is almost as high as the EI lung volume of scan 1. Similar significant shifting of the breathing baseline was found for another two subjects in this study.

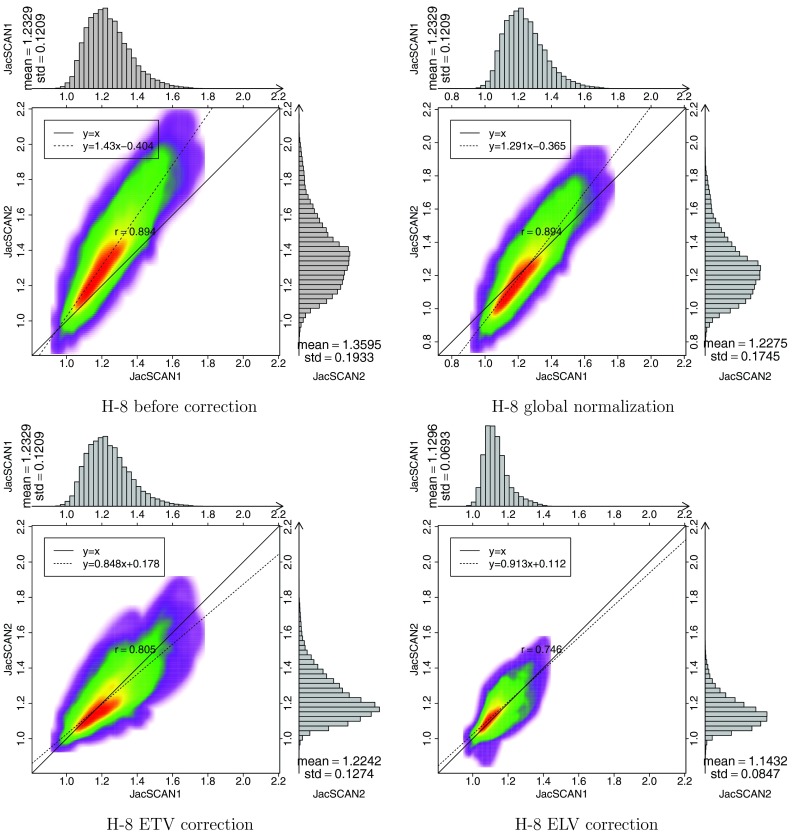
Figure 7 shows the sagittal view of colored JAC_RATIO maps before effort correction, after global normalization, after ETV, and after ELV for subject H-8. The color scale for the JAC_RATIO maps is the same 0.7 to 1.3. Global normalization factor 0.9 was used for this patient. For this subject, ELV was found to have more reproducible regions than ETV and global normalization. Figure 8 shows the voxel-by-voxel scatter plots of JAC_T1 and JAC_T2○T0 data, which were encoded with colored 2D kernel density estimates,^{13, 29} for one sample subject H-8 before and after the three effort corrections. Marginal histograms of JAC_T1 and JAC_T2○T0 are plotted along the top and right side of the figures, ideally these histograms would be mirrored images of one another. By linear regression analysis, a best fit linear model (shown as the dashed line) is calculated to represent the relationship between scan 1 and scan 2 ventilation. Line y=x is also plotted as the reference line; ideally the data would fall on the y = x regression line. The slope and y-intercept for each correction strategy is provided on the figure, showing the improved reproducibility of the different approaches.

Figure 7.

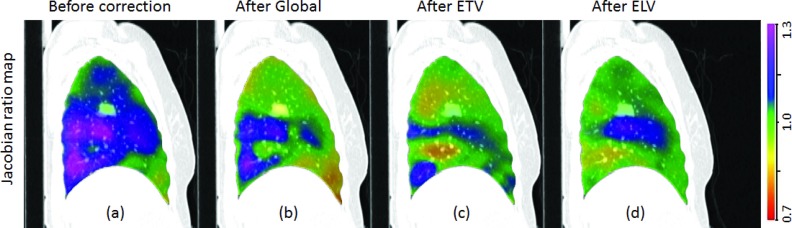
Sagittal view of JAC_RATIO before correction (a), after global normalization (b), after ETV (c), and after ELV, (d) effort correction for subject H-8. The color scale is shown on the right. If the correction was perfect, the JAC_RATIO map would be all green.

Figure 8.

Colored density scatter plot and marginal histograms of two Jacobian maps for subjects H-8. Before effort correction, after global normalization, after ETV correction, and after ELV correction, are shown, respectively. Histograms and statistics are given along the top and right side of each plot.

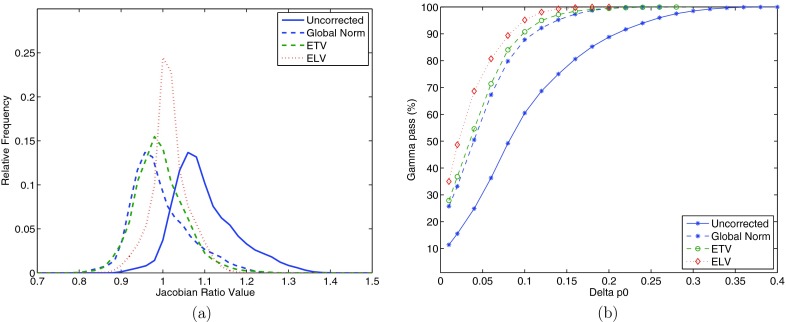
Figure 9a shows the histograms of JAC_RATIO of subject H-8 for before correction, after global normalization, after ETV correction, and after ELV correction. Since in the global normalization JAC_RATIO is simply scaled by a constant, its histogram shifts closer to one but the shape does not change. The ETV and ELV histograms become narrower and closer to one, indicating better agreement of the two ventilation maps. Figure 9b shows the gamma pass rates with increasing gamma criterion for the same subject before correction, after global normalization, after ETV, and after ELV. Delta p0 in the horizontal axis represents the tolerance criterion for Jacobian value disagreement in gamma analysis, e.g., delta p0 equals to 0.1 means Jacobian values are tolerated to disagree with each other as high as 10%. We can see for this subject all three effort correction strategies improve reproducibility. Additionally, both ETV and ELV methods, especially ELV, result in better reproducibility than the global normalization when the ventilation difference criterion in gamma evaluation is below 10%.

Figure 9.

Histograms of JAC_RATIO map (a) and gamma pass rates (b) for subject H-8 before effort correction, after global normalization, after ETV, and after ELV, shown in solid blue, dashed blue, dashed green, and dotted red, respectively.

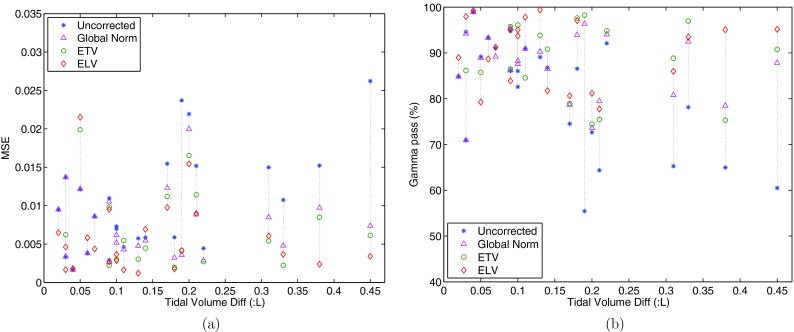
Figure 10 shows the MSE and Gamma pass rate results for each effort correction strategy for all subjects. The results are provided as a function of the relationship between the tidal volume difference in two scans and the change of reproducibility after global normalization, after ETV and/or ELV for all subjects, with regard to MSE and gamma pass rate. The horizontal axis is tidal volume difference in liters. The improvement of reproducibility can be read from reduced MSE and increased gamma pass rate. It is observed that the improvement of reproducibility is particularly significant in case of greater tidal volume difference between scan 1 and 2. We can also notice that if the tidal volume difference is small, the effect of global normalization is close to ETV and ELV, and for some subjects the effort correction strategies may deteriorate the reproducibility. ELV gave better results as tidal volume difference increases, followed by ETV, then global normalization.

Figure 10.

Relationship between the tidal volume difference in two scans and the change of reproducibility after global normalization, after ETV and/or ELV, presented with reproducibility parameters as modified mean square error (MSE) (a), and gamma pass rate (b) between JAC_T1 and JAC_T2○T0. The horizontal axis is tidal volume difference in liters.

Results: Statistical analysis

Table 1 summarizes the mean, CV of JAC_RATIO, MSE, and gamma pass rate to evaluate reproducibility before effort correction, after global normalization, after ETV, and after ELV for subjects with tidal volume difference less than 100 cc, greater than or equal to 100 cc, and all subjects (shown as cohort mean ± standard  deviation). Improvement in reproducibility is represented by that the mean of JAC_RATIO is closer to 1, the CV of JAC_RATIO and MSE decrease, and the gamma pass rate increases. The cutoff value of 100 cc is suggested based on an experimental evidence after which ETV and ELV start to have better performance overall than global normalization. As more subjects are added to this study in the future, a more accurate cutoff value may be found with statistical significance.

Table 1.

Summary of mean and CV of JAC_RATIO, MSE, and gamma pass rate for reproducibility before effort correction, after global normalization, after ETV, and after ELV in subjects with tidal volume difference less than 100 cc, greater than or equal to 100 cc, and all subjects (shown as cohort mean ± standard  deviation).

Subjects	Parameter	Before correction	After global	After ETV	After ELV
<100cc	Mean	1.00 ± 0.01	1.01 ± 0.01	1.01 ± 0.01	1.00 ± 0.01
	CV (× 10−2)	6.95 ± 2.28	6.95 ± 2.28	8.26 ± 3.53	6.54 ± 2.54
	MSE (× 10−2)	0.74 ± 0.45	0.73 ± 0.45	0.95 ± 0.76	0.65 ± 0.62
	Gamma (%)	75.4 ± 10.5	75.0 ± 10.8	75.7 ± 8.0	75.6 ± 10.8
⩾100cc	Mean	1.02 ± 0.05	1.00 ± 0.02	1.00 ± 0.02	1.00 ± 0.01
	CV (× 10−2)	7.20 ± 2.02	7.20 ± 2.02	6.30 ± 2.14	5.81 ± 2.26
	MSE (× 10−2)	1.23 ± 0.73	0.71 ± 0.44	0.62 ± 0.43	0.51 ± 0.40
	Gamma (%)	57.1 ± 14.5	68.4 ± 9.6	72.1 ± 12.6	76.3 ± 12.7
All	Mean	1.01 ± 0.04	1.00 ± 0.02	1.00 ± 0.01	1.00 ± 0.01
	CV (× 10−2)	7.11 ± 2.08	7.11 ± 2.08	6.74 ± 2.53	6.10 ± 2.34
	MSE (× 10−2)	1.05 ± 0.68	0.72 ± 0.44	0.69 ± 0.51	0.57 ± 0.49
	Gamma (%)	64.0 ± 15.8	70.9 ± 10.3	72.9 ± 11.6	76.1 ± 11.7

All effort correction strategies improved reproducibility when changes in respiratory effort were greater than 150 cc (p < 0.005 with regard to the gamma pass rate). In general for all subjects, global normalization, ETV and ELV significantly improved reproducibility compared to no effort correction (p = 0.009, 0.002, 0.005 respectively). When tidal volume difference was small (less than 100 cc), none of the three effort correction strategies improved reproducibility significantly (p = 0.52, 0.46, 0.46 respectively). For the subjects with tidal volume difference less than 100 cc, the gamma pass rate is 75.4 ± 10.5, 75.0 ± 10.8, 75.7 ± 8.0, and 75.6 ± 10.8 for reproducibility before effort correction, after global normalization, and after ELV, respectively.

Table 2 is a summary of MSE and gamma pass rate for the subjects with tidal volume difference greater than or equal to 100 cc (shown as cohort mean ± standard  deviation), for reproducibility before effort correction, after global normalization, and after ELV. Notice that MSE and gamma values at the bottom of Table 2 are slightly different from the values in Table 1 for the ⩾100  cc cohort because Table 2 lists only the subjects where ELV is applicable. The MSE improved by 36% for global normalization and 57% for ELV, and the gamma pass rate improved by 16% for global normalization and 33% for ELV. Similar comparisons can be made between global normalization and ETV, and between ETV and ELV. For cohort with tidal volume difference over 100 cc, the p-value with regard to the gamma pass rate is 0.005 between uncorrected and global normalization, 0.002 between uncorrected and ETV, 0.001 between uncorrected and ELV, 0.084 between ETV and global normalization, 0.003 between ELV and global normalization, and 0.156 between ETV and ELV. For ELV in the cohort with tidal volume difference greater than 100 cc, the improvement of reproducibility is correlated with respiratory effort difference (R = 0.744).

Table 2.

Summary of mean square error (MSE) and gamma pass rate (shown as average ± standard  deviation) for reproducibility before effort correction, after global normalization, and after ELV, for the subjects with tidal volume difference between scans greater than 100 cc.

	Mean square error			Gamma pass
	(MSE, × 10−2)			rate (%)
Subjects		After	After		After	After
>100 cc	Before	global	ELV	Before	global	ELV
H-4	0.73	0.52	0.36	65.2	66.1	87.3
H-8	2.62	0.74	0.34	36.3	67.3	80.7
H-9	1.07	0.48	0.37	51.2	69.0	74.6
H-11	0.70	0.62	0.29	70.9	73.7	84.9
H-16	2.19	2.00	1.55	51.8	55.1	64.9
H-17	1.52	0.97	0.24	44.0	54.6	81.4
H-18	1.52	0.89	0.90	42.7	57.7	52.5
H-29	1.55	1.23	0.98	58.4	61.7	63.8
H-31	0.59	0.32	0.18	68.4	82.3	90.0
H-32	0.59	0.55	0.69	66.1	68.2	62.7
H-36	1.50	0.85	0.61	44.3	59.8	68.6
H-37	0.57	0.48	0.12	71.7	72.3	92.3
H-42	0.46	0.43	0.16	74.0	74.2	88.3
Mean	1.20	0.77	0.52	57.3	66.3	76.3
Std	0.68	0.45	0.41	12.9	8.3	12.7

Results: Clinical application

The effort correction techniques can be used for longitudinal pulmonary function evaluation to reduce the measurement uncertainty that is introduced by effort differences. Figure 11 shows an example (subject H-42) of pre-RT and post-RT ventilation with or without different effort correction schemes. The Jacobian ratio maps between post-RT and pre-RT ventilation are shown in coronal view before effort correction, after global normalization, after ETV, and after ELV. To provide context for the measured changes in ventilation observed 3 months post-RT the RT dose distribution for this subject is also shown in Fig. 11a. Gamma pass rates are 27.4%, 38.9%, 56.3%, and 51.6% for before correction, after global, after ETV, and after ELV, respectively.

Figure 11.

(a) Isodose distribution in RT, the Jacobian ratio between post-RT and pre-RT ventilation (b) before effort correction, (c) after global normalization, (d) after ETV, and (e) after ELV.

DISCUSSION

There are several situations in which we want to measure ventilation changes or perform longitudinal assessment of ventilation, such as asthma, COPD, and response to radiation therapy.^{6, 7, 8, 10} To effectively measure the ventilation changes longitudinally, we need to minimize the variables and one of the variables is respiratory effort. The measure of function change is complicated by changes in respiratory effort.

In previous work, we have evaluated the reproducibility of ventilation estimates using two repeated prior-RT 4DCT scans.^{13, 14} Our present work proposes two phase-selection-based effort correction schemes (ETV and ELV), and compared them with the global normalization for the improvement of reproducibility in repeated 4DCT scans for 24 patients. Heterogeneity in lung ventilation rates demonstrates the limits of global normalization. Improvement in reproducibility was found to be correlated well with the respiratory effort difference. ELV was found to be significantly better than the other two effort correction methods when differences in tidal volume were greater than 100 cc.

In our previous work, we have shown the mean of JAC_RATIO is strongly correlated with the volumes ratios in scans 1 and 2,¹³ which hints a possible subject-specific global normalization using single scaling factor. Several other groups also suggested similar global normalization by scaling entire ventilation map with factors derived from ventilation values in a ROI or lobe that is uninvolved by radiation.^{10, 18, 19} Although true when averaged over all voxels within the lung, in this paper we have shown the ventilation rate of lung tissue is not uniform either spatially or temporally when studied at the voxel level. As shown in Fig. 3, some regions that are highly ventilated during 40%IN to 60%IN become less ventilated during 60%IN to 80%IN, or vice versa. The Jacobian histograms also showed the heterogeneity of lung expansion rates. Using the right lower lobe as the reference, the other four lobes, especially the upper and middle lobes, show various air filling rates. Hence, the global scaling normalization, which is true only with under the assumption of homogeneous lung expansion rate, may overnormalize or undernormalize regional tissue or lobes. The well-ventilated low-dose method is a type of global normalization by deriving one factor from a specific region and applying it to the whole lung. The work in this paper quantifies the spatiotemporal heterogeneity of lung ventilation and its dependence on respiratory effort. The heterogeneity of ventilation makes global normalization suboptimal when tidal volume differences between scans exceeds 100 cc. Figures 3c, 3d, 6 demonstrate that the ventilation patterns change in both space and time, which limit the applicability of being scaled globally.

The possible errors introduced by respiratory effort are of significant magnitude relative to the effect we are trying to measure, whether it is an improvement in post-RT ventilation or a reduction in post-RT ventilation. Vinogradskiy et al.¹⁰ found 8.25% increase in average in ventilation seven weeks after RT in regions that contained the tumor and shrank after RT. Ding et al.⁶ found 7.2% reduction in ventilation for one subject after 24 Gy dose delivered to ipsilateral lung regions at the distance of 20–25 mm to the center of tumor region. According to Fig. 6b, a 9.5% variation in tidal volume may cause up to a 10% change in ventilation without any effort correction. Figure 6c shows when global normalization is used variations in ventilation on the order of 10% are possible with a 18.6% variation in tidal volume. In our cohort of subjects, 83.3% and 62.5% showed a greater than 9.5% and 18.6% variation in tidal volume between scans separated by around 15 min. We believe this effect needs to be addressed to accurately resolve changes in pulmonary function following RT. It is not clear how many errors remain when ETV or ELV are used, but they are shown to result in less variation in repeat scans than global normalization.

Figure 7 shows colored ventilation maps in sagittal view for subject H-8 before and after effort correction. While the global normalization shows obvious ventilation variability in the dorsal lung, the reselection of phases in ETV and ELV effort correction methods produced JAC_RATIO maps that are closer to identity and more homogeneous. The most improvement in reproducibility was found in ELV correction for this subject.

Figure 8 shows scatter plots and histograms of JAC_T1 and JAC_T2○T0 before correction, after global normalization, after ETV, and after ELV for the same subject H-8. We can notice that the mean of JAC_T1 and JAC_T2○T0 are closer after every effort correction method. In global normalization, a scaling factor was applied to the whole lung, resulting in a vertical shift of the scatter points without affecting the distribution pattern. After ETV and ELV the marginal histograms appear more similar. The dashed line is the scatter regression line of JAC_T1 and JAC_T2○T0, and the solid line is the reference line y = x. The regression line is closer to the reference line after effort correction indicating compensated effort difference, and the better convergence of points on the regression line also reveals improved reproducible ventilation distribution in two scans. From Fig. 9a, while the global normalization simply shifted the histogram along the horizontal axis, ETV and ELV effort correction leaded to narrower histogram centered around one. The distribution of gamma pass rate in Fig. 9b further confirmed the improvement of reproducibility after the effort correction methods where ELV gave the best results for this subject, followed by ETV, and then the global normalization.

While ETV is applicable to all longitudinal pulmonary function studies using 4DCT, the ELV is an approach of choice. By measuring the volume ratio during deformation, the Jacobian of the displacement field provides a surrogate for lung ventilation. The most obvious approach to match the mean Jacobian in the lung (i.e., the global volume ratio) across different scans is ELV, which selects images with equivalent lung volumes. However, ELV is impossible in case of obvious baseline shift of lung volumes due to different breathing efforts across scans or tumor shrinkage after treatment. For example, the lung volume of scan 2 EE appears even greater than that of scan 1 EI for H-7 [refer to Fig. 5a], making ELV impossible. Compared to ELV which is based on the relationship between the definition of lung expansion and lung volume ratios, ETV is also meaningful because the reconstruction of the 0%IN phase has been shown to be the most stable and reproducible phase in a breathing cycle,³⁰ as 0%IN is typically the phase at which the lung spends relatively more time than the other phases during image acquisition. Therefore, unlike ELV, it sounds reasonable for ETV to pick phases starting with the EE phase for both baseline and followup scans.

The magnitude of effort difference varies for different subjects, and it is necessary to investigate the relationship between the degree of effort difference and the improvement of reproducibility after effort correction. In Fig. 10, more obvious improvement in reproducibility was observed for subjects with greater tidal volume difference. However, for some subjects with small tidal volume difference, e.g., less than 100 cc, the ETV and ELV may result in worse reproducibility. Arbitrary effort correction using ETV or ELV on the subjects with insignificant difference in lung volumes or tidal volumes may introduce more ventilation variation and thus deteriorate the reproducibility, because the number of phases from which ETV and ELV pick images are limited. In contrast, the global normalization uses a flexible float value which suggests global normalization may be useful in situations of small effort difference. The drawbacks may be addressed by applying global normalization after ETV or ELV to account for the small residual tidal volume differences. Additionally, in this study image interpolation was not used but might improve the results. With more subjects collected in the future study, it is essential to determine a cutoff tidal volume difference that below which we do not have to bother to do the effort correction.

All statistical parameters indicate the three effort correction methods improved reproducibility, especially when changes in respiratory effort are bigger than 100 cc, with great significance. From Table 1 we see when tidal volume difference is small, global normalization works equally with our proposed techniques. For cohort with tidal volume difference over 100 cc, ELV is significantly better than global normalization (p = 0.003), while no significance was found between ETV and global normalization (p = 0.084) or between ETV and ELV (p = 0.156). Collecting more subjects in the future will help investigate more for these effort correction methods.

As a representative case of longitudinal pulmonary function study, Fig. 11 shows the postintervention assessment of radiation-induced pulmonary function change with different effort correction schemes on respiratory effort. The treated volume was restricted to a region in the upper right lung, which corresponds to the substantial reduction in ventilation seen within the Jacobian ratio maps. Quantitative evaluation of the reduction in ventilation post radiation therapy produces different results based on respiratory effort differences. Without effort correction, while there was little function change in the treated region, the uninvolved lung had greater ventilation and contributed to the greater tidal volume in the post-RT scan. With global normalization, the reproducibility in the uninvolved lung was improved but not optimal. It is also worth noting that reduction of pulmonary function observed in the treated lung may be inaccurate due to the over-compensation of global normalization technique. With ETV and ELV, the uninvolved lung was better normalized with less perturbation to other regions and shows a more modest reduction in ventilation in the treatment volume. Our best measure of ground truth is found outside the treated volume, where post-RT values are more similar to those from the pre-RT scans. Gamma analysis results further confirmed the results shown in Fig. 11. Even though ETV and ELV did better in effort correction, the pre- and post-RT ventilation maps were still less similar and the gamma pass rates are lower than the scan-rescan study prior to RT. The post-RT ventilation may have been altered by delivered radiation, and the much longer time interval (months versus minutes) between scans. In this example, the entire lung region was used for gamma comparison including the high dose regions. The relationship between dose and function change is unknown, as is change following tumor regression or progression. The disease state of the lung may have changed after RT, and how it impacts gamma comparison is unknown. All of these changes will likely lead to a reduction in the gamma comparison in the context of reproducibility.

Although effort correction is shown to reduce the measurement uncertainty introduced by inconsistent breathing effort across scans, it may result in a loss of useful information. In Fig. 11, the subject's tidal volume increased from 0.25 L pre-RT to 0.7 L post-RT. This may be due to improved ventilation within the lung resulting from a reduction in the tumor volume. Conversely, the patient may need greater tidal volumes in order to enable the pre-RT level of gas exchange. The reason for the difference in breathing effort is unknown. Therefore, it should be recognized there might be clinical reasons for the difference in respiratory effort that are meaningful and effort correction may result in information loss. The proposed approaches in this study are effort correction methods by selecting alternative 4DCT respiratory phases, rather than a normalization operation that is directly performed on the ventilation map calculated between EE and EI. The impact of effort correction strategy on the additional information within lung function is unknown.

While the effort correction strategies proposed in this study are mainly designed for longitudinal ventilation assessment,^{6, 10} there are many clinical scenarios of 4DCT-based ventilation that do not involve longitudinal scans^{7, 8, 9} making ETV and ELV impossible, for example, using ventilation images for function avoidance to optimize RT plans. Modified versions of global normalization^{10, 18, 19} and the percentile method^{4, 7, 10, 17} might be options in the case of the single scan scenario. However, the global normalization has limitations. The scatter plot made from all subjects in Fig. 6c shows how the associated global normalization error correlates with the inverse of global normalization factor, and can be used to predict the potential drop off in accuracy for global normalization. Global normalization should be used with care in cases with large tidal volume differences, in which instances ventilation heterogeneity has been accumulated in a longer interval causing larger normalization error. It also suggests that if there are image artifacts in the EI image, global normalization can be applied to the alternate images that are close to the desired volume (e.g., 80%IN). Additionally, in one scan scenarios, ETV and ELV can also be modified to select for each patient the phases that are more stable or more consistent with other clinical end points such as pulmonary function test (PFT).

The phase-selection-based pulmonary function effort correction strategies may be influenced by reconstruction of 3D CT images at different levels in 4DCT, accuracy of lung segmentation, and lung volume change due to radiation-induced tumor shrinkage, etc. Investigation of more subjects will help analyze and compare these effort correction methods. Since the lung is spatiotemporal heterogeneous, the percentile method might not work well in all cases. There might be some population models such as atlas-based normalization that can be utilized to normalize single image. In this study, different effort correction strategies are evaluated based on the hypothesis that the reproducibility within two pre-RT scans should be the same. When applied to longitudinal data for the purpose of quantifying ventilation change, other clinical measures (e.g., PFT, perfusion image, DL_CO (carbon monoxide diffusing capacity), Xenon-CT, 6 min walk test) would be valuable to demonstrate improved correlation. The heterogeneity in lung expansion shows that effective effort correction schemes may require both a spatial and temporal component for respiratory effort correction. In the future ETV and ELV can be applied to the scans before and after RT, or images with better matching lung volumes can be simply reconstructed, to make the radiation-induced function change free of effort difference and enable more significant analysis.³¹ Moreover, the pulmonary function metrics so far reflects lung ventilation only from one phase to another phase, and more robust parameters for pulmonary function are worth being investigated to fully utilize the 4D nature of data, which may tell more information about the lung tissue dynamics.

CONCLUSIONS

In this paper we presented two effort correction strategies (ETV and ELV) to correct for respiratory effort difference by selecting alternate respiratory phases from 4DCT, and compared them with global normalization. All effort correction strategies improved reproducibility when changes in respiratory effort were great, and the improvement of reproducibility is highly correlated with the changes in respiratory effort. ELV gave better results as effort difference increase, followed by ETV, then global. Heterogeneity in lung expansion rates was quantified and analyzed, and the global normalization is demonstrated to be less accurate to correct the ventilation map with single scaling factor especially for subjects with great respiratory effort difference. Collecting more subjects in the future will help better understand the effort correction strategies.