Precision of estimates of local stability of repetitive trunk movements

Abstract

Purpose

Local dynamic stability of trunk movements quantified by means of the maximum Lyapunov exponent (λ_max) can provide information on trunk motor control and might offer a measure of trunk control in low-back pain patients. It is unknown how many repetitions are necessary to obtain sufficiently precise estimates of λ_max and whether fatigue effects on λ_max can be avoided while increasing the number of repetitions.

Method

Ten healthy subjects performed 100 repetitions of trunk movements in flexion, of trunk rotation and of a task combining these movement directions. λ_max was calculated from thorax, pelvis and trunk (thorax relative to pelvis) kinematics. Data series were analyzed using a bootstrap procedure; ICC and coefficient of variation were used to quantify precision as a function of the number of cycles analyzed. ANOVA was used to compare movement tasks and to test for effects of time.

Results

Trunk local stability reached acceptable precision level after 30 repetitions. λ_max was higher (indicating lower stability) in flexion, compared to rotation and combined tasks. There was no time effect (fatigue). λ_max of trunk movement was lower and less variable than that of thorax and pelvis movements.

Conclusions

The data provided allow for an informed choice of the number of repetitions in assessing local dynamic stability of trunk movements, weighting the gain in precision against the increase in measurement effort. Within the 100 repetitions tested, fatigue did not affect results. We suggest that increased stability during asymmetric movement may be explained by higher co-activation of trunk muscles.

Introduction

Considering the socioeconomic burden of low back pain [1], there is a pervasive need to improve clinical assessments for treatment decisions, evaluation of outcome and compensation awards [2]. While range of motion, strength or endurance are widely used in clinical practice, they may not necessarily address physical impairments related to specific neuromuscular dysfunction often observed in chronic low-back pain patients [3–5]. A key feature of trunk neuromuscular control is the ability to deal with mechanical perturbations, resulting from internal (e.g., breathing) and external (e.g., being pushed) perturbations. The ability to deal with perturbations (i.e., mechanical stability) is crucial to be able to perform reliably in a variety of tasks [6]. When stability is impaired, small perturbations can lead to uncontrolled intervertebral movement with increased risk of injury. As such, the concept of mechanical stability is closely related to the concept of clinical stability, which was defined by White and Panjabi [7] as the loss of the spine to limit its movements under physiological loads such that neurological disturbances, deformation, or pain are prevented. Panjabi has emphasized that stability is a property of a complex stabilizing system, comprising the osteoligamentous spine, the trunk musculature and the neural control system [8]. Biomechanical models can give an estimate of this system’s stability but to date no empirical method allows measuring stability in static and a fortiori in dynamic conditions. Therefore, clinicians and surgeons who deal with spinal disorders can only approximate stability impairments for diagnosis or improvements for treatment evaluation.

To assess stability of motor control, recent studies have characterized local dynamic stability (LDS) by means of the maximum Lyapunov exponent (λ_max) [9, 10]. In motor control literature, λ_max has been interpreted as the rate of divergence in kinematic state after a very small perturbation caused by internal sources, i.e., reflected in the variability of normal, unperturbed movement [11]. The kinematic state here refers to a multi-dimensional description of the movement of the system. So for trunk movement, a state space description comprises not just orientation, but also its derivatives, angular velocity, angular acceleration, etc. λ_max quantifies how fast the kinematic state diverges when the initial state is minimally perturbed. If the system is stable, trunk movements can follow a target trajectory and remain close to this trajectory over time. Perturbations of kinematics are sufficiently attenuated, because the system successfully deals with external mechanical disturbances and internal neuromuscular control errors. A higher λ_max reflects faster divergence, i.e., less attenuation of perturbations and hence lower spinal stability. In studies on trunk control, λ_max has been shown to be affected by movement pace and direction [12] and to be increased (i.e., stability is reduced) by trunk muscle fatigue [13]. It was also found that lifting light loads coincided with reduced stability compared to lifting heavier loads, presumably due to the lower muscle activity in lifting lighter loads [14]. Given these previous findings, analysis of LDS of trunk movements appears to be a promising tool for the assessment of stability of trunk movement in low-back pain patients. For example, it might allow empirical measurement of the influence of various surgical or conservative treatment strategies on neuromuscular control of the trunk.

However, several methodological issues need to be considered before using analysis of LDS in patient populations. The statistical precision of λ_max of trunk movements has to our knowledge not been assessed. Previously published experiments used arbitrary number of movements, to estimate λ_max [12–14]. However, Bruijn et al. [15] argued that, to estimate LDS of trunk kinematics in gait, 150 cycles would be needed to obtain precise estimates. Whereas studying of trunk movements’ performance and analysis of large numbers of cycles may also be advisable in view of statistical precision, this may cause fatigue, which would affect LDS. Moreover, it may not be possible in low-back pain patients.

The objectives of this study therefore were to (1) assess the precision of λ_max in tasks involving the trunk as a function of the number of repetitions and (2) determine the effect of time (fatigue) during prolonged sessions. Previously, it was found that LDS was lower in repetitive flexion–extension movements than in repetitive twisting movements [12]. Therefore, we additionally aimed to (3) compare three trunk movement sequences (sagittal plane, transverse plane and complex movements).

Methods

Participants

Ten healthy volunteers [6 males, 27 ± 4.9 years (mean ± standard deviation), 74.4 ± 5.5 kg, 181.1 ± 9.2 cm] participated in the experiment. Exclusion criteria were history of low back pain, or neurological or orthopedic disorders that could limit or interfere with trunk movements. Subjects provided informed consent and the protocol was approved by the ethical committee of the Faculty of Human Movement Sciences, VU University Amsterdam.

Procedure

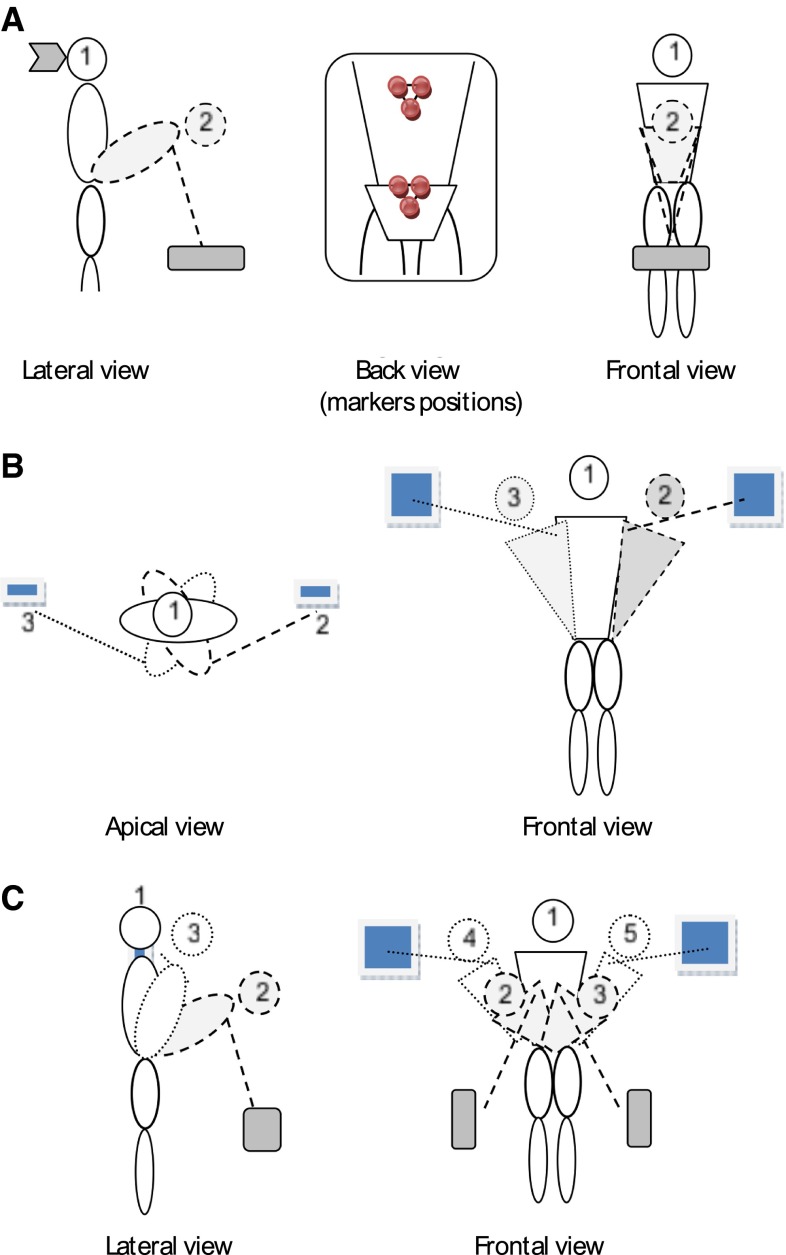
Subjects were asked to perform 100 repetitions of three different trunk movements in 3 separate trials. For the first task (sagittal plane, Fig. 1a), subjects were required to perform a freestyle rhythmic trunk flexion task between an upright standing position and a flexed position in which both index fingers touched a horizontal target positioned at knee height and at one arm length forward. This task represented a lifting task without load. For the second task (transverse plane, Fig. 1b), subjects performed a rhythmic pointing task alternating with right and left hand in upright stance moving between vertical targets positioned bilaterally at shoulder height and at one arm length laterally. For the third task (complex, Fig. 1c), subjects were asked to successively touch four targets situated at knee height on the left, at shoulder height on the right, at shoulder height left and at knee height right. The first two tasks were designed to explore the stability in a single plane of movement in a symmetric and an asymmetric condition. The complex task was designed to determine whether a more complex task is inherently unstable or generates more rapid fatigue and therefore instability.

Fig. 1.

Schematic illustration of the movement tasks studied: a symmetric flexion–extension task performed in the sagittal plane, the position of the markers are illustrated in the back view; b twisting task performed in the transverse plane; c complex task with movements in the three dimensions

As movement pace influences local stability [12] and to be as close as possible to natural movement used in daily activities, preferred pace was determined for each task prior to the experiment. In a pilot study, four subjects were asked to perform 43 movements for each task and their preferred frequency was determined. Then the mean frequency was calculated and used to set a metronome, which was used during the actual experiment. Subjects were instructed to touch the targets synchronously with the tone of the metronome. Sagittal and complex tasks were performed at 0.28 Hz, while the horizontal task was performed at 0.24 Hz.

To control for effects of fatigue, the three tasks were performed in randomized order with at least 2 min rest between each, and a Borg scale was used before and after each trial to measure perceived exertion [16].

Materials

For kinematic analysis, neoprene bands with a cluster of three infrared light emitting diodes (LEDs) were attached to the trunk at the level of T8 (thorax movement) and S1 (pelvis movement). LED movements were recorded with a 3D movement registration system (Optotrak Northern Digital Inc., Waterloo, ON) consisting of a 3 × 3 camera array. Sample rate was set at 100 samples/s and consequently time series of approximately 40,000, 45,000 and 80,000 samples were obtained for sagittal, horizontal and complex trials, respectively. Missing samples were filled in by linear interpolation. To be consistent with previous studies on trunk movement stability [12, 14], kinematic data were analyzed after filtering using a 10-Hz, low-pass, second-order filter.

State space reconstruction

To describe the kinematic state of the pelvis and thorax segments and of the thorax relative to the pelvis, first segment angles were computed from cluster orientations in the global axis system through Euler decomposition, and joint angles were determined from the orientation of the thorax (T8 marker) relative to the pelvis (S1 marker) (henceforth referred to as trunk movement). States were reconstructed in a similar way as by Graham et al. [17], using 12 dimensions, containing the 3-dimensional linear and angular velocities of a cluster marker and their time-delayed copies. Time-delayed copies are used to represent information on the higher derivatives of the kinematic state, in this case of the linear and angular velocities, and hence information on acceleration, jerk, etc. In LDS analysis, the smallest possible perturbation is approximated by comparing the each data point in the time series to the data point in which the state is most similar. To guarantee that similar states are indeed similar in all aspects, the state space description needs to contain sufficient dimensions. When too few dimensions are used, the identification of similar states may yield false nearest neighbors [18], e.g., data pairs which are similar in terms of velocity and acceleration but not in terms of jerk. Based on estimates for the embedding dimension of trunk movement by Granata and Gottipati [13], and confirmed by our data, 12-dimensional state space reconstruction is sufficient to avoid false nearest neighbors. Linear and angular velocities were normalized by the sum of the standard deviations of the three directions to give equal weight to linear and angular movement in the resulting states. Identical time delay was used for all subjects and tasks, because variations in the chosen time delay may diminish the reliability of resulting LDS [19]. To determine the delay, we used estimates of the minimum of the average mutual information on the velocity time series [20]. The delay was set to 44 samples, the median of these estimates over all subjects, markers and tasks.

Local dynamic stability

Local dynamic stability was quantified using the maximum Lyapunov exponent (λ_max). Considering an arbitrary point in the time series, the nearest neighbor is sought and the divergence of the trajectories arising from this pair of data points, i.e., the distance between the trajectories in state space as a function of time after the initial points, is calculated [9]. This procedure is repeated for all data points and the average logarithmic rate of divergence is calculated. λ_max is the slope of the linear part of this divergence curve [9], which we estimated as the slope of a linear fit to the first 72 samples, since 72 was the minimum of the intersection points of bilinear fits over all divergence curves.

Bootstrap analysis

To assess the statistical precision of the estimates of the LDS with respect to the number of repetitions, without making assumptions on data distribution, we used a bootstrap procedure [21]. The bootstrap procedure is helpful for decision making on sample size [22] and was previously used as such with respect to human movement analysis [15, 23]. For each subject, the time series were divided in windows of various lengths ranging from 10 to 50 repetitions with increments of 10 repetitions. Per window length, 100 samples were randomly selected and λ_max was calculated for each sample. Subsequently, estimates of statistical precision were obtained from the variance in results among these 100 bootstrap samples. We calculated the coefficient of variation (CoV) defined as the standard deviation over the 100 samples normalized to the mean. The ICC was calculated using the square of the standard deviation between subjects divided by square of the standard deviation of all values.

Statistics

To test for effects of task, segment/joint (thorax, pelvis, trunk) and time on λ_max, we calculated λ_max over the first, second and third 30 cycles and used univariate analysis of variance (α = 0.05). Post hoc tests were done with paired t tests using Bonferroni correction.

Results

All subjects completed the three trials. Two trials (both on the complex task) were discarded from analysis because markers were obscured from the camera’s field of view during data collection.

Statistical precision

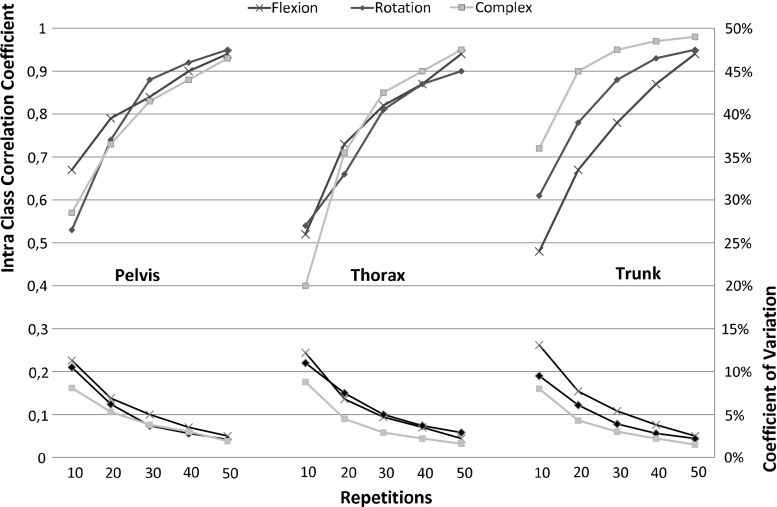
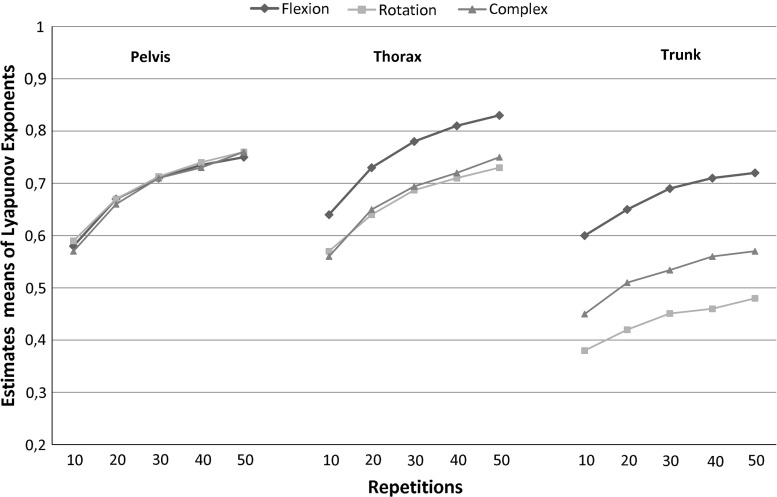
As expected, the precision increases as the number of repetitions increases (Fig. 2). As can be seen, λ_max was estimated with less precision with 10 repetitions (CoV₁₀ 8–13.1 %; ICC₁₀ 0.4–0.67) than with a higher number of repetitions. ICC values exceeded 0.8 (except for the pelvis movement in the sagittal plane task) from 30 repetitions on (CoV₂₀ 4.5–7.7 %, ICC₂₀, 0.61–0.90; CoV₃₀ 3–5.4 %, ICC₃₀, 0.78–0.95; CoV₄₀ 2.2–3.8 %, ICC₄₀ 0.87–0.97 %; CoV₅₀ 1.5–2.9 %, ICC₅₀ 0.9–0.99). λ_max of trunk movement was less variable than that of thorax or pelvis movements in global axes. As shown, the increase in precision above 30 repetitions was limited. Finally, it is important to note that the mean λ_max increased with the number of repetitions analyzed (Fig. 3)_.

Fig. 2.

Statistical precision of the maximum Lyapunov exponent as a function of number of cycles analyzed, expressed as intraclass correlation coefficients and coefficients of variation for the three tasks and for the three segment/joint movements

Fig. 3.

Mean maximum Lyapunov exponents as a function of number of cycles analyzed

Differences between thorax, pelvis and trunk movements

Statistical results are presented in Tables 1 and 2. There was significant main effect of segment/joint analyzed with overall lower λ_max for trunk movements than pelvis and thorax movements. In addition, there were significant interactions of this factor with time and task. Post hoc analyses for the interaction with time revealed that λ_max was significantly higher for pelvis and thorax movements than for trunk movements at all time points. With respect to the interaction with task, for movement in the sagittal plane, λ_max of the thorax was higher than that of pelvis and trunk. For other two tasks, λ_max was significantly higher for both the pelvis and the thorax than for the trunk.

Table 1.

Results from ANOVA (α = 0.05)

	df	F	p	Post hoc tests
Movement	2	9.698	0.002	–
Marker	2	86.904	0.000	–
Time	2	2.429	0.116	–
Mo*T	4	1.193	0.333	–
Ma*T	4	3.489	0.016	Yes
Mo*Ma	4	27.387	0.000	Yes

Independent variables are movement (Mo), marker (Ma) and time (T). The dependant variable is λ_max

df Degree of freedom

Table 2.

Results from post hoc tests

	Movement
	Flexion	Rotation	Complex
Marker
1–2	0.000	0.414	0.262
2–3	0.000	0.000	0.000
1–3	0.306	0.000	0.000

	Marker
	Pelvis	Thorax	Pelvis/thorax
Movement
1–2	No	0.007	0.000
2–3	No	0.103	0.784
1–3	No	0.044	0.018

	Time
	First 30 %	Middle 30 %	Last 30 %
Marker
1–2	0.430	0.780	0.687
2–3	0.000	0.000	0.000
1–3	0.000	0.000	0.000

Differences between tasks

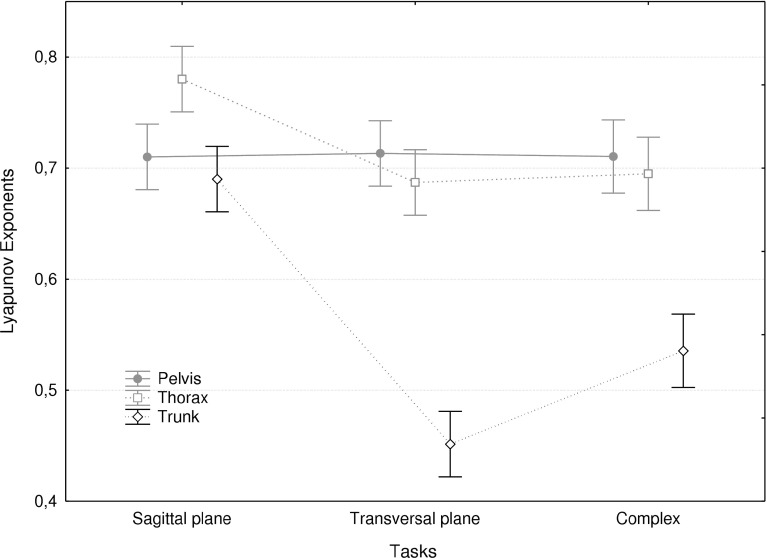
There was a main effect of task and a significant interaction with the segment/joint analyzed. As shown in Fig. 4, transverse plane and complex movements were overall more stable (lower λ_max) than sagittal plane movements. However, λ_max values for the transverse plane and complex tasks were significantly lower compared to the sagittal plane task for trunk movement only.

Fig. 4.

Mean maximum Lyapunov exponents for the three tasks and for the three segment/joint movements. Error bars indicate the standard deviation

Differences between episodes (effects of time)

There was no main effect of time. However, there was an interaction between time and segment/joint analyzed. However, post hoc testing did not reveal any significant effects of time. This was concordant with the Borg scale, where the subjects did not indicate any perception of fatigue after the experiment.

Discussion

This study was designed to assess the precision of estimates of λ_max to characterize LDS of trunk movement. Previous studies [12–14] have demonstrated the potential usefulness of the analysis of LDS for spine research, but methodological issues remained unresolved. Before this type of analysis can be applied to patients, we had to confirm that only a limited number of trials are necessary, to achieve a reliable estimate of dynamic stability. We showed that precision of estimates of λ_max was reasonable from 30 repetitions on and that no fatigue effects were apparent over the 100 repetitions of trunk movements performed. In addition, we showed that λ_max of trunk movements is lower than that of pelvis and thorax movements. Finally we corroborated and expanded previous findings, by showing that sagittal plane trunk movements had higher λ_max (lower LDS) than transverse plane and complex, three-dimensional movements.

The few authors, who have used Lyapunov exponents for assessment of trunk movement, only reported results from 30 repetitions, which based on results of other movement tasks (gait) could be assumed to yield sub-optimal precision [15]. Precision of estimates of λ_max of trunk movement during treadmill gait increased substantially with the number of cycles analyzed up to about 150 cycles [15]. For the trunk movements studied here, we observed a similar change in precision with the number of repetitions, but an acceptable precision was reached more quickly. One possible reason for this difference is the use of a metronome. By constraining the movement frequency, divergence in kinematic state may be limited and LDS increased. Another reason could be the difference in duration of cycles. Gait cycles last approximately 1 s, cycles in the present study lasted between 4 and 6 s and hence more samples per cycles are available. Finally, amplitudes of trunk movements are larger in the present task than in gait, causing a more favorable signal-to-noise ratio, which positively affects precision of estimates of λ_max [24]. Time had no effect on LDS in this experiment, which was not designed to induce fatigue. However, it was not excluded that trunk movement repetitions could cause some fatigue and affect λ_max. Unloaded trunk movement repeated 100 times in the healthy subjects tested was not associated with subjective fatigue and λ_max remained “stable” over this number of repetitions. It could however be that fatigue develops faster in specific populations, such as low-back pain patients. Given that the mean of the λ_max is affected by the number of cycles analyzed, as was shown previously [15], standardization of the number of cycles is required. Based on our results, we suggest that 30 repetitions may represent a good compromise between statistical precision on one hand and acceptance by participants and avoiding potential fatigue and pain (in patients) on the other hand.

LDS of the movement between thorax and pelvis was higher than stability of either segment. This was consistently observed over time in all three tasks, but more clearly so in transverse plane and complex movements. This could be explained by the neural control system having more precise information available on movement of segments relative to each other than on segment movements in space. Second, a relatively high impedance of the trunk may contribute to attenuate perturbations arising from variability in leg kinetics and kinematics. Van den Hoorn [25] showed lower variability of trunk movement during gait in LBP patients than in controls, whereas no differences were found when comparing thorax and pelvis movements. Therefore, we suggest that movement of the thorax relative to the pelvis may provide more relevant information on trunk neuromuscular control than segment movements and can be used for clinical experiments.

Movements in the sagittal plane were less stable than combined movements in the sagittal and horizontal plane and in the horizontal plane only. In this respect, results from the present study agree with those of Granata and England [12]. This finding appears surprising. The destabilizing moment caused by gravity increases as a sine function of the trunk inclination angle. Hence the derivative of the gravitation moment is highest at zero inclination and thus gravity can be expected to be more destabilizing in upright stance, and therefore more in the transverse plane task than in both other tasks. The effect observed may be due to higher trunk muscle co-contraction in tasks involving twisting moments. Granata and England [12] emphasized the stabilizing effect of the activity of the oblique muscles in asymmetrical tasks. Trunk twisting indeed coincides with high levels of trunk muscle co-contraction, due to the side effects that the oblique abdominal muscle have in other planes [26–29]. In line with this explanation, Graham et al. [14] showed that a load carried in the hands, which causes an increase in trunk muscle activity, coincided with higher LDS in the same trunk movement.

Considering the limited sample size of our healthy population, it is not possible to extrapolate the present results to patient populations. However, measuring in healthy people allowed us obtaining long time series to determine sufficient data for the bootstrap analysis, which would not be feasible with patients. Future studies need to assess LDS in a low-back pain population and determine test–retest reliability in this group. It would be interesting to see whether stability is similarly affected by movement symmetry and complexity as in the healthy subjects tested here and if co-contraction observed in LBP patients [30] is correlated with LDS. Moreover, when evaluating treatment options, dynamic stability may offer clinical insight into relations between effects on pain, function, and motor control, e.g., does total disk replacement in lumbar degenerative disk disease allow comparable dynamic stability compared to lumbar fusion and how does this correlate with clinical outcomes?

In conclusion, dynamic stability of trunk movement can be measured using a relatively low number of trunk movements without undue loss of statistical precision and fatigue effects were not observed over such numbers of repetitions. Thorax movements relative to the pelvis were more stable than movements of either thorax or pelvis segment. Dynamic stability was lower during sagittal plane movements than in transverse plane or complex, three-dimensional movements.