Investigation of coupled bending of the lumbar spine during dynamic axial rotation of the body

Abstract

Purpose

Little is known about the coupled motions of the spine during functional dynamic motion of the body. This study investigated the in vivo characteristic motion patterns of the human lumbar spine during a dynamic axial rotation of the body. Specifically, the contribution of each motion segment to the lumbar axial rotation and the coupled bending of the vertebrae during the dynamic axial rotation of the body were analyzed.

Methods

Eight asymptomatic subjects (M/F, 7/1; age, 40–60 years) were recruited. The lumbar segment of each subject was MRI scanned for construction of 3D models of the vertebrae from L2 to S1. The lumbar spine was then imaged using a dual fluoroscopic system while the subject performed a dynamic axial rotation from maximal left to maximal right in a standing position. The 3D vertebral models and the fluoroscopic images were used to reproduce the in vivo vertebral motion. In this study, we analyzed the primary left–right axial rotation, the coupled left–right bending of each vertebral segment from L2 to S1 levels.

Results

The primary axial rotations of all segments (L2–S1) followed the direction of the body axial rotation. Contributions of each to the overall segment axial rotation were 6.7° ± 3.0° (27.9 %) for the L2–L3, 4.4° ± 1.2° (18.5 %) for the L3–L4, 6.4° ± 2.2° (26.7 %) for the L4–L5, and 6.4° ± 2.6° (27.0 %) for the L5–S1 vertebral motion segments. The upper segments of L2–L3 and L3–L4 demonstrated a coupled contralateral bending towards the opposite direction of the axial rotation, while the lower segments of L4–L5 and L5–S1 demonstrated a coupled ipsilateral bending motion towards the same direction of the axial rotation. Strong correlation between the primary axial rotation and the coupled bending was found at each vertebral level. We did not observe patterns of coupled flexion/extension rotation with the primary axial rotation.

Conclusions

This study demonstrated that a dynamic lumbar axial rotation coupling with lateral bendings is segment–dependent and can create a coordinated dynamic coupling to maintain the global dynamic balance of the body. The results could improve our understanding of the normal physiologic lumbar axial rotation and to establish guidelines for diagnosing pathological lumbar motion.

Introduction

Vertebral segments of the human spine are known to function synergistically to maintain the stability of the human body. Altered vertebral motion has been widely assumed as a biomechanical factor causing spinal pathology [1–5]. Therefore, numerous studies have been conducted to understand spinal kinematics using both in vitro and in vivo approaches [2, 6–11]. Most cadaveric studies tested motion segments by applying a flexion–extension, bending, or axial rotation torque, with or without a compressive load to measure the vertebral motion using various techniques [8, 11–15]. Most of the in vivo studies have used skin markers or plain radiographs to measure the vertebral motion during various dynamic motion or static postures [16–18]. Three-dimensional CT and MRI imaging techniques have also been used to determine the vertebral motion during passive axial rotation of the lumbar spine [19–21]. Recently, a 3D fluoroscopic imaging technique was applied to investigate the 6DOF static range of motion of lumbar vertebrae at various weight bearing body postures [9, 10]. While these studies have dramatically improved our knowledge on the function of the human spine, however, the individual segmental vertebral motion during dynamic human body activities is still unclear. This knowledge is critical for understanding of the synergistic coordination of the vertebrae to maintain dynamic stability of the human spine.

In this paper, we investigated the in vivo characteristic motion patterns of the human lumbar spine during a dynamic axial rotation of the body. Specifically, we determined the contribution of each motion segment to the lumbar axial rotation, and examined the coupled bending and flexion/extension motion of the vertebrae during the dynamic lumbar axial rotation. We hypothesize that segmental axial rotation are similar at each segmental motion unit, but the coupled bendings are different at different levels.

Methods

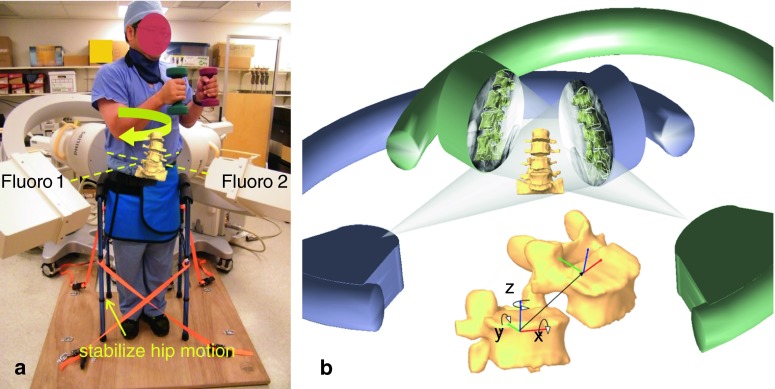
Eight asymptomatic subjects (M/F, 7/1; age, 40–60 years) were recruited in this study. The study was approved by our IRB and signed informed consent form was obtained from each subject before experiment. The lumbar segment of each subject was MRI scanned using a 3T scanner (MAGNETOM Trio, Siemens, Erlangen, Germany) with a spine surface coil and a T2-weighted fat-suppressed three-dimensional spoiled gradient recall (SPGR) sequence. Parallel sagittal images with a thickness of 1.5 mm (~85 images) without gap and with a resolution of 512 × 512 pixels were obtained (voxel size 0.45 × 0.45 × 1.5 mm). These MR images were input into the solid modeling software Rhinocerous (Robert McNeel & Associates, Seattle, WA) for construction of 3D models of the vertebrae from L2 to S1 (Fig. 1).

Fig. 1.

a Voluntary axial rotation of the body in the dual fluoroscopic image system (DFIS); b the virtual DFIS created to reproduce the in vivo vertebral motion and vertebral coordinate system. x medial–lateral translation, flexion/extension rotation; y anterior–posterior translation, left/right lateral bending; z superior–inferior translation, left/right axial rotation

The lumbar spine of the subject was then imaged using a dual fluoroscopic image system while the subject performed a dynamic axial rotation to maximal left and then to maximal right in a standing position (Fig. 1a). During axial rotation, the subject held an 8 pound (3.63 kg) dumbbell in each hand to simulate daily functional activities. The axial rotation extents are freely chosen by the subjects to reach their maximum range of motion during daily functional activities. Ten exercises were performed under the guidance of orthopedic surgeons to standardize the motion before taking the images. A complete axial rotation cycle took on average 1.5 s. The fluoroscopes captured the lumbar motion using snapshots with an 8-ms bandwidth and 30 frames/second. Our Radiation Safety Committee determined the average dose rate is 0.208 mSv/100 frames. Therefore, the radiation dosage during each axial rotation dual fluoroscopy imaging is about 0.2 mSv. Every 25 % of the motion cycle from maximum left to right axial rotation was analyzed: maximal left twist, sub-maximal left twist, neutral, sub-maximal right twist, maximal right twist.

The 3D vertebral models and the paired fluoroscopic images were input into the Rhinoceros software to reproduce the in vivo vertebral motion using an established protocol (Fig. 1b) [9, 22]. The fluoroscopic images were positioned in the software to represent two virtual fluoroscopic image intensifiers. The 3D vertebral models were introduced into the software and viewed from two virtual cameras representing the two virtual X-ray sources of the dual fluoroscopes. The 3D vertebral models could be manually manipulated in this system in 3 translations and 3 rotations, and be projected on the fluoroscopic images. The vertebral positions during the dynamic axial rotation were reproduced when their projections matching the vertebral osseous images captured during the experiment (Fig. 1b) [9, 22]. The repeatability (precision) of the method in reproducing in vivo human spine 6DOF kinematics was <0.3 mm in translation and <0.7° in orientation [22].

The 6DOF vertebral kinematics was calculated using the 6DOF motion of the superior vertebra with respect to the inferior vertebra of each motion segment unit of the lumbar spine. Local coordinate systems were located at the geometric centers of corresponding vertebra bodies (Fig. 1b). The x-axis is in coronal plane and pointed to the left direction; the y-axis is in the sagittal plane and pointed to the posterior direction; and the z-axis is perpendicular to the x–y plane and pointed superiorly. Three translations using x, y and z are defined as the motions of the superior vertebral coordinate system with respect to the inferior coordinate system: anterior–posterior, left–right and superior–inferior translations. Three rotations using α, β and γ are defined as the orientations of the superior vertebral coordinate system in the inferior vertebral coordinate system using Euler angles (in z–y–x sequence): left–right axial rotation, left–right side bending and flexion–extension (Fig. 1b). In this study, we analyzed the primary left–right axial rotation and the coupled left–right bending rotation of each vertebral segment.

A one-way analysis of variance (ANOVA) was used to test if there is a difference in the range of axial rotation or bending at different vertebral levels. The relationship between axial rotation and bending were analyzed using the Pearson’s correlation. A statistically significant difference was defined when p < 0.05.

Results

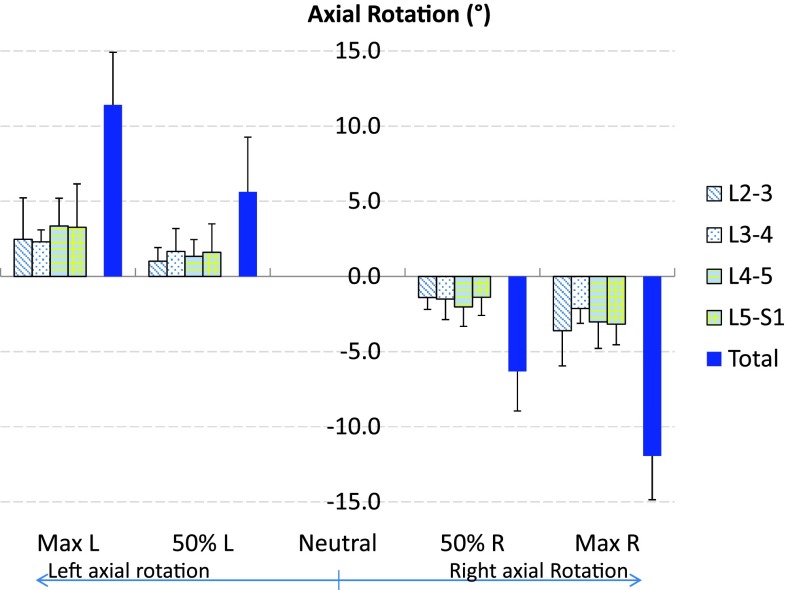
The primary axial rotations of all vertebral segments followed the direction of the body axial rotation. The range of axial rotation of L2–S1 from maximal left to right axial rotation was 23.9° ± 4.0° (Fig. 2; Table 1), where the axial rotation at maximum left twist position was 11.4° ± 3.6° and at maximum right twist position was −11.9° ± 2.9° using the standing position as a reference. Contributions of each segment to the overall lumbar axial rotation were 6.7° ± 3.0° (27.9 %) for the L2–L3, 4.4° ± 1.2° (18.5 %) for the L3–L4, 6.4° ± 2.2° (26.7 %) for the L4–L5, and 6.4° ± 2.6° (27.0 %) for the L5–S1 vertebral motion units. There was no significant difference in the range of primary axial rotation between different segmental levels.

Fig. 2.

The average range of lumbar axial rotation of the total L2–S1 spine and individual segments during left to right dynamic axial rotation of the body. Error bars represent the standard deviations of the rotation range

Table 1.

Mean and standard deviation, SD, of the total and segmental ROM of primary axial rotation and coupled bending in degrees

	Total ROM	Segmental ROM
	L2–S1	L2–L3	L3–L4	L4–L5	L5–S1
Axial Rotation	23.9	6.7 (27.9 %)	4.4 (18.5 %)	6.4 (26.7 %)	6.4 (27.0 %)
SD	4.0	3.0	1.2	2.2	2.6
Bending	1.8	−4.5 (−252.3 %)	−3.7 (−203.6 %)	4.6 (254.3 %)	5.4 (301.6 %)
SD	4.3	1.9	1.3	2.0	3.2
Corr Coef (r)	0.25	−0.78	−0.70	0.70	0.83

The percentages of segmental ROM with respect to total ROM are shown in parentheses. The minus signs indicate contralateral bending towards the opposite direction of the body axial rotation. Correlation coefficients (r) between axial rotation and bending were also shown

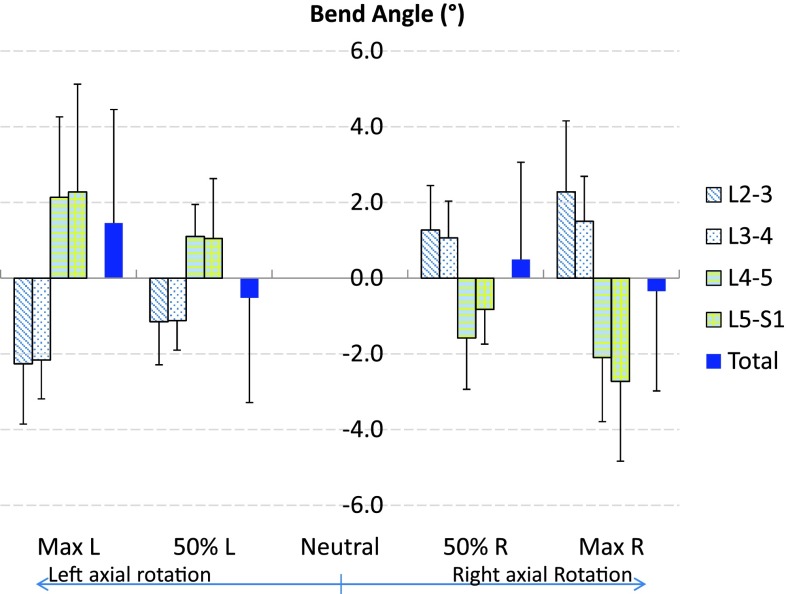
The overall range of the coupled bending from L2 to S1 levels was 1.8° ± 4.3° (Fig. 3). Contributions of each segment were −4.5° ± 1.9° (−252.3 %) for the L2–L3, −3.7° ± 1.3° (−203.6 %) for the L3–L4, 4.6° ± 2.0° (254.3 %) for the L4–L5, and 5.4° ± 3.2° (301.6 %) for the L5–S1 segment levels. The minus sign indicated that the coupled bending was towards the opposite direction of the body axial rotation. There was no significant difference in the magnitudes of the coupled bending rotations between the different segmental levels. We did not observe patterns of coupled flexion/extension rotation with the primary axial rotation.

Fig. 3.

The average coupled lateral bending of the total L2–S1 spine and individual segments during the axial rotation of the body. Error bars represent the standard deviations of the rotation range

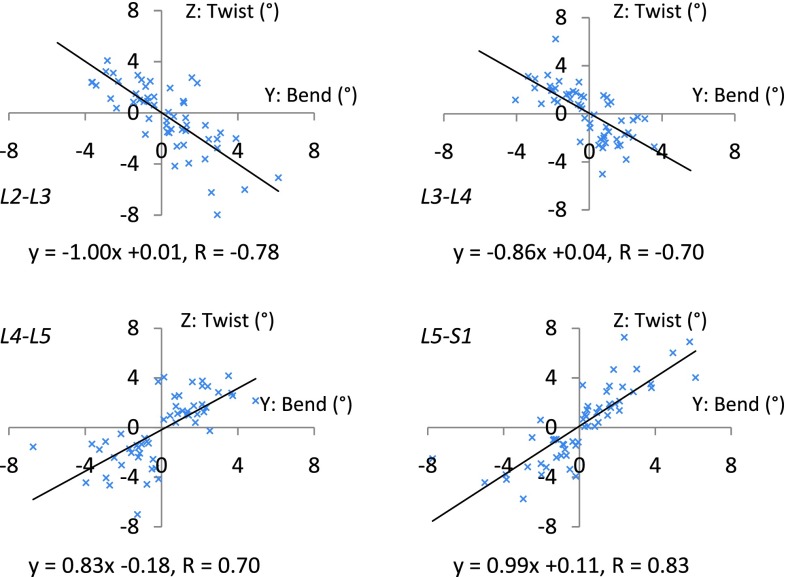
The correlation between the primary axial rotation and the coupled bending was further analyzed (Fig. 4). There was a weak correlation between the overall axial rotation and the coupled bending from L2 to S1 (R = 0.25, p = 0.07). However, there were strong negative correlations between the segmental axial rotation and the coupled bending of the upper segments of L2–L3 and L3–L4 (R = −0.78 and −0.70, respectively, p < 0.01). There were also strong positive correlations between the segmental axial rotation and the coupled bending of the lower segments of L4–L5 and L5–S1 (R = 0.70 and 0.83, respectively, p < 0.01).

Fig. 4.

Correlation of the vertebral axial rotation and coupled lateral bending. The upper lumbar (L2–L3, L3–L4) segments showed strong negative correlation (r = −0.78 and −0.70, respectively, p < 0.01) with coupled lateral bending. The lower lumbar (L4–L5), and the lumbosacral (L5–S1) segments showed strong positive correlation (r = 0.70 and 0.83, respectively, p < 0.01) with coupled lateral bending

Discussion

In this study, we investigated the in vivo vertebral rotation of human lumbar spine (L2–S1) during a dynamic axial rotation of the body from maximal left to maximal right in an upright standing position, a function as observed during golf swing, tennis games or other activities that require body axial rotation. The data indicated that all vertebrae rotated similarly in the direction of the axial rotation of the body. However, the coupled left–right bendings varied at different segmental levels. The L2–L4 bent in the opposite direction of the axial rotation, while the L4–S1 bent in the same direction of the axial rotation. The magnitude of bending of each vertebral level was higher than that of the overall bending of the L2–S1 segment.

Coupled vertebral bending during lumbar axial rotation has been reported in various in vitro and in vivo studies (Table 2) [9, 13, 18–21, 23]. Panjabi et al. [13] performed axial rotation test using cadaveric lumbar specimens by applying a compressive preload of 100 N and a torsional torque of 10 N m. They measured a rotation of ~1.5° at each vertebral level, and the data on coupled bending of L2–L4 and L4–S1 showed similar trend to our data. Pearcy et al. [18] used a bi-plane X-ray setup to study the range of body axial rotation in a static standing position. They reported on average a 2°–4° axial rotation at each vertebral level, but the coupled bending at the L4–L5 level was minimal, that was not consistent with our observation during the dynamic maximal lumbar axial rotation. Haughton et al. [20] used 3D MRI scans to investigate the passive lumbar axial rotation in a supine body position by independently axial rotation the torso and the hip by ±8°. Ochia et al. [21] used 3D CT scan to investigate the passive lumbar axial rotation in a supine body position by ±50°. Fujii et al. [19] performed in vivo non-weight bearing supine MRI scan of human lumbar spine at different passive axial rotation of the upper body by 15° increments to the maximum trunk rotation. These studies showed, on average, <2° in axial rotation at each vertebral level, and a similar trend in the coupled bending motion in the L2–L4 and L5–S1 levels as our observation. However, the L4–L5 level showed an opposite coupled bending as observed in our study. Rozumalski et al. [23] inserted K-wire into the spinous process of a volunteer-individual to perform a voluntary motion of a standing position, but did not report the direction of the coupled bending rotation. Li et al. [9] used a similar dual fluoroscopic image technique in a previous study to study quasi-static lumbar axial rotation with no weight in the hands. The reported primary axial rotation and coupled bending rotation were on average degree smaller than the current results (Table 2). However, the direction of the coupled bending rotation was also not reported in the previous study.

Table 2.

Literature on lumbar axial rotation and the coupled lateral bending motion

Ref.	Loading	Method	Lumbar axial rotation				Coupled lateral bending				Direction
			L2–L3	L3–L4	L4–L5	L5–S1	L2–L3	L3–L4	L4–L5	L5–S1	L2–L3	L3–L4	L4–L5	L5–S1
Pearcy et al. [18]	Standing	Biplanar radiograph	2 (1–3)	3 (1–5)	3 (1–5)	2 (0–3)					–	–		+
Panjabi et al. [13]	100 N Comp + 10 Nm	Testing machine	4.0	3.8	2.2	1.9	4.3	1.8	2.6	5.5	–	–	+	+
Haughton et al. [20]	Supine	MRI	0.5 ± 1.4	0.8 ± 1.0	1.7 ± 2.3	1.9 ± 0.9
Ochia et al. [21]	Supine	CT	2.1 ± 0.2	1.4 ± 0.3	0.6 ± 0.3	1.1 ± 0.3	−2.8 ± 0.3	−3.6 ± 0.3	−2.6 ± 0.5	3.0 ± 1.2	–	–	–	+
Fujii et al. [19]	Supine	MRI	1.4 ± 0.3	1.7 ± 0.6	1.7 ± 0.6	1.6 ± 0.7	−3.0 ± 1.0	−3.4 ± 0.9	−1.6 ± 0.9	0.6 ± 0.6	–	–	–	+
Li et al. [9]	Standing	DFIS	2.5 ± 2.3	2.4 ± 2.6	2.9 ± 2.1		2.6 ± 1.2	2.0 ± 2.0	3.6 ± 2.1
Rozumalski et al. [23]	Standing	Motion capture	7.9 ± 4.4	6.9 ± 2.0	7.6 ± 5.0	7.2 ± 5.0	6.5 ± 2.7	5.0 ± 1.6	5.2 ± 3.0	6.4 ± 4.1
Current study	Standing + weight	DFIS	6.7 ± 3.0	4.4 ± 1.2	6.4 ± 2.2	6.4 ± 2.6	−4.5 ± 1.9	−3.7 ± 1.3	4.6 ± 2.0	5.4 ± 3.2	–	–	+	+

+ indicates that the coupled lateral bending is in the same direction as the axial rotation, − indicates that those two motions are in the opposite directions

These data indicated that the direction of the coupled lateral bending of the L4–L5 segment during the axial rotation of the body were inconsistent among the literature data. This may be attributed to the various experimental conditions among these studies, including both in vivo and in vitro, active dynamic motion, passive motion and static positions. Our study investigated an active dynamic rotation of the human body with weights holding in hands, which represented a functional physiological loading of the human body. Therefore, a direct comparison of the experimental data of these studies is difficult.

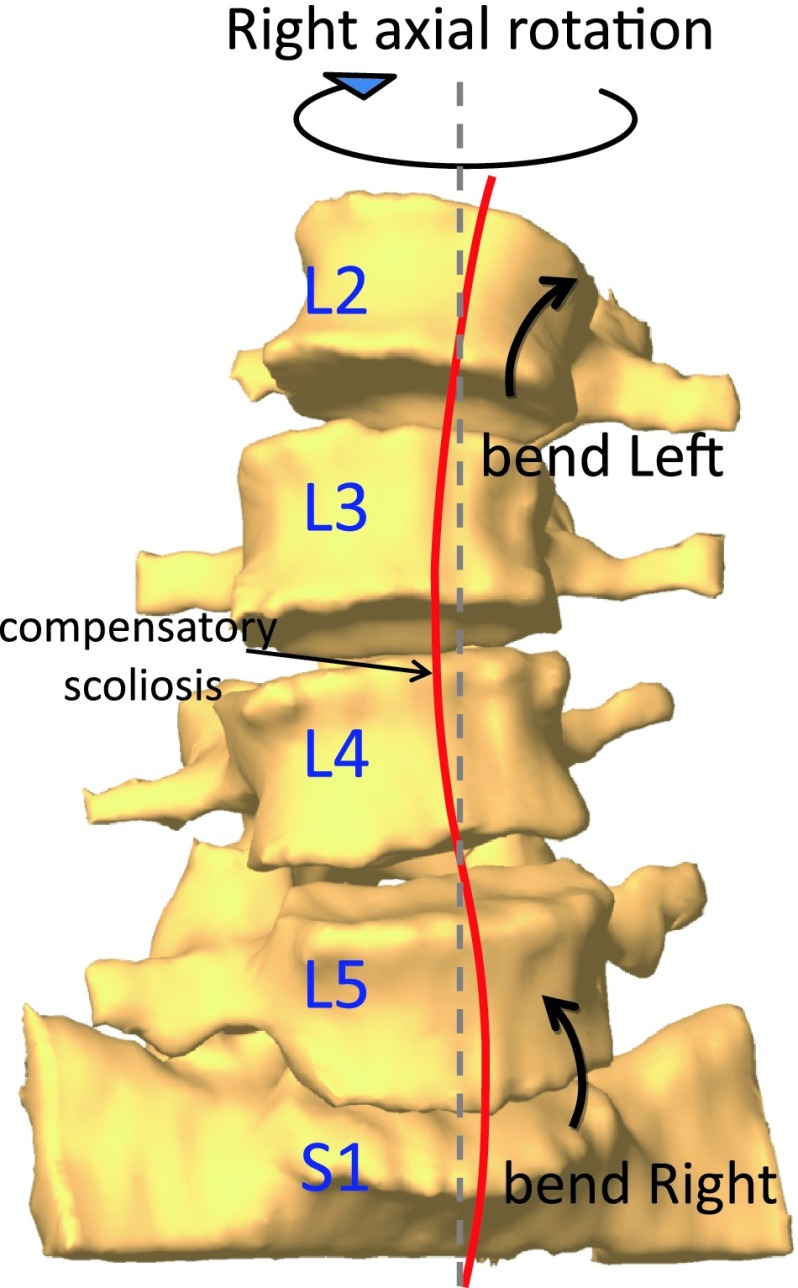
It is interesting to note that the coupled bending of the overall segment considered in this study (L2–S1) was smaller than the coupled bendings of each individual segment level. The balanced distribution of the coupled lateral bendings contributes to maintain global trunk balance, or “compensation of the spinal column”, during the dynamic body axial rotation. This balanced coupling pattern could create a temporary curvature of the spine on the coronal plane (Fig. 5), which is similar to the phenomenon of the so-called ‘compensatory scoliosis’ [18, 24–26]. The compensatory scoliosis implies a physiologic coordination of local scoliosis to maintain a global balance of the whole body posture.

Fig. 5.

Balanced distribution of the directions of the coupled lateral bending following a dynamic axial rotation of the body to maintain the global balance of the spine

The physiological phenomenon of the coupled bending during body axial rotation may have implications to contemporary spinal surgeries in treatment of lower back pain related disc degenerative diseases. From biomechanical point of view, the different bending coupling could result in varied shear deformation in the discs at different vertebral levels. An intervertebral fusion eliminates the physiological motion of the involved vertebral segments, thus may affect the physiologic ‘compensatory scoliosis’, implying a biomechanical mechanism that may be related to an increased pathology in the adjacent segments of the lumbar spine. While most contemporary artificial disc replacements are designed to preserve the segmental vertebral motion using an unconstrained articulation, an artificial disc replacement may reduce the motion at adjacent segments, thus might cause a stress release in adjacent levels. Further investigation is warranted to quantitatively examine the effect of surgical treatments of lumbar intervertebral fusion, or artificial disc replacement on the spinal segmental motion during dynamic activities of the body.

There are several limitations in this study that need to be discussed. The subject number is relatively small, although we detected differences in the coupled bending at different vertebral levels. This sample group does not allow us to analyze the age and gender effects on vertebral kinematics. Future studies should take into account both age and gender as the study variables. Due to the size limitation of the fluoroscope, we only analyzed the lumbar spine from L2 to S1. This is to focus on the lumbar segment where lower back diseases are always observed in clinic. Future study should also investigate the lumbar biomechanics during other physiological activities such as dynamic flexion–extension of the body. Despite these limitations, this study was the first to investigate the lumbar kinematics during dynamic axial rotation of the body. There might be an effect of the weight carried by the subject on the magnitude of the coupled motion. In particular, as the weight in combination with the axial rotation may load the lumbar spine with a bending moment in lateral bending which could result in increased muscle forces and thus alter the lumbar biomechanics. Future studies should investigate the effect of different magnitudes of weight carried by the subject on the lumbar segmental motion.

In conclusion, we observed that a dynamic lumbar axial rotation coupling with lateral bendings is segment–dependent and can create a coordinated dynamic coupling to maintain the global dynamic balance of the body. The results could provide an improved understanding of the normal physiologic lumbar axial rotation, in order to establish guidelines for diagnosing pathological lumbar motion in the lower lumbar levels. The results may provide useful information for contemporary implant design aimed to prevent adjacent segment degeneration after surgeries.