Sociality influences cultural complexity

Abstract

Archaeological and ethnohistorical evidence suggests a link between a population's size and structure, and the diversity or sophistication of its toolkits or technologies. Addressing these patterns, several evolutionary models predict that both the size and social interconnectedness of populations can contribute to the complexity of its cultural repertoire. Some models also predict that a sudden loss of sociality or of population will result in subsequent losses of useful skills/technologies. Here, we test these predictions with two experiments that permit learners to access either one or five models (teachers). Experiment 1 demonstrates that naive participants who could observe five models, integrate this information and generate increasingly effective skills (using an image editing tool) over 10 laboratory generations, whereas those with access to only one model show no improvement. Experiment 2, which began with a generation of trained experts, shows how learners with access to only one model lose skills (in knot-tying) more rapidly than those with access to five models. In the final generation of both experiments, all participants with access to five models demonstrate superior skills to those with access to only one model. These results support theoretical predictions linking sociality to cumulative cultural evolution.

1. Introduction

Humans may be unique among species in generating the cumulative cultural evolutionary processes that give rise to complex behavioural skills and technologies [1–4]. A growing class of theoretical models suggest that the emergence of such complex and ‘difficult to learn’ cultural traits (tools, techniques and skills), such as many of the technologies used by hunter–gatherers, is heavily influenced by the abilities of learners to access larger social networks of other individuals [5–14]. On the empirical side, field evidence consistent with these models has begun to emerge. This evidence includes analyses of the complexities of toolkits among populations [15–17] as well as detailed studies of particular archaeological, ethnographic and ethnohistorical cases [7,11,18–20]. Thus, technological sophistication may depend on sociality, on the size and interconnectedness of populations. This has led some to suggest that the key difference between human ancestors and other primates may lie in the domain of sociality and population or network structures [21–23]. Of course, there is every reason to suspect that other factors also influence cumulative cultural evolution in substantial ways [24–26].

Here, we test the relationship between sociality and cumulative cultural evolution in two laboratory experiments, where sociality is operationalized in terms of a participant's ability to access and learn from multiple experienced individuals (‘models’ or ‘cultural parents’). Experiment 1 tests the effect of the number of accessible models on cumulative cultural change over successive laboratory generations using a first generation of untrained or ‘uncultured’ participants. Experiment 2 tests the effect of the number of models on the loss of cultural complexity over successive generations by beginning with a first generation of trained ‘highly cultured’ participants.

2. Methods

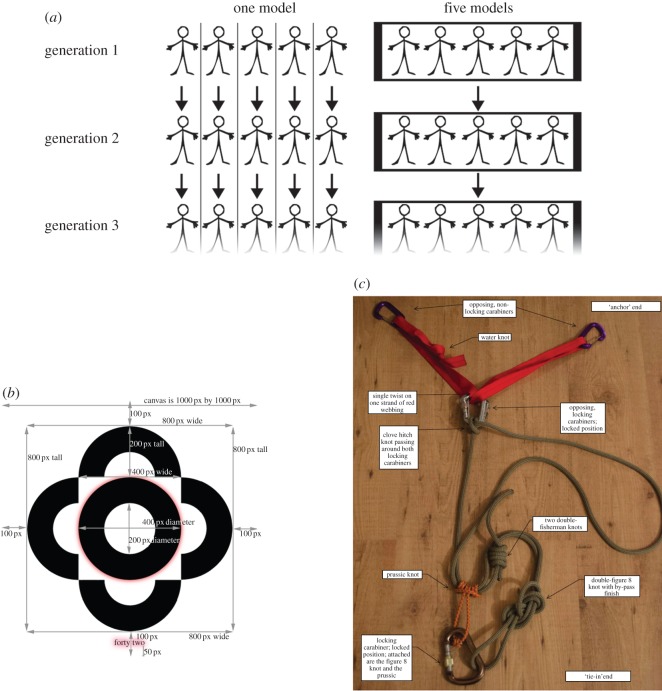
In both studies, we tested the transmission of knowledge and skill using undergraduates (n = 100) randomly assigned to one of two treatments (one model versus five models) each with 10 generations (five participants per treatment per generation). In the one-model treatment, participants in generations two to 10 had access to information from only one participant from the previous generation (one ‘cultural parent’). In the five-model treatment, participants in generations two to 10 had access to information from all five participants in the previous generation (five ‘cultural parents’). Figure 1a illustrates our experimental design. Participants’ performance was incentivized with additional entries into a $100 raffle when (i) they performed relatively better in their own generation, and (ii) those they transmitted to emerged as the best performer in the next generation. Thus, participants made the most money when both they and their cultural offspring performed the best in their respective generations (see the electronic supplementary material for details on payments). Below, we first briefly present the methods for each experiment, and then move onto the results.

Figure 1.

(a) An illustration of the experimental design. (b) The target image for Experiment 1. Note the words ‘forty two’ at the base of the image and the red glow around these words and the circle. Participants were not required to recreate the dimension arrows. (c) The knots used in Experiment 2. Participants were asked to tie this set-up to two chairs.

In Experiment 1, participants with little or no prior experience in image editing were asked to recreate a target image using a complex editing program called GIMP [27]. We also supplied a second version of the target image with annotated measurements (as shown in figure 1b). In all generations, participants were given sufficient time (up to 15 min) during which they were permitted to write up to two pages of information to assist the next generation. All generations, except generation 1, were provided with the written information, the target image (with and without measurements) and a screenshot from their cultural parent or parents and given up to 25 min to recreate the target image. Those in the one-model treatment had access to only one participant's information and image, whereas those in the five-model treatment had access to all five participant's information and images. Participants’ (n = 100, 71 female) ages ranged from 15 to 35 (M = 20.52, s.d. = 2.80). Additional participant information is provided in the electronic supplementary material.

Each participant's final image was rated in two ways. First, each image was assessed by one of three human raters using a scale designed to measure the level of reproduction of various features of the target image (alignment, size, shape, gradient, etc.). Scores on our scale ranged from 0 to 59, which we rescaled to a percentage from 0 to 100. Inter-rater reliability, calculated on a range of images from a pilot study and images from participants who exceed our maximum experience threshold, was very high (ICC (3,1) = 0.997). The electronic supplementary material provides information on the training and evaluation of raters.

Second, as a check on these human-ratings, final images were also assessed using a similarity algorithm (see the electronic supplementary material for details). The algorithm computes the normalized cross correlation metric, which yields a value between 0 and 1 for the two images by pairing them pixel by pixel and calculating a correlation. Ratings from this algorithm and our human raters were highly correlated (r = 0.87, p < 0.001). However, because the algorithm does not assess features clearly relevant to human minds (e.g. the target's degree of red glow, misalignment of image, etc.), we ran our analyses below using the above human rating scale, and relied on the algorithm's overall similarity measure only as a robustness check.

In Experiment 2, participants were asked to tie a system of connected knots commonly used in rock-climbing. Generation 1 was trained by the experimenter using standardized instructions to become ‘experts’ at tying this system of knots. Participants in all generations were given sufficient time (up to 20 min) during which they were permitted to create an instructional video detailing the tying and placement of each knot. To reduce experimenter bias, a camera was strapped to each participant's forehead, providing a first person view. All subsequent generations were provided with the video from the previous generation as well as the participant's score and were given up to 50 min to learn and recreate the knot system. The one-model treatment had access to only one participant's video and score, whereas the five-model treatment had access to all five participant's videos and scores. Participants’ (n = 100, 71 female) ages ranged from 17 to 37 (M = 20.48, s.d. = 3.15; further details in the electronic supplementary material).

To assess the performance of each participant, their final knot system was assessed by one of two human raters, using a custom rating scale inspired by a scale used to assess sutures when training surgeons [28]. The scale was used to assess the deviation of each knot and knot position from the original model. The scale scores ranged from 0 to 37, which we rescaled to percentages (see the electronic supplementary material for the complete scale). Inter-coder reliability, calculated on a range of knots from a pilot study, was very high (α = 0.99). The electronic supplementary material provides information on the training and evaluation of raters.

3. Results

(a). Experiment 1

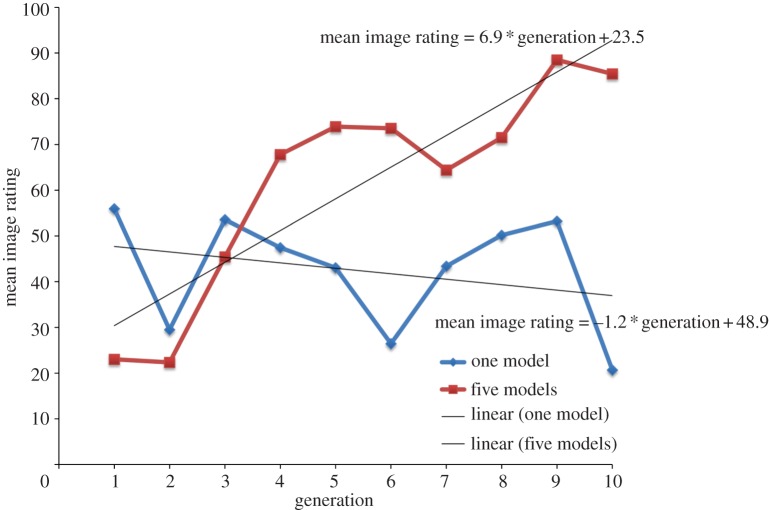
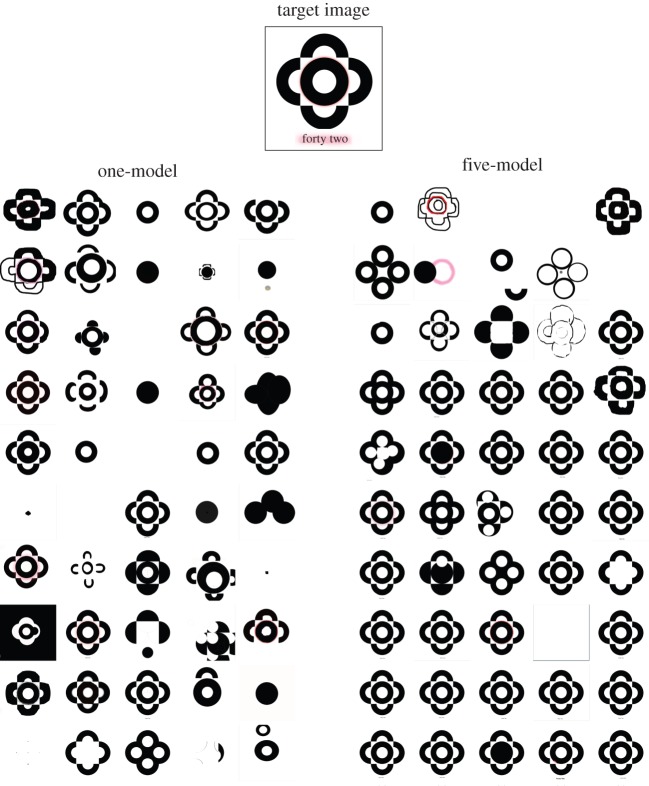
Figures 2 and 3 show the results of Experiment 1, where participants in generation 1 were novices. Over 10 generations, those who could observe the five models substantially improved in their image editing skills, in recreating the target image. Those who saw only one model demonstrated no significant improvement; if anything, they showed a decline in skill level. As the final row of figure 3 shows, the least skilled learner in the 10th generation of the five-model treatment is superior to the most skilled learner in the 10th generation of the one-model treatment.

Figure 2.

Mean image editing skills over 10 generations for the one-model and five-model treatments in Experiment 1. Scores rescaled between 0 and 100, where 100 is a perfect score. Linear lines of best fit emphasize a cumulative improvement in the five-model treatment and no improvement, and a possible decline, in the one-model treatment.

Figure 3.

Experiment 1 final images from participants in the one-model and five-model treatments. The target image is included at the top for comparison. The columns are chains of participants in the one-model treatment. Rows are generations going from top (generation 1) to bottom (generation 10). An obvious difference between the two treatments can be seen in the last row.

To further investigate the treatment differences visible in figures 2 and 3, we regressed the standardized image rating scores on the main effects and interaction of generation number and treatment, controlling for age and male (gender with male = 1). The electronic supplementary material, table S3 contains the full series of regression models we examined. Of these models, the model controlling for age and male had the highest adjusted R² and is reported in table 1, but the results are robust across all models. By alternating the dummy coding on treatment, we are able to directly compare the effect of generation on image rating score for each treatment. Our regression model (table 1) estimated an average improvement of 0.23 s.d. (equivalent to 7 percentage points) per generation in similarity-to-target image (p < 0.001), indicating the accumulation of skill. By contrast, there was only a small and non-significant effect of generation in the one-model treatment, a decline of 0.06 s.d. (2 percentage points) per generation (p = 0.19).

Table 1.

OLS regression of standardized image rating scores on the main effects and interaction of generation and treatment (one-model/five-model), controlling for male (gender, male = 1) and age (standardized). By alternating the dummy coding of treatment, we directly compare the effect of generation by looking at the generation coefficients. In the five-model treatment, image ratings improve by 0.23 s.d. per generation. By contrast, in the one-model treatment, there is no significant improvement in image ratings (and a possible decline).

	one-model	five-models
generation	−0.06 (0.04)	0.23 (0.04)**
age	−0.09 (0.08)	−0.09 (0.08)
male	−0.36 (0.19)	−0.36 (0.19)
one-model	−0.96 (0.36)**
one-model generation*	0.28 (0.06)**
five-model		0.96 (0.36)**
five-model generation*		−0.28 (0.06)**
(intercept)	0.11 (0.27)	−0.85 (0.26)**
R2	0.353	0.353
adj. R2	0.319	0.319
N	100	100

*p < 0.05; **p < 0.01.

Participants in the five-model treatment of Experiment 1 were given access to the images and notes from all five participants in the previous generation and could have learned from any or all of them. To examine selective learning biases, we broke down each participant's performance into 18 binary (present, absent) components, which gave us 810 (non-independent) observations for participants in generation two to 10. Then, using binary logistic regression, we regressed the presence or absence of each component in the participant's image on the presence or absence of each component in the participant's potential models, controlling for age, male and generation. Each potential model was ranked from best (model 1) to worst (model 5). This allowed us to examine how participants weighted the relative importance of their potential models. We used clustered robust standard errors (810 observations in 45 clusters) to control for common variance within each participant's scores. The results (table 2) indicate that the features present in the best model were the best predictor of the participant's score. However, the three next best models were also predictive of participants’ scores, indicating that participants were also looking at other models. This suggests that participants were using a skill or success bias, with the greatest weight on the most skilled model, but with some non-zero weight on everyone else except for the worst model. Such patterns offer some evidence that participants were combining information from multiple models, thereby generating novel recombinations of elements not possessed by any single one of their teachers. Of course, given the error in the estimates, we cannot be too confident in the differences observed between models 2, 3 and 4.

Table 2.

Binary logistic regression of the presence or absence of each component of the target image in each participant's attempted image on the corresponding component in each of the five potential models. We control for non-independence between participant's image components using clustered robust standard errors. The odds ratios reported reveal a large and significant bias for the best model, but also biases for the three next best models. We control for generation, male and age (see the electronic supplementary material, table S4 for full regression model). Robust standard errors in parentheses.

predictor variables	coefficients as odds ratios (standard errors)
model 1	3.910*** (1.258)
model 2	2.481*** (0.867)
model 3	1.747* (0.557)
model 4	2.187*** (0.583)
model 5	0.893 (0.260)
pseudo-R2	0.283
n	810 (45 clusters)

*p < 0.1; **p < 0.05; ***p < 0.01.

(b). Experiment 2

Figure 4 shows the results of Experiment 2, where participants in the first generation were knot-tying experts. The knot-tying skills of those in the five-model treatment decline more slowly than in the one-model treatment over the first three generations, and then level off to a higher average knot skill than those in the one-model treatment. Meanwhile, knot-tying skills in the one-model treatment continue to decline, though at a decelerating rate, through to generation 10.

Figure 4.

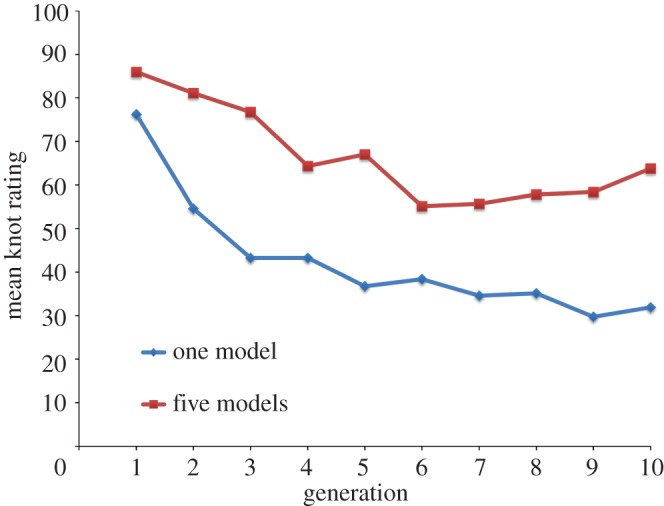
Mean knot-tying skills over 10 generations for the one-model and five-model treatments in Experiment 2. Scores rescaled to between 0 and 100, where 100 is a perfect score. The loss of skills is fastest in the first three generations and much faster in the one-model treatment than in the five-model treatment. Generations 4–10 suggest different equilibria where the five-model treatment has an equilibrium at twice the skill level of the one-model equilibrium.

To further investigate the difference between the treatments and generations in figure 4, we separately estimated a series of ordinary least square (OLS) regression models for the first three and last seven generations, controlling for age, male, ethnicity and experience with knot-tying. In the electronic supplementary material, table S5 contains the full series of regression models we examined. Of these, the models controlling for age, male and knot-tying experience had the highest overall adjusted R²-values and are reported in table 3, but results were robust across all models. Our regression model (table 3) estimated that over the first three generations, the mean skill of the five-model treatment declines by 0.25 s.d. (equivalent to 6 percentage points) per generation (p = 0.37), whereas the one-model treatment declines by 0.67 s.d. (16 percentage points) per generation (p = 0.02).

Table 3.

OLS regression of standardized knot rating scores on the generation and treatment (one-model/five-model), and their interaction, controlling for male, age (standardized) and knot-tying experience. By alternating the dummy coding of treatment, this table directly compares the effect of generation by looking at the generation coefficients. The loss of skill within both the first three generations and the last seven generations is twice as fast in the one-model treatment compared to the five-model treatment. We conducted a test of joint significance of treatment and treatment–generation interaction by statistically comparing regression models with and without these variables—see electronic supplementary material, table S6. The results indicate a statistically significant effect of treatment and treatment–generation interaction.

	one model: 1–3	five models: 1–3	one model: 4–10	five models: 4–10
generation	−0.67 (0.28)*	−0.25 (0.28)	−0.07 (0.05)	−0.03 (0.05)
five-model	0.28 (0.85)**		0.78 (0.52)**
five-model generation*	0.42 (0.38)**		0.03 (0.07)**
one-model		−0.28 (0.85)**		−0.78 (0.52)
one-model generation*		−0.42 (0.38)**		−0.03 (0.07)
age	0.07 (0.14)	0.07 (0.14)	−0.02 (0.09)	−0.02 (0.09)
male	0.41 (0.37)	0.41 (0.37)	0.34 (0.18)	0.34 (0.18)
sailing knot experience	0.11 (0.21)	0.11 (0.21)	0.01 (0.08)	0.01 (0.08)
climbing knot experience	0.19 (0.33)	0.19 (0.33)	0.07 (0.07)	0.07 (0.07)
(intercept)	1.40 (0.63)*	1.68 (0.65)**	−0.44 (0.38)	0.34 (0.38)
R2	0.518	0.518	0.524	0.524
adj. R2	0.365	0.365	0.471	0.471
n	30	30	70	70

*p < 0.05; **p < 0.01.

From generations four to 10, table 3 shows that the mean skill in the five-model treatment declines at a rate of 0.03 s.d. (0.6 percentile points) per generation (p = 0.51), whereas that in the one-model treatment declines at a rate of 0.07 s.d. (1.2 percentile points) per generation (p = 0.20). While neither of these rates of loss is significantly different from zero at conventional levels, suggesting they may be approaching equilibrium, it is worth noting that the estimated magnitude of the rate of loss in the one-model treatment remains twice as large as that in the five-model treatment. And, a test of joint significance for the addition of the treatment and treatment–generation interaction terms to model with only main effects reveals a significant increase in R² from 0.19 to 0.52, F_62,64 = 21.6, p < 0.001 (see the electronic supplementary material, table S6).

Assuming the generation 10 is in the vicinity of the final equilibrium in skill, the mean skill level in the five-model treatment is twice that of the one-model treatment. In fact, every learner in the 10th generation of the five-model treatment is superior to the most skilled learner in the 10th generation of the one-model treatment.

In Experiment 2, by contrast to Experiment 1, there was a substantial time cost to observing models, because participants could not watch all model videos in the available learning time and had to select fewer models from which to learn. Casual observations suggest that most participants watched only one video, or sometimes two. For this reason, it is not clear what the relationship should be between the various models and the specific traits acquired by the learner, so we do not present analyses of this.

4. Discussion

In a microsociety laboratory setting, our results confirm predictions made by existing formal cultural evolutionary models [6,7,9,11,29]. Specifically, they confirm how increasing the number of accessible cultural models can generate greater accumulations of technical know-how in a population, such that every individual in the final generation of the five-model population is more skilled than the most skilled individual in the final generation of the one-model population and almost all individuals in the one-model population. The results confirm that more sociable populations can sustain more complex skills, whereas less sociable populations gradually lose these skills over generations.

Our more detailed analyses of Experiment 1 indicate that learners in the five model condition learned, to at least some detectable degree, from the top four performers, though they did rely most heavily on the top performer among their cultural parents. This is important because, by drawing ideas, techniques and insights from different models, learners can end up with novel recombinations that none of their cultural parents possesses. This, in a sense, creates innovations without ‘invention’, ‘creativity’ or trial and error learning [30,31].

We chose to compare the one-model and five-model treatments for pragmatic reasons: one model represents the natural lower bound, whereas five models provide a substantial increase in model number, giving us the best chance to observe the predicted effect in a relatively small number of generations without escalating the learners’ costs of observing and evaluating a large number of models. We expect the effect of the number of models on skill level and evolutionary rate to show diminishing returns, limited by how much time participants have to evaluate and integrate culture from multiple models and the potential contribution of additional models. We could have just as easily used two to four models, though we expect that the effect sizes would have been a bit smaller.

Our findings also suggest why one prior study has failed to reveal any effects for model number on mean skill levels [32]. The theoretical models we are testing predict that if some skill or other cultural trait is sufficiently easy to learn or cognitively transparent, then increasing the number of models available to learners will have little impact over generations on mean skill level or performance [33]. We suspect that the relative ease of the task used in reference [32], which involved making a simple paper aeroplane, was too easy to learn to observe the effects we found. Such findings also address any concerns that our results were the inevitable consequence of the laboratory set-up. Future research should examine a wider range of tasks, forms of transmission and range of modelling treatments.

One concern with our set-up is that our participants, motivated by money, were primarily concerned with acquiring the specific skills and techniques necessary to match an ideal type, embodied in our target image or the system of rock-climbing knots. These tasks did not have any other immediate practical ends in themselves, such as hoisting a heavy object or communicating a message. While we think that varying the degree to which participants can focus on an immediate practical goal is well-worth exploring [34], it is important to realize that many real and practical aspects of culture have the match-to-target format. For example, an Inuit making his first kayak has no chance of figuring out all the relevant engineering principles that are implicitly embodied in a good kayak, or of knowing the kayak's performance under the extreme conditions that he will encounter weeks or months later. But, he is likely to have another sturdy and well-performing kayak on-hand, to copy. Similarly, a !Kung hunter–gatherer making his arrow poison using Diamphidia beetle larva, acacia sap, salvia and firing can only test his poison in real-time, while pursuing prey. Even then, the quality of his feedback on his poison's effectiveness will usually be murky. The best he can do in the short-term is follow the available recipe as closely as possible. We suspect functional end goals are mostly relevant for relatively easy tasks where individual learning can make a big difference.

Human and non-human primate populations vary in sociality. Chimpanzees and gorillas have mean group sizes of 51 and seven, respectively [35,36], and interact only with their immediate group members. By contrast, although hunter–gatherer groups such as the Hadza live in camps of approximately 30 individuals (11.7 adults), such bands are embedded in much larger tribal networks (approx. 500 adults; over 1000 individuals) comprising many camp sites, with whom they interact extensively [37]. Other hunter–gatherers have similar band sizes (e.g. !Kung, 23; Tiwi, 32; Mbuti, 104) and tribal networks (!Kung, 726; Tiwi, 2662; Mbuti, 1496) [38]. Horticulturalists, such as the Yanomami, live in still larger villages of well over 100 individuals [39] with a total population of around 15 000. Understanding the relationship between sociality and cumulative cultural evolution is crucial to understanding the origins and ecological success of our species [1,30,40]. Several researchers have argued that cumulative cultural evolution, by giving rise to the skills and know-how related to complex tools, clothing, watercraft, fire, cooking, weapons, social norms and water containers, effectively drove our species' genetic evolution over hundreds of thousands, if not millions, of years [22,41–44]. If true, it is essential to explore how and why our lineage crossed the threshold into a regime of cumulative cultural evolution, but others did not. This study suggests that our sociality—our social networks, conspecific tolerance, inter-group relations or population structure—may be what distinguished our ancestors from other primates, and pointed us on a different evolutionary trajectory [8].

Auspicious social conditions for crossing the cumulative cultural evolutionary threshold might emerge if ecological conditions caused a group-living species, such as chimpanzees, to begin pair-bonding [45]. This could stimulate the emergence of (somewhat) peacefully interacting groups, which could increase the size and interconnectedness of populations, opening the door to the emergence of cumulative cultural evolution. Once the cumulative cultural evolutionary threshold is crossed, autocatalytic feedback between cultural learning, tool use and sociality may kick in to synergistically drive all three [30,46].

Data accessibility

Data involved in this study are deposited in the Dryad repository: doi:10.5061/dryad.8th12.

Funding statement

J.H. acknowledges the support from the Canadian Institute for Advanced Research and the Social Sciences and Humanities Research Council of Canada.