Sample size formulae for the Bayesian continual reassessment method

Abstract

Background

In the planning of a dose finding study, a primary design objective is to maintain high accuracy in terms of the probability of selecting the maximum tolerated dose. While numerous dose finding methods have been proposed in the literature, concrete guidance on sample size determination is lacking.

Purpose

With a motivation to provide quick and easy calculations during trial planning, we present closed form formulae for sample size determination associated with the use of the Bayesian continual reassessment method.

Methods

We examine the sampling distribution of a nonparametric optimal design, and exploit it as a proxy to empirically derive an accuracy index of the continual reassessment method using linear regression.

Results

We apply the formulae to determine the sample size of a phase I trial of PTEN-long in pancreatic patients, and demonstrate that the formulae give very similar results to simulation. The formulae are implemented by an R function ‘getn’ in the package ‘dfcrm’.

Limitations

The results are developed for the Bayesian continual reassessment method, and should be validated by simulation when used for other dose finding methods.

Conclusions

The analytical formulae we propose give quick and accurate approximation of the required sample size for the continual reassessment method. The approach used to derive the formulae can be applied to obtain sample size formulae for other dose finding methods.

Introduction

The primary objective of a phase I clinical trial in cancer is the identification of the maximum tolerated dose (MTD), defined as a dose associated with a target toxicity rate. A wide variety of dose finding approaches have been proposed, including model-based designs such as the continual reassessment method (CRM) [1], random walk designs [2], stepwise procedures [3], stochastic approximation [4], and stochastic optimization [5]. While the dose finding literature has flourished in the past two decades, the determination of the sample size remains a recurring question in practice, for which the literature has thus far offered little insight. This has potentially impeded wide applications of these methods in practice, as clinicians would often appreciate and expect guidance on sample size justification early in the planning stage. An exception is the stepwise procedures in Cheung [3] who formulates dose finding as a multiple testing problem that allows us to control the probability of correct selection (PCS) at a pre-specified accuracy. This frequentist property, in turn, informs the required sample size for the stepwise procedures. However, the sample size determination process involves numerical iterations that are highly specialized. For this type of stepwise procedures which include the traditional algorithm-based A+B designs, analytical formulae are also available to calculate the expected number of patients treated at a dose level [3, 6]. For more complicated designs such as group and escalation designs [7] and the model-based Escalation With Overdose Control (EWOC) [8], sample size considerations and recommendations have been made based on computer simulation. Although a method’s operating characteristics should be evaluated thoroughly by simulation before implementation, it will be useful, particularly in consulting settings and for trial budgeting purposes, to provide a quick approximation of the required sample size.

The CRM is one of the most recognized dose finding methods among clinicians, and has seen increasing applications in practice. Its empirical and theoretical properties have been extensively studied; see [9, 10, 11] for example. The calibration of the CRM design parameters has also been written about [12, 13, 14]. These calibration techniques, however, do not provide guidance on sample size determination. Some general rules of thumbs of sample size are given in [15] but are ad hoc. The purpose of this article is to present closed form formulae for sample size calculation for the CRM. A main difficulty in deriving a formal sample size formula for the CRM is that the method is highly outcome-adaptive, and that the theoretical properties necessary for calculating PCS are intractable. Our approach hinges on the concept of a nonparametric optimal design introduced in [16]. The basic idea behind the nonparametric optimal design is to simulate toxicity outcomes of the same patient at all test doses, and estimate the entire dose-toxicity curve using the sample proportions, which achieve the Cramer-Rao lower bound for the corresponding true toxicity probabilities. Hence, this design may serve as an upper limit of performance for the CRM and any other dose finding methods.

A CRM model

In a typical phase I study, each patient is treated at a dose chosen from a set of K levels, with dose labels {d₁, …, d_K}. Let Y = Y (k) denote a patient’s toxicity outcome at dose level k with probability p_k = Pr{Y (k) = 1}. The dose finding objective is to estimate ν = arg min_k | p_k − θ | where θ is the target toxicity rate. The CRM is a model-based design that approximates p_k with a one-parameter function F(d_k, β) for some “least false” parameter value β [15]. In this article, we focus on the commonly used power function

$$F(d_k,\beta )=d_k^{\text{exp}(\beta )}$$ (1)

where β has a normal prior with mean 0 and variance 1.34 [17]. The CRM treats each patient sequentially according to the model-based recommendation based on the most recent data.

Precisely, let β̂_i denote the posterior mean of β given the first i observations, with β̂₀ = 0 denoting the prior mean. Then patient i will be given dose level ν̂_i−1 = arg min_k |F(d_k, β̂_i−1)− θ|. This process continues until a pre-specified sample size n is reached, and the final MTD estimate is given as ν̂_n.

In the CRM, the dose labels d_ks are not the actual doses administered, but are determined to yield good operating characteristics for the CRM [13]. Specifically, we will calculate d_ks for model (1) as follows: for a pre-specified starting dose ν₀ and a half-width δ ∈ (0, θ), set

$$d_{{\nu }_0}=\theta \text{and log}{d}_{k-1}\text{log}(\theta +\delta )=\text{log}{d}_k\text{log}(\theta -\delta )\text{for}k=2,\dots ,K.$$ (2)

The algorithm (2) will yield a unique set of dose labels that satisfy two properties. First, the model-based recommendation ν̂₀ based on the prior distribution will match the actual starting dose ν₀, because F(d_ν0, β̂₀) = θ. For sample size calibration purposes, we for the moment consider CRM that starts the first patient at the median dose level, that is,

$${\nu }_0=\{\begin{array}{cc}\hfill K/2\hfill & \hfill \text{for even}K,\hfill \\ \hfill (K+1)/2\hfill & \hfill \text{for odd}K.\hfill \end{array}$$ (3)

Second, the CRM design using these dose labels has an indifference interval of half-width δ; that is, it will converge to a dose with true toxicity probability on the interval θ ± δ. Based on the numerical results in [13], setting

$$\delta =0.25\theta$$ (4)

generally produces reasonable operating characteristics. As there are many ways a CRM model can be specified, extensive work on how to specify the CRM model components has been reported [13, 14]. In this article, while the sample size formulae are derived with respect to the CRM model specifically defined by (1)–(4), the results can be used to produce a quick sample size estimate and applied to CRM models defined otherwise (e.g., CRM starting at a dose below the median level); see the section “Application”.

Design objective

For the purpose of sample size calculation, we need to define an index for accuracy. Precisely, for given j = 1, …, K, let π_j = (p_1j, … p_Kj)^T denote the dose-toxicity curve with

$$\frac{p_{kj}}{1-p_{kj}}=\frac{R{p}_{k-1,j}}{1-p_{k-1,j}}\text{and}{p}_{jj}=\theta$$ (5)

for some odds ratio R > 1; that is, the true MTD is level j under π_j. Since the probability of selecting the MTD (i.e. PCS) depends on the true π_j, we take the risk-adjusted average approach considered in [18] and define the CRM’s accuracy index as $A_n(\theta ,K,R)=K^{-1}{\sum }_{j=1}^K{P}_{{\pi }_j}({\mathrm{\nu ̂}}_n=j)$, where Pπ denotes the probability computed under the probability vector π. That is, the index A_n is the average PCS under the K logistic dose-toxicity curves. The design objective then is to choose the smallest sample size n that satisfies A_n(θ, K, R) ≥ a* for given clinical parameters {θ, K, R} and accuracy a*.

Apparently, the larger R is, the steeper is the dose-toxicity curve π_j, thus representing a greater “effect size”. As in sample size calculation in other clinical contexts, this effect size R is to be pre-specified. To facilitate the elicitation of the effect size from the clinical investigators, Table 1 shows the steepness of the dose-toxicity curve indicated by the toxicity probabilities (p_j−1,j, p_j+1,j) of doses adjacent to the MTD under various values of R for some common θ. We observe that, for a given R, the toxicity probabilities of the adjacent doses become farther away from θ as a larger θ. For example, for θ = 0.30, the adjacent probabilities 0.20 and 0.43 under R = 1.75 seem to be so different from 0.30 that it may be desirable to differentiate the MTD from the adjacent doses. On the other hand, for θ = 0.10 and R = 1.75, the adjacent doses have toxicity probabilities (0.06 and 0.16) that may be considered indifferent to 0.10. These examples are of course for illustration purposes; and the effect size is to be specified to suit the particular clinical application. Generally, however, a “large” R may be appropriate for a “small” θ.

Table 1.

Odds ratio R and steepness of dose-toxicity curve. The pair in each entry indicates the toxicity probabilities associated with the doses adjacent to the MTD, i.e., (p_j−1,j, p_j+1,j).

θ	R 1.25	1.50	1.75	2.00	2.25	2.50
0.10	(0.08,0.12)	(0.07,0.14)	(0.06,0.16)	(0.05,0.18)	(0.05,0.20)	(0.04,0.22)
0.15	(0.12,0.18)	(0.11,0.21)	(0.09,0.24)	(0.08,0.26)	(0.07,0.28)	(0.07,0.31)
0.20	(0.17,0.24)	(0.14,0.27)	(0.13,0.30)	(0.11,0.33)	(0.10,0.36)	(0.09,0.38)
0.25	(0.21,0.29)	(0.18,0.33)	(0.16,0.37)	(0.14,0.40)	(0.13,0.43)	(0.12,0.45)
0.30	(0.26,0.35)	(0.22,0.39)	(0.20,0.43)	(0.18,0.46)	(0.16,0.49)	(0.15,0.52)

Review of the nonparametric optimal design

In a real clinical study, each patient is given a dose, with the outcome observed only at that dose. We may occasionally draw additional inferences under the assumption of monotone dose-toxicity relationship. For example, suppose a patient receives dose level 3 in a trial and has a toxic outcome. We then can infer by monotonicity that he would have had a toxic outcome at doses higher than dose level 3. However, we will have no information as to whether the patient would have suffered a toxic outcome had he received dose levels 1 or 2. In other words, we can only observe a partial outcome profile. In contrast, in a computer-simulated clinical study where the true π is specified, it is possible to “observe” the outcomes of the same patient at all K dose levels, that is, a complete toxicity profile. Specifically, we can draw a toxicity tolerance U_i for patient i in a simulated trial from a uniform distribution with limits 0 and 1, and set Y_i(k) = I(U_i ≤ p_k) where I(E) is an indicator function of the event E. Consequently, for a trial with sample size n, the sample proportion ${Ȳ}_{k,n}=n^{-1}{\sum }_{i=1}^n{Y}_i(k)$ is an unbiased estimate for p_k and its variance achieves the Cramer-Rao lower bound. O’Quigley et el. [16] thus propose using ν̃_n = arg min_k |Ȳ_k,n − θ| as an optimal benchmark for the estimation of ν: intuitively, because any dose finding method in a real trial uses only the partial outcome profiles, we expect that its accuracy may not exceed that of ν̃_n. Note that the benchmark design ν̃_n cannot be implemented in practice because complete toxicity profiles are not available.

A lower bound formula for sample size

While it is easy to simulate the operating characteristics of the benchmark design ν̃_n, we will exploit its theoretical properties so as to use them to provide approximation for the accuracy index of the CRM. Specifically, we show in the Appendix that for given π = (p₁, …, p_K)^T, the survivor function of ν̃_n can be approximated by

$$P_{\pi }({\mathrm{\nu ̃}}_n\ge k)\approx \mathrm{\Phi }\left\{\frac{\sqrt{n}(2\theta -p_{k-1}-p_k+0.5n^{-1})}{{\sigma }_k}\right\}$$ (6)

for k ≥ 2, where ${\sigma }_k^2=p_{k-1}(1-p_{k-1})+p_k(1-p_k)+2p_{k-1}(1-p_k)$, and Φ is the standard normal distribution function. As a simple consequence of (6), the benchmark index B_n(θ, K, R) for ν̃_n under the logistic dose-toxicity configurations {π_j} can be approximated as follows:

$$B_n(\theta ,K,R)=\frac{1}{K}\sum _{j=1}^K{P}_{{\pi }_j}({\mathrm{\nu ̃}}_n=j)\approx \frac{1}{K}+(1-\frac{1}{K})\{\mathrm{\Phi }(\sqrt{n}{\mathrm{\Delta }}_L)+\mathrm{\Phi }(\sqrt{n}{\mathrm{\Delta }}_U)-1\}$$ (7)

where

$${\mathrm{\Delta }}_L=\frac{\theta -p_{j-1,j}+0.5n^{-1}}{\sqrt{\theta (1-\theta )+p_{j-1,j}(1-p_{j-1,j})+2p_{j-1,j}(1-\theta )}}$$

and

$${\mathrm{\Delta }}_U=\frac{p_{j+1,j}-\theta -0.5n^{-1}}{\sqrt{\theta (1-\theta )+p_{j+1,j}(1-p_{j+1,j})+2\theta (1-p_{j+1,j})}}.$$

Note that p_j−1,j = θ / (θ + R − Rθ) and p_j+1,j = Rθ / (1 − θ + Rθ) under a logistic dose-toxicity curve (5). To do a “sample size calculation” for ν̃_n for given θ, K, R, we can keep iterating n until B_n(θ, K, R) ≥ a* for some pre-specified a*. Alternatively, in order to obtain a closed form sample size formula, we further approximate (7) with

$$B_n(\theta ,K,R)\approx \frac{1}{K}+(1-\frac{1}{K})\{2\mathrm{\Phi }(\sqrt{n}\mathrm{\Delta ̄})-1\}$$ (8)

where $\sqrt{n}\mathrm{\Delta ̄}=\sqrt{n}({\mathrm{\Delta }}_L+{\mathrm{\Delta }}_U)/2$. It can be proved that the absolute difference between (7) and (8) is of the order of O(n^3/2λ⁻ⁿ) for some λ > 1, while (7) converges to the true value of the benchmark index at a rate of n^−1/2. For finite sample sizes, we compare the approximations (7) and (8) with the simulated values of B_n(θ, K, R) under the clinical scenarios listed in Table 2: the largest absolute deviation between the approximated and the simulated values was 0.033, and (7) and (8) differed by no greater than 0.004 in absolute value.

Table 2.

Clinical parameters used in the simulation.

Parameter	Values
θ	0.10, 0.15, 0.20, 0.25, 0.30
K	4, 5, 6, 7, 8
R	1.25, 1.50, 1.75, 2.00, 2.25, 2.50
n	20, 25, 30, 35, 40

Result 1: For given θ, K, R, the smallest sample size required to achieve B_n(θ, R, K) ≥ a* can be approximated by rounding up ñ (a*), where

$$ñ(a)={\left\{{\mathrm{\Phi }}^{-1}\right(1-\frac{K(1-a)}{2(K-1)}\left)\right\}}^2/{\mathrm{\Delta ̄}}^2.$$ (9)

While the nonparametric optimal design ν̃_n cannot be implemented in practice, the sample size ñ (a*) can serve as a lower bound for other dose finding methods, and hence provide a benchmark for efficiency calculation.

Empirical approximation of A_n(θ, K, R) and sample size formulae

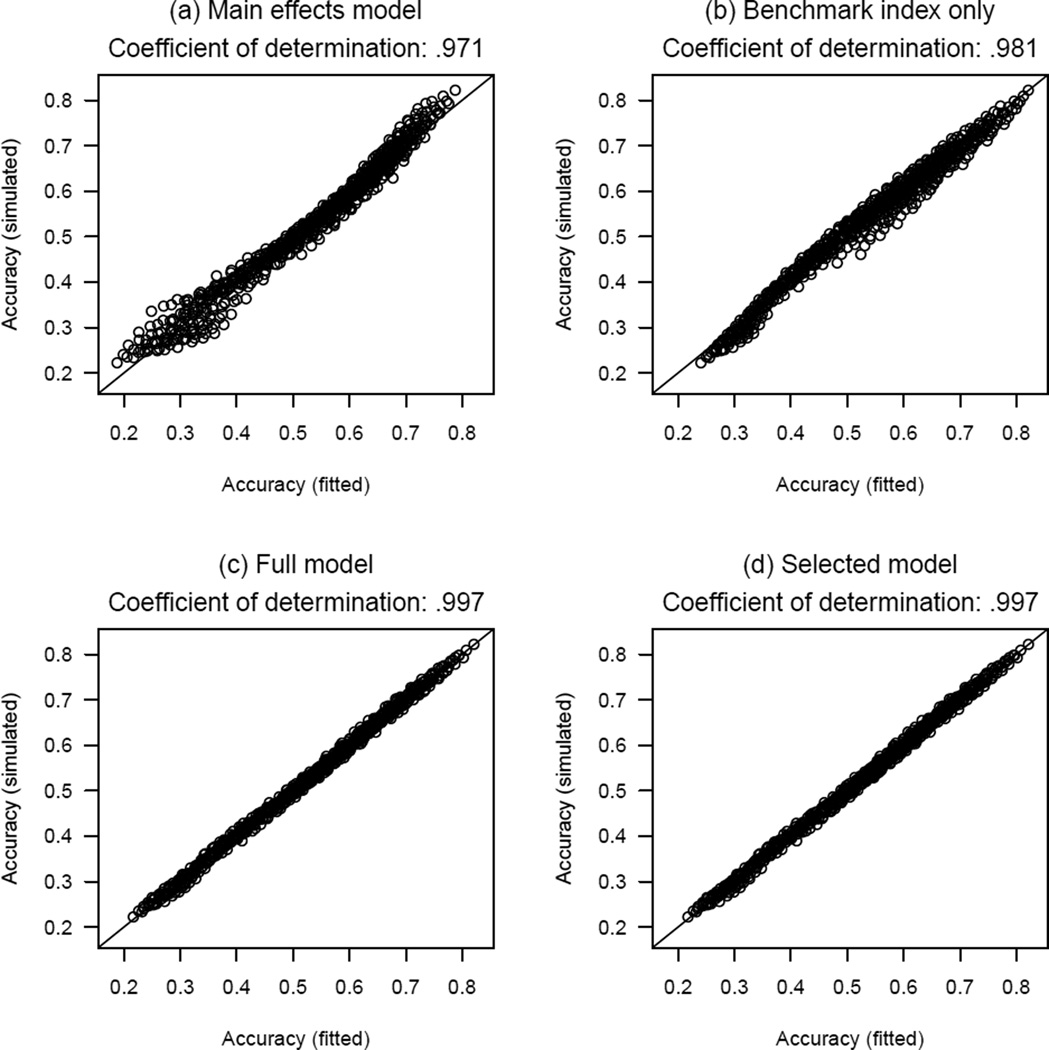
We ran simulation for the CRM defined by (1)–(4) under all possible combinations of the clinical parameters listed in Table 2, with 2000 replicates each for every logistic curve π_j for a given combination, and evaluated A_n(θ, K, R) based on the simulated trials and B_n(θ, K, R) according to (8). Table 3(a) gives the results of the main effects model that regresses logit{A_n(θ, K, R)} on θ, K, R, and n as factors. This model verifies some intuitions about how the CRM’s accuracy depends on the clinical parameters. First, accuracy increases as R and n increase. Second, accuracy improves as a less extreme θ is used: this is expected because on average 10 subjects are needed to expect a toxic outcome in order to target a dose with θ = 0.10 toxicity probability, whereas 5 are needed with θ = 0.20. Third, the accuracy decreases as K increases: this is also intuitive because choosing the right dose is more difficult among a larger number of dose levels. Figure 1(a) plots the simulated A_n(θ, K, R) versus the fitted values Â_n(θ, K, R), which shall be respectively abbreviated as A_n and Â_n. Although the correlation is extremely high, with a coefficient of determination of 0.971, the relationship appears to be non-linear. Besides, since our goal is to “predict” A_n, correlation may not be an appropriate metric to suggest whether a model is adequate. Rather, we will consider the maximum absolute difference ε_∞ ≔ ‖A_n − Â_n‖_∞ between the simulated and the fitted values in all 750 combinations of the clinical scenarios. For the main effects model, ε_∞ = 0.087, which is quite large considering the fact that the accuracy A_n is typically no greater than 0.8.

Table 3.

Linear model fits of the simulated A_n.

(a) Main effects model; intercept = −1.106
Variable	Coef.	Variable	Coef.	Variable	Coef.	Variable	Coef.
θ = 0.10	0	K = 4	0	R = 1.25	0	n = 20	0
0.15	0.182	5	−0.124	1.50	0.548	25	0.113
0.20	0.321	6	−0.232	1.75	0.912	30	0.232
0.25	0.414	7	−0.288	2.00	1.176	35	0.322
0.30	0.482	8	−0.359	2.25	1.371	40	0.410
				2.50	1.524
(b) Full model; intercept = −0.176
θ = 0.10	0	K = 4	0	R = 1.25	0	logit(Bn)	0.853
0.15	0.004	5	−0.027	1.50	0.085
0.20	0.012	6	−0.072	1.75	0.090
0.25	0.007	7	−0.082	2.00	0.053
0.30	0.000	8	−0.118	2.25	−0.016
				2.50	−0.102

Figure 1.

Scatterplots of simulated average PCS versus the fitted average PCS by various models. The coefficient of determination is the square of the sample correlation coefficient.

The second model regresses logit{A_n(θ, K, R)} on logit{B_n(θ, K, R)}, and gives

$$\text{logit}\{{Â}_n(\theta ,K,R)\}=-0.201+0.815\text{logit}\{B_n(\theta ,K,R)\}.$$ (10)

Figure 1(b) plots the simulated A_n versus the fitted Â_n based on (10). Not only is model (10) a much simpler approximation than the main effects model, it also gives a comparable coefficient of determination of 0.981. This suggests the benchmark index (8) as a good predictor for the accuracy index A_n, although (10) alone does not provide an adequate approximation over all clinical scenarios, with ε_∞ = 0.063.

Table 3(b) presents the results of a full model that includes θ, K, and R as factors and logit{B_n(θ, K, R)} as a covariate, and Figure 1(c) plots A_n versus Â_n based on this model. This full model is good for the purpose of predicting A_n, with ε_∞ = 0.022. However, because this model includes θ, K, and R as factors (as opposed to numerical variables), the model cannot be applied to clinical scenarios that are not listed in Table 2, such as when R = 1.8. Thus, we next consider θ, K, and R as numerical variables in the regression models, and use the full model as a reference for accuracy. To account for possible non-linear and non-monotone effects after adjusting for the benchmark index, we consider also quadratic terms and reciprocals. Precisely, we compared linear models using all 2⁹ = 512 combinations of {θ, θ², θ⁻¹, K, K², K⁻¹, R, R², R⁻¹} as numerical covariates, in addition to logit{B_n(θ, K, R)}. Thus, each linear model will have from 1 up to 9 covariates. Table 4 shows the model with the smallest ε_∞ for each given number of covariates, and suggests that the covariates K², R, R⁻¹ and logit{B_n(θ, K, R)} constitute the smallest model that achieves comparable predictability with the full model. Specifically, this model gives:

$$\text{logit}\{{Â}_n(\theta ,K,R)\}=2.26+0.854\text{logit}\{B_n(\theta ,K,R)\}-0.00235K^2-0.700R-1.903R^{-1},$$ (11)

and yields ε_∞ = 0.023. The fitted accuracy index Â_n in (11) can be viewed as an approximate “power curve” for the CRM. Furthermore, based on (11), to achieve an average PCS of at least a*, for given θ, K, R, we can first evaluate b* so that

$$\text{logit}(b^{*})=\{\text{logit}(a^{*})-2.26+0.00235K^2+0.7R+1.903R^{-1}\}/0.854$$ (12)

and calculate the required sample size by the CRM as ñ(b*) using formula (9). The efficiency of the CRM, for a given a*, can be defined as the ratio of the required sample size by the nonparametric optimal design to that by the CRM, that is, ñ(a*)/ñ(b*).

Table 4.

List of models with smallest ε_∞ for each given number of covariates.

Covariates	ε∞
θ, θ2, θ−1, K, K2, K−1, R, R2, R−1	0.023
θ, θ2, θ−1, K2, K−1, R, R2, R−1	0.023
θ, θ2, θ−1, K2, R, R2, R−1	0.022
θ, θ−1, K2, R, R2, R−1	0.022
θ, θ−1, K2, R, R−1	0.022
K2, R, R2, R−1	0.023
K2, R, R−1	0.023
R, R−1	0.039
K2	0.047

Some numerical results

Table 5 tabulates the sample size requirements obtained by formulae (9) and (12) under some common clinical parameters {θ, K, R} for a* = 0.5, 0.6; the sample size values exceeding 60 are excluded because these are usually infeasible numbers for phase I cancer trials. As such, Table 5 (and the formulae) can serve as a quick screening tool indicating the feasibility of a study for a given set of clinical parameters. As expected, the required sample size increases with a large K and a small effect size R. Also, we observe that a substantially larger sample size is needed to raise the accuracy from a* = 0.5 to 0.6. Unless a large effect size R is specified, achieving a* > 0.6 may require a larger-than-typical sample size in practice. For example, to achieve a* = 0.65 for a trial with θ = 0.10 and K = 5 (not listed in Table 5), we need to assume R = 2.5 in order to require a plausibly feasible, albeit large, sample size of n = 41. Therefore, the sample size formulae are useful in giving investigators realistic expectations of accuracy that they can achieve with the sample size conventionally expected: In particular, an 80% “power” (i.e., a* = 0.8) that is conventional for a phase II trial would seem to be unrealistically high for a typical phase I trial.

Table 5.

Sample size requirements in the Bayesian CRM for given clinical parameters θ, K, and R and accuracy level a*.

			a* = 0.5				a* = 0.6
θ	K	R:	1.6	1.8	2.0	R:	1.6	1.8	2.0
0.10	4		39	24	18		—	54	40
	5		51	32	23		—	—	47
	6		—	38	28		—	—	53
	7		—	43	32		—	—	58
	8		—	48	35		—	—	—
0.15	4		28	17	13		—	39	29
	5		37	23	17		—	46	34
	6		44	27	20		—	52	38
	7		50	31	23		—	57	41
	8		55	35	25		—	—	45
0.20	4		23	14	11		50	32	23
	5		30	19	14		59	37	27
	6		35	22	16		—	42	31
	7		40	25	19		—	46	33
	8		45	28	21		—	49	36
0.25	4		20	12	9		43	27	20
	5		26	16	12		51	32	24
	6		30	19	14		57	36	26
	7		34	22	16		—	39	29
	8		38	24	18		—	42	31
0.30	4		18	11	9		39	25	18
	5		23	15	11		46	29	21
	6		27	17	13		51	32	24
	7		31	20	15		56	35	26
	8		35	22	16		—	38	28

Like in other regression applications, we should be cautious about extrapolation, i.e., when applying the results derived empirically to scenarios outside the range of the clinical parameters used in the model (i.e., Table 2). For example, for θ = 0.1, K = 5, R = 1.6, and a* = 0.5, Table 5 gives a required n = 51 which is outside the range of n listed in Table 2. The usage of this table (and the formulae) should therefore be viewed as a quick starting point in consultation; and simulation should be used to verify and study the operating characteristics of the design in the subsequent trial planning. For this particular clinical setting, we ran simulation and obtained A₅₁(0.1, 5, 1.6) = 0.505 which is very close to the target a* = 0.50. We have checked entries larger than 40 in Table 5 and verified that the simulated accuracy differs from the target a* by no greater than 0.010. Likewise, for entries less than 20, simulation should be used to verify the accuracy. For example, for θ = 0.30, K = 4, R = 2.0 and a* = 0.5, Table 5 prescribes n = 9 and simulation verified A₉(0.3, 4, 2) = 0.511. In this case, the CRM seems to be very efficient requiring only n = 9 subjects. However, note that R = 2.0 for θ = 0.3 represents a rather large effect size; see Table 1 and the discussion in the section “Design objective” above. Therefore, it would be prudent to consult Table 1 for a reasonable effect size when using Table 5 or the formulae to determine the sample size.

Application

To provide a quick estimate of budget (that is, n) for a dose finding study of PTEN-long monotherapy in patients with pancreatic cancer, we calculated the required sample size using formulae (9) and (12). In the trial, the MTD was defined with target θ = 0.25. The starting dose of the trial would be determined based on a prior pharmacokinetic study, and would be the third dose level in a panel of K = 5 test doses. To obtain an average PCS of a* = 0.6 under R = 1.8, we obtained b* = 0.648 and ñ(b*) = 31.6. Thus, the sample size of the trial was set to be 32. This calculation could be easily performed on a calculator during a consultation session with the clinical investigators of the study. An R function ‘getn’ is also available in the ‘dfcrm’ package to perform the calculation; see Appendix.

Table 6 shows the operating characteristics of the CRM design defined by (1)–(4) with n = 32 by simulation under each of the 5 logistic dose-toxicity curves {π_j}. The accuracy index based on the simulation is 0.604, very close to the approximated value (0.602) based on (11).

Table 6.

Simulated operating characteristics of the CRM (ν̂_n) and the optimal nonparametric designs (ν̃_n) with n = 32 for the PTEN-long trial.

Design	Proportion selecting dose
	1	2	3	4	5
π1	.25	.38	.52	.66	.78
ν̂n (ν0 = 3, δ = .0625)	.77	.22	.01	.00	.00
ν̂n (ν0 = 3, δ = .0600)	.78	.21	.01	.00	.00
ν̂n (ν0 = 2, δ = .0575)	.80	.19	.01	.00	.00
ν̃n	.82	.17	.01	.00	.00
π2	.16	.25	.38	.52	.66
ν̂n (ν0 = 3, δ = .0625)	.24	.56	.20	.01	.00
ν̂n (ν0 = 3, δ = .0600)	.24	.56	.19	.01	.00
ν̂n (ν0 = 2, δ = .0575)	.27	.53	.19	.01	.00
ν̃n	.27	.55	.16	.01	.00
π3	.09	.16	.25	.38	.52
ν̂n (ν0 = 3, δ = .0625)	.03	.26	.52	.19	.01
ν̂n (ν0 = 3, δ = .0600)	.03	.26	.53	.19	.01
ν̂n (ν0 = 2, δ = .0575)	.03	.27	.52	.17	.01
ν̃n	.02	.24	.57	.17	.00
π4	.05	.09	.16	.25	.38
ν̂n (ν0 = 3, δ = .0625)	.00	.03	.27	.52	.18
ν̂n (ν0 = 3, δ = .0600)	.00	.03	.27	.52	.18
ν̂n (ν0 = 2, δ = .0575)	.00	.03	.29	.51	.17
ν̃n	.00	.02	.23	.56	.19
π5	.03	.05	.09	.16	.25
ν̂n (ν0 = 3, δ = .0625)	.00	.00	.04	.31	.65
ν̂n (ν0 = 3, δ = .0600)	.00	.00	.03	.31	.66
ν̂n (ν0 = 2, δ = .0575)	.00	.00	.05	.31	.64
ν̃n	.00	.00	.02	.23	.74

While the sample size formulae can give a quick answer, there is no reason not to fine-tune the CRM design using the same sample size if time permits. Using the calibration approach outlined in [13], we obtained the optimal δ = 0.0600 for the CRM defined by (1)–(3) and n = 32 under this particular set of scenarios, i.e., with starting dose at ν₀ = 3. Table 6 shows that this design has similar accuracy to the CRM with δ = 0.0625, with a slightly larger average PCS of 0.608. Generally, since we can potentially improve the operating characteristics upon the CRM design used in deriving the sample size, the formulae we derived lead to a conservative sample size. In most cases, as in this particular case, setting δ = 0.25θ according to (4) produces very competitive operating characteristics, and hence the formulae provide meaningfully close approximation.

While the sample size approximation assumes starting a trial at the median level in accordance with (3), we may apply the calculated sample size in trials with other starting dose. Suppose that the PTEN-long trial investigators postulate the prior MTD as ν₀ = 2 and start the trial at level 2 instead of level 3. Applying the calibration approach in [13] to the CRM model defined by (1), (2), and ν₀ = 2 with n = 32, we obtained the optimal δ = 0.0575 for this particular set of clinical parameters. The operating characteristics of this design, also included in Table 6, are comparable to the CRM designs that start at dose level 3, with an average PCS of 0.599, very close to the target a*. This is in line with the findings in [13, 15] that the starting dose has minimal impact on the CRM’s operating characteristics, provided that the design is properly calibrated.

Finally Table 6 also shows the operating characteristics of the optimal nonparametric design based on ν̃₃₂. The simulated average PCS is 0.650, whereas the approximation based on (7) is 0.649. The CRM designs lose about 4–5 percentage points of accuracy, or roughly 7% of 0.650, when compared to this optimal benchmark. From this viewpoint, the efficiency of the CRM is quite high. In contrast, the efficiency defined with respect to the sample size ratio is about 76%, with ñ(0.6) = 24.0. This is probably due to the fact that a large increase in sample size is needed for even a modest increase in accuracy; cf. Table 5.

Discussion

It is not the intention of this paper to comment on a dose finding method’s efficiency. Rather, the purpose is to facilitate quick assessment of the sample size, thus giving the investigators a rough idea whether a phase I dose finding trial is “adequately powered” as demonstrated in Table 5.

This work is not to replace simulation as a planning tool. As shown in our application, we can use the proposed formulae to obtain a sample size as a starting point, and then use simulation to examine possible improvements by fine-tuning the CRM, and evaluate effects of a different starting dose or CRM model specification. For sample size calculation purposes, we need to define an accuracy index, for which we use the average PCS in this article. As pointed out by a referee and also in [19], looking at a design’s behavior about the true MTD only does not fully reflect the operating characteristics of the design. Specifically, when the true dose-toxicity curve is shallow and the toxicity probabilities of the adjacent levels are close to that of the MTD, the design may have satisfactory performance by choosing the adjacent levels with high probability, even though the PCS is not very high. Therefore, we should use simulation to study the full distribution of MTD recommendation of the design under a variety of dose-toxicity curves after we have determined the sample size. Also note that while we use the logistic dose-toxicity configurations as the basis of sample size calculation, we can perform simulation under other dose-toxicity curves in the planning process. As previously pointed out in [9], the method’s consistency does not rely on the correctness of the model assumptions; in this paper, we use a misspecified power model (1) while the operating characteristics are evaluated under logistic curves.

This paper describes a general approach that explores the nonparametric optimal design as a proxy for the CRM; and the nonparametric optimal design is particularly useful because its benchmark index B_n can be computed analytically via Equations (6)–(8), thus leading to a closed form sample size expression (9). Table 3 shows that the benchmark index B_n attenuates the magnitude of the effects of the clinical parameters {θ, K, R} on A_n, and suggests that the performance of ν̃_n depends on these design parameters in a qualitatively similar way to that of the CRM. As we may expect that any reasonable dose finding designs will behave similarly, this approach can be potentially applied to derive sample size formulae for other dose finding designs. In particular, it would be of great interest to extend these results to the two-stage CRM that starts a trial with a pre-specified initial dose-escalation sequence before the first toxicity is observed [17]. As additional calibration steps for this initial sequence are needed, further work on how to exploit the benchmark index B_n for the two-stage CRM is warranted.

Finally, based on published results in the literature, we expect that various versions of model-based dose finding designs [8, 20, 21] have comparable operating characteristics, provided that they are properly calibrated. Therefore, the sample size formulae derived in this article may also be applied to approximate the required sample size for these alternative designs. This quick assessment of sample size should however be validated by simulating the detailed operating characteristics, as demonstrated in our application.

Appendix

Derivation of (6) and (7)

It is easy to verify that $\{{\mathrm{\nu ̃}}_n\ge k\}\iff \{{Ȳ}_{k,n}+{Ȳ}_{k-1,n}\le 2\theta \}\iff \{{\sum }_{i=1}^n{V}_{ik}\le 2n\theta \}$, where V_ik = I(U_i ≤ p_k) + I(U_i ≤ p_k−1) is a discrete random variable taking value on {0, 1, 2}, with mean E(V_ik) = p_k + p_k−1 and variance ${\sigma }_k^2\equiv \text{var}(V_{ik})=p_{k-1}(1-p_{k-1})+p_k(1-p_k)+2p_{k-1}(1-p_k)$. Hence,

$$P_{\pi }({\mathrm{\nu ̃}}_n\ge k)=P_{\pi }(\sum _{i=1}^n{V}_{ik}\le 2n\theta )=P_{\pi }(\sum _{i=1}^n{V}_{ik}\le 2n\theta +0.5)=P_{\pi }\{\frac{1}{\sqrt{n}}\sum _{i=1}^n\frac{V_{ik}-p_k-p_{k-1}}{{\sigma }_k}\le \frac{\sqrt{n}(2\theta -p_k-p_{k-1}+0.5n^{-1})}{{\sigma }_k}\}\approx \mathrm{\Phi }\left\{\frac{\sqrt{n}(2\theta -p_k-p_{k-1}+0.5n^{-1})}{{\sigma }_k}\right\}$$

where the approximation on the last line is by the central limit theorem. Equation (6) is thus derived. Consequently, under a logistic curve π_j ,

$$P_{{\pi }_j}({\mathrm{\nu ̃}}_n=j)\approx \{\begin{array}{cc}\hfill 1-\mathrm{\Phi }\left\{\frac{\sqrt{n}(\theta -p_{j+1,j}+0.5n^{-1})}{{\sigma }^{*}}\right\}\hfill & \text{for}j=1\hfill \\ \hfill \mathrm{\Phi }\left\{\frac{\sqrt{n}(\theta -p_{j-1,j}+0.5n^{-1})}{\sigma \prime }\right\}-\mathrm{\Phi }\left\{\frac{\sqrt{n}(\theta -p_{j+1,j}+0.5n^{-1})}{{\sigma }^{*}}\right\}\hfill & \text{for}2\le j<K\hfill \\ \hfill \mathrm{\Phi }\left\{\frac{\sqrt{n}(\theta -p_{j-1,j}+0.5n^{-1})}{\sigma \prime }\right\}\hfill & \text{for}j=K\hfill \end{array}$$

where σ*² = θ(1 − θ) + p_j+1,j(1 − p_j+1,j) + 2θ(1 − p_j+1,j) and σ′² = θ(1 − θ) + p_j−1,j(1 − p_j−1,j) + 2p_j−1,j (1 − θ). Therefore, $B_n(\theta ,K,R)=K^{-1}{\sum }_{j=1}^K{P}_{{\pi }_j}({\mathrm{\nu ̃}}_n=j)$

$$\approx \frac{1}{K}(1+(K-1)[\mathrm{\Phi }\left\{\frac{\sqrt{n}(\theta -p_{j-1,j}+0.5n^{-1})}{\sigma \prime }\right\}-\mathrm{\Phi }\left\{\frac{\sqrt{n}(\theta -p_{j+1,j}+0.5n^{-1})}{{\sigma }^{*}}\right\}\left]\right)=\frac{1}{K}+(1-\frac{1}{K})\{\mathrm{\Phi }(\sqrt{n}{\mathrm{\Delta }}_L)-\mathrm{\Phi }(-\sqrt{n}{\mathrm{\Delta }}_U)\}$$

where

$${\mathrm{\Delta }}_L=\frac{\theta -p_{j-1,j}+0.5n^{-1}}{\sigma \prime }>0\text{and}{\mathrm{\Delta }}_U=\frac{p_{j+1,j}-\theta -0.5n^{-1}}{{\sigma }^{*}}>0.$$

Equation (7) thus follows.

Derivation of the upper bound of the difference between (7) and (8)

Assume without loss of generality Δ_U ≥ Δ_L. Then define h = Δ_U − Δ̄ = Δ̄ − Δ_L. Expanding $\mathrm{\Phi }(\sqrt{n}{\mathrm{\Delta }}_L)$ about $\sqrt{n}\mathrm{\Delta ̄}$ using Taylor’s series gives

$$\mathrm{\Phi }(\sqrt{n}{\mathrm{\Delta }}_L)=\mathrm{\Phi }(\sqrt{n}\mathrm{\Delta ̄})-\sqrt{n}h\varphi (\sqrt{n}\mathrm{\Delta ̄})-\frac{n{h}^2}{2}\sqrt{n}{\mathrm{\Delta }}_L^{*}\varphi (\sqrt{n}{\mathrm{\Delta }}_L^{*})$$ (A1)

for some ${\mathrm{\Delta }}_L^{*}\in [{\mathrm{\Delta }}_L,\mathrm{\Delta ̄}]$, where ϕ is the density function of standard normal. Likewise, we have

$$\mathrm{\Phi }(\sqrt{n}{\mathrm{\Delta }}_U)=\mathrm{\Phi }(\sqrt{n}\mathrm{\Delta ̄})+\sqrt{n}h\varphi (\sqrt{n}\mathrm{\Delta ̄})-\frac{n{h}^2}{2}\sqrt{n}{\mathrm{\Delta }}_U^{*}\varphi (\sqrt{n}{\mathrm{\Delta }}_U^{*})$$ (A2)

for some ${\mathrm{\Delta }}_U^{*}\in [\mathrm{\Delta ̄},{\mathrm{\Delta }}_U]$. Adding (A1) and (A2) then gives

$$2\mathrm{\Phi }(\sqrt{n}\mathrm{\Delta })-\{\mathrm{\Phi }(\sqrt{n}{\mathrm{\Delta }}_L)+\mathrm{\Phi }(\sqrt{n}{\mathrm{\Delta }}_U)\}=\frac{n^{3/2}{h}^2}{2}\{{\mathrm{\Delta }}_L^{*}\varphi (\sqrt{n}{\mathrm{\Delta }}_L^{*})+{\mathrm{\Delta }}_U^{*}\varphi (\sqrt{n}{\mathrm{\Delta }}_U^{*})\}.$$ (A3)

It is easy to see that (A3) lies between 0 and ${(2\pi )}^{-1}{n}^{3/2}{h}^2{\mathrm{\Delta }}_U^{*}\text{exp}\{-n{\mathrm{\Delta }}_L^{*}/2\}$, with the latter converging to 0 at a rate of n^3/2λ⁻ⁿ where $\lambda =\text{exp}({\mathrm{\Delta }}_L^{*}/2)>1$ because ${\mathrm{\Delta }}_L^{*}\ge {\mathrm{\Delta }}_L>0$. It is easy to see that the difference between Equations (7) and (8) converges to zero at this rate.

R code for the PTEN-long study

An R function ‘getn’ is made available in the package ‘dfcrm’ (version 0.2-0 built on 2013-02-19). The function implements the sample size calculation proposed in this article. The following code is used to obtain the sample size for the PTEN-long study:

> library(dfcrm)
> a = 0.6
> theta = 0.25
> K = 5
> oddsRatio = 1.8
> obj = getn(a, theta, K, oddsRatio)
> obj
Target rate:                         0.25
Number of dose levels:        5
Effect size (odds ratio):        1.8
Required accuracy:              0.6
Calculated sample size:        32
> n = obj$n
> n
[1] 32
>