Models and Strategies for Factor Mixture Analysis: An Example Concerning the Structure Underlying Psychological Disorders

Abstract

The factor mixture model (FMM) uses a hybrid of both categorical and continuous latent variables. The FMM is a good model for the underlying structure of psychopathology because the use of both categorical and continuous latent variables allows the structure to be simultaneously categorical and dimensional. This is useful because both diagnostic class membership and the range of severity within and across diagnostic classes can be modeled concurrently. While the conceptualization of the FMM has been explained in the literature, the use of the FMM is still not prevalent. One reason is that there is little research about how such models should be applied in practice and, once a well fitting model is obtained, how it should be interpreted. In this paper, the FMM will be explored by studying a real data example on conduct disorder. By exploring this example, this paper aims to explain the different formulations of the FMM, the various steps in building a FMM, as well as how to decide between a FMM and alternative models.

In recent years there has been a debate in the psychological literature about whether the underlying structure of psychological disorders, such as conduct disorder, is categorical or dimensional. In the categorical view, psychological disorders are represented by diagnostic categories that indicate whether a person is affected or unaffected by a disorder and/or whether a person has a specific subtype. This has been the predominant view of psychopathology because it has the advantage of meeting clinical needs and the needs of reporting for health care planners and insurance companies (Muthén, 2006). Alternatively, psychological disorders are considered dimensional in nature and are represented as a continuous distribution, with each individual having some amount of the disorder. The advantage of the dimensional view is that each disorder can be represented as a quantitative score, or scores, which provides a more precise measure of functioning and more power for further statistical analyses than categorical outcomes (Muthén, 2006).

In the psychometric literature, each of these views has a counterpart (Bauer & Curran, 2004). The categorical view can be represented by latent class analysis, which uses categorical latent variables, called latent classes, to find homogenous groups of individuals in a sample. In this analysis, individuals are grouped into their most likely latent class based on their observed symptoms so that latent classes can then be interpreted as diagnostic categories or subtypes. The problem with latent class analysis, and the categorical approach to psychopathology, is that the categories do not consider the range in severity and impairment within and across diagnostic classes.

The dimensional view of psychological disorders has its counterpart in factor analysis. Here, continuous latent variables, called factors, are used to model the correlations among the symptoms. Each of these factors represents an underlying dimension of the disorder. One drawback of this approach is that there is, generally, no easy way to classify individuals into groups, which, as stated earlier, is currently a clinical necessity and required by insurance companies and other reporting agencies.

One solution to the debate, proposed by Muthén (2006), is the factor mixture model (FMM). The FMM uses a hybrid of both categorical and continuous latent variables, which allows the underlying structure to be simultaneously categorical and dimensional. The structure is considered categorical because the model allows for the classification of individuals into diagnostic groups through the use of latent class variables. The structure is also considered dimensional because once individuals are classified into groups, the FMM allows for heterogeneity within groups through the use of continuous latent variables. This approach is useful because it does not have the limitations of the two conventional representations of psychopathology.

While the studies that have introduced the FMM to the psychological literature have explained the conceptualization of the FMM, the use of the FMM is still not prevalent. One reason for this is that even though the concept of the FMM has been explained, there is little research about how these models should be applied in practice and, once a well fitting model is obtained, how it should be interpreted. This paper seeks to remedy these shortcomings.

This paper presents a didactic explanation of the different variations of the FMM including the various steps in building a FMM, and how to decide between a FMM and alternative models. The FMM will be explored in detail by studying a real data example concerning conduct disorder. The first section introduces LCA, FA and the FMM in technical detail while the second section focuses on the model building process and on how to compare among different types of models. The third section presents the real data example and the final section discusses the utility of the FMM. All analyses in this paper were carried out using Mplus V5.1 (Muthén & Muthén, 1998–2008). In order to elucidate the FMM, sample syntax for each model variation is available in the Appendix.

Background

Latent Class Analysis

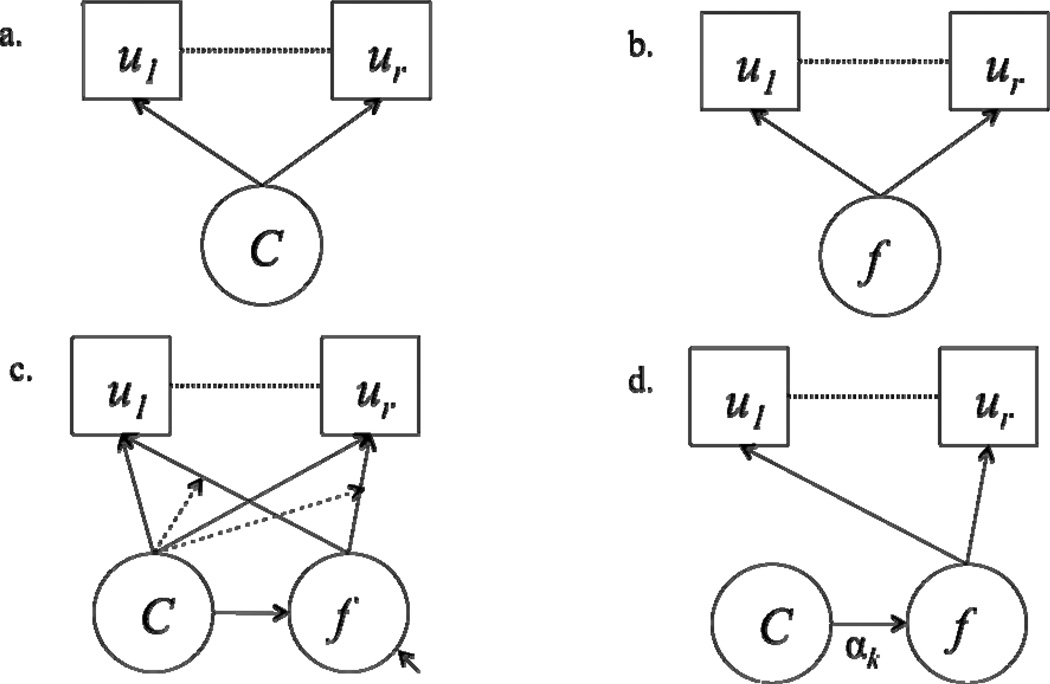
The latent class analysis (LCA) model, introduced by Lazarsfeld and Henry (1968), is used to identify subgroups, or classes, of a study population. A diagram of an example of a latent class analysis model is shown in Figure 1a. The boxes, u₁ to u_r, represent the observed response items or outcomes. The outcomes in a LCA model can be categorical, continuous, count, censored, or nominal, though this paper will specifically focus on binary items. The circle with the letter C in the middle is the unordered, categorical latent class variable with K classes. The arrows pointing from the latent class variable to the boxes above indicate that those items are measuring the latent class variable. This means that class membership is based on the observed response pattern of items. An important assumption, called the conditional or local independence assumption, implies that the correlation among the observed outcomes is explained by the latent class variable. Because of this, there is no residual correlation between the items.

Figure 1.

Model Diagrams. (a) Latent Class Analysis, (b) Factor Analysis, (c) Generalized Factor Mixture Model, (d) FMM-1, (e) FMM-2, (f) FMM-3, (g) FMM-4.

For a LCA model with categorical outcomes, there are two types of model parameters: conditional item probabilities and class probabilities. The conditional item probabilities are specific to a given class and provide information about the probability that an individual in that class will endorse a specific item. The class probabilities specify the relative size of each class, or the proportion of the population that is in a particular class.

Consider a LCA model with r observed binary items, u, and a categorical latent variable C with K classes (C = k; k = 1, 2, …, K). The marginal item probability for item u_j = 1 is

$$P(u_j=1)=\sum _{k=1}^{K}P(C=k)P(u_j=1|C=k).$$ (1)

Equation 1 states that the probability of item u_j = 1 is equal to the sum, over all latent classes, of the product of the probability of being in class k and the probability that u_j = 1 given latent class membership k. Assuming conditional independence, the joint probability of all the r observed items is

$$P(u_1,u_2,\dots ,u_r)=\sum _{k=1}^{K}P(C=k)P(u_1|C=k)P(u_2|C=k)\dots P(u_r|C=k).$$ (2)

Equation 2 says that the probability of observing a specific response pattern is the sum, over all latent classes, of the probability of being in class k multiplied by the product of the probabilities of observing each item given latent class membership k.

A product of LCA is the estimated class probabilities for each individual, called posterior probabilities, which are analogous to factor scores in a factor analysis (Muthén, 2001). These are estimates of

$$P(C=k|u_1,u_2,\dots ,u_r)=\frac{P(C=k)P(u_1|C=k)P(u_2|C=k)\dots P(u_r|C=k)}{P(u_1,u_2,\dots ,u_r)}.$$ (3)

Equation 3 states that probability of being in class k given an observed response pattern is equal to the probability of being in class k multiplied by the product of the probabilities of observing each item given latent class membership k, divided by the probability of observing a specific response pattern (i.e., Equation 2). Note that each individual is allowed fractional class membership and may have non-zero values for many classes. It is from these probabilities that class membership is assigned. An individual is assigned to be a member of a class based on their highest probability of being in a given class, even though an individual may have several classes to which they are a partial member. Once assigned to a class, an individual is assumed to be a part of that class 100%.

Factor Analysis

In factor analysis (FA), the goal is to investigate common content among the items (Lubke & Muthén, 2005) by seeing if items group together on continuous latent variables called factors. An example of a FA model can be seen in Figure 1b. As with the latent class model, there is a circle, this time with the letter f in the middle, representing the factor. But, the circle in a FA is not an unordered, categorical latent variable like in LCA, but instead, a continuous one. Because the latent variable is continuous, there is no assumption of different subpopulations of individuals, like in LCA. Instead, it is assumed that all individuals in the sample are from the same homogenous population and that differences among individuals arise because of differences on the factor. Similar to LCA, there are arrows emanating from the factor that point towards the items. This indicates that the factors are measured by those combinations of items that people tend to endorse together. The outcomes in a FA model can be categorical, continuous, count, censored, or nominal, though this paper will specifically focus on binary items.

The factor analytic model with p observed binary items, u, takes on the following form for individual i:

$${{\mathit{u}}^{*}}_i=\mathit{\Lambda }{\mathit{\eta }}_i+{\mathit{\epsilon }}_i,$$

$${\mathit{\eta }}_i=\mathit{\alpha }+{\mathit{\zeta }}_i,$$

and

$$u_{ij}=\{\begin{array}{ll}0,\hfill & \text{if}{\tau }_j<u_{ij}^{*}\hfill \\ 1,\hfill & \text{if}{u}_{ij}^{*}\le {\tau }_j\hfill \end{array}$$ (4)

where u_i are individual i’s responses, which is a p vector of observed outcomes; u*_i is individual i’s latent response vector; j is one of the items in a p vector; Λ is a p × m matrix of factor loadings, where m is the number of factors; η_i is a m vector of factor scores; ε is p vector of residuals; α is a m vector of the means of the factors; ζ_i is a m vector of residuals which is assumed to be normally distributed with mean zero and variance Ψ. The bottom part of Equation 4 relates an individual’s observed response, u_ij, to the latent response u*_ij. Usually, we specify u_ij = u*_ij if u_ij is normally distributed, but since u_ij is dichotomous a special link function relating u_ij to u*_ij is specified. The link function specifies that if u_ij is equal to zero, which indicates an individual does not endorse the item, then the latent response is below the threshold τ_j, and if u_ij is equal to one, which indicates that an individual endorses the item, then the latent response u*_ij is above the threshold τ_j. Hence, the observed dichotomous value changes when the threshold is exceeded on the latent response variable (Flora & Curran, 2004).

An important piece of information that results from a FA is the estimated factor scores, η_i. The factor scores are estimated from Equation 4, after the analysis has been conducted. The factor scores of all the individuals in a sample can be thought of as forming an approximation to the sample distribution of the factor. The factor score of an individual can be used as an indication of where that individual is located on the factor, relative to the other individuals in the sample.

Factor Mixture Model

The factor mixture model (FMM) uses a hybrid of latent class and factor analysis (Muthén, 2008) and an example of a FMM can be seen in Figure 1c. The figure shows that the FMM is a combination of LCA and FA because there is both a latent class variable, the circle with the C in the middle, and a latent continuous factor, the circle with the f in the middle. The latent class variable allows for the classification of individuals into groups while the factor models the heterogeneity of the disorder within latent class. The factor also yields quantitative scores of the disorder in the form of the factor scores.

Figure 1c shows an added flexibility of the FMM. The solid lines starting from the latent variables and ending at the symptom items indicate that the latent variables are measured by those symptoms. Additionally, there are dashed lines coming from the latent class variable and ending on the line that goes from the factor to the symptom items. This indicates that the factor structure of the model can be different in each class. The formulation of the FMM is similar to what was seen in the FA model except that the factor loadings, factor means, factor covariance matrix, and item thresholds, have the potential to be different across the classes. A factor mixture model for k = 1, 2, …, K latent classes with observed binary items, u, can be specified as follows:

$${{\mathit{u}}^{*}}_{ik}={\mathit{\Lambda }}_k{\mathit{\eta }}_{ik}+{\mathit{\epsilon }}_{ik},$$

$${\mathit{\eta }}_{ik}={\mathit{\alpha }}_k+{\mathit{\zeta }}_{ik},$$

where,

$${\mathit{\zeta }}_{ik}~\mathrm{N}(\mathbf{0},{\mathit{\Psi }}_k)$$

and

$$u_{ij}=\{\begin{array}{ll}0,\hfill & \text{if}{\tau }_{jk}<u_{ij}^{*}\hfill \\ 1,\hfill & \text{if}{u}_{ij}^{*}\le {\tau }_{jk}\hfill \end{array}$$ (5)

All of the parameters in the equation above have the same interpretation as the FA model presented in Equation 4, but now they can be class specific as indicated by the subscript k. By allowing the parameters to have the potential to be class-specific, the model becomes more flexible and allows for several variations that differ in the amount of measurement invariance. These variations will be discussed in more detail in the next section.

The FMM has distinct advantages over LCA and FA that may make it a better model to represent psychological disorders. Unlike LCA, the FMM does not have a conditional independence assumption given latent class. This suggests that individual differences in the heterogeneity of a disorder can be explored within a given class. The heterogeneity within a class is represented by the continuous factor and can be quantified by using the factor score for each individual (Lubke & Muthén, 2005; Muthén et al., 2006). One disadvantage to FA is that there is no model-based classification of individuals because individuals are assumed to be from the same homogenous population. In a FMM, classification is obtained through the latent class variable.

While there has been little research on how to do the FMM in practice, several authors have made contributions toward the development of this model. One of the first articles is by Yung (1997), which considers a FMM where all of the parameters were class-varying. McLachlan and Peel (2000) discuss a FMM where the factor structure is exploratory rather than confirmatory. Lubke & Muthén (2005) discuss the incorporation and interpretation of covariates into the FMM. Muthén (2006) and Muthén and Asparouhov (2006) consider a FMM using binary outcomes. Muthén (2008) provides an overview of the different types of FMMs and breaks them down into four branches depending on the amount of measurement invariance present and whether the factor in each model is parametric or not.

FMM: Model Variations

In this paper, four variations of the FMM and their interpretations are presented. Model presentation will start with the more restrictive models, since the interpretations tend to be simpler, and end with less restrictive models, where the interpretation can be more complex. The formula for each variation is presented in Table 1 for easier comparison among the variations.

Table 1.

Factor Mixture Model Variation Equations

Model	Equation	Link Function	Class Varying Parameters	Inputa
FMM-1 Latent Class Factor Analysis	${{\mathit{u}}^{*}}_{ik}=\mathit{\Lambda }{\mathit{\eta }}_{ik}+{\mathit{\epsilon }}_{ik},$ ${\mathit{\eta }}_{ik}={\mathit{\alpha }}_k$	$u_{ij}=\{\begin{array}{ll}0,\hfill & \text{if}{\tau }_j<u_{ij}^{*}\hfill \\ 1,\hfill & \text{if}{u}_{ij}^{*}\le {\tau }_j\hfill \end{array}$	α	1a, 1b
FMM-2 Mixture Factor Analysis	${{\mathit{u}}^{*}}_{ik}=\mathit{\Lambda }{\mathit{\eta }}_{ik}+{\mathit{\epsilon }}_{ik},$ ${\mathit{\eta }}_{ik}={\mathit{\alpha }}_k+{\mathit{\zeta }}_{ik}$ ${\mathit{\zeta }}_{ik}~\mathrm{N}(\mathbf{0},{\mathit{\Psi }}_k)$	$u_{ij}=\{\begin{array}{ll}0,\hfill & \text{if}{\tau }_j<u_{ij}^{*}\hfill \\ 1,\hfill & \text{if}{u}_{ij}^{*}\le {\tau }_j\hfill \end{array}$	α, Ψ	2
FMM-3	${{\mathit{u}}^{*}}_{ik}=\mathit{\Lambda }{\mathit{\eta }}_{ik}+{\mathit{\epsilon }}_{ik},$ ${\mathit{\eta }}_{ik}={\mathit{\zeta }}_{ik}$ ${\mathit{\zeta }}_{ik}~\mathrm{N}(\mathbf{0},{\mathit{\Psi }}_k)$	$u_{ij}=\{\begin{array}{ll}0,\hfill & \text{if}{\tau }_{jk}<u_{ij}^{*}\hfill \\ 1,\hfill & \text{if}{u}_{ij}^{*}\le {\tau }_{jk}\hfill \end{array}$	Ψ, τ	3
FMM-4	${{\mathit{u}}^{*}}_{ik}={\mathit{\Lambda }}_k{\mathit{\eta }}_{ik}+{\mathit{\epsilon }}_{ik}$ ${\mathit{\eta }}_{ik}={\mathit{\zeta }}_{ik}$ ${\mathit{\zeta }}_{ik}~\mathrm{N}(\mathbf{0},{\mathit{\Psi }}_k)$	$u_{ij}=\{\begin{array}{ll}0,\hfill & \text{if}{\tau }_{jk}<u_{ij}^{*}\hfill \\ 1,\hfill & \text{if}{u}_{ij}^{*}\le {\tau }_{jk}\hfill \end{array}$	Ψ, τ, λ	4

Note.

^aInput numbers are in reference to the example Mplus syntax in the Appendix. In the class varying parameters column: α = factor mean; Ψ = factor covariance matrix; τ = item threshold; λ = factor loading.

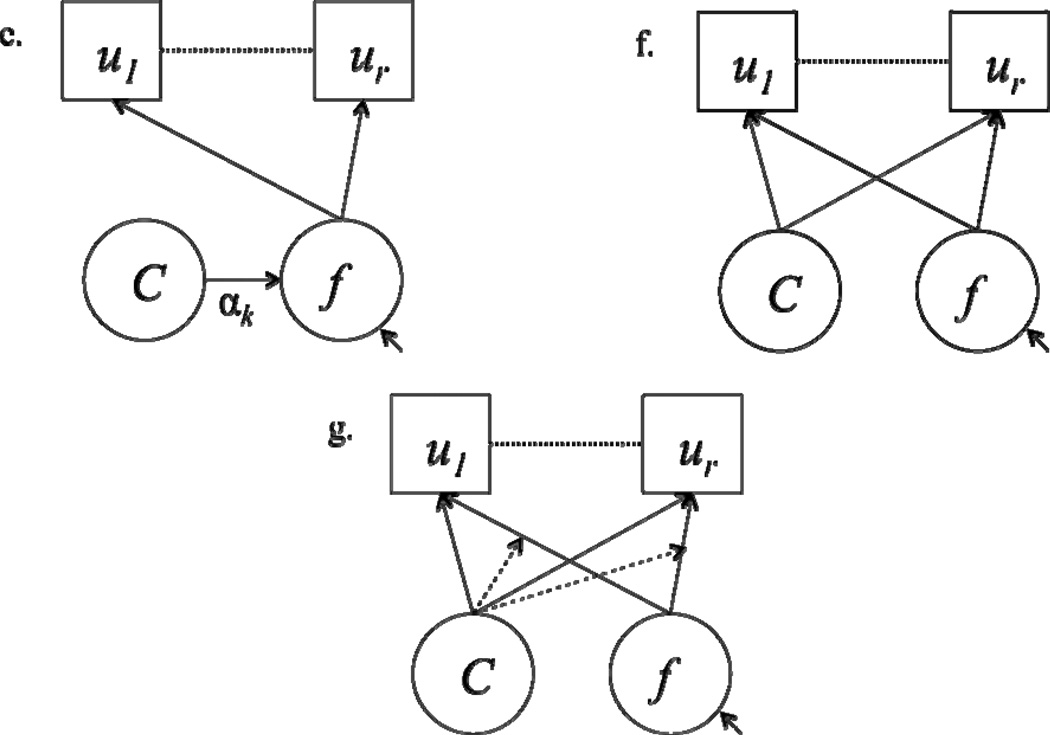
The first model variation is the latent class factor analytic (LCFA) model (Magidson & Vermunt, 2001) and is referred to as FMM-1. In this model, the only parameter that changes across classes is the factor mean, which is indicated by the subscript k on α. The item thresholds and factor loadings are held invariant across classes, suggesting that the disorder is being measured the same way across all classes. The factor covariance matrix, Ψ, is fixed at zero, indicating that there is no within-class heterogeneity in the disorder. Figure 2a shows an example plot of the factor means versus the frequency for four classes. The height of the bars in the plot represents the percentage of the sample in that class. Class Four has the highest factor mean as α₄ is further along the x-axis, but has the fewest members as the bar for Class Four is lower than the other bars. In Figure 2a, the factor distribution is shown as being strongly non-normal and discrete. In this plot, bars are used to mark the factor means instead of a distribution because the factors have no variance. This distribution of the factor is flexible because it does not assume a specific statistical distribution of the factor, such as the normal distribution, and can therefore be considered non-parametric (Muthén, 2006). This plot suggests that the only difference between individuals arises due to having different amounts of the disorder and that there are only a set number of amounts that individuals can have, which are the number of classes. It is up to the researcher to decide whether the classes in this model represent qualitatively different types of individuals or if there is a single non-normal factor distribution based on model interpretation and substantive theory. We refer the reader to Bauer and Curran (2003a) for a further discussion about whether classes represent different types of individuals or a non-normal factor distribution. Note also in Figure 2a plot that the mean of the factor in the first class is fixed to zero. This is done for identification purposes and to help set the metric of the factor distribution. In the model diagram for FMM-1, shown in Figure 1d, the latent class variable points to the factor, and not directly to the items, indicating that class membership is based on each individual’s location on the factor and that there is no class-variation in the item thresholds.

Figure 2.

Example Factor Distribution Plots. (a) FMM-1with four classes, (b) FMM-2 with two classes.

The second model variation is the FMM-2, also called a mixture factor analysis (McDonald, 1967, 2003; Yung, 1997). The FMM-2 is similar to the FMM-1 except that instead of setting the factor variances and covariances to zero, they are now freely estimated in each of the classes. Figure 2b shows an example plot of the factor distribution for two classes. In the FMM-2, the classes are now represented as distributions, rather than bars as in FMM-1, because the factors have variance. This indicates that there are many possible amounts of the disorder an individual can have, or said another way, that there is heterogeneity within class. Like the FMM-1, the FMM-2 can also be seen to represent a non-normal factor distribution, but the FMM-2 is a parametric representation of the non-normal factor distribution. The FMM-2 is a parametric representation because within latent class, the factor is assumed to be normally distributed, but when combined, all of the latent classes form a non-parametric approximation. For example, in Figure 2b, each of the normally distributed classes models one of the two peaks in the bi-modal distribution of the factor. Similar to FMM-1, the researcher must decide if these classes represent qualitatively distinct classes or if the classes are modeling a non-normal factor distribution. The model diagram of FMM-2 in Figure 1e is almost the same as the FMM-1 except that there is now an arrow pointing into the latent factor, which indicates a residual so that the within-class factor variance is now being modeled.

In the third model variation, FMM-3, the factor loadings are invariant, while the item thresholds and factor covariance matrix are allowed to change across classes. Also, the factor mean is set to zero for identification purposes and so does not appear in the equations in Table 1. The factor mean is set to zero in the remaining model variations. Figure 1f, which shows the model diagram for FMM-3, is different than the previous two model diagrams because the arrows starting from the latent class variable now point to the items rather than the factor. This shows that the item thresholds are changing across classes, which implies that the classes are now based on the responses to those items rather than the factor means and variances, as was seen in the previous two models. This suggests that one would use the FMM-3 in cases where differences between individuals are thought to arise from differences among the responses to the items rather than differences on the factor. In FMM-3, the factor covariance matrix is freely estimated in each class. Having a different factor covariance matrix for each class implies that there are different amounts of heterogeneity within each class. For example, a class that has low probabilities of endorsing any symptom of a disease might have little or no variance because individuals have none to almost no symptoms while a class with high probabilities of endorsing any symptom of a disease might have more variation because individuals might have a greater range of symptoms and impairment.

The fourth model, FMM-4, is the least restrictive model in terms of invariance of the parameters. The item thresholds, factor loadings and factor covariance matrix are all allowed to vary across classes. Because all of the measurement parameters are freely varying across classes, this suggests that the factor in the model may not be measured the same way across classes, or, phrased differently, there is a potentially different factor within each class. One would use the FMM-4 when it is believed that there are distinct subpopulations of individuals that have different interpretations of the factor. For example, when examining attention-deficit hyperactivity disorder (ADHD), one can think of two different subpopulations of individuals with ADHD. The first class is those individuals who have inattention-only ADHD and would have a factor that is measured only by inattention items on an ADHD diagnostic instrument. The second can be those individuals showing only hyperactivity symptoms and have a factor that is measured only the by the hyperactivity items on an ADHD diagnostic instrument.

FMM and Measurement Invariance (MI)

The FMM variations presented above differ in terms of how much measurement invariance (MI) is present. The amount of MI can have important implications for how a FMM is interpreted, specifically whether or not the same factors are being measured in each latent class. Several authors have discussed the presence of MI in FMMs (Lubke & Muthén, 2005; Lubke & Neale; 2006, 2008), and so this will not be discussed in detail here except to highlight how MI can impact the interpretation and model fit of FMMs.

In FMM-1 and -2, the factor loadings and item thresholds are invariant across classes, suggesting that the interpretation of the factor remains the same in each class or, put another way, the factor retains the same meaning at both the low and high values in the population. In these two variations, the latent classes are used to model the non-normality of the factor in the population. For FMM-1, Figure 2a, which plots the factor distribution for an example with four classes, shows that the factor is categorical with each latent class representing a category. For FMM-2, Figure 2b, which plots the factor distribution for an example with two classes, shows that the factor is continuous, but non-normal. The factor in a FMM-2 is a mixture of normal distributions located at different points on the factor distribution, and each normal distribution is a latent class.

In FMM-3, the item thresholds are non-invariant, while in FMM-4 both the item thresholds and the factor loadings are non-invariant. In these model variations, because the item thresholds are non-invariant, the same factor interpretation may not apply to the whole population. Instead, there is the potential for a different factor, with a different interpretation, in each latent class. The implication of this is that there are several populations, represented by the latent classes, which may have their own factor interpretation.

In our experience, the FMM-1 and -2 often do not fit real data well because the specification of invariant factor loadings and thresholds are likely to be too restrictive for certain items. In these two models, the factor loadings influence both the item mean, which changes over classes for an item j as a function of τ_j + λ_j*α_k, and the item correlation between item j and item l within class, which is λ_j*ψ* λ_l. Item means are not likely to change over classes as function of τ_j+ λ_j*α_k, but instead change as a function of τ_jk. Thus, it is unlikely that α_k is the only parameter that creates changes across classes in item means for these two models. Furthermore, it is because the factor loading has a connection between both the item mean changes over classes and the item correlation within-class that FMM-1 and -2 seldom fit real data well. These issues suggest that the interpretation of the FMM-1 and -2 associated with invariant factor loadings and thresholds will most likely not be appropriate in practice due to lack of measurement invariance and should be adjusted by incorporating measurement non-invariance as in FMM-3 and -4.

FMM: Model Building and Comparison

Because FMMs are relatively new to the literature there is a dearth of writing about the steps to build a FMM, but general guidelines for how to fit them are offered in several papers (Muthén, 2006; Muthén & Asparouhov, 2006; Muthén, Asparouhov, & Rebollo, 2006). In each of these articles, the authors analyze their data using LCA, FA, and FMMs and then compare the fit among these three types. None of these articles provide instruction on how to construct the FMMs. Specifically, no information is given on how to decide on the number of classes and factors or how to pick among the different variations of the FMM. This paper offers an explicit strategy for building FMMs, which is summarized in Figure 3.

Figure 3.

Outline of FMM Model Building Strategy.

The first step is to fit LCA models with increasing number of classes and FA models with increasing number of factors (Step 0 in Figure 3). The LCA and FA models can be seen as special cases of the FMM. LCA is a special case of FMM in which the factor covariance matrix is zero. FA can be thought of as a FMM with one latent class to which every individual in the sample belongs. The fitting of both LCA and FA models to the data is suggested to serve as a comparison in Step 4a to the FMM to investigate if there is a need for both classes and factors in the same model and to aid in the determination of when to stop fitting FMM models to the data as outlined below.

The next step is to fit a FMM with two classes and one factor, and in subsequent models increase the number of classes (Step 1 in Figure 3). After this, the number of factors would be increased to two, and the classes would once again be increased in subsequent models (Step 2 in Figure 3). This pattern of increasing the number of classes and then the number of factors would be repeated. The question arises: at what point does one stop increasing the number of classes and factors? In several papers we have reviewed, the strategy to decide on the number of classes and factors has been to take the best fitting number of classes from a LCA and the best fitting number of factors from a FA and combine them to form a FMM. After this is complete, no further investigation is conducted to see if there is a need for a smaller number of classes and factors. This practice is highly discouraged because having both factors and classes in the model may reduce the need for a greater number of classes and factors. For example, if a LCA solution has many classes that are parallel to one another, which is thought to model heterogeneity, then adding one factor will likely reduce the need for the same number of classes because the factor will now model that heterogeneity. Instead, it is suggested that the number of classes from the best fitting LCA model and the number of factors from the best fitting FA model be the end point of combinations of classes and factors in model building (Step 3 in Figure 3). Steps 2–3 should be applied to all of the FMM variations. Once this is complete, the best FMM model for the data will be selected (Step 4 in Figure 3).

A known issue with mixture models, including LCA and FMMs, is the difficulty in selecting the appropriate number of classes, called class enumeration. Several authors have discussed this issue previously, including Nylund, et al. (2007) and Tofighi and Enders (2007), among others, and will not be discussed in detail here. Briefly, despite various suggestions, there is no commonly accepted methodology on how to compare models with differing numbers of classes (Nylund, et al., 2007). When considering a plausible set of models it is wise to utilize a combination of statistical and substantive model checking (Muthén, 2003), which is the strategy that is used in this paper. Since the standard chi-square difference test (likelihood ratio test, LRT) cannot be used with mixture models (Machlan & Peel, 2000), other methods must be used to determine class enumeration. These include alternative chi-square difference tests such as the Vuong-Lo-Mendell-Rubin test (LMR-LRT; Lo, Mendell, & Rubin, 2001) and the parametric bootstrapped LRT (BLRT; McLachlan, 1987), and information criteria, such as the Bayesian Information Criterion (BIC; Schwarz, 1978).Nylund et al. (2007), which considers the performance of statistics and indices mentioned here, recommend using the BIC and LMR to narrow the number of models under consideration and then include the BLRT for a smaller set of model comparisons due to the computational demands of the BLRT. When comparing FMMs with the LMR and BLRT, only models that have the same parameterization, but differing numbers of classes can be compared. For example, a FMM-2 with two-class and one-factor can be compared with model with a FMM-2 with three-classes and one-factor, but not to a FMM-4 with three-classes and one-factor. In order to determine the appropriate number of classes, this paper follows the strategy suggested in Nylund et al. (2007), but also examines the substantive interpretation of the models, using profile plots, once the BIC and LMR have been used to winnow down the number of models under consideration.

The example will apply the strategy outlined above to build the FMM. Once a best fitting FMM has been selected, it is important to compare this model to the best fitting LCA and FA models to see if a more parsimonious solution can provide a better fit and explanation of the data (Step 4a in Figure 3). This is similar to the “best” candidate approach outlined for the Dimensional-Categorical spectrum in Masyn et al. (2010). Because the LRT cannot be used for comparing among the different model types (LCA, FA and FM), model comparison will be based on information criteria, with the lowest value indicating the best fitting model type, and substantive interpretation.

Conduct Disorder Example

This example examines the underlying structure of conduct disorder (CD) in interview data from a population-based sample of Finnish twins that were oversampled for familial alcoholism risk. The study, called FinnTwin12 (FT12; Rose et al., 2004), is longitudinal, but data for this illustration are from the first follow-up at age 14. In total, there were 1786 children in the study with about an equal number of boys and girls. The analysis focused on interview reports of thirteen dichotomous symptom items measuring CD that are from the Child Semi-Structured Assessment for the Genetics of Alcoholism, Adolescent version (C-SSAGA-A), which was developed by the Collaborative Study on the Genetics of Alcoholism (COGA; Kuperman et al., 2001). Because data from co-twins cannot be considered independent observations, the relatedness of the twins was handled by correcting the standard errors using the Type = Complex option in Mplus. The Type = Complex option uses a sandwich estimator to obtain standard errors which take into account the non-independence of the twins.

In order to obtain a diagnosis of CD, three or more symptoms must be present. In this sample, 56% of children reported no symptom presence while 12% of the sample reported having three or more symptoms present and, therefore, met criteria for a CD diagnosis. Symptom presence ranged from 0.1% (Is physically cruel to animals) to 25% of the sample (Has ever been suspended from school). For a more extensive description of the interviewed sample and analysis of CD in these 14 year-old Finnish twins see Rose et al. (2004).

Based on the fit results in Table 2 and substantive theory, the three-class LCA was chosen as the best LCA model. The two-class LCA had a lower BIC value than the three-class model, but the BLRT p-value indicated that the three-class model was a better fitting model than the two-class model.

Table 2.

Conduct Disorder Example: Model Comparison Results (n=1758)

Model	Log- likelihood	Par.	BIC	LMR p-value	BLRT p-value
Latent Class Analysis
One-Class	−5018	13	10062
Two-Class	−4586	27	9374	0	0
Three-Class	−4540	41	9387	0.33	0
Four-Class	−4524	55	9460	0.095
Five-Class	−4513	69	9543	0.132
Factor Analysis
One-Factor	−4561	26	9317
Two-Factor	−4561	27	9324
Factor Mixture Analysis
2-Class, 1-Factor
FMM-1	−4586	27	9374	0	0
FMM-2	−4537	28	9284	0.235	0.04
FMM-3	−4536	41	9379	0.029	0
FMM-4	−4526	53	9449	1	0
3-Class, 1-Factor
FMM-1	−4540	41	9387	0.034
FMM-2	*
FMM-3	−4523	55	9481	0
FMM-4	−4496	81	9600	1

Note.

^*Log-likelihood not replicated; Par. = number of estimated parameters; BIC = Bayesian Information Criterion; LMR = Lo-Mendell-Rubin test; BLRT = Bootstrapped Likelihood Ratio Test.

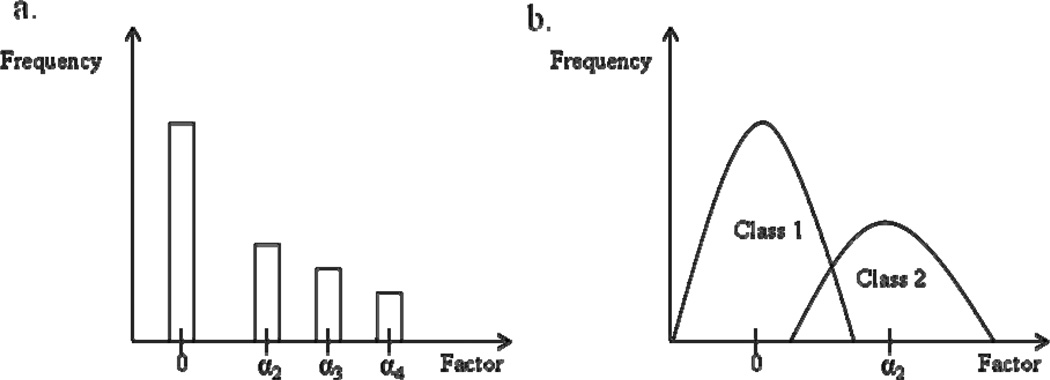
Figure 4 shows the item profile plot for the three-class solution. Class Two, 69% of the sample, has low symptom presence as indicated by low item endorsement probabilities. Because of the large size of the class and low symptom presence, this can be considered the asymptomatic class. Class Three, 26% of the sample, is defined by the items relating to suspension, lying, and truancy; with the other items having relatively low probabilities of symptom endorsement, 0.30 or lower. Potentially, some individuals in this class may meet criteria for a CD diagnosis. The first class, 5% of the sample, also has high probabilities of suspension and lying, similar to the second class, but also has high endorsement probabilities of running away, property destruction, forcing someone to participate in sexual activities, and starting fights. This class can be thought of as those individuals that are likely to meet criteria for CD.

Figure 4.

Conduct Disorder Example: Three-Class Latent Class Analysis Profile Plot.

For the FA models, a one-factor model with all thirteen of the conduct disorder symptoms loading on the factor and models with multiple factors based on substantive theory were fit to the data. When comparing the fit results of the one-and two-factor confirmatory models in Table 2, the log-likelihood is identical, but the one-factor model has one less parameter than the two-factor model, making it more parsimonious. This means that the BIC is lower for the one-factor model than the two-factor model. Since the one-factor model had a lower BIC value, it was chosen as the best fitting FA model. Normally, when comparing FA models one would use more typical indices of model comparison such as the CFI, RMSEA and SRMR, for example. For presentation purposes, we chose not to include these, and instead only present fit indices that were comparable among the different models types, LCA, FA, and FMM. But, we suggest that when one compares different FA models to examine these typical fit indices.

The bottom part of Table 2 presents results for the FMMs. Models with one factor and one to three classes were fit to the data, based on the results of FA and LCA. In Table 2, the FMM with the lowest BIC value is the two-class, one-factor FMM-2, with a value of 9284. But, for this model the LMR p-value is greater than 0.05, which indicates that a one-class, one-factor model should be chosen over this model. The next lowest BIC value in the table is 9374, which is 90 points higher than the lowest BIC value. But, additional models have BIC values that are not much higher, such as the two-class, one-factor FMM-3. For these FMMs, the LMR p-value is less than 0.05, which indicated that the two-class FMM should be chosen over the one-class model. Because there was no agreement of which model was the “best” FMM based on the BIC and the LMR p-value, the BLRT p-value was examined in the four models with the lowest BICs. In these four FMMs, the BLRT p-value was lower than 0.05 indicating that a two-class FMM should be chosen over a one-class solution. Based on these results, the two-class, one-factor FMM-2 is chosen as the “best” candidate FMM. It has the lowest BIC and the substantive interpretation of the model made the most sense.

In addition to being the best fitting model, the two-class, one-factor FMM-2 also makes the most sense for the data. The two-class, one-factor FMM-2 implies that there is one underlying latent factor of conduct disorder that has a non-normal distribution. The non-normal distribution is bi-modal with each peak being a latent class. While it can be argued that a three-class FMM might allow for better differentiation among classes, in this example the third class is a spurious class as it is comprised of only 1% of the sample and was not substantively meaningful. The FMM-1 is also unsuitable for this example because it implies that all individuals within a class are the same, which suggests that individuals in the CD class have no heterogeneity. This is unlikely to be correct as individuals with CD are not homogenous in terms of the symptoms they have. In FMM-3 and -4, the item thresholds change across classes suggesting that one of the classes endorses the symptom items at consistently different rates than the other class, independent of their factor scores. This suggests that the observed differences between classes are not entirely due to differences in the factor (Lubke & Muthén, 2005) indicating that differences between the classes are likely qualitative rather than quantitative. In this example, those individuals in the class that has higher endorsement rates of the symptom items, Class Two, also have higher factor scores suggesting that differences between the two classes are not independent of the factor. Therefore, we chose two-class one-factor FMM-2 as the best fitting model.

Table 3 displays the parameter estimates for the two-class, one-factor FMM-2 solution. The top part of the table shows the factor loadings (λ) and the item thresholds (τ), and the bottom part of the table show the factor mean (α) and factor variance (ψ) in each class. Notice that both the factor loadings and item thresholds are equivalent across classes and that the only parameters that are changing across classes are the factor mean and variances, which is the specification of the FMM-2. The CD symptoms all load on the factor significantly with the loadings ranging from 0.26 to 0.90. The loading for the symptom relating to whether an individual is consistently truant from school was fixed to one to identify the model and to set the scale of the factor. All the symptoms load on the factor suggesting that this is a general CD factor. The first class has the factor mean fixed to zero for identification and the second class has an estimated factor mean of 6.42, which suggests individuals in Class Two have higher factor scores for the CD factor. Possible interpretations of the classes are that Class One is a low or no CD symptom class and Class Two is a symptomatic CD class because the factor mean of Class Two is higher than Class One. The factor variance in Class One is not significantly different from zero, which agrees with the interpretation that Class One is a low or no CD symptom class as individuals that do not have CD are likely to not have many symptoms of CD and have will have little variation in CD symptoms. Class Two has a significant factor variance of 1.41 suggesting that CD is heterogeneous within this class, which further suggests that this class is likely composed of those individuals that have CD symptoms. Class One is the largest class with about 57% of the sample and Class Two is the smallest class with 43%. The class proportion supports the idea that Class One is a no CD symptom class as 56% of the sample reported not having any CD symptoms. For Class Two, the class proportion suggests that this class is not purely composed of individuals who have a CD diagnosis as the class proportion of 43% is much higher than the CD diagnosis rate of 12% in this sample. Instead Class Two, might be thought of as a class of individuals who have symptoms of CD.

Table 3.

Parameter Estimates for the Two-Class, One-Factor FMM-2

	Factor Loading (λ)		Item Threshold (τ)
Items	Class 1	Class 2	Class 1	Class 2
Suspend	0.90*	0.90*	0.66*	0.66*
Expelled	0.47*	0.47*	5.45*	5.45*
Stolen	0.36*	0.36*	2.35*	2.35*
Runaway	0.47*	0.47*	2.25*	2.25*
Lie	0.64*	0.64*	1.23*	1.23*
Fire	0.81*	0.81*	4.64*	4.64*
Truant	1.00a	1.00a	2.61*	2.61*
Property	0.44*	0.44*	2.89*	2.89*
Animal	0.42*	0.42*	7.59*	7.59*
Sexual	0.40*	0.40*	2.45*	2.45*
Fights	0.50*	0.50*	2.69*	2.69*
Weapon	0.26*	0.26*	5.48*	5.48*
People	0.57*	0.57*	3.80*	3.80*
Facto Mean (α)	0a	6.42*
Factor Variance (ψ)	12.27	1.41*

Note.

^* p < 0.05;

^afixed parameter

In addition to examining the parameter estimates, another way to aid in interpreting FMMs is through a profile plot that shows the probability of item endorsement at the class specific factor mean for each class. For the FMM-2, the probability of endorsing item u_j for an individual in class k, or in the case of the conduct disorder example, having symptom u_j for an individual in class k is:

$$P(u_j=1|C=k)=\frac{1}{1+e^{-(-{\tau }_j+{{\lambda }_j}^{*}{\alpha }_k)}},$$ (6)

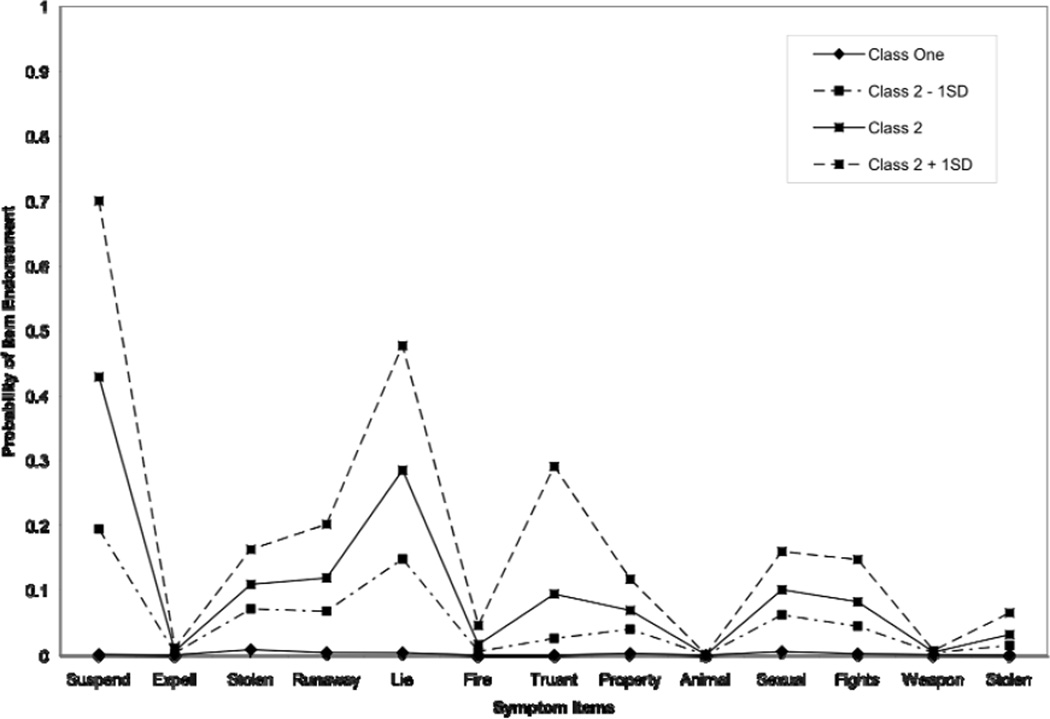
where τ_j is the item threshold, λ_j is the item factor loading, and α_k is the class specific factor mean. Figure 5 shows the profile plot for the two-class, one-factor FMM-2 solution. Class 1 is the lowest line on the profile plot, with almost all items having low probabilities of symptom endorsement, which supports the idea that individuals in this class are likely to not have any symptoms of CD. While this class is similar in its interpretation to the lowest class in the three-class LCA, the percentage of individuals in the low class differs between the two solutions suggesting that the latent classes from a LCA and a FMM are not the same. Also, the probabilities of item endorsement are lower, almost zero, in the FMM and the class proportion in the FMM is similar to the proportion of individuals in the sample that do not endorse any items, which further suggests that the low class in the FMM solution may be a true asymptomatic class. Class 2 has slightly elevated probabilities of endorsing the symptoms related to suspension, lying, and truancy, but these probabilities are still small. This class is similar to the second class in the three-class LCA solution, but with smaller item endorsement probabilities and a larger class proportion.

Figure 5.

Conduct Disorder Example: Two-Class, One-Factor FMM-2 Profile Plot. SD = standard deviation.

Notice that there are bands around Class 2 showing what the item endorsement probabilities are if an individual is one standard deviation away from the factor mean (i.e. if an individual has a lower or higher factor score than the mean of the factor). The first class does not have bands around the item profile because the factor variance in this class was non-significant. The bands around the factor mean of the second class give an idea of the variability within each class. For example, for the symptom item relating to suspension there is a great range of endorsement (0.20 to 0.70) once an individual is one standard deviation away from the factor mean. But, for the symptom item relating to expulsion, there is little variation in this item’s probability of endorsement as evidence by the bands being very close to the factor mean for that item.

Now that the “best” candidate model has been selected for each of the three model types, LCA, FA, and FMA, a comparison can be made among these “best” candidate models to see which one best describes the data. One way to decide between the models is to examine the BIC for the lowest value. For this data, the two-class, one-factor FMM-2 has the lowest BIC. Another way to decide between the models is to examine what each model implies about the underlying structure of CD in this population. The three-class LCA model implies that the underlying structure of CD is categorical with three categories, which are the three classes in the solution.

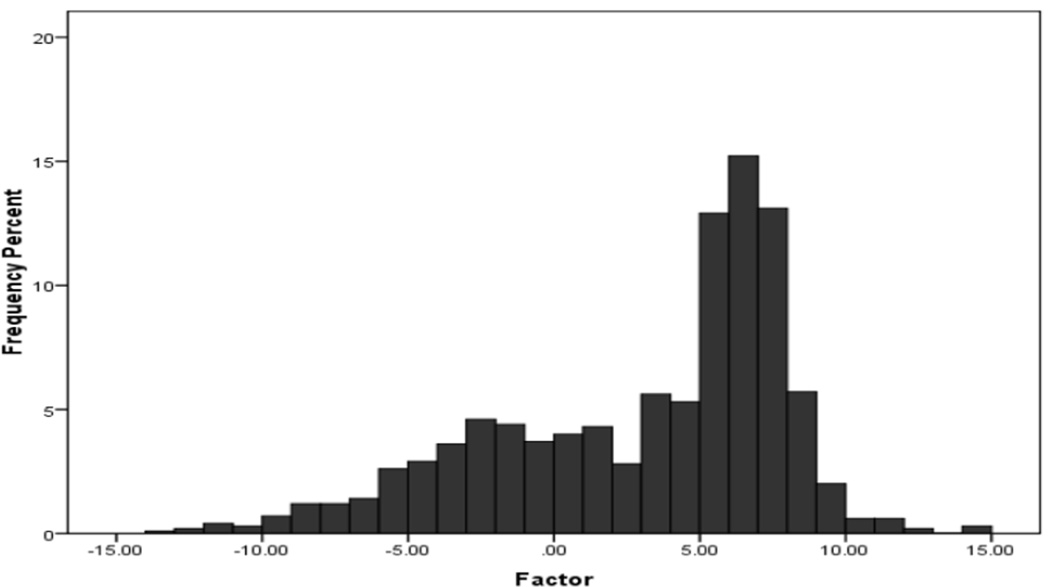
The one-factor FA solution implies that the underlying distribution of CD is continuous and normally distributed. The two-class, one-factor FMM-2 also implies that there is one underlying continuous factor of CD because of the class invariant item thresholds and factor loadings. But, unlike the one-factor FA, the distribution of the factor in FMM-2 is non-normal. The distribution of the factor in the FMM-2, shown in Figure 6, is a bi-modal distribution with a small peak at about 0 and a taller peak at about 6.5. It is these peaks and the distributions around them that form the mixtures in the FMM-2 solution. The first latent class is the small peak at the bottom of the plot with the wide distribution around it. The second class is the normal distribution further up in the plot. By having two latent classes, the FMM can model the non-normality of the factor more precisely than a FA can. Based on the results of the BIC and comparing what each model implies about the underlying structure of CD, the “best” model for this data is the two-class, one-factor FMM-2 because it models the non-normality of CD better than the other models. For an additional example with multiple factors see Clark (2010).

Figure 6.

Conduct Disorder Example: Two-Class, One-Factor FMM-2 Factor Distribution Plot.

Discussion

Despite the progress that has been made with FMMs in recent years, their use is still not prevalent. One reason, which this paper seeks to remedy, is the lack of didactic examples explaining the FMM and a set of clear steps for building a FMM, including how to decide on the number of classes and factors, and how to compare the FMM to other appropriate models. Second, FMMs can be difficult to interpret, especially when there is a lack of measurement invariance. Third, FMMs can be difficult to fit in practice because most instruments are not designed to capture both qualitative and quantitative differences among individuals.

The didactic example shed light on some issues and challenges that arise when conducting a factor mixture analysis. The example showed how difficult it can be to decide between a FMM and other appropriate models since there is often no clear “winner” based on statistical tests and indicators. The decision between different types of models must be made based on what each model implies about the underlying structure and whether that can be justified substantively. Additionally, a model should not be considered the “winner” unless there is validity evidence for the model. Validity evidence can include replication of the model in an independent sample and examining how background variables relate to the model. Bauer and Curran (2003a, 2003b, 2004) discuss this issue in detail and suggest how validation can be carried out in practice.

Despite the lack of didactic writings about the FMM, it is still an important analytic tool for conceptualizing the structure underlying psychological disorders. Using the FMM, does not force the conceptualization to be either categorical or continuous, as previous notions have suggested. Instead the FMM allows for the underlying structure to be modeled as both so that one can simultaneously classify individuals into groups and estimate the heterogeneity within those groups.

Appendix

Example Mplus Input and Model Statement Syntax for the Factor Mixture Model Variations

Input 1a: Factor Mixture Model 1 (FMM-1)

• -Two-classes, two-factors.
• -Estimating both factor means in each class.
• -Class invariant thresholds (τ), class invariant factor loadings (λ), factor covariance matrix is equal to zero (ψ = 0), class varying factor means (α_k).

DATA: File is example.dat; ! This is how to comment out text.

VARIABLE:

• Names are u1-u6; !List of variables in dataset.

• Usevariables are u1-u6;

  • ! Specifies which variables are to be used in the analysis.

• Categorical = u1-u6;

  • ! Specifies which dependent variable is categorical.

• Classes = c(2); ! Defines a latent class variable called c with two classes.

ANALYSIS:

• Type = Mixture; !Specifies doing a mixture analysis.

• Starts = 100 10; ! Specifies total number of random starts and number of final stage iterations.

• Process = 2 (STARTS);

  • ! Specifies that 2 processors are to be used in analysis and that random starts are to be spread out

  • !over the multiple processors.

MODEL:

• %Overall% ! Specifies that model below will be applied to both latent classes.

  • f1 by u1-u3; ! Defining a factor called f1 which is measured by items u1 to u3.

  • f2 by u4-u6;

  • f1-f2@0; ! Fixing factor variance at zero.

  • f1 with f2 @0; ! Fixing covariance between f1 and f2 at 0

  • [u1$1-u6$1] (1–6); ! Number in parentheses indicates fixing the threshold of this item to be the !same in class 1 and class 2.

- By default, the last class will have the factor mean fixed to zero.

Input 1b: Factor Mixture Model 1 (FMM-1)

• -Three-classes, one-factor.
• -Estimating all factor loadings.
• -Class invariant thresholds (τ), class invariant factor loadings (λ), factor covariance matrix is equal to zero (ψ = 0), class varying factor means (α_k).

MODEL: %Overall%

• f1 by u1-u6*; !* indicates that all factor loadings are to be freely estimated.

• f1@0;

• [u1$1-u6$1] (1-6);

%c#1% ! Indicates statements below apply to class 1 only.

• [f1*]; !* indicates the factor mean is freely estimated.

%c#2%

• [f1@1]; !Fixing factor mean at one.

- By default the last class will have the factor mean fixed to zero. Because all of the factor loadings are freely estimated, at least one of the factor means must be fixed for model identification and to set the metric of the factor. Here, Class 2 has the factor mean set to one.

Input 2: Factor Mixture Model 2 (FMM-2)

• -Two-classes, two-factors.
• -Class invariant thresholds (τ), class invariant factor loadings (λ), class varying factor covariance matrix (ψ_k), class varying factor means (α_k).

MODEL: %Overall%

• f1 by u1-u3;

• f2 by u4-u6;

• [u1$1-u6$1] (1–6);

%c#1%

• f1-f2;

• f1 with f2; !Specifying the correlation between f1 and f2

• [f1-f2@0];

%c#2%

• f1-f2;

• f1 with f2;

• [f1-f2*];

Input 3: Factor Mixture Model 3 (FMM-3)

• -Two-classes, two-factors.
• -Class varying thresholds (τ_k), class invariant factor loadings (λ), class varying factor covariance matrix (ψ_k), factor means fixed at zero (α_k = 0).

MODEL: %Overall%

• f1 by u1-u3;

• f2 by u4-u6;

• f1 - f2;

• f1 with f2;

• [f1-f2@0];

%c#1%

• f1 - f2;

• f1 with f2;

• [u1$1-u6$1];

%c#2%

• f1 - f2;

• f1 with f2;

• [u1$1-u6$1];

Input 4: Factor Mixture Model 4 (FMM-4)

• -Two-classes, two-factors.
• -Class varying thresholds (τ_k), class varying factor loadings (λ_k), class varying factor covariance matrix (ψ_k), factor means fixed at zero (α_k= 0).

MODEL: %Overall%

• f1 by u1-u3;

• f2 by u4-u6;

• [f1-f2@0];

%c#1%

• f1 by u2-u3;

• f2 by u3-u6;

• f1-f2;

• f1 with f2;

• [u1$1-u6$1];

%c#2%

• f1 by u2-u3;

• f2 by u5-u6;

• f1-f2;

• f1 with f2;

• [u1$1-u6$1];

-The overall statement (%Overall%) defines the factors and in the class specific statements (i.e., %c#1%, %c#2%) there is what looks like another definition of the factor, but this is not defining the factors. This allows the factor loadings to be freely estimated in both classes. Note that in the class specific statement, the factor definition starts with the second item and not the first. This is because in the overall statement where the factor is first defined Mplus defaults to fixing the loading of the first item to one. Since the loading of the first item is already fixed, it does not need to be set to be freely estimated in the class specific statement so the class specific statements begins with the second item.

Note. All of the example inputs and model statements above used dichotomous items, but factor mixture modeling can be conducted with other types of items as well with slight adjustments to the syntax above. Taking Input 3 as an example, the code can be adjusted for polytomous item by mentioning all the thresholds in the items. In the example below, the code has been adjusted for use with trichotomous items.

MODEL: %Overall%

• f1 by u1-u3;

• f2 by u4-u6;

• [f1-f2@0];

%c#1%

• f1 - f2;

• f1 with f2;

• [u1$1-u6$1];

• [u1$2-u6$2]; ! Mentioning second threshold of trichotomous item.

%c#2%

• f1 - f2;

• f1 with f2;

• [u1$1-u6$1];

• [u1$2-u6$2];

Also using Input 3 as an example, the syntax can be adjusted for continuous items by mentioning the mean of the items, rather than the threshold.

MODEL: %Overall%

• f1 by u1-u3;

• f2 by u4-u6;

• [f1-f2@0];

%c#1%

• f1 - f2;

• f1 with f2;

• [u1-u6]; ! Setting mean of items to be different across classes.

%c#2%

• f1 - f2;

• f1 with f2;

• [u1-u6];