Learning Stochastic Reward Distributions in a Speeded Pointing Task

Abstract

Recent studies have shown that humans effectively take into account task variance caused by intrinsic motor noise when planning fast hand movements. However, previous evidence suggests that humans have greater difficulty accounting for arbitrary forms of stochasticity in their environment, both in economic decision making and sensorimotor tasks. We hypothesized that humans can learn to optimize movement strategies when environmental randomness can be experienced and thus implicitly learned over several trials, especially if it mimics the kinds of randomness for which subjects might have generative models. We tested the hypothesis using a task in which subjects had to rapidly point at a target region partly covered by three stochastic penalty regions introduced as “defenders.” At movement completion, each defender jumped to a new position drawn randomly from fixed probability distributions. Subjects earned points when they hit the target, unblocked by a defender, and lost points otherwise. Results indicate that after ∼600 trials, subjects approached optimal behavior. We further tested whether subjects simply learned a set of stimulus-contingent motor plans or the statistics of defenders' movements by training subjects with one penalty distribution and then testing them on a new penalty distribution. Subjects immediately changed their strategy to achieve the same average reward as subjects who had trained with the second penalty distribution. These results indicate that subjects learned the parameters of the defenders' jump distributions and used this knowledge to optimally plan their hand movements under conditions involving stochastic rewards and penalties.

Introduction

The consequences of movements depend both on the movement plan and on the environment in which they are executed. Experiments studying visuomotor control often use deterministic environments in which there is no uncertainty about the location or the value of the movement target. Outside the laboratory, however, environments often change stochastically. On the highway, drivers in the lane next to you might change lanes without warning. Your estimate of the probability of this event determines how you position your car in your lane and the distance you maintain between cars. Environmental stochasticity significantly impacts the outcome of our movements and hence the motor strategies the brain should select.

It has been shown that humans can learn stochastic uncertainty inherent in or imposed on the sensorimotor system and integrate that knowledge in their movement plan in a statistically optimal way (Körding and Wolpert, 2004; Trommershäuser et al., 2005). However, Maloney et al. (2007) showed that optimal motor planning breaks down when costs and rewards are spatially fixed, but are awarded randomly.

Our task was designed to tie the stochasticity in the experimental environment to an ecologically reasonable causal generative model. Subjects pointed at a static target (“goal”) partly covered by three stochastic penalty regions (“defenders”). As subjects completed their pointing movements, each defender “jumped” to a position randomly drawn from a probability distribution anchored at its initial position. Subjects gained points if they hit the target unblocked by a defender; otherwise, they lost points. To perform optimally, subjects had to account for the probability distributions of each defender's jumps. They had to decide which side of the middle defender to point to and then select an aim point on that side. Thus, unlike in previous studies of sensorimotor decision making, our task included an explicit, binary decision much like choosing between two gambles in economic decision-making experiments, as well as an implicit, continuous estimate of the optimal aim point. This allowed us to address the question of whether explicit, binary decisions, which often fail to maximize expected gain in economic decision making (Kahneman and Tversky, 1979), can be optimal if framed as sensorimotor decisions, which often maximize gain when they involve implicit decisions in the estimate of aim points (Trommershäuser et al., 2003).

After ∼600 trials, subjects approached optimal performance in the first experiment. They mostly selected the “better” side of the target and adjusted their aim point within the chosen side to maximize their gain. We ran a second experiment to explore whether subjects learned a set of stimulus-action contingencies (“with this defender configuration, go there, because there you are least frequently caught”) or whether subjects generated representations of the defenders' jump distributions that would enable them to infer the optimal aim point even if the cost/reward structure was changed. We addressed this question by training subjects using one set of asymmetric penalties and testing their performance immediately after switching to a new asymmetric penalty distribution.

Materials and Methods

Apparatus

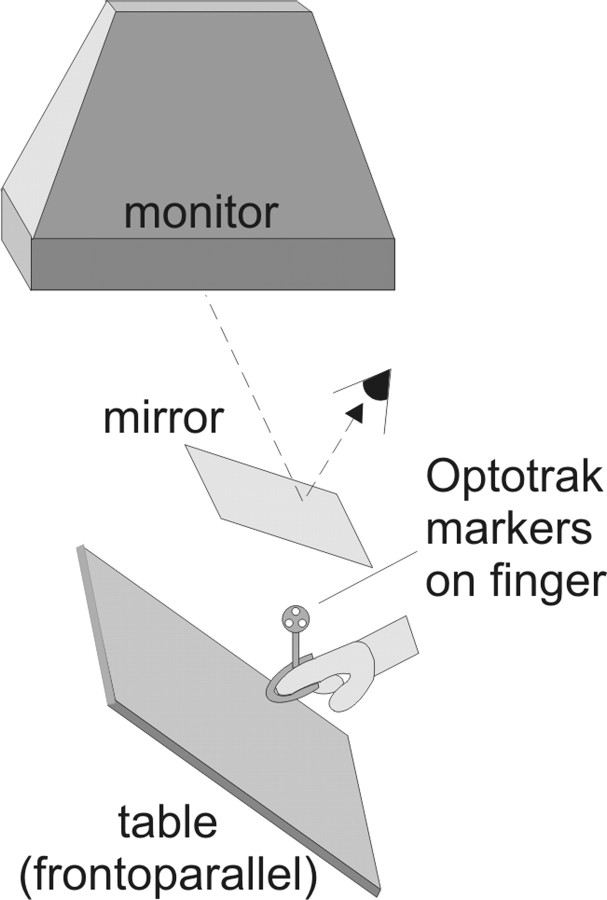
Both experiments were run on a custom workstation using Visual C++. Stimuli were presented in stereo on an NEC MultiSync (Tokyo, Japan) 1370 monitor (118 Hz; 1280 × 1024 pixel) that was facing downward toward a mirror slanted 20° upward from horizontal (Fig. 1), so that its virtual image coincided with a frontoparallel table below the mirror, at an effective viewing distance of 60 cm. The subjects' head position was fixed by a combined chin and forehead rest, and they viewed stimuli binocularly through StereoGraphics Crystal Eyes active-stereo shutter glasses at a refresh rate of 118 Hz (59 Hz for the view of each eye). Black occluders on the mirror hid any part of the monitor frame that would otherwise have been visible to the subject. A splint on the subject's right index finger was equipped with three infrared markers, the three-dimensional coordinates of which were sampled by a Northern Digital (Waterloo, Ontario, Canada) Optotrak at 120 Hz. This made it possible to extrapolate the coordinates of the real finger in space and render a virtual finger on the screen in real time so that the position of the virtual fingertip shown to the subject was coextensive with the real fingertip. When the metal splint on the finger made contact with a metal plate mounted on the frontoparallel table, a circuit was closed, allowing us to register when subjects touched the table.

Figure 1.

Set-up. A sketch of the mirror setup used for both experiments. Subjects viewed stimuli presented in stereo through the mirror, such that the stimuli appeared to be on the frontoparallel table. Optotrak markers mounted on the subject's right index finger allowed us to compute the location of the finger in the workspace and display a virtual image of the finger to the subject.

Stimuli and procedure

General stimulus and task description.

Throughout each experiment, stimuli were presented against a black background. A score indicator and a status bar were displayed on top and at the bottom of the visual display, respectively. These told subjects how many points they had earned and which proportion of the block had already been completed. As depicted in Figure 2b, subjects indicated that they were ready to start a trial by placing their virtual fingertip on a red cross on the right side of the visual display. The goal, a dim red rectangle oriented perpendicular to movement path, then appeared on the left side of the display. The distance between starting position and goal center was 15 cm, and the goal center could be located anywhere on a 30° arc around an imaginary horizontal line through the starting position (Fig. 2a). Whenever coordinates are given, we refer to the direction from starting cross to goal center as the “x-direction” and define the “y-direction” as perpendicular to it and lying in the same plane, with the coordinate system centered at the center of the goal (Fig. 2b). The goal was accompanied by a number of rectangular penalty regions. These defenders were as wide as the goal along the x-dimension (i.e., in movement direction) but covered it only partly along the y-dimension. After 750 ms, a beep go-signal was presented, indicating that subjects should start their pointing movement toward the goal. To make the pointing movement as ballistic as possible, subjects were constrained to complete the movement in <550 ms. Trials in which the finger left the starting cross before the go-signal or in which the pointing movements took longer than 550 ms were aborted and discounted, and an error message told the subject to wait for the beep or to speed up, respectively.

Figure 2.

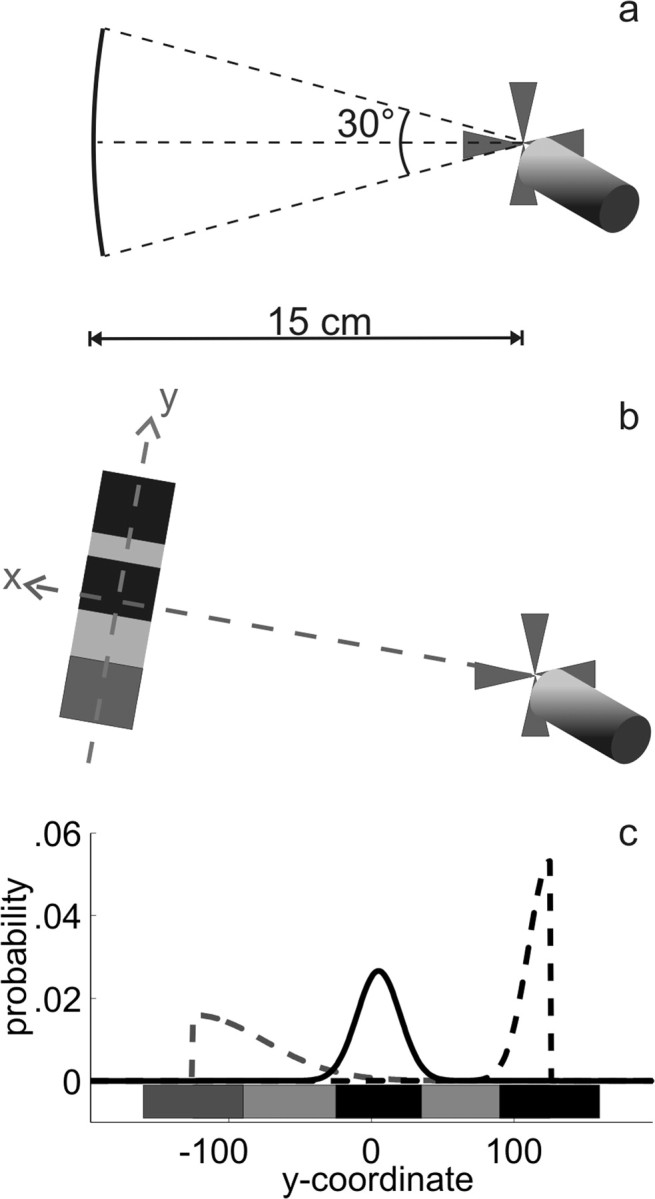
Stimuli. a, Each trial started when the subject touched a red starting cross at the right side of the display. The movement target (the goal) then appeared 15 cm from the starting point, centered on a randomly chosen position on the arc shown here. b, The rectangular dark red target (here, light gray) was accompanied by three rectangular defenders, the color of which indicated their “jump abilities” (see c). We will refer to the axis connecting starting position and target center as the x-dimension and the perpendicular axis in the table plane as the y-dimension. c, Jump distributions of the three defenders, superimposed on a sketch showing their starting positions in a standard size goal. Condition 1 is shown: the middle defender is at its leftmost starting position. In the other conditions, the middle defender and its jump distribution were closer to the right one. The jumps of the bright-red (here, black) defenders were drawn from Gaussians with a SD of 15 mm, and the jumps of the blue (here, dark gray) defender were drawn from a Gaussian with a SD of 50 mm. The jump distributions of the defenders at the goal borders were folded, so that jumps always went toward goal center, not away from it. Note that all measures given here (and in the following figures, whenever the x-axis shows y-coordinate without an explicit metric) are standard measures. The actual measures depended on subjects' SDs in the baseline task, according to which we scaled the stimuli as well as the parameters of the jump distributions. Because we chose the parameters to provide meaningful conditions given a standard endpoint variability of 10 mm in y-direction and subjects' endpoint variability in y-direction was usually four or five times smaller than that, the stimuli presented in the experiments were about four or five times smaller than our standard scale suggests.

When the finger touched down on the table after having left the starting cross, each defender jumped to a new position drawn randomly from the jump distributions shown in Figure 2c. Subjects were awarded points if they hit the goal without being blocked by a defender. They lost points if they missed the goal or were blocked by a defender. Several visual cues were provided to indicate success or failure on a trial. A small red cross was displayed where the finger had touched the stimulus, so that subjects could clearly see where they had hit. If subjects hit the goal without being blocked by a defender, the defenders exploded visually. If the subject's finger hit a defender, this defender spun around. If the subject either hit a defender or missed the goal (in either case incurring a penalty), the virtual finger shrank visually. In addition, the number of points earned in that trial was displayed at screen center, starting in the table plane and then floating upward toward the subject. Score and status bar were updated at the end of each trial. In both experiments, we used two different tasks within each daily session: an initial baseline task and the main experimental task.

Baseline task.

In the baseline task, the target was 20 mm wide and 36 mm tall and accompanied by two defenders. The defenders were bright-red rectangles centered at the top and bottom of the goal at the beginning of each trial. The top defender was 12 mm tall, and the bottom defender was 20 mm tall. When the finger touched down on the table after leaving the starting cross, the defenders jumped toward target center so that their outer borders landed exactly at the target borders. This left a space 4 mm high between the two defenders, centered 4 mm above the center of the target, hitting which was rewarded by 100 points. Subjects were told in advance that the defenders would always jump to the same positions and leave a gap between them, so that if subjects always went for this gap, they would get all available points. It was emphasized that accuracy was most important in this task, and subjects were encouraged to take their time planning the movement and to use the visual feedback given about their actual fingertip endpoint to maximize accuracy. The defender configuration was purposely chosen to have an optimal aim point that was clearly and unambiguously defined but did not coincide with the target center or the point halfway between the start position of both defenders (i.e., with a position at which subjects' visual localization ability may be specially enhanced).

Scaling the stimulus to each subject's endpoint variability.

We used the SD along the y-dimension of each subject's endpoint cloud in the baseline task at the beginning of each session as an estimate of the subject's endpoint variability along this dimension and scaled the height of the stimuli in the experimental task accordingly. In particular, we multiplied all stimulus dimensions (target and defender sizes as well as jump distribution widths) along the y-dimension with a scaling factor that was the ratio of the endpoint variability of the subject to a standard endpoint variability of 10 mm. That way, subjects with a large endpoint variability had taller stimuli than subjects with lower endpoint variability, so that the task was equally difficult for all of them. More importantly, the expected gain landscapes (functions expressing the expected total gain for movements aimed at different positions within the target; see below, Model of optimal movement planning) had the same shape for all subjects when specified in normalized units. This allowed us to average the distance between subjects' aim points and optimal aim points, their gains, etc. in a coherent way.

Main experimental task.

In both experiments, the standard goal used in the simulations assuming a 10 mm motor variability was 250 mm tall and 20 mm wide and accompanied by three defenders: two 70-mm-tall defenders centered at either border of the goal and one 60 mm tall, inside the goal (compare Fig. 2c). The size of the stimuli used in any given experimental session was scaled to subjects' endpoint variability as measured in the baseline block run at the beginning of that session and thus varied between subjects and sessions. Because subjects' endpoint variability was, on average, approximately five times smaller than the standard variability assumed in our simulations, so were the stimuli. Thus, the targets presented to the subjects were ∼50 mm tall, with defenders that were ∼14 mm tall at the bottom and top of the target and 12 mm tall inside the target. The middle defender could be centered at five different positions within the goal, yielding five different conditions (see below, Experimental parameters).

After movement completion, each defender jumped to a new position drawn randomly from a Gaussian distribution centered at its original position. Defenders differed in color according to the SDs of their jump distribution. The jump distributions of the middle and the top defenders had SDs of 15 mm, scaled according to the subject's endpoint variability, and both were colored in bright red. The SD of the bottom defender's jump distribution was 50 mm (also scaled to the subject's endpoint variability), and this defender was displayed in blue. To prevent defenders from jumping outside the goal, the jump distributions of the defenders at goal borders were “folded” such that each jump away from the target center was mirrored at the center of the jump distribution and converted into a jump toward the target center. Jump distributions are depicted in Figure 2c. When two defenders jumped such that they overlapped, one was presented slightly above the other, thus covering the parts of it where they overlapped. Which defender had “priority” was chosen arbitrarily, with the constraint that in those cases in which one defender carried a higher penalty, this one was always displayed on top.

Experimental parameters.

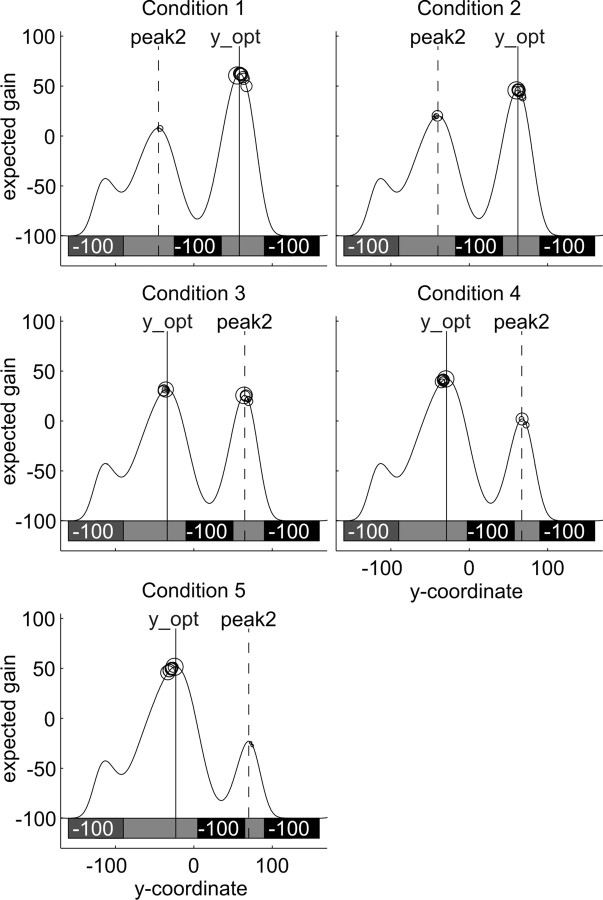
In experiment 1, possible starting positions of the middle defender were (in standardized y-coordinates) 5, 12.5, 20, 27.5, and 35 mm above the goal center. Hitting the target was rewarded by 100 points, whereas missing the target or being caught by a defender cost 100 points. Figure 3 shows the five conditions, together with the resulting expected gain landscapes for a hypothetical subject with an endpoint cloud SD of 10 mm. (For details on how the gain landscapes were calculated, see below, Model of optimal movement planning and Expected gain landscapes.). In experiment 2, possible starting positions of the middle defender were (in standardized coordinates) 5, 10, 20, 30, and 35 mm above the goal center. Hitting the target was rewarded by 200 points; missing it or being blocked by the middle defender cost 100 points. Penalties for being blocked by the top and bottom defenders were asymmetric. In one version of the task (version A), subjects were penalized 100 points if they were blocked by the top defender but were penalized 400 points if they were blocked by the bottom defender. In version B, the penalties were reversed (subjects were penalized 400 points if they were blocked by the top defender and penalized 100 points if they were blocked by the bottom defender). As shown in Figure 7, changing the penalties while keeping the defenders' start positions and jump distributions constant had a strong impact on the resulting expected gain landscape. To help subjects remember which defender had the high (400-point) penalty, we drew the defenders with faces: the two defenders who cost only 100 points were smiling, whereas the one costing 400 points had a grim expression.

Figure 3.

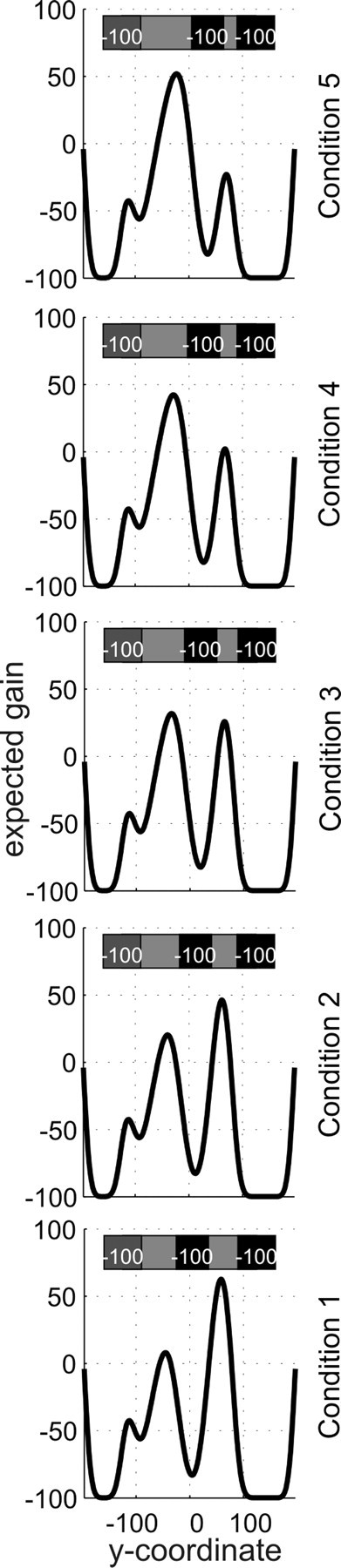
Gain landscapes in all five conditions of experiment 1. The expected gain (in points) changes as a function of where the movement planner aims. A sketch of the stimulus situation, the goal and the three defenders at their starting positions, is shown in the top part of each panel. As explained in the legend for Figure 2c, the y-coordinates given here are standard coordinates. Actual stimuli (and distribution parameters) were scaled to each individual's endpoint variability in the baseline task.

Figure 7.

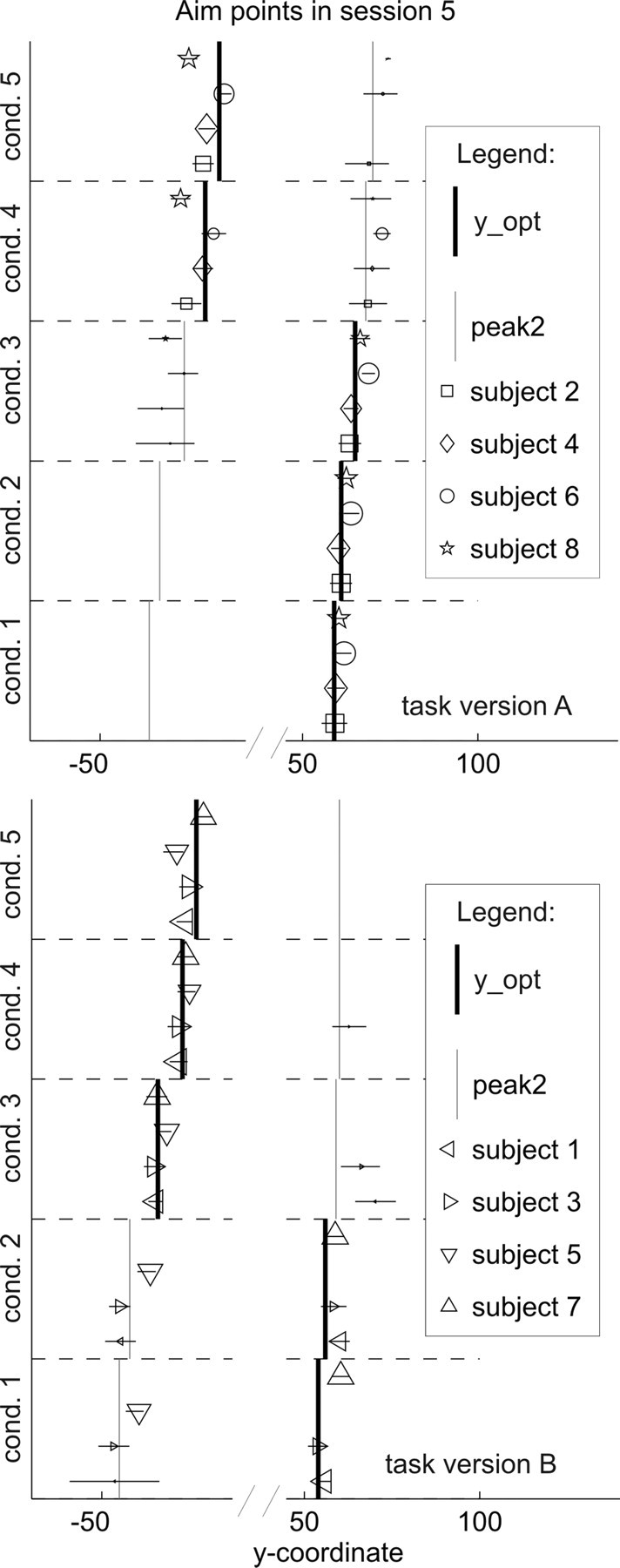
Subjects' aim points in session 5 of experiment 2: all conditions and both task versions. Marker size is scaled to the proportion of endpoints in the cluster around the depicted aim point. The x-axis is broken to show aim points in both games (both peaks of the gain landscape) while omitting the space between, where no subject ever aimed. Clearly, aim points fell close to the two maxima in the gain landscapes (indicated by the vertical lines). The majority of endpoints (indicated by bigger markers) were around the optimal aim point for most subjects and conditions. There were, however, individual biases toward one or the other side (e.g., subject 3 showed a clear preference for the left game, even in conditions in which the optimal game was the right one), and in conditions in which the two peaks of the expected gain landscapes were similar in height, most subjects showed a small proportion of sampling behavior (they occasionally played the game with the lower expected gain). Within one side, subjects' aim points followed the slight shift of the optimal aim point from condition to condition. The expected gain of subjects' aiming strategies in session 7 of experiment 2 can be seen in supplemental Figure S7 (available at www.jneurosci.org as supplemental material). cond., Condition.

Procedure.

Each session of the experiment started with a spatial calibration procedure to ensure that the stereo stimuli yielded a proper three-dimensional image, fitting the reference frame of the Optotrak, so that subjects saw their virtual finger where their real finger indeed was. We first determined the correct coordinate transformation from the reference frame of the Optotrak to the one of the monitor and the position of the subject's eyes relative to the monitor, using an optical matching procedure (Knill and Saunders, 2003). For this, we sequentially displayed a small red dot on 13 different positions on the monitor and temporarily removed the backing of the half-silvered mirror so that the subject could place an Optotrak marker where the dot appeared to be. This was done separately for the right and the left eyes and in two different depth planes. The three-dimensional position of each eye relative to screen center was calculated by minimizing the squared error between the three-dimensional position of the probe predicted by the estimated eye position and the measured three-dimensional position of the Optotrak marker. Validity of the calibration was tested by asking the subject to move the marker in the workspace and to check whether a red dot displayed at the estimated position of the marker seemed to be aligned with the real marker. Also, we ensured that the distance between the estimated eye positions was realistic. The second part of the calibration was to make sure that the visual finger appeared where the real finger was. For that, the virtual finger was presented on the screen, and subjects placed their right index finger, now equipped with a metal splint carrying three Optotrak markers, where the virtual finger seemed to be. After the transformation from the marker positions to the position of the virtual finger had been estimated, subjects moved their finger and verified that the virtual finger moved with it. Last, we closed the mirror backing and presented a cross-hair on six different positions on the table plane. Subjects touched the table such that they saw their virtual finger touch the center of the cross-hair. This way, we made sure that the finger touch points we recorded during the experiment matched with subjects' perceived touch points.

Sessions were subdivided into blocks of 100 trials each. The first session was dedicated entirely to training: subjects completed three to five blocks of the baseline task during which they could get used to the stimuli, the timing constraints, their virtual finger, and the movement itself, until endpoint variability decreased and settled on a low level. In the following sessions, subjects first received a “warm-up” block (100 trials of the baseline task) during which they could adjust to the task. A second block of the baseline task was then used to estimate their endpoint variability. After this, we changed to the experimental task. Experiment 1 comprised five 1 h sessions, one for training and four experimental sessions. The number of experimental blocks in one session varied from two to five, depending on how much time was left after calibration, warm-up, and baseline task, so that we got ∼1200 experimental trials from each subject. Experiment 2 started with one session for training, followed by four sessions of one version of the experimental task. In the last two of the seven sessions, subjects were given the other version of the experimental task (with the reversed defender penalties). Which version they started with was counterbalanced across subjects. The number of experimental blocks per session was held constant at three, so that, for each subject, we got 1200 experimental trials for the task version they started with, and 600 experimental trials for the other version.

Instructions.

To provide subjects with a generative model for the stochastic nature of the locations of the penalty regions, we introduced the target as the goal and the penalty regions as “defenders with different jump abilities” who would try to block the subjects from scoring. At the beginning of each session, subjects were informed about the payoffs associated with hitting the different regions and instructed to try and get as many points as possible. To increase motivation, we had individual as well as general high score lists, and subjects were encouraged to beat their “personal best” as well as the “absolute high score.” All subjects were naive to the purpose of the study. They were not told where to aim and received no information about the defenders' jump distributions in the experimental task. It was emphasized that the defenders would only jump the very moment the finger made contact with the table, so that it would be no use trying to be fast and hit the goal before the jump (the only chance to avoid the defenders would be to learn what their jump abilities were and then predict where they were least likely to jump to).

Subjects

Eight female subjects participated in experiment 1, and four female and four male subjects participated in experiment 2. All were students at the University of Rochester, right-handed, had normal or corrected-to-normal vision, and ranged in age from 18 to 29. None of the subjects participated in both experiments, and all subjects were naive to the hypotheses of the experiments. Subjects were treated according to the ethical guidelines of the American Psychological Association, gave their informed consent before testing, and were paid an hourly rate of $10.

Model of optimal movement planning

A model of optimal movement planning based on statistical decision theory, developed by Trommershäuser et al. (2003a,b), predicts which mean movement endpoint (x̄, ȳ) an optimal movement planner will choose, taking into account gains and losses assigned to the stimulus configuration and the subject's endpoint variability. In previous experiments, this variability has been found to follow a Gaussian distribution around the aim point (x̄, ȳ):

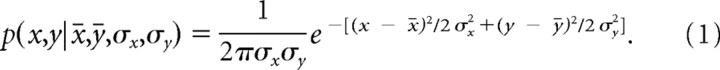In our experiments, subjects hardly ever missed the target along the x-dimension. Thus, only the endpoint variability along the y-axis was relevant to the outcome, and we can neglect the x-dimension in the following formulas. This simplifies Equation 1 to the following:

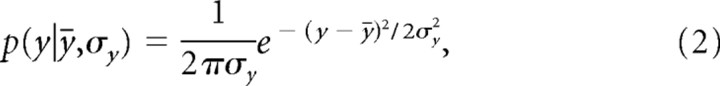where ȳ is the aim point, y is the movement endpoint, and σ_y is the SD of the endpoint distribution in y-direction, which we refer to as the subject's endpoint variability. Aim point and endpoint variability determine the probability that the movement ends at a certain endpoint.

In our task, there is a second source of uncertainty that also has to be taken into account, namely, the uncertainty regarding the locations of the defenders along the y-axis after their jumps. For each defender, his start position and jump distribution determine the probability that he will be at y after his jump. These probabilities, and the penalties associated with hitting each defender, as well as the rewards of hitting the goal unblocked by a defender, determine the gain G(y) associated with hitting a certain point y. A detailed derivation of how we compute G(y) can be found in the supplemental material (Appendix A, available at www.jneurosci.org as supplemental material).

The expected gain of aiming at ȳ can now be obtained by integrating over all endpoints y the gain of hitting them, multiplied by the probability of hitting them given aim point ȳ and endpoint variability σ_y:

An optimal movement planner that maximizes expected gain would thus aim at the optimal aim point y_opt at which the expected gain function has its maximum:

Expected gain landscapes

Figures 3 and 6 show the expected gain landscapes as a function of the average aim point ȳ in experiments 1 and 2, respectively, for a hypothetical subject with a standard endpoint variability of σ_y = 10 mm. The gain landscapes were derived assuming that subjects never missed in the x-direction (which they almost never did). The optimal aim point for each condition (y_opt) is the y-coordinate at which the expected gain landscape for that condition has its maximum. The optimal expected gain (EG_opt) is the expected gain of the optimal movement planner aiming at y_opt. In the same way, we determined the y-coordinate of the peak on the other side of the middle defender's starting position as the peak2 and the associated EG_peak2. Because we scaled the stimulus to each subject's endpoint variability in y-direction, the gain landscapes had the same shapes for all subjects, and therefore the standardized y_opt and peak2, as well as the associated expected gains, were the same for each subject and session.

Figure 6.

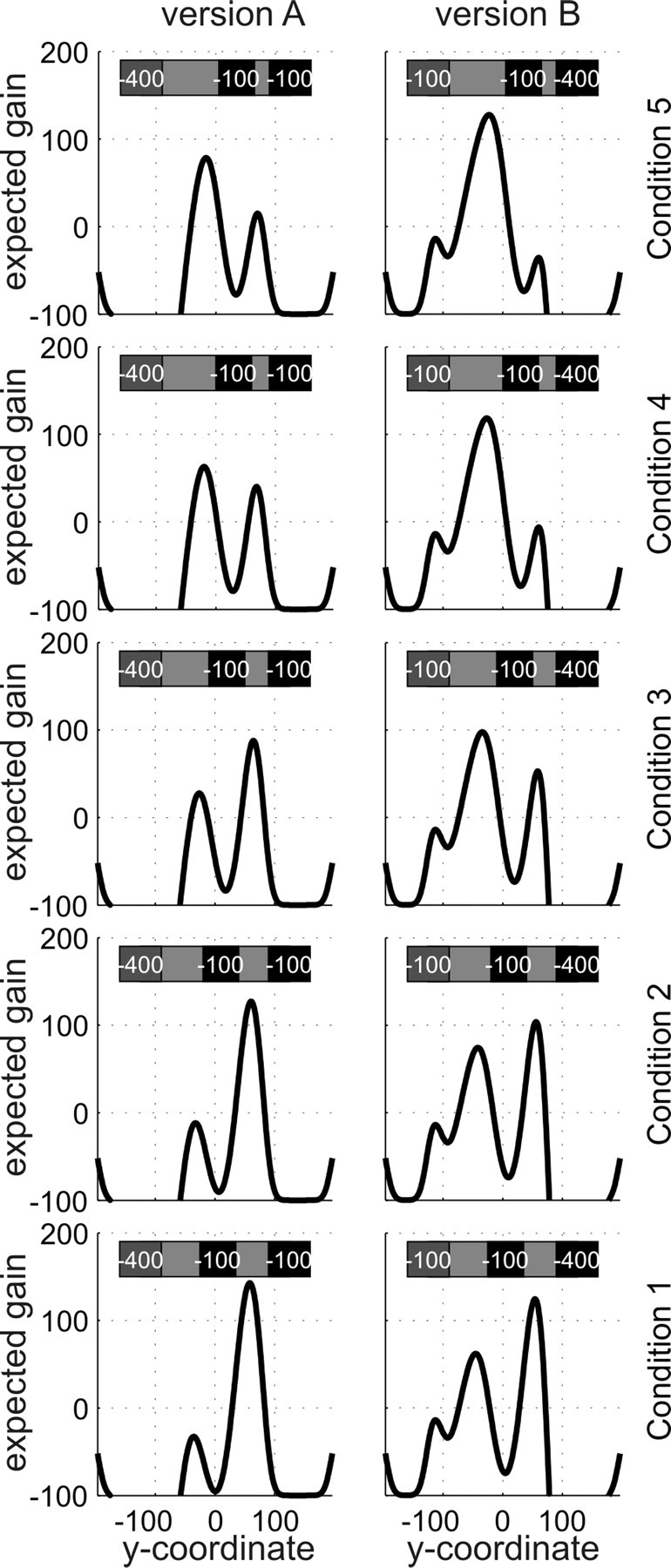
Gain landscapes in all five conditions and both versions of experiment 2. Conventions are as in Figure 3. As can be seen in the stimulus sketch in the top part of each panel, the two versions only differed in which of the defenders bore the higher penalty, but not in the starting positions of the defenders. Penalty values are printed on defenders only for illustrative reasons and were not there during the experiment. Instead, the −400 defender had a grim face, and the −100 defenders had smiling faces. A comparison of the expected gain landscapes in the left and right columns shows that changing the penalties from one version of the task to the other resulted in slight shifts of the peaks (barely visible at this scale) and affected the relative height of the local maxima such that in condition 3 the global maximum changed from one peak to the other.

The gain landscapes shown in Figures 3 and 6 were computed assuming that the endpoint variance in subjects' pointing movements measured in the baseline condition accurately represented their true variance. However, there is some uncertainty to our estimate of the subject's endpoint variance; therefore, we performed a resampling analysis to test the potential effects of errors in our measures on our estimates of subjects' true expected gain landscapes. Separately for each subject and session, we repeatedly estimated the model predictions, each time using a different estimate of the endpoint variability obtained via resampling the subject's endpoints in the baseline task (upscaled such that their SD before resampling fit with the 10 mm SD assumed by our model). From all the estimates, we then determined the mean and the 95% confidence interval borders for both the y_opt and the associated EG_opt. The re-sampling procedure arrived at the same y_opt in >95% of the cases, indicating that the y_opt is robust to small deviations from the estimated endpoint variability; we thus do not show confidence intervals around it.

The expected gain landscapes provided the basis for measuring the efficiency of the subjects' behavior and more particularly for decomposing inefficiencies in behavior to inefficiencies attributable to their explicit, discrete choice behavior (which side to point to) and inefficiencies in their implicit selection of continuous aim points within a chosen side.

Results

Baseline task performance

In the baseline task in experiment 1, SDs in the y-direction ranged from 0.11 to 0.32 cm, with a mean of 0.23 cm; in experiment 2, they varied between 0.14 and 0.26 cm, with a mean of 0.20 cm. Variability in x-direction was significantly larger in most cases but small enough that no subject missed the goal along the x-direction in >0.4% of the trials. We tested whether subjects' endpoints in the y-dimension followed a Gaussian distribution using a Lilliefors test (Lilliefors, 1967) on the baseline task data of every subject in every experimental session. Only 1 of 32 baseline task endpoint distributions in experiment 1 and 4 of 48 in experiment 2 differed significantly from a Gaussian. In neither experiment did the shape of the endpoint distribution differ significantly from a Gaussian more than once for a subject. We took these results as evidence that subjects' endpoint distributions can be modeled as Gaussian distributions. Supplemental Figure S1 (available at www.jneurosci.org as supplemental material) shows a typical endpoint distribution as found in the baseline task.

Experiment 1

Data analysis

The entire stimulus configuration for the main experimental task, including jump distributions, was scaled to match each subject's endpoint variability as measured in the baseline task of each session. The first step in the data analysis was therefore to rescale subjects' endpoint positions to the standard stimulus size used for computing the expected gain landscape. This normalized the stimulus configuration, endpoint measurements, and endpoint variability to a common scale across subjects and sessions.

In some cases, subjects' endpoints formed two clusters, one on each side of the target, corresponding to the gaps between defenders (for an example, see supplemental Figure S2, top panel, available at www.jneurosci.org as supplemental material). The clusters were nonoverlapping and could be easily classified as to which gap subjects were aiming for on each trial. On each trial, therefore, we were able to label which of the two gaps subjects selected for their pointing movement, which reflects their discrete choice as to which of two “games” to play [the top or bottom game (or right and left from the point of view shown in the figures)]. This allowed us to measure subjects' explicit choice behavior and how it evolved over trials. Computing the mean of each endpoint cluster enabled us to compare subjects' aim points with the aim points that would have been optimal in their chosen game.

Rather than measure a subject's performance in each condition and session by their actual gain, which can be highly distorted by chance, we computed the total gain for a subject's “strategy” in each condition and session. To do this, we computed a weighted average of the expected gain of the subject's aim points (using the values of the gain landscape at the aim point scaled by the proportion of trials in which the subject played the respective game). To calculate confidence intervals on our measures of subjects' gain, we re-sampled both the baseline data used to scale subjects' data and their data in the main experimental task and computed the SDs of the resampled estimates of endpoint position in the normalized stimulus space and of the resampled estimates of subjects' expected gain.

Performance in the last session

Figure 4 shows, on a standardized scale, subjects' aim points in the last session of experiment 1 superimposed on the expected gain landscapes. (In supplemental Fig. S3, available at www.jneurosci.org as supplemental material, each subject's aim points can be seen separately.) The size of the aim point marker represents the proportion of a subject's endpoints that were in the cluster around this aim point. As can be seen, the vast majority of subjects' endpoints fell close to the point of maximum expected gain (y_opt). Most of the remaining endpoints were close to the second local maximum (peak2). The principal deviation from this pattern appears in condition 3, in which the peaks of the expected gain function for both the top and bottom games were almost equally high. Thus, subjects' explicit choice behavior (between the two games) appears near optimal. In conditions 1 and 5, in which the difference between the expected gains in the two games was the greatest, subjects mostly converged on a strategy of playing only the better game. In the other conditions, subjects showed a small measure of typical sampling or foraging behavior, in which the relative frequency with which subjects chose between two options roughly matched the relative reward rates of the options (Sugrue et al., 2004; Herrnstein, 1970). Some subjects showed biases toward one game, playing it in a majority of trials even when its expected gain was lower than the one of the other game. Figure 4 also shows that in the final session subjects aimed for the peaks of the expected gain landscapes, regardless of which side of the target they pointed to. It is important to note that neither the peaks nor subjects' aim points coincide with the center of a gap between two defenders (otherwise, near-optimal performance could be explained by subjects using a simple “aim at the center of a gap” heuristic that would not require them to learn anything about the defender jumps).

Figure 4.

Subjects' aim points in the last session of experiment 1, superimposed on the expected gain landscapes. The y-coordinates of the individual aim points were divided by the subject's endpoint variability in the session, so that all aim points can be plotted in the same standard size goal, even though goals were scaled to each subject's endpoint variability. The position of the symbols on the y-axis is chosen such that they fall on the gain landscape, indicating the expected gain of the aim point (in points). Marker size is scaled to the proportion of a subject's endpoints in the cluster around the respective aim point. As can be seen here, subjects always aimed at the local maxima of the gain landscape, and the majority of endpoints (indicated by large aim point symbols) was close to the global maximum (y_opt) in all but the third condition. In the third condition, some subjects seemed to prefer the second peak over the optimal one, but because the second peak was nearly as high as the optimal peak, aiming there was not significantly worse. The expected gains of individual subjects' aiming behavior in the last session of experiment 1 can be seen in supplemental Figure S4 (available at www.jneurosci.org as supplemental material).

Development of performance over sessions:

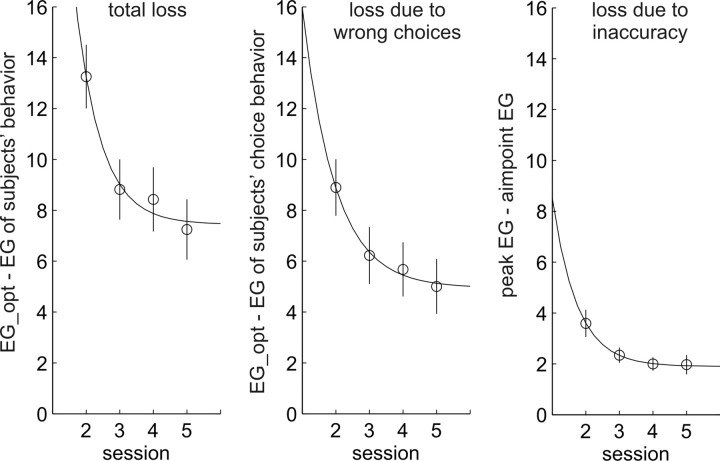
To evaluate subjects' learning over the main experimental sessions, we calculated the average loss (the difference between expected gain calculated from subjects' aim points and the expected gain of an optimal movement planner) for each subject in each session. Figure 5, left, shows the change in loss across sessions 2–5, averaged across subjects and sessions. We fitted learning curves of type y = ae^−bx + c to the data shown in Figure 5, left, and found that the time constant b was significantly different from zero (b = 1.31 ± 0.05), indicating significant learning. The data show that learning was fast, because subjects' performance asymptoted after the first two learning sessions (1/b corresponds to ∼230 trials).

Figure 5.

Losses of the subjects compared with the optimal movement planner: experiment 1. Left, Average gain losses (in points) of subjects compared with the optimal movement planner. Middle, Losses attributable to subjects' choosing the wrong game. To compute this measure, we computed the difference between the optimal gain and the gain subjects would have gotten if they chose the games they chose, but within the chosen game got the best possible outcome (no losses because of inaccuracy). Right, Losses attributable to deviations of aim points in the game the subject chose in a majority of trials from the optimal aim point in that game. Error bars indicate the ±1 SEM; curves are exponential functions fitted to the data. As expected, losses decreased over sessions as subjects learned the jump distributions. A comparison of the middle and right panels shows that subjects lost more points because they aimed at the wrong local maximum than because their aim points deviated from the maximum.

We independently measured the subjects' loss as a result of choosing the worst of the two games (the side of the target with lower peak expected gain) and their loss as a result of inaccuracy in aim points relative to the optimal aim point within a game. We calculated the loss attributable to wrong choices as the difference between the expected gain for the optimal aim point in the best game and the optimal aim point in the other game, multiplied by the proportion of trials in which subjects chose the worst of the two games. The loss attributable to inaccurate aiming within a game was computed as the average difference between the peak expected gain in that game and the expected gain of the subject's aim point in that game. Because in some sessions and conditions subjects had too few endpoints in their second cluster to reliably estimate a second aim point, we based the second loss function only on the aim points computed from subjects' biggest endpoint cluster in each session and condition. Figure 5, middle and right, show the development of the two loss functions over time.

The losses observed in the second session already reflect some amount of learning that occurred during that session; thus, they do not provide a true performance baseline before learning. Because we cannot compute reliable estimates of subjects' aim points based on single blocks, we cannot explore learning with higher temporal resolution. To provide a baseline performance level with which to compare subjects' asymptoptic performance, we compared subjects' losses with those of a naive actor who uses what would appear to be the optimal strategy before learning about the task-relevant uncertainties: to aim at the center of the largest gap. Such an observer would have a total average loss of 31.63 points, with a loss attributable to wrong choices (which he would make in conditions 1 and 2) of 16.07 points and a loss attributable to inaccuracy of 15.56 points. These compare with the subjects' average losses in the final session of 7.24 (total), 5.01 (choice loss), and 1.97 (accuracy loss).

Fitting exponential learning curves to subjects' losses, we found significant learning in both aspects of the task (choice learning: b = 1.03 ± 0.06, 1/b = 291 trials; aim point learning: b = 1.36 ± 0.05, 1/b = 221 trials). Supplemental Figure S5 (available at www.jneurosci.org as supplemental material) shows these same data as efficiencies (ratios of subjects' expected gains and the optimal movement planner's expected gain). In terms of efficiency, subjects' performance asymptoted at 83.9% (±2.5%), with a choice efficiency of 88.7% (±2.4%) and an aiming efficiency of 95.5% (±0.8%).

Experiment 2

Experiment 2 extended experiment 1 in two important ways. First, we introduced an asymmetric loss function, so that to achieve optimality subjects could not simply choose aim points based on frequency of success, but rather had to take into account the relative costs of being blocked by different defenders. Second, we switched the losses associated with each defender after session 5. This allowed us to test whether subjects simply learned stimulus-action contingencies or whether they learned something about the jump distributions that allowed them to make optimal visuomotor decisions based on the new loss functions introduced in session 6. Figure 6 shows the expected gain landscapes associated with the two versions of the task used in the experiment. Not only are the functions significantly different from those associated with the symmetric loss functions used in experiment 1, but they are also significantly different from one another.

Performance in sessions 2–5

Sessions 2–5 of experiment 2 replicated those of experiment 1, but with asymmetric cost functions. Figure 7 shows subjects' aim points across the five conditions in session 5 of the experiment. Subjects' aim points were clustered around the optimal aim points and shifted appropriately from condition to condition. Some choice inefficiency was apparent in the sampling behavior shown by subjects in the conditions in which the peaks in the expected gain functions were close to one another in height, replicating similar patterns shown in condition 3 of experiment 1. Aim points in session 7, at the end of experiment 2 and in the second session after the task version had been switched, showed the same effects (compare supplemental Fig. S6, available at www.jneurosci.org as supplemental material). Figure 8 shows subjects' average loss as a function of session number.

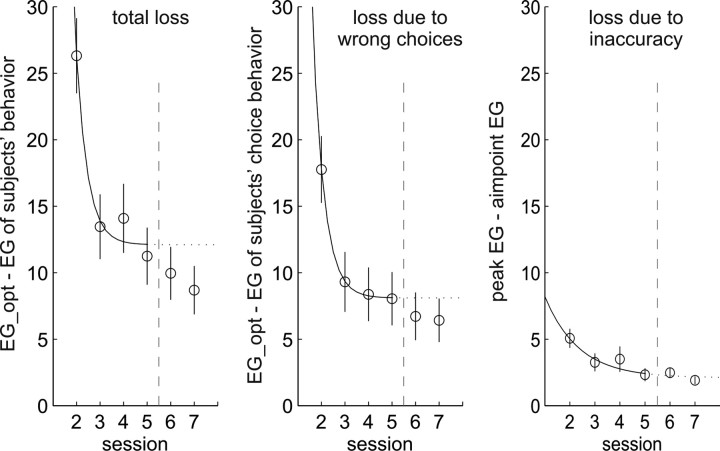
Figure 8.

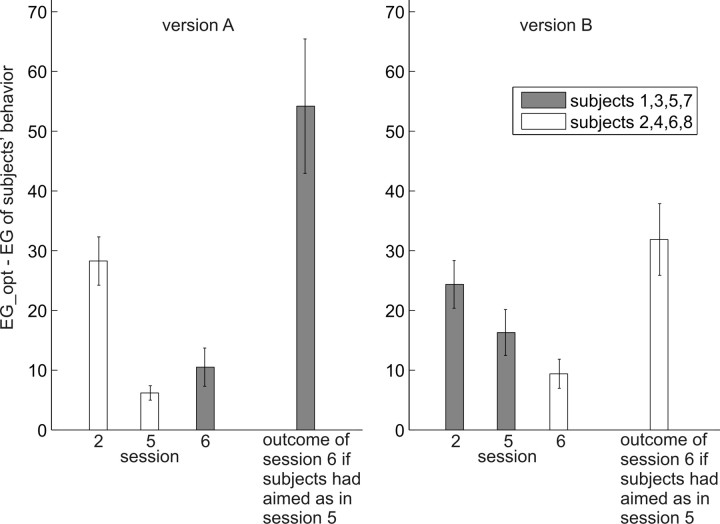
Subjects' losses in gain compared with the optimal gain, in experiment 2. Conventions are as in Figure 5. Learning curves were fitted only to the data of sessions 2–5, after which the cost function was changed. Although subjects were exposed to a novel situation in session 6, losses did not increase between sessions 5 and 6, indicating that subjects used the knowledge they had gained about the jump distributions to immediately adjust their strategies to the new payoff situation. Actually, subjects seem to be better instead of worse with regard to their choices and overall performance after the switch, which might be attributable to higher motivation because of the new challenge. Note that, although for each subject the task version, and thus the optimal gain, changed between sessions 5 and 6, the average optimal gain across all subjects did not because, as before, four subjects saw one version of the task and four saw the other version. We therefore can compare average losses in sessions before and after the change without confounding the results with differences in optimal gain between the task versions.

To get a baseline measure or performance for a subject who did not know the defenders' jump distributions, we calculated the optimal aim points for an actor who takes into account the losses associated with hitting the different defenders and his own endpoint variability. Such an actor always aims at the center of the biggest gap, because the gap is so big relative to his endpoint uncertainty that the penalties to the left and right of it do not matter. This actor would have gotten an average total loss of 96.90 points, a choice loss of 46.60 points (74.84 points in task version A and 18.36 points in task version B), and a loss attributable to inaccuracy in his chosen game of 50.30 points (74.77 in task version A and 25.84 in task version B). Our subjects' average losses in session 5 of the experiment were 11.24 (total), 8.04 (choice), and 2.33 (inaccuracy).

Fitting exponential learning curves to the data from sessions 2–5 (before the switch in loss function) gave similar results as found in experiment 1 (total learning: b = 2.07 ± 0.07, 1/b = 145 trials; choice learning: b = 2.05 ± 0.06, 1/b = 145 trials; aim point learning: b = 0.74 ± 0.06, 1/b = 405 trials).

Transfer to the new loss function in session 6

In session 6, subjects were presented with the same stimulus conditions as in sessions 2–5, but the losses associated with the two outside defenders were flipped. Figure 6 shows the changes in the expected gain function generated by the switch, both in the relative heights and in the locations of the peaks. To maintain optimality, subjects would have to follow the slight shift of the peak locations in conditions 1, 2, 4, and 5 from one task version to the other and switch to the other peak in condition 3. Neither sticking to their previous aim points nor following a simple mirror heuristic would lead to high gains. Were subjects' improvement over the four sessions before the change only attributable to fine tuning of some stimulus-action contingencies, performance should drop after the change. Alternatively, if subjects learned the jump distributions of the defenders and were able to combine this knowledge with the new loss functions in session 6, their performance should remain stable.

Figure 8 shows an initial indication that subjects learning transferred to the new loss function in session 6. Subjects' average total loss in session 6 was, if anything, lower than in session 5, although the two were not significantly different. This behavior appears both in subjects' choices and in their aim point accuracy. Supplemental Figure S8 (available at www.jneurosci.org as supplemental material) shows the same effect in terms of efficiencies. That choice performance did not drop significantly is not too surprising, because the optimal aim point changed sides in only one condition (condition 3). That aiming performance within the optimal game did not drop, however, shows that subjects appropriately changed their aim points from session 5 to session 6 to accommodate the change induced by the new loss function. Using the data from conditions 1, 2, 4, and 5, in which the optimal aim point (and subjects' choices, by and large) did not change sides, we tested whether subjects shifted their aim points from session 5 to session 6 by measuring the average change in aim point in the direction of the optimal change (a positive difference was a change in the “right” direction). Subjects' average shifts were in the correct direction and significantly different from zero (t₍₇₎ = 3.811; p = 0.007, two-tailed). Figure 10, top, shows an example of the shift between sessions 5 and 6.

Figure 10.

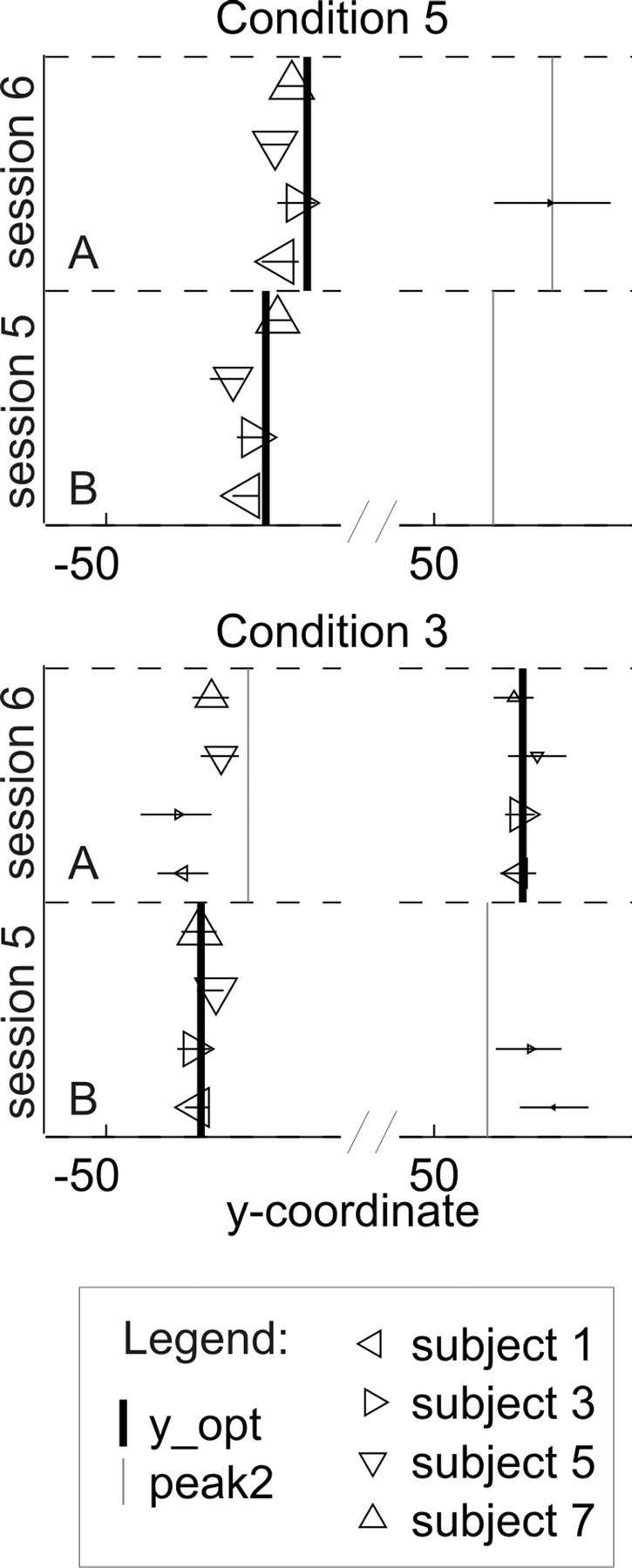
Aim points of one group of subjects before and after the switch of the cost function, in conditions 5 and 3 of experiment 2, plotted for direct comparability. The y-coordinates of the individual aim points were divided by the subject's endpoint variability in the session, so that all aim points can be shown in the same plot, although goals were scaled to each subject's endpoint variability. Marker size is scaled to the number of endpoints in the cluster around the respective aim point. The x-axis is broken to show aim points on both sides of the middle defender in the same plot. The positions of the subject symbols on the y-axis are arbitrarily chosen. Horizontal error bars indicate ±1 SEM estimate. This figure shows that, as task versions changed, subjects followed the slight shift of the optimal aim point within a game in condition 5. They did not fully follow the switch of the optimal aim point from one side of the middle defender to the other that was induced by the change in the cost function in condition 3. All subjects did, however, shift some of their endpoints to the new optimal aim point.

As an alternative analysis of transfer, we compared the loss of subjects who started the experiment with one version of the task with the loss of subjects who switched to that version on session six of the experiment. As can be seen in Figure 9, performance in session 6 was significantly better than in session 2 (results of ANOVA; F_(1,76) = 22.11, p < 0.001 for both task versions; version A: F_(1,38) = 11.89, p = 0.001; version B: F_(1,38) = 10.22, p = 0.003), even though in both cases subjects were confronted with a new loss function. Moreover, there was no significant increase in losses from session 5 to session 6, neither across task versions (F_(1,76) = 0.21; p = 0.652) nor for version A (F_(1,38) = 1.20; p = 0.214) or version B (F_(1,38) = 2.30; p = 0.137) separately. Shown in Figure 9 for comparison is the loss predicted by a simple transfer of visuomotor strategies from session 5 to session 6, clearly showing that such a strategy transfer cannot account for the experimental results. Supplemental Figure S9 (available at www.jneurosci.org as supplemental material) shows in more detail a comparison of subjects' expected gain in each condition and session of the experiment with the expected gain of an optimal movement planner.

Figure 9.

Comparison of subjects' performance in both task versions of experiment 2 before and after the new cost function was introduced. As can be seen, losses of one group of subjects (averaged across subjects and conditions) in session 2 were higher than losses of the other group of subjects in session 6, although in both cases the subjects were confronted with a new loss function. Moreover, losses did not increase significantly between sessions 5 and 6, although session 5 was the last of four sessions during which subjects could become experts for the cost function that was present during those sessions and session 6 was the first session in which they were faced with a new cost function. The rightmost bars in each panel indicate the losses we would see if subjects had just maintained the strategies they used in session 5. Clearly, subjects' performance in session 6 was significantly better than it would have been if they had maintained their session 5 strategies, indicating that they adjusted their aiming behavior to the new task version. Error bars indicate ±1 SEM.

In only one condition did transfer require switching games (condition 3). Subjects showed a significant change in this direction but did not switch perfectly (Fig. 10, bottom). Whereas in session 5 subjects chose the best game to play on 87.5% of trials in condition 3, they chose the best game to play in session 6 (after the cost function switch) only 63.4% of the time. (For comparison, in the other conditions, the percentage of correct choices was, on average, 81% in session 5 and 90% in session 6, and it did not decrease for any of those conditions.)

Discussion

Our study addressed the question of whether humans can choose sensorimotor strategies that maximize expected gain under conditions in which both the movement itself and the environment in which the movement is performed are stochastic. The stochasticity in the movement is naturally there: because of noise in the sensorimotor system, it is uncertain where the pointing movement will actually end (Fitts and Petersen, 1964). The uncertainty we imposed on our task environment was qualitatively similar and designed to be “natural” in that it was caused by the random movements of agents in the environment. Our results indicate that subjects were very good learning the optimal aim points in the task. In both experiments, the average losses attributable to having an average aim point away from the optimal corresponded to subjects being blocked by a defender only one time more than they would have been at the optimal aim point.

Subjects' total losses were dominated by inefficiencies in their choice behavior; however, even these losses were fairly low, on average, after learning. Some subjects showed biases toward one side of the target: they aimed there in a majority of trials even in conditions in which the other side promised higher expected gain. Many subjects suboptimally “sampled” the lower expected gain side of the target on a minority of trials. This behavior varied as a function of the relative expected gains associated with the two sides: subjects showed more sampling (or foraging) behavior for conditions in which the peak expected gains on the two sides were nearly equal. Both aspects of subjects' performance (choice and aim-point selection) improved over time, but the sampling behavior and biases never completely disappeared.

These results may help to answer the question why there is such a striking discrepancy between the results of experiments on economic and sensorimotor decision making. In economic decision-making experiments, in which subjects have to decide which of two gambles to play, subjects often fail to maximize expected gain and often show biases (Allais, 1953; Kahneman and Tversky, 1979). In contrast, subjects have been shown to plan movements under risk such that they optimize a loss function (Baddeley et al., 2003; Trommershäuser et al., 2003, 2005; Körding and Wolpert, 2004).

One important difference between sensorimotor and economic “decisions” seems to be how information about the stochasticity is presented to the subjects. Maloney et al. (2007) found that subjects who optimally took into account the uncertainty associated with their own pointing movement performed suboptimally when explicit uncertainty was added to the task by telling subjects that rewards and penalties would only be given with a 50% chance. From this, the authors concluded that a key difference between sensorimotor and economic decision-making experiments is that, in the latter, the information about the task-relevant stochasticity is given explicitly, whereas in the former, the uncertainty is inherent in the movement itself and thus known implicitly. Indeed, it has been demonstrated that decisions based on explicit descriptions of probabilities are different from those that are made when subjects “experience” (i.e., implicitly learn) the probabilities (Barron and Erev, 2003; Hertwig et al., 2004).

Our results suggest that subjects' failure to account for stochasticity in the task environment in the study by Maloney et al. (2007) was not attributable to the fact that the stochasticity was external to the movement but to the fact that it was explicit. Mathematically, the environmental uncertainty induced in the current study was more complex than the simple 50–50 chance of receiving the penalty attached to a penalty region, as described by Maloney et al. (2007). Nevertheless, our subjects did strikingly well. This result suggests that when observing stochastic events that have a visible natural cause (jumping defenders), subjects are able to implicitly learn near-optimal behaviors.

Subjects did show suboptimal sampling behavior in their selection of which game to play on each trial. The proportion of movement endpoints around the second highest peak increased as the relative heights of the two peaks became more similar. The sampling behavior generally decreased over time. A tentative explanation for that is that subjects based their decisions on observed statistics and that they mostly observed the defender jumps in the game they chose on a given trial. Early in the experiment, only a few jumps would have been observed, and thus subjects' estimates of the relative expected gains of the two games would have been highly uncertain. Therefore, it would be a good strategy to maintain explorative behavior (i.e., try both gaps), so that more information about both games could be accumulated. This behavior should decrease over time as more information is gathered. It should also depend on the difference between the expected gain associated with each gap. Subjects' data show both of these patterns. However, some subjects also were biased to play one game on a majority of trials even in conditions in which its expected gain was clearly lower than that of the other game. This cannot be explained in terms of foraging behavior and shows that some subjects' suboptimal choice behavior was attributable both to uncertainty about which game was optimal and to internal biases. Our data does not allow us to say from where those biases arise. They could arise from mis-estimates of the expected costs in each game or from more heuristic biases, for example, to point to the larger gap. They also could indicate the influence of some other loss function: Subjects might have a bias toward the game that is physically more comfortable for them to play.

Experiment 2 showed that subjects were able to generalize knowledge of the environmental stochasticities near-perfectly to situations with new loss functions (and hence new optimal pointing strategies). This suggests that, in fact, subjects did internalize knowledge of the statistics of defenders' jumps rather than simply learn stimulus-action contingencies. We can gain some insight into this learning process by looking at the temporal contingencies between subjects behavior on successive trials. Subjects' choice behavior provides a particular robust source of information about this aspect of learning. We computed a success change ratio by dividing the number of times subjects switched to the other game after a success by the number of success trials, and we computed a failure change ratio in the same manner. We then computed the change ratio as failure change ratio divided by success change ratio. Change ratios larger than 1 indicate that subjects were more likely to choose the other game after having been caught in one game than after having succeeded in the game they chose.

In both experiments, subjects were more likely to switch games after having been caught in the previous trial of the same condition than after having succeeded. The average change ratios were 1.79 and 1.74 in experiments 1 and 2, respectively. They were close to 1 (0.98 and 1.03 for experiments 1 and 2, respectively) when we looked at the immediately following trial (regardless whether it was of the same condition) instead of at the next trial of the same condition. This shows that the outcome of a trial did not generally affect subjects' choices in the following trial, but only in the following trial of the same condition. Interestingly, average change ratios were no larger (1.40 and 1.74 for experiments 1 and 2, respectively) when we looked only at cases in which the next trial of the same condition immediately followed the success/failure trial. Thus, the outcome of a trial was equally likely to affect the choice in the next trial of the same condition, no matter whether this trial followed immediately or with some trials between.

Both the proportion of changes after success and the proportion of changes after failure decreased over sessions in both experiments. Average failure change ratios in the last sessions of experiments 1 and 2 were 0.27 and 0.14, respectively, compared with 0.34 and 0.29 in session 2. Clearly, as subjects became more confident about what the right choice would be, they became less likely to switch games even if they were caught. In condition 3 of experiment 2, the proportion of changes after failure decreased over the first four sessions (from 0.30 to 0.15), just as in the other conditions, but in the last two sessions after task versions had been switched, it jumped back to high values (0.30 and 0.35 in sessions 6 and 7, respectively). This indicates that switching the gains increased subjects' uncertainty about which game to choose in this condition, which is not surprising because the gain change actually switched which game was the better one.

In summary, our study has shown that human sensorimotor decisions can maximize expected gain even if complex stochastic uncertainties in the task environment have to be taken into account, as long as these uncertainties can be experienced and thus implicitly learned over a few hundred trials. Moreover, subjects appear to learn information about the statistics of the environment to achieve optimality rather than simply learning stimulus-action contingencies.