Firing Rate Dynamics in the Hippocampus Induced by Trajectory Learning

Abstract

The hippocampus is essential for spatial navigation, which may involve sequential learning. However, how the hippocampus encodes new sequences in familiar environments is unknown. To study the impact of novel spatial sequences on the activity of hippocampal neurons, we monitored hippocampal ensembles while rats learned to switch from two familiar trajectories to a new one in a familiar environment. Here, we show that this novel spatial experience induces two types of changes in firing rates, but not locations of hippocampal place cells. First, place-cell firing rates on the two familiar trajectories start to change before the actual behavioral switch to the new trajectory. Second, repeated exposure on the new trajectory is associated with an increased dependence of place-cell firing rates on immediate past locations. The result suggests that sequence encoding in the hippocampus may involve integration of information about the recent past into current state.

Introduction

The hippocampus plays a key role in episodic memory (Squire, 1992; Vargha-Khadem et al., 1997; Burgess et al., 2002; Squire et al., 2004), in spatial navigation (Morris et al., 1982; Jarrard, 1993; Ferbinteanu and Shapiro, 2003), and in learning odor sequences (Fortin et al., 2002). A key common element in these tasks is the need to learn novel sequences of events or locations. Therefore, the hippocampus has been hypothesized to represent and link individual events in a sequence to form an overall memory trace (Blum and Abbott, 1996; Jensen and Lisman, 1996, 2005; Levy, 1996; Wallenstein et al., 1998; Eichenbaum et al., 1999; Lisman, 1999; Howard et al., 2005). However, direct experimental data for how hippocampal neurons encode new sequences during learning are still lacking.

A common protocol for studying hippocampally dependent learning and memory in rodents is the use of spatial navigation tasks, in which animals travel through a sequence of locations (Skaggs and McNaughton, 1996; Dragoi and Buzsáki, 2006; Suzuki, 2006; Ji and Wilson, 2007). Hippocampal neurons fire at specific locations (place fields) in a given environment (O'Keefe and Dostrovsky, 1971; McNaughton et al., 1983; Muller, 1996). Moreover, when different trajectories intersect and share a common location, hippocampal cells representing the location discharge at different rates, depending on where the animal has come from or where it will go (Frank et al., 2000; Wood et al., 2000; Ferbinteanu and Shapiro, 2003; Bower et al., 2005; Smith and Mizumori, 2006; Ainge et al., 2007a). This suggests that firing rates may be involved in encoding episodic memory (Frank et al., 2000; Wood et al., 2000; Ferbinteanu and Shapiro, 2003; Huxter et al., 2003; Leutgeb et al., 2005a,b,c, 2006; O'Keefe and Burgess, 2005). However, place fields are also found to translocate when rats alternate between two trajectories (Lee et al., 2006; Griffin et al., 2007). This raises the possibility that not only firing rate but also field location might be involved in trajectory learning.

Thus, previous results indicate that learned spatial trajectories can be reflected in differentially patterned hippocampal place-cell activity, but the dynamics of these patterns during learning is unknown. To study this, we monitored hippocampal cell ensembles while rats learned a new trajectory in a familiar environment. Rats were first trained to run a continuous figure-eight-shaped maze (see Fig. 1A), alternating between two reward sites [left (L), right (R)] via a central track along two trajectories: LR and RL (see Fig. 1B). Then, in the middle of a session, the reward at R or L was terminated and the animals were required to switch to a new unilateral LL or RR trajectory for reward.

Figure 1.

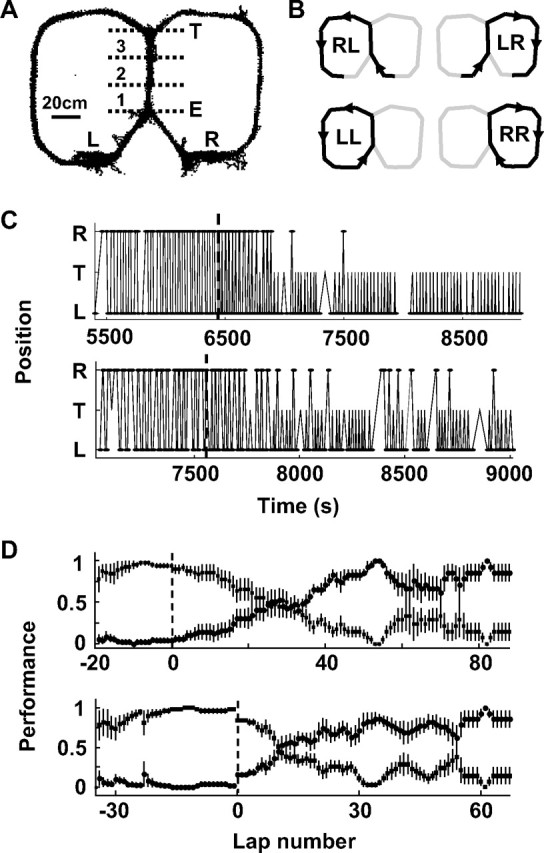
Behavioral task and performance. A, The figure-eight maze as shown in cumulative distribution of sampled locations during a typical switching session. Letters mark strategic points: L and R are the left and right reward sites, respectively; E and T are the entrance and exit of the central track, respectively. The central track was divided into three segments (1, 2, 3) for analysis. B, Schematic diagrams of running trajectories on the maze (RL, LR, LL, RR). Arrows mark running directions. C, Actual laps during two switching sessions (top and bottom, both switching from alternation LR/RL to LL). For each plot, the y-axis symbolically denotes three strategic points: L, T, and R. For example, an upward line L-T-R means an LR lap. Dashed line, Time at which reward at R was terminated. D, Average accuracy (mean ± SE), computed from all sessions, for alternation (LR/RL, ■) and unilateral (LL or RR, •) behavior. Different sessions were aligned (dashed line) either on their switching laps (top) or their actual first laps on new trajectories after the switch (bottom).

We found that the trajectory switching induced a dynamic change in firing rates, but not firing locations of the CA1 cells representing the central track, both before and after the actual behavioral change. The dynamics revealed that place cells became increasingly dependent on past locations along the new trajectories, suggesting that sequence memory in the hippocampus may require integrating past with current state information.

Materials and Methods

Behavioral task and training

Four Long–Evans rats (5–8 months old) were trained to run a figure-eight-shaped maze (see Fig. 1). The training and later recording protocol was approved by the Committee on Animal Care at Massachusetts Institute of Technology and followed National Institute of Health guidelines. Animals were trained for 2–3 weeks (once per day, 30–60 min) to alternate between LR and RL trajectories for food at reward sites L and R (alternation task). After they reached at least 80% accuracy, a tetrode array was surgically implanted. Starting 1 week after the surgery, the rats were retrained for the same alternation task for another 1 to 2 weeks until their performance recovered to presurgery levels.

On trajectory-switching days, the rats ran the same alternation task for ∼15 min as during previous trainings. Then, the reward at R was terminated and the reward at L was delivered if the animals traveled RL or the new LL trajectory. No other change was made in the maze or task. On the following 6–9 d, the animals were rewarded only for the new LL trajectory. They reached >80% accuracy for the new LL trajectory on the second or third day after the switch. After running LL for about a week, three of the four rats were trained to switch back to the alternation task, and then switch to the new RR trajectory with a similar schedule. On average, each switch took ∼7 d. The seven switching sessions from alternation to LL or RR were combined in the analysis.

Surgery and tetrode recording

A microelectrode array containing 18 independently adjustable tetrodes was implanted at coordinate (anteroposterior −4.1 mm relative to the bregma, mediolateral 2.2 mm relative to the midline) to target hippocampal neurons in dorsal CA1. Tetrodes were individually advanced to CA1 pyramidal cell layer during the 2 weeks after surgery. Recording began once units were stable and the animals were proficient in the alternation task. Spikes recorded from a tetrode with any of its four channels crossing a preset triggering threshold (60–80 μV) were acquired at 32 kHz. Single-unit clusters were manually sorted off-line using a custom-made software (Xclust, Wilson, MA), based on two-dimensional (2D) projections of spike peak-to-peak amplitudes (Gray et al., 1995). No attempts were made to match units across days for same animals. Some units may be recorded repeatedly, because tetrodes were never moved for the rest of the experiment once recording started. In any case, we sampled from the same neuronal population in CA1 on different days. Two infrared diodes were used to track the animals' positions and head directions. Diode positions were sampled at 30 Hz with a spatial resolution ∼0.67 cm. The position data used in the analysis were from the back diode, which was approximately located above the middle point of the interaural line.

Data analysis

Task performance.

Each session was divided into a series of individual laps, defined as runs between reward sites. LR and RL laps were considered correct for the alternation task, and LL (RR) laps were considered correct for the unilateral LL (RR) task. Laps that did not belong to any of four trajectories were considered incorrect for both tasks. The performance (accuracy) for a task (alternation or unilateral) was defined at each individual lap as follows. For a given lap, a window centered at the current lap and containing ±3 laps (seven laps total) was defined. Accuracy was defined as the number of correct laps divided by the total number of laps (seven) in the window. The performance curves for all sessions were aligned (lap 0) on either their switching laps, the laps at which reward at L or R was terminated, or actual first laps on new trajectories after the switch, and then averaged. Different window sizes (3–11 laps) yielded a similar average performance curve, but with different smoothness.

Firing rate maps.

The 2D maze was divided into 2 × 2 cm bins. For each bin, firing rate of a cell was computed as number of spikes fired by the cell divided by occupancy time at the bin. The rates were then spatially smoothed using a 2D Gaussian window with σ = 2 cm. The rate maps were computed separately for each trajectory, either using all the laps or a block of three consecutive laps on the trajectory.

Place-field properties and central track mean rate.

Place fields were defined on each of the three trajectories in a session (LR/RL/LL or LR/RL/RR) for a place cell [place cells were defined as overall firing rate ≥0.2 and <4 Hz and complex spike index ≥5% (McHugh et al., 1996)]. Laps were linearized into one-dimensional trajectories, which were binned with a 2 cm spatial bin size. Firing rate within each spatial bin was computed as number of spikes emitted by that cell divided by the animal's occupancy time during all laps on a trajectory. Place fields on a trajectory were determined as described previously (Mehta et al., 1997; Lee et al., 2004a, 2006). A rate threshold, which was 10% of the peak firing rate, was used to determine the boundaries of place fields. Fields with gaps smaller than 10 cm were merged into a single field. The reliability of a place field was assessed as the percentage of laps with nonzero firing rate on its trajectory. All place fields identified were reliable on at least one trajectory, with a mean reliability of 94%, median of 100%, and range [45% 100%]. Only those place cells that yielded at least one place field with its peak on or close to the central track were included for subsequent analysis (for details, see supplemental Fig. S1, available at www.jneurosci.org as supplemental material). We considered those fields of the same cell but on different trajectories as the same field, if they overlapped by at least 75%.

Once the boundary of a field, and hence field length, was defined along a trajectory, we computed the center of mass (COM) of the fields for a given lap on the trajectory. First, all the spikes within the field boundary during the lap and their corresponding positions within the field were determined. COM was the average spatial location of those spikes. Those laps during which animals stopped in the field (average speed <10 cm/s) were excluded from the analysis.

The firing rate of a place cell was computed only within the central track or maze segments, independent of the boundaries of their fields, and was computed separately for each trajectory. Those laps with low speed in the central track (average speed <10 cm/s) were excluded. Spikes within the central track during all laps on a trajectory were counted. The number was divided by occupancy time to obtain the cell's mean firing rate for that trajectory. Similarly, mean rate was also computed for each maze segment or for individual windows of three laps. In the latter case, only spikes during a window were included.

Correlation in mean rate between trajectories.

In contrast with previous studies (Frank et al., 2000; Wood et al., 2000; Ferbinteanu and Shapiro, 2003; Bower et al., 2005; Smith and Mizumori, 2006; Ainge et al., 2007a), the new trajectory (LL or RR) in our experiment shared the same past locations and differed only in immediate future locations with one old trajectory (LR or RL), and at the same time differed only in immediate past and shared the same future locations with the other old trajectory (RL or LR). By comparing activity on the central track across different trajectories, we were able to examine how an element (e.g., immediate past or future location) in a spatial sequence affects place-cell response. By “immediate,” we considered a spatial scale close to the length of a central track segment (∼16 cm) and a temporal scale associated with it (∼0.2–1.5 s). We refer to the pairs LL/LR and RR/RL as same-past, the pairs LL/RL and RR/LR as different-past, and the pair LR/RL as alternating trajectories.

Correlation in central track mean rate between same-past (different-past) trajectories was computed as follows. For each cell i, we took its central track mean rate values (x_i, y_i) on a pair of same-past (different-past) trajectories. All of the cells in all sessions that yielded at least one field with peak on the central track were combined, and the values were arranged into two vectors X(x₁, x₂,…, x_n) and Y(y₁, y₂,…, y_n). Then, the correlation (coefficient, R) is as follows:

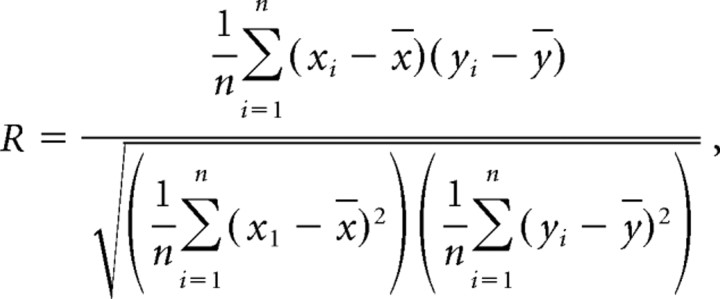where x̄ and ȳ are mean values of vector X and Y, respectively. The significance level (p value) was assessed by Pearson's r.

Firing rate dynamics.

All switching sessions were aligned (lap 0) at either their switching laps or their actual first laps on the new trajectories after the switch. Because of behavioral variations across sessions, at a given lap different sessions yielded different trajectories. To combine cells on the same trajectories across sessions, we defined windows of consecutive three laps and considered each window as a discrete time point.

To study firing rate changes on familiar trajectories after the switch, we computed a normalized rate change for each cell to quantify how its firing rate within a window of three laps changed from its mean rate during baseline laps, the 20 laps before the switch. For a given cell in a session, its rate on the central track within each lap window was computed, subtracted from the mean, and divided by the SD of its firing rates during baseline laps. The absolute value was considered the normalized rate change from the baseline. To obtain an average rate change within a period (baseline laps, laps between switching laps and actual first laps on new trajectories, or laps on familiar trajectories after the switch), the normalized rate changes of all cells in the lap windows within the period were averaged.

To study firing rate dynamics on new trajectories for a particular segment, we collected all of the fields that were active in the segment on at least one of the three allowed trajectories (mean rate, ≥1 Hz). We first computed each the average firing rate of each cell on each of the two trajectories (LR and RL) during the baseline laps. We then computed each the firing rate of each cell on the new trajectory for each window of three laps after lap 0. Based on baseline and window-by-window rates of all cells combined from all seven switching sessions, we computed rate correlation (r) for each window of three laps between the same-past and different-past trajectories. For same-past r, we collected the baseline LR rates and the LL rates in a window of all cells recorded in alternation-to-LL sessions, and also the baseline RL rates and the RR rates in the same window of all cells recorded in alternation-to-RR sessions. The firing rates of these two groups of cells were combined to form two vectors: one for baseline rates and one for the rates in the window. Same-past r was computed from the two vectors according to (1). For different-past r, we collected baseline LR rates and RR rates in a window, and combined with baseline RL rates and LL rates in the same window. As such, the correlations were computed for all of the windows with at least 10 active cells. Not every window yielded enough cells to obtain correlation values.

Results

Behavioral performance

Four rats were tested in seven switching sessions. On average, there were 83.6 ± 11.7 laps per session. The vast majority of laps (96.9%) were along one of the LR, RL, LL, or RR trajectories (Fig. 1B).

Each session started with alternation between LR and RL, after which the animals were trained to switch to the new LL (four sessions, four rats) or RR (three sessions, three of the four rats) (for details, see Materials and Methods). The switch to unilateral LL or RR trajectory was considered new learning because, before the switch, the only experience with these trajectories was rare, unreinforced, random errors (3.5%, or 0.86 lap per session). In all sessions, animals made the switch successfully, although the learning rates across sessions were variable (Fig. 1C). On average, during the 20 laps before one of the two original reward sites was no longer rewarded (switching lap), alternation performance was 96 ± 1% (mean ± SE). After the switching lap, alternation behavior dropped and unilateral behavior increased (Fig. 1D). The animals made the first lap on new trajectories after 15 ± 2 (range, 9–22) laps continuing on the old alternation task. During the last 20 laps of these sessions, 76 ± 5% of them were on the unilateral trajectories.

The central track of the maze was shared by all of the trajectories. Because our later analysis mainly focused on place fields on this portion of the maze, we divided the central track into three segments (Fig. 1A) and examined the animals' behavior in each of the segments to quantify factors that might contribute to place-cell activity. We considered three behavioral parameters: head direction, lateral position, and running speed. There were systematic differences in these parameters across trajectories (supplemental Fig. S1A, available at www.jneurosci.org as supplemental material). Head direction in segment 1 reflected the direction of entry, and in segment 3 the direction of exit. The differences in lateral position were small (<2 cm) across all of the trajectories, but significant between trajectory pairs LR/LL in segment 3. In addition, the speeds on the new unilateral trajectories were slower than the alternating trajectories.

Firing rate differences across trajectories

We first asked how place-cell activity differed across trajectories. Of 323 CA1 cells recorded, we restricted this analysis to 42 place cells with at least one field peak located on the central track (for details, see supplemental Fig. S1, available at www.jneurosci.org as supplemental material).

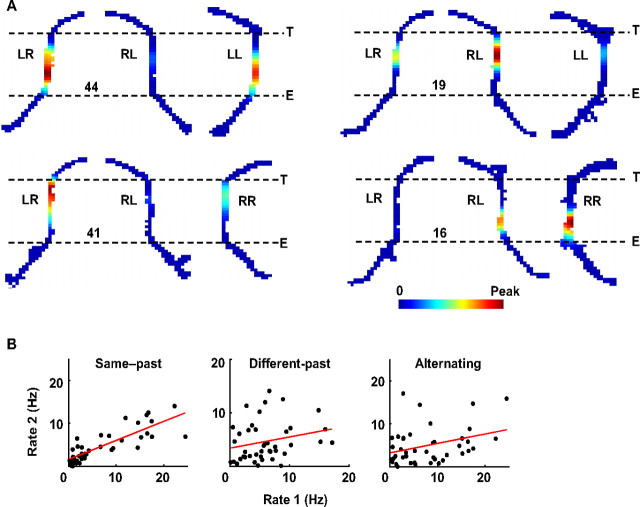
Figure 2A shows the activity of four example place cells on three trajectories (LR, RL, LL or RR) in different sessions. Although their field locations were similar across all three trajectories, there was a dramatic difference in firing rate on the central track (Fig. 2A). Their rates differed largely between different-past trajectories (LR/RR, RL/LL), but were relatively similar between same-past trajectories (LR/LL, RL/RR).

Figure 2.

Firing rates of place cells on the central track were trajectory dependent. A, Firing rate maps of four example place cells on three trajectories (LR, RL, LL, or RR). Only the central track and its surrounding segments are shown. Color codes firing rate with maps within a panel sharing the same peak rate (number in hertz). E and T are the central track entrance and exit, respectively. B, Comparison of mean firing rates of all place cells on the central track between same-past, different-past, and alternating trajectories. Each dot represents the mean rates of a place cell on two trajectories during a single switching session (e.g., LL and LR, or RR and RL for same-past). Red lines, Linear regressions.

To quantify this observation, we computed the mean rates on the central track of all of the cells, separately for different trajectories. To measure differences in firing patterns across trajectories, we computed the correlation coefficient (R) of the firing rates with same-past, different-past, and alternating (LR/RL) trajectories for the cell population (Fig. 2B). There appeared a systematic drop in firing rates on the new trajectories (population mean ± SE rate: 6.8 ± 1.1 Hz on LR and RL; 4.6 ± 0.6 Hz on LL and RR; p = 0.0016, paired t test). This rate decrease may reflect the speed change after the trajectory switch (supplemental Fig. S1A, available at www.jneurosci.org as supplemental material). Despite this global change, there was a strong correlation in the mean rates between same-past trajectories (r = 0.83, p = 1.1 × 10⁻¹¹), but only a weak correlation between different-past (r = 0.24, p = 0.12) or alternating (r = 0.33, p = 0.029) trajectories.

Place-field firing rate is known to be influenced by behavioral parameters such as head direction and running speed (McNaughton et al., 1983; Huxter et al., 2003). The firing rate variation could be a result of trajectory dependent behavioral difference. The head directions deviated equally between same-past and between different-past trajectories (supplemental Fig. S1A, available at www.jneurosci.org as supplemental material), yet the rate correlation between same-past trajectories was much larger than that between different-past trajectories. Restricting the analysis to segment 2, where there was no difference in head direction either between same-past or between different-past trajectories, produced the same results (supplemental Fig. S2, available at www.jneurosci.org as supplemental material), and moreover in segment 3, where the head direction difference between same-past was larger than that between different-past trajectories, yet the rate correlation between same-past trajectories was stronger (supplemental Fig. S2, available at www.jneurosci.org as supplemental material). Similar observations regarding the lateral position in segments 2 and 3 indicate that lateral position also could not explain the rate difference (supplemental Fig. S2, available at www.jneurosci.org as supplemental material). In addition, the running speed dropped similarly between same-past and different-past trajectories in segments 2 and 3. Therefore, it is unlikely that, despite its global influence on the firing rates, speed change is responsible for the higher correlation between same-past trajectories than between different-past trajectories.

The trajectory dependence of place-cell firing rates confirmed the previous report of “splitter” cells (Frank et al., 2000; Wood et al., 2000; Ferbinteanu and Shapiro, 2003; Bower et al., 2005). More interestingly, because firing rates between different-past trajectories were poorly correlated and these trajectories differed only in past locations, this result suggests that the difference in immediate past locations resulted in a separation in firing rate patterns of CA1 ensembles on the central track. Similarly, because the firing rates remained highly correlated between same-past trajectories, which differed only in immediate future locations, the result also suggests that the difference in immediate future locations had a relatively smaller impact on firing rate patterns of CA1 neurons. This is consistent with previous results that indicate that the majority of CA1 cells reflect retrospective coding (Frank et al., 2000; Ferbinteanu and Shapiro, 2003).

Firing rate dynamics on familiar trajectories after the switch

To examine how place cells responded to trajectory switching, we next analyzed changes in place-cell properties lap-by-lap before, during, and after the switch. To investigate whether changes in place-cell activity preceded behavioral changes, we first focused on the familiar (LR/RL) trajectories during the laps after switches and before actual first laps on new trajectories.

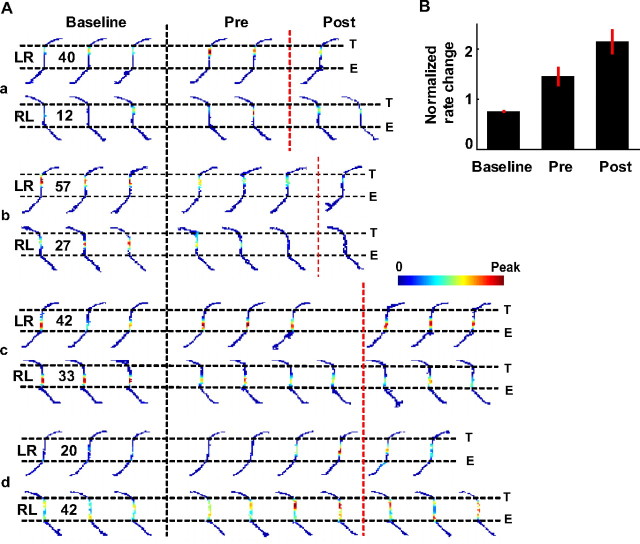
Figure 3A shows the activities of example place cells on familiar trajectories. Firing rates of these cells on the central track were stable before, but started to change after the switching laps. In contrast, the firing locations of these cells did not shift systematically.

Figure 3.

Place-field rates changed on familiar trajectories after the switch. A, Rate maps of four example place cells (a–d), each from a different session, during consecutive blocks of three laps on one of the two familiar trajectories (LR, RL). Only the central track and its surrounding segments are shown. Each row represents a cell. Color codes firing rate with the number showing peak rate in hertz. Notice the different color scales for LR and RL. E and T are the central track entrance and exit, respectively. Black dashed line, Switching laps. Red dashed lines, Actual first laps on new trajectories. B, Average normalized rate changes (mean ± SE) on the central track across all the place cells during the baseline laps before the switching (baseline), during the laps on familiar trajectories after the switching laps but before the actual first laps on new trajectories (pre), and during the laps on familiar trajectories after the actual first laps on new trajectories (post).

We computed a normalized rate change for each place cell to quantify how its rate on the central track of the familiar trajectories fluctuated from its mean rate during baseline laps (for details, see Materials and Methods), defined as 20 laps before the switching lap. We then averaged the normalized rate changes of all the cells combined from all sessions (Fig. 3B). The normalized rate change during the laps after the switch, but before actual first laps on new trajectories was significantly higher than the random rate fluctuation during the baseline laps (p = 3.0 × 10⁻⁵, signed rank test). This increase in rate change from baseline persisted even during the laps on the same familiar trajectories after the animals made their actual first laps on new trajectories (p = 8.3 × 10⁻⁷).

We also examined the normalized rate change for each window of three laps. Although the average rate change was stable during baseline laps, it gradually increased after the switching laps (supplemental Fig. S3A, available at www.jneurosci.org as supplemental material). The rate change was not dominated by fluctuations in behavioral parameters, because results were similar (supplemental Fig. S3B, available at www.jneurosci.org as supplemental material) after firing rates were corrected for their dependence on these parameters by multivariate regression (supplemental Fig. S4, available at www.jneurosci.org as supplemental material). Individual sessions showed a similar trend in rate change (supplemental Fig. S3C, available at www.jneurosci.org as supplemental material).

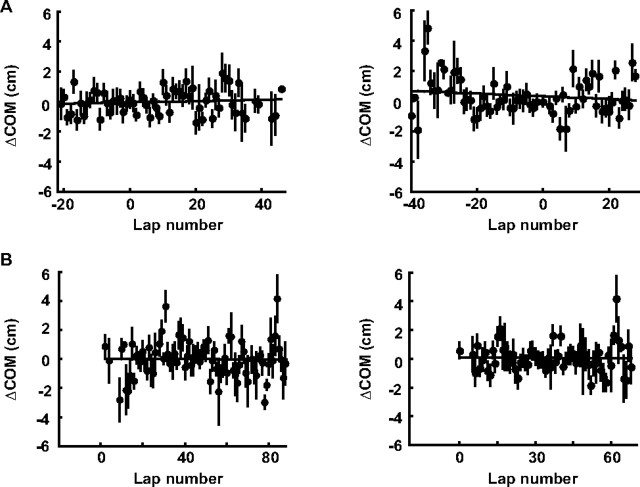
To quantify whether there was a change in firing locations, we computed place-field COMs on the familiar trajectories for baseline laps and the laps after the switch, and their shifts from the mean COM (ΔCOM). On average, COM did not show a systematic backward or forward shift on the familiar trajectories (Fig. 4A). There was no significant correlation between ΔCOM and lap number, when all the switching sessions were aligned either on their switching laps (r = 0.088, p = 0.50) or their actual first laps on the new trajectories after the switch (r = −0.14, p = 0.25). The lack of COM shift did not depend on field length on familiar trajectories (supplemental Fig. S5, available at www.jneurosci.org as supplemental material).

Figure 4.

Place-field location did not systematically shift on familiar or new trajectories. A, B, Lap-by-lap COM changes (ΔCOM, mean ± SE) on the familiar LR/RL (A) and new LL/RR (B) trajectories, averaged over all place fields with peaks on the central track. Different sessions were aligned (lap 0) on either their switching laps (left) or their actual first laps on new trajectories (right). Solid lines, Linear regressions. A positive/negative ΔCOM value means a forward/backward shift from mean COM along the direction of animals' motion.

These data indicate that place cells adjusted their firing rates, but not locations, on familiar trajectories before the behavioral switches to new trajectories, thus suggesting that changes in place-cell activity contribute to the learning involved with trajectory selection. Because before the behavioral switch the trajectories did not change, the firing rate change was likely induced by the termination of reward at one of the two sites.

Firing rate dynamics on new trajectories

To examine whether there was also change in place-cell activity during or after behavioral changes, we analyzed the dynamics of place-cell properties on the new trajectories.

Figure 5A shows the activities of example place cells in consecutive blocks of three laps on the new trajectories (LL or RR), compared with their baseline activities on two familiar trajectories (LR and RL). Whereas the field locations appeared stable across the laps on the new trajectories, the firing rates changed gradually toward a direction that became more separated from different-past trajectories and more similar to same-past trajectories.

Figure 5.

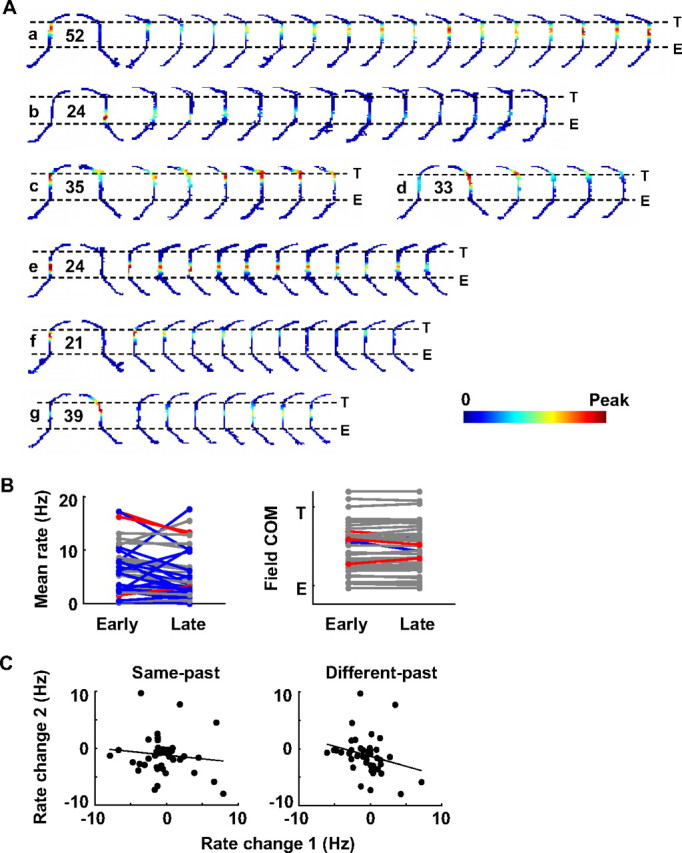
Place-cell activity showed a dynamic change on new trajectories. A, Rate maps of seven example place cells (a–g), each from a different session, during baseline laps on the two alternating trajectories (LR, RL) and during consecutive blocks of 3 laps on the new trajectories (LL or RR). Only the central track and its surrounding segments are shown. E and T are the central track entrance and exit, respectively. Each row represents a cell. Color codes firing rate with maps within a row sharing the same peak rate (number in hertz). B, Central track mean rates and field COMs of all the cells during the first (early) and last (late) two blocks of laps on the new trajectories. Each line represents a cell. Blue lines, Cells showing a significant rate change (correlation between rates or COMs and lap numbers with p < 0.05) on the new trajectories that became more similar to same-past trajectories. Red lines, Cells showing a significant change toward different-past trajectories. Gray lines, Cells without a significant change. C, Central track mean rate changes of all the cells on new trajectories, compared with the changes on same-past and different-past familiar trajectories before the first actual laps on new trajectories. Each dot represents the rate change of a place cell on a new trajectory (rate change 1: rate difference between the first and last two blocks of laps on the new trajectory) and on a familiar trajectory (rate change 2: rate difference between the baseline laps and the laps after the switching but before the actual first laps on new trajectories). Solid lines, Linear regressions.

Overall, 20 of the 42 cells showed significant changes in firing rate on the central track (correlation between rates and lap numbers, p < 0.05) toward the same-past direction, whereas three showed significant changes toward the different-past and 17 showed no significant changes (Fig. 5B). The other two cells did not yield enough spikes on the new trajectories for the analysis. Of the 23 cells with significant changes, 7 increased and the other 16 decreased their firing rates. Furthermore, the rate changes on new trajectories were not predicted by their rate changes on familiar trajectories before the behavioral switch (Fig. 5C). There was no significant correlation across the cell population between the rate changes on new trajectories and the rate changes on either the same-past (r = −0.12, p = 0.44) or different-past (r = −0.25, p = 0.098) trajectories before the actual first laps on new trajectories. This result suggests that the rate changes on new and familiar trajectories were caused by two separate processes, with the former likely by change in reward and the latter by recent experience on new trajectories.

In contrast, the vast majority of the cells (35) did not significantly shift in COM, with only two shifting toward the same-past direction and three toward the different-past (Fig. 5B). On average, there was no systematic backward or forward COM shift on new trajectories after the switch (Fig. 4B). There was no significant correlation between ΔCOM and lap number, when all of the switching sessions were aligned either on their switching laps (r = −0.015, p = 0.89) or their actual first laps on the new trajectories after the switch (r = −0.015, p = 0.90). The lack of COM shift did not depend on field length on new trajectories (supplemental Fig. S5, available at www.jneurosci.org as supplemental material).

We then examined whether there was a systematic and coherent change in firing rate across the place-cell population. Figure 6 plots spike rasters of all the cells active around the central track during laps in a session switching from alternation to LL. The cells showed distinctive and stable firing patterns on LR and RL before the switch. After the switch, the firing pattern on LL laps was initially similar to the pattern on different-past RL. The pattern then gradually became more similar to that of same-past LR. This suggests that hippocampal ensembles on the new trajectory undergo a collective dynamic change in firing rate, in which patterns become progressively less correlated with their different-past and more correlated with their same-past counterparts.

Figure 6.

Firing pattern of multiple place cells on the central track displayed a collective dynamic change on a new trajectory. Spike rasters of the cells active on the central track during individual laps in a session switching from alternation to LL. The axis labels of the first panel apply to all the panels. For every panel, each row represents a cell, and each tick represents a spike. E and T are the central track entrance and exit, respectively. Six laps before and 12 laps after the switch (lap 0) are shown. The label on top of each panel denotes lap number (black number on the left, e.g., 21, meaning it was the 21st lap after the switch), the trajectory (black letters in the middle, e.g., LL, meaning the animal was running the LL trajectory), and the time that the animal had been on the new LL trajectory (red number on the right, e.g., 1, meaning it was the first time the animal on the LL trajectory after the switch).

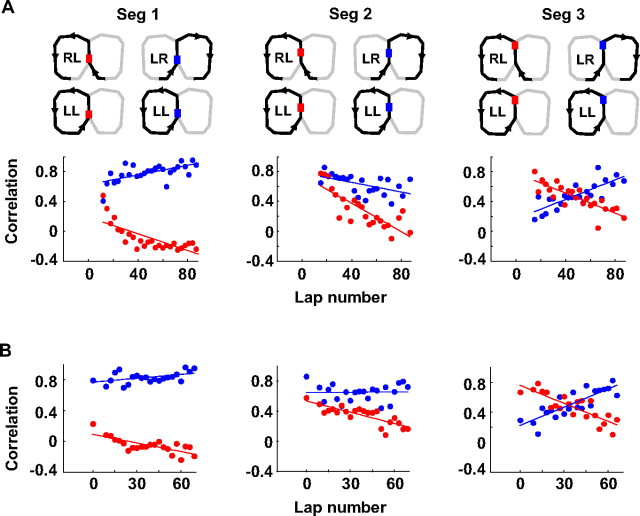
To quantify this, we computed a rate correlation (r) between same- and different-past trajectories. To check whether the dynamics varied across central track segments, the correlation was computed separately for each segment. The seven switching sessions were aligned (lap 0) on either their switching laps or their actual first laps on the new trajectories after the switch. In both cases, the 20 laps before the switch were taken as baseline laps, and all laps after lap 0 were grouped into windows of three laps. For each segment, we collected all cells that were active in the segment and calculated the firing rate of each cell within each window of three laps on the new trajectory (LL or RR), as well as its average firing rate within baseline laps on LR and RL. The rate correlation for a window was the correlation between firing rates of all the cells, combined from the seven sessions, within the window on the new trajectories and their baseline rates on either the same-past (same-past r) or different-past (different-past r) trajectories.

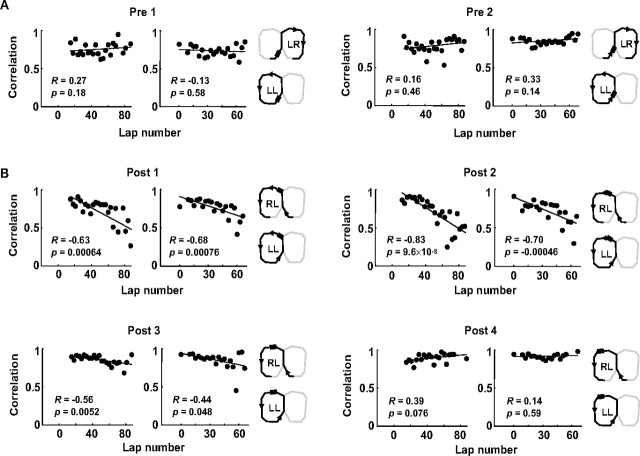
The r values with the sessions aligned on the switching laps are plotted in Figure 7A. The initial different-past r was low in segment 1, but high in segments 2 and 3. In all three segments, the different-past r decreased with lap number (correlation between r and lap number, segment 1: r = −0.75, p = 7.2 × 10⁻⁶; segment 2: r = −0.82, p = 1.9 × 10⁻⁶; segment 3: r = −0.82, p = 2.0 × 10⁻⁶). Although the drops in r were linear in segments 2 and 3, the correlation in segment 1 appeared to approach an asymptotic value around −0.25, which was also approximately the mean rate correlation between place-cell activities at two different locations on the maze. The asymptotic behavior in segment 1 suggests this value of −0.25 may be the limit for different-past trajectories r. This result indicates that the rate patterns on the new trajectories in the entire central track became increasingly separated from their different-past trajectories.

Figure 7.

Trajectory learning induced a collective firing rate change on the central track of new trajectories. A, Firing rate correlation between individual lap windows on new trajectories and baseline laps on same-past (blue) and different-past (red) trajectories. The correlation was computed for the three central track segments separately. The segments and the trajectory pairs are illustrated on the top for each panel. The trajectory pairing is only drawn for the sessions switching from alternation to LL. Cells active on the central track in these sessions were combined with those from alternation to RR to generate the plot on the bottom. Sessions were aligned (lap 0) on their switching laps. Solid lines, Linear regressions. B, Same as A, but with sessions aligned (lap 0) on their actual first laps on new trajectories after the switch.

The same-past r was initially high in segment 1 and 2, and low in segment 3. In segment 3, the same-past r rapidly increased with lap number (r = 0.80, p = 5.5 × 10⁻⁶). The increase was also observed in segment 1 (r = 0.64, p = 0.00036), despite an initial high r value. In segment 2, the same-past r decreased slightly (r = −0.53, p = 0.0093), but stayed high in the end of the sessions. It is likely the slight decrease in segment 2 was caused by behavioral variation, because the decrease was not significant after firing rate was corrected for behavioral dependence (see below). These data indicate that the rate patterns on the new trajectories over the entire central track in the end became similar to their same-past trajectories.

The results were similar when the sessions were aligned on their actual first laps on new trajectories (Fig. 7B). Different-past r significantly decreased across the three segments (segment 1: r = −0.74, p = 7.3 × 10⁻⁵; segment 2: r = −0.81, p = 4.7 × 10⁻⁶; segment 3: r = −0.84, p = 2.3 × 10⁻⁶), and same-past r increased significantly in segment 1 (r = 0.47, p = 0.029) and 3 (r = 0.83, p = 3.7 × 10⁻⁶), except that same-past r in segment 2 did not change significantly with this alignment (r = 0.0017, p = 0.99).

We then examined whether the observed change in firing rate correlations could have been generated by other noncognitive factors. First, a careful examination of lap-by-lap fluctuation in head direction, lateral position, and speed indicated that the rate dynamics could not be explained by variations in these behavioral parameters on the new trajectories (supplemental Fig. S6, available at www.jneurosci.org as supplemental material). Second, the same analysis applied to the baseline laps showed that rate correlation values did not change during these laps (supplemental Fig. S7A, available at www.jneurosci.org as supplemental material), consistent with the previous analysis showing that firing rates on the baseline laps were stable (supplemental Fig. S3, available at www.jneurosci.org as supplemental material). Furthermore, removing dependence of rate on behavioral parameters produced a similar dynamics of different-past r for all the 3 segments, and of same-past r for segment 1 and 3 (supplemental Fig. S7B, available at www.jneurosci.org as supplemental material). The same-past r in segment 2 showed a nonsignificant change after this correction. Third, normalizing firing rates across the cell population produced a similar trend in firing rate correlations, indicating that the rate dynamics was not dominated by a particular group of high-rate or low-rate cells (supplemental Fig. S7C, available at www.jneurosci.org as supplemental material).

These results indicated that immediate past locations had a strong influence on the place-cell dynamics. We next ask whether this effect was confined on the central track or could also be extended to other places on the maze. We did the same analysis to additional 30 place cells with at least one field peak in the segments before the central track (pre segments) and 52 place cells after (post segments) (Fig. 8). We found that activity patterns in pre segments remained similar with their same-past trajectories (Fig. 8A), indicating the trajectory switch per se did not alter all place fields on the maze. However, similar to the rate dynamics on the central track, the activity patterns on the new trajectories in the two immediate post segments became increasingly separated from their different-past trajectories (Fig. 8B). The effect was progressively weaker and was not observed in the distant post segment. This result suggests that the rate dynamics on the central track were extended but limited to adjacent segments.

Figure 8.

Firing rate dynamics of place fields on new trajectories was extended outside the central track. A, B, Firing rate correlation between individual lap windows on new trajectories and baseline laps on same-past trajectories for two presegments preceding the central track (A) and between individual lap windows on new trajectories and baseline laps on different-past trajectories for four post segments following the central track (B). Sessions were aligned (lap 0) on either their switching laps (left) or their actual first laps on new trajectories after the switch (right). The segments and the trajectory pairs are illustrated on the far right for each panel. Solid lines, Linear regressions with their associated correlation coefficients (R) and p values shown.

Together, these results indicate a collective firing rate change in CA1 ensembles induced by trajectory switching. With more experience on new trajectories, the firing patterns became increasingly separated from their different-past trajectories, and progressively more similar to their same-past trajectories. Therefore, trajectory learning induced a change in place-cell activity that increased the dependency on immediate past location or state.

Discussion

Episodic experiences commonly consist of novel arrangements of events occurring in familiar environments. How the hippocampus encodes different event sequences in familiar contexts is unknown. We have analyzed firing patterns of CA1 ensembles in animals as they explicitly learned a new sequence of locations (new trajectory) in a familiar environment. In agreement with the rate hypothesis (Leutgeb et al., 2005b,c), we found a dynamic change in CA1 place-field firing rates during the learning experience, without systematic change in their firing locations.

Firing rate dynamics

The observed place-field dynamics likely reflect changes in underlying synaptic input to place cells. As suggested in the path-integration proposal (Samsonovich and McNaughton, 1997; McNaughton et al., 2006), this input information may come from two possible sources: current sensory information and information associated with immediate past experience. In our experiment, both types of information could be altered across trajectories. Same-past trajectories differ in immediate future locations and would reflect differences in current sensory input because of the systematic variation in behavioral parameters such as head direction and lateral position (supplemental Fig. S1A, available at www.jneurosci.org as supplemental material), particularly in segment 3. However, different-past trajectories would reflect different immediate past input. Our results indicate a shift in relative contribution from these two types of information to place-cell activity during and after new trajectory learning. More specifically, CA1 ensemble activity was initially dominated by current input information, and then shifted to input associated with immediate past experience along a trajectory.

In our experiment, the activity patterns on the new trajectories were initially more correlated with the trajectories that shared the same current information (Fig. 7). In segment 1, the initial rate correlation was high between same-past trajectories, because of similar head direction and immediate future locations, but low between different-past trajectories because of the head direction difference. In segment 3, the initial rate correlation was high between different-past trajectories because of the similarity in head direction, lateral position, and immediate future locations, but low between same-past trajectories because of the difference in these parameters. In segment 2, the initial rate correlations were relatively high both between different-past and between same-past trajectories, because of similar head direction, lateral position, and immediate future locations across all trajectories.

With more experience on new trajectories, activity patterns became more similar with the trajectories that shared the same immediate previous experience and more different from those with different immediate previous experience. Regardless of the different initial conditions as mentioned above, activity in all three segments on new trajectories became more separated from their different-past trajectories and more correlated with their same-past trajectories (Fig. 7), indicating an increase in the influence of immediate past input on place-cell activity.

Firing rate dynamics and sequence learning

We observed that firing rate patterns changed as the animals learned new trajectories. However, it is important to understand the relationship between the observed rate dynamics and learning, that is, whether changes in neural activity precede or follow expression of learned behavior. It is presently unknown whether the exact behavioral task studied here depends on the hippocampus. A similar task has been found to be compromised by hippocampal lesions (Ferbinteanu and Shapiro, 2003), but another study shows that continuous alternation performance is not altered by the lesion unless a delay is imposed (Ainge et al., 2007b). Previous studies found that hippocampal activity changes could occur either before, during, or after the actual learning of an associational task in the primate (Wirth et al., 2003), and occur during learning of odor sequences in rats (Manns et al., 2007). Previous studies on the role of trajectory-dependent CA1 activity in alternation behavior in rats have been controversial (Ferbinteanu and Shapiro, 2003; Bower et al., 2005; Ainge et al., 2007b; Griffin et al., 2007).

In our study, we found that place-cell firing rates changed significantly on familiar trajectories before the animals switched to new trajectories (Fig. 3). This indicates that CA1 activity changes preceded actual behavioral changes, and therefore provides evidence for an active role of place-cell activity in trajectory learning. In our experiment, this active process may be induced or initiated by the change in reward contingency. However, firing rates continued to change even after the animals performed well on the new trajectories, especially in segments 2 and 3 of the central track and in post segment 1 and 2 (Figs. 7, 8). Therefore, neural activity change appears to persist after behavioral change. This suggests that CA1 may also keep track of repetitive learning experience as the new experience becomes familiar. It is likely that the rate changes before and after the behavioral switch involve different mechanisms, because they were not significantly correlated. Together, CA1 firing rate dynamics seems to play multiple roles in sequential trajectory learning, although other mechanisms could also be involved (Skaggs et al., 1996; Dragoi and Buzsáki, 2006; Shapiro and Ferbinteanu, 2006).

Place-field COM shift on new trajectories

Although we did not find any systematic shift in the COM of place fields, two previous related experiments reported that COM underwent a dramatic forward shift in similar tasks (Lee et al., 2006; Griffin et al., 2007). We hypothesize that the difference probably reflects the different experimental procedures. In these previous experiments, animals were initially trained to run a unilateral trajectory on half of a continuous T maze while the access to the other half was prevented by one or two wooden blocks. Then, the blocks were removed or shifted to a different location, and the animals were required to choose one of the two possible trajectories. Therefore, there was not only a change in the trajectory, but also a change in the maze cues. It is possible that these cue changes, as well as the potential changes in the perceived start and/or end positions of trajectories caused by the cue manipulations might have triggered the shift in place-field locations, as observed after other types of cue manipulations (Gothard et al., 1996; Lever et al., 2002; Huxter et al., 2003; Lee et al., 2004b; Leutgeb et al., 2005b). In our experiment, the change in trajectory was achieved without manipulation of cues or the structure of the maze itself. Previous studies also show that place-field COMs shift slightly backward during the first a few laps on a track (Mehta et al., 1997, 2000; Lee et al., 2004b). This phenomenon was reproduced when we analyzed place-field COM only for the baseline laps on the alternating LR/RL laps before the switch (data not shown). However, while the animals were learning the new trajectories, we did not find any systematic COM shift. This suggests that the backward shift of COM occurs after introduction into a behavioral context, but not after changes in behavior within that context.

Cellular mechanisms for the firing rate dynamics

We observed that place-cell activity during learning was increasingly influenced by the input associated with immediate past locations. Although the precise mechanisms underlying the observed dynamics remain unknown, we provide a possible explanation as follows.

Upstream activity in the entorhinal cortex (EC) reaches CA1 through two separate pathways: a direct entorhinal input from layer 3 cells and an indirect input via CA3 from layer 2 cells (Witter et al., 2000). We propose that the direct EC input mainly provides trajectory information that depends on immediate previous experience, consistent with previous studies that found that some layer 3 EC cells may function as a path integrator (Sargolini et al., 2006) and thus display trajectory-dependent firing (Frank et al., 2000; Lipton et al., 2007). The indirect CA3 input may mainly provide current spatial information to CA1 place cells, consistent with the data that normal CA3 is essential for working memory tasks and for rapid formation of place cells in CA1 (Brun et al., 2002; Lee and Kesner, 2002; Nakazawa et al., 2002, 2003; Cravens et al., 2006). In this model, the firing rate dynamics we observed can be explained by a bias toward stronger CA3 input to CA1 during early learning that shifts toward direct EC input after learning.

Our model, as well as that of Hasselmo and Eichenbaum (2005), which considers CA3 as a temporal information processor and proposes that learning mainly involves activity within the EC network, provides a different view from a class of models in which the recurrent CA3 network is considered as a sequence associator (Blum and Abbott, 1996; Jensen and Lisman, 1996; Levy, 1996; Wallenstein et al., 1998). Because our study did not record from CA3, the data did not allow us to differentiate these models. Future experiments should clarify the precise mechanism for trajectory learning in the hippocampus.