MRI of the human brain at 130 microtesla

Significance

We describe MRI in a magnetic field of 130 μT with signals detected from prepolarized protons with a superconducting quantum interference device (SQUID). We report measurements of the longitudinal relaxation time T₁ of brain tissue, blood, scalp fat, and cerebrospinal fluid. Using a combination of inversion recovery and multiple echoes, we form images in which one species can be nulled and another species emphasized. In particular, we show an image in which only blood is visible. Such techniques greatly enhance the already high intrinsic T₁-contrast obtainable at ultralow frequencies. We further present 2D brain images of T₁ and the transverse relaxation time T₂ showing that, as expected, they exhibit similar contrast.

Abstract

We present in vivo images of the human brain acquired with an ultralow field MRI (ULFMRI) system operating at a magnetic field B₀ ∼ 130 μT. The system features prepolarization of the proton spins at B_p ∼ 80 mT and detection of the NMR signals with a superconducting, second-derivative gradiometer inductively coupled to a superconducting quantum interference device (SQUID). We report measurements of the longitudinal relaxation time T₁ of brain tissue, blood, and scalp fat at B₀ and B_p, and cerebrospinal fluid at B₀. We use these T₁ values to construct inversion recovery sequences that we combine with Carr–Purcell–Meiboom–Gill echo trains to obtain images in which one species can be nulled and another species emphasized. In particular, we show an image in which only blood is visible. Such techniques greatly enhance the already high intrinsic T₁ contrast obtainable at ULF. We further present 2D images of T₁ and the transverse relaxation time T₂ of the brain and show that, as expected at ULF, they exhibit similar contrast. Applications of brain ULFMRI include integration with systems for magnetoencephalography. More generally, these techniques may be applicable, for example, to the imaging of tumors without the need for a contrast agent and to modalities recently demonstrated with T_1ρ contrast imaging (T₁ in the rotating frame) at fields of 1.5 T and above.

High-field MRI (HFMRI), based on the NMR of protons (1, 2), is a powerful clinical tool for imaging the human body (3). The protons, with magnetization M, precess about a static magnetic field B₀ at their Larmor frequency ω₀ = γB₀, where γ is the gyromagnetic ratio, 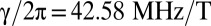. By Faraday's law, they induce an oscillating voltage 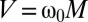in a nearby coil—shunted with a capacitor to form a tuned circuit—that is amplified and recorded. Because M scales with B₀, V scales as B₀² and hence as ω₀². 3D magnetic field gradients specify a unique magnetic field and thus an NMR frequency or phase in each voxel of the subject, so that with appropriate signal decoding one can acquire a 3D image (4).

Clinical MRI systems with 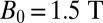achieve a spatial resolution of typically 1 mm; 3-T systems are becoming increasingly widespread in clinical practice (5), offering a higher signal-to-noise ratio (SNR) and thus higher spatial resolution. Nonetheless, there is ongoing interest in less expensive MRI systems operating at lower fields. Commercially available 0.2- to 0.5-T systems based on permanent magnets offer both lower cost and wider patient aperture than their higher field counterparts, at the expense of spatial resolution. At the still lower field of 0.03 T maintained by a room temperature solenoid, Connolly and coworkers (6, 7) obtained clinically useful SNR and spatial resolution by prepolarizing the protons in a field B_p of 0.3 T. Prepolarization (8) enhances the magnetization of the proton ensemble over that produced by the lower precession field; after the polarizing field is removed, the higher magnetization produces a correspondingly larger signal during its precession in B₀. Using the same method, Stepisnik et al. (9) obtained MR images in the Earth's magnetic field ( 50 μT).

In recent years there has been increasing interest (10–36) in NMR and MRI at fields ranging from a few nanotesla to the order of 100 μT. The enormous reduction in the detected signal amplitude compared with the high field value is overcome partly by using prepolarization and partly by detecting the signal with an untuned superconducting input circuit inductively coupled to a superconducting quantum interference device (SQUID) (37). In contrast to a conventional receiver coil, the response of the SQUID-based detector is independent of frequency, so that its sensitivity to an oscillating magnetic field does not fall off as the frequency is lowered. Furthermore, the application of a prepolarizing field B_p >> B₀ produces a proton magnetization M_p that is independent of B₀. The combination of the frequency-independent SQUID response and prepolarization yields a signal amplitude output from the SQUID that is independent of B₀ and scales as B_p.

Several authors have used ultralow-field (ULF) MRI systems to obtain in vivo images of the arm (17) and brain (26, 29, 33, 35). Zotev et al. (29) used a 7-SQUID system to obtain T₂-weighted images of the brain using multiple echoes produced by periodically reversing the direction of B₀; they also obtained values of T₁. Here, T₁ and T₂ are the longitudinal and transverse relaxation times, respectively. More recently, Vesanen et al. (35) used a 48-SQUID system to obtain T₂-weighted images using a single-echo sequence. Each of these groups has demonstrated the combination of ULFMRI and magnetoencephalography (MEG) (38, 39), using the same array of SQUIDs in a single system (15, 26, 33, 35).

ULFMRI systems make use of the myriad pulse sequences developed for HFMRI and obtain images using magnetic field gradients in much the same way. A particular advantage of ULFMRI, however, is that the T₁ difference between tissue types can be much greater than at high field (18, 34, 40, 41). In this paper, our emphasis is on using this high intrinsic T₁ contrast, combined with Carr–Purcell–Meiboom–Gill (CPMG) multiple spin echoes (42–44) and inversion recovery (IR) (41), to image selectively tissues in which there are four widely different values of T₁: the scalp fat surrounding the skull, brain tissue, cerebrospinal fluid (CSF), and blood. We present T₁ values for these components and demonstrate a variation in relaxation time greater than an order of magnitude.

We begin with a brief description of our ULFMRI system and describe the relevant pulse sequences. We report in vivo values of T₁ and use them to construct IR sequences that, coupled with multiple echoes, produce 2D images consisting solely of brain tissue, blood, or CSF. We acquire T₁ and T₂ maps of the brain, demonstrating that T₁ and T₂ weighting produces similar contrast, and show that the latter can be obtained in a much shorter time. We conclude with a discussion and outlook.

System Description and Imaging Pulse Sequences

System Configuration.

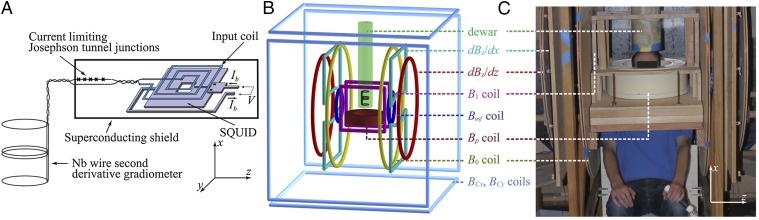
The heart of our detection system is the dc SQUID, a superconducting device that combines the phenomena of Josephson tunneling and flux quantization (37). The SQUID consists of two Josephson junctions connected in parallel on a superconducting loop (Fig. 1A). With the SQUID biased in the voltage state, the application of a steadily changing magnetic flux through the loop causes the voltage to oscillate with a period of one flux quantum, 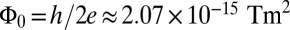. Here, h is Planck’s constant and e is the electron charge. The SQUID is operated near the flux bias 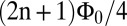, at which a small change in magnetic flux δΦ produces a voltage change δV that is amplified by conventional semiconductor electronics. The amplified signal is fed via a resistor into a coil inductively coupled to the SQUID to produce negative feedback. This flux-locked loop maintains the flux in the SQUID at a constant value and provides a voltage output that is linear in the applied flux even though the applied flux corresponds to many flux quanta. In a typical SQUID operated at 4.2 K, the flux noise is typically 1–5 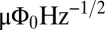. SQUIDs are fabricated from thin films, commonly in the square washer configuration shown in Fig. 1A. For most applications, a multiturn, thin-film superconducting coil is deposited on the SQUID with an intervening insulating layer. Fig. 1A shows this input coil connected to a second-derivative gradiometer, wound from Nb wire; the baseline and loop diameter are both 76 mm. A magnetic field applied to the lowest loop of this closed superconducting circuit induces a supercurrent and hence a flux in the SQUID loop. This flux transformer increases the sensitivity to nearby magnetic sources while providing a high level of rejection to distant magnetic noise sources. In our system, the magnetic field noise of the detector, referred to the lowest loop, is typically 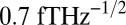. The gradiometer and SQUID are immersed in liquid helium contained in a low-noise fiberglass dewar with negligible magnetic noise (45), fabricated in-house.

Fig. 1.

System configuration. (A) Schematic of the SQUID and gradiometer. The SQUID is 1 mm across, and the resistance of the current limiter in its voltage state is ∼700 Ω. (B) Principal components of the ULFMRI system. (C) Photograph of the ULFMRI system with a subject positioned for head imaging.

Fig. 1B shows a schematic of our ULFMRI system (12). All coils are wound from copper wire. Two pairs of coils (B_Cx and B_Cy) wound on the faces of the 1.8-m cube, constructed from 37- × 87-mm lumber, cancel the Earth's field over the imaging region in the x and y directions to within ±5 μT. A Helmholtz pair wound on 19-mm plywood forms reinforces the z component of the Earth's field to produce the imaging field B₀—ranging from 125 to 135 μT—along the z axis. We choose the actual value of B₀ to minimize the noise. A Maxwell pair produces the diagonal gradient field 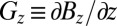, two sets of planar gradient coils produce off-diagonal fields 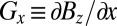and 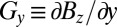(G_y is not used in this work), and an excitation coil provides oscillating pulses B₁ to manipulate the polarization. A 1.5-mm-thick aluminum shield surrounding the entire system reduces environmental magnetic field noise. A Tecmag Orion console generates the imaging pulse sequences and acquires the signals from the SQUID.

The water-cooled prepolarization coil, wound from 4 × 4-mm² hollow copper tubing, consists of 240 turns with an inner radius of 0.16 m. This coil generates a field B_p of up to 150 mT at its center along the x axis, falling to about 80 mT directly under the dewar, 0.15 m above the midplane of the coil. To avoid overheating of the polarizing coil, the maximum pulse duration, t_Bp is limited to 720 ms. The axis of the B_p coil is orthogonal to the axes of the coils producing B₀, B₁ and the gradient fields to minimize its mutual inductance to these coils. Because B_p is perpendicular to B₀, at the end of the polarization pulse, an adiabatic sweep field B_asf = 650 μT is applied along the direction of B₀ for the 10 ms during which B_p is switched off to align the spins adiabatically with B₀. A further 18-ms delay is required to allow eddy currents in the shield to decay and for relays to disconnect the polarizing coil. Immediately afterward, we apply conventional MRI pulse sequences.

Prepolarization, Spin Echoes, Spatial Encoding, and Inversion Recovery.

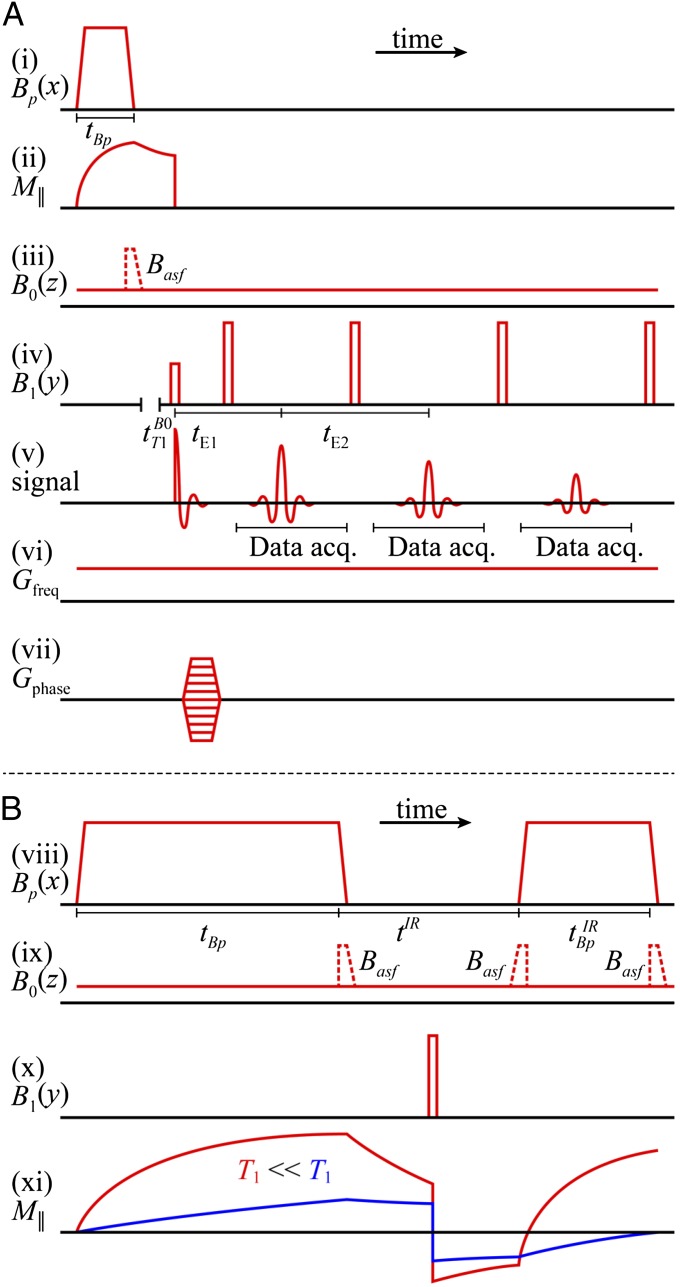
We acquire our data using a prepolarized, spin-echo imaging sequence with frequency encoding (FE) for 1D imaging and adding spin warp phase encoding (PE) (46) for 2D imaging. As appropriate, we implement CPMG multiple spin echoes and IR. The imaging sequence begins with the prepolarization pulse (Fig. 2A, i) 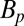, of duration 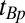, during which the proton longitudinal magnetization M_║ (Fig. 2A, ii) increases as 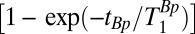toward its equilibrium value 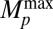. Here, T₁^Bp is the longitudinal relaxation time in the field B_p. After B_p is turned off in the presence of the adiabatic sweep field (Fig. 2A, iii), M_║ decays exponentially (Fig. 2A, ii) with time constant 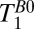, the longitudinal relaxation time in B₀. There is an optimal value 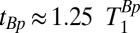, which is a compromise between polarizing for a longer time to increase M_║ and polarizing for a shorter time to increase the repetition rate of the sequence (21).

Fig. 2.

Pulse sequences. (A) Prepolarized CPMG 2D imaging sequence. (i) Prepolarizion pulse. (ii) Resulting longitudinal magnetization. (iii) B₀ field that remains on throughout data acquisition; dashed pulse is the adiabatic sweep field B_asf. (iv) CPMG pulse sequence. (v) Spin echoes. (vi) Frequency encoding gradient. (vii) Phase encoding gradients. (B) IR contrast presequence applied before the imaging sequence (A) to null out selected species. (viii) Prepolarization pulse followed by IR polarizing pulse. (ix) B₀ field and adiabatic sweep fields. (x) 180^° inverting pulse. (xi) Longitudinal magnetization.

We tip the magnetization into the x-y plane (Fig. 2A, iv) with a 90° pulse oscillating at the Larmor frequency. Subsequently, a refocusing 180° pulse applied at a time 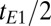after the initial excitation pulse produces the first spin echo (Fig. 2A, v) at a time 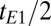later. To improve the SNR, we choose t_E1 to be short. The signal is digitized at a sampling rate of 160 kHz, producing 16,384 data points in each acquisition period 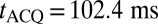. As appropriate, further refocusing pulses and spin echoes occur at multiples of t_E2 to produce a CPMG sequence (Fig. 2A, iv). The echo peak amplitudes decay exponentially with time constant .

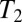For 1D imaging, frequency-encoded data are acquired in the presence of a gradient 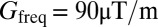that remains on throughout the pulse sequence (Fig. 2A, vi). We produce 1D images using Fourier transformation with respect to 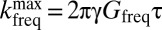, where 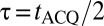. The digital resolution in the frequency-encoded dimension, established by the Nyquist sampling theorem, is 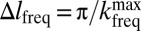, corresponding to a nominal spatial resolution of 2.5 mm. To produce 2D images a phase encoding gradient, 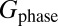, is applied in the first 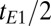period for 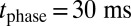so that 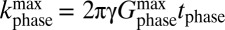(Fig. 2A, vii). We increment G_phase in steps of 4.66 μT/m to a maximum value of 107 or 140 μT/m. The digital resolution in the phase-encoded dimension, also defined by the Nyquist theorem, is 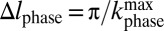, leading to a spatial resolution of 1.9 or 2.5 mm for 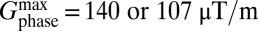, respectively. We retain only magnitude information in both 1D and 2D image data.

For some applications, we modify the imaging sequence to include a presequence that is equivalent to IR in HFMRI (Fig. 2B). The initial polarizing pulse (Fig. 2B, viii) B_p of duration 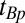, turned off with an accompanying adiabatic sweep field (Fig. 2B, ix), is followed by an evolution delay 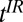, during which a B₁ 180° pulse inverts the magnetization (Fig. 2B, x and xi). The 180° pulse may be placed at any point during 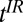. The evolution delay is followed by an IR polarizing pulse (Fig. 2A, viii) with amplitude B_p and duration 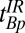. The longitudinal magnetization at the end of the IR pulse is given by

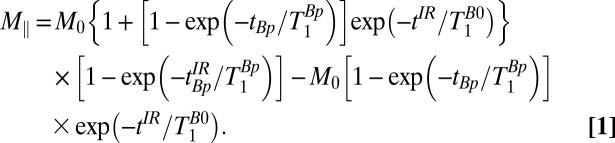The imaging pulse sequence follows. Given measured values of T₁, we use Eq. 1 to find the values of 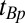, , 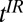and 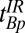required to establish a signal null for any species, as in high-field IR imaging.

Head Imaging.

We obtained detailed MRI data from two healthy men, subjects A (age 32 y) and B (age 23 y). Data from subject A are presented below. The protocol was approved by the Human Subjects Committees of the Lawrence Berkeley National Laboratory and the University of California, Berkeley, and informed consent was obtained from both subjects. The subject was seated in a chair with his head protruding through the polarizing coil (Fig. 1C) to touch the bottom of the dewar. A chinstrap attached to the dewar, and an arrangement of memory-foam cushions between the head and polarizing coil restricted motion of the head during imaging.

For 1D measurements of T₁, the subject tilted his head approximately 20° to his left, placing the central sulcus of the brain's right hemisphere under the dewar. The tilted position prevented a large blood vessel, the superior sagittal sinus (SSS), from being located directly beneath the receiver coil, enabling us to measure brain tissue T₁ with better specificity. We used 1D images to obtain T₁ values for the major brain components: gray matter (GM), white matter (WM), and CSF. However, the presence of signal from scalp fat—which is comprised primarily of long chain lipid molecules—necessitated one further pair of T₁ measurements. The skull is comprised of osseous tissue with low water content (and short T₁ and T₂) and, as in HFMRI, does not contribute significant MR signals. The frequency-encoding gradient was oriented orthogonally to the surface of the head, in the head-to-foot direction (x axis). Our 1D images are thus projections along x of all signals in the y-z plane that reside in the gradiometer field of view. This arrangement restricts scalp fat signals to that part of the head placed directly under the dewar, enabling us to separate fat signals from the brain signals beneath.

For 2D images, the subject was positioned upright with the midline of his brain oriented in the x-y plane (Fig. 1C). For 2D images, we used frequency encoding along the z axis and phase encoding along the x axis; the third dimension (y axis) was a projection onto the x-z plane of the signals parallel to y.

Relaxation Time Measurements with 1D Imaging.

Using frequency encoding, we obtained 1D images of the head on which we defined regions of interest based on features that we identified from a general knowledge of the structure of the head and brain. To measure 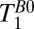, we varied the delay time, 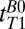, between turning off B_p and applying the 90° pulse (Fig. 2A, iv). Each 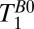-weighted signal was acquired as a separate spin echo at t_E1 = 74 ms. We used 39 values of 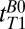distributed approximately logarithmically from 18 to 7,018 ms. We performed exponential fits of signal magnitude vs. 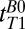to compute 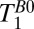for each region of interest. To obtain 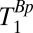, we varied the duration, t_Bp, of the 80-mT polarizing pulse (Fig. 2 A, i). Each 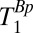-weighted signal was again acquired as a separate spin echo at t_E1 = 74 ms. We incremented the prepolarizing delay, t_Bp, from 70 to 720 ms in 13 steps of 50 ms. We computed 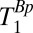for each region of interest as for the measurements of 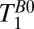. Rows 1 and 2 in Table 1 list other acquisition parameters.

Table 1.

Parameters for five pulse sequences

Row	Sequence	tBp (ms)	tIR 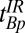(ms)	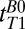(ms)	(ms)	tE1 (ms)	tE2 (ms)	No. echoes	No. averages	No. PE steps	PE resolution (mm)	FE resolution (mm)	Acquisition time
1		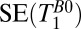420	—	—	18–7,018	74	—	1	4	—	—	2.5	5 min, 32 s
2		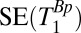70–720	—	—	18	74	—	1	4	—	—	2.5	1 min, 34 s
3	CPMG/IR CPMG	500/500	—/77	—/90	18/18	74/74	169/169	8/8	6/6	54/54	1.9	2.5	25 min, 52 s
4		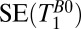500	—	—	18–4,018	74	—	1	1	47	2.5	2.5	19 min, 20 s
5		500	—	—	18	74	169	8	2	61	1.9	2.5	4 min, 26 s

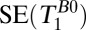, 1D spin echo sequence to acquire T₁ in B₀; 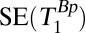, 1D spin echo sequence to acquire T₁ in B_p; CPMG/IR CPMG, interleaved CPMG and IR-CPMG sequences for 2D brain imaging; 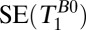, spin echo sequence to obtain 2D T₁ map; 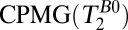, spin echo sequence to obtain 2D T₂ map.

2D Brain Imaging.

Coronal head images were obtained using interleaved CPMG and IR-CPMG sequences (Table 1, row 3). We used an interleaved acquisition, with one phase encoding step performed for each pulse sequence in turn, to minimize image subtraction errors that might arise from head motion.

The values of T₁ (determined in the 1D imaging experiments) are summarized in Table 2 and, subject to the maximum polarization time, were used to determine the pulse and delay times in the IR sequence. The sequence timing was calculated to null out the signal from the brain tissue [setting Eq. 1 equal to zero using the apparent T₁ of brain tissue, 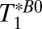(brain), and assuming that each voxel contains a single tissue component] while maximizing Eq. 1 for CSF. We fou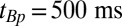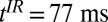nd , , and 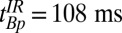. Although these estimates gave remarkably good starting points to null the brain, we empirically decreased 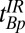from 108 to 90 ms to obtain the best possible null. Once we had optimized the value of 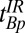, we were able to obtain images for subject B with no readjustment of the IR sequence.

Table 2.

Values of T₁ used to calculate the IR sequence for Fig. 4

Tissue	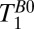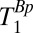(ms)	(ms)
Scalp fat	96 ± 2	223 ± 45
CSF	1,770 ± 130	4,360 ± 600
Brain	85 ± 3	453 ± 117
Blood	190 ± 39	450*

^*This value was determined by a nulling experiment that did not yield an error bar.

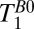and 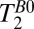Mapping.

We acquired a coronal 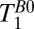map of the head using a 2D spin echo imaging sequence (Fig. 2A) with 10 values of 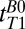distributed approximately logarithmically from 18 to 4,018 ms (Table 1, row 4). The acquisition time was 19 min, 20 s. The nominal resolution was 2.5 × 2.5 mm in-plane. The final image was computed pixelwise from a monoexponential fit of signal amplitude vs. .

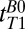A major disadvantage of maps is the long acquisition time. However, it is well known that T₂ should approach 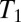at low magnetic fields (40) and the intrinsically high T₁ contrast at ULF is reflected in T₂-weighted images, as demonstrated by Zotev et al. (29). The acquisition of a multiecho train, in which the signal decays with T₂, thus permits 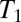-like contrast with a significant reduction of the image acquisition time. We therefore acquired 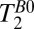-weighted images with a 2D CPMG sequence (Fig. 2A) using eight spin echoes with echo times distributed linearly between 74 and 1,257 ms (Table 1, row 5). A plot of signal amplitude vs. echo time was fitted pixelwise to a single exponential decay function to compute a T₂^B0 image. The acquisition time was 4 min, 26 s. The nominal in-plane resolution was 2.5 × 1.9 mm.

Results

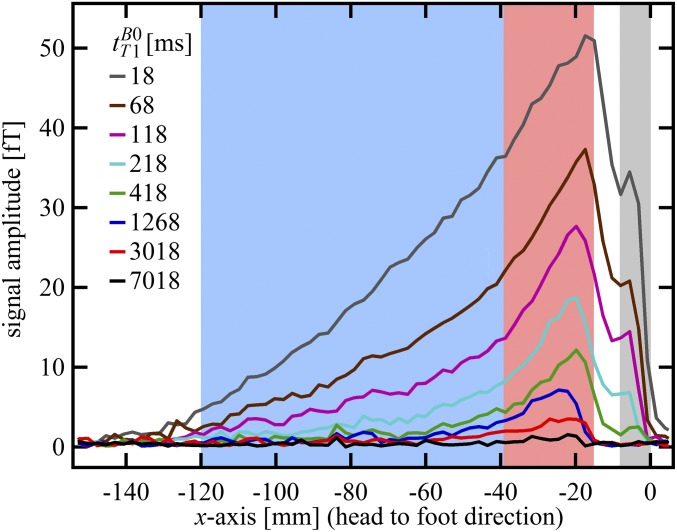
Fig. 3 shows examples of the 1D-localized signals used to determine 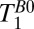. The scalp fat immediately under the dewar (x = 0) appears as a shoulder at x = –6 mm; the dip in the signal at x = –9 mm is due to the negligible skull signal. Some contaminating scalp fat signal, however, is expected in the region –17 < x < –9 mm because the skull is curved. The signal between –38 and –17 mm decays more slowly than that for x < –38 mm, and we interpret it as arising from CSF in the subarachnoid space and cortical sulci. The signal below the subarachnoid CSF (–120 < x < –38 mm) is dominated by faster relaxation, most likely from brain tissue with some contribution from CSF and blood.

Fig. 3.

One-dimensional images of the brain acquired with frequency encoding along the x axis; the nominal spatial resolution is 2.5 mm. Each 1D image was obtained at one of the eight values of 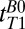listed on the figure. The bottom of the dewar and thus the top of the subject's head are at x = 0. The signal in the light gray region was integrated to perform exponential fits to obtain 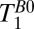(fat). The same procedure was used for the light red and light blue regions to obtain 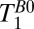(CSF) and 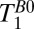(brain), respectively.

T₁ (Scalp Fat).

Scalp fat is spatially resolved in the region –9 < x < 0 mm (Fig. 3, gray region). An exponential fit of signal amplitude vs. 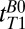for this region found 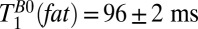. The same procedure was carried out for the polarizing field data, yielding .

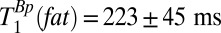T₁ (CSF).

Scalp fat and brain tissue signals decay substantially by 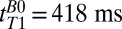, as illustrated in Fig. 3, suggesting that fitting the results for t_T1^B0 > 418 ms permits their contributions to be neglected compared with the contribution of CSF. We expect blood T₁ to be intermediate between that of the relatively immobile brain tissue water and the free water of CSF. By fitting times above 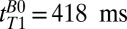and recognizing that the blood fraction is relatively small (∼10% of the total brain by volume), to a good approximation we are able to neglect the blood signal. An exponential fit to the integral of the signal in the region between –38 to –17 mm (Fig. 3, light red region) vs. 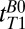for 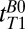= 418–7,018 ms found 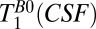= 1,770 ± 130 ms. By comparison we found 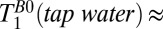2,200 ms at room temperature.

Because the maximum duration of t_Bp is 720 ms, whereas we expect 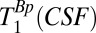to be longer than T₁^B0(CSF) ∼ 1,770 ms, it is difficult to obtain an accurate estimate of 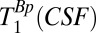using our system. Our attempts to use the signal from the region –38 < x < –17 mm and a range of t_Bp values with the maximum duration of 720 ms had unacceptably large errors. We therefore adopted an in vivo value from the literature (47), 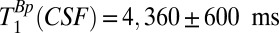, to set the IR sequence timing for 2D imaging.

T₁ (Brain Tissue).

For brain tissue we integrated the signal beneath the region of the brain dominated by CSF, that is, –120 < x < –38 mm (Fig. 3, light blue region). A single exponential fit yielded an apparent relaxation time 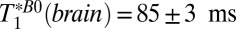. (We used this value to determine the IR timing of the 2D imaging sequence.) The acquired signal, however, contained unknown contributions from cerebral blood and CSF located deeper in the brain, as well as brain tissue. We consequently performed a triexponential fit to the signal amplitude vs. 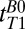for 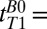18–7,018 ms, using our prior estimate of 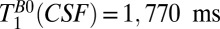as a fixed value for one of the three T₁ coefficients. This yielded 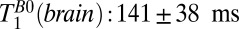and 61 ± 6 ms. These values compare reasonably well with literature values at 235 μT for GM and WM of 122 and 89 ms, respectively (48). Nevertheless, an alternative possibility is that the shorter T₁^B0 represents brain tissue and the longer 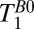represents blood. The volume fraction implied for the 61-ms component of the triexponential fit was roughly three times that of the 141-ms species. We should exercise care, however, when interpreting the volume fractions returned from the fit because each component has an unknown weighting factor that depends on the 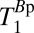of each species. We return to the assignment issue in the context of 2D imaging, below.

Even though the region –120 < x < –38 mm contains a CSF component, we attempted a single exponential fit of the polarizing field data, leading to T₁^Bp(brain) = 453 ± 117 ms. We next attempted biexponential and triexponential fits, first allowing all T₁ coefficients to fit freely and then testing fits with one T₁ held at 4360 ms (for CSF), but the results were inconclusive due to large fitting errors. This is unsurprising given that the maximum value of t_Bp, 720 ms, is less than or comparable to the likely T₁ values of the contributing sources. At 80 mT, we expect T₁(GM) and T₁(WM) to be around 900 and 500 ms, respectively (48).

T₁ (Blood).

In principle, one might hope to measure blood localized in the SSS, which follows the curvature of the head along the midline. The SSS is a large caliber vessel and is located superficially, allowing for relatively efficient signal detection. In practice, however, the curvature of the SSS relative to the plane of the gradiometer loop resulted in the contamination of blood signals by signals from scalp fat, brain tissue, and CSF, and we were unable to estimate T₁ for blood using either 1D or 2D imaging of the head. In separate experiments (Figs. S1 and S2, and Table S1), we measured T₁ of blood in the cephalic vein of the forearm to be 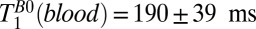and 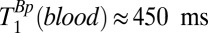. We note that 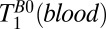is significantly longer than the value of 141 ms observed in the three-exponential fit to the brain tissue region of the 1D image, suggesting that the latter should indeed be assigned to GM.

Two-Dimensional Brain Imaging.

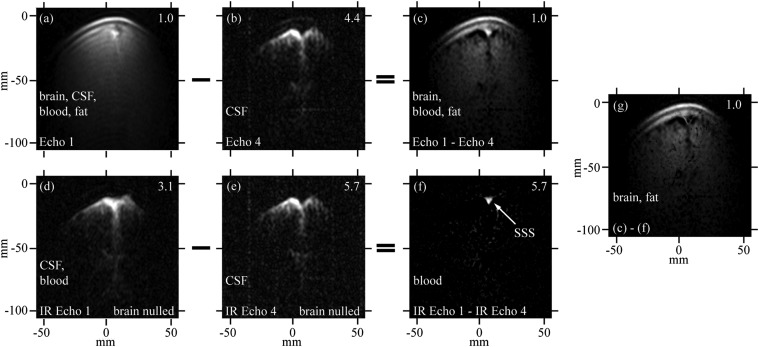
The set of coronal head images shown in Fig. 4 was obtained in ∼26 min using interleaved CPMG and IR-CPMG sequences. (Similar images for subject B are shown in Fig. S3.) The approximate thickness of these 2D images can readily be inferred from the fact that they are perpendicular to the plane of the lowest loop of the gradiometer. The maximum width of the images is ∼100 mm—as expected, somewhat greater than the diameter of the loop (49). Because the field of view of the pickup loop is rotationally symmetric, the effective image thickness in the y direction is also about 100 mm. Fig. 4A was produced from the first echo of the CPMG sequence and shows scalp fat, brain tissue, blood, and CSF. The skull is the dark crescent between the scalp and brain, and blood in the SSS appears as a bright spot. Fig. 4B shows an image produced from the fourth echo of the CPMG acquisition, which was initiated at 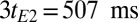after the first echo. The image is dominated by the CSF signal because of its long T₂. Lateral ventricles and CSF-filled sulci are clearly visible. Blood and brain signals have decayed nearly to zero, but a faint trace of scalp fat remains because of its high SNR due to its proximity to the gradiometer. Fig. 4C shows the result of subtracting Fig. 4B from Fig. 4A pixel by pixel. Although the subtraction allows clear contrast of several components in the head, especially between brain tissue and the CSF-filled spaces (which are signal voids after subtraction), there is no evident contrast between WM and GM.

Fig. 4.

2D images of brain. Data acquired using an acquisition of a CPMG sequence (A and B) interleaved with an IR-CPMG sequence (D and E) with the inversion recovery delays adjusted to establish a signal null for brain tissue. C and F are obtained from the subtractions A − B and D − E, respectively. G is the subtraction C − F. Image amplitudes have been scaled to enhance visualization of features: scaling factors are given in the top right corner of each image. The nominal in-plane resolution is 2.5 mm (z) × 1.9 mm (x). The total imaging time was 25 min, 52 s. Frequency and phase encoding are along the z and x axes, respectively.

Fig. 4 D and E show the first and fourth echoes of the IR-CPMG acquisition, respectively, with the IR sequence set to null signal from brain tissue. The similarity of both 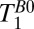and 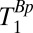for scalp fat and brain tissue also reduces the fat signal considerably. In Fig. 4D, the image is predominantly CSF and blood. A further T₂ decay of 3t_E2 = 507 ms (the fourth echo) leaves only CSF (Fig. 4E). Subtracting Fig. 4E from Fig. 4D reveals a blood-only image (Fig. 4F), the most prominent feature of which is the SSS. Finally, subtracting Fig. 4F from Fig. 4C eliminates the blood to produce Fig. 4G, which shows only brain tissue and scalp fat.

The fact that the SSS stands out so vividly against the nulled brain in Fig. 4F supports our previous tentative assignment of 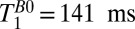to GM, rather than to blood. Thus, although we cannot differentiate GM and WM with the limited spatial resolution of our 2D images, our 1D imaging data confirm there is an intrinsic T₁^B0 contrast (29, 49).

Map.

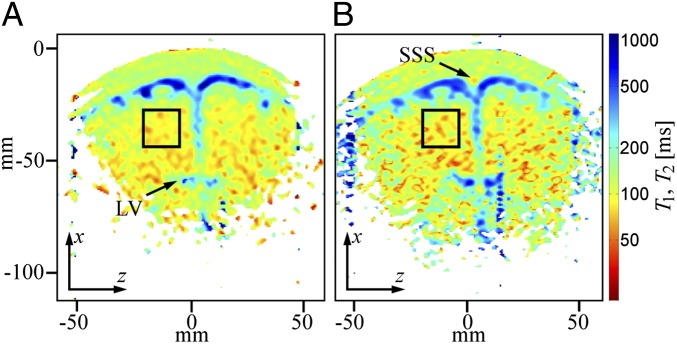
Fig. 5A shows a coronal map of the head acquired using a 2D spin echo imaging sequence. The CSF and brain tissue are especially well contrasted. The 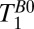(CSF) of 500–1,000 ms observed for CSF located in the subarachnoid space toward the top of the head is somewhat lower than the value 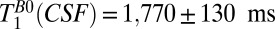obtained from the 1D imaging data. The lower value in the 2D map probably arises from partial volume contamination from scalp fat and brain tissue and from our use of a monoexponential fit to data that included short 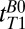values. Despite having only 10 values of 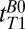, we attempted a biexponential fit to the same data and observed a longer T₁ component in the subarachnoid space that averaged around 1,500 ms, together with a shorter T₁ of around 120 ms, which is consistent with CSF contaminated by a significant partial volume effect from fat and/or brain tissue. However, the fit errors were sufficiently large that we did not attempt a detailed evaluation of the biexponential fit.

Fig. 5.

2D T₁ and T₂ maps of the brain. (A) T₁ map acquired in 19 min, 20 s. The nominal in-plane resolution is 2.5 mm × 2.5 mm. (B) T₂ map acquired in 4 min, 26 s. The nominal in-plane resolution is 2.5 mm × 1.9 mm. Black boxes indicate a region of interest used to derive an average relaxation time for brain tissue. The superior sagittal sinus location is indicated as SSS. Frequency and phase encoding are along the z and x axes, respectively.

The T₁ observed in CSF-dominated regions deeper in the brain, such as the upper portion of the lateral ventricles (LVs), also exhibits pronounced partial volume effects arising from the faster relaxing brain tissue signals; the apparent T₁ is between 200 and 500 ms, intermediate between the T₁ values for brain tissue and CSF that we obtained from the 1D data. Partial volume effects are again expected due to the low through-plane spatial resolution. The SNR is also lower in the regions farther from the gradiometer, leading to higher fit errors.

To estimate 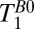in the brain tissue of Fig. 5A, we averaged voxels over an area of about 400 mm² (black box), avoiding regions with a large fraction of CSF, and found T₁^B0(brain) = 88 ± 1 ms. This value is in very good agreement with the 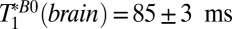obtained from the single exponential fit to the 1D images. Given the relatively low volume fraction of blood in the brain, it is perfectly reasonable that the value of 88 ms represents primarily a weighted average of GM and WM signals. The results of a biexponential fit to the same signal region, however, were inconclusive because of large fit errors.

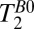Map.

Fig. 5B shows a coronal 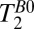map of the head using a 2D CPMG imaging sequence. The contrast in Fig. 5B is similar to that observed in the 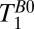map of Fig. 5A, but there are subtle differences. In the subarachnoid space 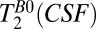is 400–800 ms, slightly shorter than the corresponding 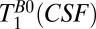values. The apparent 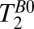(blood) of the SSS, 50–80 ms, is also short compared with 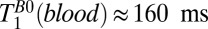in the same region of Fig. 5A. For both the CSF, which exhibits slow pulsatile flow, and the blood flowing in the SSS, we expect additional signal loss arising from the use of a constant frequency encoding gradient throughout the CPMG echo train, leading to apparent 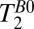values that are lower than the true values and also lower than the corresponding 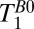values. A region of interest (black box) positioned within brain tissue, however, gives 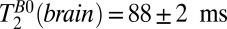, in remarkably good agreement with the value of 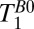from the same region in Fig. 5A. Evidently, the constant frequency encoding gradient produces negligible signal loss for the restricted motion of water in the brain tissue. A biexponential fit of signal amplitude vs. echo time was attempted for the brain region but yielded ambiguous results due to large fit errors.

In both Fig. 5 A and B, we observe contrast between tissue adjacent to the ventricles, the subarachnoid space and midline, compared with tissue farther from these CSF-dominated regions. It is tempting to assign the two tissues as GM and WM, respectively, but caution is warranted because of the partial volume effects of CSF that will be especially problematic for GM tissue located adjacent to the CSF-filled sulci. Because the apparent contrast between the brain tissue regions changes rapidly with small adjustments in the color amplitude scale, one should take care not to over interpret these images. Although we were able to identify two short 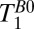values from the 1D imaging data and assigned them as GM and WM, we currently do not have the SNR or spatial resolution to separate these tissues in the 2D data unambiguously.

Discussion and Outlook

We have measured T₁ values at B₀ ∼ 130 μT for several constituents of the human head. Our quantitative results from 1D imaging agree reasonably well with previous estimates obtained at 46 μT (29) with one significant exception: we were able to separate the CSF signal from signals from other tissues, simply by waiting for the echoes from the blood and brain to decay, enabling us to obtain a more accurate estimate for T₁(CSF) of 1,770 ms. We believe, therefore, that the value of T₁(CSF) = 344 ± 9 ms reported by Zotev et al. (29) was reduced below its true value by partial volume effects, particularly from brain tissue. An earlier study found T₁ > 4 s for in vivo CSF at 235 μT (47), suggesting that our observed value may still be reduced by the presence of brain tissue.

The ratio T₁(GM)/T₁(WM) of 2.4 obtained in our work is significantly larger than the ratio of 1.2–1.5 observed at 1.5 and 3 T. This higher intrinsic brain tissue contrast is potentially less useful, however, because of the short absolute T₁ (and T₂) values. A further challenge is posed by CSF signals. The value of 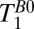(CSF) is more than an order of magnitude greater than 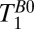(brain), whereas at high field the ratio is typically a factor of 2–4. As a consequence, at ULF the proximity of cortical GM to CSF-filled spaces such as sulci implies that partial volume effects will be a concern for voxels having dimensions of millimeters. Thus, for practical applications it remains to be seen whether sufficient GM/WM tissue contrast can be established by virtue of T₁ (or T₂) weighting alone, or if a reduction of the CSF signal—for example, by nulling—will be required. If, as we propose below, the SNR could be increased by an order of magnitude it would become feasible to acquire small voxels containing a single species. This would enable ULFMRI to exploit fully the large intrinsic T₁ (or T₂) contrast and have sufficient contrast-to-noise (CNR) to separate WM and GM in 2D (and 3D) images.

Using CPMG and IR pulse sequences, modified to accommodate the requirements of ULFMRI, we presented 2D images showing various species in the brain that can be nulled or emphasized with a high degree of flexibility. For example, by subtracting an image acquired from the fourth echo of a CPMG sequence from that acquired from the first echo, we can remove the CSF component—which has a very long T₁—to leave an image containing fat, brain tissue, and blood. By subtracting the same pair of spin echo images obtained following an IR to null out the brain tissue, we obtain an image solely of the cerebral blood. The combination of CPMG and IR sequences is a powerful technique to enhance the already substantial intrinsic T₁ and T₂ contrast at ULF.

We confirm the similarity between T₂ and T₁ contrast at ULF, as previously demonstrated by Zotev et al. (29, 49). A T₂ map of the brain resembles the corresponding T₁ map. Furthermore, compared with T₁ mapping, T₂ mapping offers the considerable advantage of a much shorter acquisition time.

The short T₁ (and T₂) values of brain tissues present a challenge for ULFMRI. Obtaining 3D voxels of 1–3 mm on a side, as are obtained routinely in HFMRI, would require increasing the SNR in our system by an order of magnitude. In fact, such an improvement is not out of the question even with a single detector. First, one could increase the value of B_p over the volume of the head from its current 80 mT to, say, 150 mT, with a somewhat larger, water-cooled polarizing coil and a reasonably sized power supply. The higher value is within accepted international safety limits for the rate of change of magnetic field for a ramp down time of 10 ms. Second, our system magnetic field noise is limited by ambient noise to about 0.7 fTHz^−1/2. A state-of-the-art SQUID with the same gradiometer, however, would have an intrinsic noise of about 0.1 fTHz^−1/2. Although attaining such low noise in the presence of environmental magnetic field fluctuations may present a significant challenge, this combination of higher polarizing field and lower noise would yield the required order of magnitude increase in SNR. The use of an array of SQUIDs (25, 35) could potentially enhance the SNR of the detected signals considerably, improving both imaging speed and spatial resolution. We note that we polarize a much larger tissue volume—the entire head—than our single gradiometer coil can possibly image, so that implementing multiple sensors would not require additional polarizing coils. Further gains in SNR are achievable by reducing the time for the relays to disconnect the polarizing coil at the end of the polarizing pulse and by reducing the decay time of the eddy currents induced in the aluminum shield. Techniques involving actively driven cancellation coils (50–52), as well as engineering magnetic shielded rooms with multiple layers and shorter eddy current decay times, are being developed to reduce the amplitude of eddy currents, and it appears likely that the eddy current problem will be solved in the near future, thereby potentially improving the SNR. Finally, other techniques developed for HFMRI are applicable to ULFMRI. Parallel imaging with multiple sensors has already been demonstrated at ULF (27, 35). Imaging times may also be shortened by filling k-space asymmetrically using partial Fourier encoding (4, 53) in the phase encoding dimension.

Given sufficient SNR and resolution to permit anatomical imaging, there are many potential novel applications for ULFMRI involving the techniques we described for brain imaging. The combination of ULFMRI with MEG (35) would improve registration between the two modalities. This could be a significant advance because all magnetic source images require MRI for their interpretation. Another possible application for ULFMRI is cancer imaging. At ULF it has been demonstrated that T₁ for ex vivo healthy prostate tissue is about 40% longer than for ex vivo tumor tissue (34), suggesting that ULFMRI has the potential for in vivo imaging of prostate cancer, and possibly other cancers, without the need of a contrast agent.

Further intriguing applications are based on 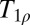contrast imaging, known as T₁ in the rotating frame. At HF, 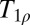contrast is produced by a long-duration spin locking B₁ field, typically 10–100 μT in amplitude, applied immediately after the application of an excitation pulse. During the spin locking period, the transverse magnetization decays in the effective field B₁. Both ULF T₁ and HF 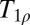contrast mechanisms are strongly influenced by slow molecular dynamics, and it seems likely that the contrast generated by spin locking at HF could be obtained intrinsically at ULF without the high power deposition required by the use of long B₁ pulses.

There are a number of recent demonstrations of 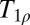contrast imaging that might be applicable at ULF. For example, the stimulated activation of gray matter has been shown to produce tissue-specific changes (54). In principle, the response to a neural stimulus could be measured in a combined MEG/ULFMRI system by recording the magnetic source signals and the T₁ changes in an interleaved fashion (15, 33). Recently, studies of ischemia following a stroke using 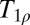contrast (55) suggest that ULF T₁ imaging may provide a linear index of ischemia duration. Accurate determination of the time elapsed since a stroke can be critically important to the choice of treatment options. Clinical applications of ULFMRI of brain might also include monitoring the progression of Alzheimer’s and Parkinson diseases, based on changes in 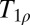contrast previously demonstrated at high field (56–58). Finally, high-field T_1ρ contrast imaging has also been suggested as a potential biomarker for gene therapy of tumors (59, 60). Although ULFMRI still requires significant development to achieve clinically useful spatial resolution with an acceptable imaging time, it may ultimately find novel clinical applications that complement those already established with HFMRI.