Pathogen selection drives nonoverlapping associations between HLA loci

Significance

Human leukocyte antigens (HLA), first identified in tissue-matching for transplantation, play a critical role in immunity. HLAs are extraordinarily diverse, but certain sets of HLA genes are more likely to be found together than others. Here, we show that associations between HLA genes can arise through their coevolutionary interaction with pathogens. Technological advances are making it easier to determine HLA types, but DNA sequence alone cannot fully predict an HLA’s functional properties. Our work offers a new evolutionary approach to tackling this problem.

Abstract

Pathogen-mediated selection is commonly invoked as an explanation for the exceptional polymorphism of the HLA gene cluster, but its role in generating and maintaining linkage disequilibrium between HLA loci is unclear. Here we show that pathogen-mediated selection can promote nonrandom associations between HLA loci. These associations may be distinguished from linkage disequilibrium generated by other population genetic processes by virtue of being nonoverlapping as well as nonrandom. Within our framework, immune selection forces the pathogen population to exist as a set of antigenically discrete strains; this then drives nonoverlapping associations between the HLA loci through which recognition of these antigens is mediated. We demonstrate that this signature of pathogen-driven selection can be observed in existing data, and propose that analyses of HLA population structure can be combined with laboratory studies to help us uncover the functional relationships between HLA alleles. In a wider coevolutionary context, our framework also shows that the inclusion of memory immunity can lead to robust cyclical dynamics across a range of host–pathogen systems.

HLAs, found on the surface of all nucleated cells, present pathogen peptides to T lymphocytes and are thus a keystone of adaptive immunity. Demonstrable associations of particular HLA alleles with resistance or susceptibility to severe disease (1, 2) underscore the importance of their role in protection against death from infection. The genes encoding HLAs are found in the 3.6-Mb-long MHC on chromosome 6 and are distinguished by their exceptional polymorphism (3), which is likely the result of selection from pathogens (4–6) Despite this enormous diversity, most human populations are dominated by a relatively small number of combinations of the alleles present at the class I HLA (A, B, C) and the principal class II HLA (DP, DQ, and DR) loci (7–12). Here we present a coevolutionary model demonstrating that pathogen selection can drive such long-term, long-range associations between HLAs. We show that this mechanistic process can be distinguished from other evolutionary effects by virtue of generating a higher degree of nonoverlap between HLA repertoires than might be expected under founder effects or hitchhiking.

A Multilocus Model for Host–Pathogen Coevolution with Allele-Specific Adaptive Immunity

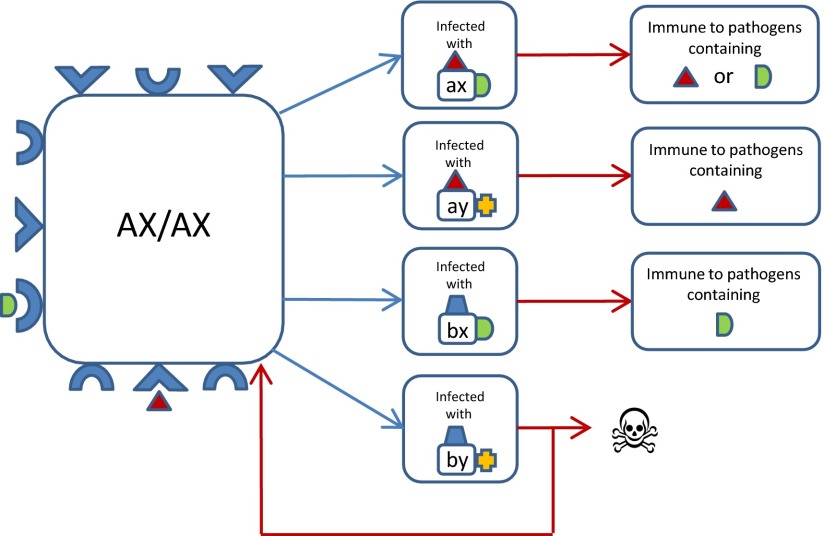
We first explored the properties of a deterministic epidemiological model (Methods) in which (i) the pathogen population was represented by four potential strains defined by two antigenic loci containing alleles (a, b) and (x, y), respectively, and (ii) we defined within a diploid host, alleles (A,B) and (X,Y) at two linked “recognition loci” (i.e., HLA loci), each only capable of responding to the corresponding parasite allele (or epitope) given in lowercase above. We assumed that immunity developed in an allele-specific manner conferring complete protection against infection by any other antigenic type containing that allele, but that there was a risk of death if a host was incapable of recognizing either allele of the infecting pathogen strain (Fig. 1).

Fig. 1.

A schematic representation of the key properties of the model. This flowchart illustrates the possible outcomes of infection by different pathogen strains for a host of genotype AX/AX who can only mount immune responses against pathogen epitopes a and x. Blue arrows indicate infection, and red arrows indicate recovery or death.

In line with previous observations, the pathogen population was observed to adopt a discrete, nonoverlapping strain structure (13). However, once any two strains (e.g., ax and by) achieve dominance, host homozygotes AX/AX and BY/BY suffer from increased mortality because each is only able to mount an immune response against one of the two circulating pathogen strains (all other host genotypes can recognize at least one allele of both strains). The numbers of these homozygotes fall until eventually the only host haplotypes left in the population are AY and BX. Thus, the strain structuring of the pathogen population by host immune selection generates nonrandom associations among the immune recognition genes of the host.

This scenario will be stable (Fig. 2A) in the absence of pathogen mutation, or when the basic reproduction number of the pathogen (R_o; a measure of its fundamental transmission potential) (14) is low. Conversely, if R_o is above a certain threshold, no genetic structuring is possible in either pathogen or host (SI Appendix, Fig. S1). Between these two extremes, we observe coevolutionary cycling (Fig. 2B) in place of permanent structuring. This dynamic emerges due to the fact that as soon as the pathogen population becomes dominated by a particular set of strains (say ax and by), haplotypes that are incapable of recognizing any one of the dominant pathogen strains (i.e., BY and AX) start to go down in frequency, and haplotypes that can recognize both the dominant pathogen strains (i.e., BX and AY) increase in frequency. Eventually the proportion of BX and AY in the population will be so high that it will be in the pathogen’s interest to switch its strain structure to (ay, bx) so as to exploit the infection reservoirs created by homozygotes of these haplotypes (BX/BX cannot become immune to ay). The system is capable of generating nonrandom associations between recognition alleles (both stable and cyclical) even when recombination is introduced between the host’s recognition loci (SI Appendix, Fig. S1).

Fig. 2.

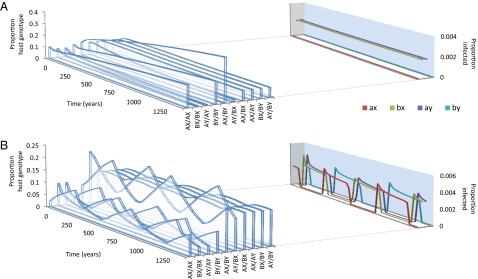
The two key behaviors of the model. See Methods for a full description of the model and its parameters. In both panels, μ₁ = 0.03; μ₂ = 2; r = 0; m = 0.0001 and σ = 10. (A) The basic reproductive number of the pathogen, R_o = 2.5; (B) R_o = 5.

To investigate the generality of these conclusions, we generated a stochastic equivalent of this deterministic model and found it to produce the same behavior in the two-locus, two-allele case, and in higher dimensional systems (SI Appendix). Nonoverlapping combinations of alleles or high complementarity equilibria (HCE) have been shown to arise in multilocus population genetic models (15) where the fitness of both host and parasite depends on the number of “matching alleles.” Our results are qualitatively different to HCE because although host recognition of pathogen epitopes has analogies with a matching allele mechanism, the structuring of the pathogen population in our model occurs through immune selection exerted by all host genotypes and would be maintained even in the absence of host heterogeneity (13). Matching allele models have so far not been shown to alternate between different nonoverlapping population structures; our results demonstrate that the integration of memory immunity can precipitate this form of coevolutionary cycling.

Structuring of HLA

Our model provides a unique mechanistic basis for the observation of nonrandom associations between host recognition loci such as HLA. Recombination between markers flanking a 7-Mb region containing the human MHC has been estimated at between 1.66% and 6.54% (16). Within our framework, pathogen selection is capable of generating nonrandom associations between host recognition alleles in the presence of recombination frequencies of up to 10% (SI Appendix, Fig. S1), and thus has the potential to maintain even long range HLA associations across recombination hotspots.

Furthermore, our model predicts that if selection from a multiepitope, strain-structured pathogen is maintaining associations between host recognition loci, alleles at those loci should not only be nonrandomly associated [i.e., in linkage disequilibrium (LD)], but also exhibit nonoverlapping repertoires (i.e., where A is principally associated with X, and B with Y). Standard metrics of LD such as D′ (17) will not capture this nonoverlapping pattern, but a previously introduced metric, f* (18), has been used to measure nonoverlapping associations among pathogen epitopes. We made a slight modification to f* (Methods) to produce a metric 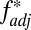, which we propose can be used as an additional feature alongside LD to begin to identify the specific effects of pathogen selection.

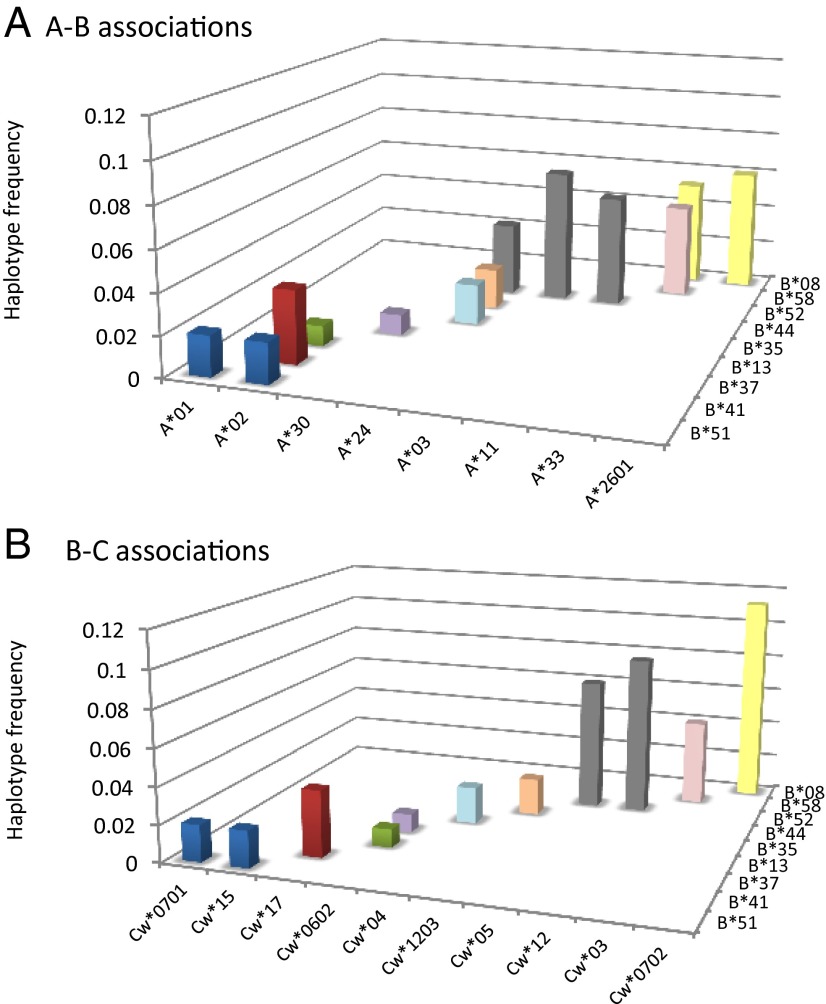
Qualitative evidence for nonoverlapping patterns between HLA is apparent in existing studies: the Burusho population of Pakistan provides a particularly striking example (Fig. 3) (12). In their survey of US bone marrow donors, Cao et al. (7) point out that whenever sequence-related (i.e., serologically indistinguishable, but with different amino acid sequences) HLA-B alleles occur at similar, moderate frequencies in a population, they tend to have nonoverlapping associations with alleles at the HLA-A or HLA-C loci. However, only by considering the entire MHC region can we establish whether HLAs are especially nonoverlapping relative to other loci with a similar demographic history. A study of 962 members of the Hutterite population of South Dakota, in which 16 loci were typed, allows us to make such comparisons (19). When we apply 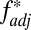to all possible pairwise combinations involving HLA-C (Fig. 4A), we find that HLA-C is highly nonoverlapping with its close neighbor HLA-B, but is also highly nonoverlapping with the much further HLA DRB1, DQA1, and DQB1 loci. Non-HLA loci in the intervening region do not display such a nonoverlapping relationship. If we repeat the exercise for TNF-α (which we would not predict to be under the same kind of pathogen selection as the HLAs), there is no particular peak in its degree of nonoverlap with physically distant loci in the region (Fig. 4B).

Fig. 3.

Nonoverlapping HLA associations in the Burusho population in Pakistan. (A) HLA-A-B associations and (B) HLA-B-C associations.

Fig. 4.

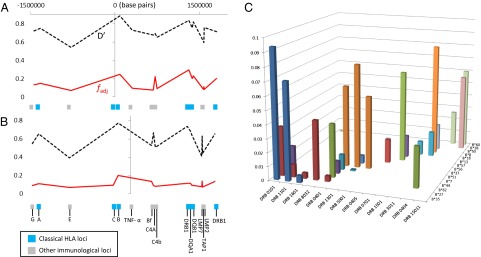
Nonoverlapping MHC associations in the Hutterite population. Here we illustrate the pairwise 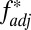and D′ values calculated from 16-locus HLA haplotypes recorded in the Hutterite population of South Dakota (19) for each indicated locus relative to HLA –C (A) or TNF-α (B). Only haplotypes for which all 16 loci were resolved were included in the analysis (97% of the total sample). (C) Frequencies of HLA-B/HLA-DRB associations within the dataset.

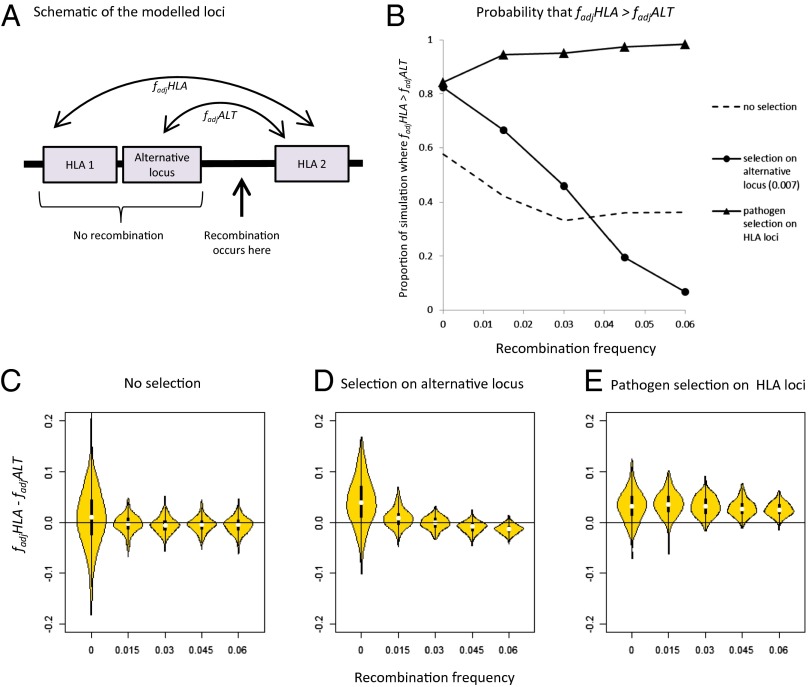
Other processes that generate LD, such as founder effects or hitchhiking, could potentially generate high 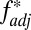between two loci; to address this, we introduced into our stochastic framework an alternative locus physically linked to one of our simulated HLA loci, but not subject to the pathogen selection acting on the HLAs (Fig. 5A). Randomly chosen alleles at the alternative locus were deemed favored at any given time, generating the sequential dominance of alleles in a manner that was entirely unrelated to the antigenic structure of the pathogen population (SI Appendix). We found that selection on the non-HLA locus was capable of generating results where HLA1/HLA2 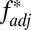scores 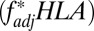were greater than HLA2/non-HLA 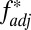scores 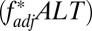, but only when very little recombination occurred between any of the loci in the system (Fig. 5 B and D). Pathogen-driven coevolution, by contrast, ensured that 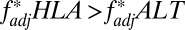even when the HLA loci were separated by recombination (Fig. 5 B and E). We can thus be more confident of pathogen selection having driven nonoverlap when considering long-range associations such as the HLA B/DRB pattern shown in Fig. 4.

Fig. 5.

Identifying a unique signature of HLA/pathogen coevolution. (A) Schematic representation of the loci within our model framework, indicating the pairs of loci between which 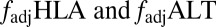measure the degree of nonoverlap. (B) Probability that 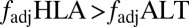under different selection regimes and levels of recombination. (C–E) Violin plots (32) produced using the vioplot package in R version 2.15.2, representing the distribution of values of 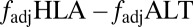for 350 simulations at each indicated selection regime and level of recombination. Only results for surviving populations are shown. The 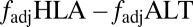values displayed are average values calculated over the final 2,500 y of 5,000-y simulations (Methods). SI Appendix describes the stochastic framework used for the simulations, and provides parameter definitions. We let there be five possible alleles at each of the two HLA loci. Parameter values were as follows: b = 0.07; m = 0.0001; φ = 0.0015; α = 0.002; Q = 5; = 1.1; Ω = 0.1; C = 2,000; k = 0.004. r was varied between 0 and 0.06, as indicated in the x axes of each panel. For “no selection,” ϖ = 0 and d = 0; for “selection on alternative locus,” ϖ = 0 and d = 0.007; and for “pathogen selection on HLA,” ϖ = 0.012 and d = 0.

Future Directions

The system we present is necessarily a minimal caricature of the MHC, and suffers from a number of limitations. Most importantly, we have only considered the effects of interaction with a single pathogen. However, though a single HLA locus undoubtedly presents peptides from a variety of pathogens (as well as self), the selective pressure upon it will mainly arise from the pathogens causing the highest mortality. Take, for example, an HLA system as described by Fig. 1 and assume that it is under assault from n pathogens whose allelic variants may be represented according the convention we have established as (a_i,b_i) and (x_i,y_i); if the most deleterious pathogen adopts the configuration (a_ix_i, b_iy_i), then the homozygotes that are most disadvantaged will still be AX/AX and BY/BY.

A second important limitation of this model is that specific host recognition loci “target” specific pathogen epitopes—in other words, why should all variants at locus 1 of the pathogen specifically be recognized by locus 1 within the host? When considering associations between class I and class II HLAs, it seems justifiable to assume that different epitopes from any given pathogen are displayed by each, but it may not be strictly correct to distinguish between class I loci (particularly A and B) on this basis.

Future work in this area should also place the HLA in its wider genomic context. The very architecture of the MHC will have an effect: in the chicken, for example, the relative proximity of the TAP and class I MHC loci may have led to tight coevolution between them, limiting the possible coexpression of class I genes (20). Furthermore, in humans, HLAs interact directly with a second family of immune system genes: Killer-cell Ig-like receptors (KIRs). KIRs display a striking haplotypic structure (21); particular KIR/HLA genotypes have been associated with different infectious disease outcomes (22, 23), and a direct effect of KIR/HLA coevolution on HLA haplotypes has recently been suggested (24).

If proven to be robust, this framework may, in principle, be able to assist in developing functional classifications of HLA alleles. It is possible to categorize HLA alleles into broad “supertypes,” based on their binding properties (25); at the same time, it is clear that a very small change in sequence (e.g., a single amino acid) can have very significant functional consequences (26). Furthermore, the ability of an HLA to bind to a specific pathogen epitope is not in itself a guarantee of an effective T-cell response to that epitope (27). If nonoverlapping allelic patterns are a signature of disease selection, they offer an alternative evolutionary approach to solving this problem. The multilocus framework described here provides a flexible platform for investigating the population-level consequences of interactions between diverse immune system genes and the pathogens they help recognize.

Methods

Deterministic Model.

We used a system of linked ordinary differential equations to capture both the population genetics of the host and the disease dynamics of the pathogen. A range of coevolutionary frameworks have been developed to combine population genetics and epidemiology (28–30); the differential equation approach, first used by Gupta and Hill (31), offers a highly flexible framework that is especially amenable to the inclusion of immunological memory.

The pathogen population was represented by four potential strains (P = 1–4) defined by two antigenic loci containing epitopes (a, b) and (x, y) respectively (SI Appendix, Table S1). Our host population was diploid, possessing recognition alleles at two linked loci (A, B) and (X, Y), making up four possible host haplotypes (h = 1–4; SI Appendix, Table S2) and giving 10 possible host genotypes (i = 1–10; SI Appendix, Table S3). To mount an immune response against a pathogen epitope represented by a particular lowercase letter, a host must possess the recognition allele represented by the corresponding uppercase letter. The various combinations of epitopes, E_j, to which a host could be immune are shown in SI Appendix, Table S4; of these, only a subset {E_k}ⁱ will be accessible to host genotype i (e.g., host genotype AXAX can only be immune to epitope sets E₁, E₃, or E₅). A host immune to the epitopes in E_j can be infected by any pathotype not displaying those epitopes. Hosts immune to the epitopes in E_k can become immune to the epitopes of E_j by being infected by strain p, where strain p contains epitopes in E_j but not in E_k.

The dynamics of this system can be described by the following set of equations:

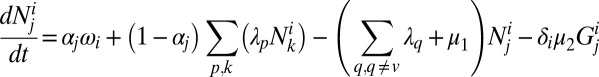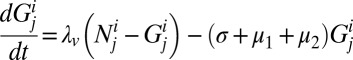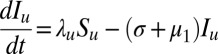Here, 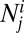is the number of hosts of genotype i who are immune to the set of epitopes E_j. 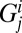is the number of these hosts who are infected with strain v, to which they can never mount an immune response and from which they risk dying at a rate 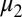; this only applies to homozygous hosts in this system (Fig. 1), so 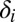= 0 for all heterozygous host genotypes. 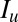is the number of hosts who are currently infected with pathogen strain u and will become immune to at least one of the epitopes of strain u. S_u is the sum of all those hosts who are not yet immune to strain u but are capable of becoming immune to at least one of the epitopes of u. All individuals recover from infection at rate 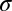and suffer a natural mortality rate .

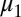The force of infection with strain p is 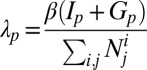, where 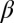is a transmission coefficient, such that 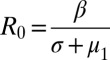for the pathogen in a population of hosts that can mount an immune response against it, and 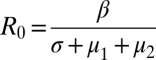in a population of hosts that cannot mount an immune response against it. In the figures and figure legends, we always quote R₀ values for a pathogen in a host population that can mount an immune response against it.

Pathogen mutation can be included in the model by allowing small perturbations in the force of infection. In the model presented here we included pathogen mutation at rate m by adjusting the force of infection term, thus

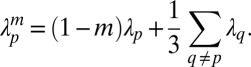The term 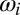represents the births into the fully susceptible compartment of genotype i (thus if j = 0, α_j = 1, if j > 0, α_j = 0). The birth term for host genotype i is given by the following:

where 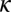is the total death rate for the entire population; 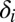is defined as above, and f_h and f_g are the frequencies of the haplotypes that make up host genotype i.

Haplotype frequencies are calculated as follows, where r is the host recombination rate. If r = 0.5, the two host loci are effectively unlinked.

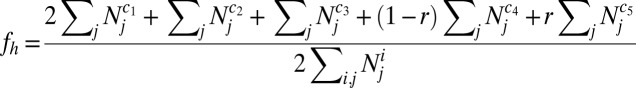See SI Appendix, Table S5 for the values of c_1–5 that correspond to a particular haplotype.

The total death rate is calculated as follows:

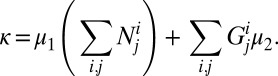Numerical simulations were carried out using the ode45 solver in MatLab version 7.10.0 (R2010b).

Stochastic Model.

A full description of the stochastic model is provided in SI Appendix, section 1. Briefly, the population was made up of N hosts, where N < C, the population carrying capacity. Each host was represented by a 19-element identifier code that recorded age, genotype, infection, and immunity status. As in the deterministic model, host genotype AX/AX was only capable of becoming immune to pathogen epitopes a and x, and risked death when infected with a pathogen it could not recognize. Infection, recovery, mortality, and reproduction were all probabilistic events.

Metrics.

We used a standard metric (Lewontin’s D′, normalized where necessary for >2 alleles per locus, as described in ref. 17) to measure LD.

The f* metric for nonoverlap between two loci was calculated as described in ref. 18 and adjusted as follows:

where 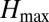= the frequency of the most frequent haplotype in the population. 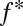takes values between 0 and 1, where values closer to 1 indicate a more nonoverlapping pattern. However, 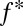= 1 for a population that consists of one haplotype only, which is not a case of true nonoverlap. For 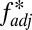, by contrast, populations containing relatively balanced frequencies of nonoverlapping haplotypes will receive the highest scores.

To calculate 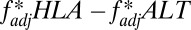from our simulations in Fig. 5, we measured 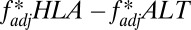every 20 y during the final 2,500 y of a 5,000-y simulation, and took the mean of those measurements.