Abstract
In this paper, we propose a new prostate computed tomography (CT) segmentation method for image guided radiation therapy. The main contributions of our method lie in the following aspects. 1) Instead of using voxel intensity information alone, patch-based representation in the discriminative feature space with logistic sparse LASSO is used as anatomical signature to deal with low contrast problem in prostate CT images. 2) Based on the proposed patch-based signature, a new multi-atlases label fusion method formulated under sparse representation framework is designed to segment prostate in the new treatment images, with guidance from the previous segmented images of the same patient. This method estimates the prostate likelihood of each voxel in the new treatment image from its nearby candidate voxels in the previous segmented images, based on the nonlocal mean principle and sparsity constraint. 3) A hierarchical labeling strategy is further designed to perform label fusion, where voxels with high confidence are first labeled for providing useful context information in the same image for aiding the labeling of the remaining voxels. 4) An online update mechanism is finally adopted to progressively collect more patient-specific information from newly segmented treatment images of the same patient, for adaptive and more accurate segmentation. The proposed method has been extensively evaluated on a prostate CT image database consisting of 24 patients where each patient has more than 10 treatment images, and further compared with several state-of-the-art prostate CT segmentation algorithms using various evaluation metrics. Experimental results demonstrate that the proposed method consistently achieves higher segmentation accuracy than any other methods under comparison.
Keywords: Image guided radiation therapy (IGRT), online update mechanism, patch-based representation, prostate segmentation, sparse label propagation
I. Introduction
PROSTATE cancer is the second leading cause of cancer death for American males [1], [2]. It is estimated by the American Cancer Society that in year 2012, around 241 740 new cases of prostate cancer will be diagnosed, and around 28 170 men will die because of prostate cancer. However, prostate cancer is often curable if diagnosed early. Image guided radiation therapy (IGRT), as a noninvasive approach, is one of the major treatment methods for prostate cancer. During IGRT, high energy X-rays with different doses from different directions are delivered to the prostate to kill the cancer cells. IGRT mainly consists of two main stages, namely the planning stage and the treatment stage. During the planning stage, an image called the planning image is obtained from the patient. Then, the prostate in the planning image is manually delineated and a treatment plan is designed in the planning image space. During the treatment stage, new image called the treatment image is obtained from the same patient on each treatment day. Then, the prostate in each treatment image is segmented so that the treatment plan designed in the planning image space can be transformed to the treatment image space. Although additional dose will be delivered to the patient during the acquisition of treatment computed tomography (CT) image (around 2 cGy), if the treatment target (e.g., prostate) is not accurately localized, higher therapeutic radiation dose (around 200 cGy) could be delivered to the surrounding healthy tissues during the treatment and could cause the severe side effects such as rectum bleeding. In addition, this will also lead to the under-treatment for the prostate tumor and finally the poor outcome for tumor control. Therefore, to improve the efficacy of radiation therapy, it is very helpful to obtain treatment CT image on treatment days prior to treatment. The treatment is usually spread out over a weeks-long series of daily fractions. Since healthy tissues can also be harmed by radiation, it is essential to maximize the dose delivered to the prostate while minimize the dose delivered to its surrounding healthy tissues, to increase the efficiency and efficacy of IGRT. Therefore, the key to the success of IGRT is the accurate segmentation of prostate in the treatment images so that the treatment plan designed in the planning image space can be accurately transformed or even adjusted to the treatment image space.
However, accurate prostate segmentation in CT images remains as a challenging task mainly due to three issues. First, the contrast between the prostate and its surrounding tissues is low in CT images. This issue is illustrated by Fig. 1(a) and (b), where no obvious prostate boundary can be observed. Second, the prostate motion across different treatment days can be large (i.e., usually more than 5 mm), which brings additional difficulty in segmenting prostate in the treatment images. Third, the image appearance on different treatment days can be significantly different even for the same patient due to the uncertainty of the existence of bowel gas. This issue is illustrated by Fig. 1(a) and (c).
Fig. 1.
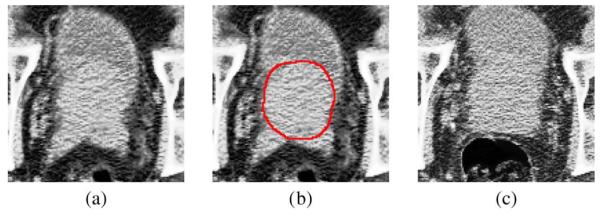
(a) An image slice obtained from a 3-D prostate CT image of a patient. (b) The manually-delineated prostate boundary shown by the red contour, superimposed on the original image in (a). (c) An image slice with bowel gas, obtained from the same patient but at different treatment day.
Many novel prostate CT segmentation methods have been proposed in the literature to deal with the three challenges mentioned above. They can be broadly classified into three main categories: deformable model based methods, registration based methods, and classification based methods. Deformable model based methods [3]–[7] construct the statistical prostate shape and appearance models to guide segmentation in the new treatment images. For instance, Feng et al. [3] integrates both the population information and patient-specific information into a statistical prostate deformable model to segment prostate in the CT images. Chen et al. [4] proposed a Bayesian framework which considered anatomical constraints from bones and learnt appearance information to construct the deformable model. Registration based methods [8]–[11] explicitly estimate the deformation field from the planning image to the treatment image so that the segmented prostate in the planning image can be warped to the treatment image space to localize prostate in the treatment images. For instance, Davis et al. [8] proposed a gas deflation algorithm to reduce the distortion brought by the existence of bowel gas, followed by a diffeomorphic registration algorithm to estimate the deformation field from the planning image to the treatment image after gas deflation. Wang et al. [12] proposed a 3-D deformation algorithm for dose tracking. Liao et al. [13] proposed a feature guided hierarchical registration method to estimate the correspondences between the planning and treatment images. Classification based methods [14]–[16] formulate the segmentation process as a classification problem, where classifiers are trained from the training images and based on which voxel-wise classification is performed for each voxel in the new treatment image to determine whether it belongs to the prostate or nonprostate region. For instance, Li et al. [14] proposed a location-adaptive classification scheme which integrates both image appearance and context features to classify each voxel in the new treatment image. Ghosh et al. [16] combined the high-level texture features and prostate shape information with the genetic algorithm to identify the best matching region in the new to-be-segmented prostate CT image. Moreover, Sannazzari et al. [17] and Chowdhury et al. [18] used both magnetic resonance imaging (MRI) and CT image modality information to help segment prostate in the CT images. It should be noted that many novel methods were also proposed for prostate segmentation in MRI [19]–[24] and ultrasound images [25]–[29]. A comprehensive survey on the existing methods for segmenting prostate in different image modalities was conducted in [30]. In our paper, we focus on prostate segmentation in the CT images.
In recent years, a novel multi-atlases label propagation framework based on the nonlocal mean principle has been proposed [31], [32]. In these papers [31], [32], each voxel is represented by a small image patch centered at this voxel as the signature. Then, the anatomical label of each voxel in the to-be-segmented target image is estimated by comparing the intensity patch-based representation of this voxel with those of the candidate voxels in the atlases. The more similar the intensity patch-based representation of a candidate voxel in the atlas image to that of the reference voxel in the target image, the higher weight this atlas candidate voxel will propagate its anatomical label to the reference voxel in the target image. This framework has many attractive properties, i.e., it allows many-to-one correspondences to identify a set of good candidate voxels in the atlases to perform label fusion, and also it does not require nonrigid image registration as good candidate voxels usually can be identified based on the nonlocal mean principle by local searching.
However, there are two major limitations in the conventional label propagation framework [31], [32], when applied to the prostate CT image segmentation. First, in [31], [32], the patch-based representation is constructed by using only the voxel intensity information, which may not be able to effectively distinguish voxels belonging to the prostate or nonprostate regions, due to low image contrast in the prostate CT images. Second, the weight of each candidate voxel for label propagation is determined by directly comparing the similarity between the patch-based representation of each candidate voxel with that of the reference voxel in the target image, which may not be robust against outlier candidate voxels and thus increase the risk of misclassification.
Therefore, we are motivated to propose a new prostate CT segmentation method in this paper, to resolve the two above-mentioned limitations in the conventional label propagation framework described above. The main contributions of the proposed method lie in the following aspects. 1) To deal with the low image contrast problem in prostate CT images, a new patch-based representation is derived in the discriminative feature space with logistic sparse LASSO [33]. The derived patch-based representation can capture salient features to effectively distinguish prostate and nonprostate voxels and can thus serve as anatomical signature for each voxel. 2) The weight of each candidate voxel during label propagation is estimated by reconstructing the proposed new patch-based signature of each reference voxel in the new prostate CT image from the sparse representation of the patch-based signatures of candidate voxels in both the planning and previous segmented treatment images of the same patient (i.e., called here as training images). The resulting sparse coefficients are used as weights for the candidate voxels. Due to the robustness property of sparse representation against outliers, the segmentation accuracy can be further improved. 3) A hierarchical segmentation strategy is proposed for first segmenting voxels with high segmentation confidence in the new treatment image, and then using their segmentations to provide useful context information for aiding the segmentation of other low-confidence voxels which are more difficult to segment. 4) An online update mechanism is further adopted in this paper, by taking each newly-segmented treatment image as a new training image to help segmentation of future treatment images. A preliminary version of this work was reported in the conference paper [34]. However, in [34], the image context feature is not considered as additional information to aid the segmentation process. In this paper, a new hierarchical labeling strategy is proposed to incorporate both image and context information for further improvement of segmentation accuracy. Moreover, our proposed method is evaluated and analyzed in a more systematic manner, and also the contribution of each proposed component is extensively evaluated in this paper. The flowchart of the proposed method is illustrated in Fig. 2. The proposed method has been extensively evaluated on a prostate CT database consisting of 24 patients with totally 330 images, where each patient has more than 10 treatment images. The proposed method has also been compared with several state-of-the-art prostate CT segmentation algorithms on various evaluation metrics. Experimental results demonstrate that the proposed method consistently achieves higher segmentation accuracy than any other methods under comparison.
Fig. 2.
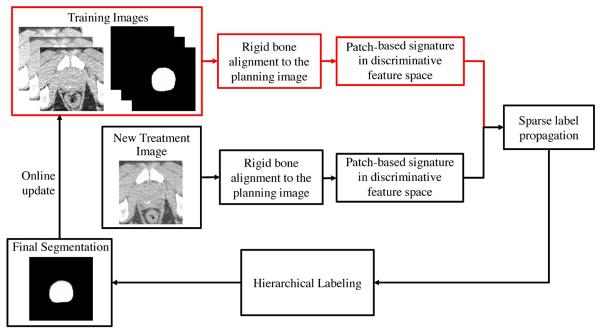
Flowchart of our method for prostate segmentation in CT images, where components associated with the training images are highlighted in red.
The rest of the paper is organized as follows. Section II introduces a new anatomical voxel signature by using patch-based representation in the discriminative feature space. Section III gives details of the proposed sparse label propagation framework, by using the derived patch-based signature to estimate the prostate likelihood of each voxel in the new treatment image and also the hierarchical segmentation strategy to further improve segmentation. The online update mechanism is further described in Section III. Section IV presents experimental results and related analysis. Section V concludes the whole paper.
II. Patch-Based Representation in the Discriminative Feature Space
Patch-based representation has been widely used as voxel anatomical signature in computer vision and medical image analysis [31], [32]. The principle of the conventional patch-based representation is to first define a small K × K image patch centered at each voxel and then use the voxel intensities of image patch as anatomical signature of . Here, K denotes the size of image patch. Patch-based representation has many attractive properties, including its simplicity for calculation and its superior discriminant power for organ recognition [31], [32].
However, due to the low contrast and also anatomical complexity of prostate CT images, patch-based representation using voxel intensities alone may not be able to effectively distinguish prostate and nonprostate voxels. To this end, we propose a patch-based representation in the high-dimensional discriminative feature space. We denote the current available M training images from the same patient as (i.e., including the planning image and the previous segmented treatment images). As illustrated in Fig. 2, each previous segmented treatment image is first rigidly aligned to the planning image, based on the pelvic bone structures similar to [13], for removing the whole-body rigid motion. Specifically, a predefined threshold value +400 is used with respect to Hounsfield units (HU), and regions with intensity of more than +400 are determined as pelvic bone structures. Then, the FLIRT toolkit [35] is used to perform rigid alignment between the identified pelvic bone structures. This is the only preprocessing step for the proposed method. For each training image , it is convolved with a set of feature extraction kernels to produce different feature maps
| (1) |
where n denotes the number of kernels for extracting n different types of features. denotes the resulting feature of Ii(i = 1, …, M) at voxel associated with the jth kernel . In this paper, 14 Haar-wavelet [36], 9 histogram-of-oriented-gradient (HOG) [37], and 30 local-binary-pattern (LBP) [38] kernels are adopted to extract features. As shown in [39], Haar and HOG features can provide complementary anatomical information to each other, and LBP can capture texture information from the input image. More advanced image features may also be used in the proposed framework [40]–[43].
Based on the feature calculated by (1), we can also obtain patch-based representation of each voxel . Suppose a K × K patch is adopted, and then each voxel has a K × K × n dimensional anatomical signature, denoted as . In this paper, 2-D patch is used for each voxel in each slice, since the slice thickness of prostate CT images (3 mm) is too larger, compared with in-plane voxel size (1 × 1 mm2), and thus the correlation between neighboring slices may be not high. However, the segmentation process in our method is performed on the whole 3-D volume of prostate CT image, which will be made clear below.
It should be noted that may also contain noisy and redundant features which will finally affect the segmentation accuracy. Therefore, feature selection should be performed in order to identify the most informative and salient features in . Note that feature selection can also be viewed as a binary variable regression problem with respect to each dimension of the original feature. Therefore, the logistic function is used as the regression function, instead of using the standard linear regression function, based on the following reasons [44]. 1) Logistic function does not require the homogeneity of variance assumption for the variables, which is required by linear regression and this assumption does not hold for binary variables. 2) For binary variables, the predicted value obtained by linear regression does not have physical meaning since for binary variables the predicted value is not a probability or likelihood. 3) Logistic regression is very robust with the assumption that the number of training samples is large. In our application, a sufficient number of sample voxels can be drawn from the planning and previous segmented treatment images of the patient.
The logistic function [44] represents a conditional probability model with the form defined by
| (2) |
where denotes the original feature signature of voxel , and y is a binary variable with y = +1 denoting that is belonging to the prostate region and y = −1 otherwise. and b are parameters of the model.
Moreover, the aim of feature selection is to select a small subset of most informative feature as anatomical signature, which can be well accomplished by enforcing the sparsity constraint during the logistic regression process. Therefore, the feature selection problem can be finally formulated as a logistic sparse LASSO problem. Specifically, P voxel samples are drawn from the training images, with their corresponding patch-based signature and also anatomical label Lc. Here, label Lc = 1 if belongs to the prostate, and Lc = −1 otherwise. Intuitively, voxels around the prostate boundary are more difficult to be correctly classified than voxels in other regions. Therefore, more samples should be drawn around the prostate boundary during the features selection process. In this paper, a parameter ζ is used to control the ratio between the number of samples drawn around the prostate boundary and the number of samples drawn from other prostate regions. Voxels which lie within 3 mm from the prostate boundary are considered as voxels around the prostate boundary. Since the ground truth prostate boundary is available for each training image, those voxels around the prostate boundary can be easily drawn. Fig. 3(a) shows a typical example of the voxel samples drawn from a training image with ζ = 5.
Fig. 3.
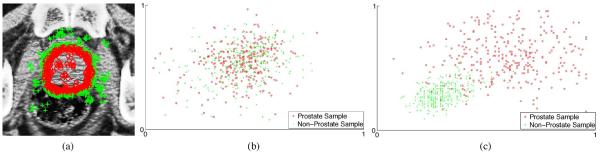
(a) Typical example showing sample voxels drawn from a training image. Samples belonging to the prostate regions are highlighted by small red circles, and samples belonging to the nonprostate regions are highlighted by green crosses. Here, more samples are drawn around the prostate boundaries, which are most difficult to be correctly classified. Scatter plots of the top two most discriminant features (selected based on the Fisher's separation criteria) are shown for (b) intensity patch-based representation and (c) patch-based representation in discriminative feature space, for the drawn samples in (a).
Based on the drawn voxel samples and their patch representations in the feature space, we aim to minimize the logistic sparse LASSO energy function in (3) [45]
| (3) |
where is the sparse coefficient vector, ∥ · ∥1 is the L1 norm, b is the intercept scalar, and λ is the regularization parameter. The first term of (3) is obtained by inputting the label values of drawn samples and their original feature signatures to the logistic function in (2), and then take the logarithm for maximum likelihood estimation. The second term of (3) is the L1 norm which aims to enforce the sparsity constraint for LASSO. The optimal solution ( and bopt) to minimize (3) can be estimated by Nesterov's method [46]. The final selected features are those with nonzero entries in (i.e., ). These selected features have superior discriminant power to distinguish prostate and nonprostate voxels. We denote the final signature of each voxel as .
Based on the selected features, we can directly measure their discriminant power to separate prostate and nonprostate voxels quantitatively, based on the Fisher's score [47]–[49].
The higher Fisher's score indicates the higher discriminative power of the representative feature. Table I lists the average Fisher score by using different types of image features to distinguish prostate and nonprostate voxels in 330 prostate CT images used in this paper, including voxel intensity, intensity-patch-based signature, patch-based signature in the feature space, and patch-based signature in the feature space after logistic LASSO based feature selection. The voxel intensity alone is served here as the baseline in this paper. It can be observed from Table I that all other three types of feature signatures outperform the baseline (i.e., voxel intensity alone), and the patch-based signature in the discriminative feature space after logistic LASSO based feature selection has the highest Fisher score.
TABLE I.
Mean Values of Fisher Score for Different Types of Feature Signatures on the 330 Prostate CT Image Volumes, to Reflect Their Discriminative Power in Separating Prostate and Nonprostate Voxels
| Features | Intensity | Intensity Patch | Patch in Feature Space | Patch in Feature Space + Logistic Lasso |
|---|---|---|---|---|
| Fisher Score | 2.15 | 5.83 | 8.89 | 12.14 |
Fig. 3 also visualizes the superior discriminant power of the proposed patch-based signature in the discriminative feature space. Specifically, we first rank each feature according to its discriminative power based on Fisher's score, and then show the joint distribution of the top two features with the highest Fisher's scores for the conventional patch-based signature [Fig. 3(b)] and for the proposed patch-based signature in the discriminative feature space [Fig. 3(c)] for the voxel samples shown in Fig. 3(a). It can be observed that the proposed patch-based signature can separate prostate and nonprostate voxels better than the conventional intensity patch-based signature.
In the next section, details will be given on how to integrate the proposed patch-based signature with a hierarchical sparse label fusion framework to segment prostate in the new treatment images.
III. Hierarchical Prostate Segmentation in New Treatment Images With Sparse Label Fusion
In this section, details of the proposed hierarchical sparse label propagation method will be given. In Section III-A, the general multi-atlases based label propagation framework is briefly reviewed and discussed. Section III-B gives the motivation and further demonstrates the advantage of enforcing the sparsity constraint in the conventional label propagation framework for estimating the prostate probability map. Section III-C introduces the hierarchical labeling strategy to integrate the image context feature from the new treatment image for guiding segmentation. Section III-D describes how to obtain the final segmentation result from the estimated prostate probability map and discusses some possible alternative strategies. Finally, Section III-E describes the online update mechanism.
A. General Multi-Atlases Based Label Propagation
Multi-atlases based image segmentation [31], [32], [50]–[54] is a hot research topic in medical image analysis and many novel methods have been proposed. Among them, one of the most popular multi-atlases based image segmentation methods is the nonlocal mean label propagation strategy [31], [32], and it can be summarized as follows. Given M pelvic bone aligned training images and their segmentation ground truths {(i, Si), i = 1, …, M} (also called as atlases), for a new treatment image Inew, each voxel in Inew is correlated to each voxel in Ii with a graph weight . Then, the corresponding label for the voxel in Inew can be estimated by performing label propagation from the atlases as below
| (4) |
where Ω denotes the image domain, and SMA denotes the prostate probability map of Inew estimated by multi-atlases based labeling. if voxel belongs to the prostate region in Ii, and otherwise.
The physical meaning of (4) can be illustrated by Fig. 4, where the patch-based representation of the reference voxel in the new treatment image is highlighted by the small green square, and the candidate voxels lying within the searching window highlighted by the purple square in each training image contribute to the estimation of prostate probability for the reference voxel. The contribution of each candidate voxel in the training image Ii during label propagation is represented by its corresponding graph weight , and its corresponding anatomical label in the ground truth segmentation image can be propagated to the reference voxel in the target image with a weight .
Fig. 4.
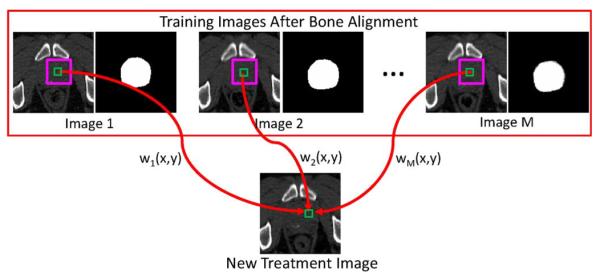
Schematic illustration of general nonlocal mean label propagation expressed by Equation (4). In this example, M training images are available, together with their segmentation ground truths. The patch-based representation of the reference voxel is denoted by the small green square in the new treatment image. The pink squares denote the searching window, where voxels lying within the searching window in each training image are served as candidate voxels. For each candidate voxel in the ith training image, its contribution is determined by the graph weight .
Therefore, the core problem to perform label propagation based on (4) is how to define the graph weight with respect to each candidate voxel , which reflects the contribution of during label fusion. In the next section, we propose a novel method to estimate the graph weight by using sparse representation of the derived patch-based signature of each voxel in the discriminant feature space.
B. Sparse Representation Based Label Propagation
As discussed in Section III-A and illustrated in Fig. 4, the core problem of the nonlocal mean based label propagation is how to define the graph weight in (4). In [31], [32], is determined based on the intensity patch difference between the reference voxel and candidate voxel . Similar to [31], [32], with the patch-based signature derived in Section II, the most straightforward way to define the graph weight is given by
| (5) |
where , with and denote the patch-based signature at of Inew and at of Inew, respectively. The heat kernel Φ(q) = e−q is used similar to [32]. γ is the smoothing parameter, and Σ is a diagonal matrix which represents the variance in each feature dimension. denotes the neighborhood of voxel in image Ii, and it is defined as the W × W × W subvolume centered at .
However, the graph weight defined by (5) may not be able to effectively identify the most representative candidate voxels in atlases to estimate the prostate probability of a reference voxel, especially when the reference voxel is located near the prostate boundary, which is the most difficult region to segment correctly. Fig. 5 shows a typical example, where Fig. 5(a) shows a prostate CT image slice with the reference voxel highlighted by the green cross (i.e., a voxel belonging to the prostate region but close to the prostate boundary). The prostate boundary of the ground truth is highlighted by the red contour. Fig. 5(b) shows this reference voxel's graph weights to the candidate voxels from training images, estimated by (5). Without loss of generality, we use blue to highlight the graph weights corresponding to the prostate sample voxels, and red to highlight the graph weights corresponding to the nonprostate sample voxels.
Fig. 5.
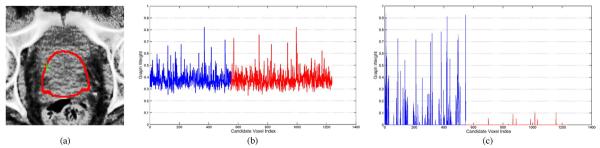
(a) Prostate CT image slice, with the reference voxel highlighted by the green cross and the prostate boundary of the segmentation ground truth highlighted by the red contour. Note that the reference voxel is in the prostate region but close to the prostate boundary. (If needed, please refer to the electronic version of the paper to better see the green cross.) (b) and (c) Graph weights to the training sample voxels, estimated by the conventional label propagation strategy and the proposed sparse label propagation strategy, respectively. Graph weights highlighted in blue are corresponding to the prostate sample voxels, while graph weights highlighted in red are corresponding to the nonprostate sample voxels.
It can be observed from Fig. 5(b) that, with the conventional label propagation strategy, lots of nonprostate sample voxels are also assigned with large weights during the label propagation step, which significantly increases the risk of misclassification.
Motivated by the superior discriminant power of sparse representation based classifiers (SRC) [55], we propose to enforce the sparsity constraint in the conventional label propagation framework to resolve this issue. More specifically, we estimate the sparse graph weights based on LASSO to reconstruct the patch-based signature of each voxel by signature of neighboring voxels in the training images. To do this, we first organize signatures , as columns in a matrix A, which is also called as dictionary. Then, we can estimate the corresponding sparse coefficient vector of voxel by minimizing
| (6) |
We denote the optimal solution of (6) as . Note that the graph weight can be set to the corresponding element in with respect to in image Ii.
Then, the prostate probability map SMA estimated by (4) can be used to localize the prostate in the new treatment image. Fig. 5(c) shows the resulting graph weight estimated by the proposed sparse label propagation strategy. It can be observed from Fig. 5(c) that by enforcing the sparsity constraint, candidate voxels assigned with large graph weights are all from the prostate regions, while candidate voxels from nonprostate regions are mostly assigned with zero or very small graph weights. These results show the advantage of the proposed sparse label propagation strategy.
C. Hierarchical Labeling Strategy
It should be noted that up to this stage, no image context information is incorporated from the new treatment image to aid the segmentation process. It is demonstrated in [14] that the image context information also plays an important role in correctly identifying the prostate region in the new treatment image. In [14], the context features are extracted from each voxel position based on the prostate probability map calculated at each iteration, without considering the confidence level of the classification result, which may accumulate and propagate the segmentation errors to the next iteration. Specifically, the use of the image context information extracted from voxels with low segmentation confidence may significantly increase the risk of misclassification (e.g., with prostate likelihood value close to 0.5).
Therefore, we are motivated to propose a hierarchical labeling strategy which incorporates the image context information of the new treatment image into the segmentation process in an effective and reliable manner. It should be noted that, in our application, voxels around the prostate center and the voxels far away from the prostate can be classified accurately, with the high and low prostate likelihood values estimated, respectively. Therefore, in the proposed hierarchical labeling strategy, only those voxels with high confidence level (i.e., with high or low prostate likelihood values in the current estimated prostate probability map) will be selected from the new treatment image as additional candidate voxels to perform label fusion in the next iteration. The schematic illustration of the hierarchical labeling strategy can be illustrated by Fig. 6, where the probability map estimated by the context information will be iteratively updated, and it will be integrated with the probability map estimated from atlases only to produce the final fused probability map. Note that only the probability map estimated by the context information will be iteratively updated, and the probability map estimated from atlases needs to be calculated only once from Section III-B. The probability map estimated from atlases is also served as the initialization of the final fused probability map.
Fig. 6.
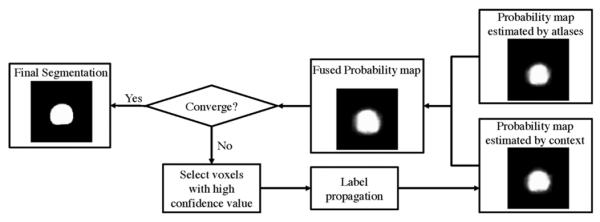
Schematic illustration of the hierarchical labeling strategy. In each iteration, only voxels with high segmentation confidence will be selected as additional candidate voxels to reflect the image context information and contribute in the label propagation process in the next iteration. The probability map estimated by the context information will be iteratively updated, and it will be integrated with the probability map estimated from atlases only to produce the final fused probability map. Note that the probability map estimated from atlases needs to be calculated only once.
Voxels with high segmentation confidence encode important context information which can be used to help the segmentation process. The selection criteria can be controlled by two parameters and in [0, 1] at each iteration k, which represent the thresholds for selecting voxels with high confidence level belonging to the prostate and nonprostate regions, respectively. We denote the new prostate probability map estimated by fusing the context information with the prostate probability map SMA estimated by multiple atlases as at iteration k. Voxels with probability map value or at the kth iteration will be selected as additional candidate voxels to perform label fusion at the (k + 1)th iteration. In the initial stage of segmentation, and are set to be higher and lower values, respectively, for selecting only the most reliable voxels from the new treatment image for reducing the risk of making wrong segmentations in the initial stages and propagating errors to future iterations. As the segmentation process continues, these two threshold values will be gradually relaxed such that more and more voxels from the current treatment image can contribute to refine the final segmentation result. In this paper, and are iteratively updated based on
| (7) |
where ∈ > 0 is the relaxation parameter used in the hierarchical labeling framework.
We denote the set of voxels x ∈ Inew which satisfy the condition or at iteration k as ψk. Then, the prostate probability map at iteration k for the current treatment image can be calculated by
| (8) |
where is the prostate probability map estimated from only the registered training images (i.e., registered atlases) based on (4) and (6). τ is the parameter controlling the weight of the prostate likelihood value estimated by atlases and the context information from the current treatment image. is the prostate probability map estimated based on the context information at iteration k, which is calculated by
| (9) |
where denotes the neighborhood of voxel in current treatment image Inew, and it is defined as the W × W × W subvolume centered at . denotes the graph weight between voxels and in current treatment image Inew. In this paper, is defined similar to (5), instead of defining it based on sparse representation. The main reason is that the number of candidate voxels selected from Inew is significantly smaller than those from training images Ii (i = 1,…,M), thus using sparse representation based on this small number of sample voxels may lead to unstable graph weights.
It should be noted that in each iteration k, only voxels (i.e., voxels with low confidence level) will be updated with new prostate probability values as illustrated in (8). The proposed hierarchical sparse label fusion strategy can be summarized by Algorithm 1.
Fig. 7 shows a typical example of the prostate probability maps obtained by using different strategies for a new treatment image of a patient. It can be observed that the conventional intensity patch-base signature (i.e., second row) fails to effectively identify the prostate regions, which is consistent with the observations in Fig. 3. On the other hand, the proposed patch-based signature in the discriminative feature space, but without sparse representation based label fusion (i.e., third row), can identify the overall outline of the prostate correctly.
|
|
|
Algorithm 1 Hierarchical Sparse Label Propagation |
| Input: M pelvic-bone-aligned training images and their segmentation groundtruths {(Ii, Si), i = 1,…, M}, and the new treatment image Inew to be segmented. |
| Output: The final prostate probability map Sfinal of Inew. |
| 1. Perform sparse label fusion based on Equations 4 and 6 to calculate SM A from registered training images, and initialize . |
| 2. Initialize and . |
| 3. Initialize ψ1 = ∅. |
| 4. FOR voxels |
| 5. IF or |
| 6. . |
| 7. END IF |
| 8. END FOR |
| 9. FOR k = 2 to K |
| 10. FOR voxels |
| 11. Calculate by Equation 9. |
| 12. Update by Equation 8. |
| 13. END FOR |
| 14. Set ψk = ∅. |
| 15. Update and by Equation 7. |
| 16. FOR voxels |
| 17. IF or |
| 18. . |
| 19. END IF |
| 20. END FOR |
| 21. END FOR |
| 22. Set . |
| 23. Return Sfinal. |
|
|
This result indicates that more anatomical characteristics can be captured in the high-dimensional feature space. Moreover, with the sparse representation based label fusion strategy, most prostate regions can be identified correctly (i.e., fourth row). However, without using the image context information, the prostate boundary still cannot be accurately located, especially in the apex area. With the hierarchical label fusion strategy described in Algorithm 1 to integrate the image context information, the final obtained probability map (i.e., the fifth row) can localize the prostate boundary accurately. Therefore, the contributions of using both the patch-based representation in the discriminative feature space and the hierarchical sparse label fusion strategy are clearly demonstrated in this example.
Fig. 7.
First row shows different slices of a prostate CT image, overlayed with the manual segmentation ground-truth indicated by the red contours. Second row shows the corresponding probability maps obtained by the conventional label propagation process with the intensity patch-based voxel signature. Third row shows the probability maps obtained with the proposed patch-based voxel signature in the discriminative feature space, but using the conventional label propagation. Fourth row shows the probability maps obtained with the proposed patch-based voxel signature in the discriminative feature space and the proposed sparse label propagation strategy, but without considering the image context information. Fifth row shows the probability maps obtained with the proposed patch-based voxel signature in the discriminative feature space by integrating the image context information into the sparse label propagation framework as detailed in Algorithm 1.
D. Final Binary Prostate Segmentation
After obtaining the final prostate probability map Sfinal by Algorithm 1, the prostate can be localized in the new treatment image by performing image registration from the segmentation ground truth of each training image Si (i = 1,…, M) to Sfinal. We denote the registered segmentation ground truth to Si (i = 1,…,M) to Sfinal as . In this paper, the affine transformation is adopted due to the relative small intra-patient shape variation, and particularly the FLIRT toolkit [35] is used for this process. Finally, the majority voting scheme is used to obtain the segmentation result of the new treatment image based on , and the morphological operations are further performed to remove the isolated voxels in the segmentation result. One of the advantages of using this strategy to obtain the final binary segmentation result, other than performing simple thresholding on the prostate probability map Sfinal, is that we can make use of the prostate shape information in the planning image and previous segmented treatment images of the same patient to preserve the topology and shape of the prostate in the final segmentation result.
It is worth noting that more advanced registration algorithms [56], [57] can also be used in this step to register the segmentation ground truth of each training image to the estimated prostate probability map Sfinal of new treatment image. For example, the multi-resolution nonrigid image registration method implemented in the Elastix registration toolkit [58], based on the fast free form deformation transformation [59], could also be used in this step.
E. Online Update Mechanism
Similar to [13], an online update mechanism is also adopted in this paper, where each segmented new treatment image will be added into the training set to help segmentation of future treatment images. It is worth pointing out that manual adjustments on the automatic segmentation results are also feasible for the online update mechanism as the manual adjustments can be completed offline when the patient has already left the table. In this paper, the automated segmentations obtained by the proposed method were used for the online update, given the fact that the proposed method can already provide accurate segmentation results in all cases (i.e., even the worst Dice ratio obtained by the proposed method can still achieve 86.9% as shown in Section IV). It is certain that manual adjustment for the automated segmentations, if available, could further increase the segmentation accuracy. But, on the other hand, this requires extra effort from the radiation oncologist.
IV. Experimental Results
The segmentation accuracy of the proposed method and the contribution of its respective component are systematically evaluated on a 3-D prostate CT image database with 24 patients. Here, each patient has more than 10 treatment images, and 24 patients totally have 330 images. Each image is collected on a Siemens Primatom CT-on-rails scanner with in-plane image size of 512 × 512 and voxel size of 1 × 1 mm2, while having interslice thickness of 3 mm. The manual segmentation of each image is also provided by a clinical expert and served as ground truth. In all the experiments, the following parameter settings are adopted for the proposed method: Patch size K = 5, and searching window size W = 15 [i.e., the size of the neighborhood used in (5)]. γ = 1 in (5), and λ = 10−4 in (3) and (6). and , with ∊ = 0.05 in (7). We set τ = 0.5 for (8). The number of iterations K in Operation 9 of Algorithm 1 is set to 5. The planning image and the first two treatment images are served as the initial training images for each patient, which means that, in clinical applications, radiation oncologists only need to manually label the planning image and the first two treatment images of the underlying patient, and the proposed method can perform automatic segmentation for the rest of the treatment images.
In this paper, four different evaluation measures are adopted to evaluate the segmentation accuracy of the proposed method: the signed centroid distance (CD), Dice Ratio, average surface distance (ASD), and the true positive fraction statistics (TPF) between the ground truth and the estimated prostate volumes.
A. Overall Segmentation Performance of the Proposed Method
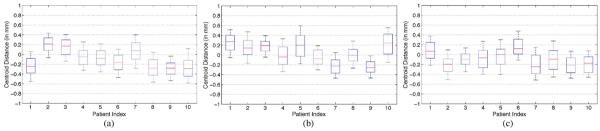
We first study the overall segmentation performance of the proposed method. Fig. 8(a)–(c) shows the whisker plot of the CD measure along the lateral (x), anterior–posterior (y), and superior–inferior (z) directions, respectively, for each patient after performing only the rigid bone alignment. It can be observed that even after the rigid bone alignment, the CD values between the ground truth and the estimated prostate volumes are still considerablely large (i.e., mostly more than 5 mm). This indicates that the prostate motion relative to bones can be large across different treatment days, which is consistent with the findings in [60].
Fig. 8.
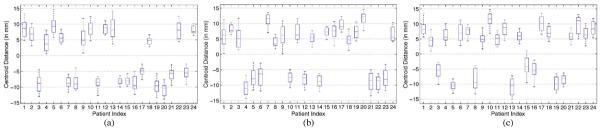
Centroid distance between the bone-aligned prostate volume and the segmentation ground truth along the (a) lateral, (b) anterior–posterior, and (c) superior–inferior directions, respectively. The horizontal lines in each box represent the 25th percentile, median, and 75th percentile, respectively. The whiskers extend to the most extreme data points.
Fig. 9(a)–(c) shows the whisker plots of CDs along the three different directions for each patient, after using the proposed method. It can be observed that the prostate position estimated by the proposed method is very close to the ground truth, (i.e., the median CDs for all the patients are mostly within 0.2 mm along all the three directions). Therefore, the high segmentation accuracy is achieved by the proposed method.
Fig. 9.
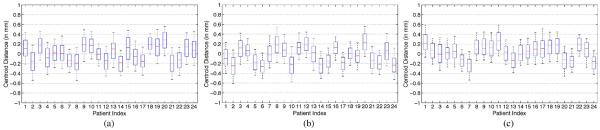
Centroid distance between the prostate volume estimated by the proposed method and the ground truth along the (a) lateral, (b) anterior–posterior, and (c) superior–inferior directions, respectively.
To further illustrate the effectiveness of the proposed method, Fig. 10(a)–(c) shows the whisker plots of ASDs, TPFs and Dice ratios of the 24 patients between the ground truth and the estimated prostate volumes by applying the proposed method, respectively. It can be observed that the proposed method can achieve small ASD values (i.e., the median ASDs for all the patients are mostly less than 1.5 mm), high TPFs (i.e., the median TPFs for all the patients are mostly above 90%), and high Dice ratios (i.e., the median Dice ratios for all the patients are mostly above 90%). The low ASD value indicates that the prostate boundaries have been localized accurately. TPF reflects whether the prostate volume is underestimated, and high TPF indicates that high percentage of the ground truth volume is overlapped with the estimate prostate volume. The high Dice ratios also shed light on the effectiveness of the proposed method.
Fig. 10.

Whisker plots of (a) average surface distance, (b) true positive fraction, and (c) Dice ratio between the estimated prostate by the proposed method and the segmentation ground truth for each patient.
The Hausdorff distance (i.e., the maximal surface distance) between the estimated prostate volume and the segmentation ground truth was also calculated to evaluate the worst-case performance of the proposed method, and the whisker plot of the Hausdorff distance of each patient is shown in Fig. 11. It can be observed from Fig. 11 that, for most patients, the median Hausdorff distance is below 2.5 mm, and the median Hausdorff distances for all the patients are below 3 mm, which illustrates the robustness of the proposed method.
Fig. 11.
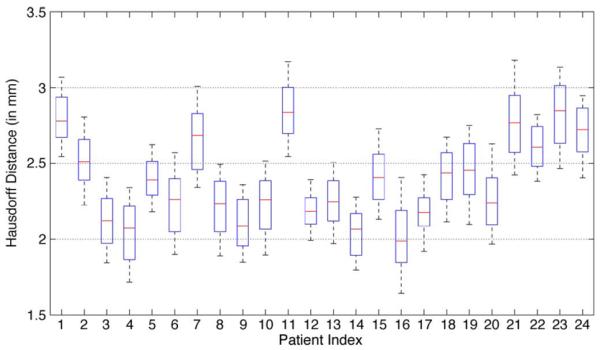
Whisker plots of the Hausdorff distance between the estimated prostate by the proposed method and the segmentation ground truth for each patient.
Typical segmentation results obtained by the proposed method are shown in Fig. 12. It can be observed that the prostate boundary estimated by the proposed method is visually very close to that of the ground truth, especially in the apex area of the prostate, which is usually the most difficult area to segment accurately. It can also be observed that the proposed method can accurately estimate the prostate boundary even in the case with existence of bowel gas, which further implies the robustness of the proposed method.
Fig. 12.
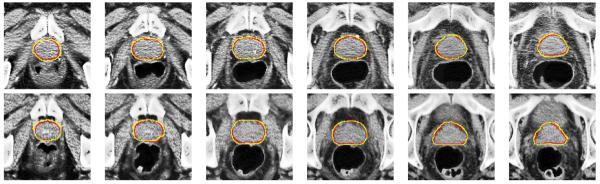
Typical performance of the proposed method on six slices of the sixth treatment image of the 16th patient (first row) and the seventh treatment image of the third patient (second row). The corresponding Dice ratios of these two treatment images are 91.04% and 90.69%, respectively. The red contours denote the manual-delineated prostate boundaries, and the yellow contours denote the prostate boundaries estimated by the proposed method.
The parameters of the proposed method such as the patch size and the size of the searching window W were determined by cross validation. Fig. 13 also shows the mean Dice ratios obtained by the proposed method with different patch size K and different searching window size W to study the sensitivity of the proposed method with respect to different parameter values. It can be observed that, when the patch size K is too small (i.e., K = 3), the Dice ratio decreases as it is not sufficient to fully capture the anatomical properties of each voxel to serve as the signature. On the other hand, if the patch size K is too large (i.e, K = 7 and K = 9), the generalizability power of the voxel signature may decrease as the signature is too specific for a reference voxel and it is hard to find similar candidate voxels in atlases to perform label propagation. Similar observations can also be found with respect to the size of the searching window W. If W is too small, good candidate voxels in atlases may be missed during the label propagation process. However, if W is too large, the confusing and outlier candidate voxels may be considered and the segmentation accuracy will be degraded during label propagation. In this paper, we found that, by setting and K = 5 and W = 15, the proposed method achieves satisfactory segmentation accuracies based on cross validation.
Fig. 13.
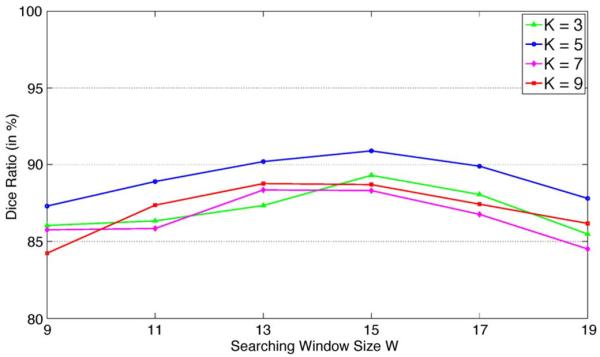
Mean Dice ratios obtained by the proposed method with different patch size K and different searching window size W.
The training phase of the proposed method takes 28.6 min on average, for completing the rigid-bone alignment and also the feature selection for the patch-based representation. It should be noted that the training phase can be completed offline, when the patient has already left the table. After the training step, it takes around 2.6 min on average to segment a whole 3-D treatment image using parallel implementation (i.e., the prostate probability of each voxel can be estimated independently), compared to 15–20 min [4] for a clinical expert to perform joint prostate and rectum volume segmentation of one treatment image. All the experiments were conducted on an Intel Xeon 2.66-GHz CPU computer with MATLAB implementation.
B. Effectiveness of the Discriminant Patch-Based Representation and Hierarchical Sparse Label Propagation Strategy
In this section, we further justify the advantage of using the discriminant patch-based representation and the hierarchical sparse label propagation strategy in a patient-specific basis. Specifically, Fig. 14 shows the average Dice ratio between the estimated prostate volume and the ground truth segmentation of each patient by using 1) the conventional label propagation framework based on intensity patch-based representation [31], [32], 2) label propagation with discriminant patch-based (DisPatch) representation derived in this paper, 3) discriminant patch-based representation with sparse label propagation (Sparse + DisPatch), and 4) the proposed method by also enforcing the hierarchical labeling strategy.
Fig. 14.
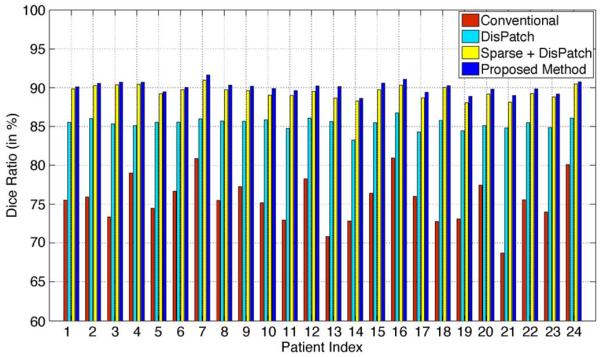
Average Dice ratios of the 24 patients obtained by using 1) the conventional label propagation strategy with intensity patch-based representation [31], [32], 2) label propagation with the proposed discriminant patch-based representation (DisPatch) in the feature space, 3) discriminant patch-based representation with sparse label propagation (Sparse + DisPatch), and 4) the proposed method by further enforcing the hierarchical labeling strategy.
It can be observed from Fig. 14 that, by using the discriminant patch-based representation in the feature space, the average Dice ratio of each patient significantly increases compare to the use of only the intensity patch-based representation in [31], [32]. Therefore, the effectiveness of the proposed discriminant patch-based representation in the feature space to resolve the issue of low image contrast in prostate CT image is clearly demonstrated, which echoes the empirical illustration shown in Fig. 3 that demonstrates the superior discriminant power of the proposed patch-based representation in feature space. Also, by enforcing the sparsity constraint during label propagation, the average Dice ratio of each patient generally can be further improved from 3% to 5%, which reflects the strength of sparse representation to identify good candidate voxels in atlases for label propagation. Finally, by adopting the hierarchical labeling strategy, the segmentation accuracy can also be slightly and consistently improved for each patient.
C. Effectiveness of the Online Update Mechanism
In this section, we study the role of the online update mechanism and the relationships between the segmentation accuracy of the proposed method and the number of available training images.
Figs. 15 and 16 show the difference of the Dice ratio with and without using the online update mechanism for the first 12 patients and the rest of the 12 patients, respectively. Note that the total number of treatment images of each patient is different. If the online update mechanism is not adopted, then only the planning image and the treatment images of the first two treatment days are served as the training images (i.e., same as the initial training set as stated in the beginning of Section IV). If the online update mechanism is adopted, each new treatment image will be included in the training set once it is segmented by the proposed method, to aid the segmentation process for the future treatment images. It can be observed from Figs. 15 and 16 that, by adopting the online update mechanism, in most treatment images the segmentation accuracy can be improved, compared to the case without using the online update mechanism (i.e., for most cases, the difference of the Dice ratio with and without using the online update mechanism is above the zero horizontal line). Therefore, the significance of the online update mechanism is clearly demonstrated. It is also worth pointing out that manual adjustment is also feasible for this online update mechanism, as it can be done offline when the patient has already left the table, which is an important and useful feature for real-world clinical applications.
Fig. 15.
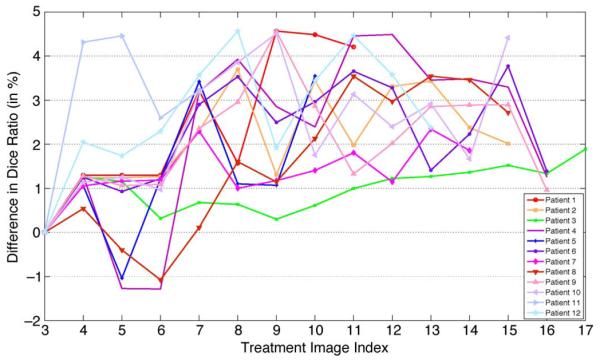
Difference of the Dice ratio of different treatment days of the first 12 patients by using the proposed method with and without using the online update mechanism.
Fig. 16.
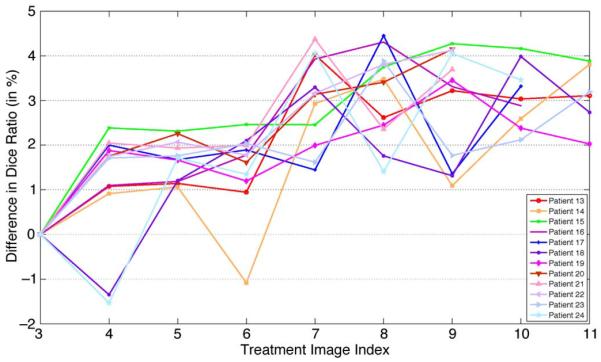
Difference of the Dice ratio of different treatment days of the other 12 patients by using the proposed method with and without using the online update mechanism.
Fig. 17 also shows the average Dice ratios obtained for each patient with and without using the online update mechanism. It can be observed that, when the online update mechanism is adopted, the average Dice ratio for each patient is consistently higher (i.e., mostly 2%–4% higher) than that without using the online update mechanism. Therefore, the importance of using the online update mechanism to progressively learn more patient-specific information from each new segmented treatment image is clearly demonstrated.
Fig. 17.
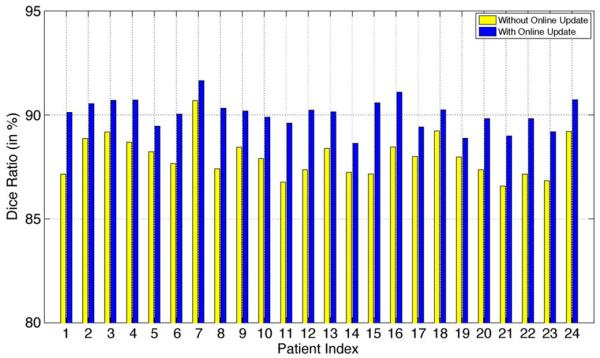
Average Dice ratio of each patient obtained by the proposed method with and without using the online update mechanism.
D. Comparison With Other Methods
In this section, the proposed method is compared with five state-of-the-art prostate CT segmentation methods proposed by Davis et al. [8], Feng et al. [3], Chen et al. [4], Liao et al. [13], and Li et al. [14]. The best segmentation accuracies reported in these papers [3], [4], [8], [13] and [14] are adopted for comparison, as those results were assumed to be obtained with the optimal parameter setting for different methods. It should be noted that in [3] and [13], the methods were evaluated on exactly the same database as used in this paper, which also consists of 24 patients with 330 images in total.
The method proposed by Davis et al. [8] is one of the representatives of the registration based methods for automatic CT prostate segmentation. This method first performs the gas deflation process to suppress the distortions brought by the existence of bowel gas. Then, diffeomorphic image registration is performed to warp the planning image and its corresponding segmentation ground truth onto the gas deflated treatment image to localize the prostate. It was evaluated based on the Dice ratio and CD evaluation measures in [8].
The methods proposed by Feng et al. [3] and Chen et al. [4] use deformable model based segmentation. In [3], both gradient and statistical features are adopted to construct the image appearance model to guide the segmentation process, while in [4] the intensity similarity and shape anatomical constraints are both considered in a Bayesian framework. These two methods are different from the proposed method as they are deformable model based methods which need to build the shape prior to guide the segmentation, while the proposed method is a multi-atlases based sparse label propagation method where no shape prior is needed. In [3], the method was evaluated based on the mean Dice ratio and mean ASD evaluation measures, and in [4] the method was evaluated based on the mean ASD, median probability of detection (PD), and the median probability of false alarm (FA).
Liao et al. [13] proposed a feature-guided deformable registration based prostate segmentation method. Specifically, an explicit Gaussian score similarity function is adopted to learn the most salient features to drive the registration process. It was evaluated on the mean Dice ratio, mean ASD, mean CDs along three different directions, median PD and median FA evaluated measures.
Li et al. [14] proposed a classification based prostate segmentation method which integrates both the image appearance and context features. It was evaluated on the mean Dice ratio, mean ASD, mean CDs along three different directions, median PD and median FA evaluated measures.
We have also included two other state-of-the-art multi-atlases based segmentation algorithms proposed by Klein et al. [22] and Coupe et al. [31] for comparison. The method proposed by Klein et al. [22] adopted the multi-resolution fast free form deformation (FFD) to register the atlases to target image and then performed majority voting (MV) scheme for label fusion. This method is denoted as (FFD + MV) in this paper. The method proposed by Coupe et al. [31] is the conventional intensity patch-based label propagation (LP) approach, and it is denoted as (Intensity LP) in this paper.
The comparisons among different approaches are summarized in Table II. It can be observed that the proposed method consistently has higher segmentation accuracy than any other methods under comparison using different evaluation measures, which reflects the superior segmentation accuracy and robustness of the proposed method. In Table II, we also report the minimum Dice ratio obtained by different approaches, which is an important measure to evaluate the robustness and stability of different approaches. Specifically, in clinical application, low Dice ratio indicates that the target defined for radiation therapy is either underestimated or overestimated. For the former case, it means that we may miss the therapy of cancerous tissue, which often leads to poor outcome of tumor control. For the latter case, the healthy tissues surrounding the prostate will be mistakenly treated with high radiation dose, which can often cause side effects on normal structures, e.g., rectal bleeding and painful urination. It is shown in [8] that the average Dice ratio of inter-rater manual segmentation is around 79%. Therefore, Dice ratio of 80% can serve as the baseline for the minimum Dice ratio to evaluate the robustness of different methods. It can be observed from Table II that the minimum Dice ratio obtained by the proposed method is 86.9%, which is significantly higher than those obtained by Feng's method [3] (i.e., 42.4%) and Li's method [14] (i.e., 75.3%). Therefore, the proposed method can provide more accurate and robust segmentation results to help automatically segment the prostate in the later-time treatment images.
TABLE II.
Comparison of Different Approaches With Different Evaluation Metrics, Where N/A Indicates That the Corresponding Result was Not Reported in the Respective Paper. The Best Results Across Different Methods are Bolded. The Last Four Rows Show the Results Obtained by the Proposed Method by Using 1) Only the Discriminative Patch Based Representation (DisPatch), 2) the Discriminative Patch Based Representation With Sparse Coding (S + DisPatch), 3) the Discriminative Patch Based Representation With Sparse Coding and Hierarchical Labeling Strategy (HS + DisPatch), and 4) the Proposed Method by Further Adopting the Online Update Mechanism, Respectively
| Methods | Mean Dice Ratio | Min Dice Ratio | Mean ASD (in mm) | Mean CD (x/y/z) (in mm) | Median PD | Median FA |
|---|---|---|---|---|---|---|
|
| ||||||
| Davis el al. [8] | 82.0 | N/A | N/A | −0.26/0.35/0.22 | N/A | N/A |
| Feng el al. [3] | 89.3 | 42.4 | 2.08 | N/A | N/A | N/A |
| Chen et al. [4] | N/A | N/A | 1.10 | N/A | 0.84 | 0.13 |
| Liao el al. [13] | 89.9 | 86.1 | 1.08 | 0.21/−0.12/0.29 | 0.89 | 0.11 |
| Li el al. [14] | 90.8 | 75.3 | 1.40 | 0.18/−0.02/0.57 | 0.90 | 0.10 |
| FFD + MV [22] | 79.4 | 57.6 | 3.18 | −0.32/0.28/0.37 | 0.78 | 0.21 |
| Intensity LP [31] | 77.7 | 51.4 | 3.47 | 0.48/−0.31/0.51 | 0.76 | 0.23 |
|
| ||||||
| DisPatch | 85.4 | 67.3 | 2.26 | −0.27/−0.25/0.23 | 0.85 | 0.14 |
| S + DisPatch | 87.6 | 76.7 | 1.54 | 0.23/0.22/−0.25 | 0.86 | 0.13 |
| HS + DisPatch | 88.3 | 82.4 | 1.23 | 0.21/0.21/−0.24 | 0.88 | 0.12 |
| Proposed Method | 90.9 | 86.9 | 0.97 | 0.17/0.09/0.18 | 0.90 | 0.08 |
To clearly demonstrate the contribution of each component of the proposed method, in Table II, we also report and compare the segmentation accuracies obtained by the proposed method by adding each component in a progressive manner. Specifically, the last four rows of Table II list the segmentation accuracies obtained by the proposed method by using 1) only the discriminative patch based representation (DisPatch), 2) the discriminative patch based representation with sparse coding (S + DisPatch), 3) the discriminative patch based representation with sparse coding and hierarchical labeling strategy (HS + DisPatch), and 4) the proposed method by further adopting the online update mechanism, respectively. It can be observed that the segmentation accuracies consistently and progressively increase by adding each component of the proposed method, which illustrates the contribution of each component in the proposed method.
E. Generalizability to Other Dataset
In order to test the generalizability of the proposed method, the proposed method was also evaluated on an additional prostate CT image dataset consisting of 10 patients with 100 images in total, where each patient has a planning image and nine treatment images. The images were obtained from the University of North Carolina Cancer's Hospital, using different CT scanners other than those used in Section IV-A. Each image has in-plane resolution 1 × 1 mm2, with interslice thickness from 3 to 5 mm, and the manual segmentation ground truth of each image is available. The same parameter setting was used for the proposed method as that in Section IV-A.
Similar to Section IV-A, the signed centroid distance (CD), Dice ratio, average surface distance (ASD), and the true positive fraction statistics (TPF) between the estimated prostate volume and the ground truth segmentations were used as metrics to evaluate the segmentation accuracy of the proposed method. Fig. 18(a)–(c) shows the whisker plot of CDs of each patient along the three different directions obtained by the proposed method. It can be observed from Fig. 18 that the proposed method still achieves satisfactory segmentation accuracy as the median CDs along all the directions are mostly within 0.3 mm. Fig. 19(a)–(c) also shows the whisker plots of ASD, TPF and Dice ratio for each patient, and the low ASD value (i.e., mostly below 1.5 mm), high TPF (i.e., mostly above 85%) and Dice ratio (i.e., mostly above 85%) values further imply the effectiveness of the proposed method.
Fig. 18.
Centroid distance between the prostate volume estimated by the proposed method and the segmentation ground truth along the (a) lateral, (b) anterior–posterior, and (c) superior–inferior directions, respectively, on the additional prostate CT image dataset.
Fig. 19.
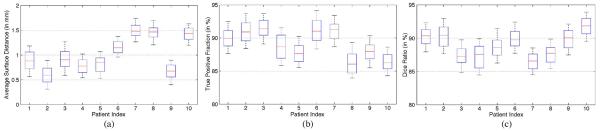
Whisker plots of (a) average surface distance, (b) true positive fraction, and (c) Dice ratio between the estimated prostate by the proposed method and the segmentation ground truth for each patient on the additional prostate CT image dataset.
The overall segmentation performance of the proposed method on this dataset is summarized in Table III and compared with two multi-atlases based segmentation algorithms as in Section IV-D. It can be observed from Table III that the proposed method still achieves higher segmentation accuracy than the other methods under comparison, therefore the generalizability and robustness of the proposed method is demonstrated.
TABLE III.
Overall Segmentation Accuracies of Different Approaches With Different Evaluation Metrics on the Additional Prostate CT Image Dataset. Best Results Across Different Methods are Bolded
Typical segmentation results of the proposed method on this additional prostate CT image dataset are also visually shown in Fig. 20. It can be observed from Fig. 20 that the estimated prostate boundary by the proposed method is very close to the segmentation ground truth, which further illustrates the satisfactory segmentation accuracy of the proposed method.
Fig. 20.
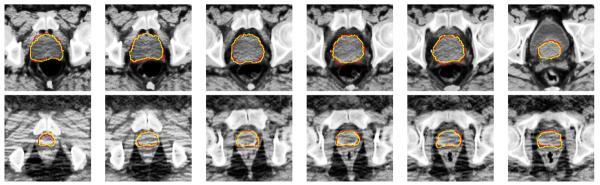
Typical performance of the proposed method on six slices of the eighth treatment image of the second patient (first row) and the third treatment image of the third patient (second row) in the additional prostate CT image dataset. The corresponding Dice ratios of these two treatment images are 90.16% and 88.82%, respectively. The red contours denote the manual-delineated prostate boundaries, and the yellow contours denote the prostate boundaries estimated by the proposed method.
V. CONCLUSION
In this paper, we propose a new method for semi-automatic prostate segmentation in CT images, which is an important step for image guided radiation therapy in prostate cancer treatment. Specifically, a new patch-based representation is derived in the discriminative feature space, by first extracting anatomical features from image patch of each voxel position, and then selecting the most informative features with the logistic LASSO regression process. Moreover, a hierarchical sparse label propagation framework is proposed. Different from the conventional label propagation strategy, the proposed label propagation method formulates the problem of determining weight of each atlas voxel in label fusion as a sparse coding problem. Specifically, the weight assigned to each atlas sample voxel is determined by its corresponding sparse coefficient to reconstruct the derived patch-based signature of the reference voxel. It is shown that, by enforcing the sparsity constraint, the new label propagation framework is more robust and can significantly reduce the risk of misclassification. To further increase the robustness of the proposed framework and incorporate the image context information in the current treatment image, the label propagation process is formulated in a hierarchical manner. Specifically, voxels with high confidence level, based on the estimated prostate probability map, are first labeled, and further used as additional sample voxels to provide the image context information for helping estimate the prostate likelihood of the remaining voxels. Finally, an online update mechanism is also adopted to progressively learn more patient-specific information from each new segmented treatment image. The proposed method has been both qualitatively and quantitatively evaluated on a prostate CT image database consisting of 24 patients and 330 images, by comparison with several state-of-the-art prostate CT image segmentation methods. It is shown that the proposed method consistently achieves higher segmentation accuracy than any other methods under comparison.
Acknowledgments
This work was supported in part by the National Institutes of Health (NIH) under Grant CA140413, in part by the National Science Foundation of China under Grant 61075010, and in part by the National Basic Research Program of China (973 Program) under Grant 2010CB732505.
REFERENCES
- [1].Cancer facts and figures 2012. Amer. Cancer Soc. [Online]. Available: http://www.cancer.org.
- [2].Shen D, Lao Z, Zeng J, Zhang W, Sesterhenn I, Sun L, Moul J, Herskovits E, Fichtinger G, Davatzikos C. Optimized prostate biopsy via a statistical atlas of cancer spatial distribution. Med. Image Anal. 2004;8:139–150. doi: 10.1016/j.media.2003.11.002. [DOI] [PubMed] [Google Scholar]
- [3].Feng Q, Foskey M, Chen W, Shen D. Segmenting CT prostate images using population and patient-specific statistics for radio-therapy. Med. Phys. 2010;37:4121–4132. doi: 10.1118/1.3464799. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [4].Chen S, Lovelock D, Radke R. Segmenting the prostate and rectum in CT imagery using anatomical constraints. Med. Image Anal. 2011;15:1–11. doi: 10.1016/j.media.2010.06.004. [DOI] [PubMed] [Google Scholar]
- [5].Smitsmans M, Wolthaus J, Artignan X, DeBois J, Jaffray D, Lebesque J, van Herk M. Automatic localization of the prostate for online or offline image guided radiotherapy. Int. J. Radiat. Oncol., Biol., Phys. 2004;60:623–635. doi: 10.1016/j.ijrobp.2004.05.027. [DOI] [PubMed] [Google Scholar]
- [6].Stough J, Broadhurst R, Pizer S, Chaney E. Regional appearance in deformable model segmentation. Inf. Process. Med. Imag. 2007:532–543. doi: 10.1007/978-3-540-73273-0_44. [DOI] [PubMed] [Google Scholar]
- [7].Freedman D, Radke R, Zhang T, Jeong Y, Lovelock D, Chen G. Model-based segmentation of medical imagery by matching distributions. IEEE Trans. Med. Imag. 2005 Mar;24(3):281–292. doi: 10.1109/tmi.2004.841228. [DOI] [PubMed] [Google Scholar]
- [8].Davis B, Foskey M, Rosenman J, Goyal L, Chang S, Joshi S. Automatic segmentation of intra-treatment CT images for adaptive radiation therapy of the prostate. Medical Image Computing Comput. Assist. Intervent. 2005:442–450. doi: 10.1007/11566465_55. [DOI] [PubMed] [Google Scholar]
- [9].Zhou L, Liao S, Li W, Shen D. Learning-based prostate localization for image guided radiation therapy. Int. Symp. Biomed. Imag. 2011:2103–2106. [Google Scholar]
- [10].Foskey M, Davis B, Goyal L, Chang S, Chaney E, Strehl N, Tomei S, Rosenman J, Joshi S. Large deformation three-dimensional image registration in image-guided radiation therapy. Phys. Med. Biol. 2005;50:5869–5892. doi: 10.1088/0031-9155/50/24/008. [DOI] [PubMed] [Google Scholar]
- [11].Martin S, Daanen V, Troccaz J. Atlas-based prostate segmentation using an hybrid registration. Int. J. Comput. Assist. Radiol. Surg. 2008;3:485–492. [Google Scholar]
- [12].Wang H, Dong L, Lii M, Lee A, de Crevoisier R, Mohan R, Cox J, Kuban D, Cheung R. Implementation and validation of a three-dimensional deformable registration algorithm for targeted prostate cancer radiotherapy. Int. J. Radiat. Oncol. Biol. Phys. 2005;61:725–735. doi: 10.1016/j.ijrobp.2004.07.677. [DOI] [PubMed] [Google Scholar]
- [13].Liao S, Shen D. A feature-based learning framework for accurate prostate localization in CT images. IEEE Trans. Image Process. 2012 Aug;21(8):3546–3559. doi: 10.1109/TIP.2012.2194296. [DOI] [PubMed] [Google Scholar]
- [14].Li W, Liao S, Feng Q, Chen W, Shen D. Learning image context for segmentation of prostate in CT-guided radiotherapy. Phys. Med. Biol. 2012;57:1283–1308. doi: 10.1088/0031-9155/57/5/1283. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [15].Haas B, Coradi T, Scholz M, Kunz P, Huber M, Oppitz U, Andre L, Lengkeek V, Huyskens D, Esch A, R. R. Automatic segmentation of thoracic and pelvic CT images for radiotherapy planning using implicit anatomic knowledge and organ-specific segmentation strategies. Phys. Med. Biol. 2008;53:1751–1772. doi: 10.1088/0031-9155/53/6/017. [DOI] [PubMed] [Google Scholar]
- [16].Ghosh P, Mitchell M. Segmentation of medical images using a genetic algorithm. Proc. 8th Annu. Conf. Genetic Evolution. Comput. 2006:1171–1178. [Google Scholar]
- [17].Sannazzari G, Ragona R, Redda M, Giglioli F, Isolato G, Guarneri A. CT-MRI image fusion for delineation of volumes in three-dimensional conformal radiation therapy in the treatment of localized prostate cancer. Br. J. Radiol. 2002;75:603–607. doi: 10.1259/bjr.75.895.750603. [DOI] [PubMed] [Google Scholar]
- [18].Chowdhury N, Toth R, Madabhushi A, Chappelow J, Kim S, Motwani S, Punekar S, Lin H, Both S, Vapiwala N, Hahn SA. Concurrent segmentation of the prostate on MRI and CT via linked statistical shape models for radiotherapy planning. Med. Phys. 2012;39:2214–2228. doi: 10.1118/1.3696376. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [19].Makni N, Puech P, Lopes R, Dewalle A, Colot O, Betrouni N. Combining a deformable model and a probabilistic framework for an automatic 3-D segmentation of prostate on MRI. Int. J. Comput. Assist. Radiol. Surg. 2009;4:181–188. doi: 10.1007/s11548-008-0281-y. [DOI] [PubMed] [Google Scholar]
- [20].Pasquier D, Lacornerie T, Vermandel M, Rousseau J, Lartigau E, Betrouni N. Automatic segmentation of pelvic structures from magnetic resonance images for prostate cancer radiotherapy. Int. J. Radiat. Oncol. Biol. Phys. 2007;68:592–600. doi: 10.1016/j.ijrobp.2007.02.005. [DOI] [PubMed] [Google Scholar]
- [21].Chandra S, Dowling J, Shen K, Raniga P, Pluim J, Greer P, Salvado O, Fripp J. Patient specific prostate segmentation in 3-D magnetic resonance images. IEEE Trans. Med. Imag. 2012 Oct;31(10):1955–1964. doi: 10.1109/TMI.2012.2211377. [DOI] [PubMed] [Google Scholar]
- [22].Klein S, Heide U, Lips I, Vulpen M, Staring M, Pluim J. Automatic segmentation of the prostate in 3-D MR images by atlas matching using localized mutual information. Med. Phys. 2008;35:1407–1417. doi: 10.1118/1.2842076. [DOI] [PubMed] [Google Scholar]
- [23].Toth R, Madabhushi A. Multi-feature landmark-free active appearance models: Application to prostate MRI segmentation. IEEE Trans. Med. Imag. 2012 Aug;31(8):1638–1650. doi: 10.1109/TMI.2012.2201498. [DOI] [PubMed] [Google Scholar]
- [24].Zhan Y, Ou Y, Feldman M, Tomaszeweski J, Davatzikos C, Shen D. Registering histological and MR images of prostate for image-based cancer detection. Acad. Radiol. 2007;14:1367–1381. doi: 10.1016/j.acra.2007.07.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [25].Zhan Y, Shen D. Deformable segmentation of 3-D ultrasound prostate images using statistical texture matching method. IEEE Trans. Med. Imag. 2006 Mar;25(3):256–272. doi: 10.1109/TMI.2005.862744. [DOI] [PubMed] [Google Scholar]
- [26].Shen D, Zhan Y, Davatzikos C. Segmentation of prostate boundaries from ultrasound images using statistical shape model. IEEE Trans. Med. Imag. 2003 Apr;22(4):539–551. doi: 10.1109/TMI.2003.809057. [DOI] [PubMed] [Google Scholar]
- [27].Ghanei A, Soltanian-Zadeh H, Ratkewicz A, Yin F. A three dimensional deformable model for segmentation of human prostate from ultrasound images. Med. Phys. 2001;28:2147–2153. doi: 10.1118/1.1388221. [DOI] [PubMed] [Google Scholar]
- [28].Zhan Y, Shen D. Automated segmentation of 3-D US prostate images using statistical texture-based matching method. Med. Image Comput. Computer-Assisted Intervent. 2003:688–696. [Google Scholar]
- [29].Zhan Y, Shen D, Zeng J, Sun L, Fichtinger G, Moul J, Davatzikos C. Targeted prostate biopsy using statistical image analysis. IEEE Trans. Med. Imag. 2007 Jun;26(6):779–788. doi: 10.1109/TMI.2006.891497. [DOI] [PubMed] [Google Scholar]
- [30].Ghose S, Oliver A, Marti R, Llado X, Vilanova J, Freixenet J, Mitra J, Sidibe D, Meriaudeau F. A survey of prostate segmentation methodologies in ultrasound, magnetic resonance and computed tomograph images. Comput. Methods Programs Biomed. 2012;108:262–287. doi: 10.1016/j.cmpb.2012.04.006. [DOI] [PubMed] [Google Scholar]
- [31].Coupe P, Manjon J, Fonov V, Pruessner J, Robles M, Collins D. Patch-based segmentation using expert priors: Application to hippocampus and ventricle segmentation. NeuroImage. 2011;54:940–954. doi: 10.1016/j.neuroimage.2010.09.018. [DOI] [PubMed] [Google Scholar]
- [32].Rousseau F, Habas P, Studholme C. A supervised patch-based approach for human brain labeling. IEEE Trans. Med. Imag. 2011 Oct;30(10):1852–1862. doi: 10.1109/TMI.2011.2156806. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [33].Liu J, Ji S, Ye J. SLEP: Sparse learning with efficient projections Arizona State Univ. 2009. [Google Scholar]
- [34].Liao S, Gao Y, Shen D. Sparse patch based prostate segmentation in CT images. Med. Image Comput. Computer-Assist. Intervent. 2012:385–392. doi: 10.1007/978-3-642-33454-2_48. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [35].Jenkinson M, Bannister P, Brady M, Smith S. Improved optimization for the robust and accurate linear registration and motion correction of brain images. NeuroImage. 2002;17:825–841. doi: 10.1016/s1053-8119(02)91132-8. [DOI] [PubMed] [Google Scholar]
- [36].Mallat G. A theory for multiresolution signal decomposition: The wavelet representation. IEEE Trans. Pattern Anal. Mach. Intell. 1989 Jul;11(7):674–693. [Google Scholar]
- [37].Dalal N, Triggs B. Histograms of oriented gradients for human detection. IEEE Comput. Soc. Conf. Comput. Vis. Pattern Recognit. 2005:886–893. [Google Scholar]
- [38].Ojala T, Pietikainen M, Maenpaa T. Multiresolution gray-scale and rotation invariant texture classification with local binary patterns. IEEE Trans. Pattern Anal. Mach. Intell. 2002 Jul;24(7):971–987. [Google Scholar]
- [39].Tu Z, Bai X. Auto-context and its application to high-level vision tasks and 3-D brain image segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2010 Oct;32(10):1744–1757. doi: 10.1109/TPAMI.2009.186. [DOI] [PubMed] [Google Scholar]
- [40].Shi Y, Qi F, Xue Z, Chen L, Ito K, Matsuo H, Shen D. Segmenting lung fields in serial chest radiographs using both population-based and patient-specific shape statistics. IEEE Trans. Med. Imag. 2008;41:285–298. doi: 10.1109/TMI.2007.908130. [DOI] [PubMed] [Google Scholar]
- [41].Liao S, Chung A. Nonrigid brain MR image registration using uniform spherical region descriptor. IEEE Trans. Image Process. 2012 Jan;21(1):157–169. doi: 10.1109/TIP.2011.2159615. [DOI] [PubMed] [Google Scholar]
- [42].Liao S, Law W, Chung A. Dominant local binary patterns for texture classification. IEEE Trans. Image Process. 2009 May;18(5):1107–1118. doi: 10.1109/TIP.2009.2015682. [DOI] [PubMed] [Google Scholar]
- [43].Guo Y, Zhao G, Pietikainen M. Discriminative features for texture description. Pattern Recognit. 2012;45:3834–3843. [Google Scholar]
- [44].Menard S. Logistic Regression: From Introductory to Advanced Concepts and Applications. Sage; Thousand Oaks, CA: 2010. [Google Scholar]
- [45].Liu J, Chen J, Ye J. Large scale sparse logistic regression. Proc. 15th ACM SIGKDD Int. Conf. Knowl. Discovery Data Mining. 2009:547–556. [Google Scholar]
- [46].Nesterov Y. Introductory Lectures on Convex Optimization: A Basic Course. Kluwer Academic; Norwell, MA: 2004. [Google Scholar]
- [47].Fisher A. The Mathematical Theory of Probabilities. Macmillan; New York: 1923. [Google Scholar]
- [48].Parry R, Essa I. Feature weighting for segmentation. Proc. ICMIR. 2004:116–119. [Google Scholar]
- [49].Liao S, Chung A. Feature based non-rigid brain mr image registration with symmetric alpha stable filters. IEEE Trans. Med. Imag. 2010 Jan;29(1):106–119. doi: 10.1109/TMI.2009.2028078. [DOI] [PubMed] [Google Scholar]
- [50].van Rikxoort E, Isgum I, Arzhaeva Y, Staring M, Klein S, Viergever M, Pluim J, van Ginneken B. Adaptive local multi-atlas segmentation: Application to the heart and the caudate nucleus. Med. Image Anal. 2010;14:39–49. doi: 10.1016/j.media.2009.10.001. [DOI] [PubMed] [Google Scholar]
- [51].Sabuncu M, Yeo B, Van Leemput K, Fischl B, Golland P. A generative model for image segmentation based on label fusion. IEEE Trans. Med. Imag. 2010 Oct;29(10):1714–1729. doi: 10.1109/TMI.2010.2050897. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [52].Warfield S, Zou K, Wells W. Simultaneous truth and performance level estimation (STAPLE): An algorithm for the validation of image segmentation. IEEE Trans. Med. Imag. 2004 Jul;23(7):903–921. doi: 10.1109/TMI.2004.828354. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [53].Asman A, Landman B. Characterizing spatially varying performance to improve multi-atlas multi-label segmentation. Inf. Process. Med. Imag. 2011:85–96. doi: 10.1007/978-3-642-22092-0_8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [54].Wang H, Suh J, Pluta J, Altinay M, Yushkevich P. Optimal weights for multi-atlas label fusion. Inf. Process. Med. Imag. 2011:73–84. doi: 10.1007/978-3-642-22092-0_7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [55].Wright J, Yang A, Ganesh A, Sastry S, Ma Y. Robust face recognition via sparse representation. IEEE Trans. Pattern Anal. Mach. Intell. 2009 Feb;31(2):210–227. doi: 10.1109/TPAMI.2008.79. [DOI] [PubMed] [Google Scholar]
- [56].Liao S, Chung A. Multi-modal image registration using the generalized survival exponential entropy. Medical Image Computing Computer Assist. Intervent. 2006:964–971. doi: 10.1007/11866763_118. [DOI] [PubMed] [Google Scholar]
- [57].Guo Y, Zhao G, Pietikainen M. Dynamic facial expression recognition using longitudinal facial expression atlases. Eur. Conf. Comput. Vis. 2012:631–644. [Google Scholar]
- [58].Klein S, Staring M, Murphy K, Viergever M, Pluim J. Elastix: A toolbox for intensity-based medical image registration. IEEE Trans. Med. Imag. 2010 Jan;29(1):196–205. doi: 10.1109/TMI.2009.2035616. [DOI] [PubMed] [Google Scholar]
- [59].Rueckert D, Sonoda L, Hayes C, Hill D, Leach M, Hawkes D. Nonrigid registration using free-form deformations: Application to breast MR images. IEEE Trans. Med. Imag. 1999 Aug;18(8):712–721. doi: 10.1109/42.796284. [DOI] [PubMed] [Google Scholar]
- [60].Schallenkamp J, Herman M, Kruse J, Pisansky T. Prostate position relative to pelvic bony anatomy based on intraprostatic gold markers and electronic portal imaging. Int. J. Radiat. Oncol. Biol. Phys. 2005;63:800–811. doi: 10.1016/j.ijrobp.2005.02.022. [DOI] [PubMed] [Google Scholar]



