Broadband Excitation Pulses for High-Field Solid-State Nuclear Magnetic Resonance Spectroscopy

Abstract

In nuclear magnetic resonance spectroscopy, experimental limits due to the radiofrequency transmitter and/or coil means that conventional radiofrequency pulses (“hard pulses”) are sometimes not sufficiently powerful to excite magnetization uniformly over a desired range of frequencies. Effects due to non-uniform excitation are most frequently encountered at high magnetic fields for nuclei with a large range of chemical shifts. Using optimal control theory, we have designed broadband excitation pulses that are suitable for solid-state samples under magic-angle-spinning conditions. These pulses are easy to implement, robust to spinning frequency variations and radiofrequency inhomogeneities, and only four times as long as a corresponding hard-pulse. The utility of these pulses for uniformly exciting ¹³C nuclei is demonstrated on a 900 MHz (21.1 T) spectrometer.

1. Introduction

In this paper, we demonstrate the use of optimal control (OC) theory^[1–3] to design pulses for solid-state nuclear magnetic resonance (NMR) spectroscopy that uniformly excite magnetization across a broad range of frequency offsets. Excitation pulses (i.e., pulses that convert longitudinal magnetization into transverse magnetization) are one of the elementary building blocks of NMR pulse sequences. Unfortunately, uniform excitation of magnetization across a range of chemical shifts is constrained by limits to the amount of radiofrequency field strength that is experimentally accessible. Consequently, a number of pulses shapes have been explored for broadband excitation in solution-state NMR spectroscopy, including composite^[4,5], Gaussian cascade^[6], polychromatic^[7], adiabatic^[8,9], ABSTRUSE^[10], and BEBOP pulses^[11–13].

Achieving uniform excitation has not been as frequent a problem in solid-state NMR spectroscopy. This is primarily because the radiofrequency coils and amplifiers used for solid-state experiments are typically designed to operate at higher power levels than those used for solution-state experiments. In addition, solid-state spectrometers have tended to use lower magnetic fields (due to the use of wide-bore magnets) than solution-state spectrometers with a corresponding reduction in the range of frequencies that need to be excited. As a result, the development of broadband excitation pulses for solid-state NMR has focused on quadrupolar nuclei^[14,15] where the range of frequencies to be excited can be orders of magnitude larger than for ¹³C or ¹⁵N. However, as solid-state NMR spectroscopy moves to using higher magnetic fields, there are now circumstances where it can be difficult to uniformly excite the spectrum for isotopes such as ¹³C.

For conventional radiofrequency pulses, magnetization will not be uniformly excited once the chemical shift offset is on the same order of magnitude as the radiofrequency field strength. For relatively small offsets in simple experiments, the effects due to non-uniform excitation can be partially counteracted by applying a first-order phase correction to the resulting spectrum. For more complicated experiments, non-uniform excitation usually results in reduced signal-to-noise and can also lead to spectral artifacts Although these effects can be reduced by increasing the radiofrequency field strength, in practice the extent to which this can be increased is always limited by saturation of the radiofrequency amplifier or arcing in the probehead. For example, on a 21.1 T spectrometer (900 MHz for ¹H), exciting the full 200 ppm ¹³C spectrum requires covering a ±23 kHz range of chemical shift offsets. A typical 3.2 or 4 mm solid-state MAS probe may only be able to generate ¹³C radiofrequency fields of 50–75 kHz, so off-resonance effects will be apparent (particularly for methyl and carbonyl signals) as the radiofrequency field is not much larger than the maximum chemical shift off-set.

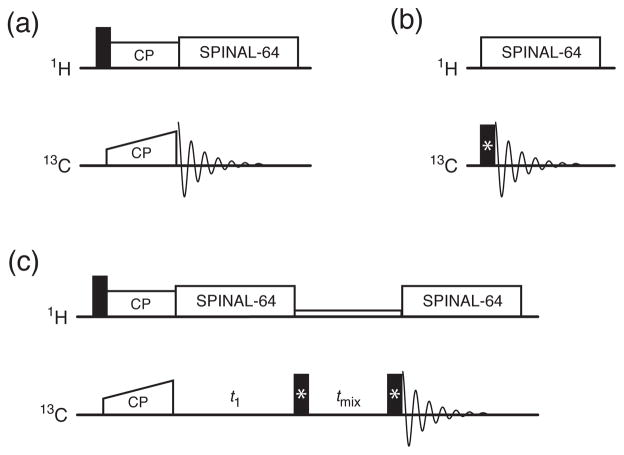
In solid-state NMR spectroscopy, broadband excitation is usually not problematic in cross-polarization magic-angle-spinning (CP-MAS) experiments (Figure 1a), as the observed signal is due to magnetization transfer from the more easily excited ¹H spectrum (where a smaller range of offsets must be covered and the available pulse powers are typically higher) rather than by direct excitation of the ¹³C nuclei (Figure 1b). However, broadband excitation pulses (which convert I_z magnetization to I_x magnetization), as well as “flip-back” pulses to restore magnetization to the longitudinal axis (I_x to I_z), are still needed for experiments such as PDSD^[16] and DARR^[17] (Figure 1c). Consequently, even in experiments where the magnetization begins on ¹H, excitation pulses designed using optimal control theory (^OCEX) can still be a useful addition. ^OCEX pulses can be turned into flip-back pulses (^OCFB) simply by time-reversing the pulse and adding a 180° phase shift, so it is not necessary to repeat the calculations to generate flip-back pulses.

Figure 1.

Pulse sequences mentioned in the text. Filled rectangles represent excitation or flip-back pulses. The ¹H–¹³C CP-MAS experiment (a) does not benefit significantly from ^OCEX pulses as the excitation pulse is on the ¹H channel. For the ¹³C-direction excitation (b) and PDSD/DARR (c) experiments, the pulses replaced with ^OCEX and ^OCFB pulses are indicated with an asterisk (*).

2. Experimental

2.1. Pulse Design

All simulations and optimal control pulse calculations were performed using SIMPSON 3.0.1^[18,19]. The source code and compiled binaries for this program are freely available for download at http://www.bionmr.chem.au.dk/bionmr/software/simpson.php. Optimal control calculations used 20 REPULSION^[20] α, β crystallite angles and 5 γ angles for powder averaging, whereas simulations of calculated pulses used 168 REPULSION angles and 10 gamma angles. Calculations with larger sets of crystallites produced results that were essentially the same but at the expense of increased computation time.

The ^OCEX pulses were generated in an iterative procedure where the best results from each step of the calculation were used as input for the subsequent step. A smoothed random RF field was used as the initial input, and at all points in the calculation the RF amplitude was capped at 50 kHz. We performed the optimization in four steps, where the parameters included in the steps of the calculation were:

1. A narrow band optimization using a single carbon chemical shift offset. The chemical shift anisotropy was set to −76 ppm and asymmetry to 0.90 (values appropriate for carbonyl carbons).

2. Chemical shift offsets were added to ensure uniform excitation over the desired chemical shift range. Eleven chemical shifts that were evenly-spaced over a 50 kHz range of offsets (corresponding to 225 ppm for ¹³C on a 21.1 T spectrometer) were used.

3. An RF inhomogeneity profile was added. The profile used was a 5% Lorentzian (full-width-half-height for the RF profile relative to the nominal RF field strength) with nine points (evenly spaced between 90% and 110% of the nominal field strength).

4. Optimization with the RF amplitude set to constant power (50 kHz).

The fourth step of the optimization was possible as the output from the third step was mostly phase-modulated with only slight variations in the amplitude. The advantage of including this fourth step is that the resulting ^OCEX pulses are of constant amplitude and, consequently, they do not depend on the linearity of the radiofrequency amplifier. This makes setting up the pulses easier. Simulations comparing pulses generated in the third and fourth step reveal that forcing the ^OCEX pulse to have a constant amplitude does not impact the pulse performance (data not shown).

The overall pulse length (10–100 μs), the spinning frequency (13 kHz), and the magnetic field (21.1 T, 900 MHz for ¹H) were all specified at the beginning of the calculation, as was the length of the steps within the pulse. The step length was set to 1 μs, so a 20 μs pulse (^OCEX₂₀) consists of 20 periods each with constant amplitude and phase. As will be seen in the next section, relatively short ^OCEX pulses (20 μs) are sufficiently broadband for our purposes and the pulses are not highly dependent on either the spinning frequency or the magnetic field. Five to ten ^OCEX pulses were calculated for each pulse length and then those with the best simulated performance were tested experimentally. Multiple calculations for each pulse length are necessary as, occasionally, the calculation procedure resulted in less optimal solutions (i.e., local minima) in comparison to other solutions.

2.2. Spectroscopy

The ^OCEX and ^OCFB pulses were tested on a Bruker (Karlruhe, Germany) Avance 900 MHz (21.1 T) spectrometer using a 3.2 mm HXY MAS probe and the pulse sequences shown in Figure 1. The MAS frequency (ν_r ) was set to 13.0 kHz. One-dimensional spectra were acquired with 32 scans and a recycle delay of 3 s. Spectra were acquired using SPINAL-64^{[21] 1}H decoupling with a decoupling field strength of ~85 kHz.

The [1,3-¹³C, U-¹⁵N]-labeled OmpG sample was prepared as described previously^[22]. The sample consisted of ≈10 mg of OmpG and E. coli lipids packed into a 3.2 mm rotor. The sample temperature was maintained at 275 K for all experiments.

3. Results and Discussion

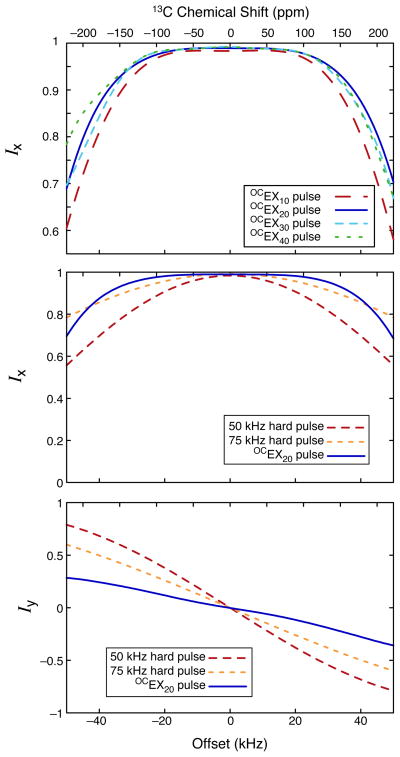
The theoretical excitation efficiencies (i.e., conversion of longitudinal (I_z) magnetization into transverse (I_x) magnetization) as a function of the chemical shift offset for 10–40 μs ^OCEX pulses are shown at the top of Figure 2. 50 and 100 μs ^OCEX pulses were also calculated but performed poorly, so only the shorter pulses are analyzed in the following. As seen in Figure 2, there is no significant improvement in the performance of the ^OCEX pulses for pulse lengths beyond 20 μs. This is because the ^OCEX pulses were designed to cover an offset range of “only” 50 kHz; the ^OCEX₂₀ pulse covers this bandwidth adequately so longer pulses are only needed for optimizations with a larger range of offsets.

Figure 2.

Conversion of longitudinal (I_z) magnetization into transverse (I_x and I_y) magnetization as a function of chemical shift offset for ^OCEX pulses and conventional hard radiofrequency pulses. The chemical shift scale corresponds to ¹³C on a 21.1 T (900 MHz) spectrometer and ν_r =13 kHz.

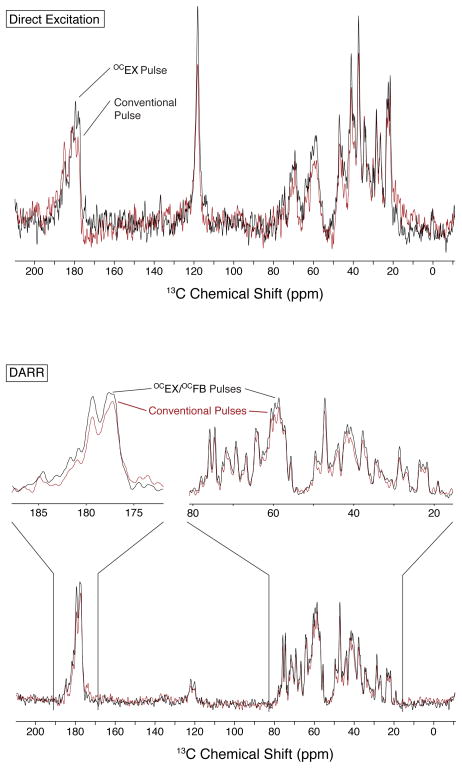
The middle and bottom of Figure 2 compares the ^OCEX₂₀ pulse to conventional 50 and 75 kHz excitation pulses (which have lengths of 5 and 3.33 μs, respectively). Not only is the ^OCEX₂₀ pulse more efficient at converting I_z magnetization into I_x over a broad range of offsets, but also less magnetization is converted to I_y magnetization. Consequently, whereas a 1D direct excitation spectrum taken using a conventional pulse may require a first-order phase correction, a similar spectrum taken using an ^OCEX pulse will usually not require such a correction. This behavior is shown at the top of Figure 3, which shows ¹³C spectra taken with conventional excitation and ^OCEX pulses. The spectra were processed using only a zero-order phase correction to highlight the uniform phase behavior of the ^OCEX pulse. For experiments with multiple excitation and flip-back pulses, the phase behavior of the ^OCEX/^OCFB pulses not only makes processing easier but also improve the signal-to-noise ratio of the resulting spectra. For example, when implemented in a 2D DARR experiment, the use of ^OCEX and ^OCFB pulses resulted in a signal-to-noise gain of 5–10%. The results from the first increments of 2D DARR spectra are shown at the bottom of Figure 3.

Figure 3.

Comparison of 1D ¹³C direction excitation NMR spectra (top) and the first increment from ¹³C DARR spectra (bottom) acquired using [1,3-¹³C, U-¹⁵N] OmpG at 900 MHz for ¹H and with ν_r =13 kHz. The black spectra are from using OCEX and OCFB pulses, whereas the red spectra are from using conventional 50 kHz pulses. No first-order phase correction was applied to the direction excitation spectra. The prominent feature in the middle of the direction excitation spectra (at 120 ppm) is from aromatic resonances that are usually attenuated in ¹H-¹³C CP-MAS spectra.

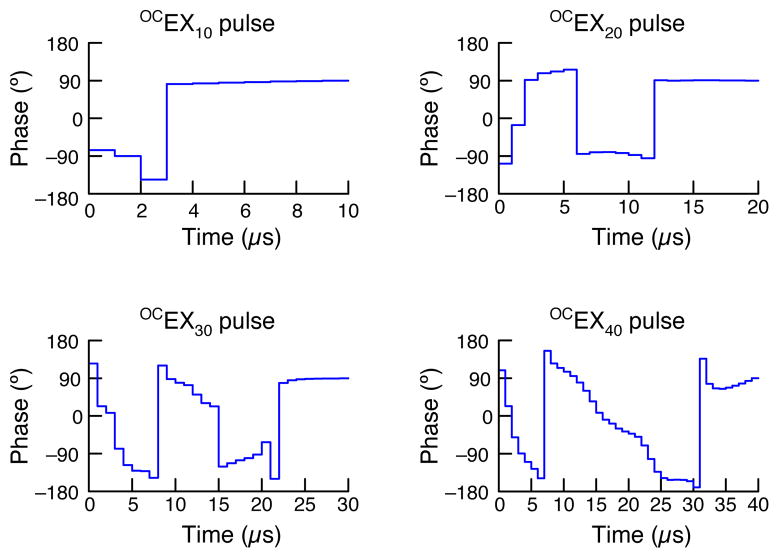
Representative ^OCEX pulses are shown in Figure 4; only the phase is shown, as the amplitude is constant (50 kHz) for all the pulses. For short pulses the solutions look similar to composite pulses whereas longer pulses appear to be quasi-adiabatic (i.e., frequency-swept). For example, the ^OCEX₁₀ pulse approximately corresponds to ${54}_{-y}^{\circ }{126}_y^{\circ }$ and the ^OCEX₂₀ pulse approximately corresponds to ${18}_{-y}^{\circ }{18}_x^{\circ }{72}_y^{\circ }{108}_{-y}^{\circ }{144}_y^{\circ }$. The pulses that we calculated have similar shapes to the BEBOP pulses devised for solution-state NMR by Kobzar et al.^[11–13]. As the BEBOP pulses were also developed using optimal control theory and the physics for magnetization excitation are essentially the same for solution- and solid-state NMR (at least for spin-½ nuclei), the similarities in the resulting pulse shapes are not surprising. The main differences are that the ^OCEX pulses in this paper are optimized to account for RF inhomogeneity and use a constant RF amplitude in addition to having an overall pulse length and power that are appropriate for solid-state NMR under magic-angle-spinning conditions.

Figure 4.

Phase profiles of the 10, 20, 30, and 40 μs ^OCEX pulses.

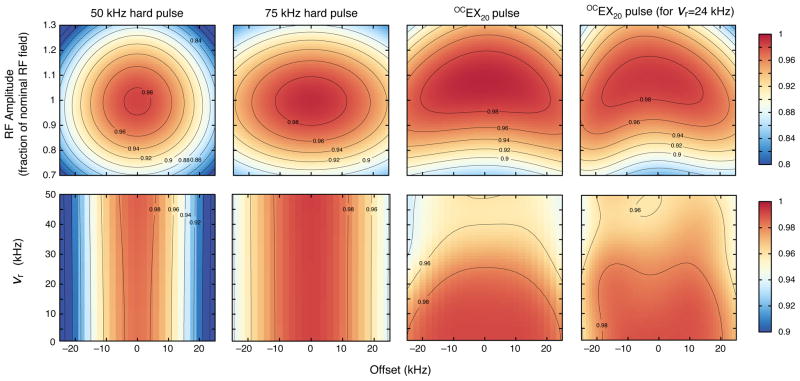
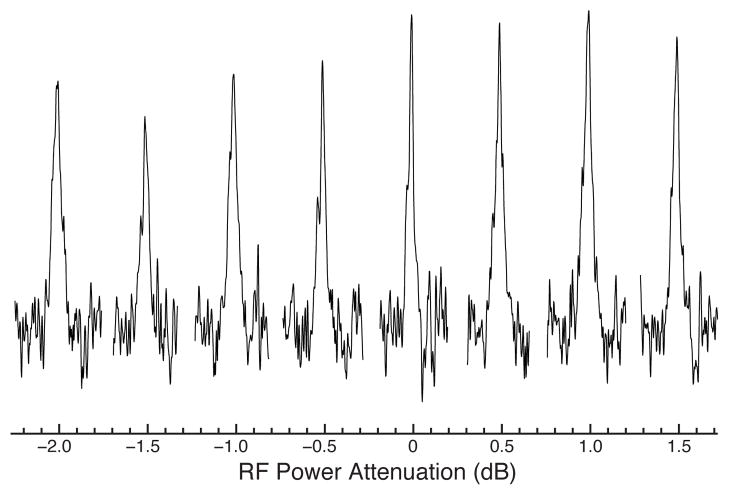
All ^OCEX pulses were optimized to include compensation for inhomogeneity of the RF field. Consequently, ^OCEX pulses should result in more signal than conventional pulses not only due to more uniform excitation but also because regions of the sample where the RF field is non-optimal can still contribute to the NMR signal. A calculation of the tolerance of the ^OCEX₂₀ pulse to RF inhomogeneity as a function of chemical shift offset is shown in the top row of Figure 5, alongside simulations for conventional pulses. The ^OCEX₂₀ pulse has transfer efficiencies in excess of 98% not only over the desired chemical shift range, but also over an approximately ±10% range in RF inhomogeneity. A side effect of this compensation for inhomogeneity is that the ^OCEX pulses are remarkably resilient to miscalibrated pulse power levels. Figure 6 illustrates the experimental excitation profile for the ^OCEX₂₀ pulse with power attenuation levels between −2 dB and 1.5 dB (in 0.5 dB steps). This robustness with respect to RF inhomogeneity is advantageous in long measurements where the sample composition and/or tuning may vary during the course of the experiment, and also means that the ^OCEX pulses are less sensitive to calibration errors than conventional pulses.

Figure 5.

Excitation efficiency as a function of RF inhomogeneity and chemical shift offset (top row) and as a function of spinning frequency (ν_r ) and chemical shift offset (bottom) for 50 and 75 kHz conventional RF excitation pulses and ^OCEX₂₀ pulses designed for 13 and 24 kHz spinning frequencies. In the top row, the first three graphs were calculated for v_r =13 kHz and the fourth for v_r =24 kHz. The color scale represents the transfer efficiency from I_z to I_x and runs from 80–100% (top row) and 90–100% (bottom row).

Figure 6.

RF power dependence for the ^OCEX₂₀ pulse at 900 MHz for ¹H and with ν_r =13 kHz. The horizontal axis corresponds to RF power attenuation (more positive values correspond to smaller RF amplitudes). The individual spectra show the aromatic region from a 1D ¹³C direction excitation experiment using [1,3-¹³C, U-¹⁵N] OmpG.

The bottom row of Figure 5 illustrates how the offset performance of both conventional and optimal control excitation pulses varies with spinning frequency. The optimal control pulses that we have calculated are not very sensitive to the spinning frequency and are superior to conventional pulses for spinning frequencies of up to 20 kHz. At higher spinning frequencies, the optimal control pulses still have relatively uniform excitation properties, but the transfer efficiency begins to decrease. That the ^OCEX and ^OCFB pulses are relatively insensitive to spinning frequency is a little unusual, as most solid-state pulses designed using optimal control are exquisitely sensitive to this parameter (and, consequently, need to be recalculated for every desired spinning frequency)^[23,24]. In the case of our ^OCEX and ^OCFB pulses, the relative insensitivity is probably due to their short length with respect to the rotor period and because they are not designed to recouple an interaction that varies with the rotor position.

We repeated the optimal control calculations with a spinning frequency of 24 kHz (instead of 13 kHz) to see if we could devise a pulse that had good offset performance over an even larger range of spinning frequencies. The transfer efficiency of one such pulse as a function of RF inhomogeneity, spinning frequency, and chemical shift offset is shown in the rightmost column of Figure 5. In comparison to ^OCEX pulses designed for a spinning frequency of 13 kHz, this pulse better covers the desired chemical shift range at spinning frequencies between 15–24 kHz but with the trade-off that it is less well compensated for RF inhomogeneity.

Designing ^OCEX pulses for spinning frequencies in excess of 24 kHz is not necessary, at least for ¹³C on a 21.1 T spectrometer. This is because higher spinning frequencies can only be achieved in MAS probes with a sample diameter smaller than 3.2 mm. Such probes have smaller coils that allow for higher RF amplitudes, which means that conventional pulses are able to adequately cover the ¹³C chemical shift range. However, for isotopes with larger chemical shift ranges (or for future spectrometers operating at even higher field strengths) excitation pulses calculated using optimal control may still be of use.

4. Conclusions

We have found that, at high fields, optimal control excitation and flip-back pulses result in improvements in experiments in which a large bandwidth needs to be efficiently excited or restored to the z-axis. In addition, the spectra that result from using these pulses have better phase properties. Although the signal improvement demonstrated in a DARR experiment is relatively modest (≈10%), pulse sequences with additional excitation and flip-back pulses will typically show even greater improvements. The ^OCEX and ^OCFB pulses are very easy to implement as they are only phase-modulated, and are robust to variations in the power level due to the inclusion of compensation for radiofrequency field inhomogeneities in their design (which makes them relatively forgiving of mismatches in the probe tuning). Unlike most optimal control pulses for solid-state NMR spectroscopy, the ^OCEX pulses perform well over a wide range of spinning frequencies. Consequently, we feel that a large number of experiments could easily benefit from the use of these OC pulses as replacements for conventional excitation and flip-back pulses.