Abstract
It is well-known that end caps and the peptide length can dramatically influence the thermodynamics of the helix–coil transition. However, their roles in determining the kinetics of the helix–coil transition have not been studied extensively and are less well understood. Kinetic Ising models and sequential kinetic models involving barrier crossing via diffusion all predict that the helix formation time depends monotonically on the peptide length with the relaxation time increasing with respect to increasing chain length. Here, we have studied the helix–coil transition kinetics of a series of Ala-based α-helical peptides of different length (19–39 residues), with and without end caps, using time-resolved infrared spectroscopy coupled with laser-induced temperature jump (T-jump) initiation method. The helical content of these peptides was kinetically monitored by probing the amide carbonyl stretching frequencies (i.e., the amide I′ band) of the peptide backbone. We found that the relaxation rates for peptides with efficient end caps are more rapid than those of the corresponding peptides without good end caps. These results indicate that efficient end-capping sequences can not only stabilize preexisting helices but also promote helix formation through initiation. Furthermore, we found that the relaxation times of these peptides, following a T-jump of 1–11 °C, show rather complex behaviors as a function of the peptide length, in disagreement with theoretical predications. Theses results are not readily explained by theories in which Ala is taken to have a single helical propensity (s). However, recent studies have suggested that s depends on chain length; when this factor is considered, the mean first-passage times of the coil-to-helix transition show similar dependence on the peptide length as those observed experimentally.
Introduction
The study of the kinetics of folding of proteins on the millisecond time scale has reached an advanced stage. Using the techniques of site-directed mutagenesis in conjunction with stopped-flow kinetics and hydrogen–deuterium exchange, it has been possible to define the sequence of events involved in folding on the millisecond time scale. In contrast, the kinetics of folding of individual segments of secondary structure or small folding motifs occur on a more rapid time scale4–25 and have been much less extensively studied.
The helix–coil transition is of great importance to protein folding. One model for protein folding suggests that secondary structural elements, such as helices, form independently of tertiary structure.26,27 Since the formation of the α-helix involves a relatively simple conformational search, it constitutes an ideal process suitable for both all-atom computer simulations13,14,17,19,23 as well as simplified kinetic treatments.15,16,18,21,22,28–31 Experimentally, rapid laser-induced T-jump methods have allowed the first investigations of the formation of α-helices.4–11 In these studies, a rapid T-jump pulse induces a shift in the equilibrium between the coil and helix states, and the subsequent relaxation toward the new thermal equilibrium point is probed by examining all of the amide groups via either IR4,8,11 or Raman7 spectroscopy, or individual residues by fluorescence spectroscopy5 or isotope-editing9,10 techniques. However, the peptides used in these studies are rather similar. Therefore, the role of the peptide sequence in defining the kinetics of helix formation has been much less determined. For example, it has long been recognized that helix-capping sequences provide very significant thermodynamic stability to the α–helix,32–37 but their role in the kinetics of folding is not yet known. The classical view would be that the initiation of a single turn of helix occurs in a more or less sequence-independent manner;38 hence the role of end caps is to lock in preexisting helices. However, it is also possible that capping sequences can effectively serve as helix initiators. These two models predict different experimental results. If the capping is not involved in initiation, the rate of helix initiation should not be much affected for peptides with different end caps. On the other hand, if capping interactions are able to initiate helix formation, then the rates of initiation of the helices should be very profoundly affected.
The peptide length is another factor that may also profoundly affect the kinetics of the helix–coil transition, as indicated by a number of theoretical studies (see below). If the kinetically and thermodynamically difficult step in the process of the coil-to-helix transition is initiation of a single turn of helix, as one proceeds in peptide length from short to long the rate of helix formation should not be much affected. Only a small increase would be observed due to a linear, length-dependent increase in the probability of initiation as the peptide is lengthened.
Although the formation of the α–helix involves only local interactions (except the long-range electrostatic interactions), it is still quite challenging to realistically compute its folding trajectory. Most molecular dynamic simulations are therefore either limited to only a few nanoseconds, which are not long enough to catch the entire folding process, or employ simplified potentials as well as implicit solvent models. Hence, the current theoretical descriptions of the kinetics of the helix–coil transition come mostly from simplified phenomenological kinetic models. For example, Schwarz treated the coil-to-helix transition as a series of sequential kinetic events, in which the fundamental process is associated with the elongation of the helix by one extra helical hydrogen bond.28 This propagation step involves an energy barrier. Schwartz showed that the time of helix formation is inversely proportional to the Zimm–Bragg nucleation constant, σ, around the midpoint of the helix–coil transition. Similarly, Brooks proposed a sequential mechanism to describe the coil-to-helix transition.15 This model suggests that while the nucleation step encounters the largest free energy barrier during the course of folding the elongation of the nucleated species needs to diffuse through a series of smaller barriers to equilibrate with the final folded state. Thus, the evolution of kinetic states describing the number of α-helical hydrogen bonds present in the folding polypeptide vs time can be treated analytically by a master equation. With this model, Brooks investigated the folding rates of helices of different length and stability, as judged by the number of α-helical hydrogen bonds and the Zimm–Bragg nucleation (σ) and propagation (s) constants.39,40 The results of Brooks indicate that indeed the meantime for the coil-to-helix transition is scaled with σ–1. Furthermore, Brooks found that both folding and unfolding rates are rather sensitive to the length of the polypeptide with less than ~16 helical hydrogen bonds, and for longer peptides the folding rate approaches an asymptotic value. Subsequently, Jun and Weaver modeled the helix–coil transition as a sequential diffusive kinetic process that is similar to that of Brooks, in which the addition or removal of a single hydrogen bond is treated as a diffusion back and forth over a square barrier.16 They found that it takes longer time for the more cooperative transitions to equilibrate. Their results also show that with other parameters fixed peptides having larger s fold faster, in agreement with the results of Brooks. In addition, they found that for a particular set of σ and s the mean folding time depends monotonically on the peptide length (or number of hydrogen bonds). Recently, based on a one-dimensional “Zimm–Bragg” Ising model Buchete and Straub derived a generalized mean first-passage time equation for the coil-to-helix transition.18 With this equation, they have evaluated the mean helix formation time as a function of a set of parameters, including the Zimm–Bragg nucleation and propagation constants, peptide length, and initial helical populations (see more details in discussion). In general, their results are similar to those obtained by Brooks and Weaver.
Herein, to investigate how peptide sequence determines the kinetics of the helix–coil transition and also compare with those results obtained by theoretical studies, we have studied the T-jump induced relaxation kinetics of a series of Ala-based α-helical peptides with either excellent or poor capping sequences:
Here, r represents d-Arg and is one of the best C caps,41 and the Ser-Pro-Glu tripeptide (SPE) serves as a helix-stabilizing N cap. Our results show definitively that good end-capping sequences can increase the rate of helix formation, whereas the peptide length has a rather complicated effect on the kinetics of the helix–coil transition.
Materials and Methods
Using the WHATIF program (G. Friend, EMBL, Heidelburg, Germany), we searched for the most frequently occurring tripeptide sequence at the N-termini of the α-helix (positions Ncap–N1–N2 as described by Aurora and Rose36). The most frequent motif was Ser-Pro-Glu which occurred 40 times in a database of 462 nonredundant proteins that contain a total of 1.0 × 105 amino acid residues (nres) and 2742 helices (nα). 29 of these sequences were found at the Ncap–N1–N2 positions. The random expectation, Pran, for this finding is given by the product of finding an Ncap–N1–N2 conformation within a randomly selected tripeptide and the probabilities of observing Ser, Pro, and Glu, which can be approximated by the following equation:
Peptides were synthesized based on standard Fmoc-protocol employing Pal resin. All samples were purified to homogeneity and characterized by electrospray-ionization mass spectroscopy. For samples used in the infrared experiments, the residual trifluoroacetic acid (TFA) from peptide synthesis, which has an infrared absorbance at 1672 cm–1 that overlaps with the peptide amide I′ band, was removed by lyophilization against 0.1 M DCl solution. For both equilibrium and time-resolved infrared experiments, the samples were prepared by dissolving the lyophilized peptides directly in 50 mM D2O phosphate buffer (pH 7) and the final concentration was 2–4 mM.
CD data were collected on an AVIV 62DS spectropolarimeter using a 1 mm quartz cell. CD samples were also prepared by dissolving lyophilized peptides directly into 20 mM phosphate buffer solution (pH 7) and their concentrations were determined optically by the tyrosine absorbance at 276 nm using ε276 = 1450 cm–1 M–1. Mean residue ellipticity was calculated using the equation θ222 = (θobs/10lc)/N, where θobs is the ellipticity measured at 222 nm in millidegrees, l is the optical path length (cm), c is the concentration of the peptide (M), and N is the number of residues.
Temperature-dependent FTIR spectra of the peptides were collected on a Nicolet Magna-IR 860 spectrometer using 2 cm–1 resolution with a CaF2 sample cell that is divided into two compartments using a Teflon spacer at an optical path length of 52 μm (determined interferometrically). Temperature was controlled with ±0.2 °C precision with a thermostated copper block. To correct for slow instrument drift, a programmable translation stage was used to move both the sample and reference side of the sample cell in and out of the infrared beam alternately, and each time a spectrum corresponding to an average of eight scans was collected. The final result was usually an average of 32 such spectra, both for the sample and the reference.
The T-jump infrared apparatus has been described in detail previously.10 Briefly, the 1.9 μm T-jump pulse (3 ns and 10 Hz) was generated via Raman shifting the fundamental output of an Nd:YAG laser in a Raman cell that was pressurized with a mixture of H2 and Ar to 750 psi. To ensure a uniform T-jump distribution within the laser interaction volume, an optical path length of approximately 50 μm was used. Furthermore, to provide information for both background subtraction and T-jump amplitude calibration in the time-resolved measurements, a sample cell with dual compartments, similar to that used in the static FTIR measurements, was used to measure the T-jump induced signals of both the sample and reference under the same conditions. Calibration of the T-jump amplitude was done similarly to that used previously, i.e., using the T-jump induced absorbance change of the buffer (D2O) at the probing frequency along with a calibration curve.
The calculation of the mean first-passage time of the helix–coil transition was carried out using Matlab. The program was verified by comparing results with those of Buchete and Straub.18
Results
Peptides used in the current study are derivatives of the poly-Ala helical sequence of Marqusee and Baldwin.42 Similar sequences have been used in our previous T-jump studies. These peptides are quite soluble in water and do not yield detectable (with IR method) aggregates at the concentration (~2-4 mg/mL) and temperature (up to 75 °C) used in the current study.
A major goal of this work was to determine whether helical end caps could serve to increase the rate of helix formation by increasing the probability of helix initiation. The helical initiation parameter is generally taken as the microequilibrium constant for forming a conformation in which three consecutive amino acids adopt an α-helical conformation. We therefore searched for a capping sequence that would greatly enhance the probability of adopting this conformation, as assessed from a survey of the protein structural database.
The Ser-Pro-Glu motif was found to be a very strong local helix-inducing sequence in the structures of folded proteins, which induces the formation of a local helical conformation in 90% of its occurrences. In the WHATIF database of 462 proteins, the Ser-Pro-Glu tripeptide sequence occurred a total of 40 times. In 36 of these occurrences, the Ser was in an extended conformation (necessary to form a favorable N-capping interaction), and the following Pro-Glu-XXX sequence was found to be in the helical region of the ϕ/ψ plot. Thus, this sequence has a very high propensity to induce a local helical conformation. Furthermore, the great majority (29) of these local helices extended into longer helices. Indeed, the Ser-Pro-Glu is observed 27-fold more frequently in an N-cap conformation in this conformational context than one would expect based on random expectation. In the N-cap conformation, the N-terminal Ser forms an N-capping interaction, and the Pro may help initiate the helix. The Glu side chain adopts a variety of different conformations, suggesting that it might stabilize the helix by electrostatic interactions that are not particularly sensitive to the geometry of the structure. An early study indeed showed that the N-terminal sequence, Ser-Pro-Glu, could substantially increase the stability of the helical structures that extend to the N-terminus.10
At the C-terminus, we also included a d-Arg residue, which was chosen because it is the most favorable C cap reported in the literature.41 This residue appears to stabilize the helix by electrostatic and potential hydrogen-bonded interactions with the carbonyl groups exposed at the C-terminus of the helix.
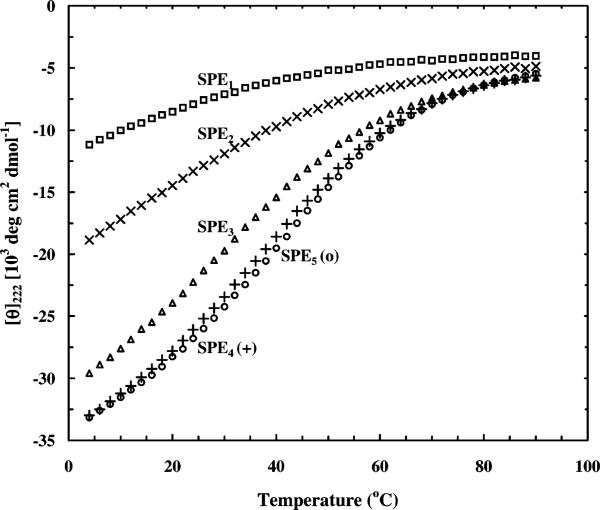
Low-temperature far UV CD spectra of these peptides show typical features associated with α-helices (data not shown). Peptides in which n = 2 should form partially helical structures near 0 °C, whereas those with n = 3 should be nearly fully helical at this temperature. Indeed, the CD data of the SPEn peptides reveal this trend (Figure 1). Furthermore, these CD thermal melting curves show that longer peptides are more stable, as indicated by their higher thermal melting temperatures (i.e., the middle point of the thermal transition).
Figure 1.
Equilibrium helix–coil transitions of SPE1 (□), SPE2 (×), SPE3 (△), SPE4 (+), and SPE5 (○) peptides as measured by the mean residue ellipticitiy at 222 nm as a function of temperature. As expected, the longest peptide in this series, SPE5, is the most stable and its thermal transition is more cooperative.
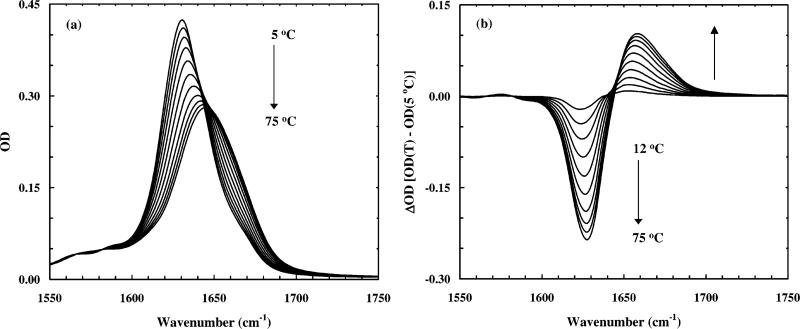
The FTIR spectra of these peptides in the amide I′ region are rather similar. As an example, only the amide I′ bands of the SPE4 peptide collected at different temperatures are shown (Figure 2a). The amide I′ absorbance of polypeptides, which arises from the backbone C=O stretching vibration, has been shown to be sensitive to conformation and is an established conformational reporter. For example, early studies indicated that solvated helices exhibit an amide I′ band around 1630 cm–1, whereas disordered structures absorb at higher wavenumbers.10 Therefore, thermally induced helix-to-coil transition in a helical peptide should induce a change in its amide I′ band. Indeed, the FTIR difference spectra of the SPE4 peptide (Figure 2b) show that its amide I′ band loses intensity at ~1630 cm–1 as temperature increases, which is concomitant with the formation of a new spectral feature at ~1655 cm–1. Similar to our previous studies, we have attributed this negative feature to the melting of the helical structures and the positive feature to the formation of nonhelical conformations. This change in the amide I′ band of polypeptides as a function of temperature is particularly important to the time-resolved studies because it provides conformational probes for us to monitor the temperature-induced helix–coil transition kinetics. Importantly, no aggregation was observed even to the highest temperature used in these measurements, as monitored by the distinct spectral features at 1624 and 1675 cm–1 associated with aggregates.
Figure 2.
(a) Temperature-dependent equilibrium and (b) difference FTIR spectra of the SPE4 peptide. These spectra were collected roughly every 7 °C, from 5 to 75 °C. Difference spectra were generated by subtracting the spectrum collected at 5 °C from the spectra collected at other temperatures. Arrows indicate the direction of changes when temperature was increased. The negative-going feature at ~1630 cm–1 corresponds to loss of helical conformations, whereas the positive-going signal ~1655 cm–1 is due to the formation of disordered structures.
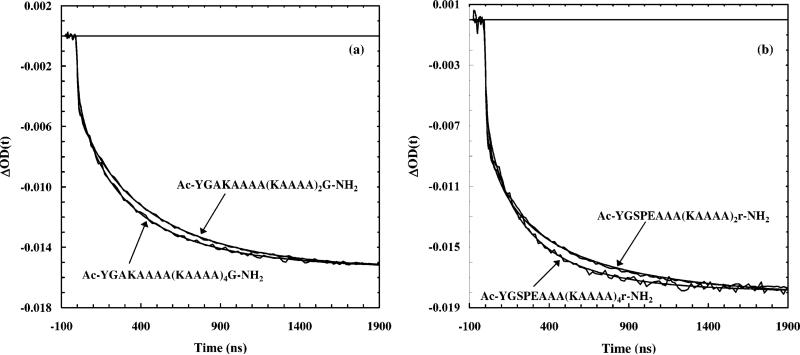
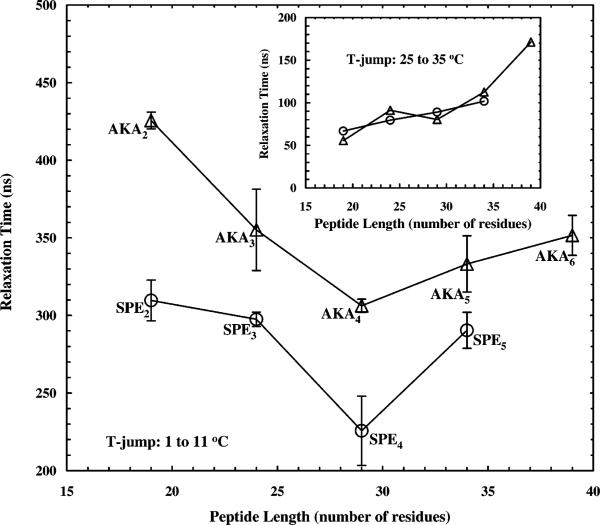
The relaxation kinetics of these peptides following a T-jump of ca. 10 °C, from 1 to 11 °C, probed at 1630 cm–1, show measurable differences among the peptides, particularly between those with and without good end caps. This indicates that the peptide sequence indeed plays an important role in determining the helix–coil transition kinetics (Table 1). As an example, the relaxation kinetics of four peptides are shown (Figure 3). Similar to and also consistent with our early results on a 19-residue peptide,10 the T-jump induced relaxation kinetics of these peptides show two distinct phases. The fast phase is significantly faster than the 10 ns rise time of the IR detection system. As discussed previously,10 two mechanisms may contribute to this fast phase, e.g., an instantaneous spectral shift and/or fast conformational changes.17 One such fast event would be the fraying of the ends of a helix. For example, with a fluorescence probe attached at the N-terminus of the Fs peptide, Eaton and Hofrichter and their co-workers5 have observed a very fast relaxation process following a nanosecond T-jump, which was attributed to the addition/removal of an additional hydrogen bond to an existing helix. Moreover, the slow relaxation phase of these peptides, which is believed to correspond to transitions between helical and nonhelical conformations, deviates to some degree from single-exponential kinetics. The extent of deviation depends on the sequence of the peptide, as well as the final temperature. For example, at high temperature where unfolding processes usually dominate, the observed relaxations can be described satisfactorily by first order kinetics, presumably because unfolding of the α-helix is a thermally activated barrier crossing process. Therefore, the nonexponential behavior observed for these peptides at low temperature appears to be a consequence of the complexity intrinsic to the coil-to-helix transition process, in agreement with our early results.10 A recent molecular dynamics (MD) simulation employing an all-atom peptide model43,44 also suggests that the kinetics of the helix–coil transition should deviate from simple exponential kinetics, and the kinetics of the helix formation may be described by a stretched exponential function with a β of approximately 0.5. While a number of mechanisms have been proposed to interpret this deviation of the helix–coil transition from a simple first-order process,10 this nonexponential behavior is fundamentally the result of the underlying distribution of the free energy barriers associated with the helix–coil equilibrium as well as the diffusing nature of the coil-to-helix transition in conformational space. Regardless of the origin of this nonexponentiality, however, to compare consistently the overall relaxation kinetics of these peptides, we need to obtain time constants that characterize the overall relaxation. Thus, we modeled the T-jump induced relaxation with a stretched exponential function plus an instantaneous component. The latter is used to account for the unresolved fast phase. Specifically, the function used to fit all the data is △OD(t) = A*[1 – B* exp(–t/τ)β], where A is the full amplitude and (1 – B) is the percentage of the instantaneous component, and 0 < β < 1 measures the extent of deviations from single-exponential kinetics. The fitting parameters (B, β, and τ) obtained from the best fits of the relaxations measured for a T-jump of 1–11 °C are listed in Table 1. It is evident from these results that the relaxation kinetics of the SPEn peptides are faster than those of the AKAn peptides. Furthermore, the relaxation times of these peptides, corresponding to a T-jump of 1–11 °C, show a concave upward dependence on the peptide length (Figure 4). Although this nonmonotonic dependence might be weak, especially toward the longer peptide length side when experimental errors are considered, and the exact minimum was not explicitly determined, this result is certainly in disagreement with early theoretical predications and needs to be further explored (see below).
TABLE 1.
Parameters Obtained from the Best Fits of the Relaxation Kinetics of the Peptides in Response to a T-Jump of 1–11 °C as Well as the Apparent Activation Energies
| peptide | AKA2 | AKA3 | AKA4 | AKA5 | AKA6 | SPE2 | SPE3 | SPE4 | SPE5 |
|---|---|---|---|---|---|---|---|---|---|
| T-jump (°C) | 1–11 | 1–11 | 1–11 | 1–11 | 1–11 | 1–11 | 1–11 | 1–11 | 1–11 |
| τ (ns) | 425 ± 5 | 355 ± 26 | 306 ± 4 | 333 ± 18 | 352 ± 13 | 310 ± 13 | 297 ± 5 | 226 ± 22 | 290 ± 12 |
| b | 0.79 | 0.72 | 0.73 | 0.91 | 0.94 | 0.59 | 0.71 | 0.72 | 0.91 |
| B | 0.74 | 0.69 | 0.81 | 0.84 | 0.63 | 0.69 | 0.68 | 0.72 | 0.70 |
| Ea (kcal/mol) | 14.0 | 9.7 | 9.6 | 8.2 | 5.3 | 11.5 | 9.2 | 8.2 | 7.9 |
Figure 3.
(a) Relaxation kinetics of AKA2 and AKA4 peptides and (b) relaxation kinetics of SPE2 and SPE4 peptides, as indicated. Note that the signals have been scaled to the same amplitude in each case. The T-jump was ~10 ± 1 °C, from ~1 to ~11 °C. The probing frequency was 1630 cm–1. The smooth lines are fits to the following function, △OD(t) = A*[1 –B* exp(–t/τ)β], convolved with the instrument response function that was determined by fitting the rise time of the D2O signal. The fitting parameters are listed in Table 1.
Figure 4.
Relaxation times of AKAn (△) and SPEn (○) peptides following a T-jump from 1 to 11 °C. It is evident that peptides of the same length but containing end caps take less time to relax to the new equilibrium point. Inset: Relaxation times of AKAn (△) and SPEn (○) peptides following a T-jump from 25 to 35 °C.
CD spectroscopy provided a rapid, if semiquantitative, indication that the helical contents of all of the peptides studied in this work were greater than 50% at 1 and 11 °C, with the possible exception of the shortest, uncapped sequence. In a T-jump experiment, the observed rate reflects the sum of the forward and reverse rate constants for a reversible reaction. Thus, under conditions in which a protein is predominantly folded the relaxation rate should be dominated by the rate of the folding reaction. The kinetics of helix formation are more complex, but the rates should reflect a weighted sum of the contributing constants and hence should also be dominated by the folding rate constants at low temperatures. Thus, the T-jump induced relaxation kinetics at 11 °C can be viewed qualitatively as the folding kinetics of the AKAn and SPEn peptides. Consistent with this picture, the concave upward dependence of the relaxation time on the peptide length observed at 11 °C gradually diminishes when the final temperature increases. For example, at 35 °C, the dependence of the T-jump induced relaxation time on the peptide length becomes monotonic (inset of Figure 4), with a relationship where a longer peptide exhibits a longer relaxation time, because at this temperature the rate of unfolding contributes significantly to, if not dominates over, the measured relaxation rate.
In an earlier work,8 we have shown that the rate of the helix–coil transition of a 19-residue helical peptide exhibits Arrhenius behavior with an apparent activation energy of ~15.5 kcal/mol. Similarly, the T-jump induced relaxation kinetics of AKAn and SPEn peptides also exhibit monotonic dependence on the final temperature, and within our experimental errors these relaxation rates can also be described by the Arrhenius relation. Because these analyses use relaxation rates obtained from stretched exponentials, the apparent activation energy cannot be considered as a true Arrhenius activation energy. Nevertheless, they provide a semiquantitative description of the relative steepness (and hence enthalpic nature) of the transitions. The apparent activation energies of these peptides decrease monotonically with increasing peptide length (Table 1). Furthermore, peptides with good end caps also have a smaller apparent activation energy than those of the same length but without good end caps, in agreement with our early results.45
Discussion
These measurements provide the first kinetic information describing how the rate of helix formation depends on chain length. In previous work, we demonstrated that the T-jump kinetics were biphasic; presumably the rapid rate reflects fraying of preformed helices while the slower rate (which is monitored in this work) reflects crossings between helical and nonhelical conformations. We will adopt this interpretation in this discussion, although we note that other interpretations cannot be ruled out. While full kinetic analysis is not yet possible, and may be best approached by all-atom molecular dynamics calculations, it is nevertheless possible to examine the consistency of existing analytical kinetic models with the current data.
A T-jump pulse induces a shift in the equilibrium between the helix and nonhelical states. Although a T-jump induced relaxation always causes the nonhelical population to increase (in this case), the observed signal nevertheless contains contributions from both folding and unfolding because the T-jump technique is essentially a relaxation method. Depending upon the final temperature, either the overall folding or overall unfolding rate could dominate the measured relaxation rate or both contribute comparably. This may be understood more clearly from a two-state folding scenario where the observed relaxation rate constant (kR) is the sum of the folding (kf) and unfolding (ku) rate constants, i.e., kR = kf + ku; whereas the ratio of kf and ku gives rise to the folding equilibrium constant (Keq) of the system, namely, Keq = kf/ku. Thus, at a temperature where folding is favored, i.e., Keq > 1, the observed relaxation rate constant is then dominated by the folding rate constant. Even though the helix–coil transition cannot be described rigorously as an equilibrium between two well-defined states, the free energy profile of a helical peptide can nevertheless be depicted as two broad basins with a barrier separating the nonhelical ensemble from the helical ensemble.46,47 Therefore, the two-state assumption has been used in T-jump studies in the past.7,48 Herein, to compare the folding kinetics of any two peptides, we may also invoke the two-state model below to describe their relaxation kinetics.
As described above, the rate constants of a two-state system can be determined if the equilibrium constant and the relaxation rate constant are known. To show that the length dependences of the relaxation times presented in Figure 4 also give the trend for the length-dependent helix folding times, below we solve for the folding time constants of the SPE2 and SPE4 peptides using their equilibrium constants derived from the CD data. It is a common practice to estimate the fractional helicity (fH) of a peptide based on its far UV mean residue ellipticity at 222 nm, i.e., [θ]222, according to the following function49,50
| (1) |
where [θ∞]222 is the mean residue ellipticity of an ideal peptide with 100% helicity, n is the length of the potential helical region, and x is an empirical correction for end effects. Although it is still controversial to what values of x and [θ∞]222 should be used, here we simply used those given by Luo and Baldwin,51 who determined that x = 2.5 and [θ∞]222 = –44 000 deg cm2 dmol–1, respectively. Using these values, we estimated that the fractional helicity of the SPE2 peptide at 11 °C is approximately 45%, which corresponds to an equilibrium constant for folding of approximately 0.83; whereas a similar analysis yielded a fractional helicity of ca. 78% and a folding equilibrium constant of 3.5 for the SPE4 peptide at the same temperature. In combination with the measured relaxation time constants, these equilibrium constants allow us to determine the helix folding times for these two peptides. They were determined to be 683 ns for the SPE2 peptide and 343 ns for the SPE5 peptide. Since the fractional helicity increases with increasing peptide length, these results definitely show that the trend observed for the relaxation times also reflects qualitatively the length dependence for helix folding.
Kinetic Effect of End Caps
It is well-known that good end caps can stabilize the helical structures of peptides.36,38,52,53 However, their effects on the kinetics of the helix–coil transition have not been studied extensively. This increase in helical stability is believed to occur via the so-called “capping” interaction mechanism where polar side chains of end caps form additional hydrogen bonds with the exposed amides at the ends of helices, since a regular helix without end caps contains four carbonyl groups at the C-terminus and four amide protons at the N-terminus without hydrogen-bonding partners. While one possibility would be that end caps can only enhance the thermal stability of helices by locking in the intervening helical structures, another scenario would be that capping interactions can actually increase the probability of helix initiation and, consequently, the rate of helix formation. Our results seem to be consistent with the latter case because a cursory inspection of these results reveals that peptides with end caps have shorter relaxation (or folding) times at low temperatures (Figures 4 and 5), where folding dominates.
Figure 5.
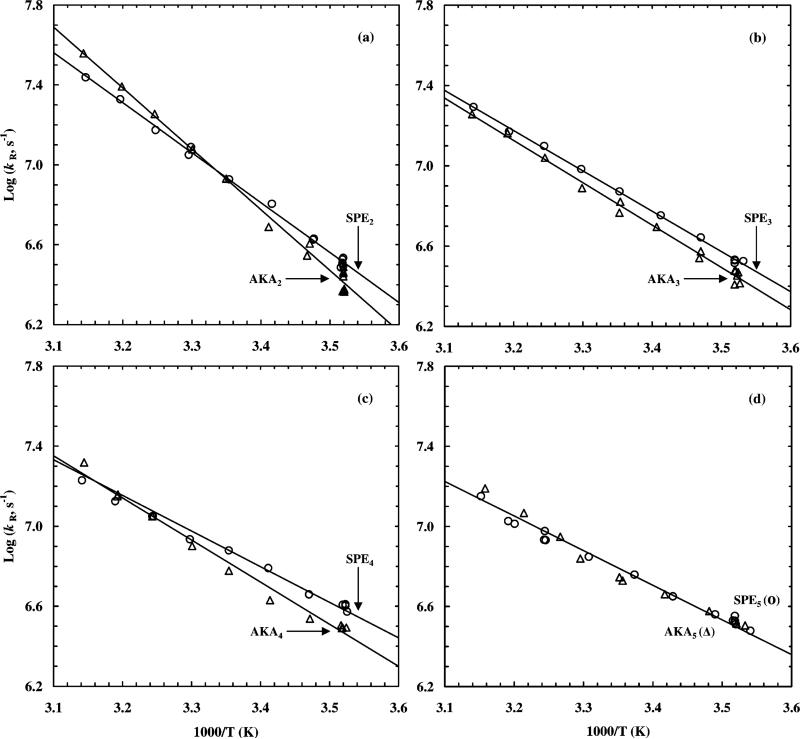
Arrhenius plots of (a) AKA2 (△) and SPE2 (○), (b) AKA3 (△) and SPE3 (○), (c) AKA4 (△) and SPE4 (○), and (d) AKA5 (△) and SPE5 (○) peptides. The T-jump amplitude for each point was roughly 10 °C. The straight lines are linear fits to the data, and the corresponding Arrhenius activation energies are listed in Table 1.
The current results clearly indicate that excellent end caps not only can serve as motifs which define the beginning and end of helices but also effectively increase the rate of helix formation, especially for shorter peptides. This effect may be understood from the theoretical models of Schwartz28 and Brooks15 as well as Buchete and Straub.18 For example, the model of Brooks suggests that the meantime for the coil-to-helix transition should be proportional to σ–1, whereas Buchete and Straub demonstrated, using a one-dimensional active Ising model as well as the “mean sequence” approximation, that the mean first-passage time (MFPT) for helix formation might be a complex function of σ and s as well as the peptide length. In particular, their results indicate that for large values of σ the calculated MFPT of the coil-to-helix transition depends monotonically, but nonlinearly on σ–1. Hence, one possible reason that peptides with efficient end caps fold faster than those of similar length but lack of good end-capping sequences is that end-capping interactions effectively increase the nucleation constant. As a matter of fact, as one of the most frequent N-terminal capping sequences, Ser-Pro-Glu may serve as a primary nucleation site with a larger σ than Ala, where Ser forms an N-capping interaction, and Pro helps to initiate the helix. In addition, the negative charge (at neutral pH) of Glu side chain might stabilize the helix by electrostatic interactions.
Length-Dependent T-Jump Relaxation Kinetics
The length dependence of the kinetics of helix formation is also consistent with the assumption that Ser-Pro-Glu is able to increase the rate of helix nucleation. This sequence has its greatest effect on the kinetics of helix formation for the shortest peptide, and the difference between the capped and uncapped peptides is gradually decreased as the sequence is elongated (Figure 5d). This is qualitatively consistent with the idea that the rate of helix formation should depend on the number of potential sites capable of nucleating the helical structure. Thus, the relative contribution of the capped vs uncapped pathway would be expected to decrease with increasing chain length. However, this result may also be interpreted according to the following picture that for long peptides the nucleation process only plays a minor role in helix formation and the overall rate of helix formation is dominated by the rate of propagation. The latter determines how fast a nucleated species can be elongated to form the final helical state. Thus, even though the nucleation constants for AKA5 and SPE5 may still be different owing to the excellent end-capping ability of SPE, their influences to the overall helix–coil transition kinetics become less important compared to those of the propagation constants. Unless the nucleation and individual propagation rates can be measured explicitly, experimentally distinguishing these two possibilities is difficult.
The temperature dependence of the rate data is also consistent with Ser-Pro-Glu playing a major role in helix initiation, as it shows the greatest contribution to the rate at low temperature (where the rate is dominated by helix formation). This is most apparent in the shortest peptide, where the midpoint occurs at relatively low temperatures. Interestingly, a crossover in the relaxation rates for SPE2 vs AKA2 is observed, with the capped peptide being most rapid at low temperature, and the uncapped peptide being more rapid at higher temperature (Figure 5a).
It is clear that for short peptides of similar length the more stable ones fold faster.45 This is also suggested by the study of Buchete and Straub,18 who have demonstrated that the MFPT for helix formation has a strong dependence on the overall stability of the helix, or σ and s. Therefore, the increase in the folding rates observed for the SPEn peptides may not be simply attributed entirely to the corresponding increase in the nucleation constant. According to the theory of Zimm–Bragg,39 the free energy change of a helix–coil equilibrium may be calculated using the following relation, △GHC = –kBT ln(σ) – nkBT ln-(s), where kB is the Boltzmann constant, T is the absolute temperature, and n is the number of helical residues. In such a treatment, the nucleation (σ) and propagation (s) constants are treated as independent parameters. Nonetheless, such assumption may not be entirely valid if the helical propensity of an amino acid is length dependent.
In fact, length dependent helical propensities of amino acids have been observed in simulations and experiments. For example, Young and Brooks have performed MD simulations with umbrella sampling on a series of Ala peptides and found that the microscopic helix propagation parameters of the residues at the N-terminus depend strongly on the length of the α-helix.54 Using a unique end-capping group, Ac–Hel, which is also a helicity reporter through its distinct 1H NMR t/c ratio, Kemp and co-workers1 have measured the helicities of a series of peptides and proposed that the helical propensity of Ala is length dependent. For example, they showed that at 2 °C Ala's helical propensity is 1.03 for peptides with 6 residues, but for peptides of longer than 10 residues, Ala's helical propensity increases to 1.26. They attributed this length dependence of Ala's helical propensity to the effect of hydrogen-bonding cooperativity, which has been observed in computational studies of hydrogen-bonded systems.55,56 Another well-known mechanism that also induces cooperativity in helix formation is long-range electrostatic interactions among individual amide dipoles.57
If the average helix stabilization per residue is length dependent, such dependence would affect profoundly the rate of helix formation because of the sequential nature of the elongation of the helix. In other words, the elongation of a helical stretch may become easier when it becomes longer and the rate of the elongation increases and ultimately saturates at a certain helical length. In addition, a length dependent helical propensity may also yield a nonmonotonic dependence on the peptide length for the helix–coil transition kinetics, as observed in the current study.
Length-Dependent Mean First-Passage Time of Helix Formation
To understand the complex dependence of the helix–coil transition kinetics on the peptide length, herein we employed the active helix Ising model of Buchete and Straub18 to calculate the mean helical folding time as a function of the peptide length. In essence, this model is a generalized version of the folding model developed by Zwanzig, Szabo, and Bagchi58 and is also similar to those proposed by Brooks15 and Thompson et al.5 Nevertheless, by computing the mean first-passage time, this model avoids the use of constraints encountered in other models, such as unidirectional propagation from the nucleation site and equilibria among contiguous helices and coils. In addition, this approach takes into account, although implicitly, the possibility of multiple nucleation sites, therefore suitable for modeling long peptides.
By considering in detail the uniresidue transition rates and neighbor-dependent configurational probabilities, Buchete and Straub derived the following generalized mean first-passage time, τ(c), for helix formation (see ref 18 for details)
| (2) |
with
where N is the total number of residues, a and b are the positions of the helical boundaries, and c is the number of residues in a coil state. The key point of this model is that the mean transition rates of the addition and dissolution of a helical site, i.e., and , are functions of the nucleation and propagation constants, the length of the peptide, and the helical fraction of a specific structure. It can be shown that eq 2 reduces to the result obtained by Zwanzig, Szabo, and Bagchi for a special case where the transition rates are treated as constants.58
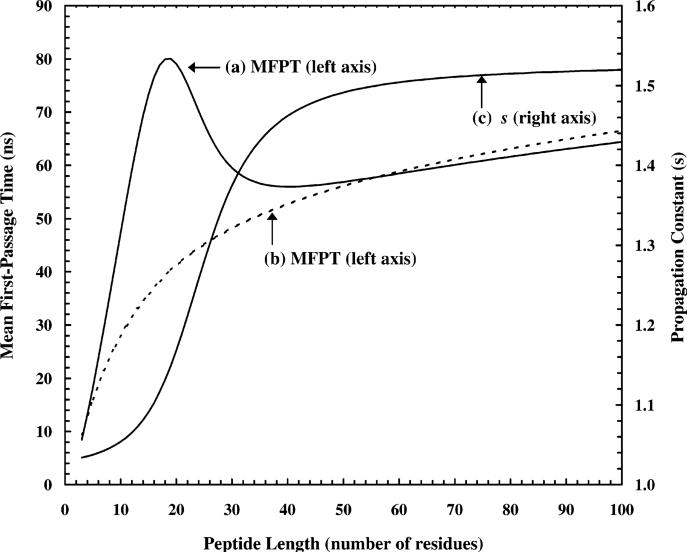
With eq 2, Buchete and Straub have studied the general characteristics associated with the kinetics of the coil-to-helix transition, including the dependence on peptide length (N) and the thermodynamic energetic parameters, σ and s. However, in these studies, they treated the interaction energies (i.e., the parameters of σ and s) as constants. Therefore, their results show that for a series similar peptides of different length, the MFPT for helix formation increases monotonically from N = 5 to N = 30, with σ = 0.002 and s = 1.5 (Figure 6), similar to the results of Brooks.
Figure 6.
Mean first-passage time of the transition from all-coil state to all-helical state as a function of peptide length. (a) Our results that were generated by using values of s described by curve c. (b) The dashed line is the result of Straub et al.,18 using σ = 0.002, and s = 1.5 (note: other Ising-like models yield similar results under the same conditions).
The results of Straub et al. also show that the helix formation time may be a complex function of σ and s. This suggests that if σ or s or both are length dependent, then the helix formation time may well deviate from a simple monotonic dependence on the peptide length. Herein, we recalculated the mean first-passage times for helix formation as a function of peptide length, in which σ = 0.002 and s was assumed to have a sigmoid shape as a function of the peptide length (Figure 6). The latter was assumed because Kemp and co-workers have observed that the helical propensity of Ala increases linearly as a function of peptide length for peptides with more than seven residues. The saturation of s at larger N is to ensure that the helical stability is bound to a certain value. Although this selection of the values of s is somewhat arbitrary and such a large cooperative effect may not be entirely realistic, the results nevertheless reproduce qualitatively the trend observed in the experiments (Figure 6). As shown, this breakdown of s into different regions modulates the mean first-passage time of the helix formation, as observed.
Although this exercise produces results qualitatively agreeing with those measured experimentally, it may be fundamentally flawed however as we interpreted the thermodynamic cooperativity, i.e., greater helical propensity for longer peptides, also as long-range kinetic cooperativity. Nevertheless, to interpret our results within the framework of the current helix–coil models, we had to adopt the assumption that the length-dependent helical propensity, which is an averaged thermodynamic parameter, can also be interpreted as a kinetic parameter because only if the individual mean transition rates (e.g., ) increase with increasing peptide length can Ising-like models yield results consistent with those observed experimentally. It is known that long-range kinetic cooperativity plays an important role in the folding of protein tertiary structure;59 however, it has not been observed in the helix–coil transition before. We note, therefore, that other interpretations cannot be ruled out. For example, the T-jump induced relaxation kinetics of the longer peptides at 11 °C may correspond mostly to conversions between all-helical and partially helical conformations, in which nucleation becomes irrelevant. Such a scenario would certainly result in a faster relaxation rate for longer peptides because of the length-dependent helical propensity.
Interestingly, the initial increase in the mean folding time for helix formation was not observed in the current study because peptides with fewer residues become increasingly unstable. As a result, it is difficult to obtain the kinetics of the helix–coil transition for very short peptides because of the small signals. On the other hand, MD simulations with implicit or explicit water potentials become increasingly popular, which have yielded folding/unfolding times for very short helical peptides. For example, in a MD simulation using an all-atom peptide model in explicit solvent, Hummer and co-workers17,23 have shown that the helix formation kinetics of an Ala pentapeptide that can form a 1.5 turns of helix occur under 1 ns. Similarly, Margulis et al.19 observed a somewhat longer helix–coil transition time, on the order of 1 ns, in their MD simulations in which they used α-carbon dihedral angles to monitor the helix–coil transition. These results are consistent with our speculation that for very short peptides (for example, less than ~15 residues) there is an initial decrease in the helix folding rate when the peptide is lengthened.
Barrier of the Helix–Coil Transition
The thermodynamics of the helix formation by this set of peptides are also difficult to assess, because of the non-two-state nature of the transition. But even at a qualitative level, the difference between the temperature dependence of the kinetics vs the thermodynamics is striking. It has been well established that the enthalpy of helix formation amounts to approximately 1.0 kcal/mol per residue.60 Thus, thermal unfolding curves of monomeric helices become increasingly steep with increasing chain length, although the van't Hoff enthalpy of the relaxation never reaches the calorimetric enthalpy due to the multistate nature of the transition as well as contributions from both folding and unfolding.
In addition to the intrinsic folding/unfolding barrier, frictions exerted by solvent molecules may also slow the folding/unfolding process. For example, Kramers’ theory suggests that in the high friction limit the reaction rate is inversely proportional to the solvent viscosity (η). The reciprocal dependence of the rate constant on the solvent viscosity would produce an additional apparent activation energy of approximately 4.5 kcal/mol, due to the temperature dependence of the solvent (D2O) viscosity. But Jas et al.48 have concluded that the rate of the α-helix folding/unfolding exhibits a fractional viscosity dependence with a relation of k ∝ η–0.6. Such dependence would produce an additional activation energy of approximately 2.7 kcal/mol for the kinetics of the helix–coil transition.8
Interestingly, the observed apparent activation energies for these peptides also show length and sequence dependent behaviors. It is evident that the apparent enthalpy of activation decreases with increasing chain length and for peptides of the same length those having good end caps also exhibit smaller activation energies. These differences reflect the differences among their underlying folding energetics of these peptides. It is possible that for long peptides they encounter smaller enthalpic barriers or even undergo barrierless transitions because of the increasingly larger cooperativity associated with longer peptides. Furthermore, these results are also consistent with the expectation that the number of possible helix initiation sites increases with chain length, thereby shifting the energetic requirements toward lower enthalpy.
Finally, the nonexponentiality of the relaxation kinetics obtained at 11 °C reflects the complexity of the underlying free energy landscape61–63 of the helix–coil transition. This is particularly true for peptides with marginal stability, such as SPE2 (Table 1). It is evident that for long peptides, e.g., SPE5, AKA5, and AKA6, whose thermal transitions are more cooperative, their relaxation kinetics are very close to being single exponential. This is due presumably to the reason that for long peptides the distribution of the helical ensemble is narrower than that of short peptides. Furthermore, this is also in accord with our speculation that the observed length dependence is owing to the dependence of the propagation constant on helical length. Because of this dependence, a single helix within an ensemble of helical structures would exhibit a unique folding time.
Conclusion
In summary, the T-jump induced helix–coil transition kinetics of a series of Ala-based helical peptides, obtained by probing the amide I′ band of the peptide backbone, exhibit complex dependence on peptide length as well as end-capping groups, indicating that the kinetics of the helix–coil transition are determined by the peptide sequence. However, when peptides get longer, the effect of the end caps to the kinetics of helix formation diminishes. In addition, calculations of the mean first-passage time corresponding to the transition from the all-coil to all-helical states, based on an active Ising model, suggest that the helical propagation constant (or rate) is length dependent in order to generate results that are qualitatively consistent with those obtained experimentally.
Acknowledgment
F.G. gratefully acknowledges financial support from the NIH (GM-065978), the NSF (CHE-0094077), and the MRSEC program of the NSF under Award No. DMR00-79909.
References
- 1.Kennedy RJ, Tsang K-T, Kemp DS. J. Am. Chem. Soc. 2002;124:934. doi: 10.1021/ja016285c. [DOI] [PubMed] [Google Scholar]
- 2.Miller JS, Kennedy RJ, Kemp DS. J. Am. Chem. Soc. 2002;124:945. doi: 10.1021/ja011726d. [DOI] [PubMed] [Google Scholar]
- 3.Engel DE, DeGrado WF. J. Mol. Biol. 2004;337:1195. doi: 10.1016/j.jmb.2004.02.004. [DOI] [PubMed] [Google Scholar]
- 4.Williams S, Causgrove TP, Gilmanshin R, Fang KS, Callender RH, Woodruff WH, Dyer RB. Biochemistry. 1996;35:691. doi: 10.1021/bi952217p. [DOI] [PubMed] [Google Scholar]
- 5.Thompson PA, Eaton WA, Hofrichter J. Biochemistry. 1997;36:9200. doi: 10.1021/bi9704764. [DOI] [PubMed] [Google Scholar]
- 6.Thompson PA, Munoz V, Jas GS, Henry ER, Eaton WA, Hofrichter J. J. Phys. Chem. B. 2000;104:378. [Google Scholar]
- 7.Lednev IK, Karnoup AS, Sparrow MC, Asher SA. J. Am. Chem. Soc. 1999;121:8074. doi: 10.1021/ja003381p. [DOI] [PubMed] [Google Scholar]
- 8.Huang C-Y, Klemke JW, Getahun Z, DeGrado WF, Gai F. J. Am. Chem. Soc. 2001;123:9235. doi: 10.1021/ja0158814. [DOI] [PubMed] [Google Scholar]
- 9.Huang C-Y, Getahun Z, Wang T, DeGrado WF, Gai F. J. Am. Chem. Soc. 2001;123:12111. doi: 10.1021/ja016631q. [DOI] [PubMed] [Google Scholar]
- 10.Huang C-Y, Getahun Z, Zhu Y, Klemke JW, DeGrado WF, Gai F. Proc. Natl. Acad. Sci. U.S.A. 2002;99:2788. doi: 10.1073/pnas.052700099. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Huang C-Y, He S, DeGrado WF, McCafferty DG, Gai F. J. Am. Chem. Soc. 2002;124:12674. doi: 10.1021/ja028084u. [DOI] [PubMed] [Google Scholar]
- 12.Clarke DT, Doig AJ, Stapley BJ, Jones GR. Proc. Natl. Acad. Sci. U.S.A. 1999;96:7232. doi: 10.1073/pnas.96.13.7232. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Daggett V, Levitt M. J. Mol. Biol. 1992;223:1121. doi: 10.1016/0022-2836(92)90264-k. [DOI] [PubMed] [Google Scholar]
- 14.Armen R, Alonso DOV, Daggett V. Protein Sci. 2003;12:1145. doi: 10.1110/ps.0240103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Brooks CL., III J. Phys. Chem. 1996;100:2546. [Google Scholar]
- 16.Jun B, Weaver DL. J. Chem. Phys. 2000;112:4394. [Google Scholar]
- 17.Hummer G, Garcia AE, Grade S. Phys. ReV. Lett. 2000;85:2637. doi: 10.1103/PhysRevLett.85.2637. [DOI] [PubMed] [Google Scholar]
- 18.Buchete N-V, Straub JE. J. Phys. Chem. B. 2001;105:6684. [Google Scholar]
- 19.Margulis CJ, Stern HA, Berne BJ. J. Phys. Chem. B. 2002;106:10748. [Google Scholar]
- 20.Levy Y, Jortner J, Becker OM. J. Chem. Phys. 2001;115:10533. [Google Scholar]
- 21.Zana R. Biopolymers. 1975;14:2425. [Google Scholar]
- 22.Go N. J. Phys. Soc. Jpn. 1967;22:416. [Google Scholar]
- 23.Hummer G, Garcia AE, Grade S. Proteins Struct. Funct. Genet. 2001;42:77. [PubMed] [Google Scholar]
- 24.Chen E, Kumita JR, Woolley GA, Kliger DS. J. Am. Chem. Soc. 2003;125:12443. doi: 10.1021/ja030277+. [DOI] [PubMed] [Google Scholar]
- 25.Ferguson N, Fersht AR. Curr. Opin. Struct. Biol. 2003;13:75. doi: 10.1016/s0959-440x(02)00009-x. [DOI] [PubMed] [Google Scholar]
- 26.Baldwin RL, Rose GD. Trends Biochem. Sci. 1999;24:77. doi: 10.1016/s0968-0004(98)01345-0. [DOI] [PubMed] [Google Scholar]
- 27.Karplus M, Weaver DL. Protein Sci. 1994;3:650. doi: 10.1002/pro.5560030413. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Schwartz G. J. Mol. Biol. 1965;11:64. doi: 10.1016/s0022-2836(65)80171-1. [DOI] [PubMed] [Google Scholar]
- 29.McQuarrie DA, McTague JP, Reiss H. Biopolymers. 1965;3:657. doi: 10.1002/bip.360030605. [DOI] [PubMed] [Google Scholar]
- 30.Poland D, Scheraga HA. J. Chem. Phys. 1996;45:2071. doi: 10.1063/1.1727893. [DOI] [PubMed] [Google Scholar]
- 31.Klimov DK, Betancourt MR, Thirumalai D. Folding Des. 1998;3:481. doi: 10.1016/s1359-0278(98)00065-0. [DOI] [PubMed] [Google Scholar]
- 32.Presta LG, Rose GD. Science. 1988;240:1632. doi: 10.1126/science.2837824. [DOI] [PubMed] [Google Scholar]
- 33.Richardson JS, Richardson DC. Science. 1988;240:1648. doi: 10.1126/science.3381086. [DOI] [PubMed] [Google Scholar]
- 34.Regan L. Proc. Natl. Acad. Sci. U.S.A. 1993;90:10907. doi: 10.1073/pnas.90.23.10907. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Aurora R, Creamer TP, Srinivasan R, Rose GD. J. Biol. Chem. 1997;272:1413. doi: 10.1074/jbc.272.3.1413. [DOI] [PubMed] [Google Scholar]
- 36.Aurora R, Rose GD. Protein Sci. 1998;7:21. doi: 10.1002/pro.5560070103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Dasgupta S, Bell JA. Int. J. Pept. Prot. Res. 1993;41:499. [PubMed] [Google Scholar]
- 38.Scholtz JM, Baldwin RL. Peptides: Synthesis, Structures, and Applications. Academic Press; New York: 1995. [Google Scholar]
- 39.Zimm BH, Bragg JK. J. Chem. Phys. 1959;31:526. [Google Scholar]
- 40.Lifson S, Roig A. J. Chem. Phys. 1961;34:1963. [Google Scholar]
- 41.Schneider JP, DeGrado WF. J. Am. Chem. Soc. 1998;120:2764. [Google Scholar]
- 42.Marqusee S, Baldwin RL. Proc. Natl. Acad. Sci. U.S.A. 1987;84:8898. doi: 10.1073/pnas.84.24.8898. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Takano M, Nagayama K, Suyama A. J. Biol. Phys. 2002;28:155. doi: 10.1023/A:1019938505594. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Takano M, Nakamura HK, Nagayama K, Suyama A. J. Chem. Phys. 2003;118:10312. [Google Scholar]
- 45.Wang T, Du D, Gai F. Chem. Phys. Lett. 2003;370:842. [Google Scholar]
- 46.Hiltpold A, Ferrara P, Gsponer J, Caflisch A. J. Phys. Chem. B. 2000;104:10080. [Google Scholar]
- 47.Levy Y, Jortner J, Becker OM. Proc. Natl. Acad. Sci. U.S.A. 2001;98:2188. doi: 10.1073/pnas.041611998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Jas GS, Eaton WA, Hofrichter J. J. Phys. Chem. B. 2001;105:261. [Google Scholar]
- 49.Chen YH, Yang JT, Chau KH. Biochemistry. 1974;31:3350. doi: 10.1021/bi00713a027. [DOI] [PubMed] [Google Scholar]
- 50.Gans PJ, Lyu PC, Manning MC, Woody RW, Kallenbach NR. Biopolymers. 1991;31:1605. doi: 10.1002/bip.360311315. [DOI] [PubMed] [Google Scholar]
- 51.Luo P, Baldwin RL. Biochemistry. 1997;36:8413. doi: 10.1021/bi9707133. [DOI] [PubMed] [Google Scholar]
- 52.Doig AJ, Baldwin RL. Protein Sci. 1995;4:1325. doi: 10.1002/pro.5560040708. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Doig AJ. Biophys. Chem. 2002;101-102:281. doi: 10.1016/s0301-4622(02)00170-9. [DOI] [PubMed] [Google Scholar]
- 54.Young WS, Brooks CL., III J. Mol. Biol. 1996;259:560. doi: 10.1006/jmbi.1996.0339. [DOI] [PubMed] [Google Scholar]
- 55.Guo H, Karplus M. J. Phys. Chem. 1994;98:7104. [Google Scholar]
- 56.Kobko N, Paraskevas L, del Rio E, Dannenberg JJ. J. Am. Chem. Soc. 2001;123:4348. doi: 10.1021/ja004271l. [DOI] [PubMed] [Google Scholar]
- 57.Wu Y-D, Zhao Y-L. J. Am. Chem. Soc. 2001;123:5313. doi: 10.1021/ja003482n. [DOI] [PubMed] [Google Scholar]
- 58.Zwanzig R, Szabo A, Bagchi B. Proc. Natl. Acad. Sci. U.S.A. 1992;99:20. doi: 10.1073/pnas.89.1.20. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Hao M-H, Scheraga HA. J. Chem. Phys. 1997;107:8089. [Google Scholar]
- 60.Lopez MM, Chin D-H, Baldwin RL, Makhatadze GI. Proc. Natl. Acad. Sci. U.S.A. 2002;99:1298. doi: 10.1073/pnas.032665199. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Ohkubo YZ, Brooks CL., III Proc. Natl. Acad. Sci. U.S.A. 2003;100:13916. doi: 10.1073/pnas.2334257100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Pappu RV, Srinivasan R, Rose GD. Proc. Natl. Acad. Sci. U.S.A. 2002;97:12565. doi: 10.1073/pnas.97.23.12565. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Gruebele M. Protein folding: the free energy surface. Curr. Opin. Struct. Biol. 2002;12:161. doi: 10.1016/s0959-440x(02)00304-4. [DOI] [PubMed] [Google Scholar]