Abstract
Point matching is crucial for many computer vision applications. Establishing the correspondence between a large number of data points is a computationally intensive process. Some point matching related applications, such as medical image registration, require real time or near real time performance if applied to critical clinical applications like image assisted surgery. In this paper, we report a new multicore platform based parallel algorithm for fast point matching in the context of landmark based medical image registration. We introduced a non-regular data partition algorithm which utilizes the K-means clustering algorithm to group the landmarks based on the number of available processing cores, which optimize the memory usage and data transfer. We have tested our method using the IBM Cell Broadband Engine (Cell/B.E.) platform. The results demonstrated a significant speed up over its sequential implementation. The proposed data partition and parallelization algorithm, though tested only on one multicore platform, is generic by its design. Therefore the parallel algorithm can be extended to other computing platforms, as well as other point matching related applications.
1 Introduction
Point matching is crucial for many computer vision and image analysis applications, such as medical image registration. It is a computationally intensive process due to the calculation of the correspondence among a large number of data points. However, the medical image registration, when used for critical applications for instance the image assisted surgery, often requires real time or near real time performance. A lot of efforts have been made to speed up the point matching method and its related application such as medical image registration. To our knowledge, there has no reports about parallelization of the landmark based image registration algorithm on the multicore platform, the IBM Cell Broadband Engine. As we will show the proposed algorithm indeed contains a distinctive advantage for parallelization by its design.
Image registration is the process to determine the linear/nonlinear mapping between two images of the same object or similar objects acquired at different time, or from different perspectives. Image registration is widely used in remote sensing, image fusion, image mosaic and especially in medical image analysis. It is very common that the images taken under different acquisition conditions, such as shifting of the patient’s positions or changing of the acquisition parameters, show different appearance. Image registration can be separated as rigid registration [1,2] and non-rigid registration [3,4]. Given two images taken at different time (usually one is called fixed image and the other is moving images), the problem can be described as finding a linear/nonlinear transformation which maps each point in the fixed image to a point in the moving image. For nonlinear registration, some of them describe the transformation based on elastic deformations, such as fluid deformation based algorithm [5,6] and Demon’s algorithm [7,8]. The others model the transformation by a function with some parameters, such as B-spline based image registration algorithm [9].
Nonrigid image registration in general is computationally expensive. With the advent of unprecedented powerful computing hardware, it becomes possible for fast nonlinear image registration using the multicore platform. In this paper, we will introduce a parallelization of a fast and robust image registration algorithm using a multicore processor platform, the IBM Cell/B.E. The algorithm starts by automatically detecting the landmarks in the fixed image followed by a coarse-to-fine estimation of the linear and nonlinear mapping. A landmark point is characterized by an affine invariant local descriptor, the multi-resolution orientation histograms. The corresponding landmarks in the moving images are identified by matching the local descriptors of candidate points. The point matching procedure is the most time-consuming therefore was accelerated by the proposed parallelization algorithm on the IBM Cell/B.E. RANdom SAmple Consensus (RANSAC) [10] is used as a robust estimator to reject outliers in the corresponding landmarks. The final refined inliers are used to estimate a Thin Spline Transform (TPS) [11] to complete the final nonlinear image registration. The algorithm is completely unsupervised and computationally efficient. We have tested the method with several different types of images. The experimental results have shown significant speed up over the sequential implementation. The parallelized algorithm has the ability to handle very large transformations and deformations, while still providing accurate registration results. The proposed image registration algorithm is explained in Section 2. In Section 3, we describe the parallelization implementation using a IBM Cell Broadband Engine (Cell B./E.) multi-core processor. The experimental results are shown in Section 4. We briefly survey the related work in Section 5. Section 6 concludes the paper.
2 Landmark Based Image Registration
The proposed nonlinear image registration algorithm can handle large scale of transformations. It begins by automatically detecting a set of landmarks in both fixed and moving images, followed by a coarse-to-fine estimation of the nonlinear mapping using the landmarks. Robust estimation is used to find the robust correspondence between the landmarks in the fixed and moving image. The refined inliers are used to estimate a nonlinear transformation T and also wrap the moving image to the fixed image.
2.1 Landmark Detection
The automatic landmark detection is the procedure used to accurately detect the prominent and salient points in the image. Harris corner detector was applied to find the points with the large gradients in both directions (x and y for 2D images). The original computation in the Harris corner detector involves the computation of eigenvalues. Instead, the determinant and trace are used in our algorithm to find the corners where α is chosen as 0.1.
| (1) |
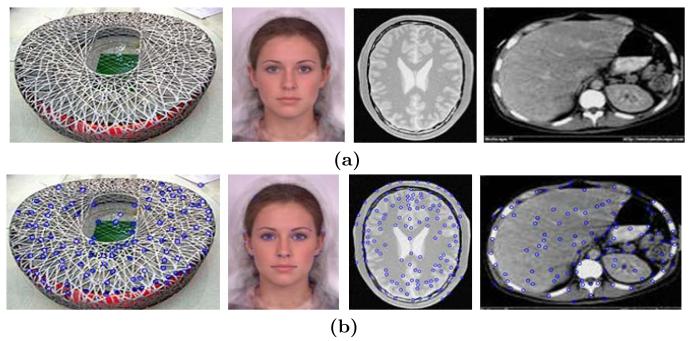
Some representative landmark detection examples are shown in Figure 1.
Fig. 1.
The landmark detection using Harris corner detector. (a) The original images. (b) The images with the landmarks overlayed.
2.2 Landmark Point Matching
After we detect the landmarks, we can extract features from the neighborhood of each landmark. The local orientation histograms are used as the features for landmark matching. The image is first convolved with the orientation filters. The filtering response in the neighborhood around the landmarks is computed to form the orientation histogram. Let Gx(i, j) and Gy(i, j) represent the gradients on pixel p(i, j) along x and y direction, respectively. The orientation histogram hk is defined as
| (2) |
where
| (3) |
and
| (4) |
The orientation histogram encodes the directions of the edges at each landmark point. It is proven to be an effective feature descriptor when the training samples were small [12].
In order to achieve robust matching of the landmarks, the extensive searching in the image space is required. This step is time consuming and often create the bottleneck for the landmark based image registration algorithm. In Section 2.4, we will show the time profile for each step in the whole procedure and it will be clear that the landmark matching dominate the execution speed.
2.3 Robust Estimation and Nonlinear Image Registration
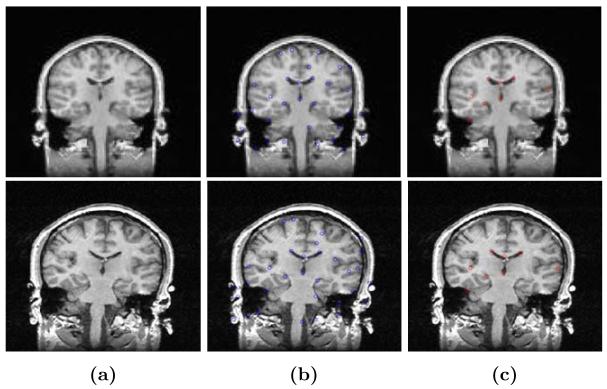
Because the original matching landmark sets contain missing landmarks. RANdom SAmple Consensus (RANSAC) [10] is used to reject outliers and robustly estimate the transformation. The RANSAC robust estimator randomly selects the minimal subset of the landmarks to fit the model. Measured by a cost function, the points within a small distance are considered as a consensus set. The size of the consensus set is called the model support M. The algorithm is repeated multiple times and the model with largest support is called the robust fit. In Figure 2 we show the results of applying robust estimation to reject the outliers in the original matching landmarks. The Harris corner detector detected 32 landmark pairs in Figure 2b. Based on the assumption of an affine transformation, the RANSAC found 8 inliers (shown in Figure 2c)and the rest 24 matching landmarks are rejected as outliers under the assumption for an Affine transformation.
Fig. 2.
Apply the robust estimation to find the robust landmark correspondence. (a)The original fixed and moving image. (b)The original pairs of matching points. (c)The robust matching points after rejecting the outliers.
The thin plate spline transform (TPS) is used to estimate the nonlinear transformation between the fixed and moving image based on the robust landmark correspondence. The TPS transformation T is calculated by minimizing the binding energy ETPS
| (5) |
where
| (6) |
with wi and vi denote the landmarks on the fixed and moving image, respectively.
TPS can provide a smooth matching function for each point in both images. The resulting nonlinear transformation is applied to map the moving image to the fixed image. For more details, we refer the readers to [11].
2.4 Image Registration Performance Bottleneck
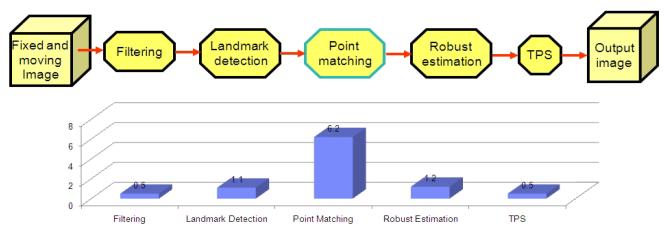
The adaptive multi-resolution landmark based image registration algorithm can provide good registration results, but requires relatively time consuming point matching procedures. In Figure 3 we show the execution time profile for each step in our algorithm for a typical 2D (192 × 192) image pair registration. It is quite obvious that the bottleneck is the point matching step. However, as we mentioned before, the point matching procedure in our proposed algorithm has a big advantage for easy parallelization by its design: data independence. Each landmark in the fixed image is independent to all the other landmarks, and its best match in the moving image is restricted to a certain area in the moving image. By fully utilizing this property, we propose to apply K-means data partitioning approach, and it has been successfully implemented on the IBM Cell Broadband Engine processor.
Fig. 3.
The time profile for the image registration algorithm
3 Parallelization on the Multicore Platform
The IBM Cell/B.E. [13,14] is a multicore chip with a relatively high number of cores. It contains a Power Processing Element (PPE) which has the similar function and configuration as the regular CPU. It also has multiple cores which are optimized for single precision float point algorithm, the Synergistic Processing Element (SPE). The PPE contains 32K L1 cache, 512K L2 cache and a large amount of physical memory (2G in our case). Unlike the PPE, the SPE has a quite different architecture compared with the standard CPU. The SPE operates on a 256KB local store to hold both code and data. The SPE also support 128 bit Single Instruction, Multiple Data (SIMD) instruction set for effective vector operations. The data transfer between SPE and PPE is through the direct memory access (DMA). DMA is quite time consuming so that a good parallel implementation should minimize the number of DMA operations.
3.1 Data Partitioning Using K-Means Clustering and Parallelization
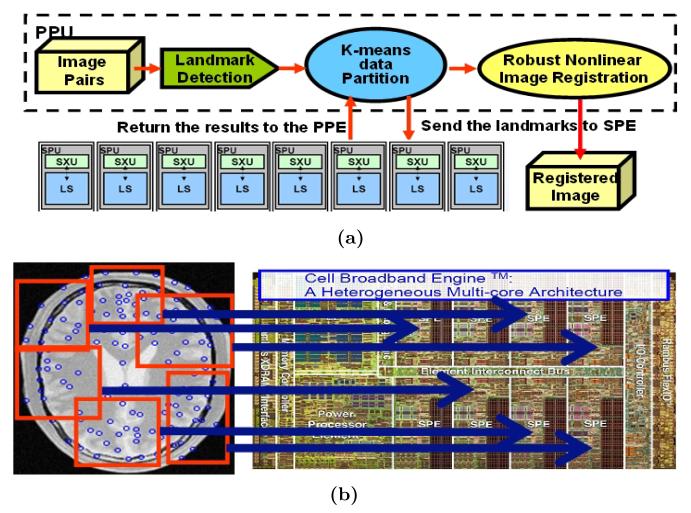
Given all the detected landmarks in the fixed image, we first apply the K-means algorithm to cluster them based on their Euclidean distance in the image, where K = 16 is set to be the number of the computing units in the IBM Cell Blade machine. Based on the boundary landmarks in each cluster center, we can calculate the largest and smallest coordinates to crop the sub-image accordingly. Because we know the size of the code running on the SPE unit in advance, we can compute the maximal size of the sub-image that can be stored on a single core (e.g. single SPE). If the image patch can fit into the local storage, the whole cluster of landmarks and their corresponding image patch are sent to the SPE for parallel processing using just one direct memory access (DMA). Because the number of DMA is critical for the performance of the parallel algorithm, the advantage of applying K-means to group the landmarks into clusters is to minimize the number of direct memory access operations. Landmarks which are spatially close to each other are grouped together and transferred into one computing core (e.g. one SPE in a Cell Processor) using one DMA call. In Figure 4a we show the procedure of parallelizing the registration algorithm. The K-means clustering and job scheduling to 16 PPEs are illustrated in Figure 4b.
Fig. 4.
The procedure of the parallel image registration algorithm. (a) The flow chart of the parallelization. (b) The data partitioning using K-means clustering.
Thread for each core or Synergistic Processing Element (SPE) is created only once in order to reduce the overhead related to thread creation. The point matching for our registration implementation is executed twice, one during the stage of linear registration and on during the stage of nonrigid registration. If we create an SPE thread each time when a point matching process starts, then all the SPE threads have to be created and destroyed repeatedly resulting additional execution time. In our implementation, all SPE threads are created before the first execution of the point matching process. These threads will be kept alive until the second point matching process is completed. It is true that the created SPE threads will be idle between the end of the first pass and the start of the second pass point matching processes, since the tasks in between are executed on PPE. This however does not cause any performance problem because those idle threads remain in the SPE spaces, which essentially has no impact to the main PPE thread.
Both the main core Power Processing Element (PPE) and SPEs are kept busy in sharing the point matching tasks. Initially we partitioned the landmark points into clusters and distribute evenly the clusters to the available SPEs. The main PPE thread waits for the completion of all active SPE threads before it proceeds to the next step of the registration process. Apparently this design overlooked the PPE computing resource, though it is indeed a different type of processor from SPE processors. It turns out that for some images, there may exist situations in which the sub-image enclosing the cluster is a little bit too large to send to a SPE by one DMA command and the space has to be further partitioned and then transferred to the SPE in more than one step. Even though such cases are rare, the second round partition is still critical to speed up the whole registration process.
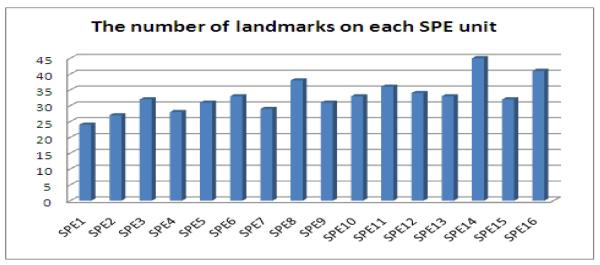
The purpose of applying K-means clustering for data partitioning is to decrease the number of direct memory access (DMA) operations. In order to fully utilize each SPE computing unit, the work load should be balanced. Because our algorithm selects the landmarks considering their spatial relationships, the K-means clustering intends to provide similar amount of landmarks in each cluster. In Figure 5 we show a typical work load distribution for one image pair on 16 SPE, it is clear that the number of landmarks assigned to each cluster roughly form a uniform distribution.
Fig. 5.
The landmark distribution on each SPE unit of the IBM Cell/B.E.
3.2 Landmarks Assembling and Transformation Estimation
The main processor or main core (e.g. PPE) is responsible to spool and destroy all the threads of computing cores (e.g. SPE). As we shown in Figure 4a, the PPE is also in charge of assembling all the matching points returned from each SPE and converts the results back to the original image coordinate systems. Robust estimation is applied to reject outliers and preserve the robust landmark correspondence. Nonlinear transformation is finally estimated to register the fixed image and the moving image.
4 Experimental Results
The testing data used in our experiments were prepared in the department of Radiology, University of Medicine and Dentistry of New Jersey and ITK [15] public image repository. The dimensionality of the test image is 192 × 192 and the x and y resolution are 1.41 mm. We tested our algorithm using the simulated affine transformations. Forty simulated 2D human abdomen CT images are generated by applying forty simulated deformations. The algorithm is compared with the multiple resolution affine registration implemented in ITK [15] and also the free software MedINRIA developed by INRIA [16]. The registration accuracy is evaluated based on whether the algorithm can successfully recover the affine transformation parameters.
| (7) |
The , , represent the estimated translation, rotation and scale parameters. The pt, pr, ps are the ground true transformation parameters. The δt = 1, δr = 0.5, δs = 0.01 are the normalization factors for translation, rotation and scale, respectively. The registration is treated as success if E ≤ 1.0. Our proposed algorithm can recover 95% of the image pairs while the ITK and MedINRIA can only recover 70% and 50% for the image pairs with large deformation. From the experimental results we show that the proposed algorithm can accurately register two images even with 2.5 times scale difference and 45 degree of rotation. It is clear from this study that our algorithm demonstrate more robust registration for large deformations compared with commonly used registration algorithm [15,16]. Some representative results are shown in Figure 6.
Fig. 6.
Comparative registration results on the human abdomen CT image pair. (a) The fixed image. (b) The moving image. (c) The registration algorithm using the MedINRIA [16]. (d) The registration algorithm using ITK [15]. (e) The registration results using our algorithm.
The parallelization code was built for two different platforms. The parallel version was tested on an IBM BladeCenter Q21 featuring 2GB of RAM and two processors running at 3.2 GHz configured as a two-way, symmetric multiprocessor (SMP) [17]. A thread running on a PPE can communicate with all 16 SPEs. The Cell/B.E. SDK 3.0 and GCC compiler were used to implement and compile the algorithm. In all our experiments, there was one main thread running on one of the PPEs and up to 16 threads on the SPEs. The sequential version was running on an x86 machine at 2.6 GHz and 4G memory. The compiler is also GCC.
All the image pairs used for testing have dimensionality (192 × 192).Because the point matching procedure dominates the running time of the registration algorithm, this step is the only part parallelized on the Cell/B.E. For fair comparison we run each implementation (sequential and parallel) 10 times. The statistics of the running speed on two platforms are shown in Table 1. Please notice that x86 refers to the sequential implementation on a x86 machine running with Linux. The Cell/B.E. (PPE only) denotes the running time on the multicore Cell processor using only the main processor PPE. The Cell/B.E. (PPE only) represents the parallel running time by fully utilizing all the 16 computing cores (SPEs). The 80% column in Table 1 represents the sorted 80% smallest running times of all 10 trials, and is commonly used to evaluate the performance of the system. Using the multicore platform, we roughly achieved 10 times of speedup over its corresponding sequential implementation. In total, the parallel version of the algorithm can register a pair of image (192 × 192) in less than five seconds.
Table 1.
The statistics of the running speed for 10 trials using the sequential and parallel multicore platform
| Mean | Variance | Median | |
|---|---|---|---|
| x86 | 5.95 | 0.26 | 5.82 |
| Cell/B.E. (PPE only) | 6.13 | 0.001 | 6.12 |
| Cell/B.E. (16 SPEs) | 0.60 | 0.0067 | 0.60 |
| Min | Max | 80% | |
| x86 | 5.33 | 6.93 | 6.22 |
| Cell/B.E. (PPE only) | 6.12 | 6.14 | 6.13 |
| Cell/B.E. (16 SPEs) | 0.50 | 0.70 | 0.70 |
5 Related Work
While research effort continues to explore methods and strategies for more efficient and rapidly converging computational methods, increasing attention has been given to hardware architecture-based parallelization and optimization algorithms for the emerging high performance architectures, such as cluster and grid computing, advanced graphical processing units (GPU) and multicore computers. In [18] a parallel implementation of multimodal registration is reported for image guided neurosurgery using distributed and grid computing. The registration time was improved dramatically to near real-time. In [19] a distributed computation framework is developed, which allowed the parallelization of registration metrics and image segmentation/visualization algorithms while maximizing the performance and portability. One key deterring factor in adopting supercomputer-based, cluster-based or grid computing architectures is availability and cost. Even for some large clinical institutions, financial limitations can be a major hurdle. The recent emergence of low cost, high computing power, multi-core processor systems have opened up an alternative venue for developing cost-effective high performance medical image registration techniques. In [20], a close to real time implementation of a mutual information based linear registration is reported. The algorithm is designed based on the Cell Broadband Engine (Cell/B.E.) multicore processor architecture. General parallel data mining algorithms on the Cell/B.E. are reported in [21,22]. In [23], a high performance distributed sort algorithm is proposed for the Cell processor. As an application, the implementation of the Radioastronomy image synthesis on the Cell/B.E. is discussed in [24]. According to our knowledge, this is the first study reporting fast and robust landmark based nonlinear image registration algorithm on a multicore platform.
6 Conclusion
In this paper, we have described a parallelization of a robust and accurate 2D image registration algorithm. The method is implemented on the IBM Cell/B.E. We have achieved about 10 times speed up, which allows our algorithm to complete the nonlinear registration of a pair of images (192 × 192) in less than five seconds. Our proposed data partitioning approach and the parallelization schema are independent to the parallel platforms and generic by its design, therefore it can be extended to other point matching related applications and other parallel platforms. The work discussed here is a part of an ongoing effort in developing full scale parallelization of a set of registration algorithms including the one reported in this paper. Future work will also include the generalization of the parallelization algorithm to handle 3D images.
Acknowledgement
This research was primarily conducted in IBM Watson Research Center funded by its internship program. It is also supported in part, by grants from the NIH through contract 5R01EB003587-04 from the National Institute of Biomedical Imaging and Bioengineering and contract 5R01LM009239-02 from the National Library of Medicine. Additional support was provided by IBM through a Shared University Research Award.
References
- 1.Maintz JBA, Viergever MA. A survey of medical image registration. Medical Image Analysis. 1998;2(1):1–36. doi: 10.1016/s1361-8415(01)80026-8. [DOI] [PubMed] [Google Scholar]
- 2.Hill DLG, Batchelor PG, Holden M, Hawkes DJ. Medical image registration. Physical Medical Biology. 1998;46:1–45. doi: 10.1088/0031-9155/46/3/201. [DOI] [PubMed] [Google Scholar]
- 3.Lester H, Arridge SR. A survey of hierarchical non-linear medical image registration. Pattern Recognition. 1999;32(1):129–149. [Google Scholar]
- 4.Zitova B, Flusser J. Image registration methods: A survey. Image Vision Computing. 2003;21(11):977–1000. [Google Scholar]
- 5.Cena B, Fox N, Rees J. Fluid deformation of serial structural MRI for low-grade glioma growth analysis. In: Barillot C, Haynor DR, Hellier P, editors. MICCAI 2004. LNCS. Vol. 3217. Springer; Heidelberg: 2004. pp. 1055–1056. [Google Scholar]
- 6.Agostino E, Maes F, Vandermeulen D, Suetens P. A viscous fluid model for multimodal non-rigid image registration using mutual information. Medical Image Analysis. 2003;7(4):565–575. doi: 10.1016/s1361-8415(03)00039-2. [DOI] [PubMed] [Google Scholar]
- 7.Thirion JP. Image matching as a diffusion process: An analogy with Maxwell demons. Medical Image Analysis. 1998;2(3):243–260. doi: 10.1016/s1361-8415(98)80022-4. [DOI] [PubMed] [Google Scholar]
- 8.Vercauteren T, Pennec X, Perchant A, Ayache N. Non-parametric diffeomorphic image registration with the demons algorithm. In: Ayache N, Ourselin S, Maeder A, editors. MICCAI 2007, Part II. LNCS. Vol. 4792. Springer; Heidelberg: 2007. pp. 319–326. [DOI] [PubMed] [Google Scholar]
- 9.Szeliski R, Szeliski R, Coughlan J, Coughlan J. Hierarchical spline-based image registration. International Journal of Computer Vision. 1994:194–201. [Google Scholar]
- 10.Fischler MA, Bolles RC. Random sample consensus: A paradigm for model fitting with applications to image analysis and automated cartography. Comm. of the ACM. 1981;24:381–395. [Google Scholar]
- 11.Chui H, Rangarajan A. A new point matching algorithm for non-rigid registration. Computer Vision and Image Understanding. 2003;89(2):114–141. [Google Scholar]
- 12.Levi K, Weiss Y. Learning object detection from a small number of examples: the importance of good features; Proc. IEEE International Conference on Computer Vision and Pattern Recognition; Washington, DC. 2004.pp. 53–60. [Google Scholar]
- 13.Kahle JA, Day MN, Hofstee HP, Johns CR, Maeurer TR, Shippy D. Introduction to the cell multiprocessor. IBM J. Res. Develop. 2005;49(4):589–604. [Google Scholar]
- 14.Chen T, Raghavan R, Dale JN, Iwata E. Cell broadbank engine architecture and its first implementation - a performance review. IBM J. Res. Develop. 2007;51(5):559–572. [Google Scholar]
- 15.ITK Software Guide. http://www.itk.org.
- 16.MedINRIA http://www-sop.inria.fr/asclepios/software/medinria/
- 17.Nanda AK, Moulic JR, Hanson RE, Goldrian G, Day MN, D’Amora BD, Kesavarapu S. Cell/B.E. blades: Building blocks for scalable, read-time, interactive and digital media servers. IBM J. Res. Develop. 2007;51(5):573–582. [Google Scholar]
- 18.Chrisochoides N, Fedorov A, Kot A, Archip N, Black P, Clatz O, Golby A, Kikinis R, Warfield S. Toward real-time, image guided neurosurgery using distributed and grid computing; ACM/IEEE Super Computing; 2006. [Google Scholar]
- 19.Warfield SK, Jolesz F, Kikinis R. A high performance approach to the registration of medical imaging data. Parallel Computing. 1998;24(9):1345–1368. [Google Scholar]
- 20.Ohara M, Yeo H, Savino F, Gong L, Inoue H, Sheinin V, Daijavad S, Erickson B. Realtime murual information based linear registration on the cell broadbank engine processor; Proc. International Symposium on Biomedical Imaging; 2007. [Google Scholar]
- 21.Buehrer G, Parthasarathy S, Goyder M. Data mining on the cell broadband engine; International Conference on Supercomputing; 2008.pp. 26–35. [Google Scholar]
- 22.Duan R, Strey A. Data mining algorithms on the cell broadband engine. In: Luque E, Margalef T, Benítez D, editors. Euro-Par 2008. LNCS. Vol. 5168. Springer; Heidelberg: 2008. pp. 665–675. [Google Scholar]
- 23.Gedik B, Bordawekar RR, Yu PS. Cellsort: high performance sorting on the cell processor; The 33rd international conference on very large databases; 2007.pp. 1286–1297. [Google Scholar]
- 24.Varbanescu AL, van Amesfoort AS, Cornwell T, Mattingly A, Elmegreen BG, van Nieuwpoort RV, van Diepen G, Sips HJ. Radioastronomy image synthesis on the cell/B.E. In: Luque E, Margalef T, Benítez D, editors. Euro-Par 2008. LNCS. Vol. 5168. Springer; Heidelberg: 2008. pp. 749–762. [Google Scholar]