Using Association Rule Mining for Phenotype Extraction from Electronic Health Records

Abstract

The increasing adoption of electronic health records (EHRs) due to Meaningful Use is providing unprecedented opportunities to enable secondary use of EHR data. Significant emphasis is being given to the development of algorithms and methods for phenotype extraction from EHRs to facilitate population-based studies for clinical and translational research. While preliminary work has shown demonstrable progress, it is becoming increasingly clear that developing, implementing and testing phenotyping algorithms is a time- and resource-intensive process. To this end, in this manuscript we propose an efficient machine learning technique—distributional associational rule mining (ARM)—for semi-automatic modeling of phenotyping algorithms. ARM provides a highly efficient and robust framework for discovering the most predictive set of phenotype definition criteria and rules from large datasets, and compared to other machine learning techniques, such as logistic regression and support vector machines, our preliminary results indicate not only significantly improved performance, but also generation of rule patterns that are amenable to human interpretation .

1. Introduction

With increasing adoption of electronic health records (EHRs), there is a growing attention in developing tools and methods for automatically identifying subjects that match a clinical trial or research protocol criteria. Typically, this is achieved by first defining the phenotype definition criteria in an algorithmic fashion, followed by the algorithm implementation within an institution’s EHR system for inexpensively and automatically generating a list of subjects that possess the desired phenotypic traits. Several national efforts, including eMERGE 1 , SHARP 2 and PGRN 3 , have demonstrated the applicability of secondary use of EHR towards high-throughput phenotype extraction. Yet the development of EHR-based phenotyping algorithms is a non-trivial and highly iterative process involving domain experts and data analysts. It is therefore desirable to develop methods that can semi-automatically generate phenotype definition criteria using existing EHR data, and potentially facilitate the algorithm development process. In particular, there is a growing need to develop methods that can reduce the significant initial effort and involvement of human experts in the algorithm development process, and instead focus on algorithm validation and implementation on large EHR systems.

To address this requirement, we extend distributional association rule mining (ARM) for semi-automatic generation for EHR-based phenotyping algorithms. ARM provides an exhaustive, although highly-efficient and robust methodology for discovering the most significant and predictive definitional criteria for a particular phenotypic trait. Our work is inspired by early results from Liao et al 4 where the authors develop an electronic algorithm to identify rheumatoid arthritis patients using logistic regression and natural language processing (NLP) techniques operating on billing codes, laboratory and medication data, achieving a 94% positive predictive value (PPV) and sensitivity of 63%. In a similar effort, Carroll et al 5 , 6 have applied Support Vector Machines (SVMs) to both non-curated and expert-defined collections of EHR features to identify Rheumatoid Arthritis cases using billing codes, medication exposures, and NLP-derived concepts as features. The authors report that SVMs trained on noncurated and expert-defined data outperformed an existing handcrafted algorithm. In this manuscript, using Type 2 Diabetes Mellitus (T2DM) as a use-case, we demonstrate that ARM not only performs significantly better compared to logistic regression and SVMs, but also has the added advantage of generating rule patterns that are amenable to human interpretation. In what follows, we provide a brief background on our overall approach and the methods developed, followed my preliminary results in applying ARM for modeling a T2DM EHR-phenotyping algorithm.

2. Materials and Methods

2.1. Distributional Association Rule

According to Simon et al. 7 , Distribution Association Rule Mining is the problem of discovering associations in a large database efficiently. A distributional association rule is a rule representing logical implications. Following the formal definition given by Agrawal et al 7 , for a set of n binary attributes I = {i ₁ ,i ₂ ,…,i _n } , called items , a rule is defined as an implication of the form X ⇒ Y where, X , Y ⊆ I and X ∩ Y = ∅ in some event (often called transaction). The set of items ( itemset s for short) X and Y are called antecedent and consequent of the rule respectively.

In a clinical setting, as illustrated in Table 1 the consequent Y corresponds to the disease outcome (for a patient) and the antecedent X corresponds to a combination of (binary) predictors: presence of abnormal lab results, diagnosis codes, medications, procedures and other pertinent information The set of predictors in the antecedent divides the patient population into two subpopulations: (i) the set of patients to whom all the predictors apply and (ii) the remaining patients (to whom at least one of the predictors does not apply). Take diabetes prediction, for example. The rule {HTN, obesity ⇒ Diabetes} applies to patients who are obese and have been diagnosed with hypertension. The rule implies that this subpopulation has statistically significantly higher risk of diabetes than the subpopulation to which it does not apply (namely, patients who are not obese and/or are not hypertensive). The statistical significance of the rules is measured by the Wilcoxon test. The output of distributional association rule mining is the set of all distributional association rules. Moreover, for all rules, the subpopulation to which the rule applies must contain at least minsup disease cases. As a user-defined threshold, minsup starts with an arbitrary choice and with some considerations of computationally easy, like random sampling in initializing a statistical model. Efficient algorithms to compute all association rules are described in Simon et al 7 , 8 and Agrawal et al 7 .

Table 1 .

Example of ARM

Diabetes	HTN	OB
True	Yes	Yes
False	No	No
False	No	Yes

2.2. Making predictions using distributional association rules

Distributional association rule mining is exhaustive in nature and discovers all significant association rules. The number of discovered rules can be combinatorial. Also the set of conditions in the rules can be overlapping and hence the subpopulations to which the rules apply can also be overlapping. In the clinical setting, to each patient, zero, one or more rules may apply. To make a prediction for a patient, we first find the most appropriate rule and then compute the prediction using that rule.

First, let us consider the problem of computing the prediction for a rule. We define the prediction by the rule as the mean risk (probability of diabetes) of the subpopulation to which the rule applies. The mean risk of a subpopulation is a statistically sound estimate and performs well as long as the subpopulation is homogeneous.

Ensuring homogeneity within a subpopulation drives our choice for the most appropriate rule. When no rule applies to a patient, we cannot ensure the homogeneity of the population, and we just return a default prediction, which is the mean risk of the entire study population. When only a single rule applies to a patient, the prediction for that patient is the prediction by that single rule: the mean probability of diabetes computed over the patients to whom the rule applies.

When multiple rules apply to a patient, we choose the most specific rule, that is, the rule involving the highest number of predictors. Intuitively, the rule with the highest number of conditions is the most likely to define a homogeneous patient subpopulation. Recall, that no matter how specific the rule, it applies to at least minsup cases (and some controls), thus it provides us with a reliable estimate of the subpopulation mean risk. Once we obtain a probability estimate for diabetes, we assign a label of ‘diabetic’, ‘normal’ or ‘unknown’ to each patient.

2.3. Data Preparation for this study

To demonstrate the feasibility of our approach, we used T2DM as our use case and the patient cohort (N=2581) from our existing eMERGE study 9 on peripheral arterial disease (see Table 2 ) While the EHR data available for this cohort comprises demographics, hospital admission and discharge notes, progress notes, outpatient clinical notes, medication prescription records, radiology reports, laboratory data and billing and administrative data, for developing the ARM model, we only used demographics, billing data and lab measurements. Since ARM is a supervised learning model, and hence requires appropriate class labels for the training data, we first executed the eMERGE T2DM algorithm 10 to identify “T2DM cases” and “T2DM controls”. These assigned labels were further validated with a T2DM rule-based algorithm developed internally by local domain experts at Mayo Clinic to provide a very high level of confidence in the correctness of the labels.

Table 2 .

Demographic Characteristics-Peripheral Arterial Disease

	PAD cases (n = 1687)	Controls (n = 1725)	p Value
Age, years	66±11	61±8	<0.0001
Men	1073 (64%)	1035 (60%)	0.0303
Race			NS
White	1592 (92%)	1566 (93%)	–
Black or African American	5 (0.3%)	11 (0.6%)	–
Native American Indian or Alaskan	2 (0.1%)	5 (0.2%)	–
Asian	4 (0.2%)	0 (0%)	–
Other	7 (0.4%)	10 (0.6%)	–
Unknown	110 (6.4%)	89 (5.3%)	–
Missing	5 (0.3%)	6 (0.4%)	–
Geographical distribution			<0.0001
Minnesota	918 (54%)	1047 (61%)	–
Iowa	204 (12%)	96 (5%)	–
Wisconsin	125 (7%)	77 (4%)	–
Illinois	109 (6%)	120 (7%)	–
Michigan	67 (4%)	62 (4%)	–
Other	264 (16%)	323 (19%)

Age is presented as mean±SD.

Categorical variables are presented as percentages (%).

PAD, peripheral arterial disease.

2.4. Item/Feature Extractions and ARM Model Building

For ARM, like any other machine learning models, it is essential to find good features ( items in ARM terminology). For our T2DM use case in this study, we extracted all diagnosis and lab data as well as the class labels for the eMERGE patient cohort (N=2581). Diagnosis data includes 150 different CPT-4 codes, 15 SDIAG (secondary use diagnosis) codes and 15 SPROCO (secondary use procedure) codes, while lab test data comprised 32 different lab measurements relevant for Diabetes. We used AHRQ’s (Agency for Healthcare Research and Quality) Clinical Classification Software 11 to classify the entire diagnosis data into 250 distinct categories. Since items are binary features, we dichotomized the features into ‘ yes ’ or ‘ no ’ as follows: For a diagnosis code, the dichotomized feature indicates the presence of the diagnosis code; and for a laboratory result, the dichotomized feature indicates abnormal results—a measurement outside the healthy range.

ARM aims to discover all rules—combinations of diagnosis codes and/or abnormal (unhealthy) laboratory results that indicate increased risk (probability) of diabetes. To this end, ARM utilizes the Apriori algorithm, which discovers these combinations through exhaustive enumeration. Conceptually, it first considers individual items that apply to at least minsup diabetes cases. Then it iteratively proceeds to pairs, triplets and higher-order sets of items. The algorithm terminates, when no more itemsets can be generated that applies to at least minsup diabetes cases. ARM only reports those itemsets as rules, where the affected patients (patients to who present all the diagnosis code and abnormal lab results in the itemset) have statistically significantly higher risk of diabetes than the unaffected patients. Bonferroni correction is used to adjust for simultaneous hypothesis testing.

3. Results

We start our evaluation by establishing a baseline. A naive method to find diabetic patients is to search the EHR repository for diabetes-related diagnosis codes. Specifically, we construct a baseline classifier, which predicts a patient to be diabetic if it finds one of the diagnosis codes in the AHRQ group of ‘diabetes mellitus without complications’. Table 3 resents the confusion matrix of this naive classifier. The rows of the table correspond to the predicted diabetes status and the columns correspond to the actual outcome. Among 1613 patients with no diabetes, 1572 are correctly predicted to not have diabetes. Among 966 patients who are labeled as true diabetic, 945 are correctly predicted to be diabetic. Hence, in our data set, the precision of the baseline classifier is 0.866 and its recall is 0.969, making it a reasonable classifier.

Table 3 .

CM (Confusion Matrix) for V48 vs Label

True DM	No	Yes
Dx Code
No	1470	30
Yes	145	936

3.1. The ARM Model

While the baseline classifier achieves reasonably high precision and recall, for the purpose of phenotyping, such performance may be insufficient. Recall that ARM has a single parameter, minsup , denoting the number of cases (diabetic patients) that needs to be determined. This parameter controls how tightly the model fits the data. If minsup is high, only the most obvious rules are found; if it is low, the model may “overfit” the data: coincidental rules can be discovered. In our work, we use 208 as the minsup, which is one sixth of the total number of patients ( 1295 patients in total in the training set). For this study, ARM discovered 1159 rules. In Table 4 we report the 5 rules with the highest precision. The columns of the table include Support , SupportD , Precision and Item set. Support refers to the number of patients to whom the antecedent of each AR (association rule) applies, while SupportD refers to the number of cases (diabetic patients) to whom that antecedent of each AR applies. The precision of a rule is the fraction of cases among the patient to whom the rule applies. In other words, precision is supportD divided by support. The item set denotes the set of conditions that the antecedent of the rule is comprised of. The meaning of these conditions and the number of rules that utilized these conditions are listed in Table 5 .

Table 4 .

Top Rules Ranking List

NO.	Support	SupportD	Precision	Item set
1	281	270	0.961	V48 V86 V142 V245 V82080
2	280	269	0.96	V48 V57 V74 V86 V245 V82080
3	274	263	0.95	V48 V52 V57 V74 V244 V246 V82080
4	278	263	0.94	V48 V52 V57 V87 V82080
5	278	263	0.94	V48 V57 V86 V216 V221 V82080

Table 5 .

Meaning and ranking of Items

Items	Times	Diagnosis Meaning
V48	5	Diabetes mellitus without complication
V82080	5	Hemoglobin A1c, B
V57	4	Deficiency and other anemia
V86	3	Hypertension with complications and secondary hypertension
V74	2	Retinal detachments; defects; vascular occlusion; and retinopathy
V52	2	Gout and other crystal arthropathies
V245	2	Residual codes; unclassified
V246	1	Adjustment disorders
V221	1	Open wounds of head; neck; and trunk
V216	1	Other fractures
V244	1	Other screening for suspected conditions (not mental disorders or infectious diseases)
V142	1	Acute and unspecified renal failure

All of the top 5 rules (involving 12 items) have a precision higher than 94% and all of them include the item V48 (Diabetes mellitur without complication) and V82080 (Hemoglobin A1c, B). Recall, that the naïve classifier uses only the diabetes diagnosis code and achieved a precision of .866. All of the top rules achieved precision higher than that of the naïve classifier, suggesting that at least some of the extra conditions (on top of the diagnosis code) contribute positively. Intuitively, the extra conditions indeed are indicative of T2DM: renal failure, increased risk of fracture, decreased wound healing—are all coincident with or are outright consequences of diabetes.

3.2. Comparison with State-of-the-Art Machine Learning and Statistical Models

In order to make comprehensive comparisons, we run the dataset with logistic regression, decision-tree (DT) and SVM besides ARM with the same set of features. We use the R statistical computing environment. In total, our dataset comprised of 2581 patient subjects that were randomly split into two halves, with half of them serving as training data and the other half as testing data. We ran 10 fold cross validations on the training data, and used the trained model for making predictions on the testing dataset. Instead of a binary label for T2DM outcome, all four models compute the probability of diabetes. To transform a probability into a binary label, we can use a cutoff : we predict that a patient is diabetic if his probability of diabetes exceeds thus use-supplied cutoff . By changing this cutoff, we can adjust the prediction to better fit the requirements: we can select a high cutoff, when higher precision is required; or we can select a lower cutoff when higher recall is required.

Table 6 shows the results for the four models at three different values of cutoff . Among the four models, ARM obtained the best results. When its cutoff is 0.92, ARM has well-balanced recall and precision: both as high as 0.89. Thus, its F-score is 0.895. Note that the highest F-score for ARM is 0.914, which is attained at a cutoff of 0.95. The most comparable model is decision tree (DT). It is similarly interpretable as ARM and also has similar and balanced performance. It is, however, instructive to point out that whenever the precisions of ARM and DT are similar, the recall of DT tends to be a little lower. Decision trees are constructed through recursively partitioning the patients into two groups without overlap such that one group is enriched with cases and the other with controls. Consequently, each patient can be classified by at most a single leaf in the tree. In contrast, many association rules may apply to the same patient. This allows association rules to “re-use” patients, and hence estimate probabilities of diabetes from larger samples. When the number of cases in a leaf is too small, it is not possible for a decision tree to reliably divide that node further and still robustly estimate the probability of diabetes. Therefore, these cases are misclassified, resulting in a slightly lower recall for decision trees the cutoff at 0.9, then we classify all patients with a predicted probability of diabetes at or above 0.9 as diabetic. Since all patients who are predicted diabetic have a predicted probability of diabetes of at least 0.9, the precision of the classifier should be at or above 0.9. For ARM, the difference between the cutoff and the achieved precision is relatively small, but for the other models, the difference can be very large. This indicates that the competing models have difficulty in assessing the probability of diabetes for patients with high true probability of diabetes. In a general application, this issue would not be of practical importance, but in our phenotyping application, the patients we aim to find are precisely the patients with high probability of diabetes.

Table 6 .

Measure Metrics for All Models

Model	ARM			DT			LR			SVM
cutoff	0.95	0.93	0.92	0.88	0.75	0.70	0.95	0.7	0.6	0.7	0.6	0.55
Precision	0.9	0.887	0.868	0.903	0.888	0.881	0.904	0.889	0.883	0.904	0.893	0.881
Recall	0.112	0.894	0.966	0.812	0.889	0.925	0.693	0.796	0.819	0.784	0.858	0.878
F-score	0.199	0.895	0.914	0.855	0.8885	0.902	0.785	0.840	0.849	0.839	0.875	0.879

Another standard technique to compare classification models is ROC curves 12 Furthermore, it is also the primary tool for selecting a good cutoff. To avoid clutter, in Figure 1 we show the ROC curves only for ARM and SVM. As we expect based on the similar F scores, for the most part, the two ROC curves are overlapping. Where they differ is in the top left corner—the section of the ROC curve where cutoffs are selected from. In other words, since the difference in performance is concentrated on the narrow range where cutoffs are typically selected from, the small difference in performance that we saw in Table 5 , translates to real-world performance difference.

Figure 1 .

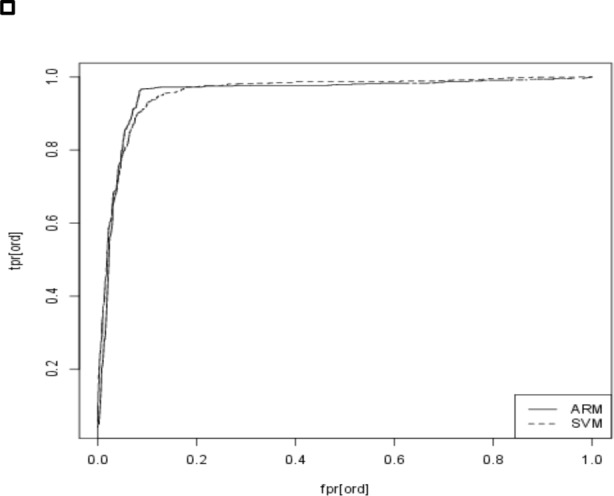
ROC curve for ARM and SVM classifiers

4. Conclusion and Future Work

In this paper, we present a machine-learning framework to do semi-automatic phenotyping algorithm development using EHR data at Mayo Clinic. Our framework—distributional ARM—is a supervised learning technique that is not only scalable with large datasets, but is also robust and efficient. As part of our T2DM use case, we demonstrate its superior performance compared to traditional machine learning techniques. Furthermore, the rules generated from ARM are amenable to human interpretation. Without doubt, with the right feature engineering method, interpretable results can be extracted from all discussed models, however, ARM directly offers an interpretable model, which simplifies or even enables further refinements of the model. With the right minsup setting, ARM is computationally very efficient; all computation could be completed within a few seconds on a modern laptop computer.

In our future work, we plan to expand and evaluate our approach on a range of phenotypes including rheumatoid arthritis and depression that include more complex patters, as well as more complex patterns and interactions between various algorithmic definition criteria. In addition, we will explore employing features or attributes from clinic notes obtained by deploying NLP tools and methods.