Abstract
Adaptation of vein bypass grafts to the mechanical stresses imposed by the arterial circulation is thought to be the primary determinant for lesion development, yet an understanding of how the various forces dictate local wall remodeling is lacking. We develop a dynamical system that summarizes the complex interplay between the mechanical environment and cell/matrix kinetics, ultimately dictating changes in the vein graft architecture. Based on a systematic mapping of the parameter space, three general remodeling response patterns are observed: 1) shear stabilized intimal thickening, 2) tension induced wall thinning and lumen expansion, and 3) tension stabilized wall thickening. Notable is our observation that the integration of multiple feedback mechanisms leads to a variety of non-linear responses that would be unanticipated by an analysis of each system component independently. This dynamic analysis supports the clinical observation that the majority of vein grafts proceed along an adaptive trajectory, where grafts dilate and mildly thicken in response to the increased tension and shear, but a small portion of the grafts demonstrate a maladaptive phenotype, where progressive inward remodeling and accentuated wall thickening lead to graft failure.
Keywords: dynamical system, remodeling, vein graft, biomechanics, hemodynamics
1. Introduction
Myocardial infarction, stroke, and limb loss continue as leading causes of mortality and morbidity in our society [1]. Vein bypass grafting has evolved as the most successful therapeutic modality for treating the stenotic or occluded arteries that are responsible for these clinical outcomes. However, despite significant advances to optimize bypass grafting, long-term success remains limited. Plagued by constriction (negative remodeling) and accelerated scarring within the wall (intimal hyperplasia), significant luminal narrowing and intraluminal thrombus formation remain frequent complications [2]. In an effort to improve outcomes, researchers have applied a variety of approaches to modify the biology that controls vascular remodeling and intimal hyperplasia [3]. Unfortunately, attempts have been largely ineffective due to an incomplete understanding of the specific cause - effect linkages through which the underlying pathologic mediators (e.g. hemodynamic factors, biochemical mediators, and cellular effectors) lead to this occlusive phenotype [4]. Work in our laboratory has confirmed that wall shear stress and intramural wall tension stand as a key regulators of the vascular architecture [5,6], and we have established that local inflammation (mediated by blood monocytes) is an important accelerator of intimal hyperplasia [7]. However, lacking is an understanding of the dynamic interplay between the physical forces and cellular elements that modulate local variations in wall remodeling, and ultimately success or failure of the graft.
In the current manuscript, we propose a simple theoretical framework to organize the current undersanding of the components that drive pathologic vascular remodeling and failure. Our goal is to provide a more indepth examination of the control variables that are observed at the macroscopic level. In isolation, each of the various feedback mechanisms promotes a monotonic change and stable solution in the dynamical system; however, in aggregate they lead to substantial non-linearities that provide insight into the highly variable outcomes that are observed clinically.
2. Heuristic and Conceptual Diagram
2.1. Mediators of Vein Graft Adaptation
In response to environmental stimuli, the vein graft wall demonstrates significant plasticity and provides a mechanism to maintain integrity through a wide range of imposed conditions. Following transfer of the vein from the low pressure/continuous flow venous sytem to the high pressure/pulsatile flow arterial system, vein grafts undergo a series of adaptations. These adaptations encompass two distinct processes: intimal hyperplasia and wall remodeling. Intimal hyperplasia is characterized by migration of smooth muscle cells into the intima with proliferation and deposition of extracellular matrix, resulting in narrowing of the lumen. In contrast, remodeling is characterized by preservation (or loss) of lumen area through reorganization of the cellular and extracellular components within the media. Following vein graft implantation, both forms of adaptation are initiated, and it is the balance between these two processes that dictates the degree of luminal narrowing and ultimately the success or failure of the revascularization [8, 9]. Figure 1 illustrates the range of phenotypes that are observed in human vein grafts, six months following implantation. Comprised of both a heuristic and experimental understanding, the phenomenology of vein graft adaptation has been summarized in Figure 2.
Figure 1.
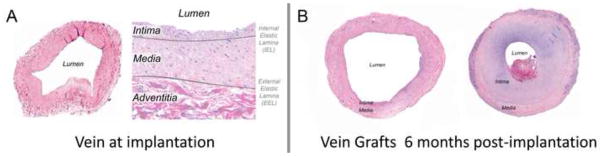
Vein histology at the time of graft implantation, demonstrating intimal and medial layers (A). Vein grafts obtained from different patients, six months following implantation (B). Markedly different phenotypes, ranging from preservation of the lumen to severe intimal thickening and lumen narrowing are commonly encountered.
Figure 2.
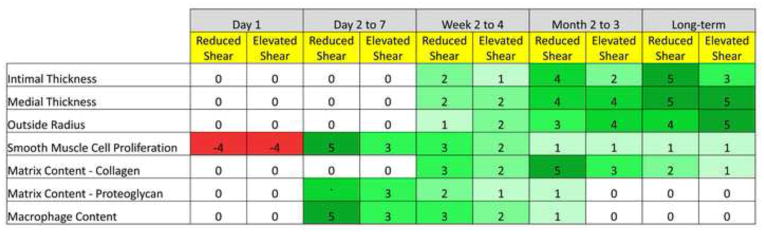
Biologic processes that dominate vein graft adaptation, as a function of time and wall shear stress. A scale ranging from −5 to 5 is used to represent a reduction or increase in the parameter, respectively. A graduated coloring scheme is also used with red illustrating a reduction and green illustrating an increase in the parameter.
A variety of approaches have been used to describe these overlapping events and undertand their combined influence on vein graft architecture. In work performed in our laboratory, adaptation geometry has been described using a classic biologic population model [8]. Integrated with an extensive data set derived from in vivo experimentation and validated against a unique focal stenosis geometry, this model provides insight into the temporal change in graft geometry in the weeks to months following graft implantaton. Developed exclusively as a phenomenological geometric model, however, this approach lacks insight into the biology that dictates these structural change. To address this deficiency, we have proposed a hybrid Partial Differential Equation (PDE) - Agent Base Model (ABM) that explicitly describes tissue adaptation at the cellular level [9]. The PDE component is founded in continuum mechanics and provides the hemodynamic flow conditions, while the ABM component describes the cellular activity within the wall. While providing signficant enhancements over the population model, this approach fails to integrate the feedback mechanisms that are critical to understanding the dynamics of the system. To this end, we propose here a conceptual framework aimed at integrating the multi-factorial complexities and feedback loops that are inherent in vein graft adaptation.
2.2 Conceptual Diagram
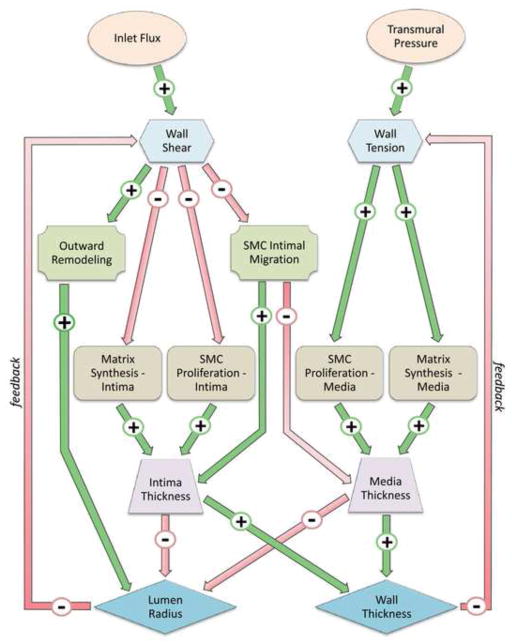
Vein graft plasticity can be described as a function of the local biomechanics and the population dynamics of smooth muscle cells. The most dominant mechanical stimuli are wall shear stress and intramural wall tension. The dynamics of the smooth muscle cells are characterized by the rate of proliferation and its capacity to deposit or degrade extracellular matrix. The structural outcome for the vein graft is examined as a function of time, using geometrical quantities such as intimal and medial thickness and lumen cross-sectional area. The inter-relationships among these various factors (Table 1) are integrated into a heuristic model of vein graft adaptation (Figure 3). Conections between nodes are expressed by an oriented link in the graph, where A → B indicates a direct influence of node A on node B. If A induces an increase in B, the corresponding linkage is indexed with a plus sign. If A induces a reduction in B, the corresponding linkage is negative.
Table 1.
Dominant factors controlling vein graft adaptation.
Forcing environmental parameters:
|
Mechanical parameters:
|
Remodeling variables:
|
Cell population variables:
|
Compartmental size:
|
Global Outcomes:
|
Figure 3.
Dynamical system schematic illustrating the primary interacting elements in vein graft adaptation.
We can identify three closed cycles linking Shear Stress and Lumen Radius, one cyle with all positive signs (i.e. Shear → Outward Remodeling → Lumen Radius → Shear) and two cycles with mixed signs along the path. Similarly, we observe two closed cycles linkages involving Wall Tension and Wall Thickness. In addition, several cross coupling relations between Shear - Wall Thickness and Wall Tension - Lumen Radius are also noted. With such complexity, a wide range of unpredictable scenario are likely to be present a variety of cyclic phenotypes, such as bifurcations and transitions to chaos. In the current analysis, novel nonlinear phenomena, unanticipated from the conceptual diagram, emerge from the simulation.
3. Mathematical Model
3.1. Hemodynamic and Tensile Forces in a Thick Cylinder
Assuming Poiseuille flow in a straight cylindrical pipe, where z is the axial coordinate and R1 is the radius of the lumen, blood flow Q is given by:
| (1) |
where ΔPblood is the pressure drop in a vessel of length L, and μ is the dynamic viscosity. If we consider the the pressure drop of the fluid inside the lumen to be small compared to the transmural pressure, the shear stress at the wall is given by the analytical formula:
where U is the maximum (centerline) velocity of the blood.
For describing the mechanical deformation of the wall, the classical analytical thick cylinder solution is used, where the transmural pressure ΔPwall = P2 − P1 generates the load and the wall deformation. Assuming the vein graft has a thick wall (R2 − R1) with uniform linear elastic mechanical properties and σz = 0, the radial stress σr and hoop stress σθ are then given by [10]:
and
Note that the radial stress matches the internal and external pressure at the wall, which in the current analysis are assumed to be constant. Postulating that the radial stress is not influenced by the adapation events, and the hoop stress is the primary component that impacts outward remodeling, σθ can be expressed as:
| (2) |
with
For simplicity, we will drop the subscript θ from σθ in subsequent formulations.
While the stress distribution in the radial symmetric, thick cylinder case is independent of the stiffness and compression ratio of tissue (i.e. the Young modulus E and Poisson ratio ν are independent of σ), this is not true for the displacement u, which is given by:
where
and λ and μ are the Lamé coefficients:
Although this analytical solution might be modified to take into account any pre-assumed stretching of the vein graft in the longitudinal direction, this is omitted in the current analysis.
3.2. Dynamical System
We have formulated the dynamical system in such a way that perturbations on input velocity and/or transmural pressure are the initial driving forces for adaptation.
Letting τ0 be the shear stress and σ0 be the intramural hoop stress at time t = 0, we postulate that there should be three types of control mechanisms:
-
The first mechanism is driven by shear stress, where the vein graft response evolves to drive the local shear stress τ towards the baseline shear stress condition τ0. This control mechanism is expressed in the dynamical system with coefficients dependent on Δτ = τ(t) − τ0. To illustrate this concept using a dummy example, assume the dynamics of the lumen are given by the differential equation Ȧ = αΔτ A, where the equilibrium point corresponds to Δτ = 0. Depending on the sign of the coefficient α, this equilibrium might be stable or unstable. If we expressing shear stress as a function of the lumen area, the following autonomous equation is obtained:
If α is positive, the vein graft is directed towards the baseline shear stress condition, with a stable phenotype. If α is negative, the lumen progresses toward either unchecked outward dilation or complete occlusion, depending on the initial condition A(0).
-
A second control mechanism is driven by the intramural hoop stress, Δσ = σ − σ0. Using the same dummy example (Ȧ = αΔσ A) and using a thin cylinder approximation (i.e. R1, R2 ≈ R), we obtain the linear model:
Note that the two above control mechanisms are region specific, with cells reacting to the local mechanical environment to which they are exposed.
-
The third control mechanism is dominated by flux. Assuming the overall system maintains a prescribed blood supply Q0, our example equation can be written as Ȧ = αΔQ A. Replacing the flux by its analytical formula, we obtained the generalized logistic model
where the coefficients βj, j = 1,2 depend on ΔPblood, μ, and L.
Returning to the construction of the dynamical system (Figure 3), we can express all growth rates as a function of the difference between the mechanical condition at time t and a prescribed baseline setting:
Meanwhile the velocity profile in the straight pipe is maintained to conserve the flux Q0.
Using this approach, the dynamics of the system components can be established. Assuming the simplest form, a linear dependence for each parameter on the mechanical quantities τ and σ, yields the following expressions:
| (3) |
| (4) |
| (5) |
| (6) |
| (7) |
In equations (3) to (6), the migration of SMC from the media to the intima is assumed to be non-reversible and accentuated by reductions in wall shear stress. The coefficient for migration is factored by Δτ− = min(Δτ,0). Using an estimate of the mean density of SMC in the media adjacent to the internal elastic lamina (IEL), we obtain the expression
to represent the migration of SMC through the elastic lamina toward the intima.
Further refinement in the model is obtained by assuming a phenotypic modulation of SMC to maintain a constant SMC to extracellular matrix (ECM) ratio[11]. We modify equation (4) to maintain equilibrium of these elements, where
| (8) |
We have integrated a unidirectional feedback that is responsive to both reduced shear stress and elevated wall tension. To represent this, we substitute Δτ and Δσ, with the expressions Δτ− and Δσ+, respectively. Finally, the response to mechanical stress is assumed to saturate above a certain limit, supporting the use of a coefficient of the type
Within the derivation, we have assumed that the hemodynamic flux stays constant in the graft. While this approximation is applicable for most geometries, it begins to fail as the lumen approaches near occlusion. To account for this issue, the time integration of the dynamical system is suspended if the lumen radius is less than an a priori bound Rmin. This hypothesis corresponds to the general observation that in the circulation there exist a general control feedback to modulate distal resistance to maintain constant flux in all downstream branches, independent of the extent of a more proximal stenosis. Finally, note that all coefficients α in the dynamical system are positive, such that the sign preceeding α reflects the positive or negative index.
The simulation is initiated with a perturbation of the inflow velocity, and the system responds as a function of the resulting difference on shear stress Δτ. Similarly, Δσ measures the difference between the mean hoop stress at time t and its initial value. We observe that the dynamical system, equations (3) to (7), is truly non linear, secondary to the dependence of σ and τ on the areas of the lumen, intima, and media. We observe that Δτ = Δσ = 0 are the critical points of the dynamical system, where all derivatives of time become zero). From a mathematical point of view, τ0 and σ0 can be viewed as controlled parameters.
Work both in our laboratory [12] and other [13] has demonstrated the transmigration of monocytes and their conversion to macrophages to be a critical driving force in vein graft adaptation. To integrate this time-dependent component into the model, we modify the right hand side of the dynamical system using an activity factor A(t). As such, all events are weighted by a time factor that mimics the macrophage activity:
| (9) |
As outlined in Figure 2, the density of macrophages in the graft wall reaches a maximum around time Ti and decays at time scale δTi. This simple model of inflammation provides two additional parameters
and insertion into the the dynamical system (3) to (7) yields the following expressions
| (10) |
| (11) |
| (12) |
| (13) |
| (14) |
While other groups have utilized a more extensive model of vascular inflammation [14], the integration of a global modifying factor to simulate these effects provides a straight forward approach that can be readily rescaled with regard to time.
4. Results
As describe above, the simple dynamical system encompasses two primary feedback loops, acting through shear stress and wall tension. In the initial analysis, each of these loops will be analyzed independently. To faciliate this evaluation, the effect of inflammation will be neglected by setting the macrophage activity to zero.
4.1. Testing the Feedback Control Loops
The dynamics of the model around the equilibrium are analyzed as a function of the external forcing parameters, input velocity and pressure. All simulation results are obtained using the Matlab ode45 differential equation solver, which is based on an explicit Runge-Kutta formula and the Dormand-Prince pair [15]. The range of solutions are examined through a 50% increase in shear stress and a 20% reduction in tension, with qualitative observations described below.
4.2. Influence of Shear and the Lumen Area-Shear Feedback Loop
Focusing on the dynamics of the intima (α1 = α2 = 0.1 and αj = 0, for j = 3..7), Figure 4A and 4B shows the effect of a 50% decay in shear stress. It is interesting to note that this pattern approximates the standard results of a logistic model, characterized by rapid exponential growth of the intima, saturation due to the inhibitory effect of an increasing shear stress, and a reduction in lumen area. Although neglected in this portion of the analysis, it is interesting to note that growth of the intimal layer may stop before reaching an equilibrium if the expressions for macrophage activity are included.
Figure 4.
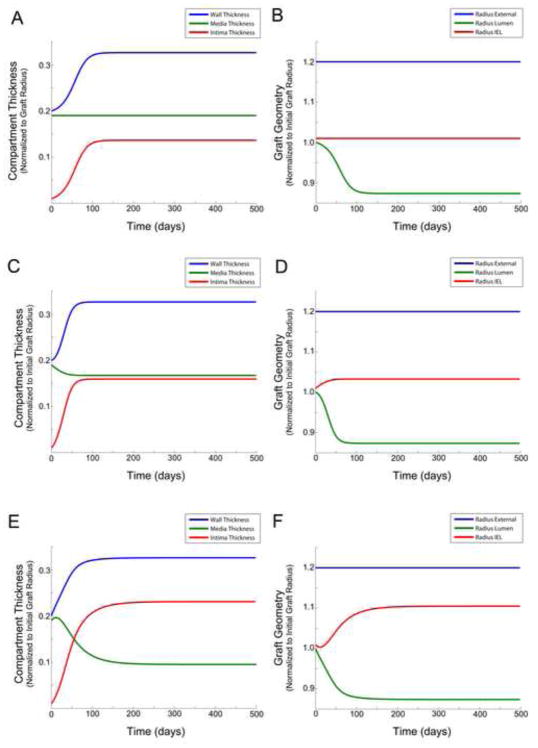
Influence of shear on the graft geometry with inclusion of an active lumen area - shear feedback loop and excluding the effect of wall tension (A – B), with an active lumen area - shear feedback loop and the inclusion of smooth muscle cell migration from the media to intima (C – D), and with an active lumen area - shear feedback loop and the inclusion of extracellular matrix production and smooth muscle cell production in response to altered wall tension (E – F). Compartment/layer thickness (A, C, E) and graft radius (B, D, F).
Examining the effect of SMC migration, by tuning α5 = 0.02 (Figure 4C and 4D), the anticipated increase in intimal thickness and reduction in medial thickness is observed. The effect on lumen narrowing, however, is relatively modest, where we observe no notable influence on the final equilibrium of the system but a more rapid rise to these asymptotic geometries.
Including the dependency of both ECM synthesis and SMC proliferation as a function of tension (with α3 = α4 = 0.05), a general reduction in media thickness and increase in intimal thickness is observed (Figure 4E and 4F). While the global outcome (i.e. the asymptotic geometries of the lumen and external diameter of the graft) is not significantly affected, the influence on the early dynamics of remodeling are notable. A small transient oscillation in layer thickness is observed, predominantly due to a secondary indirect coupling of tension and shear stress.
4.3. Influence of Wall Tension and the Wall Thickness-Tension Feedback Loop
Figure 5 shows the effect of a 20% decay in tension, while removing all dependency on shear stress (i.e. α1 = α2 = α5 = α6 = 0) and including both an outward remodeling and medial thickening dependency on wall tension (i.e. α7 = 0.01 and α3 = 0.001, α4 = 0.05,). We observe both layer thicknesses and the lumen diameter to increase toward an asymptote.
Figure 5.
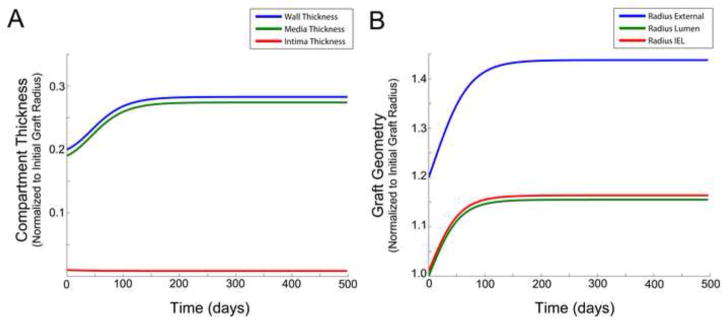
Influence of wall tension on graft geometry, with an active wall thickness – intramural wall tension feedback loop and excluding the effect of shear. Compartment/layer thickness (A). Graft radius (B).
4.4. Nonlinear Coupling between Outward Remodeling and Wall Thickening
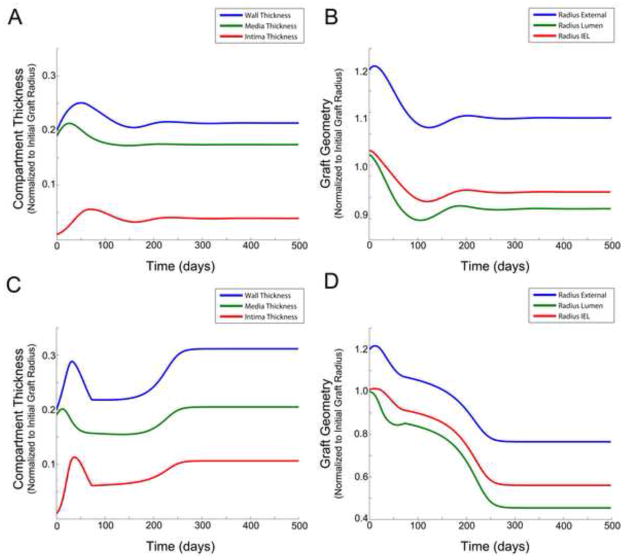
In the simulations described above (sections 4.2 and 4.3), we have obtained results that could have generally been anticipated from the vein graft adaptation heuristic. However if we couple both the shear-lumen area and tension-wall thickness feedback mechanisms (i.e. using non zero coefficients for all αj), we begin to identify emergent, unanticpated behaviors that result from the interactions. Examples of these findings, obtained with α1 = α2 = 0.1, α3 = 0, α4 = 0.1, α5 = 0.001,α6 = 0.003, α7 = 0.01 and α1 = α2 = 0.2, α3 = 0.02, α4 = 0.1, α5 = 0.008, α6 = 0.001, α7 = 0.01, are provided in Figure 6. In stark contrast to the monotonic growth patterns of a standard logistic model, significant oscillations in the early phase of graft adaptation are observed. These early dynamics, and ultimately the final equilibrium morphology of the graft, are implicitly linked to the balance among the various biologic processes that drive vein graft adaptation. In Figure 6A and 6B, the dependence of SMC proliferation and ECM production on shear is modest, and intimal thickening with narrowing of the lumen is limited. In Figure 6C and 6D, where SMC and ECM kinetics are highly dependent on shear, lumen diameter is maintained until a critical threshold is reached, and rapid loss of lumen is observed. Somewhat non-intutitive is the transient growth then reduction in layer thicknesses, which appears to result from the early production of SMC and ECM within the media, followed by the migration of SMC into the intima.
Figure 6.
Influence of nonlinear coupling between outward remodeling and wall thickening on graft geometry. Compartment/layer thickness (A) and graft radius (B), where (α1 = α2 = 0.01; α3 = 0; α4 = 0.1; α5 = 0.001; α6 = 0.003; α7 = 0.1). Compartment/layer thickness (C) and graft radius (D), where (α1 = α2 = 0.2; α3 = 0.02; α4 = 0.1; α5 = 0.008; α6 = 0.001; α7 = 0.01)
Instability within the model may lead to either graft occlusion or uncontrolled outward expansion and aneurysm development. While these phenotypes are observed within the spectrum of clinical outcomes, model predictions become increasingly inaccurate due to violation of the underlying assumption of constant flux, which is not maintained as the radius becomes either too large or small. Interestingly, if the target is driven by flux instead of shear stress and tension, the solutions become even more unpredictable. Figure 7 provides an example of the simulation obtained with a 20% reduction in flux, while the objective for shear stress and tension are maintained at their baseline values.
Figure 7.
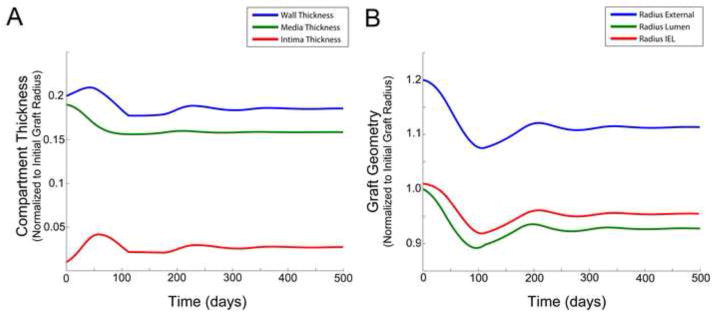
Simulation results obtained with a 20 per cent reduction in flux, while shear stress and tension are maintained at their baseline values. Compartment/layer thickness (A) and graft radius (B).
Inclusion of the inflammation model terms, equations (10) to (14), induces additional complexities to the early phase adaptation. Interestingly, the time scale of the macrophage activity drives the system to a non “quiescent” state that maybe substantially removed from equilibrium. In situations where the early remodeling is highly dynamic (such as observed in Figure 7), the macrophage driving force may decline to zero and become fixed at any point during the oscillation.
In summary, we have obtained from the nonlinear dynamical system a range of simulation results that in its simplest form reproduces a logistic model yet in its most complex forms provides a wide variety of temporal behaviors that are analogous to the spectrum of vein graft phenotypes that are observed clinically.
4.5. Stochastic Model and Rare Events
To systematically explore the parameter space, a Monte Carlo simulation was employed. The simplified model (3) to (7) was used, with the additon that we enforce a balance on ECM/SMC ratio in the intima with equation (8) and c = 0.3. This latter modification was required as at later simulation times, the ECM had a tendency to be systematically eliminated from the intima. Subsequent evaluation of this additional boundary condition has shown no notable impact on the predicted geometric outcomes. Similar to the analyses in section 4.2 to 4.4, a target of a 50% increase of shear stress and a 20% decrease of tension was assigned. For simplicity, we again neglected the influence of inflammation by fixing the inflammation factor to unity.
Using the same differential equation ode solver, the parameter space was examined with a uniform distribution of αj, j = 1..7, in (0,0.1). A classic Latin Hypercube Sampling (LHS) commonly used in global sensitivity analysis was employed [16], and Figure 8A provides the distribution of global morphologies (i.e. external radius versus lumen radius) obtained with 1000 simultation runs. Interestingly, this systematic exploration of the parameter space reveals that approximately 10% of the parameter combinations lead to extensive outward remodeling and aneurysmal degeneration of the vein graft wall. If α1 = α2 = 0.01 are fixed to maintain a minimum level of SMC and ECM production and the other coefficients are assigned random values (αj, j = 3..7, in (0,0.1)), the phenomena of aneurysmal degeneration is not observed.
Figure 8.
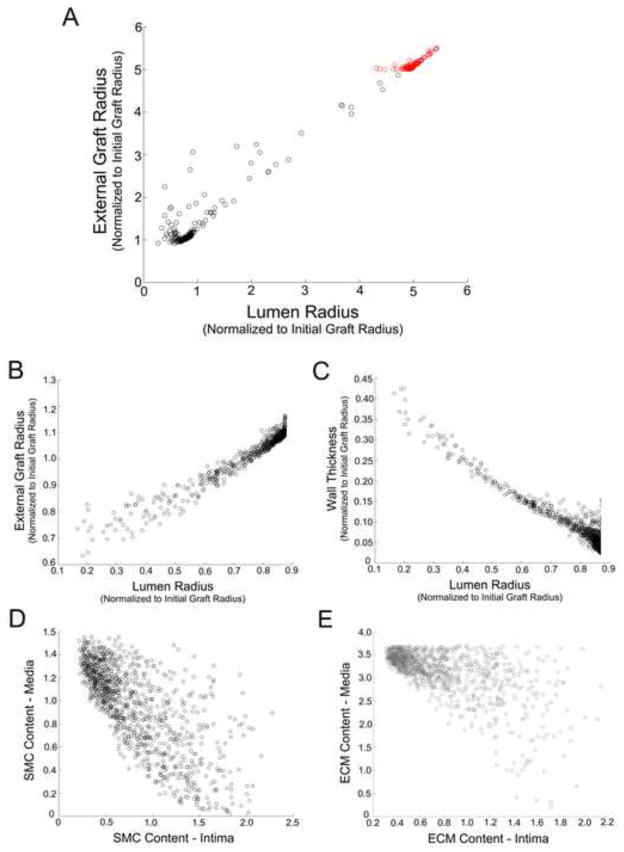
Parameter space exploration of the dynamical system using a Montecarlo simulation. (A) Model parameters T = 400 for αj, j = (1..7)∈(0, 0.01); 1000 iterations. Red symbols demonstrate those simulations where a greater than 5-fold increase in the external radius is predicted. (B – E) Model parameters T = 400 for α1 (1)=α2(2)=0.1 and αj, j=(3..7)∈(0, 0.01); 1000 iterations. External radius versus lumen radius (A – B). Wall thickness versus lumen radius (C). SMC content in the media versus intima (D). ECM content in the media versus intima (E).
Figure 8B to 8E provides a more indepth examination of the outcomes obtained from 1000 simulation runs, where α1 = α2 = 0.01 and αj, j = 3..7, in (0,0.1). High grade stenosis defined as a greater than 80% reduction in lumen radius is relatively rare, occurring in less than 5% of the runs. There is an inverse correlation between the wall thickness and lumen radius (Figure 8C), with greater than 10% reductions in lumen radius demonstrating a strong linear relationship with increased wall thickness. The relative portions of SMC and ECM in the media and intima appear to be only loosely correlated (Figure 8D and 8E). Of particular note, the ratio of ECM/SMC in the intima, which is enforced by equation (8), is not a global attractor.
Motivated by recent publications in the field [17, 18], we examined the Partial Rank Correlation Coefficient (PRCC) for the set of 1000 simulation runs (Figure 9). A sensitivity analysis around α1 = α2 = 0.01; αj = 0 for j = 3..7 reveals that lumen radius and wall thickness are linearly related to α6 and α7, the outward/inward remodeling coefficients defined by equation (14). Within this sensitivity analysis, a random perturbation on all αj of order 0.01 was performed. We observed that the wall thickness is positively correlated to the wall tension gradient and negatively correlated to the wall shear gradient through the outward/inward remodeling equation (14). In a similar manner, acting through coefficients α6 and α7, the lumen radius is positively correlated to shear and negatively correlated to tension. In agreement to the clinical observation where the underlying biology of the remodeling vein graft is very dynamic (Figure 2), a sharp transition for all correlation coefficients following the first month after implantation is identified (Figure 9). Finally we interpret the low correlation results for α1 to α5 as a consequence of the complex cell and matrix dynamics that characterize the adaptation process, leading to multiple solution outcomes that do not conform to a simple linear relationship. In contrast, the complexity of the outward/inward remodeling dynamics, governed by coefficients α6 and α7, is limited and well described by first order relationships.
Figure 9.
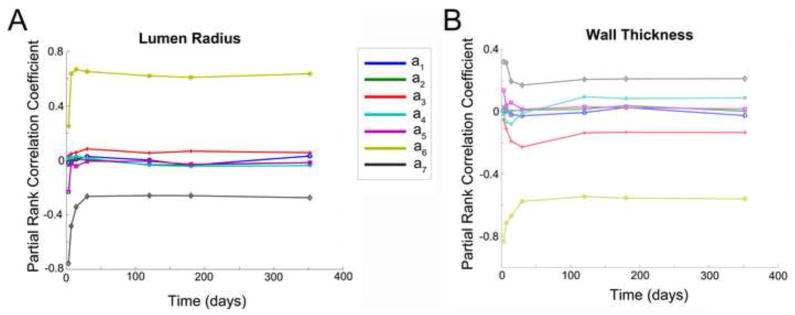
Time evolution of the Partial Rank Correlation Coefficient obtained from a Montecarlo simulation of the dynamical system for a(1)=a(2)=0.1 and a(3..7) = 0; 1000 iterations. Lumen radius (A) and wall thickness (B).
4.6. Summation
Based on a systematic mapping of the parameter space, three general remodeling response patterns are observed.
Shear stabilized intimal thickening
Ensuing from a dominant lumen area-shear feedback loop, low shear stress promotes SMC proliferation, migration of SMC toward the lumen, and an increase in wall thickness. The overall increase in wall thickness provides stabilization of the wall in the face of an elevated transmural pressure, but a limited ability for outward remodeling. This reduction in lumen diameter leads to higher wall shear. This process converges in time, leading to a stable solution when the shear stress becomes sufficiently high to drive both SMC proliferation and ECM synthesis to zero.
Tension induced wall thinning and lumen expansion
Elevated intramural tension induces outward expansion while inhibiting SMC proliferation and ECM production. The resulting decay in wall thickness leads to expansion of the graft and further elevations in wall tension. This destabilization continues until it is halted by an increasing differential between the internal and external pressure. While potentially a dominant adapation event, our simulation has shown that as long as a minimum amount of intima hyperplasia is induced (i.e. α1, α2 > 0), then unchecked outward expansion does not occur. It is interesting to consider this potential destablization in light of the ongoing effort to develop pharmacologic agents that mitigate the intimal hyperplastic response. Such approaches to perserve the vein graft lumen may be at the expense of structural stability, manifested by unchecked outward remodeling and aneurysmal degeneration.
Tension stabilized wall thickening
Reductions in intramural wall tension promote SMC division and ECM deposition, as described by coefficients α3 and α4 in equations 5 and 6. The resulting increase in wall thickness leads to a further reduction in wall tension. which is halted when wall tension reaches an asymptote and SMC/ECM production is driven to zero.
Exploration of the parameter space and the accompanying simulations demonstrate varying combinations of these response patterns, which may or may not lead to structural stability. In fact, a very large number of possible scenarios are observed where the radius of the vein graft varies non monotonically. This is further underscored when we examine small variation on the parameter αj, j = 1..7, where we find that the global outcome (lumen narrowing or wall thickening) is not linearly correlated to parameters α1 to α5 (Figure 8).
5. Discussion and Conclusions
Surgical manipulation of the vein combined with the acute exposure to elevated shear and tensile forces elicit a complex series of biologic events in the vein wall that begin immediately on implantation. Repair of the damaged vein graft is initiated by the local synthesis of a variety of growth factors. Activated by these various factors, SMC begin to replicate within the media and migrate from media to intima, where continued proliferation and abundant matrix deposition is stimulated. While this process is self-limited in the majority of vein grafts, progressive thickening of the intima leads to severe luminal narrowing, reductions in flow, and intraluminal thrombosis (Figure 1).
Results from our simulations demonstrate that the proposed dynamical system can provide a wide range of possible scenarios, from severe stenosis and occlusion to progressive dilation and aneurysm formation. Despite the relative uniformity of the surgical trauma and hemodynamic insult, vein grafts demonstrate significant focality in their lesion development [17]. With a peak incidence between 4 and 12 months following implantation, 30 to 45% of autogenous grafts will fail or require revision secondary to significant narrowing of the lumen [18]. Although initially postulated that these graft lesions are associated with valve leaflets, detailed evaluation of this issue demonstrated substantial remodeling within valve sites. Transient reductions in lumen diameter were a frequent observation at these sites, but significant plasticity and later outward remodeling was commonplace, such that progression to high-grade stenosis occurred in less than 20% of these lesions [19]. The current analysis is the first detailed examination to predict an oscillatory pattern of vein graft adaptation, where substantial wall thickening progresses and then regresses within several months of implantation.
As noted above, structural changes in implanted vein grafts have been intimately linked to the local hemodynamic environment, and wall shear stress has been thought to be the key driving forces that regulate this adaptive process. Founded on these observations, the standard paradigm of vascular remodeling has been established, where a reduction in shear stress accelerates the intimal hyperplasic response and leads to luminal narrowing. Resulting from the reduced lumen diameter, shear stress increases, and the rate of intimal growth and additional narrowing of the lumen is inhibited. While this idealized feedback loop is attractive in its simplicity, it predicts an equilibrium state and fails to provide a mechanistic understanding for the severe stenotic lesions that lead to human vein graft failure. We have shown that a coupled analysis of both shear stress and intramural wall tension reveal unanticipated trajectories of vein graft morphology that are in close alignment with clinical observations.
While much of the emphasis in vein graft pathology has been focused on intimal thickening, the balance between outward expansion and wall thickening more appropriately dictates morphology of the graft. As demonstrated by Glagov, the normal vascular adaptive response is an increase in overall circumference to prevent luminal narrowing [2, 20]. In response to hemodynamic and biochemical stimuli, SMC degrade and reorganize the rigid matrix structure of the wall to facilitate these changes. Examination of early vein graft morphology demonstrates a 20% increase in diameter within the first month following implantation, with failure of this outward remodeling correlated with subsequent graft failure [21]. The current dynamic analysis supports the concept that the majority of vein grafts precede along a “normal” adaptive trajectory, where grafts dilate in response to the increased shear, but a notable fraction demonstrate a “maladaptive” phenotype, where progressive inward remodeling and accentuated wall thickening leads to graft failure.
Although integrating the dominant elements of vascular remodeling, the current model has been designed as an initial approximation and fails to encompass the full complexity of these events. For example, the composition of the extracellular matrix proteins and relative distribution of cells to matrix changes over time, leading to time-dependent variations in the mechanical properties of the wall. Integration of a hyperelastic model linked to the composition of the wall could provide additional enhancements in this regard. Simplified expressions were used to model the effect of inflammation, and its corresponding influence on the graft wall. This is at best a first-order approximation of the coordinated series of cytokine and cell-based events that govern the inflammatory process. To be more precise, this coupling between inflamation and tissue adaptation is an integrated response, where chemokine release by the wall induces transformation of the SMC phenotype and further augmentation of the leukocyte recruitment pathways [22, 23]. Also of note is the lack of integration of the model with the physiology of the intact patient, where the vasculature is highly responsive to changes in perfusion. Alterations in vein graft morphology, and the resulting influence on the pressure gradient between the inlet and outlet of the graft, invariably lead to compensatory changes in both the distal microvascular resistance and flux in the vein graft. While integration of such complexities can be easily accomplished, the improved model granularity comes at the expense of increased parameter uncertainity and is best reserved for more focused analysis of the individual components of the adaptation response.
Despite these limitations, the current model is successful in the primary goal of utilizing global parameters to explore the nonlinearities that characterize vein graft adaptation. Particularly notable is our observation that the integration of multiple feedback mechanisms leads to a variety of non-linear responses, which would be unanticipated by an analysis of each system component independently. Further insight can be accomplished through development of a more realistic spatio-temporal model. Using partial differential equation or agent-based modeling approaches, such increased system granularity can be achieved, with the global dynamical system serving as a calibration tool and/or consistency check for these more complex modeling approaches [24].
Highlights.
We develop a dynamical system to examine vein graft adaptation.
Evaluates the complex interplay between the biomechanics and cell/matrix kinetics.
Multiple feedback mechanisms leads to a variety of non-linear responses.
Supports the clinical observation concerning maladaptive graft phenotypes.
Acknowledgments
This work was supported in part by NIH Grant 1R01 HL095508.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Roger VL, Go AS, Lloyd-Jones DM, Benjamin EJ, Berry JD, Borden WB, et al. Heart disease and stroke statistics—2012 update: a report from the American Heart Association. Circulation. 2012;125:e2–e220. doi: 10.1161/CIR.0b013e31823ac046. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Glagov S. Intimal hyperplasia, vascular modeling, and the restenosis problem. Circulation. 1994;89:2888–2891. doi: 10.1161/01.cir.89.6.2888. [DOI] [PubMed] [Google Scholar]
- 3.Conte MS, Bandyk DF, Clowes AW, Moneta GL, Seely L, Lorenz TJ, et al. Results of PREVENT III: a multicenter, randomized trial of edifoligide for the prevention of vein graft failure in lower extremity bypass surgery. J Vasc Surg. 2006;43:742–751. doi: 10.1016/j.jvs.2005.12.058. [DOI] [PubMed] [Google Scholar]
- 4.Berceli SA, Tran-Son-Tay R, Garbey M, Jiang Z. Hemodynamically driven vein graft remodeling: a systems biology approach. Vascular. 2009;17:24–31. doi: 10.2310/6670.2008.00083. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Jiang Z, Wu L, Miller BL, Goldman DR, Fernandez CM, Abouhamze ZS, et al. A novel vein graft model: adaptation to differential flow environments. Am J Physiol Heart Circ Physiol. 2004;286:H240–H245. doi: 10.1152/ajpheart.00760.2003. [DOI] [PubMed] [Google Scholar]
- 6.Fernandez CM, Goldman DR, Jiang Z, Ozaki CK, Tran-Son-Tay R, Berceli SA. Impact of shear stress on early vein graft remodeling: a biomechanical analysis. Ann Biomed Eng. 2004;32:1484–1493. doi: 10.1114/b:abme.0000049033.65547.cf. [DOI] [PubMed] [Google Scholar]
- 7.Jiang Z, Yu P, Tao M, Ifantides C, Ozaki CK, Berceli SA. Interplay of CCR2 signaling and local shear force determines vein graft neointimal hyperplasia in vivo. FEBS Lett. 2009;583:3536–3540. doi: 10.1016/j.febslet.2009.10.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Hwang M, Garbey M, Berceli SA, Tran Son Tay R. Ruled-based simulation of multicellular biological systems - a review of modeling techniques. Cell Mol Bioeng. 2009;12:285–295. doi: 10.1007/s12195-009-0078-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Hwang M, Garbey M, Berceli SA, Wu R, Jiang Z, Tran Son Tay R. Rule-based model of vein graft remodeling. PLoS ONE. 2013;8:e57822. doi: 10.1371/journal.pone.0057822. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Kleinstreuer C. Biofluid Dynamics: Principles and Selected Applications. 1. CRC Press; 2006. [Google Scholar]
- 11.Boyle CJ, Lennon AB, Pendergast PJ. In silico prediction of the mechanobiological response of arterial tissue: application to angioplasty and stenting. J of Biomech Eng. 2011;133:081001. doi: 10.1115/1.4004492. [DOI] [PubMed] [Google Scholar]
- 12.Hwang M, Berceli SA, Garbey M, Kim NH, Tran Son Tay R. The dynamics of vein graft remodeling induced by hemodynamic forces - a mathematical model. Biomech Model Mechan. 2010;11:411–23. doi: 10.1007/s10237-011-0321-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Glagov S, Bassiouny HS, Sakaguchi Y, Goudet CA, Vito RP. Mechanical determinants of plaque modeling, remodeling and disruption. Atherosclerosis. 1997;131:S13–S14. doi: 10.1016/s0021-9150(97)06117-0. [DOI] [PubMed] [Google Scholar]
- 14.Boyle CJ, Lennon AB, Early M, Kelly DJ, Lally C, Prendergast PJ. Computational simulation methodologies for mecanobiological modeliing: a cell-centered approach to neointima development of stents. Phil Trans R Soc, A. 2010;368:2919–2935. doi: 10.1098/rsta.2010.0071. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Dormand JR, Prince PJ. A family of embedded Runge-Kutta formulae. J Comp Appl Math. 1980;6:19–26. [Google Scholar]
- 16.Marino S, Hogue IB, Ray CJ, Kirshner DE. Review: a methodology for performing global uncertainty and sensitivity analysis in systems biology. J Theor Biol. 2008;254:178–196. doi: 10.1016/j.jtbi.2008.04.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Szilagyi DE, Elliott JP, Hageman JH, Smith RF, Dall’Olmo CA. Biologic fate of autogenous vein implants as arterial substitutes: clinical, angiographic and histopathologic observations in femoro-popliteal operations for atherosclerosis. Ann Surg. 1973;178:232–246. doi: 10.1097/00000658-197309000-00002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Roddy SP, Darling RC, Maharaj D, Chang BB, Paty PSK, Kreienberg PB, et al. Gender-related differences in outcome: an analysis of 5880 infrainguinal arterial reconstructions. J Vasc Surg. 2003;37:399–402. doi: 10.1067/mva.2003.99. [DOI] [PubMed] [Google Scholar]
- 19.Vesti BR, Primozich J, Bergelin RO, Strandness E. Follow-up of valves in aaphenous vein bypass grafts with duplex ultrasonography. J Vasc Surg. 2001;33:369–374. doi: 10.1067/mva.2001.111744. [DOI] [PubMed] [Google Scholar]
- 20.Gibbons GH, Dzau VJ. The emerging concept of vascular remodeling. N Engl J Med. 1994;330:1431–1438. doi: 10.1056/NEJM199405193302008. [DOI] [PubMed] [Google Scholar]
- 21.Owens CD, Wake N, Jacot JG, Gerhard-Herman M, Gaccione P, Belkin M, et al. Early biomechanical changes in lower extremity vein grafts--distinct temporal phases of remodeling and wall stiffness. J Vasc Surg. 2006;44:740–6. doi: 10.1016/j.jvs.2006.06.005. [DOI] [PubMed] [Google Scholar]
- 22.Clarke M, Talib S, Figg NL, Bennett MR. Vascular smooth muscle cell apoptosis induces interleukin-1–directed inflammation: effects of hyperlipidemia-mediated inhibition of phagocytosis. Circ Res. 2010;106:363–372. doi: 10.1161/CIRCRESAHA.109.208389. [DOI] [PubMed] [Google Scholar]
- 23.Hoch JR, Stark VK, Rooijen N, Kim JL, Nutt MP, Warner TF. Macrophage depletion alters vein graft intimal hyperplasia. Surgery. 1999;126:428–437. [PubMed] [Google Scholar]
- 24.Tran-Son-Tay R, Hwang M, Garbey M, Jiang Z, Ozaki CK, Berceli SA. Experiment-based model of vein graft remodeling induced by shear stress. Ann Biomed Eng. 2008;36:1083–91. doi: 10.1007/s10439-008-9495-y. [DOI] [PubMed] [Google Scholar]