Energy-efficient pulse-coupled synchronization strategy design for wireless sensor networks through reduced idle listening

Abstract

Synchronization is crucial to wireless sensor networks due to their decentralized structure. We propose an energy-efficient pulse-coupled synchronization strategy to achieve this goal. The basic idea is to reduce idle listening by intentionally introducing a large refractory period in the sensors’ cooperation. The large refractory period greatly reduces idle listening in each oscillation period, and is analytically proven to have no influence on the time to synchronization. Hence, it significantly reduces the total energy consumption in a synchronization process. A topology control approach tailored for pulse-coupled synchronization is given to guarantee a k-edge strongly connected interaction topology, which is tolerant to communication-link failures. The topology control approach is totally decentralized and needs no information exchange among sensors, and it is applicable to dynamic network topologies as well. This facilitates a completely decentralized implementation of the synchronization strategy. The strategy is applicable to mobile sensor networks, too. QualNet case studies confirm the effectiveness of the synchronization strategy.

I. Introduction

The distributed allocation of component nodes in space is a key feature of wireless sensor networks. In wireless sensor networks, spatially distributed autonomous sensors measure physical/environmental conditions, process data, and cooperate with each other to achieve area monitoring, direction guidance, and information fusion. In many of these applications, synchronization of time references in different sensor nodes is a prerequisite condition. Moreover, in various wireless media access control (MAC) protocols, time synchronization is essential to schedule the access to a shared physical medium. Therefore, synchronization is of crucial importance in wireless sensor networking.

Plenty of protocols have been proposed to synchronize sensor networks in recent years. RBS (Reference-Broadcast Synchronization) [1] selects a reference node to periodically broadcast beacon messages. All other nodes use the arrival time of the beacon as a reference point for comparing their clocks. RBS eliminates transmitter-side non-determinism but it is only designed for single-hop networks. TPSN (Timing-sync Protocol for Sensor Networks) [2] works on multihop sensor networks by building and maintaining a spanning tree and then using hop-by-hop synchronization along the edges to synchronize all nodes to the root. Instead of maintaining a spanning tree, FTSP (Flooding Time Synchronization Protocol) [3] chooses root dynamically, and it also simplifies multi-hop synchronization by using periodic floods from the selected root. The spanning tree based structure of TPSN and FTSP can potentially incur large skews between close-by nodes due to the large stretch of the tree structure. Sommer and co-workers proposed GTSP (Gradient Time Synchronization Protocol), which avoids the problem by following a completely distributed scheme where nodes synchronize to all of their neighbors [4]. They also proposed the ‘PulseSync’ protocol to reduce the growth rate of error with network size by reducing the propagation time from the reference node to the whole network [5]. By exploiting constructive interference, Glossy provides a novel flooding architecture for wireless sensor networks along with accurate time synchronization [6].

However, the need for exchanging a large number of packets is common to the above synchronization protocols, which entails large energy expenditures [7]. This contradicts the requirement of energy efficiency, which is crucial to extend the functional lifetime of sensor nodes. The requirement of energy efficiency is more stringent in mobile ad hoc networks (MANET), where random movement of nodes changes network topology frequently [8], and hence, synchronization algorithms need to be implemented frequently. Repeated synchronization-algorithm implementation leads to increased energy consumption, which poses a challenge to wireless sensor networks, where energy is the single most important resource due to battery-powered sensor nodes. In fact, minimum energy consumption in portable communication devices has been one of the major design goals in recent IC (Integrated Circuit) designs [9].

This paper proposes an energy-efficient pulse-coupled synchronization strategy for wireless sensor networks. ‘Pulse-coupled’ means that oscillators interact with each other using pulse-based communication, i.e., they interact with each other in a pulsatile rather than smooth manner. Pulse-based communication has been used to describe many biological synchronization phenomena such as the flashing of fireflies, the contraction of cardiac cells, and the firing of neurons [10], [11]. Recently, with the progress of ultra-wide bandwidth (UWB) impulse radio technology [12], pulse-coupled oscillator based synchronization scheme has been applied to synchronize wireless sensor networks [7], [13], [14], [15], [16], [17], [18], [19]. Since pulse-coupled oscillators can be synchronized via pulse transmitting instead of packet exchanging, it avoids wasting the limited computational capability of sensor nodes that is required by packet based synchronization algorithms. Moreover, the pulse-coupled synchronization scheme does not require any memory to store the information of neighboring nodes, which is of great appeal to low-cost sensor nodes. Therefore, the pulse-coupled oscillator based synchronization scheme has received increased attention in the communication community recently. For example, [13] discussed the implementation of pulse-coupled oscillators in a wide band network, [15] verified the effectiveness of pulse-coupled oscillators using a TinyOS simulator. The authors in [16] and [17] discussed the scalability of pulse-coupled strategy when used in the synchronization of sensor networks. The authors in [18] and [20] considered strongly globally pulse-coupled oscillators with a refractory period and gave the maximally allowable refractory period when applied to synchronize sensor networks.

In pulse-coupled oscillators, the pulse-based interaction can be captured as a phase response function [21], [22]. A phase response function tabulates the shift in an oscillation phase induced by a pulse as a function of the phase at which the pulse is received. In this paper, we design an energy-efficient synchronization strategy for wireless sensor networks by intentionally introducing a large refractory period in the phase response function. The new strategy reduces energy consumption in a synchronization process because the intentionally introduced large refractory period reduces idle listening (i.e., listening to receive possible traffic that is not sent) in a synchronization process. This is motivated by the observation that idle listening is the major source of energy-inefficiency [23]. In most of existing MAC protocols such as Code Division Multiple Access (CDMA) and IEEE 802.11, nodes listen continuously to the channel because they do not know when they might receive messages. This idle listening has been shown to consume 50 – 100% of the energy required for receiving [24]. In the proposed synchronization strategy, a large refractory period is intentionally introduced in every sensor’s phase response function in a synchronization process. Within the refractory portion of an oscillation period, sensors turn off their radio and any arriving signal is ignored, hence power consumption is avoided during this time. We prove analytically that this intentionally introduced refractory period has no influence on the time to synchronization. Given that the total energy consumed in a synchronization process is determined by the product of single-period energy consumption and the time to synchronization (number of oscillation periods), the total energy consumption in the synchronization process is greatly reduced in the proposed strategy since single-period energy consumption is greatly reduced by the intentionally introduced refractory period.

The paper is organized as follows: Sec. II gives a brief introduction to pulse-coupled oscillators and relevant graph theory. Sec. III proves analytically the synchronization of pulse-coupled oscillators with a refractory period that may be larger than half oscillation period in the phase response function. Synchronization time is also given in this section. The results are valid for general coupling structures even when the topology is dynamic. Sec. IV proposes a new pulse-coupled synchronization strategy for wireless sensor networks. By introducing a refractory period in the sensors’ response, a sleep mode is added in sensors’ transmission/reception, hence idle listening and energy consumption in a synchronization process are remarkable reduced. Sec. V discusses the implementation issues of the new synchronization strategy. By exploiting the relationship between node degree and connectivity, we propose a totally decentralized topology control approach to guarantee a k-edge strongly connected interaction topology. The topology control approach is tailored for pulse-coupled synchronization. It is robust to link failures and applicable to mobile sensors. QualNet case studies are given in Sec. VI to confirm the effectiveness of the results.

II. Preliminaries

A. Pulse-coupled oscillators and phase response function

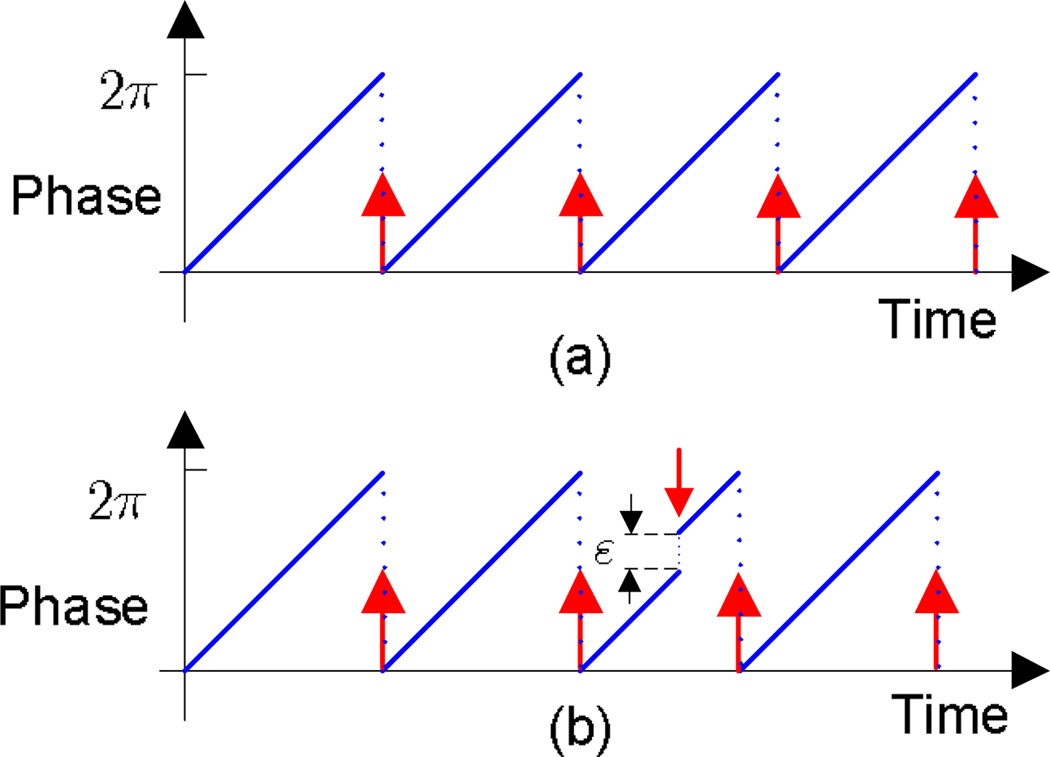
In pulse-coupled oscillators, the phase of each oscillator, φ_i, evolves from 0 to 2π. When it reaches 2π, an oscillator fires (emits a pulse) and its phase returns to 0, after which the cycle repeats. When an oscillator receives a pulse from a neighboring oscillator, it shifts its phase by a certain amount. A schematic of pulse-coupled oscillators is given in Fig. 1. When there is no interaction between oscillators, each oscillator’s phase evolves freely from 0 to 2π repeatedly. When there is an interaction between oscillators, an oscillator modifies its phase upon receiving a pulse, and the magnitude of the modification (phase shift) ε depends on the exact timing of the incoming pulse relative to the phase of its own oscillation. The phase shift induced by an incoming pulse is usually described by a phase response function [21], [22]. In this paper, we consider delay-advance phase response functions:

Fig. 1.

Phase evolution of pulse-coupled oscillators. (a) Isolated oscillators (b) Coupled oscillators (ε: phase shift)

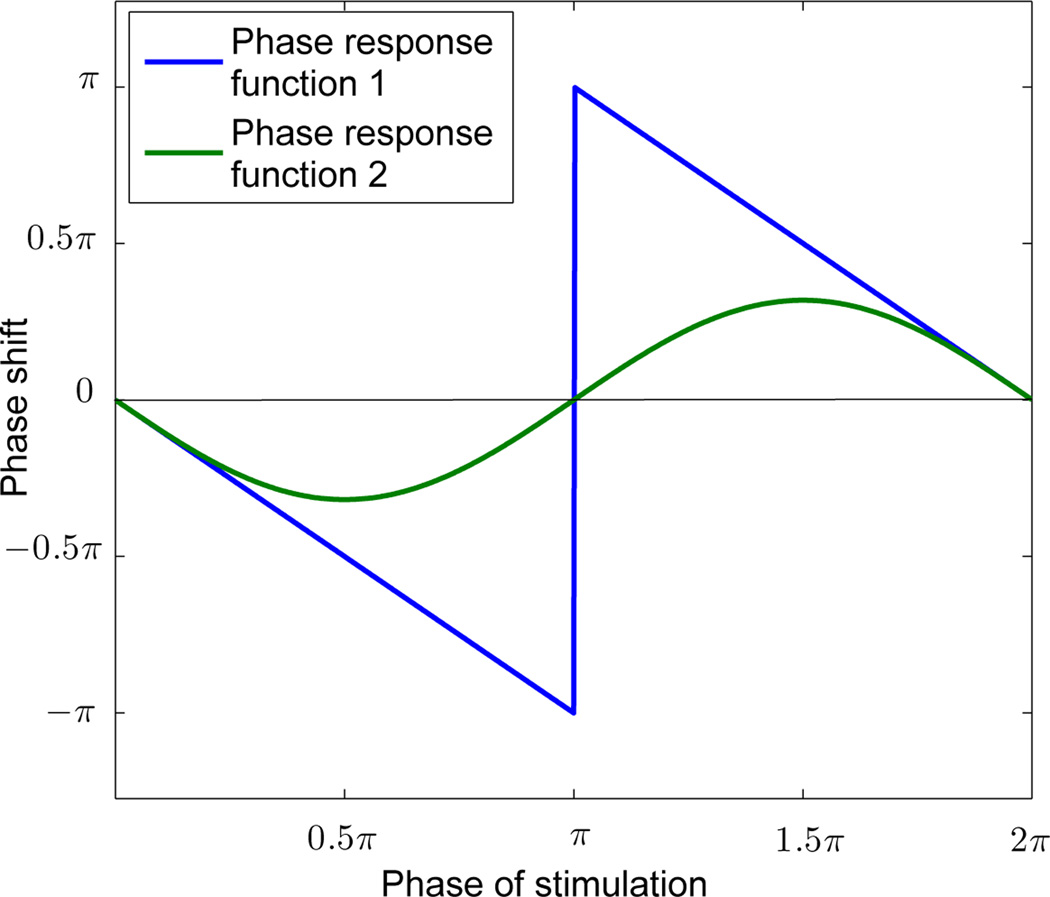
Definition 1: [21] A phase response function is called a delay-advance phase response function if the value of phase shift is negative in the interval (0, π), positive in the interval (π, 2π), and zero at phases 0 and 2π.

Two examples of delay-advance phase response functions are shown in Fig. 2. From Definition 1, we can see that under such a phase response function, the phase of oscillation can be either delayed (if a pulse is received when an oscillator’s phase is within (0, π)) or advanced (if a pulse is received when an oscillator’s phase is within (π, 2π)). In practice, coupling strength also influences phase shifts, so in the following, we multiply the phase shift in the phase response function by a weighting factor l to describe the actual phase shift induced by a pulse. l is restricted to the interval (0, 1].

Fig. 2.

Two examples of delay-advance phase response functions.

Remark 1: To guarantee finite-time synchronization, it is necessary to require that the weighted phase response function has slope −1 in the vicinity of phase 2π. Hence, throughout the paper, we fix the weighted phase response function (l× phase response function) to 2π − φ when φ ∈ [2π − μ, 2π) for a μ ≪ 1.

B. Graph formulations

A pulse-coupled oscillator network can be formulated as a directed graph G = (V, E), where V = {υ₁, υ₂, …, υ_N} is a set of vertices corresponding to oscillators in the network and E is a set of directed edges corresponding to the interaction between a pair of oscillators [25]. An edge (υ_i, υ_j) means that υ_j can receive pulses from υ_i but not necessarily vice versa. A directed path in graph G is a sequence of edges (υ_i1, υ_i2), (υ_i2, υ_i3), (υ_i3, υ_i4), …. A graph G is said to be strongly connected if there is a directed path from each vertex in the graph to every other vertex. For a node υ, the number of edges entering υ is called the indegree of the vertex and is represented as δ⁻(υ); the number of edges leaving υ is called the outdegree of the vertex and is represented as δ⁺(υ). The value δ(υ) ≜ min(δ⁻(υ), δ⁺(υ)) is called the degree of node υ. The value ${\delta }^{-}(G)\triangleq \underset{\upsilon \in V}{\text{min}}{\delta }^{-}(\upsilon )$ is called the indegree of graph G, and ${\delta }^{+}(G)\triangleq \underset{\upsilon \in V}{\text{min}}{\delta }^{+}(\upsilon )$ is called the outdegree of graph G.

III. Synchronization of pulse-coupled oscillators with a general structure in the presence of a refractory period

In this section, we will prove analytically that perfect synchronization can be achieved for pulse-coupled oscillators even when there is a refractory period in their phase response function. We will also discuss time to synchronization. The results are quite general: the coupling structure is not restricted to conventional all-to-all topology studied in most existing literature [18], [26], [27], it can even be time-varying; the interaction strength can be either strong or weak; the refractory period can be small or large, it can even be over half of the oscillation period.

A. A synchronization condition

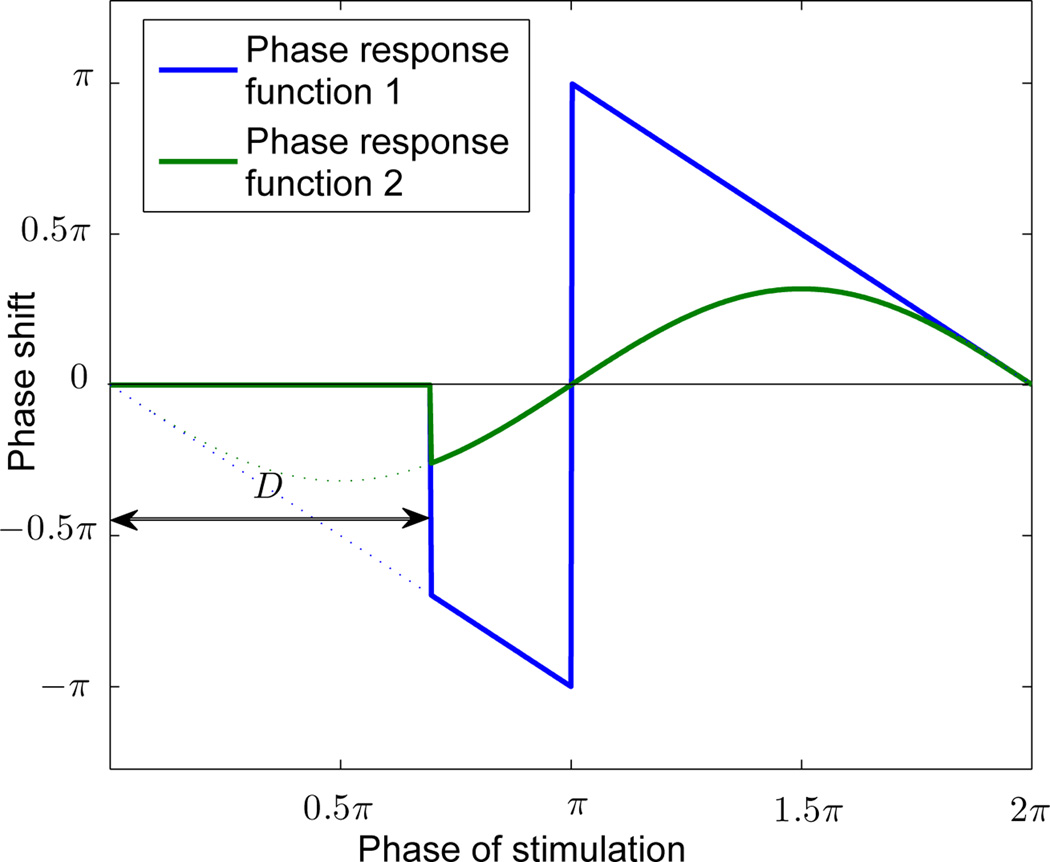
In the presence of a refractory period, the phase response function is modified as exemplified in Fig. 3. The two phase response functions have a refractory period of length D. When an oscillator’s phase is within the interval [0, D), the oscillator will ignore external pulses and its phase will evolve freely towards 2π. That is, if there a pulse that arrives when an oscillator’s phase φ is within [0, D), the pulse will have no influence on φ. But if a pulse arrives when φ is outside of the refractory period, it will cause an offset in φ with value determined by the phase response function.

Fig. 3.

Phase response functions with a refractory period of length D.

Consider a pulse-coupled oscillator network composed of N oscillators. We assume that all oscillators have the same oscillation period and have a refractory period of length D in the phase response function. We can prove that the oscillators can be perfectly synchronized if certain conditions are satisfied. The detailed results are given in Theorem 1:

Theorem 1: For pulse-coupled oscillators with a length D refractory period in the phase response function (the phase response function can be any delay-advance phase response function defined in Definition 1), suppose the oscillators’ initial phases are given by φ₁, φ₂, …, φ_N, respectively, where φ_i ∈ [0, 2π) for i = 1, 2, …, N. If the maximal phase difference, i.e., $\underset{1\le i,j\le N}{\text{max}}\{|{\phi }_i-{\phi }_j|\}$, is less than some Λ̄ ∈ (0, π] and the interaction topology is strongly connected, then the oscillators can be perfectly synchronized for any D not larger than 2π − Λ̄.

Proof: Suppose that the ith oscillator has the maximal phase ${\phi }_i={\phi }_{\text{max}}=\underset{j=1,2,\dots ,N}{\text{max}}{\phi }_j$. If more than one oscillator have phase equal to φ_max, any of them can be nominated as oscillator i. Without loss of generality, we assume that the period is 2π and the initial time instant is t = 0. Denote the maximal phase difference at t = 0, i.e., $\underset{1\le i,j\le N}{\text{max}}\{|{\phi }_i-{\phi }_j|\}$, as Λ. We have Λ < Λ̄ according to the assumption.

We first consider the case that D < Λ̄ is satisfied. Since oscillator i has the largest phase, its phase evolves to 2π without perturbation and it reaches 2π at t = 2π − φ_max. At this time instant, all the other oscillators have phase between 2π − Λ (which is larger than π) and 2π. In the following time interval of length Λ, every oscillator will fire once. By the assumption of a strongly connected topology, the oscillator that fires the last (denote it as oscillator j) receives at least one pulse during its phase evolution from 2π − Λ to 2π, and its phase is increased. (The value of phase response function is positive in (π, 2π).) Denote the phase increase as ε (which is dependent on coupling strength l and the phase-dependent phase response function, and hence may be time-dependent). Given that the initial phase difference is Λ, and the phase of the oscillator that fires the last in this round of firing (oscillator j) is expedited by ε, oscillator j fires at a time instant no later than t = 2π − φ_max + Λ − ε. Note that no oscillator can fire for a second time before t = 2π. This is because oscillator i who fires first cannot be expedited by other nodes’ firing since Λ is less than π, and the phase response function is negative in the interval [D, π). The same arguments hold for the other oscillators, too. So after oscillator j’s firing, there will be no firing in the network before t = 2π. Therefore, at t = 2π, oscillator j has the smallest phase, which is no less than 2π − (2π − φ_max + Λ − ε) = φ_max − Λ + ε. Note that at t = 2π, the largest phase is no larger than φ_max. (It may or may not belong to oscillator i.) So at t = 2π, the phase difference is no larger than φ_max − (φ_max − Λ + ε) = Λ − ε.

We can see that after a time interval of length 2π, the phase difference is decreased by ε > 0. By iterating this argument, we can prove that the phase difference will be reduced by ε > 0 after each time interval 2π until synchronization is achieved. Hence the network can be synchronized.

Next, we consider the case that D ≥ Λ̄ is satisfied. Still assume that at t = 0, the ith oscillator has the largest phase φ_max. So its phase evolves towards 2π without perturbation and reaches 2π at time instant 2π − φ_max. Similar to the D < Λ̄ case, under the assumption of a strongly connected coupling topology, we can derive that the oscillator firing the last in this round (denote it as oscillator j) fires at a time instant no later than t = 2π − φ_max + Λ − ε. When it fires, the ith oscillator has a phase no larger than Λ − ε and hence it is still in the refractory period since Λ − ε < Λ < Λ̄ ≤ D. So the ith oscillator is not influenced by the firing of the other oscillators and it always has the foremost phase in the whole network. Hence we know the ith oscillator’s phase is φ_max at t = 2π. At this time instant, the node firing the last in this round has the smallest phase φ_max − Λ + ε. So the phase difference is no larger than φ_max − (φ_max − Λ + ε) = Λ − ε, which is ε less than the phase difference at t = 0. By iterating this argument, we can prove that the phase difference is reduced by ε after each time interval 2π until synchronization is achieved. Hence the network can be synchronized.

Remark 2: In contrast to most synchronization conditions for pulse-coupled oscillators which require that the coupling topology is all-to-all [11], [18], [20], [26], [27], the results in Theorem 1 hold for more general coupling topologies that are strongly connected. The results can also be used to bi-directionally connected oscillators. In that case, the strongly connected condition reduces to requiring that the topology is connected.

Remark 3: In Theorem 1, the coupling strength can be weak [28] or strong. This is different from the results in [18] and [20], which require that the coupling is strong such that an arriving pulse will trigger an oscillator to fire immediately.

Remark 4: Note that different from the results in [11], [26], [27], [29], which may fail for some initial phases (although with a measure 0), our results can guarantee perfect synchronization for any initial phase satisfying the conditions.

Remark 5: Although the phase-difference reduction ε may be time varying, according to the above analysis, it is proportional to the value of phase response function in (π, 2π), which is positive, so ε is always positive (when phase difference is non-zero) and can always reduce the phase difference to zero.

B. Synchronization time

Next we analyze the time to synchronization of the previously described pulse-coupled oscillator networks. From the proof of Theorem 1, we know the time to synchronization is determined by ε, the phase-difference reduction in each iteration. Given that ε is influenced by the phase response function, coupling strength, and the number of pulses received by an oscillator in one interaction, we have the following theorem for the time to synchronization:

Theorem 2: For pulse-coupled oscillators with a length D refractory period in the phase response function, (the phase response function can be any delay-advance phase response function defined in Definition 1), if their maximal phase difference Λ is less than some Λ̄ ∈ (0, π], D is not larger than 2π − Λ̄, and the interaction topology is strongly connected with the indegree of interaction graph given by δ⁻(G), then the time to synchronization is proportional to

$$\frac{\mathrm{\Lambda }}{l\mathrm{\Psi }\delta -(G)}$$ (1)

where l denotes the coupling strength, Ψ denotes the average phase response in the advance stage (i.e., [π, 2π)) and is given by

$$\mathrm{\Psi }=\frac{1}{\pi }{\int }_{\pi }^{2\pi }\psi (\phi )p(\phi )d\phi$$ (2)

with ψ(φ) denoting the value of phase response function when phase is φ, and p(φ) denoting the rate (or probability) that an oscillator receives a pulse at phase φ.

Proof: According to the proof of Theorem 1, we know that phase difference Λ will be decreased by ε every 2π, hence the time to synchronization is proportional to initial phase difference Λ, and inversely proportional to ε. Since ε represents the phase increase in the oscillator that fires the last in each round of firing, we know ε is proportional to the product of the number of pulses an oscillator receives and phase increase caused by a single pulse. The number of pulses an oscillator receives in an oscillation period is proportional to the number of oscillators that can influence it, i.e., its indegree δ⁻(υ_i). So it is no less than δ⁻(G) according to the definition of the indegree of a graph. The phase increase caused by a single pulse can be represented by the product of coupling strength l and the average of phase response function in the phase advance region, which is proportional to Ψ in (2). So we know that the time to synchronization is determined by (1).

Remark 6: From Theorem 2, we can see that the time to synchronization is independent of D, the length of refractory period. Moreover, given that a larger indegree of interaction graph means a stronger connection between the oscillators, Theorem 2 indicates that a stronger interaction leads to a faster synchronization rate.

C. Dynamic topology

Next, we show that the results on synchronization condition and synchronization time remain true even when the coupling topology is dynamic. The results are summarized in Theorem 3:

Theorem 3: For pulse-coupled oscillators with a coupling topology that changes in every oscillation period, i.e., G(V, E) = G(V, E(k)) where E(k) denotes the edge set at time instant t = k×2π (k = 0, 1, 2, …), if the refractory period is not larger than 2π − Λ̄ with Λ̄ ≤ π denoting an upper-bound on phase difference, then synchronization can be achieved under any delay-advance phase response function if there exists some finite integer n such that at any time instant k, the coupling topology G(V, Ē) is strongly connected. Here Ē = E(k)∪E(k+1)∪…∪E(k+n) denotes the union of edge sets E(k), E(k + 1), …, E(k + n).

Proof: From the statements in Theorem 3, we know that if G(V, Ē) is strongly connected for some integer n, the union of the edges in any n successive oscillation periods forms a strongly-connected graph for vertex set V. Then following the proof of Theorem 1, we can see that the evolution of phase difference in the dynamic topology case follows the same way as that in the static topology case if we change the iteration period in the analysis from one oscillation period 2π to n oscillation periods 2nπ. That is, the phase difference decreases by at least ε every n oscillation periods. Hence the theorem is proven.

Remark 7: Theorem 3 indicates that if the network is strongly connected in the time interval [t₀, t₀ + 2nπ] for any t₀, i.e., there is a directed path between every pair of oscillators in the time interval [t₀, t₀ + 2nπ], then the network can be synchronized. This means that even when there is no directed path between two nodes at every time instant, the network can still be synchronized if a directed path exists by splicing the interaction of several time instants. Hence sensor mobility facilitates synchronization.

Remark 8: If there are intermittent link failures, i.e., failures that are not permanent and can be recovered, then it can be proven that the interaction topology in this case is still strongly connected in the sense of Theorem 3 if the topology without failure is strongly connected. Hence the oscillator network can still be synchronized even in the presence of intermittent link failures. Oscillator networks with permanent link failures will be addressed in Sec. V-B.

IV. A new synchronization strategy for wireless sensor networks

Based on the results in the previous section, we propose a new energy-efficient pulse-coupled synchronization strategy for wireless sensor networks. Our basic idea is to reduce idle listening by intentionally introducing a large refractory period in sensors’ responses to arriving signals. It is worth noting that existing studies on pulse-coupled synchronization of wireless sensor networks have shown that a small refractory period is necessary to stabilize the network [13], [14], [30].

In pulse-coupled synchronization of wireless sensor networks, each sensor has an embedded clock and is equipped with a transceiver [13], [14], [30]. By employing pulse-coupled interaction, the embedded internal clocks in all sensors can be synchronized. When there is a refractory period, a sensor ignores all the signals arriving within the refractory period and hence the pulses that arrive during the refractory period do not change the phase of the internal clock. Outside of the refractory period, the clock in a sensor can influence and be influenced by the clocks in other sensors through pulse emission and pulse reception.

Since in the refractory period, a sensor does not need to transmit/receive any signal, it can turn off its transceiver and switches to a sleep mode. But the phase of its interval clock still evolves freely towards 2π. When the phase exceeds the refractory period, the sensor wakes up, turns on its transceiver, and switches to an active mode. This sleep-active switching strategy has important ramifications for wireless sensor networks since the sleep mode reduces idle listing, which is the main source of energy waste. So it is well motivated to design a synchronization protocol that uses the largest allowable refractory period and hence reduces idle listening to the maximal extent, leading to the maximal reduction in energy consumption. Making use of the analytical results in the previous section, we propose the following energy-efficient synchronization strategy for wireless sensor networks:

Energy-efficient synchronization strategy: For each sensor, construct an internal clock as a periodic timer that evolves from 0 to 2π repeatedly and emits a UWB (ultra-wide bandwidth) monocycle pulse when its phase reaches 2π; A sensor stays in sleep mode when the phase of its internal clock is within the interval [0, D). When in the sleep mode, a sensor shuts down its transceiver but the phase of its timer still evolves freely towards 2π; For each sensor, when the phase of its internal timer exceeds D, it turns on its transceiver and switches to active mode in order to be able to receive pulses; For each sensor in active mode, upon receiving a UWB monocycle pulse, it modifies the phase of its internal clock according to the given coupling strength l and its delay-advance phase response function.

In the synchronization strategy, since each sensor behaves as a pulse-coupled oscillator, the internal clocks of the network will be synchronized according to our analytical results in Sec. III. By using the sleep mode, idle listening is reduced and energy consumption in each oscillation period is reduced to $\frac{2\pi -D}{2\pi }$ of its original value. However, in order to reduce the total energy consumption in a synchronization process, the time to synchronization should not be increased significantly compared with the small refractory period case. (A small refractory period is necessary to stabilize synchronization [13].) This is because the total energy consumption is determined by the product of single-period energy consumption and the time to synchronization (number of oscillation periods used to achieve synchronization), and hence, if the time to synchronization is increased significantly compared with the small refractory period case, then the energy saved by reducing idle listening in each oscillation period will be counteracted by the increased synchronization time. Fortunately, as shown in Theorem 2, the intentionally introduced large refractory period will not lead to a larger time to synchronization compared with the small refractory period case where the refractory period is used for stability purpose [13], because Theorem 2 proves that the time to synchronization is independent of the length of refractory period. Hence the total energy consumption in a synchronization process is indeed reduced. Therefore, the benefits of the new synchronization strategy can be summarized as follows:

1. Reduced energy consumption (as analyzed above);

2. Applicable to mobile sensor networks. As proven in Sec. III-C, the new synchronization strategy can be used even when the topology keeps changing with time;

3. Reduced memory. The pulses exchanged among the sensors are identical and are independent of the origins of the pulses. Therefore, at the receiver of every single sensor, received pulses need not be distinguished and can be treated identically, no matter where a pulse is from. Hence no information about the source/destination address is needed in the exchanged messages and synchronization is achieved without needing memory to store the time or information of other sensors;

4. Robust to link failures. Link failure is a common scenario in wireless sensor networks due to collision, interference, radio noise, etc. Hence tolerance to link failures is crucial. As indicated in Remark 8, the new synchronization strategy is robust to link failures;

5. Totally decentralized and scalable. The synchronization strategy can be implemented in a totally decentralized manner. And since the process of synchronization is independent of network size, the strategy is scalable;

6. Increased precision due to low layer implementation. The pulse-coupled synchronization strategy can be implemented entirely with hardware at the frontend of the receiver [13], hence the imprecision due to higher layer processing delays is prevented.

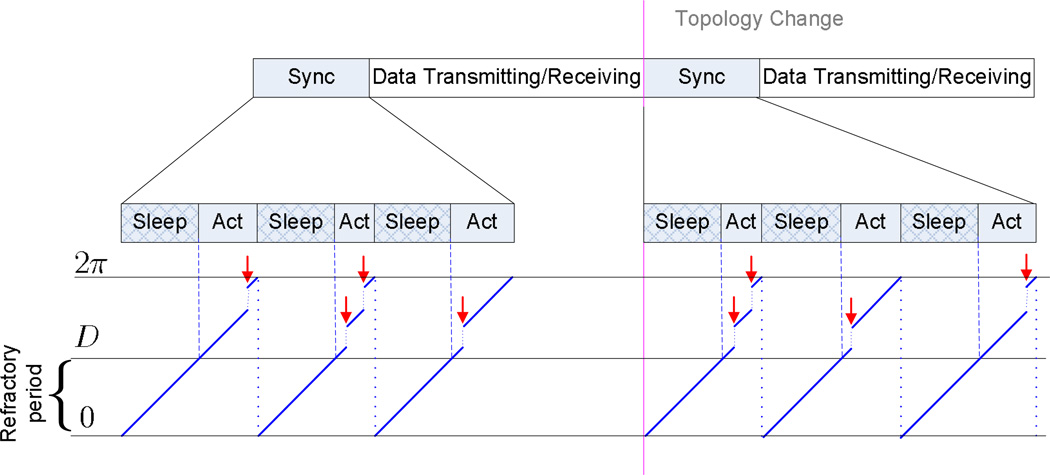
A schematic of the new protocol is given in Fig. 4. A sensor network implements the synchronization strategy before data exchanging. When topology is changed, the synchronization strategy needs to be implemented again.

Fig. 4.

Energy-efficient synchronization strategy with active-sleep mode. (‘Act’: ’Active mode’; Red arrows: arriving pulses)

V. Implementation of the synchronization strategy

A. Length of the refractory period D

As discussed in Sec. IV, a refractory period of length D will reduce $\frac{D}{2\pi }$ of energy consumption in one oscillation period, but will not influence the time to synchronization. So the length of the refractory period should be set to the maximally allowable value, i.e., 2π − Λ̄ according to Theorem 1 to reduce the energy consumption in a synchronization process. Here Λ̄ is an upperbound on phase difference. It can be measured during initial deployment of wireless sensors. And after deployment, it can be calculated according to the drifting rate of internal clocks, which is determined by the quality of electric circuits (e.g., quartz) and is measurable in practice.

Since a smaller Λ̄ means a larger D, and hence leads to more energy reduction, we can use a ‘reset’ packet to reduce Λ̄: Any sensor that wants to run the synchronization strategy broadcasts a ‘reset’ packet (with its ID specified in the packet) and resets its phase to 0 to initiate a synchronization process. Every sensor receives the packet resets its phase to 0 and immediately passes the packet to its neighbors. A sensor having received the ‘reset’ packet once will ignore all subsequently arriving identical ‘reset’ packets to prevent broadcast storms. Note that although the ‘reset’ packet cannot synchronize the network due to the existence of processing time (denote it as T_p), it can reduce the maximal phase difference to the level of m × T_p, where m is the maximal number of hops the ‘reset’ packet uses to cover the whole network.

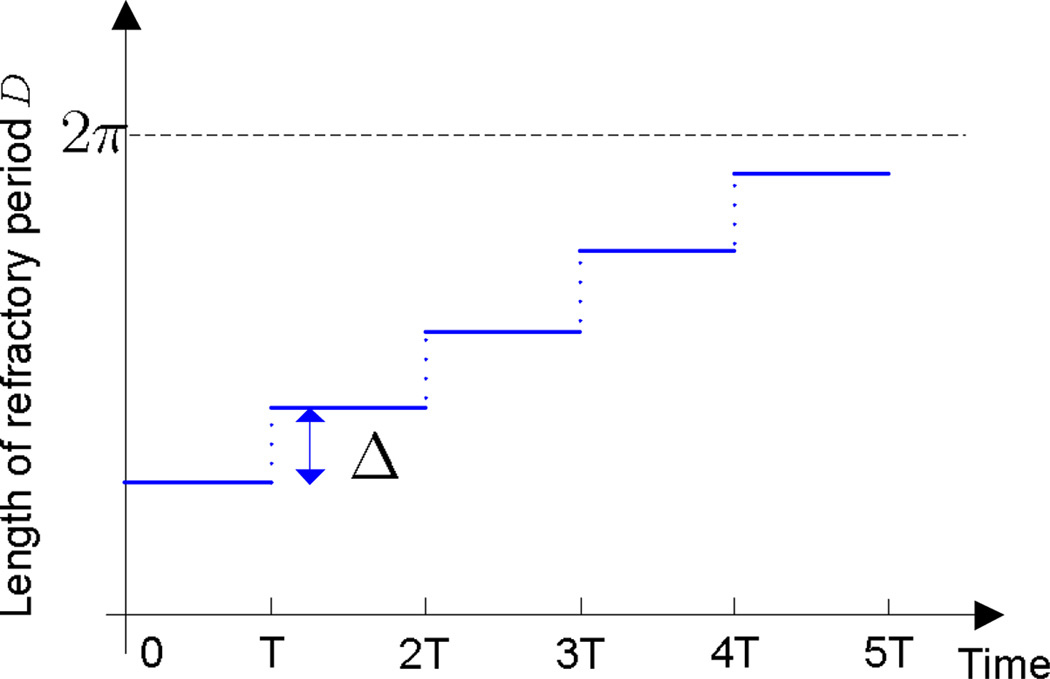
We can also adopt an adaptive refractory period scheme to reduce energy consumption further. As proven by Theorem 1, the phase difference is reduced by at least ε every oscillation period. Hence the maximally allowable refractory period increases by ε every oscillation period. Given this observation, we can increase D by Δ (Δ ≤ ε) every oscillation period to reduce energy consumption further. A schematic of the adaptive refractory period scheme is given in Fig. 5. Note that according to Theorem 2, ε is determined by the phase response function, coupling strength, and the indegree of coupling topology, hence Δ should be determined according to specific circumstances.

Fig. 5.

A schematic of the adaptive refractory period scheme. The length of refractory period is increased by Δ every oscillation period.

B. Topology control

As indicated in Theorem 1, in the proposed synchronization strategy, a strongly connected topology is vital to guarantee the final synchronization of a sensor network. In real implementations, it is impossible for a single node to check if the network to which it belongs is strongly connected. This problem is even worse when all the nodes are mobile. Since in this case the topology keeps changing all the time and a single node needs to prevent disconnecting the topology when it moves. Because our purpose is to design a totally decentralized synchronization strategy, we do not want to introduce a centralized station to control the interaction topology. In this section, we circumvent this problem by exploiting the relationship between the indegree and the connectivity property of a graph. We propose a totally decentralized approach to ensure a strongly connected topology. That is, in our topology control approach, each sensor does not need to know the information of other sensors.

We prove that strong connectivity can be ensured if the minimal degree of sensors (a degree of a sensor is defined as δ(υ) = min{δ⁻(υ), δ⁺(υ)}) is no less than a certain threshold value, and hence by making the neighbors of each sensor (neighbors of a sensor i means sensors that can talk to sensor i) over a certain value, we can ensure that the coupling topology is strongly connected. The results are detailed in Theorem 4:

Theorem 4: If a directed graph G(V, E) with N vertices V = {υ₁, υ₂, …, υ_N} satisfies $\delta (G)\ge [\frac{N}{2}]$ with

$$\delta (G)=\underset{{\upsilon }_i\in V}{\text{min}}\{{\delta }^{-}({\upsilon }_i),{\delta }^{+}({\upsilon }_i)\}$$ (3)

and [•] denoting the maximal integer no larger than ‘•’, then graph G is strongly connected.

Proof: Assume to the contrary that G is not strongly connected. Then the vertices of graph G can be divided into two nonempty disjoint subsets A and V − A such that either of the following two statements holds:

1. There are no edges between A and V − A, i.e., there is no edge between a vertex in A and a vertex in V − A;

2. There are edges between A and V − A, i.e., there are edges between a vertex in A and a vertex in V − A, but all the edges have the same direction (either all from A to V − A, or all from V − A to A).

Next we prove that both of the two statements contradict with the fact $\delta (G)\ge [\frac{N}{2}]$.

1. If there are no edges between A and V − A, then since the vertices in A have degree no less than $[\frac{N}{2}]$, A contains at least $[\frac{N}{2}]+1$ vertices. Using the same argument, we know V − A also has at least $[\frac{N}{2}]+1$ vertices. Then the total number of vertices is at least $2[\frac{N}{2}]+2$, which is larger than N and hence is impossible.

2. If there are edges between A and V − A but all the edges have the same direction, then without loss of generality we assume that the edges are all directed from A to V − A. Because the vertices in A have indegree no less than $[\frac{N}{2}]$, there are at least $[\frac{N}{2}]+1$ vertices in A. Similarly, because the vertices in V −A have outdegree no less than $[\frac{N}{2}]$, there are at least $[\frac{N}{2}]+1$ vertices in V − A. Therefore there are no less than $2[\frac{N}{2}]+2>N$ vertices in V, which contradicts the fact that there are N vertices in V.

From Theorem 4, if every sensor can be reached by no less than $[\frac{N}{2}]$ sensors and it receives information from no less than $[\frac{N}{2}]$ sensors (these sensors are not necessarily the same with those that can reach this sensor), then the network is guaranteed to be strongly connected.

In wireless sensor networks, the network links may fail randomly and the transmitted data can be corrupted by noise. This happens, for example, in an erasure network, where a transmission is occasionally lost, and, in the case of a successful transmission, the data may be distorted due to channel imperfections. In this case, it is of crucial importance to maintain strong connectivity even when there are link failures. In Sec. III-C and Remark 8, we have shown that the new synchronization strategy is tolerant to intermittent link failures. In the following, we will prove that our topology control approach in Theorem 4 can guarantee the strong connectivity of interaction topology even in the presence of permanent link failures.

To this end, we need to introduce the definitions of ‘k-edge strongly connected’ and ‘edge strong connectivity’ [31]:

Definition 2: A network is said to be k-edge strongly connected if it remains strongly connected after the removal of any m edges for any integer m satisfying 0 ≤ m < k.

Definition 3: The maximal value of k for which a directed graph G is k-edge strongly connected is called the edge strong connectivity of G, and is denoted as λ(G).

From Definition 2, we can see that if the interacting topology of a sensor network is k-edge strongly connected, then the network is tolerant to any link failures as long as the number of link failures is less than k. In fact, using the strategy in Theorem 4, we can guarantee that the network topology is δ(G)-edge strongly connected, where δ(G) is the degree of graph G and is defined in (3). But before we proceed to give the results, we need the definition of set-connection number, Lemma 1, and Lemma 2 below:

Definition 4: For V’s two disjoint vertex subsets A and B, denote δ⁻(A, B) as the number of edges directed from a vertex in A to a vertex in B, and denote δ⁺(A, B) as the number of edges directed from a vertex in B to a vertex in A, then the set-connection number δ(A, B) is defined as the minimum of δ⁻(A, B) and δ⁺(A, B), i.e., δ(A, B) ≜ min{δ⁻(A, B), δ⁺(A, B)}.

Lemma 1: A directed graph G with vertex set V is k-edge strongly connected if and only if there exists no nonempty proper subset A (i.e., A ⊆ V, but A ≠ V) such that the set-connection number δ(A, V − A) is less than k.

Proof: The proof is given in Appendix A.

Lemma 2: A directed graph G with vertex set V has edge-strong connectivity k if and only if $\underset{A\subseteq V,A\ne V}{\text{min}}\{\delta (A,V-A)\}=k$ is satisfied.

Proof: The proof is given in Appendix B.

Based on Lemma 1 and Lemma 2, we can now proceed to give Theorem 5:

Theorem 5: If a directed graph G(V, E) with N vertices V = {υ₁, υ₂, …, υ_N} satisfies $\delta (G)\ge [\frac{N}{2}]$ with δ(G) defined in (3), then graph G is δ(G)-edge strongly connected.

Proof: According to Theorem 4, we know G is strongly connected, i.e., edge-strong connectivity λ(G) satisfies λ(G) > 0. From the definition of edge-strong connectivity λ(G) in Definition 3, it follows λ(G) ≤ δ(G) where δ(G) is defined in (3). In order to prove that λ(G) is equal to δ(G), we only need to prove that λ(G) < δ(G) cannot be true. Assume to the contrary that λ(G) < δ(G) is true. According to Lemma 2, we know there exists a nonempty subset A of G such that δ(A, V − A) (please refer to Definition 4) is equal to λ(G). Hence either of the following statements is true:

1. The number of edges directed from a vertex in A to a vertex in V − A is λ(G);

2. The number of edges directed from a vertex in V − A to a vertex in A is λ(G).

Or both of them are true.

Without loss of generality, we assume that the number of edges directed from a vertex in A to a vertex in V − A is λ(G). Clearly, these λ(G) edges are originated from p ≤ λ(G) vertices in A. Next, we show that A has at least one vertex that has no edges directed to a vertex in V − A. Assume to the contrary that A has no other vertex except the p vertices having edges directed to a vertex in V − A. Note that the outdegree of vertices in A is no less than δ(G), which is larger than λ(G) according to our assumption, so the total number of outgoing edges of the p vertices in A is no less than p × δ(G). Given that λ(G) of them are directed to V − A, the outgoing edges between nodes in A is no less than p × δ(G) − λ(G). But the maximally allowable number of outgoing edges for a graph of p vertices is p × (p − 1), which is less than p × δ(G) − λ(G). This is because p ≤ λ(G) < δ(G) holds (according to our assumption), which further leads to

$$p\times (p-1)-(p\times \delta (G)-\lambda (G))=p\times (p-\delta (G))-(p-\lambda (G))\le (p-\delta (G))-(p-\lambda (G))=\lambda (G)-\delta (G)<0$$ (4)

So the assumption of only p vertices in V is incorrect and there is at least one vertex υ_i in A such that it has no edge directed to a vertex in V − A. Hence all υ_i’s outgoing edges are directed to vertices in A, meaning that the number of vertices in A is no less than δ(G) + 1 given that υ_i’s out degree is no less than δ(G). Similarly, since the vertices in V − A have indegree no less than δ(G), which is larger than the number of total edges directed from A to V − A, i.e., λ(G), we can prove that there exists at least one vertex υ_j in V − A such that all its ingoing edges are originated from vertices in V − A. Hence the number of vertices in V − A is no less than δ(G) + 1 since υ_j’s indegree is no less than δ(G). Combining the fact that both A and V − A have no less than δ(G) + 1 vertices and $\delta (G)\ge [\frac{N}{2}]$, we know that the total number of vertices in V is no less than $2[\frac{N}{2}]+2$, which is larger than N. This contradicts the fact that there are N vertices in V.

The same contradiction can be obtained if we assume that the number of edges directed from V − A to A is λ(G).

Summarizing the above derivations, we have λ(G) = δ(G), meaning that G is δ(G)-edge strongly connected.

Therefore, by making each sensor have no less than $[\frac{N}{2}]$ neighbors, we can guarantee an overall $[\frac{N}{2}]$-edge strongly connected interaction topology. (By sensor i’s neighbors we mean the sensors that can talk to sensor i.) This is true even when the sensors are mobile. Moreover, using this method, the final synchronization of the network is ensured even when there are permanent link failures as long as the number of failures is less than $[\frac{N}{2}]$. (Since channels are considered directed, for a bidirectional channel, a failure in one direction is considered one link failure, and a failure in both directions should be regarded as two link failures.)

Remark 9: According to the derivation in Theorem 1 and Theorem 2, we know that the number of neighbors of a sensor is equal to the number of pulses it receives in one oscillation period. Hence by counting the number of pulses received in one oscillation period, a sensor can estimate the number of sensors in its neighborhood.

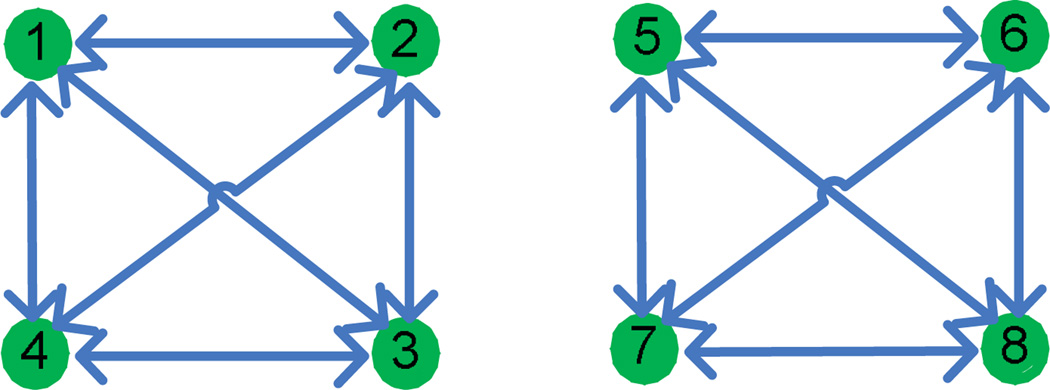
Remark 10: In fact, to guarantee the connectivity for an arbitrary network, it is necessary to require that every node has no less than $[\frac{N}{2}]$ neighbors. For example, consider a bi-directional network as shown in Fig. 6. There are 8 nodes. Although every node already has $[\frac{N}{2}]-1=[\frac{8}{2}]-1=3$ neighbors, the topology is still not connected and the network can never be synchronized. So to guarantee a connected topology for an arbitrary network, it is necessary to require that every nodes has at least $[\frac{N}{2}]=[\frac{8}{2}]=4$ neighbors. If, due to the existence of walls, a particular node only has 1 or 2 neighbors, our energy-efficient synchronization algorithm is still applicable if the topology is strongly connected (with definition given in Sec. II-B), but in this case, since the condition in our failure-tolerant topology control approach cannot be satisfied, the network topology is vulnerable to link failures. In fact, in this case, if the connection(s) between the node and its neighbor (two neighbors) is (are) broken due to link failure, then the node becomes isolated and the network cannot be synchronized.

Fig. 6.

An example to show that having no less than $[\frac{N}{2}]$ neighbors is necessary to guarantee connectivity for an arbitrary network.

To implement the failure-tolerant topology control, all nodes are assigned with no less than $[\frac{N}{2}]$ neighbors in initial deployment. If nodes are mobile, then after each movement, a node counts the number of neighbors by counting the number of pulses received in one oscillation period (c.f. Remark 9). If the number is no less than $[\frac{N}{2}]$, then the topology remains strongly connected and the movement is retained. Otherwise, to avoid the possibility of disconnecting the network, the node has to go back to its original position (it has no less than $[\frac{N}{2}]$ neighbors there). Of course, in the latter case, the node can also retain the movement and use some advanced algorithm (e.g., k-neigh [32] or k-XTC in [33]) to acquire $[\frac{N}{2}]$ neighbors by increasing transmission power. However, this makes the topology control approach complex and hence is not adopted here. Also, to keep the topology control approach as simple as possible, no action is taken if the number of neighbors is over $[\frac{N}{2}]$. It is worth noting that a node cannot just simply choose $[\frac{N}{2}]$ from all available neighbors since it does not know the source of received pulses.

Remark 11: To maintain the natural scalability of pulse-coupled synchronization strategy, the exchanged pulses should be identical and no source/destination information such as node ID should be embedded in them (for example, they have been realized by using impulsive waveform and pseudorandom sequence in [7]). Our topology control approach is tailored for this pulse-coupled synchronization strategy and can guarantee a $[\frac{N}{2}]$-edge strongly connected topology without distinguishing pulse sources and irrespective of the realization of exchanged pulses. Whereas existing topology control approaches all require the source of exchanged messages to build and maintain a connected network [32].

C. Transmission

In each sensor, when the phase of embedded timer reaches 2π, the sensor resets its phase to 0 and sends out a pulse. For impulse-radio UWB network, this can be achieved by sending a monocycle pulse with specified energy [34]. For IEEE 802.11 protocols, a pulse can be realized by using preambles [35].

D. Reception

Due to the broadcast nature of wireless transmission, there may be interference at the receiver. Moreover, channel noise could also prevent the detection of arriving pulses. This once again underscores the necessity of failure-tolerant k-edge strongly connected interaction topology. In order to detect a pulse, an energy detection unit can be used to compare the arriving signal’s energy with a specified threshold value. If the energy exceeds the threshold value, then a pulse is detected. A sophisticated detector such as a generalized maximum-likelihood detector can be used to improve the detection performance [36].

So far, we can see that using the new pulse-coupled strategy, synchronization can be achieved by exchanging pulses instead of complex packet messages. Moreover, by controlling the number of neighbors of a sensor locally, we can achieve a globally strongly connected interaction topology. The topology control method is applicable to mobiles sensors and is tolerant to both intermittent link failures and permanent link failures.

VI. QualNet Case Studies

In this section, we use a high-fidelity network evaluation tool (QualNet) to illustrate the proposed synchronization strategy. QualNet is a commercial network platform that can be used to evaluate wireless communication networks. It was first released in 2000 by Scalable Network Technologies and has been widely used to predict the performance of MANETs, satellite networks and sensor networks, among others [37].

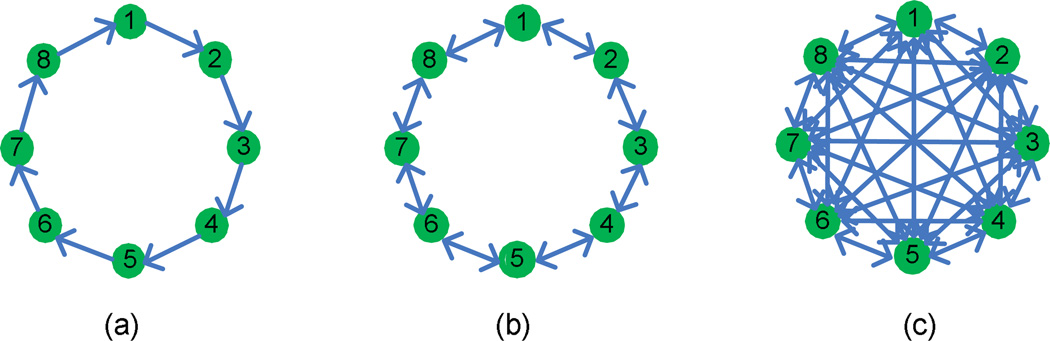
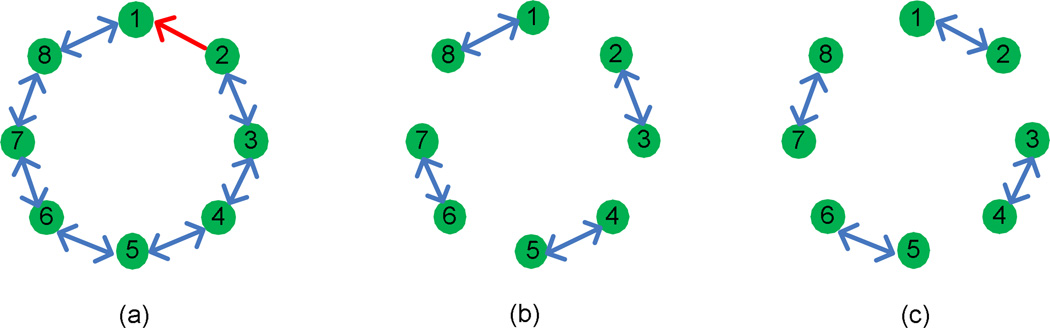
We consider N = 8 pulse-coupled sensors with natural period of embedded timers equal to 1s. The interaction topologies used in implementation are shown in Fig. 7. All of the three topologies are strongly connected. According to the definition of ‘k-edge strongly connected’, we know that the three topologies are 1-edge strongly connected, 2-edge strongly connected, and 7-edge strongly connected, respectively. (Note that a bi-directional interaction means two unidirectional edges.) In all the implementation, similar to [15], when a node’s firing period (the interval between two successive fires) remains unchanged for 5 consecutive oscillation periods, it considers that synchronization is achieved and stops pulse emitting. The time to synchronization is calculated off-line and is defined as the interval from synchronization algorithm initiation to the instant when all nodes fire simultaneously for two consecutive oscillation periods.

Fig. 7.

The coupling topologies of the wireless sensor networks used in the QualNet implementations: (a) unidirectional interaction; (b) bidirectional interaction; (c) all-to-all interaction

We first implemented the wireless sensor network under the topology in Fig. 7 (a). Initial phases were randomly chosen from the interval (0, 0.7π). So according to Theorem 1, the network can be synchronized under a refractory period not larger than 1.3π. To find the influence of the refractory period, we implemented the network under different refractory periods (D = 0.2π, 0.4π, …, 1.0π, 1.2π) and different coupling strengths (l = 0.1, 0.2, …, 0.8, 0.9), respectively. The network was found synchronized in all the above cases, confirming the analytical results in Theorem 1. We also compared the time to synchronization under different refractory periods and coupling strengths. For each parameter pair (refractory period D and coupling strength l), we ran the implementation for 100 times and each time we chose the initial phases randomly from the uniform distribution on (0, 0.7π). The time to synchronization is defined to be the average over the 100 runs. In all cases, the network was synchronized, and the times to synchronization are given in Table I. From Table I, we can see that the time to synchronization decreases with an increase in the coupling strength l, but it is hardly influenced by the length of refractory period, which confirms the theoretical predictions in Theorem 2. Note that there may be small fluctuations in the time to synchronization under different refractory periods since the time to synchronization is averaged over 100 runs with randomly chosen initial phases.

TABLE I.

Influence of refractory period and coupling strength on the time to synchronization [s] under coupling topology Fig. 7 (a)

Coupling strength l	0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.8	0.9
Refractory period D
0.2π	177.75	95.56	58.87	44.49	32.35	25.51	19.97	14.79	10.71
0.4π	175.50	93.96	61.84	44.47	33.74	25.11	19.41	14.81	10.48
0.6π	178.97	94.17	61.70	44.50	33.63	24.97	19.32	14.60	10.41
0.8π	178.97	94.17	61.70	44.50	33.63	24.97	19.32	14.60	10.41
1.0π	178.97	94.17	61.70	44.50	33.63	24.97	19.32	14.60	10.41
1.2π	178.97	94.17	61.70	44.50	33.63	24.97	19.32	14.60	10.41

Based on a similar setup, we also implemented the network under the topology in Fig. 7 (b) and the topology in Fig. 7 (c), respectively. Synchronization was achieved in all cases and the times to synchronization are given in Table II and Table III, respectively. We can see that under the two coupling topologies, the time to synchronization is still influenced by the coupling strength but hardly influenced by the length of refractory period. Similar to the unidirectional case, there may be small fluctuations in the time to synchronization under different refractory periods since the time to synchronization is averaged over 100 runs with randomly chosen initial phases.

TABLE II.

Influence of refractory period and coupling strength on the time to synchronization [s] under coupling topology Fig. 7 (b)

Coupling strength l	0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.8	0.9
Refractory period D
0.2π	81.80	46.60	34.05	27.43	22.39	18.65	16.88	10.36	8.34
0.4π	83.46	48.11	32.80	27.94	21.68	18.84	15.94	10.35	8.36
0.6π	85.83	47.47	32.80	27.81	21.74	18.59	15.76	10.35	8.39
0.8π	85.98	47.90	32.89	27.86	21.70	18.45	15.93	10.35	8.39
1.0π	85.98	47.90	32.89	27.86	21.70	18.45	15.93	10.35	8.39
1.2π	85.98	47.90	32.89	27.86	21.70	18.45	15.93	10.35	8.39

TABLE III.

Influence of refractory period and coupling strength on the time to synchronization [s] under coupling topology Fig. 7 (c)

Coupling strength l	0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.8	0.9
Refractory period D
0.2π	25.47	15.15	10.57	8.32	6.53	5.06	4.02	2.98	2.04
0.4π	27.16	16.03	11.15	8.40	6.53	5.06	4.02	2.98	2.04
0.6π	28.17	16.03	11.15	8.40	6.53	5.06	4.02	2.98	2.04
0.8π	28.17	16.03	11.15	8.40	6.53	5.06	4.02	2.98	2.04
1.0π	28.17	16.03	11.15	8.40	6.53	5.06	4.02	2.98	2.04
1.2π	28.17	16.03	11.15	8.40	6.53	5.06	4.02	2.98	2.04

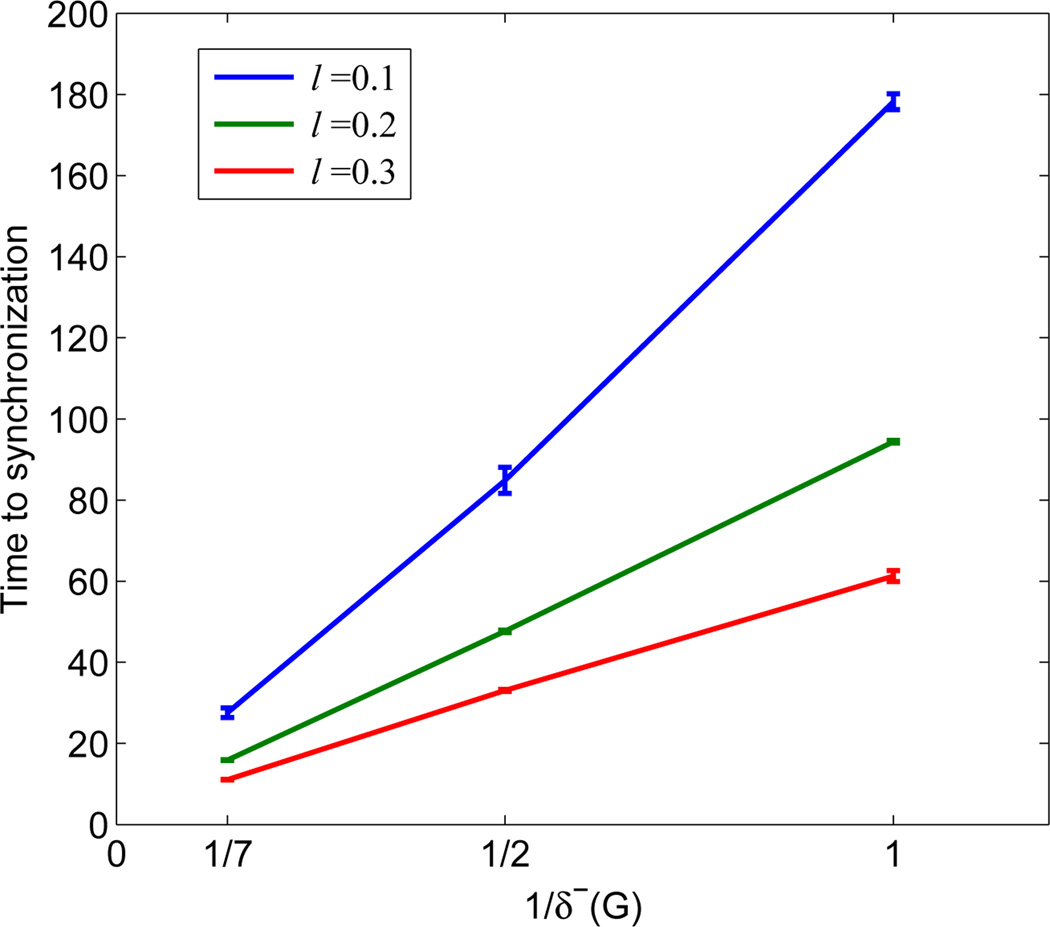
Using the results in Table I, Table II, and Table III, we can analyze the influence of network topology (indegree δ⁻(G)) on the time to synchronization. Fig. 8 plots the relationship between the time to synchronization and the reciprocal of coupling topology’s indegree δ⁻(G). Since the indegrees of the topologies in Fig. 7 (a), Fig. 7 (b) and Fig. 7 (c) are 1, 2, and 7, respectively, the abscissas in the plot are 1/1, 1/2, and 1/7, respectively. For each topology, the time to synchronization is averaged over all six refractory periods (D = 0.2π, 0.4π, 0.6π, 0.8π, 1.0π, 1.2π) and the deviation from average value (variance) is also given, which is represented by an error bar. From the plot, we can see that the time to synchronization is indeed almost inversely proportional to the indegree of coupling topology, which confirms the analytical prediction in Theorem 2.

Fig. 8.

The influence of interaction topology (indegree δ⁻(G)) on the time to synchronization.

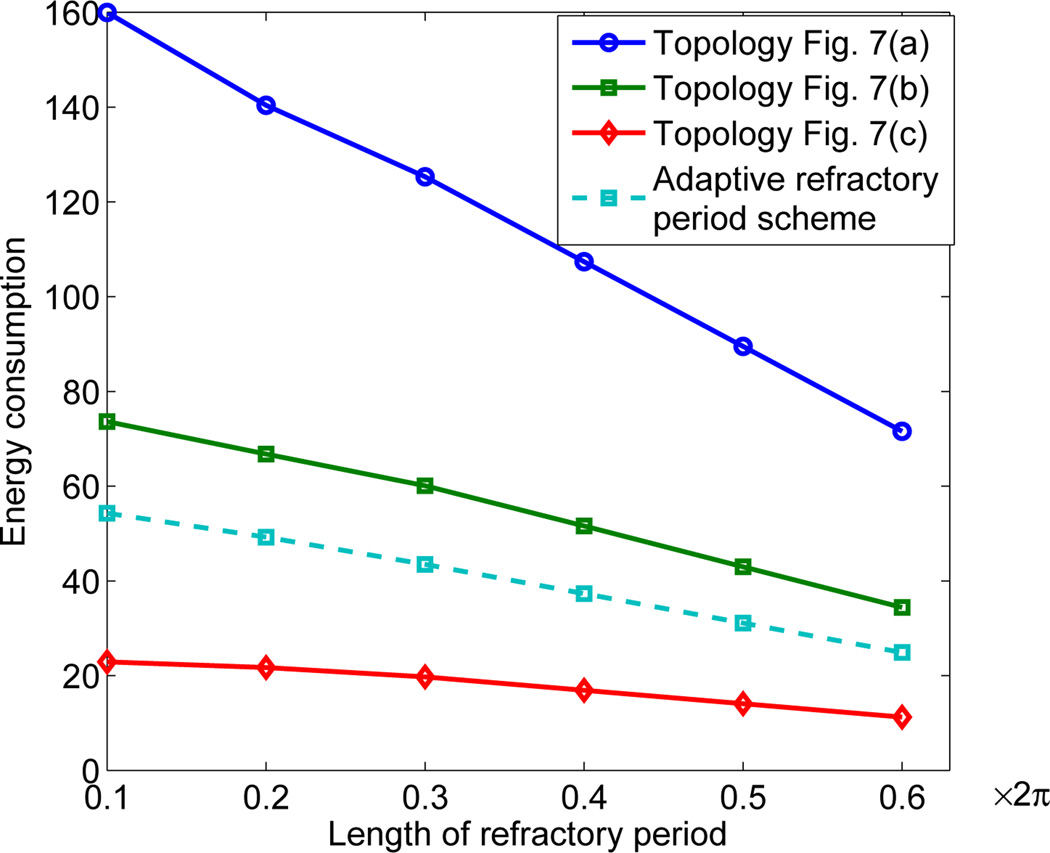
The total energy consumption is proportional to the time to synchronization and inversely proportional to the length of refractory period. In the implementation, energy consumption for the three coupling topologies were also obtained. The result is given by the three solid lines in Fig. 9. It can be seen that for all topologies used in the implementation, by using the largest allowable refractory period, energy consumption is reduced by about a half.

Fig. 9.

Energy consumption under different lengths of refractory period (l = 0.1). In the adaptive refractory period scheme, the x-axis is the initial length of refractory period.

Given that the topology in Fig. 7 (b) is 2-edge strongly connected, synchronization should be retained after a link failure in any unidirectional communication. Since the topology is symmetric, we removed the communication from sensor 1 to sensor 2 (which amounts to changing the interaction between sensors 1 and 2 from bidirectional to unidirectional). The resulting interaction topology is given in Fig. 10 (a). Using this coupling topology, we implemented the wireless sensor network under different refractory periods and coupling strengths. In all cases the network was still synchronized, confirming the failure-tolerance of our synchronization strategy. The times to synchronization are given in Table IV. Comparison with Table II shows that the time to synchronization is increased due to the reduced connectivity.

Fig. 10.

The coupling topology of wireless sensor network: (a) topology Fig 7 (b) with one link failure; (b) interaction pattern 1 in the dynamic topology; (c) interaction pattern 2 in the dynamic topology

TABLE IV.

Influence of refractory period and coupling strength on the time to synchronization [s] under coupling topology Fig. 10 (a)

Coupling strength l	0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.8	0.9
Refractory period D
0.2π	148.29	73.26	48.33	35.99	28.19	23.12	19.72	16.59	13.42
0.4π	149.27	74.23	48.23	36.01	28.78	23.06	19.77	16.87	13.10
0.6π	149.29	74.19	48.20	36.03	28.66	23.01	19.79	16.63	13.97
0.8π	148.41	73.44	48.20	36.03	28.06	23.01	19.79	16.45	13.92
1.0π	149.25	74.33	48.20	36.03	28.81	23.01	19.79	16.45	13.92
1.2π	149.31	74.19	48.20	36.03	28.66	23.01	19.79	16.45	13.92

We also ran the network using the adaptive refractory period scheme under the topology in Fig. 7 (b). In the implementation, we increased the refractory period by $\mathrm{\Delta }=\frac{2\pi -D}{15}\times l$ each oscillation period until synchronization was achieved. The times to synchronization are given in Table V. We can see that these times to synchronization are almost identical with those in Table II, confirming again that the length of refractory period does not influence the time to synchronization even when it is adaptive. The energy consumption is also recorded and given in Fig. 9 (the dashed cyan line). Comparison with the energy consumption under the same topology but a static refractory period (the solid green line) confirms that the adaptive refractory period scheme can indeed reduce energy consumption further.

TABLE V.

Influence of adaptive refractory period and coupling strength on the time to synchronization [s] under coupling topology Fig. 7 (b)

Coupling strength l	0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.8	0.9
Initial refractory period D
0.2π	83.00	46.72	33.34	27.98	21.88	18.84	16.34	10.36	8.34
0.4π	85.87	48.58	32.58	27.87	21.78	18.81	16.65	10.35	8.36
0.6π	87.09	48.08	32.83	27.96	21.83	18.79	16.66	10.35	8.39
0.8π	87.24	48.08	32.83	27.96	21.83	18.79	16.66	10.35	8.39
1.0π	87.24	48.08	32.83	27.96	21.83	18.79	16.66	10.35	8.39
1.2π	87.24	48.08	32.83	27.96	21.83	18.79	16.66	10.35	8.39

To study the synchronization of the network under dynamic topologies, we implemented the wireless sensor network under an interaction topology switching between Fig. 10 (b) and Fig. 10 (c) in a round-robin manner. Since neither Fig. 10 (b) nor Fig. 10 (c) is strongly connected, the network cannot be synchronized under either of these coupling topologies. However, by alternately switching between the two topologies, the interaction became strongly connected in the sense of Theorem 3. Hence the network should be synchronized under this switching topology according to Theorem 3. Implementation result confirmed the prediction, and the times to synchronization were also recorded, which are given in Table VI.

TABLE VI.

Influence of refractory period and coupling strength on the time to synchronization [s] under a topology switching between Fig. 10 (b) Fig. 10 (c) in a round-robin manner

Coupling strength l	0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.8	0.9
Refractory period D
0.2π	172.46	94.58	65.38	50.60	42.65	33.95	31.51	23.86	19.17
0.4π	176.42	91.87	67.55	51.74	39.00	34.68	31.35	23.07	18.35
0.6π	178.14	94.03	67.79	50.86	39.00	34.09	30.75	22.20	18.09
0.8π	178.23	94.43	67.91	51.05	39.13	34.21	30.79	22.06	18.37
1.0π	178.23	94.43	67.91	51.05	39.13	34.21	30.79	22.06	18.37
1.2π	178.23	94.43	67.91	51.05	39.13	34.21	30.79	22.06	18.37

Using QualNet, we also compared our synchronization strategy to traditional packet-based synchronization algorithms in terms of both energy consumption and synchronization accuracy. The algorithm used for comparison is FTSP [3], which is widely regarded as the state-of-the-art clock synchronization protocol for wireless sensor networks [5]. As in [15], Since coupling strength and the length of refractory period are design parameters in our synchronization strategy, in the comparison, we fixed them to 0.9 and 1.2π, respectively. All the energy consumption and synchronization error are averaged over 100 runs. The comparison results under different topologies are given in Table VII, which indicate that our synchronization strategy is indeed an appealing option to consider for wireless sensor networks. Under the same re-synchronization period of 30 seconds (i.e., in the case of FTSP, sync beacons are sent every 30 seconds), we also compared the radio duty cycle. The results are given in the last row of Table VII. It can be seen that our synchronization strategy has smaller radio duty cycles and hence longer sleep phases. This explains its higher energy efficiency than FTSP.

TABLE VII.

Comparison of our synchronization strategy to FTSP under different topologies in terms of both energy consumption and synchronization accuracy

Topology	Fig. 7 (a)		Fig. 7 (b)		Fig. 7 (c)		Fig. 10 (a)		Fig. 10 (b) & (c)
Protocol	Proposed	FTSP	Proposed	FTSP	Proposed	FTSP	Proposed	FTSP	Proposed	FTSP
Energy consumption [mJ]	4.16	11.33	3.35	7.19	0.81	2.08	5.56	10.56	7.34	15.71
Synchronization error [µs]	20.23	21.20	11.94	13.60	1.09	3.00	9.47	20.19	11.70	13.78
Radio-duty cycle	13.8%	37.7%	11.1%	23.9%	2.7%	6.9%	18.5%	35.2%	24.4%	52.3%

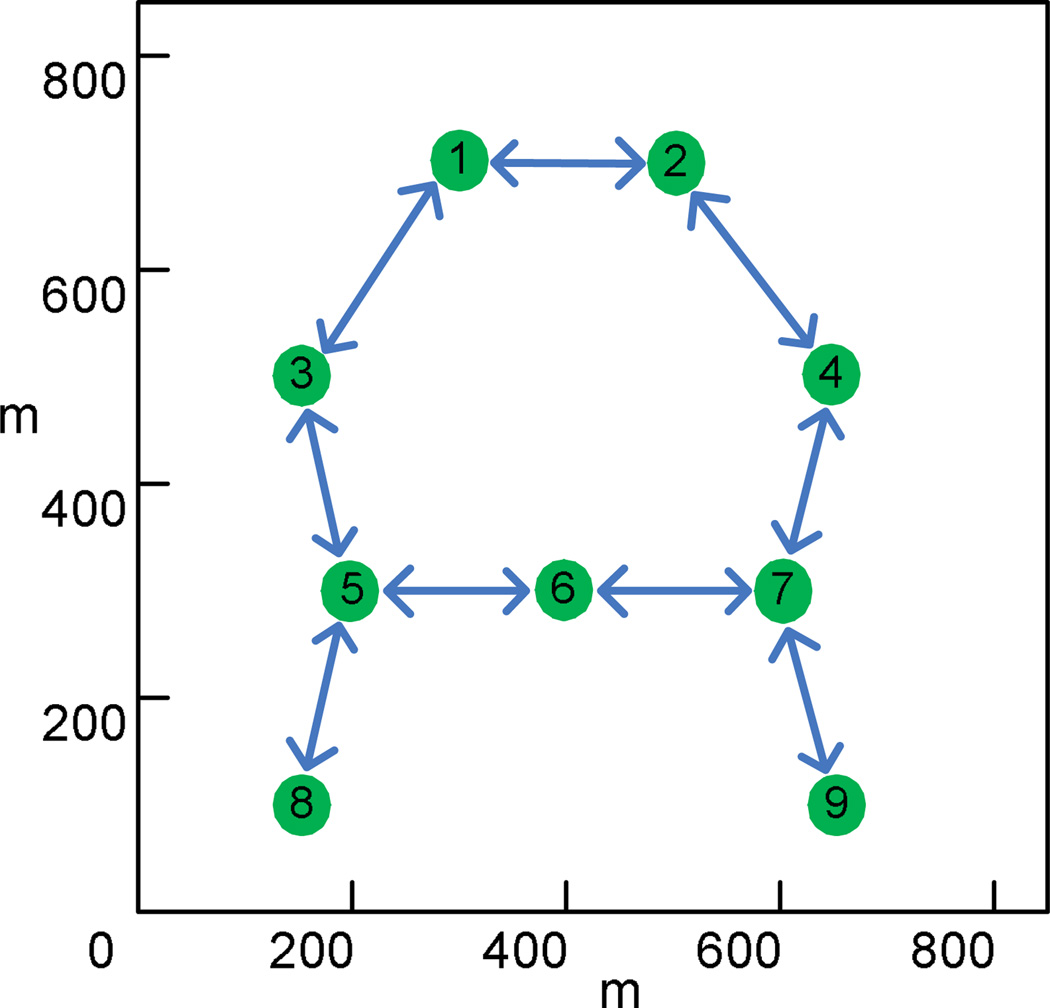
To show the applicability of the synchronization strategy to more general mobile networks, in the QualNet environment, we tested our algorithm with the random waypoint network [32], which is the most widely used mobility model in the ad hoc network community. The network is composed of 9 nodes. The initial distribution and initial interaction status of the 9 nodes are given in Fig 11. The initial interaction topology is strongly connected according to the definition in Sec. II-B. Among the 9 nodes, node number 5, node number 6, and node number 7 are fixed in position and the rest of the nodes are mobile. Every mobile node chooses at random a destination in the square [0, 800m] × [0, 800m] and moves towards it along a straight line with a velocity chosen at random in the interval (0m/s, 10m/s). When it reaches the destination, it remains stationary for a pause time of 10 seconds, and then it starts moving again according to the same rule. Every node has the same transmission range of 250m. Both the fixed refractory period scheme and the adaptive refractory period scheme (where the refractory period was increased by $\mathrm{\Delta }=0.9\times \frac{2\pi -D}{600}$ each oscillation period until synchronization was achieved) were implemented. The times to synchronization and energy consumptions under different (initial) refractory periods are given in Table VIII. They are all averaged over 100 runs with initial phases in each run randomly chosen from the uniform distribution on (0, 0.7π). It is clear that the time to synchronization is independent of the length of refractory period and a larger refractory period reduces energy consumption.

Fig. 11.

The initial distribution and initial interaction status of the random waypoint mobile network.

TABLE VIII.

Time to synchronization [s] (1st element of each 2-tuple) and energy consumption [mJ] (2nd element of each 2-tuple) under the random waypoint network (l = 0.9)

(Initial) refractory period D	0.2π	0.4π	0.6π	0.8π	1.0π	1.2π
Scheme
Fixed refractory period	(142.27, 128.0)	(142.25, 113.8)	(142.25, 99.5)	(142.25, 85.3)	(142.25, 71.1)	(142.25, 56.9)
Adaptive refractory period	(142.27, 114.3)	(142.25, 101.6)	(142.25, 88.9)	(142.25, 76.2)	(142.25, 63.5)	(142.25, 50.8)

We also tested the influence of the degree of network mobility on the proposed synchronization strategy. The simulation setup was the same as the random waypoint network case except that we varied the fraction of mobile nodes (1 out of 9 nodes, 2 out of 9 nodes, …, 9 out of 9 nodes) that were allowed to move according to the random waypoint rule. The synchronization strategy worked well in all cases. For each case, the averaged time to synchronization and energy consumption over 100 runs are given in Table IX. In fact, the results show that the time to synchronization and energy consumption reduce with an increase in the fraction of mobile nodes, which corroborates the prediction in Remark 7 that mobility facilitates synchronization.

TABLE IX.

Influence of mobility on the time to synchronization and energy consumption (l = 0.9, D = 1.2π)

Total number of mobile nodes	1	2	3	4	5	6	7	8	9
Time to synchronization [s]	290.91	279.73	260.30	244.18	175.46	174.97	174.52	153.56	136.10
Energy consumption [mJ]	116.36	111.89	104.12	97.67	70.18	69.98	69.80	61.42	54.44

VII. Conclusions

An energy-efficient pulse-coupled synchronization strategy is proposed for wireless sensor networks. The basic idea is to introduce a large refractory period in the phase response function. Different from the intuition that a refractory period reduces synchronization accuracy, it is proven analytically that perfect synchronization is achieved under the proposed strategy. The time to synchronization is proven to be independent of the large refractory period. Given that the total energy consumption is determined by the product of single-period energy consumption and the time to synchronization (number of oscillation periods used to achieve synchronization), the proposed synchronization strategy greatly reduces energy consumption through reducing idle listening in each oscillation period. By exploiting the relationship between connectivity and the indegree of a graph, we also propose a topology control scheme. The scheme is tolerant to link failures and totally decentralized, hence successfully guaranteeing a decentralized implementation of the proposed synchronization strategy. In addition, the synchronization strategy is applicable to dynamic networks. Its effectiveness is illustrated by detailed QualNet case studies.

Biographies

Yongqiang Wang was born in Shandong, China. He received his B.E. degree in Electrical Engineering & Automation, B.E. degree in Computer Science & Technology from Xian Jiaotong University, Shanxi, China, in 2004. From 2007–2008, he was with the University of Duisburg-Essen, Germany, as a visiting student. He received his M.Sc. and Ph.D. degrees in Control Science & Engineering from Tsinghua University, Beijing, China, in 2009. He is now with the University of California, Santa Barbara as a project scientist. His research interests are systems modeling and analysis of biochemical oscillator networks, synchronization of wireless sensor networks, networked control systems, and model-based fault diagnosis.

Dr. Wang is the recipient of 2008 Young Author Prize from IFAC Japan Foundation for a paper presented at the 17th IFAC World Congress in Seoul.

Felipe Núñez was born in Santiago de Chile. He received his B.Sc. and M.Sc. degrees in Electrical Engineering from the Pontificia Universidad Católica de Chile in 2007 and 2008, respectively. Currently, he is working towards his Ph.D. degree at The University of California, Santa Barbara. His research interests include control of networks, hybrid dynamical systems, model predictive control, fuzzy systems, mineral processing, modern philosophy, and tarology.

Francis J. Doyle, III received his B.S.E. degree from Princeton in 1985, C.P.G.S. degree from Cambridge in 1986, and Ph.D. degree from Caltech in 1991, all in chemical engineering. He is the Associate Dean for Research in the College of Engineering at UCSB, and he is the Director of the UCSB/MIT/Caltech Institute for Collaborative Biotechnologies. He holds the Duncan and Suzanne Mellichamp Chair in Process Control in the Department of Chemical Engineering as well as appointments in the Electrical Engineering Department and the Biomolecular Science and Engineering Program. He has been awarded the distinction of Fellow in multiple professional societies, including the IEEE, IFAC, AIMBE, and the AAAS. He served as the editor-in-chief of IEEE Transactions on Control Systems Technology from 2004 to 2009 and is the Vice President for Publications in the IEEE Control Systems Society. His research interests are in systems biology, network science, modeling and analysis of circadian rhythms, drug delivery for diabetes, model-based control, and control of particulate processes.

Appendix

A. Proof of Lemma 1

Sufficiency (⇐)

If there is no nonempty proper subset A of V satisfying δ(A, V − A) < k, suppose to the contrary that G is not k-edge strongly connected. Then according to the definition of ‘k-edge strongly connected’, there exist m edges, 0 < m < k, such that removing them from G makes G not strongly connected. Represent the graph after edge removal as Ḡ. Note that Ḡ and G have the same vertex set V. Since Ḡ is not strongly connected, V can be decomposed into two nonempty subsets Ā and B̄ ≜ V − Ā such that either of the following statements is true:

1. There are no edges between Ā and B̄;

2. There are edges between Ā and B̄, but they all have the same direction (either all from Ā to B̄, or all from B̄ to Ā).

So according to Definition 4, δ(Ā, B̄) = 0 is satisfied for Ḡ. Therefore δ(Ā, B̄) ≤ m < k is satisfied for G, which contradicts the initial assumption that there exists no nonempty proper set A such that δ(A, V − A) < k is satisfied.

Necessity (⇒)

If G is k-edge strongly connected, suppose there exists a nonempty proper subset A of V such that δ(A, V − A) is m, which is less than k. Represent the edges directed from a vertex in A to a vertex in V − A as E(A, V − A) and the edges directed from a vertex in V − A to a vertex in A as E(V − A, A), respectively. Represent further the numbers of the two kinds of edges as m₁ and m₂, respectively. Since min{m₁, m₂} = m according to the definition of δ(A, V − A) in Definition 4, we have that either m₁ or m₂ is equal to m, or both of them are equal to m. Without loss of generality we suppose that m₁ is equal to m. Then removing these m₁ edges makes the edges between A and V − A all directed from V − A to A, i.e., the network is not strongly connected anymore. This contradicts the assumption that G is k-edge strongly connected. Hence the lemma is proven.

B. Proof of Lemma 2

According to the definition of edge-strong connectivity in Definition 3, we know if a graph has edge-strong connectivity λ(G) equal to k, then G is k-edge strongly connected but not (k + 1)-edge strongly connected. Thus, making use of Lemma 1, one gets Lemma 2.