Computer-Aided Drug Design: Using Numbers to Your Advantage

Abstract

Computer-aided drug design could benefit from a greater understanding of how errors arise and propagate in biomolecular modeling. With such knowledge, model predictions could be associated with quantitative estimates of their uncertainty. In addition, novel algorithms could be designed to proactively reduce prediction errors. We investigated how errors propagate in statistical mechanical ensembles and found that free energy evaluations based on single molecular configurations yield maximum uncertainties in free energy. Furthermore, increasing the size of the ensemble by sampling and averaging over additional independent configurations reduces uncertainties in free energy dramatically. This finding suggests a general strategy that could be utilized as a posthoc correction for improved precision in virtual screening and free energy estimation.

The expectation for computational modeling in chemistry and biology has been for it to become a fast, cheap, and reliable workhorse for making predictions concerning biomolecular systems. As many in the drug design field well know, this expectation has not yet been fulfilled. Accurately predicting properties of drug-like molecules is difficult, and predicting their binding affinities to protein targets is even more challenging. Although in principle we know the equations we need to solve from statistical mechanics, practically treating biomolecular systems requires many approximations and simplifications for the problem to be amenable to computation. These practical limitations have inspired the generation of numerous computational models, which, by their very construction and approximations used, all yield some amount of prediction error. Understanding and estimating these prediction errors is a significant challenge.

In molecular modeling, errors are usually attributed to two sources: sampling and computed energetics. Sampling errors come from an incomplete representation of a statistical ensemble, perhaps by neglecting some important but rarely populated states. Sampling errors will almost certainly arise when modeling very high-dimensional systems. As Levinthal famously noted, neither computers nor nature could practically perform an exhaustive sampling of the ∼10³⁰⁰ configurations available to a typical protein.¹ Of course, the majority of these states are insignificantly populated, and thus importance sampling via molecular dynamics (MD) or Monte Carlo (MC) simulations are preferable. Indeed, in recent years the ability to sample via MD has exploded due to the use of GPUs and special purpose hardware, which has opened up new frontiers in understanding the role of sampling in modeling chemical and biological processes.^2,3 Energetic errors originate from the approximate modeling of the potential energy of a given configuration of a system. In computer-aided drug design, we are typically limited to the use of force field models, which treat molecules as point charges bound by spring-like potentials and Lennard-Jones interactions. The benefit of using force fields is obvious: speed of computation. Their weaknesses can be severe: sensitivity to parameters, neglect of electronic degrees of freedom (polarization), and inability to model bond breaking are some of them. Nonetheless, given enough sampling, force fields can be used to model processes including protein folding and protein–ligand association.⁴⁻⁶

Since approximate energy models can sometimes work well and other times fail, we began to develop methods that estimate potential energy modeling errors on the fly.^7,8 Of particular interest, we studied how potential energy modeling errors propagate in statistical ensembles and found an interesting phenomenon: sampling can actually diminish the effects of energetic errors. That is, imprecise potential energy functions can still be used to make accurate predictions in computational chemistry if the statistical ensemble is adequately sampled. Our model experiment is set up as the following: imagine you sample a potential energy surface by estimating the energy at random points with an approximate energy function, which has a known precision of 1.0 kcal/mol. You continue sampling randomly until your free energy estimate converges. How does the 1.0 kcal/mol precision affect this free energy evaluation?

We can model this situation through Monte Carlo error propagation, in which a distribution of free energy estimates is constructed by repeatedly evaluating the free energy after perturbing the microstate energies according to probability density functions describing their inherent imprecision. In eq 1, the expression for free energy in the discrete canonical ensemble, we add a perturbation to each microstate energy, which is randomly drawn from a normal distribution centered at zero with a standard deviation of 1.0 kcal/mol (here we use the notation N(μ,σ) to mean a random variable from a normal distribution with mean μ and standard deviation σ). Thus, we assume in this example that each microstate has no systematic error, and 1.0 kcal/mol random error representing energy model imprecision. After evaluating the free energy many times with different random microstate energy perturbations, the standard deviation of the distribution of free energies yields an estimate of uncertainty in free energy.

1

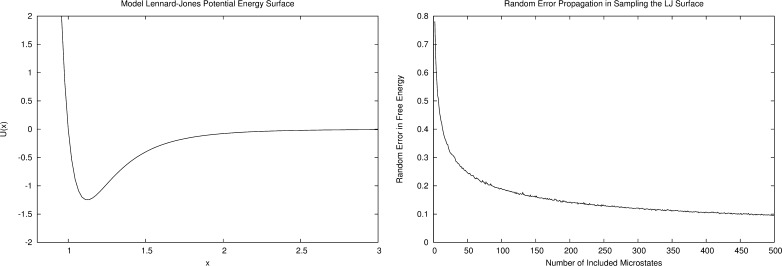
We performed this experiment on the Lennard-Jones surface of Figure 1a. The C++ code for this simulation is available on the Internet at http://www.merzgroup.org. What we found was that, as we add more randomly selected microstates to our statistical ensemble, each with an energy modeled with a precision of 1.0 kcal/mol, the uncertainty in free energy decreases (Figure 1b). With one included microstate, we find the trivial result that the uncertainty in free energy is 1.0 kcal/mol. As 1 to 50 random microstates are added, the free energy uncertainty decreases dramatically. This suggests that any computational model that uses a single configuration to estimate free energies will contain the maximum amount of error from the approximate energy function, but one that samples additional independent configurations will benefit from this sampling–uncertainty buffering effect, which minimizes uncertainty from energy function errors. In addition to converging toward the free energy value, increased sampling provides a secondary effect of buffering energy modeling errors. This finding led us to propose a free energy estimation protocol in which independent samples taken from MD or MC simulations are clustered by structure and then averaged over to produce minimum-uncertainty free energy differences between clusters.

Figure 1.

(a) Lennard-Jones potential energy surface used in our computational experiment. (b) Standard deviation of free energy estimations (kcal/mol units) at each ensemble size. Each microstate included in each ensemble is modeled with a potential energy function with a precision of 1.0 kcal/mol.

We applied this analysis to a real biological system, the T4-lysozyme L99A mutant, which is an excellent model system for studying protein–ligand interactions.⁹ After an exhaustive grid-based conformational sampling of each ligand inside a rigid, optimized binding site, we estimated the uncertainties associated with each protein–ligand complex microstate energy based on our previous analyses of potential energy model errors.^7,8 We then evaluated the free energies of binding using a variable number of microstates in the protein–ligand complex ensemble (Figure 2). As with the Lennard-Jones system, we found that using single microstates led to the maximum free energy errors, but averaging over a few microstates led to dramatically decreased uncertainties in free energy. The details of this work will be provided in an upcoming publication.¹⁰

Figure 2.

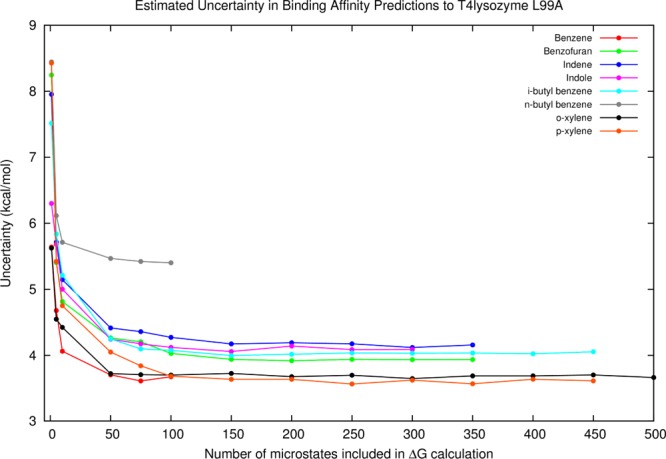
Uncertainties (standard deviation) in calculated free energies of binding for different binders to T4-lysozyme L99A at different ensemble sizes. The ff99SB force field and generalized Born solvent model were used as the energy model, and units are in kcal/mol. As sampling increases, the expected error in free energy is diminished.

Our finding was rooted in error analysis applied to statistical mechanics, but variants of our observation are found elsewhere, both inside and outside of chemical modeling. Charifson and later Wang demonstrated how using a consensus of multiple scoring functions outperforms single scoring functions in binding affinity estimation.^11,12 In the statistical modeling and machine learning communities, the use of ensemble methods like bootstrap aggregation (bagging) and boosting have become standard practice since they consistently decrease uncertainties in predictions.¹³ Genheden and Ryde recommend using multiple independent MD simulations to enhance the precision of MM/PBSA results.¹⁴

We believe that computer-aided drug design would benefit greatly from a better understanding of how modeling errors arise and propagate. Such knowledge might inspire new algorithms that intrinsically minimize uncertainties, such as the one mentioned here. In addition, the ability to routinely estimate our modeling uncertainties would open the door to using standard statistical tests and, importantly, let us generate quantitative estimates of confidence in our predictions. Our published methods for quantitative error estimation depend on knowledge of potential energy model performance, but the sampling-uncertainty buffering effect suggests a general procedure that could be implemented as a posthoc correction to current end-point methods for improved precision. Two other procedures, bootstrapping and consensus scoring, should also be more commonly utilized in our prediction models to both increase precision and estimate uncertainties. The benefits of all three procedures originate from the use of ensembles (in configuration, measurement, or model space) larger than N = 1. Perhaps this could be a new mantra for computer-aided drug design: “use numbers to your advantage.”

This work was funded by the National Institutes of Health (GM044974 and GM066689 to K.M.M., and AI093459 to W.Y.).

Views expressed in this editorial are those of the author and not necessarily the views of the ACS.

The authors declare no competing financial interest.

Funding Statement

National Institutes of Health, United States