Skip to main content
PMC home page
Plant Physiology logoLink to Plant Physiology
. 2013 Oct 23;163(4):1558–1567. doi: 10.1104/pp.113.228262

Wide-Angle X-Ray Scattering and Solid-State Nuclear Magnetic Resonance Data Combined to Test Models for Cellulose Microfibrils in Mung Bean Cell Walls1

Roger H Newman 1,2,*, Stefan J Hill 1,2, Philip J Harris 1,2
PMCID: PMC3846134  PMID: 24154621

Peak shapes in an x-ray diffractogram of primary cell walls indicated 18-chain microfibrils with mixed cross-sectional shapes and occasional twinning, consistent with a cellulose-synthesizing complex assembled from six CESA trimers.

Abstract

A synchrotron wide-angle x-ray scattering study of mung bean (Vigna radiata) primary cell walls was combined with published solid-state nuclear magnetic resonance data to test models for packing of (1→4)-β-glucan chains in cellulose microfibrils. Computer-simulated peak shapes, calculated for 36-chain microfibrils with perfect order or uncorrelated disorder, were sharper than those in the experimental diffractogram. Introducing correlated disorder into the models broaden the simulated peaks but only when the disorder was increased to unrealistic magnitudes. Computer-simulated diffractograms, calculated for 24- and 18-chain models, showed good fits to experimental data. Particularly good fits to both x-ray and nuclear magnetic resonance data were obtained for collections of 18-chain models with mixed cross-sectional shapes and occasional twinning. Synthesis of 18-chain microfibrils is consistent with a model for cellulose-synthesizing complexes in which three cellulose synthase polypeptides form a particle and six particles form a rosette.

Cellulose is unique among plant polysaccharides, in that it is synthesized as microfibrils rather than individual chains. In land plants (embryophytes) and charophycean green algae, each microfibril emerges from a rosette of six particles on the plasma membrane, so it is reasonable to assume that a microfibril contains a multiple of six (1→4)-β-glucan chains, but the value of that multiple remains uncertain. Herth (1983) suggested that each particle contains six cellulose synthase (CESA) polypeptides and that each CESA polypeptide synthesizes a single chain, so that each microfibril contains 36 chains. Scheible et al. (2001) published a representation of a 36-CESA rosette as a hexagon of hexagons, and similar representations have appeared in recent reviews (Bessueille and Bulone, 2008; Mutwil et al., 2008; Taylor, 2008; Guerriero et al., 2010). A 36-CESA rosette was compatible with most descriptions of the microfibrils in primary cell walls up to the time of the Delmer (1999) review. The larger microfibril dimensions reported for some secondary walls have been attributed to aggregation, e.g. cellulose synthesized by raft-like structures of rosettes rather than individual rosettes (Guerriero et al., 2010). However, a growing number of studies of primary cell walls have indicated microfibrils of 24 to 30 chains (Carpita, 2011; Thomas et al., 2013a) or possibly 18 chains (Guerriero et al., 2010), or even fewer (Niimura et al., 2010). No single instrumental technique is capable of measuring microfibril cross-sectional dimensions with sufficient precision to test these alternatives. This paper explores the use of a combination of two complementary techniques.

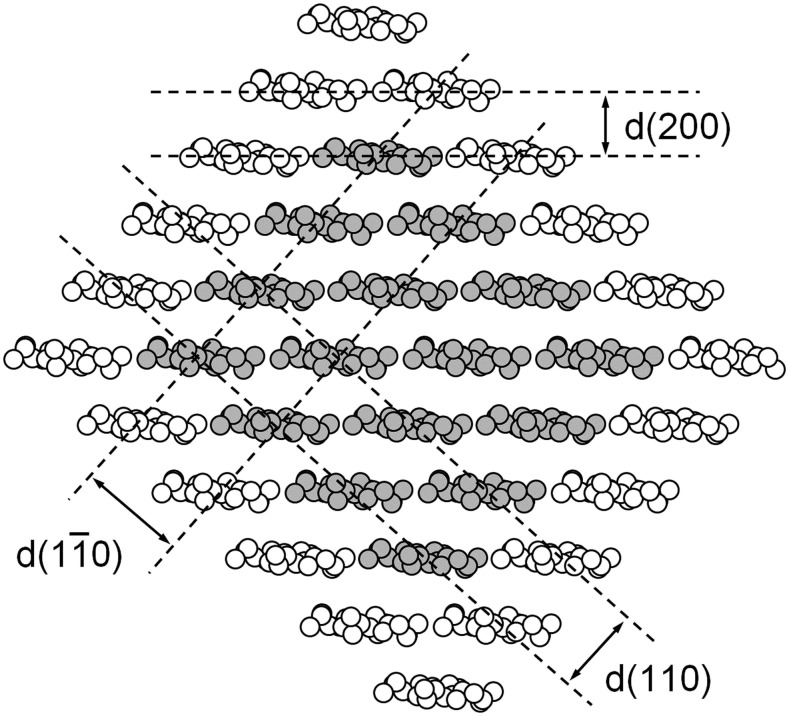
All of the available instrumental techniques for estimating the number of chains per microfibril depend on assumptions concerning the cross-sectional shape of a typical microfibril. Atomic force microscopy (AFM) can be used to measure the thickness of a microfibril deposited on glass or a mica plate (Davies and Harris, 2003; Niimura et al., 2010), but the probe tip is usually too blunt to provide precise information about the width of a microfibril. Attempts at correcting for probe tip dimensions can give nonsensical answers (Kirby et al., 2006). Small-angle neutron scattering can be used to determine a mean center-to-center distance for packing of microfibrils in a dry sample, and this distance is approximately equal to the microfibril diameter if the microfibrils have circular cross sections (Thomas et al., 2013b). The relative strengths of solid-state 13C NMR signals can be used to determine the mean number of (1→4)-β-glucan chains in the (200) crystal planes of the cellulose Iβ crystal form (Fig. 1), and this number can be used to calculate the number of chains in a microfibril if a square cross-sectional shape is assumed (Newman, 1999). A square cross section exposes only (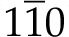Inline graphic)and (110) planes, with the exposed chains (Fig. 1, white) showing NMR signals displaced from those assigned to chains that are not exposed (Fig. 1, gray). The larger the number of chains in a microfibril, the smaller the relative contribution from the monolayer of exposed chains. The width of the (200) peak in a wide-angle x-ray scattering (WAXS) diffractogram can be used to estimate the number of (200) crystal planes, but the calculation requires selection of an appropriate ‘shape factor’ for the assumed cross-sectional shape. Here again, a square cross-sectional shape is sometimes assumed (Newman, 1999). Newman and Davidson (2004a) suggested combining WAXS and NMR as complementary techniques for characterizing the shapes of cellulose microfibrils. This paper takes that approach further by using computer simulation of WAXS peak shapes (Newman, 2008) rather than just the width of one WAXS peak.

Figure 1.

Figure 1.

Open in a new tab

Cross-sectional view of a 36-chain cellulose microfibril showing carbon and oxygen atoms but not hydrogen. Chains shaded gray are hydrogen bonded to two adjacent chains, and those shown as white are hydrogen bonded to just one adjacent chain. Broken lines indicate the three crystal planes that contribute the tallest peaks in a WAXS diffractogram, labeled according to the cellulose Iβ unit cell of Nishiyama et al. (2002).

Mung bean (Vigna radiata) primary cell walls were chosen because of the availability of exceptionally precise 13C NMR data for isotopically enriched samples (Bootten et al., 2004). A synchrotron beamline was used to obtain a WAXS diffractogram with a high signal-to-noise ratio for a specimen similar to that used in the NMR study, so that WAXS peak shapes were well defined. Microfibril models were constructed, and those conflicting with results from either or both of NMR and WAXS were rejected.

RESULTS

WAXS Peak Assignments

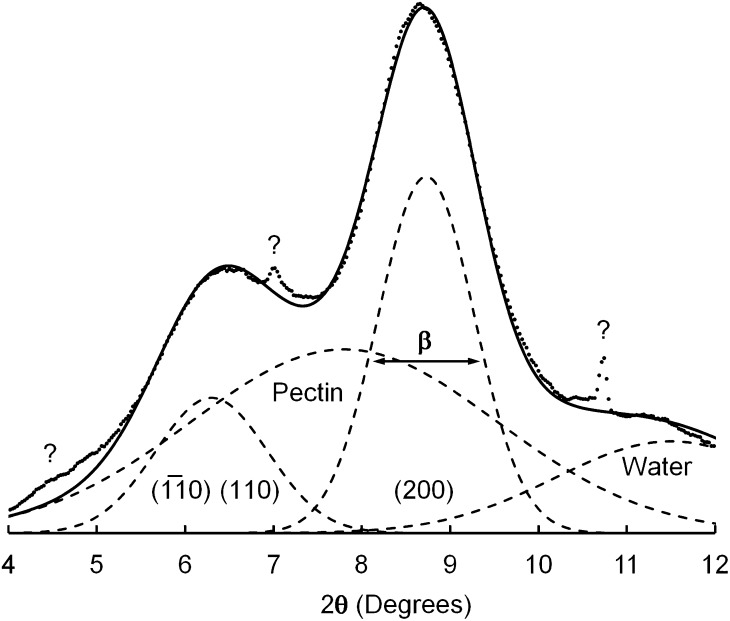
The specimen was prepared by stacking dried films, so that the microfibrils were mostly confined to planes normal to the x-ray beam. The experimental diffractogram (Fig. 2, dots) was therefore dominated by equatorial reflections, peaks associated with the (hk0) planes illustrated in Figure 1. The tallest component appeared at a diffraction angle (2θ) of 8.7°, corresponding to a lattice spacing of 0.41 nm, and was assigned to the (200) planes of cellulose I. This lattice spacing was larger than typical values of approximately 0.39 nm reported for cellulose Iβ (Wada et al., 1997), but lattice expansion is commonly associated with cellulose crystallites having cross-sectional dimensions no more than a few nanometers (Ioelovich and Larina, 1999). A broader peak at 2θ = 6.3°, corresponding to a lattice spacing of 0.56 nm, was assigned to unresolved contributions from (110) and(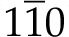Inline graphic)planes of cellulose I. Inability to resolve the contributions from (110) and from (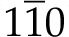Inline graphic) and planes is sometimes taken as evidence for a cellulose IV crystal structure, but computer simulations have shown that observation of a single peak is consistent with cellulose I crystallites having cross-sectional dimensions no more than a few nanometers (Newman, 2008). A weak but relatively sharp peak at 2θ = 7.0°, corresponding to a lattice spacing of 0.51 nm, was tentatively assigned to the (002) planes of cellulose I. This assignment was consistent with a unit cell dimension c = 1.02 nm (Nishiyama et al., 2002) and with the value of 2θ for a peak assigned to (004), observed outside the range plotted in Figure 2. An even sharper peak at 2θ = 10.7°, labeled with a question mark in Figure 2, was attributed to an unidentified impurity. Neither of the peaks labeled with question marks in Figure 2 was observed in a diffractogram of the adhesive tape alone.

Figure 2.

Figure 2.

Open in a new tab

WAXS diffractogram of mung bean cell walls (dots) after subtraction of the diffractogram of adhesive tape, for radiation of wavelength 0.06199 nm. Dashed lines represent four best-fit component peaks, and a solid line represents the sum of those components.

The experimental diffractogram was deconvoluted to give four component Gaussian peaks, the two contributions from cellulose as discussed above and two contributions from other substances. The four components are represented by dashed lines in Figure 2. A component at 2θ = 11.3°, corresponding to a lattice spacing of 0.32 nm, was assigned to water. Liquid water shows a WAXS peak at a lattice spacing of 0.31 nm (Hura et al., 2003), and adsorbed water contributes a peak at a similar lattice spacing even when it is present at low levels in plant tissue at equilibrium with laboratory air (Hill et al., 2010). A relatively broad component at 2θ = 7.9°, corresponding to a lattice spacing of 0.45 nm, was assigned to amorphous polysaccharides. Such polysaccharides included xyloglucan, for which a published diffractogram includes a broad peak corresponding to a lattice spacing of 0.51 nm (Taylor and Atkins, 1985). Solvents of pectic polysaccharides were avoided in preparation of the specimen, because removal of noncellulosic polysaccharides can cause sharpening of the (200) peak in a WAXS diffractogram of primary cell walls (Wardrop, 1949). Removal of noncellulosic material might facilitate the aggregation of adjacent parallel microfibrils, so that they can coalesce into larger structures (Mühlethaler, 1967; Fernandes et al., 2011).

WAXS Diffractogram Peak Width

The component assigned to (200) planes (Fig. 2) had a full width at half height of β = 0.0225 radians (1.29°). The number of (200) planes can be estimated from the value of β (in radians) using the Scherrer relationship (Murdock, 1930):

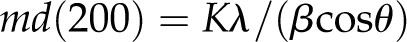graphic file with name pp_228262_E1.jpg (1)

Here, m is the total number of (200) planes, λ is the wavelength of the radiation, and K is a shape factor, which depends on the cross-sectional shape of the crystallite. A value K = 0.9 was selected as typical of the values suggested by Murdock (1930). Equation 1 gives a microfibril thickness of md(200) = 2.5 nm; so for a lattice spacing of d(200) = 0.41, as estimated above, m = 6.1.

If the mean number of (1→4)-β-glucan chains in a sheet is n, then the number of chains in a microfibril is mn. Newman and Davidson (2004a), in their study of cellulose microfibrils in florideophycean algae, used 13C solid-state NMR to obtain an estimate of n as follows. Cellulose microfibrils are not crystalline, in the strict definition of that word, because chains exposed on surfaces (Fig. 1, white) are not identical to those contained in the crystalline core (Fig. 1, gray). A 13C NMR spectrum shows distinct chemical shifts for C-4 in chains exposed on surfaces (approximately 84 parts per million [ppm]) or contained within the interior of a crystallite (approximately 89 ppm; Newman and Davidson, 2004b). The difference in chemical shift has been attributed to differences in molecular conformation, resulting from disruption of interchain hydrogen bonding at crystal surfaces (Newman and Davidson 2004b). One chain is exposed at each edge of a sheet, and there are n − 2 chains contained in the interior of a sheet of n chains, so:

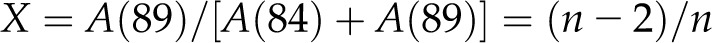graphic file with name pp_228262_E2.jpg (2)

where A represents the area under the relevant peak. This can be rearranged to:

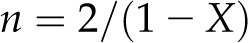graphic file with name pp_228262_E3.jpg (3)

Bootten et al. (2004) described NMR studies of a sample of mung bean cell walls similar to that studied in this work. They used proton spin relaxation parameters to separate a subspectrum of cellulose, measured the areas A(89) and A(84) of 13C NMR signals at 89 and 84 ppm, respectively, and reported X = 0.37. Substitution of X = 0.37 in Equation 3 gives n = 3.2, so the approximate number of chains in a microfibril is mn = 19.

While a combination of Equations 1 and 3 led to an estimate of mn = 19 for the mean number of chains in a microfibril, it must be emphasized that this was an approximate value. One of the weak points in the logic was the use of K = 0.9 in Equation 1. Murdock (1930) calculated values of K between 0.84 and 0.90 for different planes in a crystal of square cross-sectional shape, Scherrer’s original relationship used K = 0.94 (Murdock, 1930), and Ioyelovich (1991) rounded the value to K = 1.0 for studies of cellulose. This source of uncertainty alone means that the number of chains could be as low as 18 or as high as 21.

Uncertainties in the value of X, used in Equation 3, contributed to the uncertainty in the estimated number of chains. Bootten et al. (2004) used two different NMR methods to measure X and averaged data from three cell wall preparations, leading to an estimate of X = 0.37 ± 0.02. Consideration of this additional source of uncertainty indicated that the number of chains could be as low as 17 or as high as 22. While the (200) peak width did not provide a precise result, it was consistent with an 18-chain model and not consistent with a 36-chain model.

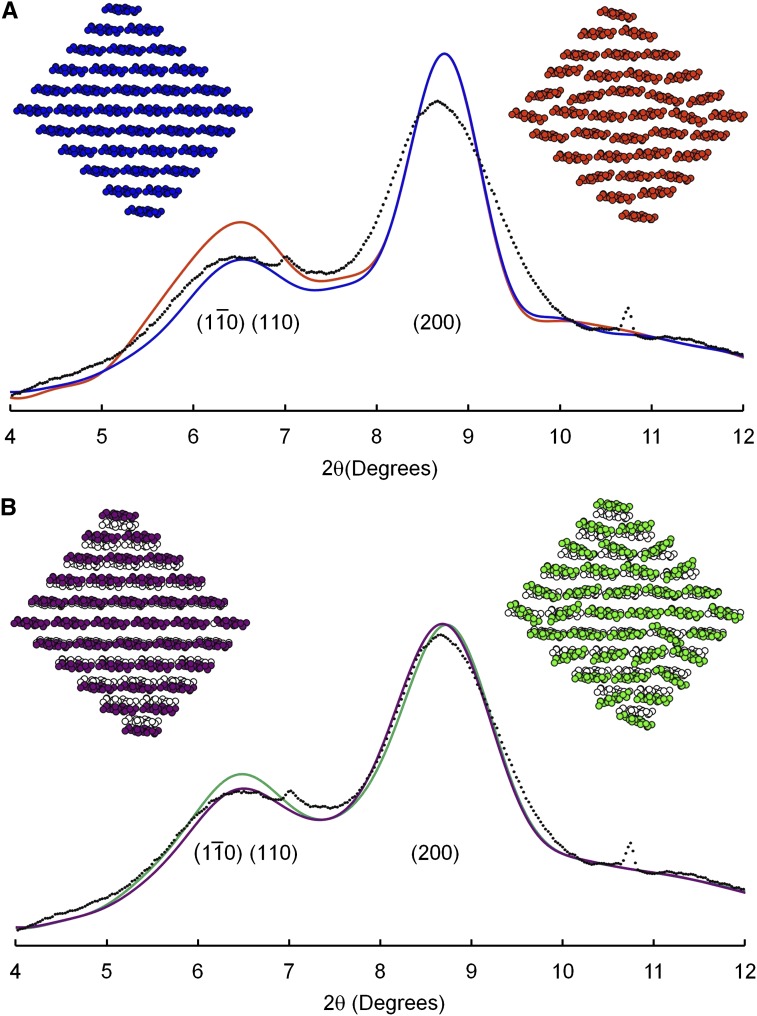
WAXS Diffractograms for 36-Chain Models

The cross-sectional shape in Figure 1 was chosen as an example of a 36-chain model with X = 0.44, which is considerably higher than the published value of X = 0.37 for mung bean cell walls as discussed above. The corresponding diffractogram was calculated by computer software described in “Materials and Methods” and was added to the two contributions from noncellulosic matter discussed in the previous section. The result (Fig. 3, blue line) was a poor fit to the peak shapes in the experimental data. In particular, the calculated (200) peak was considerably sharper than the experimental peak. The peak assigned to overlapping contributions from (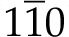Inline graphic) and (110) planes was likewise sharper than the corresponding peak in the experimental diffractogram, but this comparison presented a less conclusive test for the microfibril model because the calculated peak could have been broadened by increasing the input value of the unit-cell angle γ. Other 36-chain models were considered but not illustrated because the models with values of X closer to the experimental value of 0.37 showed even sharper (200) peaks in the calculated diffractograms, while the models that showed broadening of the (200) peak showed values of X even further from the experimental value.

Figure 3.

Figure 3.

Open in a new tab

WAXS diffractogram of mung bean cell walls (dots) after subtraction of the diffractogram of adhesive tape, for radiation of wavelength 0.06199 nm, and diffractograms calculated for a 36-chain microfibril model without disorder (blue) and with type 1 disorder (orange; A) and two models with type 2 disorder as described in the text (purple and green; B).

Defective molecular packing can broaden WAXS peaks. This possibility can sometimes be tested by measuring the width of the (400) peak in a diffractogram of a cellulose fiber (Ioyelovich, 1991; Thomas et al., 2013a), but, in this case, the relevant peak could not be resolved from other broad peaks in the neighborhood. Instead, the possibility of defective molecular packing was tested by introducing defects into model microfibrils and calculating diffractogram.

The most obvious deviation from a perfect crystal structure is the occurrence of mixtures of two crystal forms, cellulose Iα and Iβ, in plant cell walls. These two crystal forms differ primarily in the longitudinal displacement of neighboring sheets of chains (Nishiyama et al., 2002, 2003). When the two crystal structures are viewed in cross section, the two arrangements of chains are similar. The equatorial WAXS peaks are therefore similar (Wada et al., 1997). Precise x-ray measurements have revealed small difference in the spacings between sheets of chains, with the spacing greater by 0.004 nm for celluloses rich in Iα relative to those rich in Iβ (Imai et al., 1997; Langan et al., 2005). The consequences for primary-wall cellulose were assessed by calculating WAXS diffractograms for the 36-chain model in Figure 1, but with d(200) adjusted by ± 0.002 nm. The two diffractograms were then added together, to simulate results for a mixture of equal numbers of microfibrils packed on Iα and Iβ lattices. The resultant diffractogram (not shown) was indistinguishable from that shown in blue in Figure 3a.

Nishiyama et al. (2012) calculated diffraction patterns for twisted microfibrils, such as those illustrated by Fernandes et al. (2011), and showed that the peaks were broader than those calculated for untwisted microfibrils. The broadening was attributed, at least in part, to changes in lattice parameters arising from energy minimization for the twisted model. Energy was not minimized in this work, so the consequences of twist could not be explored. The possibility of broadening through changes in lattice parameters will be discussed below.

Random disorder was introduced into the lattices of model microfibrils. The simplest kind of lattice disorder is known as disorder of the first kind, or uncorrelated disorder (Eads and Millane, 2001). This type of disorder was imposed on 36-chain microfibrils by repacking the chains to introduce random voids. Averaging the calculated diffractograms for collections of such microfibrils showed negligible changes in the width of the (200) peak, so the results are not illustrated. Uncorrelated disorder was also introduced by making random changes in the rotation of each chain around its axis, and displacement of each axis relative to a perfect lattice, with the consequences for each chain considered independent of consequences for neighboring chains. Specifically, chains were rotated about their axes, with a sd of 8°, chains were displaced above and below sheets, with a sd of 0.04 nm, and chains were displaced from side to side within sheets, with a sd of 0.02 nm. Ten such models were constructed. One is colored orange in Figure 3A. The three sds were chosen so that they were just large enough to cause unrealistically small separations between the atoms of neighboring chains. The orange model in Figure 3A shows several examples of chains that have been brought into such close proximity that the hydrogen atoms (not shown) would have to share the same positions in space. Despite the unrealistic level of disorder, the calculated (200) peak was not detectably broadened. The orange curve in Figure 3A shows an average of the diffractograms for all 10 model microfibrils. The relative heights of peaks were affected but not their widths.

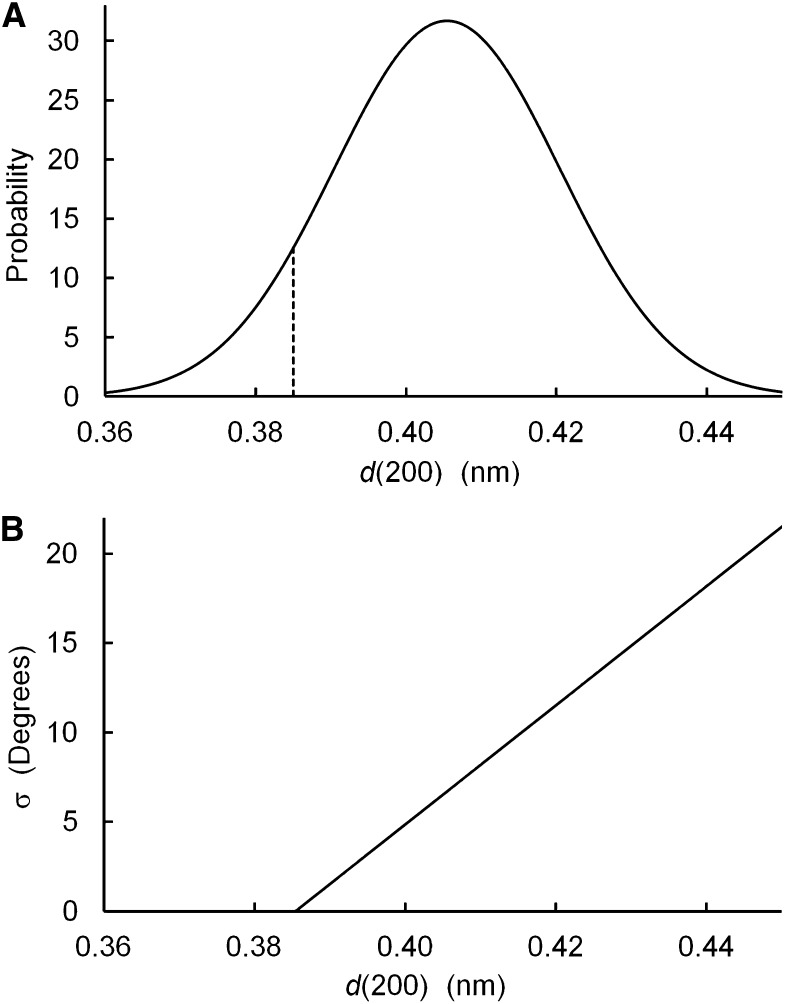
Peak broadening was achieved by introducing correlated disorder, disorder of the second kind. The value of d(200) was allowed to differ between microfibrils but held constant within each microfibril, with values determined by a normal distribution (Fig. 4A). The disorder was therefore correlated in the sense that if one value of d(200) was altered within a microfibril, then all had to be altered. Ten such 36-chain models were constructed. The purple model in Figure 3B shows one such model, superimposed on the unaltered model shown in black and white. The sd of d(200) was 0.015 nm, chosen so that the average of the 10 diffractograms (Fig. 3B, purple line) showed broadening of the (200) peak to a width similar to that of the experimental diffractogram. In the second step, the chains were allowed to rotate around their axis, with rotation angles determined by a normal distribution. The sd of the rotation angle was a function of d(200; Fig. 4B), defined so that in microfibril models that were tightly packed, i.e. those with d(200) = 0.385, there was no disorder in the chain rotation angle. Disorder was permitted for larger values of d(200), perhaps providing a mechanism for spreading the sheets of chains further apart, in that disordered layers seem less likely to pack together efficiently. Correlated differences in the degree of disorder and the value of d(200) might be associated with differences in the degree of twisting of microfibrils around their axes, as illustrated by Fernandes et al. (2011).

Figure 4.

Figure 4.

Open in a new tab

Parameters used to introduce type 2 disorder into model microfibrils: probability of a given value of d(200) in a microfibril (A) and sd of the chain rotation angle (B).

Ten such 36-chain models were constructed, including the green model in Figure 3B. The average of the 10 calculated diffractograms (Fig. 3B, green line) showed no further broadening beyond that shown by the purple line, the first step in the introduction of correlated disorder, in which values of d(200) were correlated between pairs of sheets within a microfibril but randomized between microfibrils.

Other models for disorder were considered, involving distributions of spacings within microfibrils rather than between microfibrils. For example, the spacings between chains might increase with radial distance from the center of the microfibril or the value of d(200) might be a function of the number of chains in the relevant layers. While those models for disorder might well contribute to peak broadening, calculations indicated asymmetric peak shapes that were quite unlike the near-Gaussian shapes observed in the experimental diffractogram.

While Figure 3B shows that it is possible to broaden the (200) peak to the width seen in an experimental diffractogram, it is important to note that the magnitude of the disorder is unrealistic. The distribution of values of d(200; Fig. 4A) has 8% of microfibrils with d(200) < 0.385 nm. This is the value of d(200) measured for cellulose Iβ in the relatively large crystallites found in tunicates, when those crystallites are cooled to 100 K (Langan et al., 2005). It seems unlikely that the relatively narrow microfibrils of primary-wall cellulose would contain sheets of chains that are even more densely packed than in tunicate cellulose. Figure 4A also shows 10% of microfibrils with d(200) > 0.425 nm, an increase by 0.04 nm relative to d(200) for tunicate cellulose. Such a large increase of the interplanar spacing seems unlikely, considering that adjacent (200) planes are held together by short-range nonbonded interactions. The 36-chain models therefore failed to provide good matches to either NMR or WAXS experimental data.

WAXS Diffractograms for 24- and 18-Chain Models

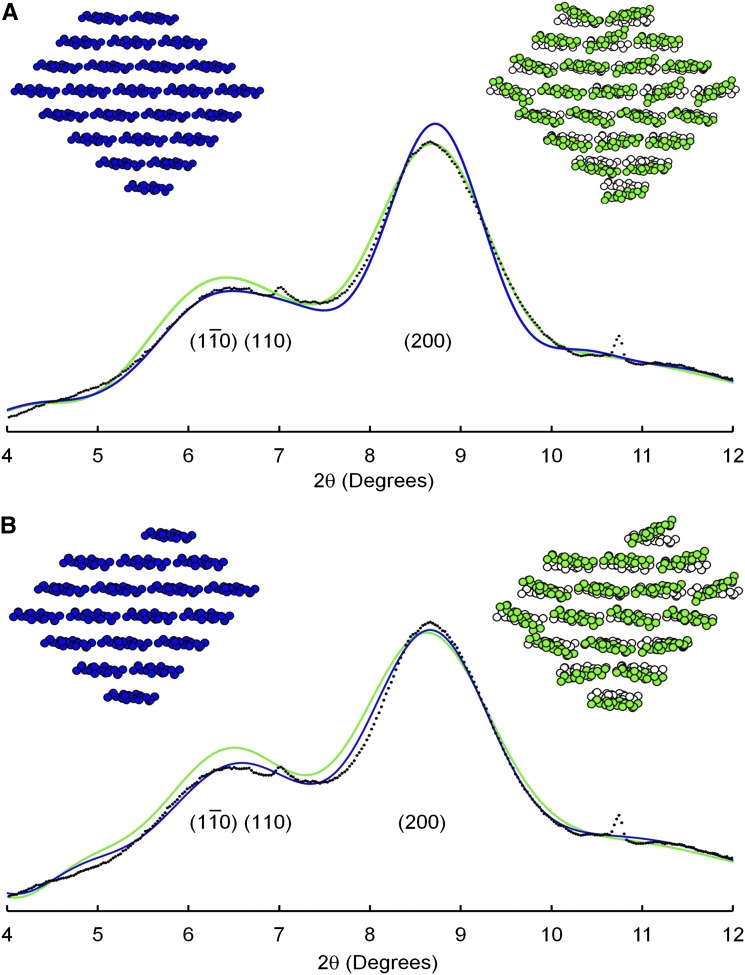
The 24-chain microfibril shown as blue in Figure 5A was chosen as an example of molecular packing with X = 0.37, indistinguishable from the experimental value. The calculated diffractogram (Fig. 5A, blue line) shows a (200) peak that is too sharp, relative to the experimental diffractogram. Thomas et al. (2013b) considered the same 24-chain model in their study of celery (Apium graveolens) collenchyma cellulose, using the Scherrer equation rather than calculating the full diffractogram as in this work. The Scherrer equation indicated that the WAXS diffractogram for the 24-chain model would be broader than the experimental diffractogram. Thomas et al. (2013b) also considered a stack of eight four-chain planes, for which the Scherrer equation indicated a reasonable fit to experimental data. The full calculations (not illustrated) showed instead a diffractogram in which the (200) peak was even sharper than that represented by the blue line in Figure 5A. These comparisons between the Scherrer equation and full numerical calculations illustrate the advantage of the latter approach to interpretation of WAXS diffractograms.

Figure 5.

Figure 5.

Open in a new tab

WAXS diffractogram of mung bean cell walls (dots) after subtraction of the diffractogram of adhesive tape, for radiation of wavelength 0.06199 nm, and diffractograms calculated for 24-chain (A) and 18-chain microfibril models (B) without disorder (blue) or with Type 2 disorder (green).

Calculated diffractograms for 24-chain models can be broadened by introducing correlated disorder (Fig. 5A, green model) as in the case of the 36-chain microfibrils (Fig. 3B). Using the same level of disorder as for 36-chain models led to the green line in Figure 5A, with a (200) peak slightly broader than the experimental curve. Disordered 24-chain models were therefore consistent with both NMR and WAXS experimental data.

The 18-chain microfibril shown as blue in Figure 5B has X = 0.33, a little lower than the experimental value, and the calculated diffractogram (Fig. 5B, blue line) shows an almost perfect match with the experimental diffractogram. The calculated (200) peak is so broad that introducing correlated disorder (Fig. 5B, green model and line) shows little further broadening, even for an unrealistically large magnitude of disorder as discussed above.

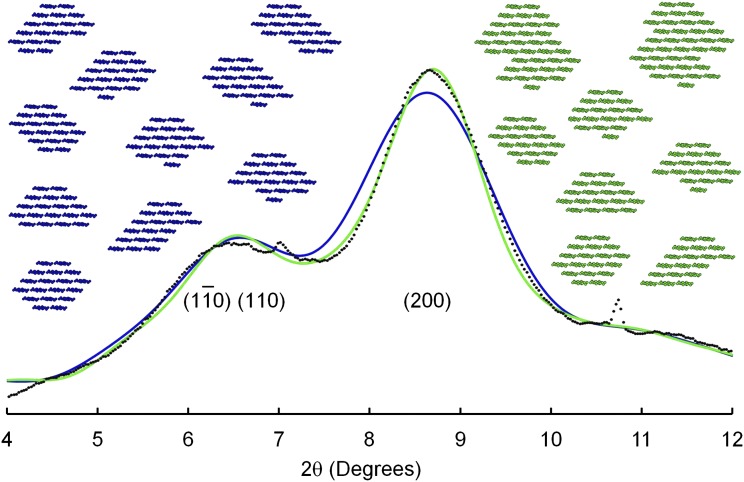
It seems unlikely that the chains emerging from a cellulose-synthesizing complex will always crystallize into identical cross-sectional shapes. The experimental results of Niimura et al. (2010) were consistent with mixtures of shapes, and no published work disproves the hypothesis of mixtures, so mixtures were considered. The 10 blue models in Figure 6 show 10 different cross-sectional shapes, all built from 18 chains. Values of X were in the range 0.28 to 0.44, with a mean value of 0.36, a value very similar to the experimental value. The diffractogram calculated for this collection (Fig. 6, blue) was similar to the experimental curve, except for broadening of the (200) peak. Two pairs of microfibrils were allowed to coalesce, as suggested by Thomas et al. (2013b) and as shown in the green models in Figure 6. This coalescence or twinning might arise through a pair of cellulose-synthesizing complexes traveling across the membrane in such close proximity that the emerging chains crystallize as a single microfibril. The value of X rose to 0.40, and the calculated (200) peak (Fig. 6, green line) sharpened to show a good fit to the experimental curve. Similar good fits (not shown) were obtained for other collections of discrete 18-chain microfibrils mixed with twinned microfibrils, and values of X were sometimes closer to the experimental value. The collection shown in Figure 6 was chosen for illustration because it included two hexagonal cross sections, both readily assembled from six submicrofibrils of three chains, such as might emerge from each of the six particles in a rosette.

Figure 6.

Figure 6.

Open in a new tab

WAXS diffractogram of mung bean cell walls (dots) after subtraction of the diffractogram of adhesive tape, for radiation of wavelength 0.06199 nm, and diffractograms calculated for mixtures of microfibril models, without twinning (blue) or with twinning (green).

Collections of 18-chain models, whether disordered or not, were therefore consistent with both NMR and WAXS experimental data.

DISCUSSION

Comparisons with Literature

Although the experimental work described in this paper was confined to mung bean cell walls, comparisons with literature data showed that the experimental NMR and WAXS data were typical of data published for the primary cell walls of other species.

Solid-state 13C NMR experiments, of similar design to those used for mung bean cell walls (Bootten et al., 2004), have been reported for the primary cell walls of nine other plant species (Newman et al., 1994, 1996; Koh et al., 1997; Ha et al., 1998; Smith et al., 1998; Thimm et al., 2002; Ratnayake et al., 2011). The median and mean values of X were 0.35 and 0.36, respectively, with a sd of 0.05. The value of X = 0.37 reported for mung bean cell walls (Bootten et al., 2004) was close to the mean value for the nine other species.

WAXS diffractograms have been published for the primary cell walls of blackberry (Rubus fruticosus; Lai-Kee-Him et al., 2002), celery (Thimm et al., 2002), carrot (Daucus carota; Georget et al., 1999), and strawberry (Fragaria spp.; Niimura et al., 2010). In all of those cases, the diffractograms showed broad peaks similar to the peaks in the diffractogram of mung bean cell walls. A WAXS diffractogram of celery collenchymal cellulose showed relatively sharp peaks (Thomas et al., 2013b). The sharpness might have been associated with the method of isolation of the cellulose, i.e. acid hydrolysis of noncellulosic matter followed by drying. Thomas et al. (2013b) discussed the possibility of aggregation of microfibrils under such conditions. Coalescence of cleaned microfibril surfaces could lead to twinning as illustrated in the green model of Figure 6, causing an increase in the mean microfibril thickness relative to the value for unprocessed cell walls.

Niimura et al. (2010) used AFM to measure thicknesses of 1 to 2 nm for microfibrils isolated from the primary walls of three species. Their results indicated microfibrils that were even thinner than the 18-chain models illustrated in Figure 6. It is not easy to reconcile their results with the NMR and WAXS results reviewed above. Further AFM experiments seem necessary to test the reliability of that method.

Chains per Microfibril

The 36-chain models did not provide good fits to the experimental data. While it was possible to broaden the WAXS diffractograms to match the experimental diffractograms, by introducing unrealistically high levels of correlated disorder, that approach was successful only for a model with an unacceptably high value of X = 0.44. Constructing models with values of X closer to the experimental value of 0.37 made it necessary to introduce even higher levels of correlated disorder to broaden the WAXS peaks.

While it was possible to construct 24-chain models that showed good fits to both NMR and WAXS data, it was necessary to assume an absence of twinning, coalescence of pairs of adjacent microfibrils for at least a portion of their length. The twinned microfibrils, or segments of microfibrils, would contain 48 chains and contribute relatively sharp peaks to the WAXS diffractograms. If twinning were to be introduced into collections of 24-chain microfibrils, the diffractograms would be sharpened and additional disorder would have to be introduced to account for the broadening observed in the experimental diffractogram. Twinning would also increase the mean value of X above the experimental value. The quality of the fits between calculated and experimental diffractograms should therefore be regarded with caution, until the level of twinning can be established. Experimental techniques such as small-angle X-ray scattering and small-angle neutron scattering have indicated aggregation of microfibrils in both primary and secondary cell walls (Fernandes et al., 2011; Thomas et al., 2013b), but those experiments have not provided quantitative information about the level of twinning within the aggregates.

The collections of 18-chain discrete and twinned microfibrils provided the most realistic fits to the experimental evidence. The diffractogram peak widths were already so broad that introducing uncorrelated or correlated disorder had little influence on peak shapes. Differences in the levels of twinning might account for small variations in peak widths between diffractograms of cell walls taken from different species.

Models for Cellulose-Synthesizing Complexes

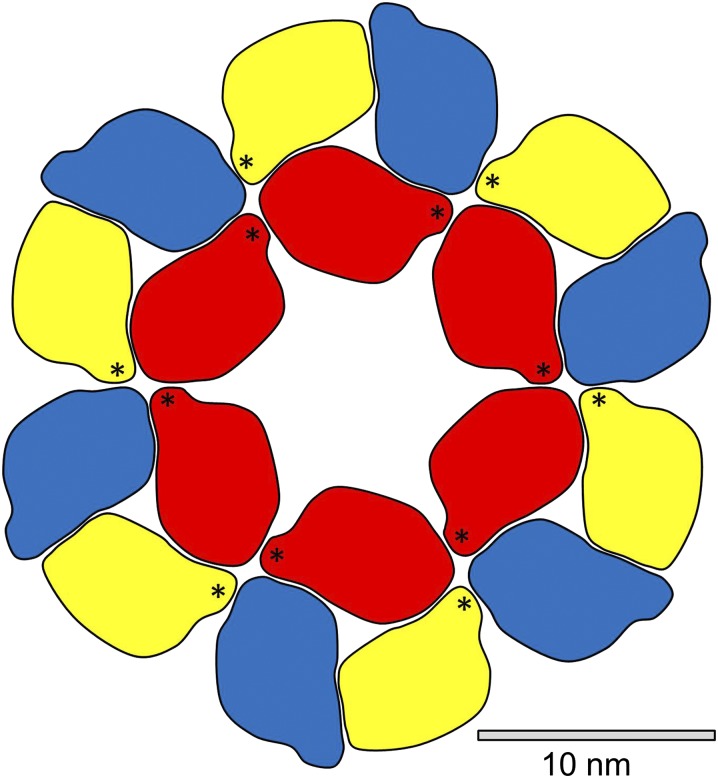
Cellulose-synthesizing complexes are visible as hexagonal rosettes of six particles when plant plasma membranes are examined using freeze-fracture electron microscopy. The diameters of the rosettes have been reported as between 25 and 30 nm (Lerouxel et al., 2006). Computer modeling has indicated that six CESA polypeptide molecules can be packed into a particle with a diameter of 12.6 nm (Sethaphong et al., 2013). Assembling six such particles in a hexagonal structure would result in a complex with a diameter of approximately 36 nm. This model is approximately 20% larger than complexes observed in experimental images.

Sethaphong et al. (2013) also used computer modeling to assemble a particle from three CESA polypeptides but did not attempt modeling of six such particles to make a rosette. A three-CESA particle is represented in stylized form in Figure 7, with the three components distinguished by red, yellow, and blue coloring. Five additional particles were added to Figure 7 to form a rosette of diameter 30 nm. This model shows a good fit to the rosettes seen in experimental images, e.g. an exceptionally detailed image of a rosette on a Eucalyptus tereticornis plasma membrane (Fujino and Itoh, 1998). The model in Figure 7 is based on an assumption that the particles can be packed as hard objects. Computer modeling will be needed to provide a more reliable picture of the interactions between adjacent particles and hence a more accurate estimate of the diameter of the rosette.

Figure 7.

Figure 7.

Open in a new tab

Representation of a cellulose-synthesizing complex assembled from 18 CESA polypeptides. Outlines were drawn around each CESA polypeptide in a detailed model of a three-CESA particle published by Sethaphong et al. (2013), and six such particles were assembled as hard objects. Stars mark plant-conserved regions.

It is possible to formulate simple rules for self-assembly of such a rosette, e.g. (1) red binds to yellow, yellow to blue, and blue to red within a particle and (2) red binds to red between particles and yellow binds to blue but neither yellow nor blue bind to red. The model shows two linkages between each pair of particles, where one linkage might be sufficient, so these three rules are not unique. Stars in the yellow and red CESAs of Figure 7 mark plant-conserved regions, which are thought to participate in the oligomerization of CESAs (Sethaphong et al., 2013). The plant-conserved regions are clearly well positioned for that role.

Scheible et al. (2001) and Timmers et al. (2009) have described models for self-assembling 36-CESA rosettes, likewise starting with three different types of CESA, but their models require additional rules to terminate growth at precisely 36 CESAs. In the 18-CESA model of Figure 7, growth is conclusively terminated because only blue CESAs are exposed on the outer edge of the rosette, and the potential inter-CESA linkage points of those blue CESAs are considered ineffective.

An x-ray crystallographic study of bacterial CESA has shown that a CESA polypeptide synthesizes a single glucan chain (Mazur and Zimmer, 2011), and computer modeling has indicated that a plant CESA polypeptide likewise contains a single active synthetic site (Sethaphong et al., 2013). The 18-CESA model illustrated in Figure 7 would therefore synthesize an 18-chain microfibril, consistent with the microfibrils illustrated in Figure 6.

In the discussion above, it has been assumed that all CESA polypeptides are actively involved in synthesizing (1→4)-β-glucan chains. It is possible that the channels in some of the CESA polypeptides become blocked, so that assembly of an 18-chain microfibril requires a cellulose-synthesizing complex containing more than 18 CESA polypeptides. Computer modeling will be needed to test whether it is possible to assemble more than 18 CESA polypeptides in a complex of the dimensions observed in electron microscopic images.

MATERIALS AND METHODS

Germinated seedlings of mung bean (Vigna radiata) were bought from a local store. The cotyledons, roots, and apical hook were removed, and the hypocotyls (5 g) were homogenized in 20 mm Tris-HCl buffer (pH 7.2; 10 mL) in a pestle and mortar. All procedures were carried out at 4°C. Breakage of the cells was monitored using bright-field microscopy after staining with Ponceau 2R, which stains cytoplasmic proteins red (Harris, 1983). The homogenate was centrifuged (1,800g; 5 min), and the pellet was washed twice by centrifugation and filtered onto nylon mesh (pore size, 11 μm). The cell walls on the mesh were washed with water until the filtrate was clear. The solvent was exchanged by successively washing with ethanol, methanol, and finally n-pentane. The suspension of cell walls was cast on a flat surface and stored over silica gel to dry as a film. This was examined histochemically for the presence of starch using bright-field microscopy after treating with a solution of iodine in potassium iodide (0.2 g iodine and 2 g potassium iodide in 100 mL water). No starch granules were detected.

Seven layers of the film of dried cell walls were stacked to prepare a specimen with an area density of 8 mg cm–2. The specimen was encased between two layers of Tesa 51408 adhesive tape (Beiersdorf AG). The manufacturer’s data sheet for the tape specified Kapton (35 μm thick) with a silicone adhesive backing (25-μm thick). The specimen was mounted so that the beam was normal to the plane of the stack of films.

WAXS patterns were collected on the small-angle X-ray scattering/WAXS beamline at the Australian Synchrotron. Radiation with a wavelength of 0.06199 nm was used. A Mar165-CCD detector (Rayonix LLC) was located 300 mm from the specimen. The beam size was 50 μm × 100 μm, and the detector pixel size was 0.158 mm. The exposure time was 10 s for each of 10 sampling points. The 10 datasets were averaged, and counts were averaged over arcs within a 60° segment on the area detector, extending from the beam stop, to produce a diffractogram, a plot of counts against the angle 2θ between transmitted and reflected rays. The width of each arc was approximately Δ(2θ) = 0.027°. A blank diffractogram was obtained by repeating the procedure for two layers of tape without cell walls. The blank diffractogram was subtracted from the experimental diffractogram to eliminate contributions from Kapton and silicone adhesive.

Computer simulations used the software described by Newman (2008). This software will be made available on request. The computer software summed the intensity of radiation scattered from each atom, allowing for differences in phase angles, and then rotated the model and repeated the calculation. A total of 359 orientations around the microfibril axis were considered for each value of 2θ, and the value of 2θ was increased from 3° to 12° in steps of 0.04°. Models for the (1→4)-β-glucan chains were constructed using atomic coordinates for cellulose Iβ (Nishiyama et al., 2002). Hydrogen atoms were omitted because the corresponding scattering factors were considered too low to justify the large increase in computing time that would be required. The chains were placed on a monoclinic lattice with unit cell parameters considered appropriate for plant cellulose (Newman, 2008): a = 0.816 nm, b = 0.808 nm, and γ = 96.5°. All of the chains were rotated –5° around their axes, relative to the rotation angles reported by Nishiyama et al. (2002), to improve the relative peak heights in the simulated diffractograms. It is too early to comment on whether this small deviation of the optimal rotation angles from published values is a feature of the packing of chains into microfibrils with relatively small cross-sectional dimensions, or at least of packing of chains into the monolayer exposed on the surface, or perhaps arose from a small distortion of the diffractogram by underlying contributions from noncellulosic matter. No value was required for the unit cell parameter c, because the computer software calculated contributions associated with (hk0) planes.

Acknowledgments

We thank Nigel Kirby and staff at the Small and Wide Angle Scattering Beamline at the Australian Synchrotron for assistance in obtaining the experimental data.

Glossary

CESA

cellulose synthase

AFM

atomic force microscopy

WAXS

wide-angle x-ray scattering

ppm

parts per million

References

  1. Bessueille L, Bulone V. (2008) A survey of cellulose biosynthesis in higher plants. Plant Biotechnol 25: 315–322 [Google Scholar]
  2. Bootten TJ, Harris PJ, Melton LD, Newman RH. (2004) Solid-state 13C-NMR spectroscopy shows that the xyloglucans in the primary cell walls of mung bean (Vigna radiata L.) occur in different domains: a new model for xyloglucan-cellulose interactions in the cell wall. J Exp Bot 55: 571–583 [DOI] [PubMed] [Google Scholar]
  3. Carpita NC. (2011) Update on mechanisms of plant cell wall biosynthesis: how plants make cellulose and other (1→4)-β-d-glycans. Plant Physiol 155: 171–184 [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Davies LM, Harris PJ. (2003) Atomic force microscopy of microfibrils in primary cell walls. Planta 217: 283–289 [DOI] [PubMed] [Google Scholar]
  5. Delmer DP. (1999) Cellulose biosynthesis: exciting times for a difficult field of study. Annu Rev Plant Physiol Plant Mol Biol 50: 245–276 [DOI] [PubMed] [Google Scholar]
  6. Eads JL, Millane RP. (2001) Diffraction by the ideal paracrystal. Acta Crystallogr A 57: 507–517 [DOI] [PubMed] [Google Scholar]
  7. Fernandes AN, Thomas LH, Altaner CM, Callow P, Forsyth VT, Apperley DC, Kennedy CJ, Jarvis MC. (2011) Nanostructure of cellulose microfibrils in spruce wood. Proc Natl Acad Sci USA 108: E1195–E1203 [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Fujino T, Itoh T. (1998) Changes in the three dimensional architecture of the cell wall during lignification of xylem cells in Eucalyptus tereticornis. Holzforsch 52: 111–116 [Google Scholar]
  9. Georget DMR, Cairns P, Smith AC, Waldron KW. (1999) Crystallinity of lyophilised carrot cell wall components. Int J Biol Macromol 26: 325–331 [DOI] [PubMed] [Google Scholar]
  10. Guerriero G, Fugelstad J, Bulone V. (2010) What do we really know about cellulose biosynthesis in higher plants? J Integr Plant Biol 52: 161–175 [DOI] [PubMed] [Google Scholar]
  11. Ha MA, Apperley DC, Evans BW, Huxham IM, Jardine WG, Viëtor RJ, Reis D, Vian B, Jarvis MC. (1998) Fine structure in cellulose microfibrils: NMR evidence from onion and quince. Plant J 16: 183–190 [DOI] [PubMed] [Google Scholar]
  12. Harris PJ (1983) Cell walls. In JL Hall, AL Moore, eds, Isolation of Membranes and Organelles from Plant Cells. Academic Press, London, pp 25–53 [Google Scholar]
  13. Herth W. (1983) Arrays of plasma-membrane “rosettes” involved in cellulose microfibril formation of Spirogyra. Planta 159: 347–356 [DOI] [PubMed] [Google Scholar]
  14. Hill SJ, Kirby NM, Mudie ST, Hawley AM, Ingham B, Franich RA, Newman RH. (2010) Effect of drying and rewetting of wood on cellulose molecular packing. Holzforschung 64: 421–427 [Google Scholar]
  15. Hura G, Russo D, Glaeser RM, Head-Gordon T, Krack M, Parrinello M. (2003) Water structure as a function of temperature from x-ray scattering experiments and ab initio molecular dynamics. Phys Chem Chem Phys 5: 1981–1991 [Google Scholar]
  16. Imai T, Sugiyama J, Itoh T, Horii F. (1999) Almost pure Ia cellulose in the cell wall of Glaucocystis. J Struct Biol 127: 248–257 [DOI] [PubMed] [Google Scholar]
  17. Ioelovich M, Larina E. (1999) Parameters of crystalline structure and their influence on the reactivity of cellulose I. Cellul Chem Technol 33: 3–12 [Google Scholar]
  18. Ioyelovich MY. (1991) Supermolecular structure of native and isolated cellulose. Polym Sci 33: 1670–1676 [Google Scholar]
  19. Kirby AR, Ng A, Waldron KW, Morris VJ. (2006) AFM investigations of cellulose fibers in bintje potato (Solanum tuberosum L.) cell wall fragments. Food Biophys 1: 163–167 [Google Scholar]
  20. Koh TH, Melton LD, Newman RH. (1997) Solid-state 13C NMR characterization of cell walls of ripening strawberries. Can J Bot 75: 1957–1964 [Google Scholar]
  21. Lai-Kee-Him J, Chanzy H, Müller M, Putaux JL, Imai T, Bulone V. (2002) In vitro versus in vivo cellulose microfibrils from plant primary wall synthases: structural differences. J Biol Chem 277: 36931–36939 [DOI] [PubMed] [Google Scholar]
  22. Langan P, Sukumar N, Nishiyama Y, Chanzy H. (2005) Synchrotron X-ray structures of cellulose Ib and regenerated cellulose II at ambient temperature and 100 K. Cellulose 12: 551–562 [Google Scholar]
  23. Lerouxel O, Cavalier DM, Liepman AH, Keegstra K. (2006) Biosynthesis of plant cell wall polysaccharides - a complex process. Curr Opin Plant Biol 9: 621–630 [DOI] [PubMed] [Google Scholar]
  24. Mazur O, Zimmer J. (2011) Apo- and cellopentaose-bound structures of the bacterial cellulose synthase subunit BcsZ. J Biol Chem 286: 17601–17606 [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Mühlethaler K. (1967) Ultrastructure and formation of plant cell walls. Annu Rev Plant Physiol 18: 1–24 [Google Scholar]
  26. Murdock CC. (1930) The form of the x-ray diffraction bands for regular crystals of colloidal size. Phys Rev 35: 8–23 [Google Scholar]
  27. Mutwil M, Debolt S, Persson S. (2008) Cellulose synthesis: a complex complex. Curr Opin Plant Biol 11: 252–257 [DOI] [PubMed] [Google Scholar]
  28. Newman R, Ha MA, Melton LD. (1994) Solid-state 13C NMR investigation of molecular ordering in the cellulose of apple cell walls. J Agric Food Chem 42: 1402–1406 [Google Scholar]
  29. Newman RH. (1999) Estimation of the lateral dimensions of cellulose crystallites using 13C NMR signal strengths. Solid State Nucl Magn Reson 15: 21–29 [DOI] [PubMed] [Google Scholar]
  30. Newman RH. (2008) Simulation of x-ray diffractograms relevant to the purported polymorphs cellulose IVI and IVII. Cellulose 15: 769–778 [Google Scholar]
  31. Newman RH, Davidson TC. (2004a) Crystalline forms and cross-sectional dimensions of cellulose microfibrils in the Florideophyceae (Rhodophyta). Bot Mar 47: 490–495 [Google Scholar]
  32. Newman RH, Davidson TC. (2004b) Molecular conformations at the cellulose-water interface. Cellulose 11: 23–32 [Google Scholar]
  33. Newman RH, Davies LM, Harris PJ. (1996) Solid-state 13C nuclear magnetic resonance characterization of cellulose in the cell walls of Arabidopsis thaliana leaves. Plant Physiol 111: 475–485 [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Niimura H, Yokoyama T, Kimura S, Matsumoto Y, Kuga S. (2010) AFM observation of ultrathin microfibrils in fruit tissues. Cellulose 17: 13–18 [Google Scholar]
  35. Nishiyama Y, Johnson GP, French AD. (2012) Diffraction from nonperiodic models of cellulose crystals. Cellulose 19: 319–336 [Google Scholar]
  36. Nishiyama Y, Langan P, Chanzy H. (2002) Crystal structure and hydrogen-bonding system in cellulose Iβ from synchrotron x-ray and neutron fiber diffraction. J Am Chem Soc 124: 9074–9082 [DOI] [PubMed] [Google Scholar]
  37. Nishiyama Y, Sugiyama J, Chanzy H, Langan P. (2003) Crystal structure and hydrogen bonding system in cellulose Iα from synchrotron x-ray and neutron fiber diffraction. J Am Chem Soc 125: 14300–14306 [DOI] [PubMed] [Google Scholar]
  38. Ratnayake RMS, Sims IM, Newman RH, Melton LD. (2011) Effects of cooking on the cell walls (dietary fiber) of ‘Scarlet Warren’ winter squash (Cucurbita maxima) studied by polysaccharide linkage analysis and solid-state 13C NMR. J Agric Food Chem 59: 7186–7193 [DOI] [PubMed] [Google Scholar]
  39. Scheible WR, Eshed R, Richmond T, Delmer D, Somerville C. (2001) Modifications of cellulose synthase confer resistance to isoxaben and thiazolidinone herbicides in Arabidopsis Ixr1 mutants. Proc Natl Acad Sci USA 98: 10079–10084 [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Sethaphong L, Haigler CH, Kubicki JD, Zimmer J, Bonetta D, DeBolt S, Yingling YG. (2013) Tertiary model of a plant cellulose synthase. Proc Natl Acad Sci USA 110: 7512–7517 [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Smith B, Harris PJ, Melton LD, Newman RH. (1998) Crystalline cellulose in hydrated primary cell walls of three monocotyledons and one dicotyledon. Plant Cell Physiol 39: 711–720 [Google Scholar]
  42. Taylor IEP, Atkins EDT. (1985) X-ray diffraction studies on the xyloglucan from tamarind (Tamarindus indica) seed. FEBS 181: 300–302 [Google Scholar]
  43. Taylor NG. (2008) Cellulose biosynthesis and deposition in higher plants. New Phytol 178: 239–252 [DOI] [PubMed] [Google Scholar]
  44. Thimm JC, Burritt DJ, Sims IM, Newman RH, Ducker WA, Melton LD. (2002) Celery (Apium graveolens) parenchyma cell walls: cell walls with minimal xyloglucan. Physiol Plant 116: 164–171 [DOI] [PubMed] [Google Scholar]
  45. Thomas LH, Altaner CM, Jarvis MC. (2013a) Identifying multiple forms of lateral disorder in cellulose fibres. J Appl Cryst 46: 972–979 [Google Scholar]
  46. Thomas LH, Forsyth VT, Sturcová A, Kennedy CJ, May RP, Altaner CM, Apperley DC, Wess TJ, Jarvis MC. (2013b) Structure of cellulose microfibrils in primary cell walls from collenchyma. Plant Physiol 161: 465–476 [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Timmers J, Vernhettes S, Desprez T, Vincken JP, Visser RG, Trindade LM. (2009) Interactions between membrane-bound cellulose synthases involved in the synthesis of the secondary cell wall. FEBS Lett 583: 978–982 [DOI] [PubMed] [Google Scholar]
  48. Wada M, Okano T, Sugiyama J. (1997) Synchrotron-radiated x-ray and neutron diffraction study of native cellulose. Cellulose 4: 221–232 [Google Scholar]
  49. Wardrop AB. (1949) Micellar organisation in primary cell walls. Nature 164: 366. [DOI] [PubMed] [Google Scholar]

Articles from Plant Physiology are provided here courtesy of Oxford University Press

RESOURCES