Abstract
Epigenetic effects attributed to genomic imprinting are increasingly recognized as an important source of variation in quantitative traits. However, little is known about their relative contribution to phenotypic variation compared to those of additive and dominance effects, and almost nothing about their role in phenotypic evolution. Here we address these questions by investigating the relative contribution of additive, dominance and imprinting effects of quantitative trait loci (QTL) to variation in ‘early’ and ‘late’ body weight in an intercross of mice selected for divergent adult body weight. We identified 18 loci on 13 chromosomes; additive effects accounted for most of the phenotypic variation throughout development, and imprinting effects were always small. Genetic effects on early weight showed more dominance, less additive and, surprisingly, less imprinting variation than that of late weight. The predominance of additivity of QTL effects on body weight follows the expectation that additive effects account for the evolutionary divergence between selection lines. We hypothesize that the appearance of more imprinting effects on late body weight may be a consequence of divergent selection on adult body weight, which may have indirectly selected for alleles showing partial imprinting effects due to their associated additive effects, highlighting a potential role of genomic imprinting in the response to selection.
Introduction
Variation in quantitative traits is often affected by many small-effect quantitative trait loci (QTL, e.g. Falconer and Mackay 1996; Lynch and Walsh 1998). Such QTL can have a number of different patterns of effect on trait expression, such as additive effects (which measure the independent effects of alleles at a locus) or dominance effects (which measure the interaction between alleles at a locus). In addition to these ‘genetic’ sources of variation, epigenetic effects, where no variation in the underlying DNA sequence is involved, are increasingly recognized as a significant factor that may contribute to phenotypic variation in a number of different traits (e.g. Jablonka and Lamb 1998; Hager and Johnstone 2003, 2006; Bossdorf et al. 2007). In particular, genomic imprinting effects have been shown to influence the expression of a variety of quantitative traits, most notably size and growth related traits (Itier et al. 1998; Li et al. 1999; Reik et al. 2003; Cheverud et al. 2008; Wolf et al. 2008a). In a quantitative genetic framework, genomic imprinting can broadly be defined as the unequal expression of maternally and paternally inherited alleles (Wolf et al. 2008b), which may be caused by DNA methylation, non-coding RNA and histone modifications (Feil & Berger 2007). Phenotypically, genomic imprinting is manifested as a difference in trait expression between the alternative ordered heterozygotes (e.g. A1A2 versus A2A1; Wolf et al. 2008b). Imprinting of a locus generally results in expression of either the paternal or the maternal allele and corresponding silencing of the other allele (Bartolomei and Tilghman 1997; Reik and Dean 2001; Wood and Oakey 2006), but partial imprinting, where the two parental alleles are expressed to different degrees or have differential effects, has also been reported (e.g. Hayward et al. 1998; Morison et al. 2005; Wolf et al. 2008a). Thus, overall phenotypic variation is modulated by genetic as well as epigenetic sources of variation. However, the degree to which these different sources of variation contribute to trait variation remains poorly understood. Such information seems particularly pertinent to the study of phenotypic evolution because the various types of genetic effects play different roles in a trait's response to selection and in the effect that selection has on patterns of genetic variation within and between populations. In this study, we address this issue by characterizing the relative contribution of genetic (additive and dominance) and epigenetic (imprinting) effects to phenotypic variation in a cross between divergent selection lines using a novel multivariate framework.
One of the best-studied quantitative traits in animals is body weight and growth (e.g. Falconer 1953; Cheverud et al. 1996; Vaughn et al. 1999; Brockmann et al. 2004). Body size may be a particularly important trait because it is a key predictor of individual fitness in animals (and is also related to a number of weight-associated diseases such as obesity; Brockmann and Bevova 2002). Previous research has characterized the contribution of additive, dominance (e.g. Vaughn et al. 1999) and epistatic effects (e.g., Cheverud and Routman 1995) to the genetic architecture underlying phenotypic variation in body weight. By contrast, most research on epigenetic imprinting effects has utilized non-QTL approaches, such as gene-targeting techniques. Several studies in mice demonstrated that genomic imprinting can crucially affect body weight (De Chiara et al. 1990; Reik et al. 2003). For example, Li et al. (1999) have shown that pups that inherited a mutated copy of a paternally expressed gene (Peg3) were born small and growth retarded. In addition to postnatal and pre-weaning effects, other studies demonstrated that imprinting also influences body weight and other traits at later stages in life (Itier et al. 1998), and in humans, parent-of-origin-dependent effects on birthweight have been studied using genome-wide linkage analyses (e.g. Lindsay et al. 2004). These results are corroborated by several QTL studies of size-related traits utilizing different approaches. For example, de Koning and colleagues (de Koning et al. 2000) used a model to separate the expression of paternally versus maternally derived alleles and demonstrated the existence of an imprinted locus for fat thickness in pigs. By contrast, Nezer et al. (1999) compared a Mendelian model of inheritance with an F2 model ordered by the paternal allele to show that a paternally expressed QTL exists at IGF2 in pigs affecting a range of body composition traits. More recently, several studies have demonstrated that a QTL analysis using both parental and offspring genotypes can be successfully employed to detect imprinted QTL on complex traits (Cheverud et al. 2008; Wolf et al. 2008a; Leamy et al. 2008). Furthermore, using a QTL approach one can ascertain whether parent-of-origin-dependent effects are caused by maternal genetic effects or genomic imprinting (Hager et al. 2008). While together results of the aforementioned studies show that a proportion of variation in adult body weight is affected by imprinting effects, very little is known about the relative contribution of imprinting effects to phenotypic variation in quantitative traits compared to those of additive and dominance effects. Furthermore, we know almost nothing about the role of imprinting effects in trait evolution (but see Spencer 2002) and the relative importance of imprinting compared to genetic effects.
While the evolutionary response to selection is determined by the additive genetic variance, (Fisher 1930), additive genetic variation can arise not only from additive gene action, but also from dominance, imprinted or epistatic effects of loci (Cheverud and Routman 1995; Willis and Orr 1993; Cheverud 2000). In contrast, imprinting effects usually do not contribute to the additive genetic variance (Spencer 2002; 2008) because they do not contribute to the average effect of alleles (which is generally the average phenotype associated with an allele in a population, measured as a deviation from the phenotypic mean; Falconer and Mackay 1996). This is because the two reciprocal heterozygotes typically occur in equal numbers (i.e. alleles are found equally often in these alternative states) and, as a result, imprinting effects do not contribute to a mean difference in the average phenotype associated with different alleles at a locus. However, despite this fact, genomic imprinting can still play an important role in determining the pattern of effect of loci and their contribution to the additive genetic variance. Since genomic imprinting affects the expression of alleles in both homozygotes and heterozygotes (alleles are expressed depending on their parent-of-origin regardless of genotype) it can influence the additive and dominance effects of alleles. As a result, genomic imprinting can affect how a locus contributes to an evolutionary response to selection. For example, in the case of pure monoallelic expression, genomic imprinting removes the possibility for interactions between alleles in heterozygotes, and thus the physiological, mechanistic, basis of dominance variation (unless there are closely linked interacting loci, as in the callipyge locus in sheep; Georges et al. 2003). In the case of paternal or maternal expression, imprinting contributes to differences between the average phenotypes of homozygotes (where each homozygote expresses the alternative allele at a locus) and, therefore, monoallelic expression associated with imprinting should lead to additive expression at a locus. Thus, the phenomenon of genomic imprinting, like physiological dominance and epistasis (i.e., the presence of these non-additive effects as a result of molecular or developmental effects; Cheverud 2000, Wade 2001; see also Brodie 2000) can influence the contribution of a locus to the evolutionary response to selection.
In light of our previous work that demonstrated a diversity of imprinting effects on weight and growth traits, here we explore the contribution of genomic imprinting effects to trait variation relative to the contribution of genetic effects. In this study, we aim to analyze genetic and epigenetic sources of variation for body weight traits in mice using an intercross between inbred mouse strains selected for large and small adult body weight in separate selection experiments. Using the F3 generation of this intercross population we specifically examine the relative contribution of additive, dominance and genomic imprinting effects to quantitative trait variation. Our design enables us further to determine whether parent-of-origin-dependent effects were caused by genomic imprinting and not maternal genetic effects, which can be confounded in other designs (see Hager et al. 2008). Finally, we discuss the implications of our results for the evolutionary consequences of selection on the genetic architecture underlying the selected traits.
Methods
Study population and phenotypes
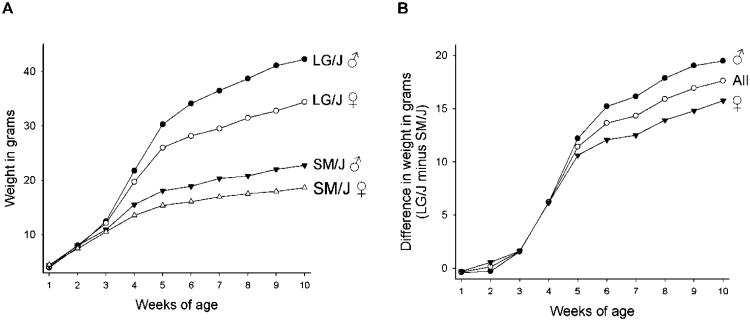
Our experimental population is the intercross between the inbred mouse strains Large LG/J and Small SM/J, which were originally produced by artificial selection for large or small body weight at 60 days of age (Chai 1956). These lines now differ by ca. 8.5 within-strain standard deviations in adult body weight (at 63 days of age) in both sexes (Kramer et al. 1998; see Fig. 1a), and are thus ideal to investigate genetic and epigenetic sources of variation for body weight. For clarity, we refer to these lines as Large and Small throughout, though their official strain designations are LG/J and SM/J, respectively (the LG/J strain derived by Goodale 1938; the SM/J strain derived by MacArthur 1944). The study population was generated by mating ten males of the Small strain to ten females of the Large strain resulting in the F1 population of 52 individuals. These F1 individuals were then mated at random to produce 510 F2 animals, representing our parental generation. Random mating among F2 animals yielded 200 full-sib families of the F3 generation with a total of 1632 individuals. Further details of the husbandry can be found in Vaughn et al. (1999) and Hager et al. (2008).
Figure 1.
a). Growth of the Small (SM/J) and Large (LG/J) inbred strains of mice. A) Weights at each of the first 10 weeks of age (in grams) are shown for males and females of the two strains. Data are from Kramer et al. (1998). b) The difference between the Large and Small strains in weekly weights for males, females and all individuals together (labelled ‘All’).
Weight measures were obtained weekly beginning at 1 week of age using digital scales. We analyzed weekly weights from week 1 to week 10 and pre-weaning growth from week 1-3 and post-weaning growth from week 3-10. Growth was calculated as the difference in absolute body weight between the weeks that defined the growth period. Although all weekly weight measures show a general autoregressive correlation structure, principle component analysis of the genetic and phenotypic correlation matrices (see Kramer et al. 1998 for the matrices) revealed that the weekly weights separated into an early set of weights (weeks 1 to 4) and a late set (weeks 5 to 10). Previous genetic analyses (Cheverud et al. 1996; Vaughn et al. 1999) also support this separation since genetic effects tend to be mostly limited to within these two groups. Therefore, multivariate analyses were performed using these two phenotypic ‘modules’, which we refer to as ‘early’ and ‘late’ body weight (see below).
Genotyping
DNA was extracted from livers of F2 and F3 mice using Qiagen DNeasy tissue kits and samples were scored for 384 polymorphic SNP markers across the 19 autosomes using the Golden Gate Assay by Illumina, San Diego, USA. The X chromosome with 16 markers was excluded from this analysis because the genotype distribution created by the breeding design precludes mapping the parent-of-origin effects on the X chromosome in the F3 generation. We note that the exclusion of the X-chromosome could potentially under-estimate the importance of imprinting effects if there are X-linked imprinted QTL, but such a bias is expected to be small (given the relatively small proportion of the genome being excluded, though two imprinted genes have been identified on the X to date; geneimprint.com, November 2008). X-linked imprinted effects will also be restricted to variation in females since there cannot be parent-of-origin dependent effects associated with the male X chromosome (all males receive their X-chromosome from their mothers). Fifteen autosomal markers were unreliably scored and were excluded. A genetic map of the 353 remaining markers based on Haldane's centiMorgans (cM) was produced using R/QTL and validated against the genome coordinate locations in the Ensembl database (www.ensembl.org). The average map distance between markers in the F2 generation is 4 cM. Markers are evenly placed throughout the genome except for monomorphic regions between LG/J and SM/J (Hrbek et al. 2006).
Unlike in traditional QTL analysis where only three genotypes are analyzed, we distinguish all four possible genotypes (LL, SS, LS, SL, where ‘L’ and ‘S’ refer to the allele derived from Large and Small respectively), which are ordered according to the parent-of-origin, with the paternal allele given as the first allele and the maternal as the second. Ordered genotypes for the F3 generation and unordered genotypes for the F2 generation were inferred using the haplotype reconstruction program Pedphase (Li and Jiang 2003). The inclusion of ordered genotypes allows for the identification of parent-of-origin-dependent effects in addition to additive and dominance effects. Thus, by using an F3 generation for our mapping analysis, where we can directly differentiate the parent-of-origin of alleles for all individuals rather than the F2 generation, enables us to expand our view of genetic architecture by considering the parent-of-origin dependent effects of alleles.
QTL Analysis
For our analysis we assigned the four ordered genotypes at the marker loci (LL, LS, SL, SS) additive (a), dominance (d) and parent-of-origin (i) genotypic index scores following Mantey et al. (2005) given by: which yields estimates of the parameters: . where the genotypic values are , r is the reference point for the model (the midpoint between homozygotes), a is the additive genotypic value (half the difference between homozygotes), d is the dominance genotypic value (the difference between the mean of the heterozygotes and the mid-point of the homozygote means), and i is the parent-of-origin or imprinting genotypic value (half the difference between heterozygotes). We also created a genotype class variable, where individuals were grouped by their ordered genotype at a locus.
To identify QTL we conducted a genome scan using a model with the four ordered genotypes as a fixed class variable (following Wolf et al. 2008a). This model tests the overall null hypothesis of no QTL. Therefore, significant QTL could have any combination of additive, dominance or parent-of-origin-dependent effect (unlike in Wolf et al. 2008a where we specifically searched for loci showing imprinting effects only). The three effects are orthogonal in the model and it is thus possible that all three may co-occur at a locus, but they need not for the locus to show a significant effect. QTL were characterized in terms of their pattern of effect (additive, dominance and imprinting) after they had been identified. Therefore, our analysis should provide an unbiased picture of the patterns of effect of loci.
We performed the genome scan to detect QTL using a repeated measures mixed model fitted by restricted maximum likelihood (REML) with family as a random effect and the four ordered genotypes as fixed effects using SAS version 9.1 (SAS Institute, Cary, NC, USA). For ‘early weight’, the weights measured for weeks 1 to 4 were treated as repeated measures of the same ‘weight’ trait and the correlation between weeks was modeled using the Toeplitz autoregressive structure (Kincaid 2005), which approximates the phenotypic correlation structure (Kramer et al. 1998). Likewise, for ‘late weight’, the weights measured for weeks 5 to 10 were treated as repeated measures using the same model structure. This enabled us to analyze the 10 weekly weights using just two multivariate sets to search the genome for QTL, thereby reducing the number of independent tests performed. Probability values were transformed to a logarithmic probability ratio (LPR) in order to make them comparable to the LOD scores typically seen in QTL analyses (LPR = −log10(probability)). Once QTL locations were identified we performed post hoc analyses to characterize the pattern of effect of QTL on the individual weekly weight traits and the two growth traits. In these analyses, the significance of the individual genetic effects for each of the 12 traits was determined using a mixed model with the a, d and i index values as fixed regression effects and family as a random effect (fitted again using REML in the Mixed Procedure of SAS).
Significance thresholds for QTL detection in the genome scan were determined using a Bonferroni correction that implements the effective number of markers method, which has been demonstrated to be less artificially conservative than a simple Bonferroni correction (Li and Ji 2005). Due to correlations between linked markers, the genome has 133 effective markers, which results in a genome-wide Bonferroni threshold LPR at the 5% level (i.e., α = 0.05) of 3.41. Following Chen and Storey (2006), a modified genome-wide error rate should be applied as opposed to the traditional genome-wide error rate or the false discovery rate when several QTL can be expected to affect traits as in our study. This is achieved by applying the significance criterion to the highest LPR on each chromosome and yields overall the best results by increasing the discovery of true positives while at the same time avoiding problems using the false discovery rate in gene mapping experiments. We therefore determined the chromosome-wide significance threshold for each chromosome, again based on the effective number of markers.
We further tested the possibility that parent-of-origin effects can also be caused by maternal genetic effects, rather than genomic imprinting (Hager et al. 2008), by restricting the analysis to offspring of heterozygous mothers since there is no variation in maternal genetic effects amongst these females and differences between heterozygous offspring will be due to genomic imprinting. Patterns of imprinting were characterized by comparing the relative fit of different possible imprinting patterns (see Wolf et al. 2008a for details).
To determine the relative proportion of variance explained by the loci overall and by each of the effects, we calculated the approximate variance contributed by a locus (Vg):
which is the genetic variance of a locus in a population with two alleles at approximately equal frequency in Hardy-Weinberg equilibrium. This approach was adopted as REML does not compute sums of squares and the corresponding R2. Thus, the proportion of variance explained is Vg/Vp (where Vp is the phenotypic variance) and the variance explained by the additive effect is given by ½a2/Vp; the corresponding values for the dominance and imprinting effects are ¼d2/Vp and ½i2/Vp, respectively.
When chromosomes contained more than one significant QTL we assumed that all loci more than 50cM apart represented separate QTL. Moreover, inspection of the multivariate scan and the LPR for the three effects was used to determine whether two closely located loci are different if, for instance, one showed a highly significant dominance effect but no additive effect and the other locus the reverse pattern.
Results
Our genome scan to detect QTL affecting early and late weight identified a total of 18 QTL on 13 different chromosomes (denoted adiX.Y where ‘adi’ indicates and the multivariate model for additive, dominance and imprinting effects, X identifies the chromosome and Y the QTL number on that particular chromosome). Our results are summarized in Table 1 and show that, overall, most loci showed an additive effect, followed in frequency by dominance and then genomic imprinting effects. Of the 18 detected loci, 15 were significant at the genome-wide level while three loci exceeded the chromosome-wide level (Table 1). Of the 15 QTL reaching genome-wide significance, several QTL showed distinct effects in both growth periods, with five QTL being significant at the genome-wide level for both early and late weights and ten loci exceeding the genome-wide significant threshold in one set of weights only, suggesting that different QTL may modulate early and late growth in mice. By contrast, five QTL were significant at the genome-wide level for both early and late weights.
Table 1.
QTL affecting early and late body weights in the Large × Small intercross. The multivariate set affected by the trait is given after the QTL name where ‘E’ refers to the early weight set and ‘L’ for the late set. Given are the F2 location in cM (‘Locat.’), the coordinates based on mouse build 36 (‘Coord.’) and the locus LPR followed by the traits weekly weights (‘wk1-wk10′), pre-weaning growth (‘g1-3′) and post-weaning growth (‘g3-10′). Where the locus was significant at the genome level for both sets the higher LPR is given and identified. For each affected trait we note whether the effect was an additive, dominance or imprinting effect (a = additive, d = dominance, i = imprinting). We further give the pattern for imprinting effects in parentheses where ‘p’ refers to paternal expression and ‘under’to polar underdominance. QTL not in bold exceeded the modified genome-wide threshold but not the standard genome-wide threshold. Further details can be found in the Methods. The coordinates for adi4.2 are unknown.
| Traits | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| QTL | Locat. | Coord. | LPR | wk1 | wk2 | wk3 | wk4 | wk5 | wk6 | wk7 | wk8 | wk9 | wk10 | g1-3 | g3-10 |
| adi1.1 (E,L) | 8.26 | 31.1 | 6.8 (L) | a | a | a | a | a | a | a | a,i (p) | a,i (p) | a | a | a |
| adi1.2 (E) | 34.70 | 75.2 | 4.3 | a, d | a, d, i (p) | d | d | d | a, d | a, d | a, d | a, d | d | d | |
| adi2.1 (L) | 76.23 | 158.2 | 3.32 | a | a | a | a | a | a | a | |||||
|
| |||||||||||||||
| adi3.1 (L) | 77.79 | 141.5 | 3.43 | a | a | a | a | a, i (p) | i (under) | i (under) | i (under) | a, i (under) | |||
|
| |||||||||||||||
| adi4.1 (L) | 33.50 | 78.9 | 8.38 | a | a, i (p) | a | a | a | a | a | a | a | a, i (p) | a, d | |
|
| |||||||||||||||
| adi4.2 (E) | 61.67 | Unk | 4.75 | d | d | d | d | d | d | d | d | d | d | ||
|
| |||||||||||||||
| adi5.1 (E) | 68.01 | 131.6 | 3.69 | a | a | a | a | a | a | a | |||||
|
| |||||||||||||||
| adi6.1 (E) | 0 | 3.79 | 3.18 | a | a | a | a | a | a | a | a | a | |||
|
| |||||||||||||||
| adi6.2 (E, L) | 58.30 | 123.1 | 12.97 (L) | a, d | a, d | a, d | a, d | a | a | a | a | a | a | a, d | a |
|
| |||||||||||||||
| adi7.1 (E, L) | 27.70 | 56.3 | 11.92 (L) | a | a, d | a, d | a | a | a, i (p) | a, i (p) | a, i (p) | a, i (p) | a, i (p) | a, i (p) | a, i (p) |
|
| |||||||||||||||
| adi7.2 (E, L) | 44.07 | 99.8 | 9.60 (L) | a, d | a, d | a, d | a, d | a, d | a | a | a | a, d | a, d | d | a |
|
| |||||||||||||||
| adi8.1 (E, L) | 4.22 | 13.6 | 9.41 (E) | a, d | a, d | a, d | a, d | a, d | a, d | a, d | a, d | a, d | a, d | a, d | a, d |
|
| |||||||||||||||
| adi8.2 (L) | 33.90 | 53.6 | 5.47 | a, d | a, d | a, d | a, d | a, d | a, d | a, d | a, d | a, d | a, d | a, d | |
|
| |||||||||||||||
| adi9.1 (L) | 21.43 | 42.8 | 3.71 | a | a | a | a | a | a | a | a | ||||
|
| |||||||||||||||
| adi10.1 (L) | 46.26 | 105.4 | 5.46 | a | a | a | a | a | a | a | a | a | a | ||
|
| |||||||||||||||
| adi12.1 (L) | 42.8 | 89.8 | 3.65 | d | d | d | d | d | d | d | d | ||||
|
| |||||||||||||||
| adi14.1 (L) | 37.75 | 81.2 | 3.51 | a | a | a | a | a | a | a | |||||
|
| |||||||||||||||
| adi15.1 (E) | 35.12 | 76.7 | 2.85 | a | a | a | a | a | |||||||
The highest LPR was observed for adi6.2 with a value of 12.97 (Table 1). The predominant QTL effect observed was additive with all loci showing an additive effect either for all traits affected by a given locus (e.g. adi1.1 and adi4.1) or only for specific traits (e.g.adi4.2; Table 1). In addition to yielding information on which individual traits are affected by loci identified in the multivariate analysis, the mixed model analysis revealed also whether, for a given trait, the locus showed several effects, e.g. additive and dominance effects. Nine loci showed only one effect type for a given trait (mostly additive) whereas the nine other loci exhibited at least two effect types for a given trait. Locus adi1.2 was the only one that showed all three effect types for one trait (week 2 body weight). Moreover, a locus could also have joint additive and imprinting or dominance effects (e.g. adi7.1). While the two loci adi8.1 and adi8.2 are located closely together, inspection of the LPR distribution for additive and dominance effects revealed two separate QTL with distinct patterns as the former locus shows very strong additive but small dominance effects whereas the latter has a very strong dominance signal with a small additive effect (Supplementary Table).
Genotypic effects
Where additive effects occurred, they were positive indicating that the LL homozygote was significantly larger than the SS homozygote, with one exception (adi3.1). For this locus, we obtained significant negative estimates for the additive effect (i.e. the LL homozygote was smaller than the SS homozygote, see Supplementary Table).
With regard to dominance effects, the most commonly observed pattern of effect was the L allele dominant over the S allele (occurring 46 times at six loci). The only other dominance pattern was overdominance. This pattern was shown by three QTL for at least one trait (adi1.2, adi4.2 and adi12.1). With the exception of adi1.2 and adi4.2 all other loci maintained their dominance effect pattern for all affected traits. By contrast, adi1.2 showed overdominance for weight traits from week 3 to week 5 but then the L allele showed a dominance effect over the S allele until week 10. Finally, at adi4.2 ten traits were influenced by dominance effects, of which nine showed the overdominance pattern and one trait (week 3) showed the L allele dominant over the S allele.
A total of five loci showed imprinting effects for some of the affected traits, where the majority affected later weights (Table 1). Four other parent-of-origin-dependent effects were due to maternal genetic effects and are not discussed further but are given in the Supplementary Table. All five loci showed the paternal expression pattern where the genotypes inheriting the same allele from their fathers have similar phenotypes. Locus adi3.1 showed, in addition, a polar underdominance pattern for week 7 to week 10 body weights. This pattern is characterized by one of the two heterozygotes being different from all other three genotypes. In this case, the LS heterozygote was smaller than the other heterozygote as well as the two homozygotes.
Proportion of variance explained
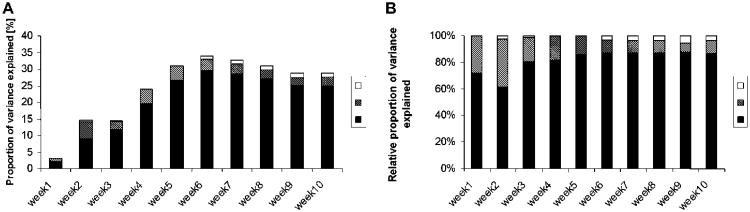
The proportion of phenotypic variance explained by additive, dominance and genomic imprinting effects increased from 3.2% for week 1 weight to 23.9% at week 4 (Table 2). This rose to a maximum of one third of phenotypic variance accounted for at week 6 and then remained around or just under 30%. The largest effects were found for additive genetic effects, followed by dominance and then imprinting effects (Fig. 2a). Interestingly, the greatest variation in phenotypic variance explained was found for additive effects while dominance effects largely remained within the 2-5% range throughout. Genomic imprinting effects were mostly restricted to after week 6.
Table 2.
QTL effects and number for each trait. In the second column, the table lists for each trait the overall number of all QTL affecting the trait, the third only those with an additive effect, the fourth column those with a dominance effect and the fifth column those with an imprinting effect. This is followed by the overall R2 value in percent for all loci, and the R2 values in percent for the additive, dominance and imprinting effect, respectively.
| Trait | Loci | a effects | d effects | i effects | Total R2 | R2 a effects | R2 d effects | R2 i effects |
|---|---|---|---|---|---|---|---|---|
| Week 1 | 9 | 8 | 5 | 0 | 3.2 | 2.3 | 0.9 | 0 |
| Week 2 | 11 | 11 | 6 | 1 | 14.6 | 9.0 | 5.2 | 0.4 |
| Week 3 | 14 | 12 | 7 | 1 | 16.9 | 11.6 | 5.1 | 0.2 |
| Week 4 | 16 | 13 | 7 | 0 | 23.9 | 19.5 | 4.4 | 0 |
| Week 5 | 17 | 14 | 6 | 0 | 31.0 | 26.6 | 4.4 | 0 |
| Week 6 | 17 | 15 | 5 | 2 | 34.0 | 29.6 | 3.4 | 1.0 |
| Week 7 | 17 | 14 | 5 | 2 | 32.6 | 28.5 | 3.0 | 1.1 |
| Week 8 | 16 | 13 | 5 | 3 | 30.9 | 27.0 | 2.7 | 1.2 |
| Week 9 | 16 | 13 | 6 | 3 | 29.4 | 25.2 | 2.7 | 1.5 |
| Week 10 | 16 | 13 | 6 | 2 | 28.7 | 24.8 | 2.8 | 1.1 |
| Early growth | 12 | 9 | 6 | 2 | 14.6 | 10.5 | 3.4 | 0.7 |
| Late growth | 12 | 11 | 4 | 1 | 21.6 | 20.1 | 1.1 | 0.4 |
Figure 2.
Variance explained by QTL. a) The proportion of phenotypic variance explained by additive (a), dominance (d) and parent-of-origin-dependent effects (i) for weekly weights from week 1 to week 10. b) The relative proportion of phenotypic variance (i.e., relative to the total variance attributable to QTL) explained by additive (a), dominance (d) and parent-of-origin-dependent effects (i) for weekly weight from week 1 to week 10. Here, the sum of the proportion of phenotypic variance explained by a, d and i equals 100% and shown are the relative proportions for the individual genotypic effects. For example, for week 2 weight, imprinting effects explained about 4% of the overall phenotypic variance while dominance explained about 40% and additive effects the remaining 56%.
Focusing on the relative proportion of phenotypic variance explained (Fig. 2b) we found that, for week 1 and 2 body weights, dominance effects accounted for between 30% and 40% with the remainder being additive effects. Dominance effects remained prominent until week 4, after which their relative contribution as a percent of the genetic variance decreased to around 10%. Overall, imprinting effects played a relatively minor (2.3% to 6.6%) role but were stronger at later stages.
Discussion
The key objective of our study was to examine the relative contribution of the traditional genetic additive and dominance effects as well as epigenetic imprinting effects as a source of phenotypic variation in lines derived by artificial selection for divergent body weight. By using a multivariate approach, we were also able explore in detail the pleiotropic nature of QTL underlying phenotypic variation in a set of correlated body weight traits. We detected a total of 18 QTL, with five loci affecting ‘early’ weights (body weights measured up to week 4 of age), eight loci affecting ‘late’ weights (body weights from 5 to 10 weeks of age) and five loci affecting both early and late weights. This result lends support to earlier studies that found evidence for two distinct mechanisms governing the two growth periods (Falconer et al. 1978; Cheverud et al. 1996; Atchley et al. 1997). The supposed latent cause for these two growth periods is that during early stages cell numbers are increased while at later stages cell size is increased (Atchley et al. 1997; Vaughn et al. 1999).
Genetic and epigenetic effects
Overall, the diversity of effects detected by the full model is greater at later ages than at earlier ages. Surprisingly, imprinting effects were stronger at later ages, although they remain overall small compared to dominance and additive effects. Dominance effects decreased over time, being a major part of genetic architecture early (explaining 30-40% of the genetic variance contributed by the QTL in weeks 1 and 2) and a relatively minor part at later ages (explaining only between 7% and 14% of the QTL variance after week 5). Turning to the estimates of effect sizes in our study, we found standardized effects that ranged from 0.10 |a|/SD to 0.33 |a|/SD (where |a| denotes the absolute value of a), and is within the range of previous studies on this intercross (Kenney-Hunt et al. 2006). We note that the average value of the standardized additive effect calculated for our study is 0.17, a value exceeding, but of similar magnitude to, that predicted by Falconer (1955) for body size (0.12).
One locus deviated in its pattern of the additive effect from other loci in that the Small allele resulted in higher rather than lower weight than the Large allele for all affected traits (adi3.1; Supplementary Table). Such a ‘contra’ effect might be expected for early weight traits but not for later weights. Cheverud et al. (1996) suggested that the ‘contra’ effects of the Small allele during early growth periods can be explained by the history of the strains that were selected for large and small body weight at 60 days of age (Goodale 1938; Macarthur 1944). It may be due to this selection criterion that alleles influencing early growth are not fixed as expected in adults (i.e. the Large allele increasing weight) but rather by drift (Cheverud et al. 1996). The squared genetic correlation between week 1 and week 10 weights in this population is low (10%) so selection on adult weight would be expected to have a very small correlated response in early weights. We note that the locus has no significant effect on weight at weeks 7, 8 and 9, which is within the period during which the original lines were selected for (body weight at day 60). Therefore, the fixation of the allele with such ‘contra’ effects on early weights may be explained by drift.
Genomic imprinting and evolutionary response
The pattern of selection that produced the Small (SM/J) and Large (LG/J) lines of mice would be expected to lead to the fixation of loci showing additive effects on adult body size (the target of the divergent selection) since such loci are expected to account for the evolutionary divergence of selection lines. Indeed, as expected, most allelic effects are additive with nearly all showing a pattern where the allele derived from the Large strain exerts a positive effect on body size (i.e., the alleles from the Large strain cause mice to be larger while alleles from the Small strain result in smaller individuals). Not surprisingly, loci affecting later weeks (especially after week 4) account for more phenotypic variation than the loci affecting earlier weights. This follows the pattern of divergence in body weight between the strains (Fig. 1b), which is expected given that these QTL presumably are what contributed to the evolutionary difference in body size between the strains.
Our results generally indicate small genomic imprinting effects that are more apparent at later stages. While selection on body weight in the two original mouse lines would have favored (and ultimate led to the fixation) of alleles with additive effects, alleles at imprinted loci showing a uniparental expression pattern (paternal or maternal expression) may nonetheless also have been favored during this process and can be detectable if they affect body weight due to the associated additive effects. Indeed, it is possible that the presence of imprinting may render the effects of alleles additive since we would expect that a completely imprinted locus (i.e., one showing strict monoallelic expression) should necessarily show additivity because the average of the two homozygotes would have to be the same as the average of the two different heterozygotes (i.e. there is no dominance). Therefore, a further consequence of selection for imprinted gene expression (as outlined by theories for the evolution of genomic imprinting, e.g. Haig and Graham 1991; Wolf and Hager 2006) could be increased additivity (again due to the associated additive effects with parental imprinting), which in turn may enhance the response to selection. In this sense, imprinting may increase the capacity to generate heritable and selectable variation (evolvability sensu Kirschner and Gerhart 1998; Wagner 2005) of a population and thus its ability to respond to selection (see also Houle 1992; Hansen and Houle 2008).
Looking at the proportion of loci with imprinting effects compared to the total number of detected loci, a striking discrepancy between the predicted proportion of imprinted murine genes and our empirical results becomes apparent. In a simulation study, Luedi et al. (2005) estimated that 2.5% of all genes in mice are potentially imprinted, while we found that 27% of the loci with effects on adult body weight show a significant imprinting effect. This suggests that there is an overrepresentation of imprinted loci in the genetic architecture of body size. The discrepancy between the proportion of imprinted loci across the genome predicted by Luedi et al. (2005) and our study may, in part, be explained by the fact that we have focused on growth related traits whereas Luedi et al. (2005) predicted the occurrence of imprinted genes across the entire genome, irrespective of the potential effects of such genes. If genes affecting growth and size related traits are more likely to show imprinting, as might be predicted by the conflict hypothesis for the evolution of genomic imprinting (e.g. Wilkins & Haig 2003), then the discrepancy may not be surprising, though it is not clear whether the set of genes predicted to be imprinted by Luedi et al. are actually enriched for growth associated genes. Furthermore, it seems possible that selection itself could have led to imprinted gene expression, perhaps through the evolution of modifier loci, because imprinting may enhance evolvability (see above). However, the underlying mechanisms of such a process and why the selection regime would have favored genomic imprinting remain unclear at present.
While the aim of this study was not to detect parent-of-origin-dependent effects per se, all the detected imprinted loci confirm previously described lo ci (Wolf et al. 2008a) or are very close to such (adi1.1, adi7.1 and adi3.1). With the exception of adi7.1, all loci showing imprinting effects are outside genomic regions in which known imprinted genes are located (cf. www.geneimprint.com). However, adi7.1 maps to a large imprinting cluster on chromosome 7 where several major imprinted genes such as example Peg3 are found. One weak imprinting effect for week 2 weight at adi1.2 might suggest a second cluster of imprinted genes on chromosome 1 although we view this imprinting effect with caution as the effect is weak and just exceeds the lowest significance threshold. Comparing these results with those of prior work on the detection of imprinting effects (Wolf et al. 2008a), it is clear that the detection of QTL using multivariate analyses of additive, dominance and imprinting effects is driven by the strong additive effects and is a promising approach to assess joint effects and the relative contribution of these three effects. Specifically, the peak for the full model (including a, d, i) often does not coincide with the peak for the imprinting effect. Thus, if the research aim is to identify one of the three genotypic effects (see Wolf et al. 2008a), it seems more appropriate to focus on the specific effect individually. Although our results in the present study do not indicate an important role for genomic imprinting effects in comparison with dominance and additive effects, one should be cautious to conclude that imprinting effects on complex traits are rare. Both gene-targeting and QTL studies identified several imprinted loci with effects on trait variation and clearly demonstrated strong pleiotropic effects on a number of traits caused by imprinted genes (e.g. Li et al. 1999; Wilkinson et al. 2007; Wolf et al. 2008a).
To our knowledge, this is one of the first studies to investigate genetic and epigenetic sources of variation for quantitative traits in conjunction using a multivariate QTL model. Moreover, we provide some of the first insights into the possible role of imprinting effects in trait evolution. We find that loci showing additive effects, which necessarily underlie selected differences between populations fixed for different alleles (as in differentially selected inbred lines), also often show imprinting effects (with over 30% of the loci having additive effects on adult body weight showing imprinting). Therefore, imprinting may be a reasonably common feature of loci involved in trait evolution, perhaps because a necessary consequence of monoallelic expression are associated additive effects.
Supplementary Material
Supplementary Table: The table lists the identified QTL (adiQTL). First, the QTL is identified, followed by marker name, the F2 map location in cM and the genome coordinate based on mouse build 36 (www.ensembl.org), followed by the trait affected. The next section details the additive, dominance and parent-of-origin-dependent effects with standard error and p-value. If a significant imprinting effect was detected, the pattern is described after the p-value. ‘Paternal’ refers to paternal expression, ‘maternal’ to maternal expression and ‘polar under’ to polar underdominance (see Wolf et al. 2008a for details). Where the parent-of-origin-dependent effect is significant but is not caused by genomic imprinting, ‘MGE’ refers to maternal genetic effect. Similarly, the dominance patterns are given were significant with ‘L > S’ referring to the L allele being dominant over the S allele and ‘Over’ to overdominance. This is followed by the standardized genotypic effects and the sum of standardised genotypic traits for each trait where SD is the standard deviation. Then, the locus LPR together with the appropriate genome- and chromosome-wide thresholds are given. Finally, we list the genotypic values (means) of the four ordered genotypes with their standard error SE and sample size n.
Acknowledgments
This research was supported by grants from the Biotechnology and Biological Sciences Research Council, UK (BBSRC), an Underwood Fellowship from the BBSRC and NIH grant DK055736. RH is supported by a NERC Research Fellowship.
Contributor Information
Reinmar Hager, Email: reinmar.hager@cantab.net.
James M. Cheverud, Email: cheverud@pcg.wustl.edu.
Jason B. Wolf, Email: jason@evolutionarygenetics.org.
References
- Atchley WR, Cowely DE, Xu S. Restricted index selection for altering developmental trajectories in mice. Genetics. 1997;146:629–640. doi: 10.1093/genetics/146.2.629. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bartolomei MS, Tilghman SM. Genomic imprinting in mammals. Annu Rev Genet. 1997;31:493–525. doi: 10.1146/annurev.genet.31.1.493. [DOI] [PubMed] [Google Scholar]
- Bossdorf O, Richards CL, Pigliucci M. Epigenetics for ecologists. Ecol Lett. 2007;11:106–115. doi: 10.1111/j.1461-0248.2007.01130.x. [DOI] [PubMed] [Google Scholar]
- Brodie ED., III . Why evolutionary genetics does not always add up Pp 3-19. In: Wolf JB, Brodie E, Wade M, editors. Epistasis and the Evolutionary Process. Oxford University Press; New York: 2000. [Google Scholar]
- Brockmann GA, Bevova MR. Using mouse models to dissect the genetics obesity. Trends Genet. 2002;18:367–376. doi: 10.1016/s0168-9525(02)02703-8. [DOI] [PubMed] [Google Scholar]
- Brockmann GA, Karatayli E, Haley CS, Renne U, Rottmann OJ, Karle S. QTLs for pre- and postweaning body weight and body composition in selected mice. Mamm Genome. 2004;15:593–609. doi: 10.1007/s00335-004-3026-4. [DOI] [PubMed] [Google Scholar]
- Chai C. Analysis of quantitative inheritance of body size in mice. I. Hybridization and maternal influence. Genetics. 1956;41:157–164. doi: 10.1093/genetics/41.2.157. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen L, Storey LD. Relaxed significance criteria for linkage analysis. Genetics. 2006;173:2371–2381. doi: 10.1534/genetics.105.052506. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cheverud J. Detecting epistasis among quantitative trait loci. In: Wolf JB, Brodie E, Wade M, editors. Epistasis and the Evolutionary Process. Oxford University Press; New York: 2000. pp. 58–81. [Google Scholar]
- Cheverud JM, Routman EJ. Epistasis and its contribution to genetic variance components. Genetics. 1995;139:1455–1461. doi: 10.1093/genetics/139.3.1455. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cheverud JM, Routman EJ, Duarte FAM, van-Swinderen B, Cothran K, Perel C. Quantitative trait loci for murine growth. Genetics. 1996;142:1305–1319. doi: 10.1093/genetics/142.4.1305. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cheverud JM, Hager R, Roseman C, Fawcett G, Wang B, Wolf JB. Genomic Imprinting Effects on Adult Body Composition in Mice. Proc Natl Acad Sci USA. 2008;105:4253–4258. doi: 10.1073/pnas.0706562105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- DeChiara TM, Efstratiadis A, Robertsen EJ. A growth-deficiency phenotype in heterozygous mice carrying an insulin-like growth factor II gene disrupted by targeting. Nature. 1990;345:78–80. doi: 10.1038/345078a0. [DOI] [PubMed] [Google Scholar]
- de Koning J, Rattniek AP, Harlizius B, van Arendonk JAM, Brascamp WE, Groenen MAM. Genome-wide scan for body composition in pigs reveals important role of imprinting. Proc Natl Acad Sci USA. 2000;97:7947–7950. doi: 10.1073/pnas.140216397. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Falconer DS. Selection for large and small size in mice. J Genet. 1953;51:470–501. [Google Scholar]
- Falconer DS. Patterns of response in selection experiments with mice. Cold Spring Harbor Symp Quant Biol. 1955;20:178–196. doi: 10.1101/sqb.1955.020.01.018. [DOI] [PubMed] [Google Scholar]
- Falconer DS, Gauld I, Roberts R. Cell numbers and cell sizes in organs of mice selected for large and small body size. Genet Res. 1978;31:387–301. doi: 10.1017/s0016672300018061. [DOI] [PubMed] [Google Scholar]
- Falconer DS, Mackay TFC. Introduction to quantitative genetics. Longman; Harlow: 1996. [Google Scholar]
- Feil R, Berger F. Convergent evolution of genomic imprinting in plants and mammals. Trends Genet. 2007;23:192–199. doi: 10.1016/j.tig.2007.02.004. [DOI] [PubMed] [Google Scholar]
- Fisher RA. The genetical theory of natural selection. Clarendon; Oxford: 1930. [Google Scholar]
- Georges M, Charlier C, Cockett NE. The callipyge locus: evidence for trans interaction of reciprocally imprinted genes. Trends Genet. 2003;19:248–252. doi: 10.1016/S0168-9525(03)00082-9. [DOI] [PubMed] [Google Scholar]
- Goodale H. A study of the inheritance of body weight in the albino mouse by selection. J Hered. 1938;29:101–112. [Google Scholar]
- Hager R, Johnstone RA. The genetic basis of family conflict resolution in mice. Nature. 2003;421:533–535. doi: 10.1038/nature01239. [DOI] [PubMed] [Google Scholar]
- Hager R, Johnstone RA. The influence of phenotypic and genetic effects on maternal provisioning and offspring weight gain in mice. Biol Lett. 2006;2:81–84. doi: 10.1098/rsbl.2005.0403. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hager R, Cheverud JM, Roseman C, Wolf JB. Maternal effects as the cause of parent-of-origin-dependent effects that mimic genomic imprinting. Genetics. 2008;178:1755–1762. doi: 10.1534/genetics.107.080697. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hansen TF, Houle D. Measuring and comparing evolvability and constraint in multivariate characters. J Evol Biol. 2008 doi: 10.1111/j.1420-9101.2008.01573. [DOI] [PubMed] [Google Scholar]
- Haig D, Graham C. Genomic imprinting and the strange case of the insulin-like growth factor II receptor. Cell. 1991;64:1045–1046. doi: 10.1016/0092-8674(91)90256-x. [DOI] [PubMed] [Google Scholar]
- Hayward BE, Moran V, Strain L, Bonthron DT. Bidirectional imprinting of a single gene: GNAS1 encodes maternally, paternally and biallelically derived proteins. Proc Natl Acad Sci USA. 1998;95:15474–15480. doi: 10.1073/pnas.95.26.15475. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Houle D. Comparing evolvability and variability of quantitative traits. Genetics. 1992;130:195–204. doi: 10.1093/genetics/130.1.195. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hrbek T, de Brito RA, Wang B, Pletscher LS, Cheverud JM. Genetic characterization of a new set of recombinant inbred lines (LGXSM) formed from the intercross of SM/J and LG/J inbred mouse strains. Mamm Genome. 2006;17:417–429. doi: 10.1007/s00335-005-0038-7. [DOI] [PubMed] [Google Scholar]
- Itier JM, Tremp GL, Léonard JF, Multon MC, Ret G, Schweighoffer F, Tocqué B, Bluet-Pajot MT, Cormier V, Dautry F. Imprinted gene in postnatal growth role. Nature. 1998;393:125–126. doi: 10.1038/30120. [DOI] [PubMed] [Google Scholar]
- Jablonka E, Lamb MJ. Epigenetic inheritance in evolution. J Evol Biol. 1998;11:159–183. [Google Scholar]
- Kenney-Hunt JP, Vaughn T, Pletscher SL, Peripato A, Routman' E, Cothran K, Durand D, Norgard E, Perel C, Cheverud JM. Quantitative trait loci for body size components in mice. Mamm Genome. 2006;17:526–537. doi: 10.1007/s00335-005-0160-6. [DOI] [PubMed] [Google Scholar]
- Kincaid C. Guidelines for selecting the covariance structure in mixed model analysis; Proceedings of the Thirtieth Annual SAS Users Group International Conference, SAS Institute Inc.; Cary, NC, USA. 2005. [Google Scholar]
- Kirschner M, Gerhart J. Evolvability. Proc Natl Acad Sci USA. 1998;95:8420–8427. doi: 10.1073/pnas.95.15.8420. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kramer MG, Vaughn TT, Pletscher LS, King-Ellison K, Adams E, Erikson C, Cheverud JM. Genetic variation in body weight gain and composition in the intercross of Large (LG/J) and Small (SM/J) inbred strains of mice. Genet Molec Biol. 1998;21:211–218. [Google Scholar]
- Leamy LJ, Klingenberg CP, Sherratt E, Wolf JB, Cheverud JM. A search for quantitative trait loci exhibiting imprinting effects on mouse mandible size and shape. Heredity. 2008;101:518–526. doi: 10.1038/hdy.2008.79. [DOI] [PubMed] [Google Scholar]
- Li LL, Keverne EB, Aparicio SA, Ishino F, Barton SC, Surani MA. Regulation of maternal behaviour and offspring growth by paternally expressed Peg3. Science. 1999;284:330–333. doi: 10.1126/science.284.5412.330. [DOI] [PubMed] [Google Scholar]
- Li J, Ji L. Adjusting multiple testing in multilocus analyses using the eigenvalues of a correlaton matrix. Heredity. 2005;95:221–227. doi: 10.1038/sj.hdy.6800717. [DOI] [PubMed] [Google Scholar]
- Li J, Jiang T. Efficient rule-based haplotyping algorithms for pedigree. J Bioinfo Comp Biol. 2003;1:41–69. [Google Scholar]
- Lindsay RS, Kobes S, Knowler WC, Hanson RL. Genome-wide linkage analysis assessing parent-of-origin effects in the inheritance of birth weight. Human Genet. 2004;110:503–509. doi: 10.1007/s00439-002-0718-2. [DOI] [PubMed] [Google Scholar]
- Luedi PP, Hartemink AJ, Jirtle RL. Genome-wide prediction of imprinted murine genes. Genet Res. 2005;15:875–884. doi: 10.1101/gr.3303505. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lynch M, Walsh B. Genetics and analysis of quantitative traits. Sinauer; Sunderland: 1998. [Google Scholar]
- MacArthur J. Genetics of body size and related characters. I. Selection of small and large races of the laboratory mouse. Am Nat. 1944;78:142–157. [Google Scholar]
- Mantey C, Brockmann GA, Kalm E, Reinsch N. Mapping and exclusion mapping of genomic imprinting effects in mouse F2 families. J Hered. 2005;96:329–338. doi: 10.1093/jhered/esi044. [DOI] [PubMed] [Google Scholar]
- Morison IM, Ramsay JP, Spencer HG. A census of mammalian imprinting. Trends Genet. 2005;21:457–465. doi: 10.1016/j.tig.2005.06.008. [DOI] [PubMed] [Google Scholar]
- Nezer C, Moreau L, Brouwers B, Coppieters W, Detilleux J, Hanset R, Karim L, Kvasz A, Leroy P, Georges M. An imprinted QTL with major effect on muscle mass and fat deposition maps to the IGF2 locus in pigs. Nature Genet. 1999;21:155–156. doi: 10.1038/5935. [DOI] [PubMed] [Google Scholar]
- Reik W, Dean W. DNA methylation and mammalian epigenetics. Electrophoresis. 2001;22:2838–2843. doi: 10.1002/1522-2683(200108)22:14<2838::AID-ELPS2838>3.0.CO;2-M. [DOI] [PubMed] [Google Scholar]
- Reik W, Constância M, Fowden A, Anderson N, Dean W, Ferguson-Smith A, Tycko B, Sibley C. Regulation of supply and demand for maternal nutrients in mammals by imprinted genes. J Physiol. 2003;547:35–44. doi: 10.1113/jphysiol.2002.033274. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spencer HG. The correlation between relatives on the supposition of genomic imprinting. Genetics. 2002;161:411–417. doi: 10.1093/genetics/161.1.411. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spencer HG. Effects of genomic imprinting on quantitative traits. Genetica. 2008 doi: 10.1007/s10709-008-9300-8. [DOI] [PubMed] [Google Scholar]
- Vaughn TT, Pletscher LS, Peripato A, King-Ellison K, Adams E, Erikson C, Cheverud JM. Mapping quantitiative trait loci for murine growth: a closer look at genetic architecture. Genet Res. 1999;74:313–322. doi: 10.1017/s0016672399004103. [DOI] [PubMed] [Google Scholar]
- Wade MJ. Epistasis, complex traits, and mapping genes. Genetica. 2001;112:59–69. [PubMed] [Google Scholar]
- Wagner A. Robustness, evolvability, and neutrality. FEBS letters. 2005;579:1772–1778. doi: 10.1016/j.febslet.2005.01.063. [DOI] [PubMed] [Google Scholar]
- Willis JH, Orr HA. Increased heritable variation following population bottlenecks: The role of dominance. Evolution. 1993;47:949–957. doi: 10.1111/j.1558-5646.1993.tb01249.x. [DOI] [PubMed] [Google Scholar]
- Wilkins JF, Haig D. What good is genomic imprinting: The function of parent-specific gene expression. Nat Rev Genet. 2003;4:1–19. doi: 10.1038/nrg1062. [DOI] [PubMed] [Google Scholar]
- Wilkinson LS, Davies W, Isles AR. Genomic imprinting effects on brain development and function. Nat Rev Neurosci. 2007;8:832–843. doi: 10.1038/nrn2235. [DOI] [PubMed] [Google Scholar]
- Wolf JB, Hager R. A maternal-offspring coadaptation theory for the evolution of genomic imprinting. PLoS Biol. 2006;4:2238–2243. doi: 10.1371/journal.pbio.0040380. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wolf JB, Cheverud JM, Roseman C, Hager R. Genome-wide analysis reveals a complex pattern of genomic imprinting in mice. PLoS Genet. 2008a;4(6):e1000091. doi: 10.1371/journal.pgen.1000091. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wolf JB, Hager R, Cheverud JM. Genomic imprinting effects on complex traits: A phenotype-based perspective. Epigenetics. 2008b;3:295–299. doi: 10.4161/epi.3.6.7257. [DOI] [PubMed] [Google Scholar]
- Wood AJ, Oakey RJ. Genomic imprinting in mammals: Emerging themes and established theories. PLoS Genet. 2006;2:1677–1685. doi: 10.1371/journal.pgen.0020147. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary Table: The table lists the identified QTL (adiQTL). First, the QTL is identified, followed by marker name, the F2 map location in cM and the genome coordinate based on mouse build 36 (www.ensembl.org), followed by the trait affected. The next section details the additive, dominance and parent-of-origin-dependent effects with standard error and p-value. If a significant imprinting effect was detected, the pattern is described after the p-value. ‘Paternal’ refers to paternal expression, ‘maternal’ to maternal expression and ‘polar under’ to polar underdominance (see Wolf et al. 2008a for details). Where the parent-of-origin-dependent effect is significant but is not caused by genomic imprinting, ‘MGE’ refers to maternal genetic effect. Similarly, the dominance patterns are given were significant with ‘L > S’ referring to the L allele being dominant over the S allele and ‘Over’ to overdominance. This is followed by the standardized genotypic effects and the sum of standardised genotypic traits for each trait where SD is the standard deviation. Then, the locus LPR together with the appropriate genome- and chromosome-wide thresholds are given. Finally, we list the genotypic values (means) of the four ordered genotypes with their standard error SE and sample size n.