Structural Effects of Network Sampling Coverage I: Nodes Missing at Random

Abstract

Network measures assume a census of a well-bounded population. This level of coverage is rarely achieved in practice, however, and we have only limited information on the robustness of network measures to incomplete coverage. This paper examines the effect of node-level missingness on 4 classes of network measures: centrality, centralization, topology and homophily across a diverse sample of 12 empirical networks. We use a Monte Carlo simulation process to generate data with known levels of missingness and compare the resulting network scores to their known starting values. As with past studies (Borgatti et al 2006; Kossinets 2006), we find that measurement bias generally increases with more missing data. The exact rate and nature of this increase, however, varies systematically across network measures. For example, betweenness and Bonacich centralization are quite sensitive to missing data while closeness and in-degree are robust. Similarly, while the tau statistic and distance are difficult to capture with missing data, transitivity shows little bias even with very high levels of missingness. The results are also clearly dependent on the features of the network. Larger, more centralized networks are generally more robust to missing data, but this is especially true for centrality and centralization measures. More cohesive networks are robust to missing data when measuring topological features but not when measuring centralization. Overall, the results suggest that missing data may have quite large or quite small effects on network measurement, depending on the type of network and the question being posed.

1. Introduction

A common justification for network research is that, unlike traditional statistical approaches, we do not pretend our respondents are independent. As Freeman (2004) points out in a quote from Barton (1968):

“For the last thirty years, empirical social research has been dominated by the sample survey. But as usually practiced, …, the survey is a sociological meat grinder, tearing the individual from his social context and guaranteeing that nobody in the study interacts with anyone else in it.”

Social network researchers often make this point a little smugly – after all, social life is connected, so why pretend otherwise? We are, however, less likely to tout the tradeoff needed to capture network effects: in giving up independence, we also (usually) give up sampling. As typically practiced¹, network measures assume a census of the relevant respondents and their relations (Wasserman and Faust, 1994; Laumann et al 1983). This raises an obvious question: how robust are network measures when our observed sample is incomplete?

This question is critically important for medium-sized settings where network measures are used for building policy, such as within schools (Valente et al. 2003; Steglich et al. 2012) or organizations (Moore et al. 2004). In these settings, the network is too large for an expert informant to reliably describe and too small to make effective use of the sorts of macro-structure regularities featured in extremely large networks (Albert and Barabasi 2002; Newman, Watts and Strogatz 2002). In such cases, respondents may be absent the day of survey administration or have opted-out of the survey for privacy reasons, leading to potentially significant coverage error (Butts 2003). Every network has some level of this error, but we are just beginning to get estimates of the bias these coverage errors introduce (Wang et al. 2012; Huisman 2009; Borgatti et al 2006, Kossinets 2006, Costenbader & Valente 2003, Galaskiewicz 1991).

Our goal with this set of studies is to extend network sample coverage research to help provide simple, practical guidance for data collection and analysis.² The more specific goals are threefold: first, to describe the maximum level of missing data that will yield an acceptable level of bias; second, to explain why some networks are more or less robust to missing data than others; and third, to extend past work that has generally focused on a single data type and/or measure. To that end, we will describe the effects of missingness on more measures and across more diverse networks than previously studied. This will provide researchers with a clear, sensible and interpretable guide to the effects of missing data across a wide range of data types and measures.

Ultimately, we hope to identify the effects of different types of missingness and the effectiveness of simple correction strategies over a diverse range of network structures to provide practical research guidance to network researchers. Since this goal requires work beyond the scope of a single paper, we approach the project in three parts. In this first study, we examine measurement error under simple random missingness. There are multiple ways in which missingness can be biased, but missing-at-random is a reasonable starting point commonly used in other work (Borgatti et al 2006, Kossinets 2006, Costenbader & Valente 2003). Missing-at-random also provides a comparison for the non-random missingness we explore in part II and matches recent advances in this line of work (Huisman 2009). Finally, after laying the groundwork on the effects of missingness, we explore simple imputation procedures designed to correct for missing data (part III), focusing on models that fill in information from sampled respondents.

We begin this paper by describing past work on missing network data. We then describe the networks used in the simulation, the measures of interest, and the sampling scheme used to measure the effect of missing data. The second half of the paper summarizes our results and is divided into four sections: one for centrality, centralization, topology and homophily.

1.1 Background & Prior Work

This project fits nicely in a small, growing tradition of simulating network errors from observed data to evaluate bias (Huisman 2009; Borgatti et al 2006, Kossinets 2006, Costenbader & Valente 2003, Galaskiewicz 1991). Monte-Carlo simulations of the effects of data error on network measurement are a natural way to gauge robustness, particularly since the mathematics of sampling networks are daunting (Frank 1971; 1978; Granovetter 1976) and test-retest designs are subject to real change in the underlying network (Zemljic & Hlebec 2005). The simulation approach parallels work done on non-network survey data problems, where researchers use simulation to capture the effect of missing data on various model parameters—such as correlation and regression coefficients (see for example, Kim and Curry 1977; Kaufman 1985; Jinn and Sedransk 1989; Yuan and Bentler 2000; Akritas et al. 2002).

In the absence of clear analytic solutions for most network measures, simulation is a straightforward, analytically tractable approach. The basic procedure emerging in this literature is to: (1) identify (or construct) a population of networks, (2) calculate known measures on those networks, (3) sample from them in various ways that represents missingness, (4) re-compute the substantive measures on the now distorted networks and (5) compare the results. Prior work has examined small Erdös random graphs of varying density (Borgatti et al 2006), as well as collections of empirical networks that range from small (less than 200 nodes) face-to-face networks (Huisman 2009; Costenbader & Valente 2003, Galaskiewicz 1991) to large (16,000 node) 2-mode networks (Kossinets 2006) to even larger online networks (Wang et al. 2012). This work has shown a dependency in the resulting measurement bias as a function of network density, size and assortative mixing. Looking across papers, this work also suggests that the scale of node-missingness effects is contingent on the underlying structure of the graph. It is not entirely clear, however, which features matter most and whether this varies by network measure. As such, we will closely examine a small number of widely varying structures to provide variation for substantive exploration.

Most prior work has examined the robustness of centrality scores (Johnson et al, 1989; Galaskiewicz 1991; Costenbader & Valente 2003; Borgatti et al 2006), suggesting that many centrality scores are robust in the face of modest node missingness. For example, Costnbader & Valente (2003) show that in-degree is remarkably stable; with correlations remaining in the 0.9 range even with 50% missing (see also Galaskiewicz 1991). More system-dependent measures, such as betweenness centrality, showed lower correlations, averaging 0.5 at 50% coverage, though Borgatti et al. (2006) show correlations in the 0.7 range for 50% missingness in Erdos graphs, even for system-dependent measures such as betweenness and closeness centralities. These studies all show a consistent and smooth decline in accuracy as missingness increases.

Kossinets (2006) is among the few studies to look at features other than centrality³, focusing instead on indicators of global network structure. Examining small world statistics (clustering & path length, Watts and Strogatz 1998), fractional size of the largest component and degree assortative mixing, his results similarly suggest a smoothly increasing bias as missing data levels increase. He finds widely ranging levels of tolerable differences, dependent on both the measure of interest and the type of missing data. Huisman (2009) similarly considered non-centrality measures, focusing on degree, reciprocity, clustering, assortative mixing (on degree) and distance. He considered different missing mechanisms as well as directed/undirected versions of the same data, finding the effect of missingness to be fairly similar across analyses. The directed network did, however, have larger bias for clustering while the undirected network had larger bias for degree and distance.

Most of this work demonstrates clearly that network estimates are degraded with lower sample coverage, but that there is a wide variability in these effects across measures. For practical purposes, researchers want to know how much damage has been done when survey response rates are less than perfect, and typically need this information for multiple network measures. Thus, while Kossinets (2006) and Huisman (2009) explore many network features, their limitation to a single network form makes generalization difficult. Similarly, centrality studies provide information across a wide-ranging set of networks, but focus on a single dimension of network structure. More recently, Wang et al. (2012) focus on different types of measurement error, considering coding problems that are likely to emerge in large, automatically collected data sources. Wang et al. (2012) thus capture a variety of error processes but explore a limited number of networks and network measures.

We thus build on this important prior work by extending analyses to a wide set of networks that cover a variety of underlying features. Importantly, we assess both estimate bias (mean difference from true) and precision (variability around the mean) for measures related to centrality, centralization, global network topology and homophily.

2. Data and Methods

2.1 Network Samples

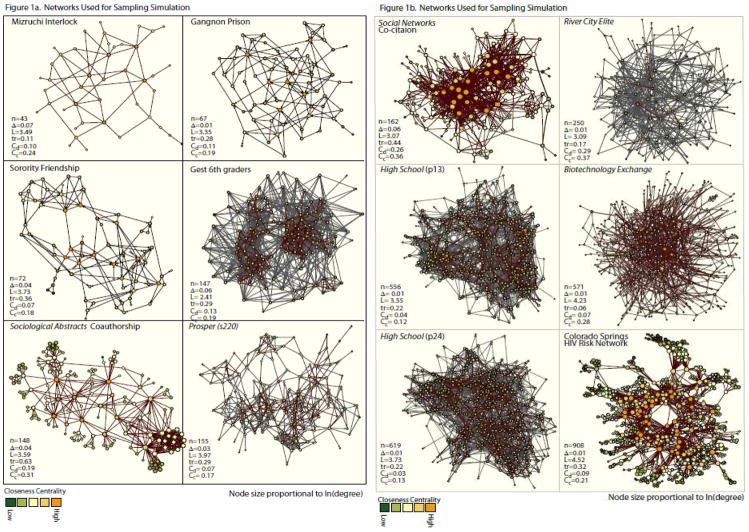
We want a set of networks that researchers from multiple substantive fields could use as analogs to their own work. We limit our study to relatively small (<1000 nodes) networks for both practical and theoretical reasons. Practically, many of the network structure statistics we calculate are time-intensive and non-linearly so with network size, so this limitation helps on computation time. Theoretically, mid-sized networks are likely the least amenable to large-scale random-graph summaries and perhaps most sensitive to small levels of missingness due to key players. These settings, typically within organizations, are also more likely the focus of intensive management efforts. Figures 1a and 1b present sociograms and simple descriptive statistics for each of the 12 networks we study.

Figure 1.

The sampled networks range in size from 43 to 908 nodes, covering many of the contexts commonly studied in social networks research.⁴ These include data on elites (corporate interlocks: “Mizruchi Interlock” and “River City Elite”), young youth networks (“Gest 6^th graders”, “Prosper s220”),⁵adolescent & young adult networks (“Sorority Friendship”, “High School (p13 & p24)”, the Gagnon prison network (MacRae 1960), science networks (a portion of the sociological abstracts collaboration graph and the Social Networks article co-citation graph, the biotechnology exchange network) and epidemiological networks (Colorado Springs HIV risk network-Morris and Rothenberg 2011).⁶ For each figure, we include the observed values for size (n), density (Δ), average path length (L), transitivity (Tr), degree centralization (C_d) and closeness centralization (C_c). Nodes are colored by the relative closeness centrality. Directed edges are represented by an arc while undirected edges are not. The substantive variability in these networks should help us determine how much sampling bias is contingent on network structure.

2.2 Network Position Measures

We focus on four classes of measures: centrality, centralization, topology and homophily. For centrality, we measure degree, closeness, betweenness, and Bonacich power scores. For directed networks, we distinguish between in and out degree but treat the network as undirected for the other three scores. For Bonacich power centrality, we choose β as 0.75 times the largest Eigenvalue. Since centrality is an individual-level score, we measure system reliability as the Pearson’s correlation coefficient between the true and observed scores.

2.3 Network Structure Measures

All other scores are measured at the graph level and we calculate a simple relative bias score as:

$$\mathit{bias}=\frac{\mathit{Observed}-\mathit{True}}{\mathit{True}}$$ (1)

This score tells us the percentage difference of the observed value under sampling relative to the true value observed in the complete network. Positive values indicate that node-sampling inflates the score. Negative values indicate that the score is deflated. In addition to overall bias, we are also interested in the variability of the score as a function of sampling. Thus all figures include the mean, inner-quartile range and 10^th/90^th percentiles.

2.3.1 Centralization

We calculate network centralization scores for each individual centrality measure using Freeman’s standard (1979) formula. These capture the dispersion in centrality -- the extent to which the network is “star-like”, with high values indicating highly unequal distributions and low values indicating fairly equal distributions. Centralization scores are strongly affected by density, so comparisons across networks are difficult, though trends within networks should be informative. As we discuss in the results sections, other indicators for distribution inequality may be more robust to sampling errors.

2.3.2 Topology

We focus on 6 measures of network topology. The first measures capture connectivity, focusing on the fraction of the population in the largest component and bicomponent, key indicators of structural cohesion (Moody & White 2003). A component of a network is a maximal set of nodes reachable through at least a single path.⁷ The largest component thus marks the limiting extent of people reachable through the network. By definition, a component may be disconnected by the removal of a single node. Bicomponents, in contrast, are maximal sets that can only be disconnected by removing 2 or more nodes, and each pair of nodes is linked through at least two node-independent paths. As such, bicomponents offer a potentially more robust structure for diffusion than components (Moody & White 2003).

The third topological measure is the average path distance between nodes. A path in a network is a sequence of adjacent edges linked by nodes, and the shortest path connecting two nodes is the geodesic; if two nodes are unreachable the distance between them is infinite. While average distance is an easily interpretable statistic within a connected network, infinite values due to unconnected pairs make calculating a simple summary score such as the mean impossible. As such, we use ‘closeness’ instead of distance, calculated as 1/distance. Since the lim(dist→inf) of 1/dist is zero, we score unconnected pairs as zero. High average closeness values indicate that the network is compact, with many pairs separated by small distances.

The extent to which triples are closed in a network captures local clustering, or the likelihood that “a friend of a friend is a friend.” We measure local clustering with the transitivity ratio—the proportion of all two-step paths that are also 1-step paths. Networks with high transitivity are locally clustered.

While transitivity captures the extent of locally closed triads, the full triad census summarizes much more of the topological information in a network (Wasserman and Faust, 1994). Holland and Leinhardt (1976) and Wasserman (1977) provide scoring to test for the shape of the network macro structure based on tau statistics, conditional on the distribution of dyads. Johnsen (1985, 1986) provides a number of models that capture clustering and hierarchy in networks. Here we calculate tau statistics based on a ranked cluster (RC) model. For directed networks⁸, the ranked-cluster model describes settings where ordered sets of m-cliques are arranged in a hierarchy. For our purposes, we are less interested in the actual level of hierarchy than in the stability of the distribution given missing data.

Perhaps the most general treatment of a network’s topology is a block-model (White et al 1976). A blockmodel ideally reduces a complex network to a manageable number of equivalent positions that capture the underlying network structure. Unfortunately, there is no single-indicator summary for a block-model, making it difficult to contrast the “true” partition with the partition identified in the missing-data perturbed network. We can, however, ask how similar any two arbitrary network partitions are with the rand statistic. The rand statistic (Rand 1971) tells us the proportion of pairs in one partition that are similarly grouped (together or apart) in a second partition.⁹ Thus, to capture the robustness of the global network structure, we first partition the network with ConCorr (arbitrarily set to depth 3), then compare the partition observed in each sampled network to that observed in the full network (for all pairs remaining in both networks). We are not claiming that each of these networks is best fit by a depth=3 ConCor partition. Rather, we simply want a way to capture the overall robustness of the role structure to sampling, and the ConCorr partition provides a simple mechanism for doing so using a well-known and commonly used technique.¹⁰ In principle, high rand statistics at low sampling levels should indicate that one can effectively enumerate summary network positions with the sampled data, regardless of the topological complexity of the network.

2.3.3 Homophily

The measures described above focus purely on network structure, but many researchers are interested in the intersection of network structure with behavior (e.g. Cohen 1983; Haynie 2001; Bramoullé, Djebbari, Fortin 2009; Steglich, Snijders, and Pearson 2010). In most cases, researchers ask how similar connected nodes are to each other with respect to a given attribute. We focus on two sorts of homophily here. First, homophily with respect to structure is best captured with network degree homophily, also known as the level of assortative mixing. We calculate assortative degree mixing as the edgewise correlation on degree. High positive values indicate that nodes with many ties are connected to others with many ties and those with few to others with few. Strong negative values indicate disassortative mixing, where people with many ties are connected to those with few.

The challenge to measuring attribute homophily on a diverse sample of networks is finding an attribute sufficiently consistent across networks to provide comparison. Since no such attribute exists naturally in these data, we assign attributes to nodes in each network in a way that creates a known level of homophily. To do so, we first randomly “seed” the network with values of a uniform random variable. We then apply a peer-influence model (Friedkin 1990) to adjust the values of the variable across nodes until a minimum level of homophily is achieved. These attributes are then fixed for the nodes across all runs. Here we use two levels of homophily to test for strength effects, where high homophily measures may be more (or less) robust to missing data. We again measure homophily as edgewise correlation, using values of .35 and .75.

Table 1 summarizes the measures and provides the known values for each of the networks studied.

Table 1.

Sample Network Descriptive Statistics

	Inter-lock	Prison	Sorority	6th Grade	Co-author	Prosper	Co-citation	Elite	HS 13	Bio-tech	HS24	HIV Risk
Directed?	No	Yes	Yes	Yes	No	Yes	No	Yes	Yes	No	Yes	No
Centrality
In – Degree	3.02 (1.93)	2.72 (2.02)	2.89 (1.75)	8.86 (5.26)	6.16 (5.98)	3.83 (2.69)	9.32 (10.62)	2.39 (7.59)	6.06 (4.42)	3.85 (4.99)	5.71 (3.96)	6.05 (8.12)
Out – Degree	3.02 (1.93)	2.72 (1.48)	2.89 (1.85)	8.86 (4.67)	6.16 (5.98)	3.83 (2.36)	9.32 (10.62)	2.39 (1.63)	6.06 (2.90)	3.85 (4.99)	5.71 (2.99)	6.05 (8.12)
Symmetric Degree	3.02 (1.93)	5.43 (2.73)	5.78 (2.88)	17.7 (7.73)	6.16 (5.98)	7.65 (3.85)	9.32 (10.62)	4.78 (7.83)	12.1 (6.04)	3.85 (4.99)	11.43 (5.84)	6.05 (8.12)
Closeness	0.36 (0.08)	0.18 (0.08)	0.15 (0.09)	0.35 (0.12)	0.32 (0.06)	0.18 (0.09)	0.38 (0.09)	0.03 (0.02)	0.22 (0.05)	0.26 (0.04)	0.2 (0.06)	0.25 (0.04)
Betweenness	0.06 (0.07)	0.03 (0.05)	0.04 (0.05)	0.01 (0.02)	0.02 (0.06)	0.02 (0.03)	0.01 (0.02)	0 (0)	0.01 (0.01)	0.01 (0.02)	0.01 (0.01)	0 (0.02)
Bonacich Power	0.82 (0.58)	0.86 (0.52)	0.86 (0.51)	0.9 (0.43)	0.58 (0.82)	0.82 (0.57)	0.63 (0.78)	0.64 (0.77)	0.83 (0.55)	0.6 (0.8)	0.83 (0.56)	0.57 (0.82)
Centralization
In – Degree	0.10	0.08	0.06	0.14	0.19	0.08	0.26	0.29	0.04	0.07	0.03	0.09
Out – Degree	0.10	0.08	0.06	0.15	0.19	0.02	0.26	0.03	0.01	0.07	0.01	0.09
Symmetric Degree	0.10	0.06	0.05	0.08	0.19	0.05	0.26	0.15	0.03	0.07	0.02	0.09
Closeness	0.27	0.12	0.17	0.16	0.35	0.11	0.48	0.06	0.08	0.36	0.08	0.28
Betweenness	0.20	0.17	0.16	0.06	0.37	0.16	0.12	0.01	0.05	0.24	0.03	0.17
Bonacich Power	0.20	0.18	0.14	0.13	0.26	0.16	0.22	0.41	0.13	0.29	0.12	0.23
Topology
Component Size	43	67	72	147	148	155	162	250	556	571	619	908
Bicomponent Size	27	62	59	145	75	147	118	195	545	336	605	517
Distance	0.36	0.18	0.15	0.35	0.32	0.18	0.38	0.03	0.22	0.26	0.2	0.25
Transitivity	0.11	0.28	0.36	0.29	0.63	0.29	0.44	0.17	0.22	0.02	0.22	0.32
TauRC	−0.91	2.35	4.65	17.75	17.65	7.22	−27.36	163.6	23.66	−91.61	22.91	−104.22
Homophily
In-degree	−0.07	0.02	0.03	0.1	0.31	−0.01	0.03	−0.29	0.05	−0.13	0.13	−0.13
Out-Degree	−0.07	−0.13	−0.03	−0.08	0.31	−0.06	0.03	0	0.14	−0.13	0.16	−0.13
High attribute	0.75	0.75	0.77	0.88	0.78	0.82	0.84	0.79	0.93	0.75	0.8	0.77
Low attribute	0.36	0.39	0.37	0.35	0.38	0.37	0.35	0.39	0.37	0.38	0.38	0.4

Standard deviations are in parentheses.

2.4 Network Sampling Setup

For each network, we randomly select a proportion of nodes to remove, reconstruct the network without these nodes or any of their contributing edges, and compute the scores of interest. These are then recorded for comparison to the known values. We repeat this process 1000 times for each level of missingness, evaluated at 1, 2, 5, 10, 15, 20, 25, 30, 40, 50, 60, and 70 percent. We use a simple “listwise” procedure to reconstruct the network. Only those nodes sampled are included in the reconstructed network. This is the standard method used in prior work (Galaskiewicz 1991; Costenbader & Valente 2003; Borgatti et al 2006) and reflects a common idea that unsampled nodes are also unknown.¹¹ Practically, we ignore any nominations from a sampled node to a non-sampled node.

2.5 Analysis strategy

The amount of information generated by this research design presents a formidable data-summary challenge: we have mean and variability scores for 12 networks across 12 levels of missingness over 22 network measures. Our strategy is to first provide graphical summaries for each network to provide a qualitative portrait of the missingness effect. We then summarize over all of the networks using marginal distributions or regression models. We refer to the graphical summaries as mosaic plots. Figure 2 presents a simple example of one network and one measure to guide the interpretation of the remaining summary figures. Here we examine the robustness of in-degree for the River City elite network. The first panel shows the scatter plot of observed in-degree after sampling (y-axis) by the true in-degree (x-axis), for one draw at 5 missingness levels. As we can see, the slope of each line drops as missingness increases. Thus, as missing data levels increase, there is lower fidelity to the true value, or a lower correlation between true and observed in-degree. The second panel summarizes this result over 1000 iterations, plotting the mean level as a dark line, the inner-quartile range as dark grey and the 10^th/90^th percentile as light gray.

Figure 2.

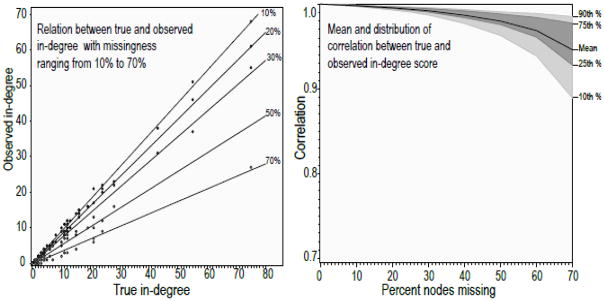
Missingness comparison example, River City Elites and in-degree

We can see that the overall slope of the mean line in panel two is flat, indicating that in-degree is quite robust in this network. Fitting a linear term to this line yields a −0.006 slope (on 10% units); we can then expect a correlation of 0.982 between the true and observed score if we were to sample only 70% of the nodes in this network. Moreover, the variation around the line is quite small. We calculate a total deviation score (υ) to measure this variability. Total deviation is equal to the square root of the total sum of squares of the observed minus the mean divided by n. As deviation increases, the total uncertainty in our estimate increases. This effectively captures the relative size of the shaded region in each panel. The total deviation here is .0005, which is among the smallest we will observe.¹²

3. Results

3.1 Network Position scores

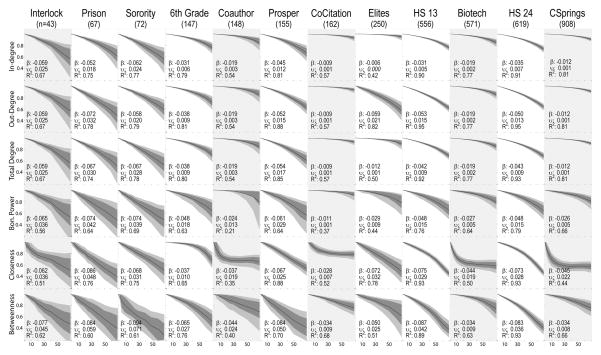
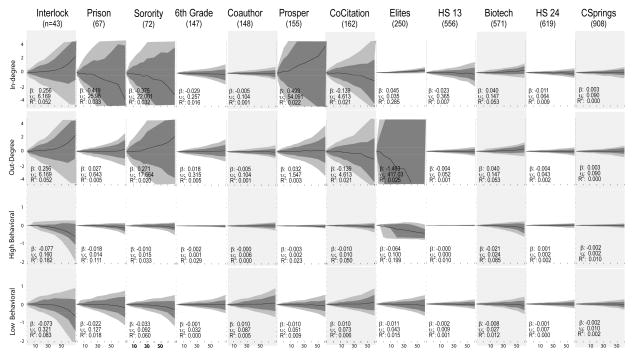
Figure 3 presents the summary results for the 6 centrality scores. Since in- and out-degree are the same as total degree for the undirected networks, we have shaded those columns for ease of reference. Looking across the rows lets us compare networks with respect to their sensitivity to missingness, while looking down the columns lets us compare the relative effects within networks of different centrality scores. The generally declining slopes tell the obvious story that accuracy is lower as less of the network is sampled. The range of these effects is quite large, however. For the co-citation network, for example, sampling only 50% of the nodes would leave us with expected degree scores that correlate at about 0.95 with the true value [1−5*(0.01) =.95], dropping to a correlation of 0.93 if we sampled only 30%. On the other hand, a 50% sample from the Gangon prison network would leave us with a total degree score that correlates at 0.66 with the true score, dropping to 0.54 at a 30% sample, and the results would be much worse for betweenness centrality.

Figure 3.

Centrality Score Robustness

Each subgraph plots the distribution of the correlation between the true centrality score and the score computed on the network with nodes removed at random. The dark line represents the mean, inner-quartile range with dark gray and 10th/90th percentiles with light gray. β is the regression coefficient of correlation regressed against percent missing (divided by 10), and thus represents the expected drop in correlation for each 10% decline in sample coverage. For example, if we sampled 80% of the Sorority population, we would expect a correlation for closeness centrality of [1−2*(0.068)=] 0.86. υ represents the average observed deviation (square-root of total sum of squares divided by n) and R² is the proportion of the variance explainable with the linear regression term. Shaded columns indicate undirected networks.

In the directed networks, we see that in-degree is usually more robust to sampling than out-degree, though that effect may be strongest for the highly-centralized (in-degree) networks, such as the River City Elites. For the four measures based largely on degree (Bonacich Power being a degree-weighted score), we see generally higher total variation among the smaller networks (even though these are based on percent of nodes removed, not absolute number), with the exception of the 6^th-grade Prosper network. This may be due, in part, to the strong sex-segregation here – effectively giving us two small networks weakly linked rather than one larger network. The River-City elite network has a very robust in-degree profile, but a weak out-degree profile. Since this is a “who do you think is influential” network, there is strong agreement on the most important players in the setting and thus in-degree is robust. The two high-school networks have a fairly strong negative slope (−0.05; → a correlation of 0.75 at 50% sampling), but this is also very narrowly distributed.

The more dependent a score is on system features, the greater effect missing data has on the resulting bias, and often so in a non-linear way. Closeness centrality, for example, often shows a sharp decline in fit for small amounts of missingness that later levels off. In general, closeness centrality is quite sensitive to moderate levels of missing data. So, while the average linear slope is −0.037 for the Coauthorship network, the effect of missingness levels out after 10% missing at a correlation of about 0.7. Betweenness centrality has a more linear response to missingness, but the slope is generally quite steep, and the effect is evident for both small and large networks. Table 2 summarizes these curves by giving the proportion missing data that would produce a target correlation between the true and observed score, based on a quadratic model fit to our simulation results (to better capture the curves evident in Figure 3). Thus, we see that in the interlock network, you would achieve a correlation with the true degree score of 0.9 or greater if you had up to 23% missing node data, while having between 23% and 40% will likely yield a correlation of at least 0.8.

Table 2.

Maximum percent missing to retain target correlation with true score

Network	Target Correlation	In-Degree	Out-Degree	Total Degree	Bonacich Power	Closeness	Betweenness
Interlock	0.90	--	--	23	20	8	12
	0.80	--	--	40	36	19	25
Prison	0.90	27	17	19	15	10	21
	0.80	45	31	35	29	21	24
Sorority	0.90	20	23	18	13	16	5
	0.80	37	40	34	26	31	13
6th Graders	0.90	43	38	38	29	46	22
	0.80	64	58	58	48	60	38
Coauthor	0.90	--	--	58	54	3	24
	0.80	--	--	*	*	12	47
Prosper	0.90	31	26	25	22	18	10
	0.80	51	45	43	39	33	21
Co-Citation	0.90	--	--	*	*	12	33
	0.80	--	--	*	*	36	60
Elites	0.90	*	23	*	45	15	25
	0.80	*	40	*	67	30	45
HS 13	0.90	43	25	34	30	21	17
	0.80	64	44	54	49	36	30
BioTech	0.90	--	--	58	47	0	44
	0.80	--	--	*	70	8	62
HS 24	0.90	39	27	32	30	25	17
	0.80	60	46	52	48	39	31
CSprings	0.90	--	--	*	47	0	38
	0.80	--	--	*	*	7	62
Mean (Std Dev)	0.90	39 (16.1)	25.6 (6.4)	42.9 (20.9)	35.2 (17.4)	14.5 (12.7)	22.3 (11.5)
	0.80	55.9 (11.9)	43.4 (8.2)	55.5 (14.6)	51.8 (17.0)	27.7 (15.2)	38.2 (16.9)

^*Cases where percent missing is above 70, our observed maximum. In these cases, 70 is used to calculate overall means. The maximum percent missing was calculated based on a quadratic fit to the data.

As a simple summary of the effect of network structural features on the centrality score sensitivity to missingness, Table 3 presents the correlation between measures of network structure and the beta slope coefficients from Figure 3.^13,14

Table 3.

Correlation of missingness robustness scores and network structure: centrality

	In Degree		Out Degree		Degree		Bon Power		Closeness		Betweenness
	Slope β	Var υ	Slope β	Var υ	Slope β	Var υ	Slope β	Var υ	Slope β	Var υ	Slope β	Var υ
Size	0.48	−0.56+	0.41	−0.50+	0.46	−0.55+	0.41	−0.61*	0.08	−0.16	0.34	−0.52+
Density, undirected	−0.55+	0.55+	−0.31	0.37	−0.54+	0.57*	−0.52+	0.60*	0.05	−0.00	−0.40	0.47
Indegree Std. Dev.	0.92**	−0.84**	0.75**	−0.70**	0.93**	−0.86**	0.93**	−0.88**	0.66*	−0.66*	0.83**	−0.85**
Outdegree Std. Dev.	0.66*	−0.61*	0.93**	−0.84**	0.73**	−0.67*	0.80**	−0.72**	0.85**	−0.77**	0.77**	−0.77**
Degree Std. Dev.	0.87**	−0.85**	0.67*	−0.69*	0.84**	−0.85**	0.84**	−0.86**	0.61*	−0.72**	0.67*	−0.77**
Mean of true score	0.47	−0.54	0.66*	−0.70*	0.01	−0.20	−0.85**	−0.71**	0.72**	−0.56+	−0.08	−0.17
Directed Network	−0.38	0.24	−0.74**	0.58*	−0.53+	0.40	−0.59*	0.43	−0.70*	0.39	−0.74**	0.64*
Limited Degree	−0.01	−0.17	−0.50+	0.29	−0.17	−0.02	−0.23	0.03	−0.47	0.14	−0.46	0.22
% in Largest Bicomponent	−0.37	0.19	−0.61*	0.44	−0.52+	0.36	−0.53+	0.34	−0.55+	0.21	−0.72**	0.53*

Note: Positive correlations mean that networks with higher values of that measure (e.g. size) are more robust to measurement error.

⁺P<= 0.1;

^*+P<= 0.05,

^**P<= 0.01

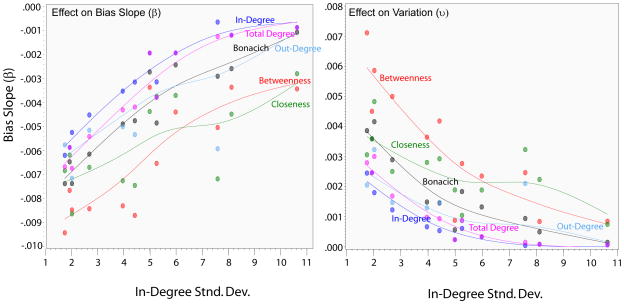
While regressions with 12 cases have limited statistical power, the only measure that is consistently significant is the dispersion of degree, particularly in-degree¹⁵. The more unequal the degree distribution, the more robust the centrality scores will be to random missingness. These correlations are extremely strong, often in the range of 0.9. Since the dispersion of degree is a form of network centralization (centralization scores correlate at about 0.7 with the standard deviation scores in this sample of networks), these results suggest that when the network is highly centralized, random missingness will have only a minor effect on the reliability of the centrality scores. This is exactly what we expect given the literature on network robustness coming out of the preferential attachment literature (Albert, Jeong, and Barabasi 2000); when networks are highly centralized they tend to be robust to random missingness (but may be at greater risk to targeted missingness, see part II). It is important to note, however, that there is a non-linear relationship between the effect of missing data and centralization. As indegree standard deviation grows larger so too does the bias slope (so lower bias), but this rate of increase decreases at higher levels of centralization. Figure 4 below summarizes this (non-linear) effect of in-degree centralization for robustness. Inversely, more cohesive networks tend to be less robust to missing data.¹⁶

Figure 4.

Dependence of centrality sensitivity to missingness by in-degree Centralization

The effects are qualitatively similar for variability in the centrality correlations, with the overall network degree centralization having a pronounced effect. When in-degree is highly dispersed, there is lower variability in the response to missingness, suggesting, again, that the networks are more robust to random missingness when they are centralized. In addition, there are consistent effects for size, such that larger networks have lower variability and higher correlations with the true scores, though these effects do not hold controlling for centralization.

3.2 Network Structure

As we turn our attention to the network structure measures, we move from a simple node-level correlation to a bias coefficient. We calculate bias as the percent difference from the true score, so a value of 0.5 would mean that the observed score is 50% larger than the true score, while a value of 1 is double that observed. For reference in the mosaic plots, we have added lines at −.5 and .5. A flat mean line suggests that the resulting network score is unbiased when data are missing at random, a positive sloping line that the observed score is too large, and a negative slope that the resulting score underestimates the true value. A bell-shaped shaded region implies that the uncertainty of the estimate increases with more missing data.

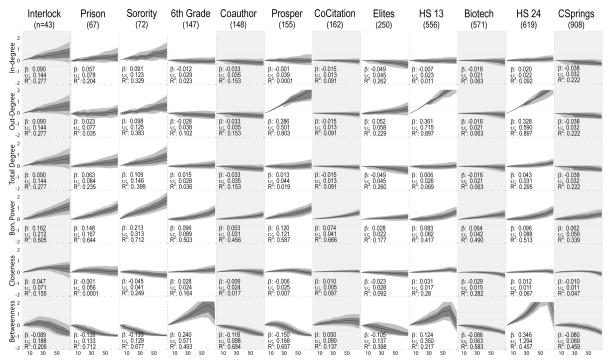
3.2.1 Network Centralization

Figure 5 presents the mosaic bias plot for network centralization. The first impression from this figure is of one of inconsistency across scores and networks. Some clarity can be had by focusing on the 4 degree-based measures, then sorting by network size. Among the smallest networks (first 3 columns), you see large uncertainty and a smoothly increasing bias. Among the larger networks, bias tends toward zero, with fairly flat lines and narrow uncertainty bands. The exceptions are the out-degree centralization scores for the prosper network and the two high-school networks. These three all have a fixed-nomination design and are less robust to missing data. Note this bias is somewhat less when direction is ignored, consistent with Butts’ findings (Butts 2003). Fixed out-degree networks have larger bias because they have lower centralization (as degree is truncated) and degree centralization responds more strongly to missing data when centralization is low; here, degree centralization is not driven by the very high degree nodes, making it more susceptible to random removal of nodes. We can see this clearly in Table 5, where degree standard deviation is positively correlated with robustness to missing data, although this effect weakens at higher levels of degree standard deviation.

Figure 5.

Centralization Score Robustness

Each subgraph plots the distribution of the bias between the true centralization score and the score computed on the network with nodes removed at random. The dark line represents the mean, inner-quartile range with dark gray and 10th/90th percentiles with light gray. β is the regression coefficient of bias regressed against percent missing (divided by 10), and thus represents the expected change in bias for each 10% decline in sample coverage. υ represents the average observed deviation (square-root of total sum of squares divided by n) and R² is the proportion of the variance explainable with the linear regression term. Shaded columns indicate undirected networks.

Table 5.

Correlation of missingness robustness scores and network structure: centralization

	In Degree		Out Degree		Degree		Bon Power		Closeness		Betweenness
	Slope β	Var υ	Slope β	Var υ	Slope β	Var υ	Slope β	Var υ	Slope β	Var υ	Slope β	Var υ
Size	0.38	−0.53+	−0.26	0.26	0.37	−0.52+	0.49	−0.46	0.16	−0.62*	−0.11	0.26
Density, undirected	−0.28	0.44	0.28	−0.27	−0.29	0.44	−0.59*	0.54+	−0.21	0.51+	−0.16	−0.01
Indegree Std. Dev.	0.41	−0.65*	0.36	−0.36	0.51+	−0.68*	0.77**	−0.76**	0.34	−0.69*	0.33	−0.17
Outdegree Std. Dev.	0.39	−0.54+	0.38	−0.38	0.47	−0.56+	0.47	−0.53+	0.34	−0.64*	0.34	−0.2
Degree Std. Dev.	0.54+	−0.74**	0.2	−0.2	0.6*	−0.76**	0.74**	−0.74**	0.34	−0.78**	0.09	0.05
Mean of true score	0.02	−0.2	0.66*	−0.65*	0.16	−0.25	0.61*	−0.51+	0.04	−0.2	0.43	−0.53+
Directed Network	0.08	0.03	−0.51+	0.51+	−0.06	0.1	−0.28	0.29	0.01	0.1	−0.59*	0.43
Limited Degree	0.47	−0.34	−0.61*	0.62*	0.38	−0.32	0.18	−0.2	0.17	−0.16	−0.62*	0.56+
% in Largest Bicomponent	0.29	−0.11	−0.6*	0.62*	0.15	−0.05	−0.28	0.22	0.07	−0.01	−0.63*	0.56+

Note: Positive correlations mean that networks with higher values of that measure (e.g. size) are more robust to measurement error. The direction of the bias is ignored when calculating the correlations.

⁺P<= 0.1;

^*+P<= 0.05,

^**P<= 0.01

Bonacich centrality is a nice bridge between system and local, and shows a marginally larger sensitivity to missingness, with slope coefficients larger across the networks than observed for the pure degree scores. The relation to missingness is smooth and monotonic, with the networks appearing more centralized as missingness increases. Again, larger, more centralized networks are less prone to bias under conditions of missing data (with this effect weaker at higher levels of centralization). For example, the Interlock network (small, with low degree standard deviation) yields an average bias above .5 with 32 percent of the network missing, while the Colorado Springs network (larger, with higher degree standard deviation) yields an average bias of .5 with 77 percent of the network missing. See Table 4 for more details.

Table 4.

Maximum percent missing to remain under target bias: centralization

Network	Target Bias	In-Degree	Out-Degree	Total Degree	Bonacich Power	Closeness	Betweenness
Interlock	.25	19	19	19	16	20	19
	.5	43	43	43	32	*	49
Prison	.25	38	35	36	21	35	13
	.5	*	*	68	40	*	29
Sorority	.25	23	30	22	10	48	9
	.5	50	54	45	23	*	23
6th Graders	.25	*	51	*	38	64	9
	.5	*	*	*	58	*	17
Coauthor	.25	54	54	54	51	*	24
	.5	*	*	*	*	*	46
Prosper	.25	60	9	70	21	*	23
	.5	*	18	*	43	*	44
Co-Citation	.25	*	*	*	43	*	25
	.5	*	*	*	67	*	*
Elites	.25	49	45	49	69	66	18
	.5	*	*	*	*	*	41
HS 13	.25	*	9	*	39	*	11
	.5	*	17	*	63	*	21
BioTech	.25	*	*	*	41	*	35
	.5	*	*	*	*	*	60
HS 24	.25	*	9	58	38	*	8
	.5	*	18	*	58	*	12
CSprings	.25	55	55	55	41	*	43
	.5	*	*	*	*	*	65
Mean (Std Dev)	.25	54 (18.5)	38 (22.9)	53.6 (18.8)	35.7 (16.4)	60.3 (16.8)	19.8 (11.0)
	.5	66.1 (9.3)	53.3 (23.1)	65.5 (10.1)	55.3 (16.6)	70 (0)	39.8 (19.4)

^*Cases where percent missing is above 70, our observed maximum. In these cases, 70 is used to calculate overall means. The maximum percent missing was calculated based on a quadratic fit to the data.

The system centrality measures tell two stories. Closeness centralization is remarkably robust across networks. In most networks the relation centers on zero, suggesting that the closeness centralization score would be accurately measured even with significant levels of random-missing data. Only the smallest network, with 43 nodes, has a visible positive slope or generally large variability. Betweenness centrality, in contrast, is widely variable across networks, with two general patterns. In nine of the twelve test cases, betweenness centralization presents a smoothly decreasing bias with missingness levels. In the other three networks, we observe a rapidly increasing bias that quickly returns to zero. This is likely occurring due to the low starting values of the betweenness scores. Small changes quickly increase the percent score, but when missingness is nearly complete, the centralization score tends toward zero and thus returns to the observed value.¹⁷ We note that this effect also appears to be driven largely by the normalizing denominator for centralization, since the analogous figures for the standard deviation of betweenness centrality is monotonic.

Taken as a whole, the major predictors of bias and variance for centralization are size and degree deviation (greater size and centralization are associated with less bias and variance), although directed/undirected status and percent in the largest bicomponent is important for out-degree and betweenness. In both cases, directed, more cohesive networks are less robust to missing data and have larger variance. More cohesive networks are actually more robust to missingness when percent in the largest bicomponent is smaller (between .5 and.6 for our data), but less robust at higher levels of cohesiveness.

3.2.2 Topology

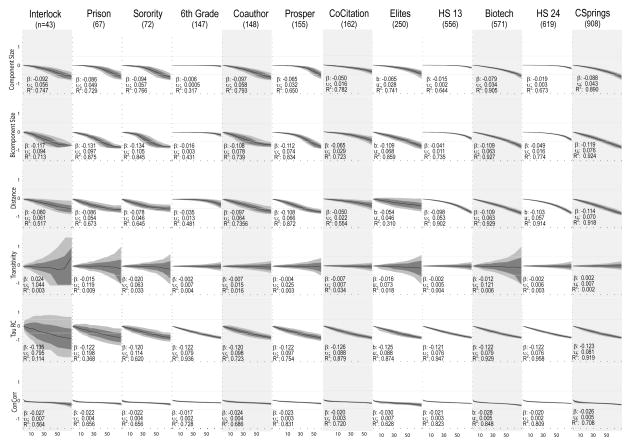
The mosaic plots in Figure 6 show analogous results for 6 measures of global network structure. Turning first to simple measures of connectivity, we see that connectivity decreases with sample missingness. The proportion of the population in the largest connected component tends toward a “rotated-J” shape, staying flat until about 30% of the population is removed, then turning fairly steeply to smaller average component sizes. The variability around component size is quite narrow, and combined these indicate that basic connectivity is robust to random missingness. The pattern is not merely a reflection of size; as the 6^th grade friendship network (n=147) and the two high-school networks (n=556 & 619 respectively) have nearly flat response curves with extremely narrow bounds. On average, it is necessary to remove 74 percent of the network before the bias crosses the .5 level and 55 percent before the bias crosses the .25 level (see Table 6).

Figure 6.

Topology Score Robustness

Each subgraph plots the distribution of the bias between the true topology score and the score computed on the network with nodes removed at random. The dark line represents the mean, inner-quartile range with dark gray and 10th/90th percentiles with light gray. β is the regression coefficient of bias regressed against percent missing (divided by 10), and thus represents the expected change in bias for each 10% decline in sample coverage. υ represents the average observed deviation (square-root of total sum of squares divided by n) and R² is the proportion of the variance explainable with the linear regression term. Shaded columns indicate undirected networks.

Table 6.

Maximum percent missing to remain under target bias: topology

Network	Target Bias	Component Size	Bicomponent Size	Distance	Transitivity	Tau RC	ConCorr
Interlock	.25	34	19	31	29	4	*
	.5	58	40	62	39	13	*
Prison	.25	45	23	20	40	12	*
	.5	63	42	50	60	31	*
Sorority	.25	41	24	20	49	16	*
	.5	59	43	58	*	36	*
6th Graders	.25	*	*	67	*	17	*
	.5	*	*	*	*	37	*
Coauthor	.25	32	20	25	*	17	*
	.5	56	43	51	*	37	*
Prosper	.25	53	39	23	65	17	*
	.5	69	55	47	*	37	*
Co-Citation	.25	55	49	54	*	16	*
	.5	*	*	*	*	35	*
Elites	.25	49	27	36	47	17	61
	.5	*	49	*	*	35	*
HS 13	.25	*	63	39	*	17	*
	.5	*	*	57	*	37	*
BioTech	.25	41	29	27	38	17	56
	.5	64	51	49	60	36	*
HS 24	.25	*	59	38	*	17	*
	.5	*	*	56	*	37	*
CSprings	.25	38	24	25	*	17	*
	.5	60	45	46	*	37	*
Mean (Std Dev)	.25	49.8 (14.0)	37.2 (18.4)	33.8 (14.4)	57.3 (15.6)	15.3 (3.8)	68.1 (4.6)
	.5	64.9 (5.5)	54 (12.5)	57.2 (9.1)	65.8 (9.3)	34 (6.8)	70 (0)

^*Cases where percent missing is above 70, our observed maximum. In these cases, 70 is used to calculate overall means. The maximum percent missing was calculated based on a quadratic fit to the data.

While component size gives the upper limit of reachability, bicomponent size captures the extent of the population that is re-connected through multiple cycles. The proportion in the largest bicomponent tracks the component size results strongly, although with slightly steeper slopes in the smaller networks. The correspondence of these two curves suggests that estimates of connectivity will be fairly robust to random missingness, at least so long as 70% to 80% of the sample is captured. The Biotech, Couathorship and Colorado Springs networks are the exceptions to this rule, exhibiting more bias than the other networks. Tellingly, these three networks have low levels of cohesion. Networks with low cohesion are subject to disconnection with missing data and thus underestimate the size of the largest bicomponent and component. This is clear in Table 7, where percent in the largest bicomponent is positively correlated with robustness in the bicomponent/component columns.

Table 7.

Correlation of missingness robustness scores and network structure: topology

	Component Size		Bicomponent Size		Distance		Transitivity		Tau RC		ConCorr
	Slope β	Var υ	Slope β	Var υ	Slope β	Var υ	Slope β	Var υ	Slope β	Var υ	Slope β	Var υ
Size	0.2	−0.32	0.18	−0.32	−0.56+	0.38	0.08	−0.32	0.25	−0.37	−0.15	−0.07
Density, undirected	0.1	0.07	0.15	0.04	0.64*	−0.62*	0.05	0.2	−0.13	0.27	0.54+	−0.3
Indegree Std. Dev.	0.16	−0.31	0.28	−0.39	0.3	−0.34	−0.11	−0.39	0.01	−0.41	−0.06	0.03
Outdegree Std. Dev.	0.03	−0.15	0.23	−0.3	0.09	−0.25	0.06	−0.3	0.02	−0.29	0.17	−0.25
Degree Std. Dev.	0.44	−0.55+	0.52+	−0.62*	0.39	−0.5+	−0.14	−0.53+	0.14	−0.54+	0.18	−0.19
Mean of true score	NA	NA	0.51+	−0.47	0.27	−0.26	−0.21	−0.4	−0.03	−0.01	NA	NA
Directed Network	0.49	−0.4	0.25	−0.21	0.2	−0.24	−0.39	−0.35	0.42	−0.31	0.39	−0.34
Limited Degree	0.74**	−0.69*	0.54+	−0.55+	0.16	−0.22	−0.08	−0.32	0.25	−0.31	0.29	−0.28
% in Largest Bicomponent	0.72**	−0.63*	0.51+	−0.47	0.24	−0.39	−0.17	−0.29	0.29	−0.25	0.63*	−0.58*

Note: Positive correlations mean that networks with higher values of that measure (e.g. size) are more robust to measurement error. The direction of the bias is ignored when calculating the correlations.

⁺P<= 0.1;

^*+P<= 0.05,

^**P<= 0.01

We next turn our attention to the “small-world” statistics, focusing on mean closeness (normalized by log(sample size)) and the transitivity ratio (the proportion of directed triads that are closed). Recall we capture the number of steps between nodes with a closeness score (1/distance) so as the score trends negative, the average closeness is going down, and thus the distance is going up, though not dramatically. As missingness increases, we see over-estimates of the distance between pairs; this, intuitively, must be due to the loss of “bridging” nodes that lower path-lengths disproportionately. Such nodes are likely a minority, but the odds of hitting one of them increase with missingness, leading to an under-estimate of path length. Over all of the networks, it requires 63 percent of the nodes to be removed before bias reaches .5 (see Table 6). The bias on mean distance is especially high when density is low: in sparse networks, the connections between nodes are more dependent on a given path, making distance harder to measure with high levels of missing data.

The transitivity ratio remains largely constant as the proportion missing increases, showing a nearly flat line for all networks except the smallest (interlock). There appears to be a minor negative bias for the next two largest networks (Sorority & Prison), reaching mean bias of about −25% when the network is missing 70% of the cases. But for most networks, the transitivity ratio remains unbiased in the face of heavy randomly missing data. For all networks, the error variability increases with missingness, although this is especially true in the smaller networks.

The combined effect of over-estimating the distance between nodes and a consistent transitivity estimate suggests that small-world statistics will be under-estimated under conditions of missing data; with the average path length being larger than it should be in the presence of missing data while the clustering coefficients will remain largely stable.

The final two measures capture indicators of global network shape. In the first case, we use the distribution of triads (relative to chance expectations) as an indicator of overall network structure. The results for the tau statistic are very consistent: the tau statistic trends lower with increasing missingness (approaching zero), and we see a −50% bias at about 30% missing across all networks (the slope of − 0.12 is nearly the same across networks). The one exception is the smallest network, which has a slightly more negative slope and extreme variability.

Finally, for the ConCorr partitions, the rand statistic decreases slightly relative to the true value, but the line is remarkably flat as more data is removed. This indicates that even in the face of dramatically high missing data, one would likely classify pairs of nodes similarly (those in the same position together, those in different partitions apart), and thus would likely draw similar substantive conclusions.¹⁸ Our blockmodel measure only deals with the partitioning of nodes and ignores the larger macro picture encapsulated in an image matrix. We have thus run additional analyses where the measure of interest is based on the partitioning of nodes and the image matrix (see also Žnidaršič, Ferligoj, and Doreian 2012). The results are included in the Appendix and suggest, generally, that a measure based on the image matrix and node partitioning is less robust to missing data. On average, one can only have 40% missing data and still maintain a bias score under .5, as opposed to almost 70% in the case of just the partitioning.

Looking over all networks and all topology measures (see Table 7), networks that are more cohesive are more robust to the removal of missing nodes. The variance results are more heterogeneous, with some measures exhibiting high levels of variance, and others very little, but in general networks that are more centralized have less variable profiles.

3.2.3 Homophily

Figure 7 presents the results for structural and attribute homophily. If the prior topology results are remarkable in their consistency and robustness in the face of missing data, the assortative mixing statistics tell just the opposite story, with dramatically inconsistent results and significant bias as missingness increases. Note first that to fit these figures we had to increase the length of the y-axis (so the range is now +/− 4), and even in the face of this we often get out-of-range variability. In half of the networks we find almost no bias (slope near 0 and relatively narrow variability bands that cross the zero line), in two we have positive bias and in the remaining 4 negative bias.

Figure 7.

Homophily Score Robustness

Each subgraph plots the distribution of the bias between the true homophily score and the score computed on the network with nodes removed at random. The dark line represents the mean, inner-quartile range with dark gray and 10th/90th percentiles with light gray. β is the regression coefficient of bias regressed against percent missing (divided by 10), and thus represents the expected change in bias for each 10% decline in sample coverage. υ represents the average observed deviation (square-root of total sum of squares divided by n) and R² is the proportion of the variance explainable with the linear regression term. Shaded columns indicate undirected networks.

For both in and out degree mixing, the bias and variance scores correspond directly with the true degree-degree correlations. Networks with negative but absolutely small correlations (Interlock and Prosper for in-degree and Interlock, Prosper and Sorority for out-degree) have strongly positive slopes and large variance. Here, the low initial starting points exaggerate the proportional, or bias based, measure of error. The slopes are positive as the missing data pushes the degree-degree correlations to higher values (by condensing the range of the degree distribution). Conversely, networks with positive but small correlations have strongly negative slopes and large variances. This explains the results for the Sorority, Prosper and Co-citation network for in-degree, as well as the extreme plot for the Elite network for out-degree (where the true correlation is close to 0).

The behavioral results appear largely consistent with the earlier structural results, and are remarkably consistent in the face of high levels of missingness. The “high behavioral” simulation asks what happens to the edgewise correlation score for an attribute that is highly-correlated (0.7+) in the original network. The “low behavioral” analysis does the same for an attribute that correlates at 0.35 or better. When the homophily attribute is very strong, data missing-at-random has almost no effect in 9 of the 12 networks, with only the smallest or most centralized networks having a strong difference. Thus the elite network tends to underestimate the correlation, as does the biotech network (both highly centralized), while the interlock network has the largest variability.

The mean story is almost the same for the lower correlation score, but the variability is much higher, suggesting that as missingness increases we become systematically less likely to be able to draw an observation close to the mean line. Smaller and less centralized networks are less robust to missing data and also have higher levels of variance (note that the effect of centralization weakens or even reverses at higher levels of centralization). See Table 9. For the same level of missing data, smaller networks have fewer dyads informing the homophily estimate and thus have higher bias and uncertainty.

Table 9.

Correlation of missingness robustness scores and network structure: homophily

	Indegree		Outdegree		High Behavioral		Low Behavioral
	Slope β	Var υ	Slope β	Var υ	Slope β	Var υ	Slope β	Var υ
Size	0.6*	−0.42	0.19	−0.08	0.32	−0.32	0.53+	−0.6*
Density, undirected	−0.45	0.28	0.16	−0.24	−0.02	0.04	−0.35	0.42
Indegree Std. Dev.	0.61*	−0.51+	−0.23	0.29	0.11	−0.16	0.5	−0.41
Outdegree Std. Dev.	0.44	−0.37	0.31	−0.28	0.38	−0.36	0.38	−0.27
Degree Std. Dev.	0.65*	−0.51+	−0.16	0.24	0.27	−0.31	0.64*	−0.57+
Mean of true score	0.06	0	0.05	0	0.4	−0.37	0.19	−0.23
Directed Network	−0.31	0.38	−0.21	0.26	0.16	−0.22	0.23	−0.31
Limited Degree	0.03	0.17	−0.22	0.33	0.12	−0.15	0.43	−0.42
% Largest Bicomponent	−0.29	0.36	0.06	−0.01	0.27	−0.31	0.27	−0.29

Note: Positive correlations mean that networks with higher values of that measure (e.g. size) are more robust to measurement error. The direction of the bias is ignored when calculating the correlations.

⁺P<= 0.1;

^*+P<= 0.05,

^**P<= 0.01

4. Conclusion

This paper has explored the effect of missing data on a variety of network measures using a large number of empirical networks. Following past work (Borgatti et al. 2006), we examined the effect of missing data by removing nodes at random from a known network, calculating the statistics of interest on the reduced network and comparing those estimates to those from the true network. We restricted the study to missing-at-random node removal as a means of simplifying the presentation and discussion. We considered empirical networks of varying size and features while examining network measures of centrality, centralization, topology and homophily. By including a large number of networks and measures, we were able to fully describe how and, more importantly, when, missing data would lead to seriously flawed and uncertain estimates.

The results, on the whole, suggest that many network measures can be measured accurately even with high levels of missing data. The exact relationship between bias and missing data varies, however, by the network of interest. For example, larger, more centralized networks are generally more robust to missing data. Other results are more contingent, depending on both the network measure and the network type. Networks that are more cohesive are less robust for centrality measures but more so for measures of topology. Similarly, directed networks are less robust than undirected networks for most centrality measures, but there are few systematic differences for the other network measures.

The overall level of bias is also clearly a function of the network measure itself, as some measures are more susceptible to missing data than others—although, of course, all measures are less accurate as missingness increases. For example, all centrality measures have higher bias with more missing data, but degree based measures are more robust than closeness or betweenness centrality. This differs from some past studies that found little difference across centrality types (Borgatti et al. 2006). Our results may differ from past studies as they focused on Erdos random networks, which are considerably less clustered and hierarchical than the empirical networks considered here. This also reiterates the importance of examining missing data on networks with a wide variety of features, including those typically found in observed social networks (Wang et al. 2012). The topology results suggest that structural measures can be captured well with high levels of missing data, with transitivity and Concorr particularly robust. Distance and the tau statistic are comparatively more prone to error as missingness increases. Finally, for the homophily measures, behavioral similarity shows almost no bias as missing data increases, while mixing by degree performs considerably poorer.

What are the practical implications of these results? First, the results suggest that different collection strategies are necessary for networks of different sizes—at least as it pertains to dealing with the problem of missing nodes. Larger networks are more robust to missing respondents but are also more prone to missing data in the first place. The onus is thus larger in smaller networks to find those last few respondents, but this should also be easier to accomplish. Alternatively, in larger networks, the cost of finding specific respondents may be prohibitive: they may be harder to find while the gain in accuracy is small. Second, if one is faced with large levels of missing data, it may be necessary to use a network measure robust to missingness. For example, if one is interested in homophily but there are high levels of missing data, it may be advantageous to focus on behavioral homophily, as opposed to degree-degree mixing. Or, for macro-structural measures, it may be more useful to examine blockmodeling solutions than distance or bicomponent size. Finally, the results suggest that a researcher must be clear about their tolerance for bias. A researcher interested in a certain network type and network measure would have to collect very different amounts of data to achieve different levels of accuracy. Tables 2, 4, 6, and 8 offer a convenient means to asses target levels, but it is still necessary to know how much bias is acceptable to answer the question at hand.

Table 8.

Maximum percent missing to remain under target bias: homophily

Network	Target Bias	Indegree	Outdegree	High Behavioral	Low Behavioral
Interlock	.25	1	1	38	25
	.5	11	11	58	44
Prison	.25	1	17	*	31
	.5	1	33	*	61
Sorority	.25	1	1	*	41
	.5	1	1	*	68
6th Graders	.25	24	20	*	61
	.5	46	41	*	*
Coauthor	.25	37	37	*	37
	.5	66	66	*	*
Prosper	.25	1	6	*	51
	.5	1	20	*	*
Co-Citation	.25	1	1	*	43
	.5	8	8	*	*
Elites	.25	54	1	26	53
	.5	*	1	*	*
HS 13	.25	20	50	*	*
	.5	40	*	*	*
BioTech	.25	30	30	66	64
	.5	56	56	*	*
HS 24	.25	46	55	*	*
	.5	*	*	*	*
CSprings	.25	41	41	*	*
	.5	*	*	*	*
Mean (Std Dev)	.25	21.4 (20.1)	21.7 (20.4)	63.3 (14.9)	51.3 (15.9)
	.5	36.7 (30.1)	37.3 (28.4)	69 (3.5)	66.9 (7.7)

^*Cases where percent missing is above 70, our observed maximum. In these cases, 70 is used to calculate overall means. The maximum percent missing was calculated based on a quadratic fit to the data.

This paper, while useful in its own right, has also laid the groundwork for future work on missing data in social networks. The simplifying assumption of missing-at-random will be dropped in Part II of this study. Following the work of Huisman (2009) we will examine how missing data affects the validity of network measures when missingness is correlated with centrality. The results will be based on two types of centrality (degree and closeness) as well as 4 correlations between centrality and missingness (−.75, −.25, .25 and .75). In the final part of the project, we will consider practical options for dealing with missing data problems. We will consider different treatments of the partial information, while incorporating a small ego network sample into the estimation process. The hope, in the end, is to provide a practical, comprehensive guide for workers in the field: a researcher will know how biased their estimates are likely to be and how best to deal with such limitations.

Highlights.

• We examine the effect of missing data on measures of centrality, topology and homophily.

• We examine measurement bias and variability across 12 empirical networks.

• Measurement bias varies systematically across network measures and network types.

• Larger, more centralized networks are generally more robust to missing data.

• Cohesive networks are robust to missing data when measuring topology but not centralization.

Appendix: Alternative Measures for ConCorr

This appendix describes the results from 2 supplemental ConCorr analyses. The ConCorr results in the main text use the rand statistic to measure the effect of missing data. The rand statistic captures how many pairs of people are correctly placed into the same/different blocks, compared to the true partition on the full network. As an alternative, this appendix provides the results for the adjusted rand statistic, which accounts for chance expectations (and only counts pairs placed into the same group). Specifically, the adjusted rand can be written as:

$$AR=\frac{\#\mathit{Pairs}in\mathit{Same}\mathit{Group}-\mathit{Expected}\#of\mathit{Pairs}in\mathit{Same}\mathit{Group}}{\mathit{Max}\#of\mathit{Possible}\mathit{Pairs}in\mathit{Same}\mathit{Group}-\mathit{Expected}\#of\mathit{Pairs}in\mathit{Same}\mathit{Group}}$$

In addition to the adjusted rand statistic, we also provide results for a completely different type of blockmodel measure—one that takes into account both node partitioning and the image matrix. The rand statistic only captures the partitioning of nodes into blocks but says little about the macro structure implied by the blockmodel. We have thus rerun the analysis using a measure dependent on the image matrix as well as the node partitioning. Specifically, we begin the analysis by computing the blockmodel on the network of interest. We then use the densities (note not 0s and 1s) in the image matrix, as well as the block memberships, to create a predicted probability matrix. In this predicted probability matrix, the probability of a tie between person i and j is the probability of a tie between the blocks that i and j are in (i.e. the densities in the image matrix). We then correlate the elements of the true probability matrix with the elements of the same matrix estimated under conditions of missing data (restricted to those cases who are sampled in that iteration). The measure thus incorporates both the image matrix, as those densities are used to fill in the predicted probabilities, and the partitioning, as the partitioning determines which densities in the image matrix are selected for each i, j pair.

Table A1.

Maximum percent missing to remain under target bias: ConCorr Results

Network	Target Bias	ConCorr: Unadjusted Rand	ConCorr: Adjusted Rand	ConCorr: Predicted Probability Matrix
Interlock	.25	*	2	3
	.5	*	14	20
Prison	.25	*	1	4
	.5	*	16	24
Sorority	.25	*	1	9
	.5	*	17	34
6th Graders	.25	*	9	23
	.5	*	34	65
Coauthor	.25	*	9	57
	.5	*	28	*
Prosper	.25	*	11	16
	.5	*	32	45
Co-Citation	.25	*	9	22
	.5	*	34	*
Elites	.25	61	4	1
	.5	*	21	13
HS 13	.25	*	5	9
	.5	*	26	39
BioTech	.25	56	1	8
	.5	*	9	27
HS 24	.25	*	3	7
	.5	*	22	30
Csprings	.25	*	1	5
	.5	*	14	25
Mean (Std Dev)	.25	68.1 (4.6)	4.7 (3.8)	13.7 (15.4)
	.5	70 (0)	22.2 (8.5)	38.5 (19.9)

^*Cases where percent missing is above 70, our observed maximum. In these cases, 70 is used to calculate overall means. The maximum percent missing was calculated based on a quadratic fit to the data.