Best Practices for Measuring Students’ Attitudes toward Learning Science

This review presents an overview of some of the common assessment tools available to measure students' attitudes toward learning science. The review also provides widely endorsed, straightforward recommendations for analysis methods with theory and empirical evidence to support analysis plans.

Abstract

Science educators often characterize the degree to which tests measure different facets of college students’ learning, such as knowing, applying, and problem solving. A casual survey of scholarship of teaching and learning research studies reveals that many educators also measure how students’ attitudes influence their learning. Students’ science attitudes refer to their positive or negative feelings and predispositions to learn science. Science educators use attitude measures, in conjunction with learning measures, to inform the conclusions they draw about the efficacy of their instructional interventions. The measurement of students’ attitudes poses similar but distinct challenges as compared with measurement of learning, such as determining validity and reliability of instruments and selecting appropriate methods for conducting statistical analyses. In this review, we will describe techniques commonly used to quantify students’ attitudes toward science. We will also discuss best practices for the analysis and interpretation of attitude data.

Science, technology, engineering, and math (STEM) education has received renewed interest, investment, and scrutiny over the past few years (American Association for the Advancement of Science [AAAS], 2010; President's Council of Advisors on Science and Technology, 2012). In fiscal year 2010 alone, the U.S. government funded 209 STEM education programs costing more than $3.4 billion (National Science and Technology Council, 2011). At the college level, education researchers have predominantly focused greater effort on demonstrating the results of classroom interventions on students’ intellectual development rather than on their development of “habits of mind, values and attitudes” toward learning science (National Research Council, 2012). However, students’ perceptions of courses and attitudes toward learning play a significant role in retention and enrollment (Seymour and Hewitt, 1997; Gasiewski et al., 2012). Motivation has a strong direct effect on achievement (Glynn et al., 2007), and, in some courses, students’ attitudes may provide a better predictor of success than quantitative ability (Steiner and Sullivan, 1984).

The current national effort to comprehensively adopt active-learning strategies in college classrooms (Handelsman et al. 2004; Wood and Handelsman, 2004; AAAS, 2010) provides additional reasons to assess students’ attitudes. Although use of active-learning strategies has repeatedly demonstrated impressive gains in student achievement (Michael, 2006; Freeman et al., 2007, 2011; Armbruster et al., 2009; Haak et al., 2011), these gains may be strongly tied to changes in learning orientation (at least for problem-based methods; Cruce et al., 2006). Additionally, researchers have characterized significant levels of student resistance (Powell, 2003; Yerushalmi et al., 2007; White et al., 2010) and discomfort with the ambiguity, lack of a “right” response, and multiplicity of views found in these methods (Cossom, 1991). For all these reasons, many researchers have increased their focus on measuring students’ engagement, perceived learning gains, motivation, attitudes, or self-efficacy toward learning science.

There are a wide variety of excellent tools available to gather data on student perceptions. Qualitative analysis tools, such as student interviews, provide rich data that can reveal new insights and allow for flexibility and clarification of students’ ideas (Slater et al., 2011). However, analyzing written comments or transcripts can be very labor intensive. Quantitative analysis tools, such as survey instruments, can allow for easier compilation of student responses that attach numerical scores to students’ opinions about different aspects of a curriculum along a continuum, say, 1–5, with 1 being “not useful” to 5 being “very useful” for each aspect. The familiar end-of-semester student evaluations of courses and teachers use a combination of quantitative survey items and qualitative open-ended comments. In addition, the Student Assessment of Their Learning Gains Internet site alone has almost 7800 instructors creating surveys that query students’ perceptions of gains in learning (www.salgsite.org). To draw the most valid conclusions possible from data collected through such tools, it is important for faculty to choose analyses most appropriate for the task. This review is designed to present an overview of some of the common assessment tools available to measure students’ attitudes toward learning science. The review will also provide widely endorsed, straightforward recommendations for analysis methods with theory and empirical evidence to support analysis plans. Our goal is to help education researchers plan attitudinal studies such that they avoid common pitfalls. We would also like to provide advice and references for supporting your approaches to analyzing and displaying attitudinal data.

INVENTORIES (SCALES) FOR ASSESSING STUDENTS’ ATTITUDES

Pen-and-paper assessments used to gauge psychological characteristics such as attitude are commonly referred to interchangeably as inventories, surveys, instruments, or measurement scales. Psychologists use such tools to assess phenomena of interest, such as beliefs, motivation, emotions, and perceptions that are theoretical constructs not directly observable and often composed of multiple facets. The more psychologists know about the theoretical underpinnings of a construct, the more likely they are to develop reliable, valid, and useful scales (DeVellis, 2003). Psychological constructs are often described as latent, meaning they are not directly observed but are instead inferred from direct measurements of theoretically related variables (Lord and Novick, 1968; Borsboom et al., 2003). The most important methodological concern to stress about scales designed to measure a latent construct is that they are not solely a collection of questions of interest to the researcher. Instead, scales are composed of items that have been subjected to tests of validity to show that they can serve as reasonable proxies for the underlying construct they represent (DeVellis, 2003). Bond and Fox (2007) use the history of the development of temperature measures as an analogy for better understanding measurement theory in the social sciences. Although people customarily refer to the reading on a thermometer as “the temperature,” Bond and Fox explain that a thermometer reading is at best an indirect measure. The estimate of temperature is indirect, because it is determined from the known effects of thermal energy on another variable, such as the expansion of mercury or the change in conductivity of an electrical resistor. Similarly, in the social sciences, numerical representations of psychological attributes (e.g., attitude toward science) are derived from theoretical explanations of their effect on a more readily observable behavior (e.g., response to a set of survey items). In this way, an attitudinal scale score serves as a proxy for the latent construct it is purported to measure, and researchers need to be prepared to defend the validity and limitations of their scale in representing it (Clark and Watson, 1995).

Just as one would not consider a single question adequate to evaluate a student's knowledge about a biology topic, one would not evaluate a complex construct, for example, engagement, with a single item. A scale developed to evaluate engagement would undergo a rigorous, iterative validation process meant to determine the aspects of the underlying construct the scale represents and empirically test the hypothesized relationships between the construct and its observable proxy (Clark and Watson, 1995). A measurement scale is composed of a collection of purposely constructed items backed up by empirical evidence of interrelationship and evidence that they represent the underlying construct (Carifio and Perla, 2007). A minimum of six to eight items is recommended to provide for adequate considerations of generalizability, reliability, and validity (Cronbach et al., 1972). Table 1 lists scales for assessing attitudes in college-level biology students who have met standard criteria set for common tests of validity and reliability.

Table 1.

Inventories for assessing students’ perceptions about biology (college-level)

	Instrument
Domain evaluated	Name	Reference	Description
Engagement	Student Course Engagement Questionnaire	http://serc.carleton.edu/files/NAGTWorkshops/assess05/SCEQ.pdf; Handelsman et al., 2005	Twenty-three Likert items assessing perceived skills engagement, participation/interaction engagement, emotional engagement, and performance engagement
Learning gains	Classroom Activities and Outcomes Survey	Terenzini et al., 2001	Twenty-four Likert items rating progress in learning skills related to engineering or general scientific inquiry
		Student Assessment of Learning Gains (SALG)	http://salgsite.org; Seymour et al., 2000	Multiple Likert items within 10 major categories rating gains in learning, skills, and attitudes due to components of a class
		Survey of Undergraduate Research Experiences (SURE)	www.grinnell.edu/academic/csla/assessment/sure; Lopatto, 2004	Twenty Likert items assessing perceived learning gains as a result of participation in undergraduate research
	Undergrad Research Student Self-Assessment	www.colorado.edu/eer/research/undergradtools.html; Hunter et al., 2007	Multiple Likert items assessing perceived gains in skills related to participation in research, yes/no questions categorizing specific experiences, and open-response items
Motivation	Achievement Goal Questionnaire	Elliot and Church, 1997; Finney et al., 2004	Likert items rating performance approach and avoidance goals, and mastery goals
		Motivated Strategies for Learning Questionnaire (MSLQ)	www.indiana.edu/~p540alex/MSLQ.pdf; Pintrich, 1991; Pintrich et al., 1993	Two sections: Motivation section contains 31 Likert items assessing goals and value beliefs; Learning Strategies section contains 31 items assessing cognitive strategies and 19 items related to students' managing resources
	Science Motivation Questionnaire (SMQ)	www.coe.uga.edu/smq; Glynn et al., 2011	Thirty Likert items comprising six components of motivation: intrinsic, extrinsic, relevance, responsibility, confidence, and anxiety
Self-efficacy	College Biology Self-Efficacy	Baldwin et al., 1999	Twenty-three Likert items indicating confidence in performing tasks related to biology courses and at home
Views/attitudes	Biology Attitude Scale	Russell and Hollander, 1975	Twenty-two items: 14 Likert-type and eight semantic differential measuring students’ perceptions of liking or disliking biology
		Colorado Learning Attitudes about Science Survey (CLASS)–Biology	Semsar et al., 2011	Thirty-one Likert-type items for measuring novice-to-expert-like perceptions, including enjoyment of the discipline, connections to the real world, and underlying knowledge and problem-solving strategies.
		Environmental Values Short Form	Zimmermann, 1996	Thirty-one Likert items assessing level of agreement with statements describing concern for different environmental issues
		Views About Sciences Survey (VASS)	http://modeling.asu.edu/R%26E/Research.html; Halloun and Hestenes, 1996	Fifty items: Students choose a value describing their position with regard to two alternate conclusions to a statement probing their views about knowing and learning science in three scientific and three cognitive dimensions.
		Views on Science and Education (VOSE)	www.ied.edu.hk/apfslt/download/v7_issue2_files/chensf.pdf; Chen, 2006	Fifteen items for which several statements or claims are listed. Respondents choose their level of agreement to these series of predetermined statements/claims to provide reasoning behind their opinion.
	Views on Science-Technology-Society (VOSTS)	www.usask.ca/education/people/aikenhead; Aikenhead and Ryan, 1992	One hundred fourteen multiple-choice items that describe students’ views of the social nature of science and how science is conducted

The basic assumption behind attitude scales is that it is possible to uncover a person's internal state of beliefs, motivation, or perceptions by asking them to respond to a series of statements (Fraenkel and Wallen, 1996). Individuals indicate their preference through their degree of agreement with statements on the scale. Items containing these statements are constructed with three common response formats: dichotomous agree/disagree, semantic-differential, and Likert formats (Crocker and Algina, 2008). In all cases, the items consist of two parts: a question stem and a response option (Figure 1). Dichotomous items contain just two response options (1 = yes, 2 = no; or 0 = disagree, 1 = agree) following a simple declarative statement. Semantic-differential items use a bipolar adjective (opposite-meaning) list or pair of descriptive statements that examinees use to select the response option out of a range of values that best matches their agreement. These semantic-differential items measure connotations. (Figure 1 contains semantic-differential items from Lopatto [2004].) As demonstrated in Table 1, Likert items are the most common response formats used in attitude scales. They offer multiple response categories that usually span a 5-point range of responses, for example, A = “strongly agree” to E = “strongly disagree,” but may span any range. (Figure 1 contains Likert response–format items from Russell and Hollander [1975] and Seymour et al. [2000].) Generally, internal-consistency reliability is increased and sufficient variances obtained when more than four response options are used (Masters, 1974; Comrey, 1988). In addition to the increase in reliability when moving from the dichotomous 2-point range to a 4- or 5-point range, statisticians have demonstrated an increase in type II error rates in 2-point response formats (Cohen, 1983). Response options may be delineated by numbers, percentages, or degrees of agreement and disagreement. Response options may also be structured in several equivalent ways: a numbering system, letters to indicate the responses, or just end points indicated (Frisbie and Brandenburg, 1979; Lam and Klockars, 1982).

Figure 1.

Common inventory items for assessing attitude. The three most common types of items used in attitude inventories or scales include: dichotomous, semantic-differential, and Likert-type items. All three formats consist of a question stem followed by several response options. Each of these three types differ in the number and types of response options. Dichotomous items contain just two response options, while semantic-differential and Likert-type items are polytomous. Semantic-differential items use a bipolar adjective list or pair of descriptive statements that examinees use to select a response option out of a range of values that best matches their agreement. Likert-type items include a declarative statement followed by several levels of agreement along a span of (usually) five to seven response options. Semantic-differential items from Lopatto (2004). Likert response–format items from Russell and Hollander (1975) and Seymour et al. (2000).

TYPES OF DATA COLLECTED IN ATTITUDINAL SURVEYS

Psychologist Stanley Smith Stevens is credited with developing the theory of data types that are pertinent for pen-and-paper tests used to measure psychological constructs (Stevens, 1946). He set forward “basic empirical operations” and “permissible statistics” for the four levels of measurement scales, terms, and rules he developed to describe the properties of different kinds of data: nominal, ordinal, interval, or ratio (Table 2). Data collected in a nominal format describe qualitative traits, categories with no inherent order, such as demographic information like nationality or college major. Responses to dichotomous items are considered nominal when 0 and 1 merely serve as descriptive tags, for example, to indicate whether someone is male or female (Bond and Fox, 2007). However, dichotomous items may be used to generate ordinal rather than nominal data. For example, the disagree/agree or unsatisfied/satisfied responses to dichotomous items generate data for which a value of 1 represents a meaningfully greater value than that represented by 0. Ordinal data are nominal data with an added piece of quantitative information, a meaningful order of the qualities being measured. This means these data can be rank-ordered (first, second, third, …). In addition to these agree/disagree dichotomous items, responses to semantic-differential items ask participants to place themselves in order along a continuum between two adjectives. Likert items ask participants to rank a set of objects or statements with response options over a range of values: “strongly disagree,” “disagree,” “neutral,” “agree,” and “strongly agree.” These would also commonly be described as ordinal, because the response choices on a particular item are arranged in rank order of, in this case, least amount of agreement to most (Jamieson, 2004; Carifio and Perla, 2007; Norman, 2010). Both nominal and ordinal data are described as categorical, whereas the two other levels of measurement—interval and ratio—are quantitative (Agresti, 2007). Quantitative data can be further classified as discrete quantitative, only being able to take on certain values, or as continuous quantitative, theoretically able to take on any value within a range (Steinberg, 2011).

Table 2.

Levels of measurement provided by data and appropriate statistical techniques

	Level of measurement
	Categorical		Quantitative
Type of data:	Nominal	Ordinal	Interval	Ratio
Characteristics	Qualitative (unordered)	Hierarchical (rank)	Equal intervals (rank) (equal intervals)	Equal ratios (rank) (equal intervals) (includes zero)
Examples	Gender (male, female)	Preference (first, second, third)	Temperature (15°C)	Age in years (20)
		Individual Likert items	Interrelated items comprising Likert scale
Appropriate statistics
Distribution	Nonparametric		Parametric
Central tendency	Mode	Median	Mean/SD
Analysis methods	Inferential categorical data analysis, Fisher's exact test		IRT, ANOVA, t tests, regression

CATEGORICAL (NONPARAMETRIC) VERSUS QUANTITATIVE (PARAMETRIC) DATA ANALYSIS PROCEDURES

In inferential statistics, tests are conducted to determine the plausibility that data taken from a smaller random sample are representative of the parameters measured were the data to be observed for the entire population (Moore, 2010). (See Table 3 for a glossary of statistical terms.) Researchers commonly refer to the statistical tools developed for analyzing categorical data with a nominal or ordinal dependent variable as nonparametric and include the median test; Mann-Whitney U-test; Kruskal-Wallis one-way analysis of variance (ANOVA) of ranks; and Wilcoxon matched-pairs, signed-ranks test (Huck, 2012). These tests involve fewer assumptions than do the parametric test procedures developed for use with quantitative interval- or ratio-level data (such as the assumptions of normality of the distributions of the means and homogeneity of variance that underlie the t and F tests). Parametric statistics are so named because they require an estimation of at least one parameter, assume that the samples being compared are drawn from a population that is normally distributed, and are designed for situations in which the dependent variable is at least interval (Stevens, 1946; Gardner, 1975). Researchers often have a strong incentive to choose parametric over nonparametric tests, because parametric approaches can provide additional power to detect statistical relationships that genuinely exist (Field, 2009). In other words, for data that do meet parametric assumptions, a nonparametric approach would likely require a larger sample to arrive at the same statistical conclusions. Although some parametric techniques have been shown to be quite robust to violations of distribution assumptions and inequality of variance (Glass et al., 1972), researchers will sometimes convert raw scores into ranks to utilize nonparametric techniques when these assumptions have been violated and also when sample sizes are small (Huck, 2012).

Table 3.

Glossary

ANOVA (analysis of variance): An overall test of whether means differ between groups. Useful when there are three or more categorical independent variables and a quantitative dependent variable. Special case of linear regression.
ANCOVA (analysis of covariance): Test of whether means differ between groups after controlling for covariate(s). Useful for removing bias of nonexperimental independent variables that are likely to influence the dependent variable. Multiple regression with dummy-coded variables is an alternative method for examining group effects while controlling for confounds.
Central tendency: Refers to a central value that summarizes with one number a cluster of numerical data. The most common measures of central tendency are mean, median, and mode. Less common measures include geometric mean and harmonic mean.
Chi-square test: Useful as a test for association between two nominal variables that each have two or more possible values. Tests whether the relative proportions of one variable are independent of the other. Consider using Fisher's exact test when sample is small or some response option frequencies are very low.
Cochran-Mantel-Haenszel test: Tests for association between two dichotomous variables while controlling for another dichotomous variable. Example situation: recoding a Likert item as a binary variable (1 = agree, 0 = neutral or disagree), then analyzing whether being in one of two treatment groups is associated with responding “agree,” while controlling for another dichotomous variable, such as gender.
Coefficient alpha (aka Cronbach's alpha [α]; KR-20): An estimate of a scale's internal consistency (a form of reliability). Based on item covariances, quantifies the homogeneity of items that make up a scale. Ranges from 0 to 1, with α ≥ 0.80 and α ≥ 0.90 commonly described, respectively, as good and excellent levels of internal consistency.
Item: The basic component of a test or attitudinal measure. Refers to the text of the question or item itself, as opposed to the response format of the item.
Item response theory (IRT; latent trait theory; Rasch model): Psychological measurement theory in which responses to items can be accounted for by latent traits that are fewer in number than the items on a test. Most applications of this theory assume a single latent trait and enable the creation of a mathematical model of how examinees at different ability levels for the latent trait should respond to an individual item. This theory does not assume that all items are of equal difficulty, as is commonly done in classical test theory. Because it allows for comparison of performance between individuals, even if they have taken different tests, it is the preferred method for developing scales (especially for high-stakes testing, such as the Graduate Record Exam). Danish mathematician, Georg Rasch, one of the three pioneers of IRT in the 1950s and 1960s, is credited with developing one of the most commonly used IRT models—the one-parameter logistic model for which all items are assumed to have the same discrimination parameter.
Kruskal-Wallis H (aka Kruskal-Wallis one-way ANOVA): A nonparametric overall test of whether medians differ between groups. Useful when there are three or more categorical independent variables and an ordinal dependent variable.
Level of measurement: Refers to theoretical descriptions of data types. Includes nominal data (categorical with no inherent order), ordinal (ordered categories), interval (quantitative data with equal distances from on unit to the next), or ratio (all properties of interval plus a true zero).
Mann-Whitney U (aka MWW; Wilcoxon rank-sum): A nonparametric test of whether two medians are different. Useful when there are two categorical independent variables and an ordinal dependent variable.
Question stem: The first part of an item that presents the problem to be addressed or statement to which the examinee is asked to respond.
Reliability: The consistency or stability of a measure. The extent to which an item, scale, test, etc., would provide consistent results if it were administered again under similar circumstances. Types of reliability include test–retest reliability, internal consistency, and interrater reliability.
Response format: Following a question stem or item on a test or attitudinal measure, an array of options that may be used to respond to the item.
Dichotomous: Examples include true/false, yes/no, and agree/disagree formats.
Semantic differential: Two bipolar descriptors are situated on each side of a horizontal line or series of numbers (e.g., “agree” to “disagree”), which respondents use to indicate the point on the scale that best represents their position on the item.
Likert: Response levels anchored with consecutive integers, verbal labels intended to have more or less even differences in meaning from one category to the next, and symmetrical response options. Example: Strongly disagree (1), Somewhat disagree (2), Neither agree nor disagree (3), Somewhat agree (4), Strongly agree (5).
Scale: Although there are several different common usages for scale in psychometric literature (the metric of a measure, such as inches; collection of related test items; an entire psychological test), we use the term to mean a collection of empirically related items on a measure. A Likert scale refers to multiple Likert items measuring a single conceptual domain. A Likert item, on the other hand, specifically refers to a single Likert item that consists of multiple response options.
t test (aka Student's t test): A statistical test of whether two means differ. Useful when there are two categorical independent variables and one quantitative dependent variable.
Validity: In psychometrics, the extent to which an instrument measures what it is designed to measure. Demonstrated by a body of research evidence, not by a single statistical test. Types of validity include content validity, criterion validity, and construct validity.

The assumption that parametric tests should only be used with interval-level dependent variables is central to the ongoing debate about appropriate analyses for attitudinal data. Statistics such as mean and variance—what are commonly the parameters of interest—are only truly valid when data have meaningfully equidistant basic units; otherwise, using these statistics is “in error to the extent that the successive intervals on the scale are unequal in size” (Stevens, 1946, p. 679). Data from well-designed psychological measurement scales, however, can have properties that appear more interval than ordinal in quality, making classification based on Stevens’ guidelines more ambiguous (Steinberg, 2011). This has led to a great deal of conflicting recommendations over whether to use parametric or nonparametric data analysis procedures for scales based on ordinal data from dichotomous and semantic-differential items, but particularly for Likert-type items (Knapp, 1990; Carifio and Perla, 2008). For example, some sources argue that assigning evenly spaced numbers to ordinal Likert-response categories creates a quantitative representation of the response options that is more interval than ordinal and, therefore, practically speaking, could be analyzed as interval quantitative data. This argument supports computing means and SDs for Likert-response items (Fraenkel and Wallen, 1996) and utilizing parametric statistical analysis techniques (e.g., ANOVA, regression) designed for interval data (Norman, 2010). Others argue that equivalency of distances between ranked responses in a Likert-response format should not be assumed and, thus, treating responses to a Likert item as ordinal would lead to a more meaningful interpretation of results (Kuzon et al., 1996; Jamieson, 2004; Gardner and Martin, 2007). Stevens (1946) even offered this pragmatic suggestion: “In the strictest propriety, the ordinary statistics involving means and SDs ought not to be used with these [ordinal] scales, for these statistics imply a knowledge of something more than the relative rank-order of data. On the other hand, for this ‘illegal’ statisticizing there can be invoked a kind of pragmatic sanction: In numerous instances it leads to fruitful results” (p. 679).

The reasoning behind varying perspectives on appropriate procedures for analysis of data involving ordinal items has been addressed in further detail elsewhere (Harwell and Gatti, 2001; Carifio and Perla, 2007, 2008; Norman, 2010). Marcus-Roberts and Roberts (1987) sum it up best by saying that although it may be “appropriate” to calculate means, medians, or other descriptive statistics to analyze ordinal or ranked data, the key point is “whether or not it is appropriate to make certain statements using these statistics” (p. 386). The decision to analyze ordinal responses as interval quantitative data depends heavily on the purpose of the analysis. In most cases, ordinal-response measurement scales are used to gather data that will allow inferences to be made about unobservable constructs. To simply accept the data as interval would be to ignore both the subjectivity of these opinion-type questions and the response format the numbers represent. The decision clearly needs to first take into account how the sample investigated can be analyzed to infer characteristics about the population as a whole. The sample in this case includes: 1) the individuals surveyed and 2) the number and nature of the questions asked and how they represent the underlying construct. In the following section, we will provide recommendations for analyzing ordinal data for the three most common response formats used in attitudinal surveys. We will argue that, for semantic-differential and Likert-type items, the question of which analysis to perform hinges on the validity of making conclusions from a single item versus a scale (instrument subjected to tests of validity to support representation of an underlying construct).

RECOMMENDED STATISTICAL ANALYSES FOR ATTITUDINAL DATA

Dichotomous Items

There are a variety of statistical test procedures designed for nonparametric data that are strictly nominal in nature. We will focus on providing recommendations for analysis of dichotomous items producing ordinal data because these are most common in attitudinal surveys. For an excellent overview and treatment of comparisons of many different types of categorical data, we recommend reading the chapter “Inferences on Percentages and Frequencies” in Huck (2012, Chapter 17, pp. 404–433) and in Agresi (2007, Chapters 1–4, pp. 1–120). Let us consider a hypothetical research question: Imagine that a researcher wishes to compare two independent samples of students who have been surveyed with respect to dichotomous items (e.g., items that ask students to indicate whether they were satisfied or unsatisfied with different aspects of a curriculum). If the researcher wishes to compare the percentage of the students in one group, who found the curriculum satisfying, with the percentage of students in the second group, who did not, he or she could use Fisher's exact test, which is used for nonparametric data, often with small sample sizes, or an independent-samples chi-square test, which is used for parametric data from a larger sample size (Huck, 2012). The independent-samples chi-square test has the added benefit of being useful for more than two samples and for multiple categories of responses (Huck, 2012). This would be useful in the scenario in which a researcher wished to know whether the frequency of satisfaction differed between students with different demographic characteristics, such as gender or ethnicity. If the researcher wished to further examine the relationship between two or more categorical variables, a chi-square test of independence could be used (Huck, 2012).

Semantic-Differential and Likert Items

As described in Table 2, a semantic-differential or Likert item on its own is most likely ordinal, but a composite score from a measurement scale made up of the sum of a set of a set of interrelated items can take on properties that appear much more continuous than categorical, especially as response options, items, and sample size increase (Carifio and Perla, 2007). For these reasons, many researchers use parametric statistical analysis techniques for summed survey responses, in which they describe central tendency using means and SDs and utilize t tests, ANOVA, and regression analyses (Steinberg, 2011). Still, taking on qualities that appear more continuous than ordinal is not inherently accompanied by interval data properties. A familiar example may better illustrate this point. Consider a course test composed of 50 items, all of which were written to assess knowledge of a particular unit in a course. Each item is scored as either right (1) or wrong (0). Total scores on the test are calculated by summing items scored correct, yielding a possible range of 0–50. After administering the test, the instructor receives complaints from students that the test was gender biased, involving examples that, on average, males would be more familiar with than females. The instructor decides to test for evidence of this by first using a one-way ANOVA to assess whether there is a statistically significant difference between genders in the average number of items correct. As long as the focus is superficial (on the number of items correct, not on a more abstract concept, such as knowledge of the unit), these total scores are technically interval. In this instance, a one-unit difference in total score means the same thing (one test item correct) wherever it occurs along the spectrum of possible scores. As long as other assumptions of the test were reasonable for the data (i.e., independence of observations, normality, homogeneity of variance; Field, 2009), this would be a highly suitable approach.

But the test was not developed to blindly assess number of items correct; it was meant to allow inferences to be made about a student's level of knowledge of the course unit, a latent construct. Let us say that the instructor believes this construct is continuous, normally distributed, and essentially measuring one single trait (unidimensional). The instructor did his or her best to write test items representing an adequate sample of the total content covered in the unit and to include items that ranged in difficulty level, so a wide range of knowledge could be demonstrated. Knowing this would increase confidence that, say, a student who earned a 40 knew more than a student who earned a 20. But how much more? What if the difference in the two scores were much smaller, for example, 2 points, with the lower score this time being a 38? Surely, it is possible that the student with the 40 answered all of the easier items correctly, but missed really difficult questions, whereas the student with the 38 missed a few easy ones but got more difficult questions correct. Further, would a point difference between two very high scores (e.g., between 45 and 50) mean the same amount of knowledge difference as it would for the same difference between two midrange scores (e.g., 22 and a 27)? To make such claims would be to assume a one-to-one correspondence between a one-unit change in items correct and a one-unit change in knowledge. As Bond and Fox (2007) point out, “scales to which we routinely ascribe that measurement status in the human sciences are merely presumed … almost never tested empirically” (p. 4).

The above example illustrates how data with interval qualities can emerge from nominal/ordinal data when items are combined into total scores, but that the assumption of interval properties breaks down when, without further evidence of a one-to-one correspondence, we use the observed total score to indirectly measure a latent construct, such as knowledge or attitude toward a course. As a solution to this problem, many in the measurement field point to item-based psychometric theory, such as Rasch modeling and item response theory (IRT), techniques that allow ordinal data to be rescaled to an interval metric (Harwell and Gatti, 2001). This is accomplished by using the response data for each item of large samples of respondents as empirical evidence to assess and calibrate the mathematical measurement model of their instrument (Ostini and Nering, 2006; Bond and Fox, 2007). In short, item response approaches do not assume equal contributions across items to measuring a construct, but instead assume that the probability of a particular response to an item—such as choosing “strongly agree” for a statement related to having a positive attitude toward learning science—is a function of item parameters (e.g., how endorsable the item is) and person parameters (i.e., how much of the latent trait the person possesses). (See Ostini and Nering, 2006.) Once these parameters are reasonably estimated, the measurement model for the instrument allows the researcher to estimate a new respondent's location along the latent trait being measured by using an interval continuous scale (Bond and Fox, 2007). A comprehensive treatment of the work involved in developing an IRT-based measure is beyond the scope of this article, but we recommend the article “Rescaling Ordinal Data to Interval Data in Educational Research” by Harwell and Gatti (2001) for an accessible account and examples of how IRT can be used to rescale ordinal data. We also recommend the book Applying the Rasch Model: Fundamental Measurement in the Human Sciences by Bond and Fox (2007), which provides a context-rich overview of an item-based approach to Likert survey construction and assessment.

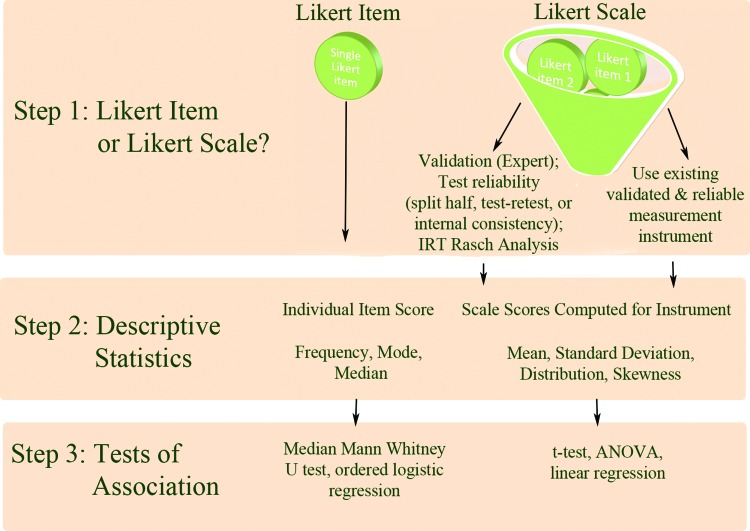
So, to summarize, for surveys that contain either semantic-differential and Likert-type items, decisions about analysis begin by first determining whether you are analyzing data from a single item or from a scale composed of validated interrelated items (ideally with IRT item characteristics curves to determine the probability of a particular response to an item as a function of the underlying latent trait). Figure 2 presents a decision matrix based on this initial step and offering recommended descriptive statistics and appropriate tests of association in each case.

Figure 2.

Best practice flowchart. This flowchart can help with decisions that you make while planning your study. It diagrams appropriate approaches to represent and analyze your data once you are in the analysis stage.

LIKERT DATA ANALYSIS EXAMPLE FROM BIOLOGY EDUCATION

In a study published in a science education research journal, the authors gave a survey of attitudes, concepts, and skills to students in a science research program. Students were surveyed pre-, mid-, and postprogram. The survey consisted of Likert-style items (coded 1–5). Students surveyed were engaged in either a traditional model program or a collaborative model program.

Likert Scale Analysis

In the article, the authors tested the internal reliability (using Cronbach's α) of each set of items (attitudes, concepts, and skills) within the survey to see whether it would be reasonable to analyze each set of items as three separate scales. They wanted to exclude the possibility that all items correlated equally well together, thus indicating they perhaps described a unidimensional, single, latent trait. Also, if the items did not correlate together as predicted, the authors would not have had evidence supporting the validity of the items comprising a scale and should not then sum them to create scores for each scale. The researchers set a criterion that each scale had to meet an α of 0.70 or greater for this to be an appropriate procedure. Scale scores were then analyzed as the dependent variable in separate repeated-measures ANOVAs with gender, ethnicity, and treatment group as between-subject factors.

What Is Defendable about This Approach?

The authors checked the reliability of their Likert item sets prior to summing them for analysis. Analyzing a Likert scale (i.e., sum of Likert items), as opposed to single Likert items, likely increased the reliability of the outcome variable. Providing an estimate of the internal consistency of each Likert scale increased confidence that items on each scale were measuring something similar.

What Might Improve This Approach?

The authors reported the internal consistency (a form of reliability) for each of the three scales and the results of their ANOVAs involving these scales, but no other descriptive information about the data, such as measures of central tendency or dispersion. The authors used ANOVA without providing evidence that the data assumptions of this parametric test were met. Although ANOVA is robust in the face of some violations of basic assumptions, such as normality and homogeneous variances with equal sample sizes (Glass et al., 1972), describing the data would help the reader to better judge the appropriateness of the analyses. Further, the authors’ use of ANOVA treats the dependent variable as interval, but no argument for doing so or limitation of interpretation was provided. For example, the authors could conduct exploratory factor analysis in addition to computing internal reliability (using Cronbach's α) to provide evidence of the clustering of items together in these three categories. Also, if they had adequate numbers of responses, they could use Rasch modeling (IRT) to determine whether the items were indeed of equal difficulty to suggest interval qualities. (See Table 4 for more sources of information about the specifics of ANOVA and its assumptions.) It is also worth noting that, in psychological measurement, many other aspects of reliability and validity of scales are standard in preliminary validation studies. Evidence of other aspects of the scale's reliability (e.g., split-half, test–retest) and validity (e.g., convergent validity, content validity) would bolster any claims that these scales are reliable (i.e., provide consistent, stable scores) and valid (i.e., measure what they purport to measure). Table 4 also contains resources for further information related to these common issues in measurement theory. If the data were judged to be a poor fit with the assumptions of ANOVA, the authors could have chosen a nonparametric approach instead, such as the Mann-Whitney U-test.

Table 4.

Suggested further reading

ANOVA and assumptions	Keppel and Wickens, 2004
Basics of categorical data analysis for behavioral science	Agresti, 2007; Azen and Walker, 2011
Basics of measurement theory	Crocker and Algina, 2008
Basic statistical methodology	Field, 2009
Design and analysis of survey questionnaires	Fowler, 1995; Groves et al., 2004; Presser et al., 2004
Item response theory	Ostini and Nering, 2006; Bond and Fox, 2007
Scale development basics	DeVellis, 2003; Adams and Wieman, 2011
Validity	Clark and Watson, 1995

LIKERT-ITEM ANALYSIS

In the same article, the authors targeted several individual Likert items from the scale measuring self-perceptions of science abilities. The student responses to these items were summarized in a table. The authors chose these particular items, because students’ responses were indicative of key differences between two types of educational programs tested. The items were included in the table, along with the proportions of students responding “definitely yes” regarding their perceived ability level for a particular task. The authors then conducted separate Fisher exact tests to tests for differences in proportions within the “definitely yes” categories by time (pre-, mid-, and postcourse) and then by program model.

What Is Defendable about This Approach?

When analyzing individual Likert items, the authors used a nonparametric test for categorical data (i.e., Fisher's exact test for proportions). As these Likert items were ordinal to the best of the authors’ knowledge, a nonparametric test was the most fitting choice.

What Might Improve This Approach?

The authors transformed the items into dichotomous variables (i.e., 1 = definitely yes; 0 = chose a lesser category) instead of analyzing the entire spectrum of the 5-point response format or collapsing somewhere else along the range of options. There should be substantive reasons for collapsing categories (Bond and Fox, 2007), but the authors did not provide a rationale for this choice. It often makes sense to do so when there is a response choice with very few or no responses. Whatever the author's reason, it should be stated.

RECOMMENDATIONS

Validation of an attitudinal measure can be an expensive and labor-intensive process. If you plan to measure students’ science attitudes during the planning phases of your study, look for measurement instruments that have already been developed and validated to measure the qualities you wish to study. If none exist, we recommend collaborating with a measurement expert to develop and validate your own measure. However, if this is not an option—for instance, if you are working with pre-existing data or you do not have the resources to develop and validate a measure of your own—keep in mind the following ideas when planning your analyses (Figure 2).

Avoid Clustering Questions Together without Supportive Empirical Evidence

In some analyses we have seen, the researcher grouped questions together to form a scale based solely on the researcher's personal perspective of which items seemed to fit well together. Then the average score across these item clusters was presented in a bar graph. The problem with this approach is that items were grouped together to make a scale score based on face validity alone (in this case, the subjective opinion of the researcher). However, no empirical evidence of the items covariance or relationship to some theoretical construct was presented. In other words, we have no empirical evidence that these items measure a single construct. It is possible, but it is not always easy, to predict how well items comprise a unidimensional scale. Without further evidence of validity, however, we simply cannot say either way. Failing to at least include evidence of a scale's internal consistency is likely to be noticed by reviewers with a measurement background.

Report Central Tendency and Dispersion Accordingly with the Data Type

For Likert items (not scales), we recommend summarizing central tendency using the median or the mode, rather than the mean, as these are more meaningful representations for categorical data. To give the reader a sense of the dispersion of responses, provide the percentage of people who responded in each response category on the item. In the case of a well-developed scale, it is more appropriate to compute mean scores to represent central tendency and to report SDs to show dispersion of scores. However, keep in mind the admonitions of those who champion item response approaches to scale development (e.g., Bond and Fox, 2007): If your measure is of a latent construct, such as student motivation, but your measure has not been empirically rescaled to allow for an interval interpretation of the data, how reasonable is it to report the mean and SD?

For Scales, Statistical Tests for Continuous Data Such as F and t tests May Be Appropriate, but Proceed with Caution

Researchers are commonly interested in whether variables are associated with each other in data beyond chance findings. Statistical tests that address these questions are commonly referred to as tests of association or, in the case of categorical data, tests of independence. The idea behind a test of independence (e.g., chi-square test) is similar to commonly used parametric tests, such as the t test, because both of these tests assess whether variables are statistically associated with each other. If you are testing for statistical association between variables, we do not recommend analyzing individual Likert items with statistical tests such as t tests, ANOVA, and linear regression, as they are designed for continuous data. Instead, nonparametric methods for ordinal data, such as the median Mann-Whitney U-test, or parametric analyses designed for ordinal data, such as ordered logistic regression (Agresti, 2007), are more appropriate. If you are analyzing a Likert scale, however, common parametric tests are appropriate if the other relevant data assumptions, such as normality, homogeneity of variance, independence of errors, and interval measurement scale, are met. See Glass et al. (1972) for a review of tests of the robustness of ANOVA in the cases of violations of some of these assumptions. Remember, though, just like an F-test in an ANOVA, statistical significance only refers to whether variables are associated with each other. In the same way that Pearson's r or partial eta-squared with continuous data estimate the magnitude and direction of an association (effect size), measures of association for categorical data (e.g., odds ratio, Cramer's V) should be used in addition to tests of statistical significance.

If you are using statistical methods appropriate for continuous data, gather evidence to increase your confidence that your data are interval, or at least approximately so. First, research the psychological characteristic you are intending to measure. Inquire whether theory and prior research support the idea that this characteristic is a unidimensional continuous trait (Bond and Fox, 2007). Test to see that the data you have collected are normally distributed. If you have developed your own items and scales, provide response options with wordings that model an interval range as much as possible. For example, provide at least five response options, as Likert items with five or more response options have been shown to behave more like continuous variables (Comrey, 1988). If possible, run your analyses with nonparametric techniques and compare your results. If your study will include nonparametric data that may only show small effects, plan from the start for a suitable sample size to have enough statistical power.

SUMMARY

Student attitudes impact learning, and measuring attitudes can provide an important contribution to research studies of instructional interventions. However, the conclusions made from instruments that gauge attitudes are only as good as the quality of the measures and the methods used to analyze the data collected. When researchers use scores on attitudinal scales, they must remember these scores serve as a proxy for a latent construct. As such, they must have supporting evidence for their validity. In addition, data assumptions, including the level of measurement, should be carefully considered when choosing a statistical approach. Even though items on these scales may have numbers assigned to each level of agreement, it is not automatically assumed that these numbers represent equally distant units that can provide interval-level data necessary for parametric statistical procedures.