The strong Nagata conjecture

Abstract

It is proved that there exist wild coordinates in the polynomial algebra in three variables over a field of characteristic zero. This result implies the famous Nagata conjecture.

Let P_n = K[x₁, x₂,..., x_n] be the polynomial algebra in n variables x₁, x₂,..., x_n over a field K of characteristic 0. A K-automorphism φ ∈ Aut_KP_n is called elementary if φ preserves all but one x_i for i = 1,..., n. In other words, a K-automorphism φ ∈ Aut_KP_n is elementary if it can be expressed as

where 0 ≠ a ∈ K, q ∈ K[x₁,..., x_j–1, x_j + 1,..., x_n]. A K-automorphism φ ∈ Aut_KP_n is called tame if φ can be decomposed as a product of elementary automorphisms. Otherwise φ is called wild. A polynomial p ∈ P_n is called a coordinate polynomial (or just a coordinate for short) if there exists φ ∈ Aut_KP_n such that φ(p) = x₁. Moreover, a coordinate p ∈ P_n is called a tame coordinate if there exists a tame automorphism φ ∈ Aut_KP_n such that φ(p) = x₁. Otherwise p is called a wild coordinate. The notion of the tame and wild coordinates plays an important role in the study of automorphisms of polynomial algebras in refs. 1–5. Jung (6) in 1942 [Char(K) = 0] and van der Kulk (7) in 1953 [Char(K) > 0] proved that all automorphisms of P₂ are tame. As an immediate consequence, all coordinates of P₂ are tame as well. Nagata (8) conjectured in 1972 that there exist wild automorphisms in Aut_KP₃. The famous Nagata conjecture was recently proved by Shestakov and Umirbaev (9–11). However, the following strong version of the Nagata conjecture remains open.

Strong Nagata Conjecture

There exist wild coordinates of P₃. The history of the strong Nagata conjecture naturally goes back to 1972 when the Nagata conjecture was formulated. However, it was formulated formally in June 2002 by J.-T.Y. in an algebra seminar held at the University of Hong Kong. Obviously the strong Nagata conjecture implies the Nagata conjecture but not vice versa, since it is possible that an image f of x under a wild automorphism φ:(x, y, z) → (f, g, h) of P₃ = K[x, y, z] can be taken to x by a tame automorphism.

In this article, we settle the strong Nagata conjecture affirmatively. Our result is the following.

Main Theorem

There exist wild coordinates of P₃. In particular, all wild coordinates of K[z][x, y] (see refs. 1 and 2) are also wild coordinates of P₃ = K[x, y, z]. Moreover, the image of x, y, z under a wild automorphism in Aut_K(P₃) must contain at least two wild coordinates.

Before proving the main theorem in the next section, let us describe the main idea of this article introduced by J.-T.Y. when he formulated the strong Nagata conjecture in the same algebra seminar [this idea was motivated by a similar idea used by Shpilrain and Yu (12) to effectively classify parametrized curves; see also ref. 13]: a given coordinate p = p(x, y, z) ∈ P₃: = K[x, y, z] can be faithfully parametrized as a triple , where p(x(u, v), y(u, v), z(u, v)) = 0 and K[x(u, v), y(u, v), z(u, v)] = K[u, v]. It can be seen that p = p(x, y, z) is a tame coordinate of P₃ if and only if there exists a sequence of elementary automorphisms of P₃ that takes the triple (x(u, v), y(u, v), z(u, v)) to (0, u, v). This condition can be effectively determined by an algorithm motivated by ideas of Shestakov and Umirbaev (9–11). By the algorithm, we are able to prove that all wild coordinates of K[z][x, y] (1, 2) are also wild coordinates of P₃ = K[x, y, z], hence we obtain many wild coordinates of P₃. Note that a tame automorphism takes a wild coordinate to a wild coordinate; this way we also obtain many wild coordinates.

In the sequel we use the following conventions: (i) K is a field of characteristic zero; (ii) all automorphisms are K-automorphisms unless specified otherwise, and AutP_n always means Aut_KP_n; (iii) algebraic (linear) independency (dependency) always means K-algebraic (K-linear) independency (dependency); (iv) an automorphism φ of P_n with φ(x_i) = p_i is denoted (p₁,..., p_n) sometimes, and each p_i is called a coordinate of φ; and (v) p̄ denotes the highest homogeneous part of a polynomial p ∈ P_n.

Proof of the Main Theorem

We start with some preliminaries. In ref. 14, the Poisson bracket of elements of the algebra P_n was defined. If f, g ∈ P_n, then

The Poisson bracket satisfies the Leibniz identity, i.e.

[1]

For every element f ∈ P_n the highest homogeneous part f̄ and the degree deg f can be defined in an ordinary way, if we put deg (x_i) = 1, where 1 ≤ i ≤ n.

The next lemma was proved in ref. 14.

Lemma 1. Two polynomials f, g ∈ P_n are algebraically dependent if and only if [f, g] = 0.

Lemma 2. Elements f, g ∈ P_n are algebraically dependent if and only if there exists t ∈ P_n such that f, g ∈ K[t].

Proof: It was proved in ref. 14 that the centralizer C(f) = {h ∈ P_n|[f, h] = 0} of any element f ∈ P_n\K is a polynomial algebra in one indeterminate, i.e., there exists t ∈ P_n such that C(f) = K[t]. By Lemma 1, g ∈ C(f) if and only if f and g are algebraically dependent.

Two generated subalgebras of the algebra P_n were studied in ref. 14. The lower degree bound of an element in such a subalgebra obtained there plays a major role in the study of the automorphisms in AutP₃ in refs. 9–11 as well as in the study of coordinates of P₃ in this article. Recall that a pair of elements (f, g) of the algebra P_n is called reduced (15), if f̄ ∉ K[ḡ] and ḡ ∉ K[f̄]. According to ref. 14, an algebraically independent reduced pair of elements (f, g) of the algebra P_n is called *-reduced if f̄ and ḡ are algebraically dependent.

Let f, g be a *-reduced pair of elements of P_n and k = deg f < m = deg g. Put

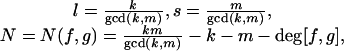where gcd(k, m) is the greatest common divisor of k and m. We sometimes call the above *-reduced pair (f, g) an l-reduced pair in the sequel. Let G(x, y) ∈ K[x, y]. It was proved in ref. 14, if deg_y G(x, y) = lq + r, 0 ≤ r < l, then

[2]

and if deg_x G(x, y) = sq₁ + r₁, 0 ≤ r₁ < s, then

[3]

We consider the set of triples θ = (f₁, f₂, f₃), where f_i ∈ P_n. deg θ:= deg f₁ + deg f₂ + deg f₃ is called the degree of the triple θ. Recall that an elementary transformation of the triple (f₁, f₂, f₃) changes only one coordinate f_i to the element of the form αf_i + g, where 0 ≠ α ∈ K, g ∈ K[{f₁, f₂, f₃} – f_i]. The notation θ → τ means that the triple τ can be obtained from θ by a single elementary transformation. Moreover, θ ⇒ τ means that there exists a sequence of triples θ = θ₀, θ₁,..., θ_s = τ such that

As usual, an automorphism θ of the algebra P₃ such that θ(x_i) = f_i, 1 ≤ i ≤ 3, is also denoted by the triple θ = (f₁, f₂, f₃). Note that the automorphism θ ∈ AutP₃ is tame if and only if

A triple θ = (f₁, f₂, f₃) of elements of the algebra P₂: = K[u, v] is called a tame triple, if

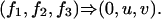Otherwise it is wild.

A polynomial f₁ in the triple (f₁, f₂, f₃) of P₂ is reducible, if there exists g ∈ K[f₂, f₃] such that f̄₁ = ḡ, otherwise it is irreducible. Put , where 0 ≠ c ∈ K, then deg() < deg(f) and deg(, f₂, f₃) < deg θ. In this situation we say f₁ is reduced in θ by the triple (, f₂, f₃). We may define the reducibility of f₂ and f₃ similarly. θ is elementarily reducible (or θ admits an elementary reduction) if one of f_i is reducible.

In the sequel the next lemma is useful.

Lemma 3. Let f, g, h ∈ P₂ and let K[f, g, h] = P₂. If f, g are algebraically dependent, then there exists at ∈ P₂ such that K[f, g] = K[t] and P₂ = K[t, h].

Proof: By Lemma 2 there exists a t ∈ P₂ such that f, g ∈ K[t]. So P₂ = K[t, h]. If K[f, g] is a proper subring of K[t], then K[f, g, h] is a proper subring of K[t, h] = P₂. Therefore K[f, g] = K[t].

Lemma 3 implies the following.

Lemma 4. Let f, g, h ∈ P₂ and let K[f, g, h] = P₂. If f, g are algebraically dependent, then there exists a coordinate t ∈ P₂, and a sequence of elementary transformations taking (f, g) to (0, t).

Proof: By Lemma 3 and the famous Abhyankar-Moh-Suzuki Theorem (13) we obtain a proof.

Theorem 1. Let f, g, h ∈ P₂ such that K[f, g, h] = P₂. Then the elementary reducibility of the triple (f, g, h) is algorithmically recognizable.¶

Proof: We only need to prove the reducibility of an element in the triple is algorithmically recognizable. By Lemma 4, we may assume that f, g, h are pairwisely algebraically independent. Now we are going to recognize the reducibility of an element, say, h of the triple. If f̄ and ḡ are algebraically independent, then h is reducible if and only if h̄ ∈ K[f̄, ḡ]. Since f̄ and ḡ are homogeneous, this can be effectively determined. If ḡ ∈ K[f̄] and ḡ = cf̄^k, where c is a nonzero element of K, then h is reducible in (f, g, h) if and only if it is reducible in (f, g-cf^k, h). Since deg (f, g-cf^k, h) < deg (f, g, h), we may apply induction in this case.

Now we may assume (f, g) is a -reduced pair and deg (f) < deg (g). Suppose that there exists *_G(x, y) ∈ P₂ such that h̄ = the highest homogeneous part of G(f, g). Then 2 and 3 give a upper bound k for deg_x (G) and deg_y (G). Hence G(f, g) is in the vector space generated by fⁱg^j, i, j < k. The highest homogeneous part of elements in this space can be effectively determined by triangulation.

Now we are going to define four types of (nonelementary) reductions for triples of P₂; all of these reductions are compositions of at most four elementary transformations of a special type. These definitions are motivated by the definitions of the four types of nonelementary reductions for automorphisms in AutP₃ in refs. 9–11.

Definition 1: Let θ = (f₁, f₂, f₃) be a triple of P₂ such that deg f₁ = 2k, deg f₂ = ks, s ≥ 3 is an odd number, 2k < deg f₃ ≤ ks, f̄₃ ∈ K[f̄₁, f̄₂]. Suppose that there exists 0 ≠ α ∈ K such that the elements g₁ = f₁, g₂ = f₂ – αf₃ satisfy the conditions:

1. g₁, g₂ is a two-reduced pair and deg g₁ = deg f₁, deg g₂ = deg f₂;

2. The element f₃ of the triple (g₁, g₂, f₃) is reduced by a triple (g₁, g₂, g₃) with the condition deg [g₁, g₃] < deg g₂ + deg [g₁, g₂]. Then we say that θ admits a reduction (g₁, g₂, g₃) of type I.

Definition 2: Let θ = (f₁, f₂, f₃) be a triple of P₂ such that deg f₁ = 2k, deg f₂ = 3k, 3k/2 < deg f₃ ≤ 2k, and f̄₁, f̄₃ are linearly independent. Suppose that there exist α, β ∈ K, where (α, β) ≠ (0, 0), such that the elements g₁ = f₁ – αf₃, g₂ = f₂ – βf₃ satisfy the conditions i and ii in Definition 1. Then we say that θ admits a reduction (g₁, g₂, g₃) of type II.

Definition 3: Let θ = (f₁, f₂, f₃) be a triple of P₂ such that deg f₁ = 2k, and either deg f₂ = 3k, k < deg f₃ ≤ 3k/2, or 5k/2 < deg 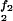, deg f₃ = 3k/2. Suppose that there exist α, β, ∈ K such that the elements g₁ = f₁ – βf₃, g₂ = f₂ – βf₃ – αf3 satisfy the conditions:

1. g₁, g₂ is a two-reduced pair and deg g₁ = 2k, deg g₂ = 3k;

2. There exists an element g₃ of the form.

where 0 ≠ s ∈ K, g ∈ K[g₁, g₂]\K, such that deg g₃ ≤ 3k/2, deg[g₁, g₃] < 3k + deg[g₁, g₂].

If (α, β, β) ≠ (0, 0, 0) and deg g₃ < k + deg[g₁, g₂], then we say that θ admits a reduction (g₁, g₂, g₃) of type III. On the other hand, if there exists 0 ≠ μ ∈ K such that deg(g₂ – ) ≤ 2k, then we say that θ admits a reduction (g₁, g₂ – g₃) of type IV.

Definition 4: A simple triple in P₂ is defined inductively as follows: A triple 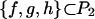is a simple triple if deg (f, g, h) = 2 and K[f, g, h] = P₂. A triple β of deg β = k > 2 is a simple triple, if there exists an elementary reduction or a reduction of one of the types I–IV to β, and after such a reduction, the resulting triple β of deg β < k is simple.

The above definition of a simple triple of P₂ is motivated by the definition of a simple automorphism in AutP₃ in refs. 9–11.

Theorem 2. A triple 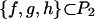is tame if and only if it is simple.

Proof: It is obvious that a simple triple is a tame one according to Definition 4. To prove the converse, first note that by Lemma 2, we may assume that f, g, h are pairwisely algebraically independent for a tame triple (f, g, h) of P₂. Then the proof of theorem 1 in ref. 9 shows that (f, g, h) is either elementarily reducible, or admits a reduction of one of the types I–IV.

Theorem 3. Let f, g, h ∈ P₂ such that K[f, g, h] = P₂. Then the tameness of the triple (f, g, h) is algorithmically recognizable.

Proof: By Theorem 2, we only need to prove that the simple reducibility of (f, g, h) is algorithmically recognizable. The elementary reducibility of (f, g, h) is algorithmically recognizable by Theorem 1, if (f, g, h) admits a reduction of one of types I–IV, then the proof is similar to the proof of theorem 3 in ref. 9.

Remark 1: If p ∈ P₃ is irreducible and p(f, g, h) = 0, then we do not know whether the hypothesis of the above theorem implies that p is a coordinate of P₃. The famous embedding conjecture of Abhyankar-Sathaye claims that in this case p is a coordinate. See, for instance, ref. 16. On the other hand, Lemma 5 below shows that p is a tame coordinate if and only if (f, g, h) is a tame triple.

Lemma 5. Let be a tame triple with deg(f_i) ≤ 1 for some i ∈ {1, 2, 3}. Then θ admits an elementary reduction.

Proof: It is easy to see from Definitions 1–3 that in this case θ does not admit a reduction of types I–IV.

Now we consider coordinates of P₃ = K[x, y, z]. If one of the coordinates of θ = (f, g, h) ∈ AutP₃ is wild, then obviously θ is a wild automorphism. But even if θ is a wild automorphism, it does not necessarily imply that all coordinates of the θ are wild. For example, the Nagata automorphism σ: = (x – 2wy – w²z, y + wz, z) of P₃, where w = y² + xz, is wild (9–11), but the coordinate z of σ is obviously tame.

Let p ∈ P₃ be a coordinate,

[4]

a surjective homomorphism with Ker(φ) = pP₃ and φ(x, y, z) = (x(u, v), y(u, v), z(u, v)). Then the triple (x(u, v), y(u, v), z(u, v)) gives a faithful parametrization of p(x, y, z): p(x(u, v), y(u, v), z(u, v)) = 0 and K[x(u, v), y(u, v), z(u, v)] = K[u, v].

Lemma 6. Let p ε P₃ be a coordinate of P₃ and let (x(u, v), y(u, v), z(u, v)) be a faithful parametrization of the p. Then the coordinate p is tame if and only if the triple (x(u, v), y(u, v), z(u, v)) is tame.

Proof: Put x̂ = x(u, v), ŷ = y(u, v), ẑ = z(u, v). Assume that p is a tame coordinate and let (p, q, r) be a tame automorphism. Then

Since p(x̂, ŷ, ẑ) = 0, the same sequence of elementary transformations produces

where f = q(x̂, ŷ, ẑ), g = r(x̂, ŷ, ẑ). By surjectivity of the φ from 4, we have K[u, v] = F[f, g]. It follows that (f, g) is an automorphism of P₂ = K[u, v]. By Jung's theorem (see ref. 6) (a, b) ⇒ (u, v). Obviously,

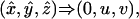and the parametrization (x̂, ŷ, ẑ) is tame.

Now assume that

The same elementary transformations give

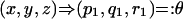such that φ(p₁) = 0. Since Ker(φ) = pP₃, then p₁ = pt, where t ∈ P₃. We have

Since θ^–1(p) is also a coordinate, we obtain that deg (θ^–1(t)) = 0 and 0 ≠ t ∈ K. Since (p₁, q₁, r₁) is a tame automorphism, p₁ is a tame coordinate; so is p.

Recall that the well-known Nagata automorphism σ ∈ AutP₃ is defined as follows (see ref. 8):

Theorem 4. The coordinates f and g of the Nagata automorphism σ are wild.

Proof: Note that

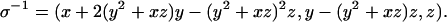Since σσ^–1 = id, then by putting x = 0, y = u, z = v in σ^–1 we get a parametrization

of the f; and by putting x = u, y = 0, z = v we get a parametrization

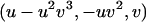of the g. It is easy to see that the highest homogeneous parts of the elements in both triples are pairwise algebraically independent, and the highest homogeneous part of an element is not contained in the subalgebra generated by the highest homogeneous part of the other two elements in the same triple, hence both triples do not admit elementary reduction. Moreover, both triples do not admit any reduction of one of types I–IV by Lemma 3 since deg (v) = 1. Therefore, both triples are not simple. By Theorem 2, both f and g are wild coordinates of P₃.

Lemma 7. Let p be a coordinate of the algebra P_n and let φ be a tame automorphism in AutP_n. Then p is a tame coordinate if and only if φ(p) is a tame coordinate.

Proof: The conclusion is obvious by the definition of a tame coordinate.

Theorem 5. Let θ = (f, g, z) ∈ AutP₃. If θ is a wild automorphism, then both coordinates f and g are wild.

Proof: Put θ^–1 = (p, q, z). Then the homomorphism φ (see 4) defined by

gives a faithful parametrization of the f.If ξ is wild, then f is wild by Lemma 6. Suppose that ξ is tame. By Lemma 5, ξ is elementarily reducible. Hence there exists a sequence of elementary automorphisms of P₃:= K[x, y, z] preserving z such that

The same sequence produces

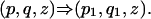It follows that ψ(p₁) = 0, where ψ: P₃ → K[u, v] is the surjective homomorphism defined by ψ(x) = 0, ψ(y) = u, ψ(z) = v. Then p₁ = xt and as in the proof of Lemma 5 we can take p₁ = x. Therefore, both automorphisms (p₁, q₁, z) and (p, q, z) = θ^–1 are tame. Consequently, θ is also tame. The contradiction completes the proof.

Remark 2: As a consequence, a wild coordinate of K[z][x, y] is always a wild coordinate of P₃ = K[x, y, z], hence by Drensky and Yu (1, 2) (where all wild coordinates of K[z][x, y] are effectively classified), we obtain many wild coordinates of P₃.

Theorem 6. Let θ = (f, g, h) be a wild automorphism in AutP₃. Then at least two coordinates among the coordinates f, g, h of θ are wild coordinates of P₃.

Proof: Suppose that h is a tame coordinate and let φ ∈ AutP₃ be a tame automorphism with φ(h) = z. Then θ₁ = φθ = (φ(f), φ(g), z) is also a wild automorphism. By Theorem 5, the coordinates φ(f) and φ(g) are wild. Now the wildness of both coordinates f and g follows from Lemma 7.

The conclusion of the main theorem follows from Theorems 4–6.

Some Open Problems

Recall that an element q of the free associative algebra A_n:= K〈x₁,..., x_n〉 is called a primitive element if there exists an automorphism φ ∈ AutA_n such that φ(q) = x₁. Tame and wild automorphisms and primitive elements of A_n can also be defined naturally.

Problem 1. Let p ∈ P₃ be a coordinate. Can p be lifted to a primitive element p′ of the free associative algebra A₃? In other words, does there exist a primitive element p′ ∈ A₃ such that the natural homomorphism (the abelianization) from A₃ to P₃ takes p′ to p?

Remark 3: If the answer to Problem 1 is yes for some wild coordinate p of P₃, then obviously p′ is a wild primitive element of A₃, hence there exist wild primitive elements and wild automorphisms of A₃ that would settle a famous conjecture of Cohn (17) affirmatively. On the other hand, if the answer is no for some coordinate q of P₃, then we would obtain a new proof of the Nagata conjecture without using the previous results of Shestakov and Umirbaev (9–11).

Suppose that f₁,..., f_k ∈ P_n and K[f₁,..., f_k] = P_n. Then obviously n ≤ k. The following two problems are naturally raised.

Problem 2. Does there exist an automorphism φ ∈ AutP_k such that

[5]

Problem 3. Does there exist a tame automorphism φ ∈ AutP_k such that

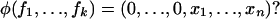[6]

Note that Problem 2 is the algebraic formulation of the problem of rectifiability of an embedding in affine algebraic geometry (see ref. 8).

If k = n, then Problem 2 becomes the problem of recognizing automorphisms of P_n and was solved by van den Essen (16) by the Gröbner basis method; and Problem 3 becomes the Nagata conjecture for P_n.

The case k = 2, n = 1 of both Problems 2 and 3 have positive solutions if Char(K) = 0 (that is the well-known Abhyankar-Moh Theorem) and a negative solution if Char(K) > 0 (13).

The case k ≥ 2n + 2of Problem 2 was solved positively in refs. 18–21 (see also refs. 12 and 22–24). In fact, the automorphisms obtained in refs. 12 and 18–24 are all tame, hence also give the positive solutions of the case k ≥ 2n + 2 of Problem 3.

The case n = k = 3 of Problem 3 was solved negatively by Shestakov and Umirbaev (9–11). Note that some other examples considered in refs. 1, 2, and 25 are also wild by refs. 9–11.

Also Theorems 4 and 5 give the answer to the case n = 3, k = 2 of Problem 3 negatively.

It is natural to raise the following.

Problem 4. Let p ∈ P₃ be a given coordinate. Does there exist an algorithm to determine whether p is tame or wild?

This problem is closely related to the following question: for a given polynomial p ∈ P₃, how do we effectively determine whether p is a coordinate? Moreover, if p is a coordinate, how do we effectively construct an automorphism φ ∈ AutP₃ such that φ(p) = x?

Theorem 7. Let p be a given coordinate of P₃ and let θ = (f, g, h) be a given automorphism in AutP₃ taking p to x. Then there exists an algorithm to determine whether the coordinate p is tame or wild.

Proof: Suppose θ = (f, g, h). Then the homomorphism φ (see 4) defined by

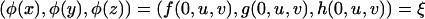gives a faithful parametrization of p. By Lemma 6, ξ is a wild triple if and only if p is a wild coordinate of P₃. Then apply Theorem 3.

Finally, in view of Theorems 5 and 6, we may propose the following.

Problem 5. Is AutK[x, y, z] essentially generated by ? Or, more precisely, is it true that any automorphism in AutK[x, y, z] can be decomposed as a product of automorphisms fixing z and linear automorphisms?