Percolation and criticality in a mitochondrial network

Abstract

Synchronization of mitochondrial function is an important determinant of cell physiology and survival, yet little is known about the mechanism of interorganellar communication. We have recently observed that coordinated cell-wide oscillations in the mitochondrial energy state of heart cells can be induced by a highly localized perturbation of a few elements of the mitochondrial network, indicating that mitochondria represent a complex, self-organized system. Here, we apply percolation theory to explain the mechanism of intermitochondrial signal propagation in response to oxidative stress. A global phase transition (mitochondrial depolarization) is shown to occur when a critical density of mitochondria accumulate reactive oxygen species above a threshold to form an extended spanning cluster. The scaling and fractal properties of the mitochondrial network at the edge of instability agree remarkably well with the idea that mitochondria are organized as a percolation matrix, with reactive oxygen species as a key messenger.

Spatial and temporal coordination of information in both physical and biological systems is crucial for mounting an effective response to sudden environmental changes. Such systems often evolve to operate close to the edge of dynamic instability (1–5). The heart is a prime example; when subjected to stress (e.g., ischemia and reperfusion), the normally well coordinated oscillations of electrical and contractile activity become unstable (6–8), giving rise to arrhythmias involving interactions among many cells in the syncytium. At the subcellular level, adapting energy production to meet a variable metabolic demand depends on the coordinated action of thousands of mitochondria in the cardiac myocyte, which are distributed between myofilaments in a lattice-like network of nonlinear elements. This arrangement is conducive to spatiotemporal patterns of self-organization, for instance, oscillations and/or propagating waves (9, 10). However, it is not known how individual mitochondria interact with their neighbors or how metabolic signals are communicated over cellular distances. Elucidating this mechanism is vitally important, because the rapid and irreversible loss of mitochondrial inner membrane potential (ΔΨ_m) is a decisive factor in necrotic or apoptotic cell death.

We have recently described synchronized whole-cell oscillations of ΔΨ_m, NADH, and reactive oxygen species (ROS) production induced by controlled depolarization of mitochondria in a small volume of the cardiomyocyte (10). The accumulation of mitochondrial ROS up to a critical threshold level was a key determinant of propagation and synchronization of the response throughout the mitochondrial network, thus resembling a system at the critical state [i.e., characterized by an extreme susceptibility to external factors (11)]. We proposed that the cell-wide propagation of the local perturbation (10) was mediated by ROS liberated from a mitochondrion triggering a mechanism of regenerative ROS-induced ROS release (a term coined by Zorov et al. (12)]. An open question was how the local production of ROS by a mitochondrion (size ≈1–2 μm) could trigger a synchronized depolarization across the length of a cell (>100 μm), especially given the short half-life and buffering capacity of the cell for the central messenger, superoxide ().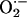

Here, we apply percolation theory, which describes how neighbor–neighbor interactions determine the macroscopic spatiotemporal properties of an excitable matrix, to demonstrate that a spanning cluster of oxidatively stressed mitochondria forms in the mitochondrial network just before the first cell-wide depolarization of ΔΨ_m. Specific predictions regarding the fractal geometry and scaling properties of a percolation matrix (13, 14) were verified experimentally, providing support for the hypothesis that local interactions among mitochondria can lead to criticality and global synchronization of ΔΨ_m by percolation.

Methods

All experiments were carried out at 37°C on freshly isolated adult guinea pig ventricular myocytes prepared and handled for experimental recordings as described (7). We monitored NAD(P)H autofluorescence, mitochondrial membrane potential (ΔΨ_m) with the cationic potentiometric fluorescent dye tetramethylrhodamine ethyl ester (TMRE), and ROS production with the ROS-sensitive fluorescent probe 5-(–6)-chloromethyl-2′,7′-dichlorodihydrofluorescein diacetate, as described (10). Images were recorded by using a two-photon laser-scanning microscope (Bio-Rad MRC-1024MP) with excitation at 740 nm (Tsunami Ti:Sa laser, Spectra-Physics). Owing to the overlap in the cross sections for two-photon excitation of the three fluorophores of interest [NADH, TMRE, and CM-DCF (5-(–6)-chloromethyl-2′,7′-dichlorof luorescein)], this wavelength permitted recording of redox potential, ROS production, and ΔΨ_m simultaneously (10).

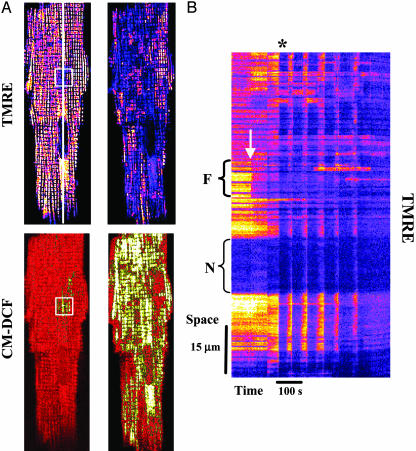
Images were analyzed offline by using imagej software (Wayne Rasband, National Institutes of Health, http://rsb.info.nih.gov/ij). For visualization of the spatiotemporal responses of NADH, TMRE, and CM-DCF a 2- to 3-pixel-wide line was drawn along the length of the myocyte (as shown in Fig. 1 A), and the average fluorescence profile along the line was determined for the entire time series of 2D images for a given experiment (time-line image) (as shown in Fig. 1B).

Fig. 1.

Cell-wide synchronized mitochondrial oscillations after local generation of ROS. (A) Cardiomyocyte loaded at 37°C with TMRE (ΔΨ_m indicator, upper images) and 5-(–6)-chloromethyl-2′,7′-dichlorohydrofluorescein diacetate (ROS-sensitive, lower images). By using two-photon laser excitation, and after 10–20 control images were collected, a small region of a cardiac myocyte (20 × 20 pixels, 8.7 × 8.7 μm square, ≈81 μm³ volume, and <1 μm focal depth) was excited in a single flash resulting in rapid loss of ΔΨ_m (A, white square in upper left) and local generation of ROS (A, white square in lower left). Thereafter, ΔΨ_m remained depolarized in the flashed area throughout the experiment (see B). The right images in A show the first whole-cell ΔΨ_m depolarization (B, asterisk) after a delay time (see text for further explanation). (B) Time-line image of TMRE created by analyzing a line drawn along the longitudinal axis of the cell (shown in A, upper left; see Methods). The arrow points out the timing of the flash and the brackets point out the flash region (Upper) and the nucleus (Lower). The synchronous ΔΨ_m mitochondrial oscillations are evident as vertical blue bands. The mitochondria that do not belong to the spanning cluster remained visibly polarized.

To quantitatively determine the fraction of polarized mitochondria and their levels of ROS as a percentage of the total mitochondrial population from 2D TMRE and CM-DCF images, we applied grid analysis. In brief, a binary mask of the cell TMRE or CM-DCF fluorescence was made, and the cell area, excluding nuclei, was divided into small squares approximately the size of individual mitochondria (≈2 × 2 μm; see Fig. 2B). The average fluorescence within each grid object was measured, and the fraction of polarized mitochondria with respect to the total number of objects at time 0 was calculated for the image series. A cutoff value halfway between the two peaks in the histograms of the distribution of mitochondria fluorescence was used to determine whether a given grid object was classified as “polarized” or “depolarized.”

Fig. 2.

Threshold of ROS required for cell-wide mitochondrial oscillations. (A) Time course of average whole-cell fluorescence of TMRE and CM-DCF, the latter normalized to initial intensity (F/F₀). Oscillations in ΔΨ_m were initiated only when the ROS signal increased by >20% (horizontal dashed line) over the duration of the experiment. The relationship between TMRE and CM-DCF signals and the ROS threshold can be clearly appreciated from the vertical and horizontal reference lines drawn, respectively. Arrow indicates the timing of the flash. (B) Grid analysis of TMRE or CM-DCF fluorescence as applied to a cardiomyocyte (see Methods). (C) Development of the mitochondrial spanning cluster from the flash and up to the time of the first whole cell ΔΨ_m depolarization (see Fig. 1B, asterisk). At p_c = 0.56 (last image on right) a mitochondrial cluster with a critical density, comprising ≈60% of the mitochondrial population, spans the cell. At p_c the mitochondrial cluster has a D_f = 1.82 as calculated by the box counting method (17). (D) Analysis of the fraction of polarized mitochondria from 2D TMRE and CM-DCF images as a percent of the total mitochondrial population was performed as described (ref. 10; see also Methods). The relationship between TMRE and CM-DCF signals can be clearly appreciated from the vertical reference line drawn. Arrow indicates the timing of the flash.

Results

According to the method we described recently, two-photon laser excitation was used to produce a local perturbation in the mitochondrial network of a myocyte to trigger a response in the remainder of the cell. The laser flash induced ΔΨ_m depolarization (Fig. 1A, box in upper left of the TMRE image) and ROS generation (Fig. 1 A, square in the lower left of the CM-DCF image) in a small volume of a cardiac myocyte in the presence of glucose (10). After a significant delay (43 ± 9 s; n = 13; five experiments), this “flash” induced synchronized and cell-wide oscillations in ΔΨ_m (Fig. 1B), NADH, and ROS involving up to ≈70% of the mitochondrial population (Fig. 1 A Right).

The onset of the first cell-wide mitochondrial depolarization was preceded by the build-up of ROS in a cluster of mitochondria spanning almost the whole cell (Fig. 1 A Right). The attainment of a critical level of ROS, ≈20% above baseline (10), was synchronous with the first global depolarization of the mitochondrial network (Fig. 2A).

Whole-Cell Mitochondrial Spanning Cluster Formation. To apply percolation theory, the two-photon imaging method (≈1 μm focal depth) allowed us to treat the data as a 2D single mitochondrial layer. Because the mitochondrial network in cardiomyocytes is arranged in a quasi-square lattice, we treated it as a grid, with each element of the grid being occupied by roughly one to two mitochondria (Fig. 2B). We created a binary mask over the myocyte area, excluding the cell's nuclei and tracked the time-dependent response of ΔΨ_m and ROS production in individual mitochondrial elements.

Just before the first global ΔΨ_m depolarization, the formation of a large cluster of mitochondria with ROS levels above threshold was observed (Fig. 2C). This “spanning cluster” involved 56 ± 7% of the mitochondrial lattice (Fig. 2D; n = 8, six independent experiments). This value was consistent with a critical density of mitochondria at the percolation threshold (p_c), which, for a square lattice in percolation theory is equal to ≈0.593 or 59% (13, 15). The value of p_c obtained should be considered an approximation because we have assumed a “quasi-square” geometry and have not taken into account the natural structural variations of the cell (e.g., the presence of nuclei). As expected, at p_c, the probability for a single mitochondrion to belong to the largest cluster increases dramatically (see Appendix). A few mitochondria (which had ROS levels below threshold) were excluded from the spanning cluster (Fig. 1 A) and remained polarized throughout the depolarization.

Another signature feature of percolation processes at p_c is that they are organized as fractals. This property implies that local processes can scale to produce macroscopic behavior. At p_c, the mass of the spanning cluster increases with the size of the lattice, L, as a power law, L^Df, with D_f as the fractal dimension (13, 14, 16). Fractal box counting (14, 15) analysis of our data yielded a fractal dimension of D_f = 1.82, close to that exhibited by percolation clusters and cytoskeletal lattices at p_c (D_f = 1.90) (1, 14, 17, 18). A complex system like a percolation matrix, when close to criticality, may undergo phase transitions characterized by critical exponents (11, 13–15). An estimation of these exponents for the mitochondrial network is provided in Appendix.

Nearest Neighbor Interactions and Superoxide Diffusion. The critical density of mitochondria at a p_c of 0.56 suggests that each mitochondrion in the spanning cluster is affecting its four immediate neighbors (see Appendix). Therefore, we next investigated, in quantitative and qualitative terms, if diffusion of 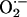produced by a mitochondrion interacting with its neighbors was mechanistically feasible. This model was based on the proposal (10) that cell-wide propagation is mediated by regenerative ROS-induced ROS release between neighboring mitochondria.

At the percolation threshold, one possible mechanism is that a mitochondrion in the spanning cluster produces a burst of 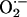, which then diffuses to its neighbor with a particular spatial concentration profile that is a function of the rate of 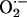scavenging (Fig. 3). For the response to be regenerative, the 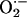-induced opening of a ROS-activated target channel on the neighbor (which we believe to be an inner membrane anion channel; ref. 10) will depend on two main conditions: (i) the mitochondrial neighbor must belong to the spanning cluster (i.e., it possesses a near-threshold level of ROS in the mitochondrial matrix), and (ii) a suprathreshold level of cytoplasmic 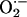must reach the target mitochondrion (Fig. 3). A global phase transition (through percolation) then occurs when a cluster forms with the critical density of mitochondria exceeding the ROS threshold (Fig. 2).

Fig. 3.

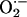Model of diffusion between neighboring mitochondria in the spanning cluster. The concentration profiles of 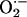were calculated from the solution of a diffusion model (31):

[1]

where c, x, and t are messenger concentration, distance, and time, respectively. When the solution of Eq. 1 is supposed to depend on a spatial parameter, z = x – vt, we obtain:

[2]

whose solution is:

[3]

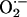The concentration gradients of between mitochondria as a function of its rate of scavenging, v, were calculated according to Eq. 3 and the following boundary conditions: c(0) = C_max, and c(∞) = 0. The higher the rate of scavenging, the steeper the gradient and the lower the 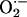concentration reaching the second mitochondrion. A maximal distance between two neighboring mitochondria of 0.5 μm was determined. The ROS threshold of 20% was obtained experimentally by image analysis (see Fig. 2 A), and the two mitochondria at the critical state are assumed to belong to the spanning cluster, i.e., they possess a level of ROS very close to the threshold. For those conditions in which ROS near Mito 2 exceeds the threshold, ROS-induced ROS release is predicted. Considering the volume of an average mammalian cell of the order of 4 × 10^–12 liters (32) and of single mitochondria, 10^–15 liters (≈500–1,000 mitochondria in a plane; e.g., see Fig. 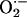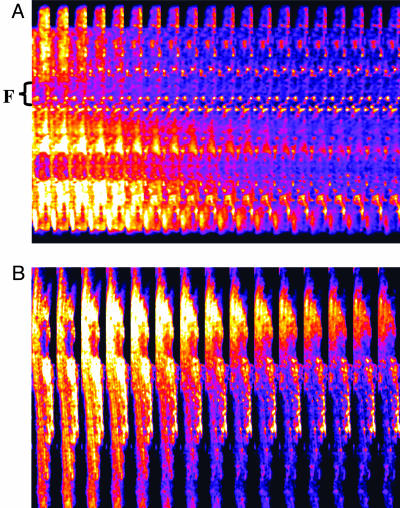2B), we estimate that the levels of released between neighboring mitochondria would have to be at least in the micromolar range for propagation to occur in the presence of superoxide dismutase (k_cat ≈ 1 nmol/s).

Although the transition in the mitochondrial spanning cluster appears abrupt, the phase transition should be slow enough to be resolved as waves of depolarization with faster image acquisition and/or interventions that slow propagation, as described for spontaneous metabolic oscillations (9). Indeed, at higher temporal resolution, depolarization waves could be detected with a speed of 22 μm·s^–1 (Fig. 4A). The total time for global cell depolarization was 4.2 ± 0.4 s (n = 15, ten independent experiments; Fig. 2 A), in agreement with the observed speed of the depolarization wave (i.e., it takes ≈4 s for a 22 μm·s^–1 wave to travel the length of a 100-μm myocyte). In the presence of the ROS scavenger N-acetyl-l-cysteine, we could resolve a depolarization wave with a propagation velocity of 3.5 μm·s^–1, even at a slow acquisition rate, confirming the aforementioned dependence of the local gradients on the cytoplasmic 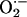-scavenging capacity (Fig. 4B).

Fig. 4.

Wave propagation during laser flash-induced whole cell mitochondrial ΔΨ_m oscillations in cardiomyocytes. Cardiomyocytes labeled with TMRE were subjected to a laser flash, and images were collected at a frame rate of 0.512 s. Under these conditions, waves traveling at speeds of 22 μm·s^–1 could be detected (A). In the presence of the ROS scavenger N-acetyl-l-cysteine (4 mM), and with slower image acquisition (3.5 s), waves traveling at 3.5 μm·s^–1 were observed (B).

Discussion

Analysis of mitochondrial metabolic oscillations triggered by a local perturbation of ROS reveals that the mitochondrial network of the isolated cardiac cell is an excellent biological example of a system operating near the critical state. Relatively mild stressors, such as substrate deprivation (7), or, in the present case, a highly localized increase in ROS, can induce a phase transition in the entire cell. This first ΔΨ_m depolarization can be described by percolation theory as a universal phase transition, which has the properties of similar structure at different scales, a fractal organization (power law dependence), and a percolation threshold (13, 14). Similarly, many physical and biological dynamic systems evolve to a state of self-organization, in which the collective behavior of the system can be very sensitive to local fluctuations (11). This state improves the response to environmental changes but, in the present example, may foster instability.

Our mechanistic hypothesis (10), supported by the available experimental data, suggests that the local liberation of ROS from the mitochondria, produced by leakage of electrons from the electron transport chain, triggers propagating, regenerative ROS-induced ROS release in the entire mitochondrial network. ROS liberation from mitochondria is transported through inner-membrane anion channels that exert the dual role of both dissipating energy to depolarize ΔΨ_m and transporting 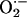out of the matrix in a positive feedback loop. Using a computational model of mitochondrial bioenergetics (19)† that incorporates the main features of our hypothesis, we have demonstrated that the behavior of individual mitochondria can undergo bifurcations and display stable limit cycles, which resemble the characteristics of the whole-cell oscillations. In this case, the transition from steady-state behavior to oscillation occurs after a suprathreshold perturbation, or hard excitation (20), and depends on the balance between ROS production and cytoplasmic ROS scavenging. The present analysis indicates that the depolarization involves almost the entire cell because the mitochondria belong to a spanning cluster; i.e., most mitochondria are at or near the threshold concentration of ROS (Figs. 1 and 2). This finding explains why a delay occurs between the initial perturbation and the first global ΔΨ_m depolarization, the latter occurring simultaneously with the formation of the spanning cluster (Fig. 2).

The 4-s time for global cell depolarization to take place is faster than it would take for pure diffusion to propagate the ROS signal throughout the cell. Effectively, if the Einstein relation for a diffusion process [(Δx)² = 2Dt] is applied, a total of 14 s would have been required for the ROS signal to travel the length of a myocyte in the absence of scavenging (assuming a diffusion coefficient, D = 700 μm²·s^–1, and Δx = 100 μm). If scavenging is also taken into account, the time required for diffusion will certainly be much longer. Our description is also biochemically consistent with the fact that the short half-life and limited diffusion rate of 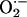would restrict its influence to the short intramitochondrial distances, i.e., 0.5–1 μm. Indeed, the k_cat of Cu,Zn superoxide dismutase is ≈10⁶ mM^–1·s^–1 (21, 22), which would predict dismutation turnover rates of 1 s for nanomolar levels of 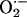(Fig. 3).

The observation that some mitochondria resisted depolarization in the face of cell-wide synchronization (Fig. 1 A Right) argues against a simple regenerative wave based on ROS-induced ROS release. The mitochondria were also required to be near threshold and belong to the percolation cluster.

The biological importance of the results described in the present work cannot be overstated. The existence of phase transitions in mitochondrial energetics can be seen as a crisis in oxidatively stressed cells close to the point where their behavior may become unstable and abruptly change, i.e., criticality. This instability is likely to occur in the postischemic myocardium and will determine the course of necrotic and apoptotic cell death. A common feature of crises in disparate systems is that they emerge from collective processes leading to bifurcations between stable and novel regimes (1, 11). Nonlinear analysis has been applied to the study of abnormal cardiac electrical conduction and arrhythmias (23–28) and the behavior of neural networks (4); however, the present phenomenon appears to be the premier example of these concepts in an intraorganellar network. The mitochondrial transitions are closely linked to changes in cellular electrical excitability (7, 8, 10) and, presumably, to dispersion of action potential repolarization in the whole heart, suggesting that criticality at the microscopic level may be translated into the death of the organism.

Appendix: Determination of Critical Exponents

The tools used for studying phase transitions have also been applied to percolation (13, 15), and the critical exponents of a phase transition have been determined. Critical phase transitions are characterized by an order parameter, Z, which describes, for example, the magnetic transition of a magnet, the population inversion threshold of a laser, or flow-through of a porous material (11, 29). Three critical exponents, β, ν, and δ, describe how the order parameter, the correlation length, and the characteristic time parameters scale with the percolation probability, ε, near p_c (ε ≪ 1) (11, 13, 14, 29).

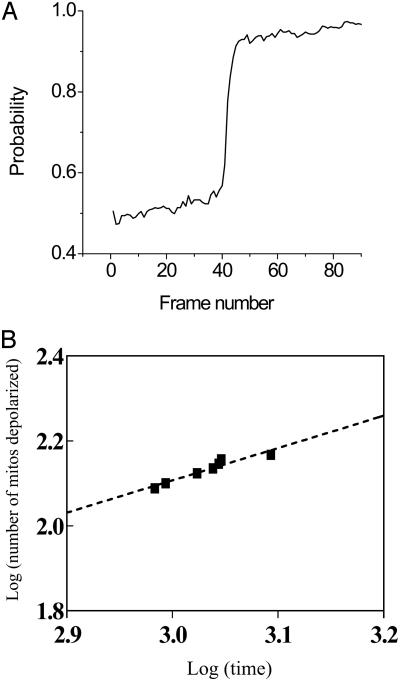
For 2D percolation, the values of the critical exponents are well known; the correlation length exponent, ν, equals 4/3 exactly (13), β equals 5/36 ≈ 0.139 (13, 14), and the characteristic time exponent δ equals 1.533 (15, 30). We calculated the ratio of the critical exponents corresponding to the first global depolarization of ΔΨ_m (e.g., see asterisk on Fig. 1B). The slope of the double log plot of the number of depolarized mitochondria versus time equals (15) the ratio of the critical exponents [(ν – β)/δ]. By substitution, the theoretical value for (ν – β)/δ is 0.779. The experimentally determined value we obtained was 0.777 ± 0.069 (Fig. 5C; n = 8, six independent experiments). This numerical value should be taken only as approximate because of the very narrow span of the power law behavior shown in Fig. 5B, whereas the critical exponents have previously been obtained from simulations of enormous lattices (to avoid finitesize effects) far bigger than the mitochondrial one.

Fig. 5.

Quantitative analysis of the mitochondrial network. (A) The probability of a mitochondrion belonging to the spanning cluster increases dramatically at percolation threshold, p_c (see also Fig. 2D). This was calculated from frequency histograms of “grid objects” (mitochondria) with CM-DCF fluorescence intensity above baseline. The baseline was obtained averaging the maximal fluorescence value from the frequency distribution of the initial 10–20 images before the flash. The probability was calculated as total number of mitochondria with values above baseline over the total number of objects in the grid. (B) The quantitative relationship between the critical exponents at the first global ΔΨ_m depolarization can be calculated from double-log plots of the number of depolarized mitochondria versus time near p_c (within approximately ±3–5% of p_c) for the first global depolarization (15). The straight line conforms to a power law and the total number of depolarized mitochondria scales as t^{(ν – β)/δ}, with t being time. Thus, the slope gives ν – β/δ (= 0.760; r² = 0.920, for the example presented).

The critical exponents depend only on the dimensionality of the embedding space (e.g., two dimensions for a square lattice) and the “degrees of freedom” of the variable considered, and are independent of the type of lattice being studied (this feature of percolation is referred to as universality). Although the critical exponents β, ν, and δ are independent of the size of the interacting neighborhood, that is, their values are indistinguishable for 4, 8, and 24 nearest neighbors on the square lattice, the critical densities at p_c differ, being 0.593, 0.407, and 0.168, for the coordination numbers 4, 8, and 24, respectively (15). We found a critical density of mitochondria at a p_c value of 0.56, indicating that each mitochondrion in the spanning cluster is affecting its four immediate neighbors.