Chaos may enhance information transmission in the inferior olive

Abstract

Despite unique well characterized neuronal properties, such as extensive electrical coupling and low firing rates, the role of the inferior olive (IO), which is the source of the climbing fiber inputs to cerebellar Purkinje cells, is still controversial. We propose that the IO stochastically recodes the high-frequency information carried by its synaptic inputs into stochastic, low-rate spikes in its climbing fiber output. Computer simulations of realistic IO networks showed that moderate electrical coupling produced chaotic firing, which maximized the input-output mutual information. This “chaotic resonance” may allow rich error signals to reach individual Purkinje cells, even at low firing rates, allowing efficient cerebellar learning.

Over a century of cerebellar research has provided us with comprehensive understandings of cerebellar anatomy and physiology. It is well known, for instance, that the output neurons of the cerebellar cortex, the Purkinje cells, receive two major types of synaptic inputs: >100,000 parallel fibers and a single climbing fiber, an axon from an inferior olive (IO) neuron; whereas summation of parallel fiber inputs generate “simple spikes,” a single IO spike generates a “complex spike” through the powerful climbing fiber input. Furthermore, the major anatomical and electrophysiological properties of the IO neurons are well characterized (1). First, these neurons generate dendritic and somatic spikes at low firing rates in vivo (three spikes per sec at most) (2). Second, they are electrotonically coupled by gap junctions (3), more extensively than any other cells of the mammalian brain (4). Third, they exhibit subthreshold oscillations in vitro (5, 6). However, despite this detailed knowledge, we still lack a clear understanding of the function of the cerebellum, and two seemingly contradictory major hypotheses have been proposed, each based on a dramatically different view of the IO (7, 8).

According to the cerebellar learning hypothesis (9-13), when conjointly activated with parallel fibers, IO spikes modify cerebellar input-output transformations, in agreement with the known long-term depression (LTD) at the parallel fiber-Purkinje cell synapse (14). Recent cerebellar motor learning theories (12, 15-19) make two further postulates relevant to this hypothesis. First, the IO neurons must fire at a low firing rate so that complex spikes encoding error signals do not interfere with simple spikes carrying motor control commands (12, 15). Second, the IO must transmit error signals (15, 20) with high-temporal resolution for cerebellar learning for efficient motor control.

Alternatively, the cerebellar timing hypothesis states that the IO exerts its influence on motor control in real time via synchronous and rhythmic discharges (21). This hypothesis is in agreement with the facts that IO neurons are extensively electrically coupled via gap junctions (8) and that IO neurons fire with some degree of rhythmicity and pair-wise synchrony both in vitro (22) and in vivo (21). It is further supported by the general view that electrical junctions synchronize firings of coupled neural oscillators (6, 23). Note, however, that this hypothesis makes no mention of the widely accepted cerebellar plasticity, such as LTD. Conversely, the cerebellar learning theories have yet to accommodate studies showing that the IO neurons are extensively electrically coupled, and fire with some degree of rhythmicity and pair-wise synchrony.

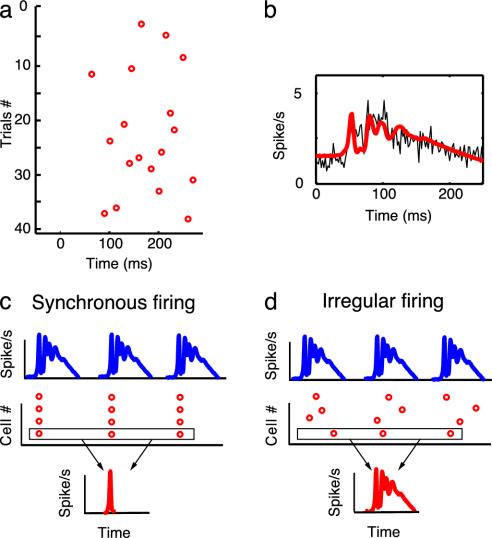
Here, we propose a theory of the role of the IO that is not only coherent with all of the IO data reviewed above, but also explains the facts that although the IO neurons themselves have low firing rates, their inputs have high firing rates (24). We postulate that the major role of the IO is to reduce the firing rate carrying the error signal for cerebellar learning while maintaining its information content. Although the observed low firing rates may appear to contradict the assumption that the IO output carries high-resolution error signals, recent data show that peristimulus histograms (PSTH) of complex spikes do contain high frequency components (Fig. 1 a and b) (15). This means that IO spikes are generated at different timings in each trial, so that the accurate error signal is available for individual Purkinje cells after repeated trials. Although the error signal waveform is not explicitly reconstructed, the cumulative effects of LTD, known to have time constants up to several hours (14), virtually average the climbing fiber inputs (12, 15, 16) (see Discussion). LTD can thus restore high-frequency information content of the error signal for individual Purkinje cells. If the IO discharges were rhythmic and synchronized, the PSTH would have a very sharp peak at the onset of a volley of synaptic inputs, and the IO would not transmit information-rich signals (Fig. 1c). In contrast, if the IO discharges were irregular and desynchronized, after summation, the PSTH would be similar to the input waveform (Fig. 1d). That is, if the spike timing is varied on each learning episode, each individual Purkinje cell can restore IO input content by temporal averaging through LTD.

Fig. 1.

Data showing that PSTH of complex spikes contain high-frequency components. (a) Complex spikes recorded in a Purkinje cell during OFR in a monkey. The raster plot shows the large variability in the timing of complex spikes from trial to trial during 40 presentations of visual stimulus motion. (b) Temporal average of 487 trials from the individual Purkinje cell shows that the PSTH (2-msec time bins) carries high-frequency information (thin black line). The thick red line shows that a generalized linear model can accurately reproduce IO neuron firing rate; data are from ref. 15 with permission. (c and d) Diagrams illustrating the advantage of irregular and desynchronized firing of IO neurons. (c) A cluster of IO cells receive a common synaptic inputs of high firing rates (Top), and they fire regularly and synchronously by electrical coupling (Middle). Because all of the IO cells in a cluster fire synchronously at the synaptic input onset, they do not respond to the remaining part of the input; moreover, repetitive presentation of the same input induces very similar responses. Thus, the PSTH of each cell, or a cluster of IO cells, exhibits a sharp peak at the onset (Bottom). (d) On the other hand, if in response to the input (Top), IO firing is irregular and desynchronized (Middle), the same input induces different responses for each neuron over trials. Thus, the PSTH is more similar to the input waveforms (Bottom): the temporal resolution of the transmitted information is high after temporal averaging. [b is reproduced with permission from ref. 15 (Copyright 1998, Am. Physiol. Soc., Bethesda).]

How then could irregular and desynchronized firing arise in coupled IO neurons? Although strong electrical coupling synchronizes neurons, moderate electrical coupling can theoretically desynchronize neurons (25-28) and can make the discharges of individual cells irregular (25). This possibility is consistent with the apparently random IO firing in vivo (15, 29) (see Fig. 1a for an example) and the chaotic subthreshold IO oscillations in vitro (30). To test this hypothesis, we simulate small networks of realistic IO cell models and study the effect of electrical coupling on both spiking behavior and input-output information transmission.

Methods

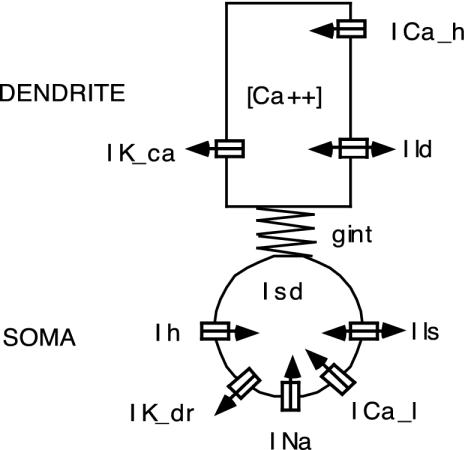
Cell Model. The single IO cell model (see Fig. 2) consisted of a somatic and a dendritic compartment to represent the known location of the ionic currents, gap junctions, and synaptic inputs (25). The somatic compartment included a low-threshold calcium current (I_Cal), an anomalous inward rectifier current (I_h), a Hodgkin-Huxley type sodium current (I_Na), and a delayed rectifier potassium current (I_Kdr). The somatic low-threshold calcium current had a window of conductance around the resting potential, which caused excitation in response to hyperpolarizing current pulses. The dendritic compartment contained a high-threshold calcium current (I_Cah), a calcium-activated potassium current (I_KCa), and an electrical junction current (I_c) (25). The dendritic high-threshold calcium current was noninactivating, which generated prolonged plateau potentials in response to depolarizing inputs. Dendritic calcium influx activated the calcium-dependent potassium current, which abruptly terminated the plateau potentials after 20-30 msec. Because the inactivation of this current had a long time constant, dendritic spikes were followed by a prolonged hyperpolarization during which the cell was less responsive to its inputs.

Fig. 2.

Two-compartment biophysical model of an IO cell. The somatic ionic currents include a low-threshold calcium inward current (I_Cal), an anomalous inward rectifier current (I_h), the Hodgkin-Huxley type inward sodium (I_Na) and outward delayed rectifier potassium (I_Kdr) currents, and a leakage current (I_ls). The dendritic currents include a high-threshold inward calcium current (I_Cah), an outward calcium-dependent potassium current (I_KCa), and a leakage current (I_ld). Because the dendritic potassium current I_KCa is calcium-dependent, Ca²⁺ concentration dynamics is included in the model. g_int is the coupling conductance between the two compartments. The electrotonic coupling between this cell and multiple other cells is not shown.

Our cell model was previously developed to account for in vitro experiments. To replicate the low firing rate of IO cells and increased excitability in vivo, as well as to incorporate new data on electrical coupling (31), we slightly modified the model as follows. To decrease the firing rate, we increased the pump-out time constant of the dendritic calcium concentration

1

To increase the excitability, we used the following maximal current conductances: g_Na = 110 mS/cm², g_Cal = 2 mS/cm², g_h = 0.15 mS/cm²; the forward rate constant of the sodium current was changed to α_m = (V + 48)/1 - e^(-(V+48)/3) to reduce the number of sodium spikes during the plateau potential. As the nonlinearity of the gap junctions seems to be more pronounced than we previously modeled (31), we weighted the maximal coupling conductance g_c by f(V) = 0.8e^{(-(V 2}/10²)) + 0.2, where V was the membrane potentials difference between two coupled dendrites. This model adequately reproduces the coupling nonlinearity observed when one cell is strongly depolarized compared to its neighbor (possibly because of Ca²⁺-dependent inactivation of coupling).

Synaptic Inputs. To show that irregular firing can lead to high information transfer of error signals to individual Purkinje cells at low firing rates, we added, to each cell, synaptic inputs carrying realistic error signal in an eye-movement task. Neurons in the pretectal nucleus of the optic tract innervate the IO, and exhibit high firing rates up to 400 spikes per sec during ocular following response (OFR) (24). Furthermore, their PSTH is similar in shape to the PSTH of complex spikes (15, 24). Thus, for simplicity, we assumed the IO synaptic input to be the complex-spike PSTH rescaled between 10 and 200 spikes per sec. OFR error inputs, each lasting 252 msec, were presented every 1-2 sec (uniform distribution, mean 1.5 sec). This waveform was then used as an input to 20 Poisson process spike generator: 10 were common to all cells and 10 were prepared separately for each cell. These spike trains arrived at 20 excitatory synapses on each cell.

To study the effect of noise on information transmission, each cell received additional 20 excitatory and 20 inhibitory Poisson synaptic inputs (adding only excitatory inputs would quickly silent the cells by increasing the average membrane potential), each carrying noisy inputs of mean firing rate 10 spikes per sec.

We modeled the excitatory synapses with

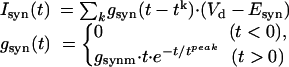2

where g_synm is the maximal synaptic conductance, t^k is the time of kth spike arrival, t^peak = 2.5 msec is the time to peak, and V_d is the dendritic membrane potential. The synaptic current reversal potential was E_syn = -10 mV is for the excitatory synapses and -75 mV for the inhibitory synapses. We used this synaptic model both for the OFR inputs (with g_synm = 0.03 mS/cm²) and for the excitatory and inhibitory noise inputs, see below (with varying maximal synaptic conductance).

Network Structure. To account for the variability in cellular properties observed in real neurons, we then built small networks of heterogeneous neurons with heterogeneous coupling. In our simulations we used two types of networks: (i) chain networks of 9 × 1 cells, in which each cell is coupled to its two nearest neighbors (except for the two cells at the extremities); and (ii) grid networks of 2 × 2, 3 × 3, and 9 × 3 cells, where the cells are connected to their two, three, or four neighbors depending on their positions in the grid. To account for the variability in cellular properties, the maximal conductance g_Cal of the low threshold calcium current were drawn from uniform distributions, with maximum deviations set at ±20% of the mean (larger deviations led to some cells not firing at all). Furthermore, the coupling strengths g_c were also taken from uniform distribution, with maximum deviation set at 20% of the mean for all networks. A hyperpolarizing current of I_hyp = -0.1 μA/cm² was injected in both the soma and the dendritic compartments.

Lyapunov Exponents. To verify whether the irregular firing was chaotic, we computed the Lyapunov exponents (32) for different network structures and different coupling strengths. To compute the Lyapunov exponents, we simulated 10 different 2 × 2, 1 × 9, and 3 × 3 networks (computation of the Lyapunov exponents was impracticable for 9 × 3 networks); each network had different g_Cal and g_c drawn from uniform distributions. We started the computation of the exponents at 50 sec after an initial perturbation and recorded the exponent values at 100 sec, when the values converged. We linearized the 40 or 90 dimension (10 variables for each cell) system by deriving the analytical form of Jacobian at time t, J_t, calculated the evolution of an orthonormal set of vectors V_t and computed the exponents in terms of the length of the principal axes.

Coupling Coefficients and Input Conductance. To examine whether the coupling strength leading to chaos and high information transfer in our models were biologically realistic, we computed the coupling coefficients (CCs), which are defined as the ratio of change in steady state membrane potentials of a prejunctional cell to that of the postjunctional cell. To compute the CCs, we first hyperpolarized all cells to -67 mV by injection of I_hyp = -1 μA/cm². To determine the CCs, we injected a tonic depolarizing current of 0.2 μA/cm² in the soma of a “master” cell, and recorded the steady state voltage change in both this master cell and a neighboring cell. To best reproduce experimental conditions, we used two cells coupled to four other cells in the 3 × 9 networks. We estimated the input resistance from the voltage response to a -0.2 μA/cm² current injection. The input conductance is the inverse of the input resistance.

Mutual Information. We quantified the influence of electrical coupling on the low firing code of IO output by computing how much information about the input could be extracted from the IO output spike trains, i.e., the mutual information. To measure the mutual information robustly, we constructed 10 different samples of 2 × 2, 3 × 3, and 3 × 9 networks; each network had different g_Cal and g_c drawn from uniform distributions. Then, for each network, we ran 10 simulations (each with a different random seed for Poisson spike generators); responses to the first two OFR inputs were considered as transients and discarded. To keep the number of spikes roughly constant, we used for analysis the responses to 135 OFR inputs for the 2 × 2 networks, the responses to 60 inputs for the 3 × 3 networks, and the responses to 20 OFR inputs for the 9 × 3 networks. We detected the presence of spikes by differentiating the membrane potential and applying a threshold.

The mutual information was given from the formula

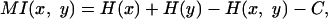3

where x is the OFR histogram made from Poisson spikes, y is the IO output, H(x), H(y), and H(x, y) are marginal and joint entropies of inputs and outputs, and C is a correction term necessary to compensate for the small number of spikes (33). We made PSTH of both the OFR inputs and the corresponding IO output spikes with 0.5 msec time bins, filtered them with a Gaussian filter(standard deviation: 5 msec), and computed the entropies from the histograms (10 equally distant bins) of x, y, and (x, y).

Results

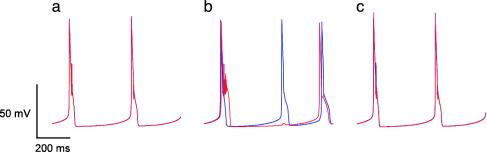
Properties of Single Cells and Homogenous Coupled Networks. We previously showed that two identical coupled IO neurons could generate desynchronized antiphase firing (25). We show here that moderate coupling in a small 3 × 3 network of identical IO cells, each connected to its nearest neighbors, can generate desynchronized and irregular firing (Fig. 3). For a physiologically plausible coupling strength, if all of the initial conditions were identical, firing was synchronized and rhythmic (Fig. 3a). If the middle cell was initially delayed only by 1 msec compared to all of the other cells, the current flowing into this cell via the gap junctions generated a dendritic spike (first red spike in Fig. 3b), then the cells' spikes became desynchronized. Because of the activation of calcium-dependent potassium current the middle cell failed to fire a somatic spike when the other cells did, and then fired (a somatic spike) earlier than others did in the next cycle (Fig. 3b). This shows that a coupled IO network has the two basic mechanisms for providing chaos: (i) sensitivity to initial conditions and (ii) “expansion and folding,” that is, expansion of small delay in spike timing and its reversal into early spiking. For stronger coupling, a 1-msec delay in the middle cell did not induce desynchronization but resulted in regular and periodic firing (Fig. 3c).

Fig. 3.

Demonstration of the sensitivity to initial conditions for medium coupling strength for a network of identical cells. Shown are the membrane potentials for two coupled cells in a 3 × 3 network of identical cells. Blue line, middle cell; red line, left neighbor. (a) Intermediate coupling strength (g_c = 0.04 mS/cm²) and same initial conditions for all neurons: the two cells fire somatic spikes in synchrony. (b) Same coupling strength (g_c = 0.04 mS/cm²), but the middle cell is initially delayed by only 1 msec compared to all of the other cells. The middle cell (red) generates a dendritic spike as shown by the shoulder after the sodium spike. (c) Same initial conditions as in b, but with strong coupling (g_c = 0.5 mS/cm²): firing is regular (somatic spikes).

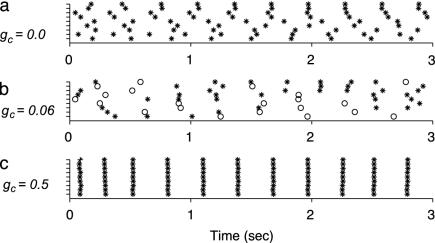
Moderate Coupling Leads to Chaotic Spiking in Heterogeneous Networks. Fig. 4 shows the spiking behavior of the nine (3 × 3) middle cells of a 9 × 3 network, which received constant current input. Without electrical coupling (Fig. 4a), each cell generated periodic somatic spikes. The average firing rate was 3.1 spikes per sec; however, because of cellular heterogeneity, the difference in firing rates between the slowest and fastest cells was 0.7 spikes per sec. With intermediate coupling strength (mean g_c = 0.06 mS/cm², Fig. 4b), the firing pattern of individual cell appeared chaotic, often with one or several dendritic spikes generated between somatic spikes, because of the long after-hyperpolarization following dendritic spikes, the average firing rate was reduced to 1.8 spikes per sec. With strong coupling (mean g_c = 0.5 mS/cm²; Fig. 4c), spiking became almost synchronous, and, as in the uncoupled case, the cells generated only regular somatic spikes (firing rate: 3.5 spikes per sec). This increase in synchrony, rhythmicity, and firing rate is consistent with biological data under conditions of increased coupling strengths (22).

Fig. 4.

Spiking behavior of coupled IO cells without synaptic inputs for a network of nonidentical cells. The nine cells shown are the middle 3 × 3 cells of a 9 × 3 network. Raster plots for respective coupling strengths g_c = 0.0, 0.06, and 0.5 mS/cm² are shown. Open circles, dendritic spikes; asterisks, somatic spikes.

To quantify the synchrony between cells, we computed the mean pair-wise correlation coefficients (21) (at zero delay using a 10-msec time bin) between the center cells and its four immediate neighboring cells, in 3 × 3 networks. The mean pair-wise correlation coefficients increased monotonically with coupling: 0.012 ± 0.017 for g_c = 0.06 mS/cm², 0.11 ± 0.08 for g_c = 0.1 mS/cm², and 0.66 ± 0.053 for g_c = 0.5 mS/cm².

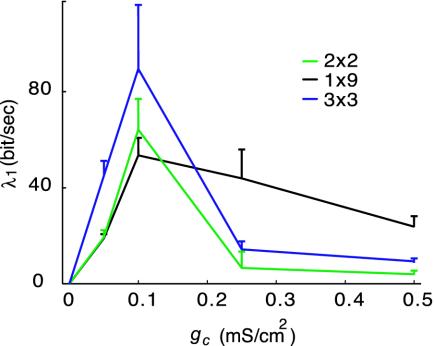
As seen above, moderate electrical coupling can also have the less intuitive property of making firing chaotic. For both weak (g_c <0.06 mS/cm²) and strong (g_c >0.5 mS/cm²) coupling strengths, the largest Lyapunov exponent (λ₁) was close to zero for all networks, an indication of near-rhythmic firing. For intermediate coupling strengths however the largest Lyapunov exponent was largely positive, an indication of strong chaotic behavior (Fig. 5).

Fig. 5.

Largest Lyapunov exponent as a function of coupling strength g_c for different networks of nonidentical cells. When the largest exponent was large, the network exhibited marked chaotic behavior. When the largest exponent was close to 0, firing was almost rhythmic.

Our results offer an explanation to the seemingly contradictory reports on rhythmic (21, 22) or arhythmic (29) IO neuron firing. It is known that the coupling strength is under control of γ-aminobutyric acid (GABA)ergic innervation that originates from the cerebellar nuclei (22). When the GABAergic input is present in vivo (corresponding to intermediate coupling in the model), the cells discharge with little rhythmicity and synchrony. When the GABAergic input is blocked in vitro (corresponding to strong coupling in the model), however, the discharges are rhythmic and synchronous. Furthermore, our results show that although moderate electrical coupling leads to some degree of synchrony between cell pairs, it makes the cells arhythmic when the whole network becomes desynchronized. This puzzling result may be interpreted as chaotic itinerancy (34): clustering of subgroups of synchronized elements can vary over time in coupled systems of chaotic elements. This is consistent with multicellular recording data showing coherence in small subgroups of cells that varied over time (35).

Moderate Coupling Increases Information Transfer. When synaptic inputs carrying realistic error signal in an eye-movement task were added, the overall change in firing behavior with coupling was similar to that without inputs; without coupling, these cells generated predominantly somatic spikes. Moderate coupling (g_c = 0.06 mS/cm²) yielded both somatic and dendritic spikes, and IO discharges were irregular and desynchronized overall. With strong coupling, the cells only generated almost synchronized somatic spikes.

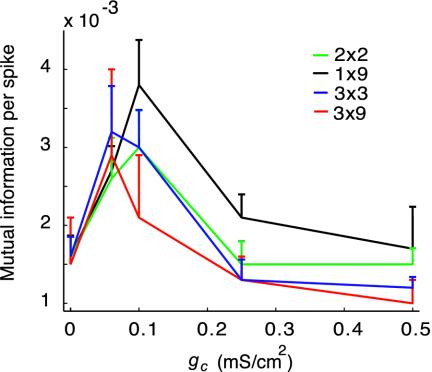
The mutual information per spike for a single cell at the center of the 3 × 3 networks was 48% greater for g_c = 0.06 mS/cm² than that with no coupling. Furthermore, the mutual information carried by whole networks increased by 37% in average compared to no coupling, and, because of the reduction in firing rate, the mutual information per spike increased by 102% on average (Fig. 6). Note that the coupling strength that produced the largest Lyapunov exponent (Fig. 5), g_c = 0.1 mS/cm², also yielded a large information transfer. To test the generality of our results, we further computed the mutual information for whole 2 × 2, 1 × 9, and 9 × 3 networks: in all cases, moderate electrical coupling produced a large increase in mutual information per spike (see Fig. 6).

Fig. 6.

Network mutual information per spike as a function of coupling strength g_c for different networks of nonidentical cells.

The coupling strength leading to chaos and high information transfer in our models were biologically realistic, as shown by the coupling coefficients. We found CC ≈ 0.045 for g_c = 0.06 mS/cm². These values were compatible with experimentally observed CCs (between 0.002 and 0.17, with most CCs between 0.01 and 0.05) (31).

Physiological Noise Inputs Do Not Lead to Similar Increase in Information Transfer. The above results show that chaotic behavior of coupled neurons without synaptic inputs appeared to underlie increased input-output information transmission. This is reminiscent of “stochastic resonance,” a phenomenon wherein the response of a nonlinear system to a weak input signal is optimized by the presence of a particular, nonzero level of noise (36). For example, in threshold units such as sensory neurons, moderate noise levels improve their responses by bringing them above threshold (37). Stochastic resonance has been observed in sensory systems (37), but not in the central nervous system.

Our results in 3 × 3 uncoupled networks showed that, although the average mutual information per spike did not increase for a maximal noise input conductance of 0.05 mS/cm², it increased on average 33% for 0.5 mS/cm², and 97% for 2 mS/cm². To examine whether 2 mS/cm² was biologically plausible, we compared the total synaptic conductance 3,200 nS with the cell input conductance 12.4 nS. The total synaptic conductance, consisting of 20 synapses of 2 mS/cm², was computed from the surface area of the model dendritic compartment (25) as 20 × 2 mS/cm² × 8,000 μm². Given a reversal potential for excitatory synapse E_syn = -10 mV, activation of only 0.1% of the total synaptic conductance would produce 11.7 mV depolarization. Because this is clearly too large, we conclude that physiological ranges of synaptic conductance for noisy inputs cannot produce large increase in mutual information.

Discussion

Our results suggest that electrical coupling in IO cells may induce chaos, which allow information-rich but low firing-rate error signals to reach individual Purkinje cells, thereby providing the cerebellar cortex with essential information for efficient learning without disturbing on-going motor control.

The chaotic firing leads to the generation of IO spikes at different timings at each trial. Because of the IO low firing, the accurate error signal can only be available for individual Purkinje cells after repeated trials; the cumulative effects of LTD allows the Purkinje cells to reconstruct the error signal. To illustrate how this can be the case, let us look at the OFR system, which has been thoroughly studied both experimentally (15) and in simulations (16, 38). An OFR movement is elicited by the sudden motion of a large-field visual stimulus. This visual stimulus yields a wide variety of responses in medial superior temporal (MST) neurons (38), which are relayed to the Purkinje cells via the granule cells. Although it is impossible to record from granule cells in vivo because of their tiny sizes, simulations showed that they provide Purkinje cells with a variety of temporal basis functions (such as Gaussian radial basis functions with different time delays), with the origin of time taken at the onset of movement. Conjoint activity in parallel fibers and climbing fiber induce LTD. Thus, if, for instance, one IO spike reaches a Purkinje cell 150 msec after the stimulus motion onset, all parallel fiber synapses activated ≈150 msec after the stimulus motion onset will be depressed. Using the same OFR error signal we use in the present paper, we demonstrated that the simple spike firing temporal waveform of a Purkinje cell reconstruct, after learning, was an approximate (but not exact, see ref. 12) mirror image of the complex spike PSTH (16, 38).

Although we took the OFR control as an illustrative example, our view of the IO applies to all types of movement control; in all cases, the IO must transmit error signal with high-temporal resolution for cerebellar learning for efficient motor control. In particular, when the movements are rapid and need accuracy like the saccadic or fast arm movements, a feed-forward motor command must be accurately learned (for example, see refs. 17 and 39). The proposed chaotic firing can achieve this learning without compromising the on-line motor command. Furthermore, our proposal also extends to the role of the cerebellum in classical conditioning. Indeed, it has been recently proposed (40, 41) that cerebellar-dependent classical conditioning, such as eye blink conditioning (in which the animal learns how to close its eyelid at the time of an air puff), followed the same principles as motor control for eye movements (VOR and saccade): feed-forward use of sensory information via temporally specific learning. Furthermore, the learning rules that models LTD in both classical conditioning and motor control are variations of functionally similar error correcting rules; compare, for instance, the learning rules for classical conditioning in ref. 42 and motor control in ref. 12. Because the classical conditioning response (the closure of the lid) is a fast and accurate motor response, the IO that carry the teaching (or error) signal should have the same role we proposed here. Indeed, the motor command to control the eyelid has a temporal waveform in the 200-msec range (see figure 4.5 in ref. 40). This need for a motor command with an extended duration could, a priori, seem to run against the need for a precise timing of the eye lid in response to the air puff; however, simulations in ref. 40 showed that, even with an IO input that was artificially smeared, the eye-blink occurs exactly at the time of the air puff.

We showed here that electrical coupling could provide the source of disorder that induced a “chaotic resonance” (43) in IO networks. This resonance led to an increase in information transmission in IO cells by distributing the high-frequency components of the error inputs over the sporadic, irregular and non-phase-locked spikes by the following electrophysiological mechanisms. Isolated (noncoupled) IO cells tend to generate mainly rhythmic somatic spikes for constant current inputs. Because somatic spikes, unlike dendritic spikes, do not induce long-lasting hyperpolarization, the firing rates are relatively high. For very strong coupling, even inhomogeneous cells are almost perfectly synchronized, and thus behave like a single cell. Consequently, only somatic spikes of relatively high frequency with rhythmicity are generated (see figure 3 in ref. 22). If phasic synaptic inputs that contain motor error signals are fed to either uncoupled or strongly coupled cells, the properties of the above autonomous system (without chemical synaptic inputs) are maintained. That is, only somatic spikes are generated with relatively high firing frequency, and those spikes tend to be phase locked to the onset of error signals and synchronized between IO neurons. Thus, for either no or strong coupling, information transmission per spike is low.

In contrast to these two cases, medium electrical coupling induces dendritic spikes, phase jitters between neighboring neurons, and chaos. The balance between excitatory and inhibitory currents flowing through the gap junctions was essential for chaos (see ref. 44). In the presence of even very small differences in spike timing between coupled neurons, depolarizing currents flowing through gap junctions can generate dendritic spikes. Then, dendritic spikes and resulting after-hyperpolarizations introduce complex phase shifts in neighboring neurons by excitation/inhibition, and thus induce chaos. Because chaos makes the spikes less time-locked to error signals, mutual information increases. It is possible to experimentally test this model by computing the Lyapunov exponents from recordings of spiking IO neurons (or complex spikes) while experimentally varying the electrical coupling strength.