Statistics for Nonparametric Linkage Analysis of X-Linked Traits in General Pedigrees

Abstract

We have compared the power of several allele-sharing statistics for “nonparametric” linkage analysis of X-linked traits in nuclear families and extended pedigrees. Our rationale was that, although several of these statistics have been implemented in popular software packages, there has been no formal evaluation of their relative power. Here, we evaluate the relative performance of five test statistics, including two new test statistics. We considered sibships of sizes two through four, four different extended pedigrees, 15 different genetic models (12 single-locus models and 3 two-locus models), and varying recombination fractions between the marker and the trait locus. We analytically estimated the sample sizes required for 80% power at a significance level of .001 and also used simulation methods to estimate power for a sample size of 10 families. We tried to identify statistics whose power was robust over a wide variety of models, with the idea that such statistics would be particularly useful for detection of X-linked loci associated with complex traits. We found that a commonly used statistic, S_all, generally performed well under various conditions and had close to the optimal sample sizes in most cases but that there were certain cases in which it performed quite poorly. Our two new statistics did not perform any better than those already in the literature. We also note that, under dominant and additive models, regardless of the statistic used, pedigrees with all-female siblings have very little power to detect X-linked loci.

Introduction

Statistical methods for linkage analysis are usually divided into “parametric” and “nonparametric” methods. Although there is ongoing debate about the appropriateness of this division and about which methods are best under what circumstances (e.g., see Abreu et al. ¹⁹⁹⁹; Sham et al. ²⁰⁰⁰), it seems fair to say that the nonparametric, or “allele-sharing,” statistics have been particularly important in mapping studies of complex traits. In this article, we consider some of the issues involved in applying allele-sharing statistics to detect X-linked loci involved in complex traits.

Although parametric methods have been used extensively for X-chromosomal linkage analysis (e.g., see Nyholt et al. ¹⁹⁹⁸; Vallada et al. ¹⁹⁹⁸; Xu et al. ¹⁹⁹⁸), there has been limited development and use of nonparametric methods for detection of X linkage. Weeks et al. (1995) developed an X-linked version of the affected-pedigree-member method, based on identity-by-state sharing. Cordell et al. (1995) extended the sib-pair method of Risch (1990a, 1990b, 1990c) and Holmans (1993) to the X chromosome, and Dupuis and Van Eerdewegh (2000) developed a similar theory for the pseudoautosomal region. Two of the most popular software packages for nonparametric linkage analysis—GENEHUNTER (Kruglyak et al. 1996) and Allegro (Gudbjartsson et al. 2000)—have implemented X-chromosome statistics. However, these statistics are not actually defined or described in the literature, and GENEHUNTER dropped the X-linkage option after version 1.3. Since there is certainly evidence suggesting the involvement of X-chromosome loci in complex traits (e.g., see Hamer et al. ¹⁹⁹³; Nyholt et al. ¹⁹⁹⁸; DeLisi et al. ²⁰⁰⁰; Liu et al. ²⁰⁰¹), we saw a clear need for a more complete study of allele-sharing statistics for X linkage in general pedigrees.

In this article, we first describe the X-chromosome allele-sharing statistics implemented in Allegro and in GENEHUNTER version 1.3. We then use analytic methods and simulation to compare the power of those statistics, as well as that of two new statistics that we propose. We consider a number of different pedigree types and genetic models. Our goal is to find a statistic whose power is robust over a wide variety of situations, since one does not expect to know much, in advance, about the trait model when studying a complex trait. Our methodological approach is very similar to that used in our recent study of autosomal allele-sharing statistics (Sengul et al. 2001).

Subjects and Methods

Pedigrees

We studied both nuclear families and extended pedigrees. The nuclear families consisted of parents with unknown trait phenotypes and two to four affected siblings of all possible sex combinations. We considered four different extended-pedigree structures, which obviously does not account for all possibilities but which allowed us to investigate the effects of several important pedigree features. The extended pedigrees consisted of affected individuals (shaded symbols in figs. 1 and 2) and individuals with unknown trait phenotypes (unshaded symbols in figs. 1 and 2). The first extended pedigree, which we call the “MMT” pedigree (fig. 1A), would normally be considered inconsistent with X-linked inheritance, since it contains a male-to-male transmission, in which there are affected males in two consecutive generations. However, this pedigree is perfectly compatible with a model that includes X linkage along with phenocopies and/or heterogeneity. The second extended pedigree, which we call “NMMT,” is similar, except that it does not include male-to-male transmission (fig. 1B). We also considered two different pedigrees involving affected sibships that are first cousins through sisters; pedigree “CSFF” contains only female affected individuals (fig. 1A), and pedigree “CSMF” contains both male and female affected individuals (fig. 1B). Figures 1 and 2 show unique numerical labels for each founder allele at a hypothetical marker; we use these in discussing identity-by-descent (IBD)–sharing configurations below.

Figure 1.

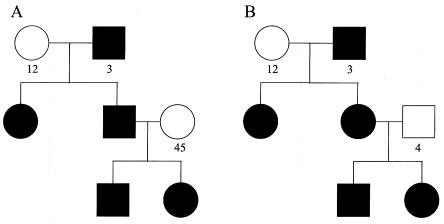
MMT pedigree (A) and NMMT pedigree (B). The numbers denote unique founder alleles; unshaded symbols denote unknown phenotypes.

Figure 2.

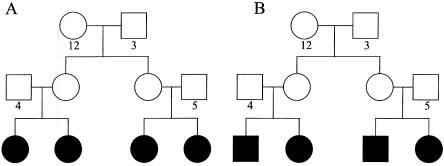
CSFF pedigree (A) and CSMF pedigree (B). Notation is as in figure 1.

Genetic Models

We considered single-locus two-allele dominant, additive, and recessive models with full and reduced penetrance and with varying levels of phenocopies. Table 1 lists all of the single-locus models, with the female penetrances denoted by f₀, f₁, and f₂ and with the male penetrances denoted by g₀ and g₁. In all cases, the phenocopy rate is the same for males and females (g₀ = f₀ for dominant and additive models; g₀ = f₀ = f₁ for recessive models). All models have allele frequency, q, equal to 0.1. The population trait frequencies vary between ∼5% and ∼10% for males (K_male) and between ∼0.5% and ∼20% for females (K_female). Table 1 also presents the relative risks to sibs of a proband, for male-male pairs (λ_mm), male-female pairs (λ_mf), and female-female pairs (λ_ff), computed by the formulae presented by Cordell et al. (1995).

Table 1.

Single-Locus Genetic Models

Model	q	f0	f1	f2	g0	g1	Kmale	Kfemale	λmm	λmf	λff	Description
Dominant:
1	.1	0	.5	.5	0	.5	.050	.095	5.5	3.1	4.1	No phenocopies, reduced penetrance
2	.1	.005	1	1	.005	1	.105	.194	5.1	3.0	4.0	5% of cases are phenocopies, full penetrance
3	.1	.005	.5	.5	.005	.5	.055	.099	4.7	2.8	3.8	5% of cases are phenocopies, reduced penetrance
4	.1	.05	.5	.5	.05	.5	.095	.136	2.0	1.6	2.3	Half of cases are phenocopies, reduced penetrance
Additive:
5	.1	0	.25	.5	0	.5	.050	.050	5.5	3.3	4.4	No phenocopies, reduced penetrance
6	.1	.005	.5	1	.005	1	.105	.104	5.1	3.0	4.1	5% of cases are phenocopies, full penetrance
7	.1	.005	.25	.5	.005	.5	.055	.054	4.7	2.9	3.8	5% of cases are phenocopies, reduced penetrance
8	.1	.05	.25	.5	.05	.5	.095	.091	2.0	1.5	1.7	Half of cases are phenocopies, reduced penetrance
Recessive:
9	.1	0	0	.5	0	.5	.050	.005	5.5	5.5	55.0	No phenocopies, reduced penetrance
10	.1	.005	.005	1	.005	1	.105	.015	5.1	3.9	24.9	5% of cases are phenocopies, full penetrance
11	.1	.005	.005	.5	.005	.5	.055	.010	4.7	3.0	14.4	5% of cases are phenocopies, reduced penetrance
12	.1	.05	.05	.5	.05	.5	.095	.055	2.0	1.2	1.4	Half of cases are phenocopies, reduced penetrance

The phenocopy rates in the single-locus models can be interpreted as including heterogeneity effects, and the single-locus models are also good approximations to certain interaction models that produce small marginal effects. However, we also did a limited investigation of explicit two-locus models. Model “H-rare” is a rare-allele dominant heterogeneity model. At each locus, the disease allele has frequency 0.01; penetrance is 0 for anyone with no disease alleles and is 1.0 for anyone with one or more disease alleles. Model “H-common” is a common-allele dominant heterogeneity model; it has the same penetrance matrices as does model “H-rare”, but the disease-allele frequency at each locus is 0.07. Finally, model “Additive” is an additive model. The disease-allele frequency at each locus is 0.05, there is a phenocopy rate of 0.2 for females and males, and each disease allele at either locus adds an additional 0.2 to the penetrance, so that, for example, a female who is homozygous for the disease allele at both loci has penetrance 1.0.

Allele-Sharing Statistics

We considered five different allele-sharing statistics for testing X linkage. All of the statistics can be applied to any pedigree type. Each statistic measures IBD among affected relatives, but somewhat differently. Our notation for the IBD-sharing configurations is that used by Whittemore and Halpern (1994); founder alleles are given unique numbers (as in figs. 1 and 2), and then the IBD-sharing configurations of family members are described in terms of which founder alleles are inherited by each person. Configurations are understood to include inheritance patterns that are equivalent up to permutation of the founder-allele labels; for example, if we have a mother and father with genotypes labeled 12 and 34 at an autosomal marker, then the IBD-sharing configurations among two offspring may be either (13 13), (13 14), or (13 24), and it is understood that the (13 13) configuration also includes (14 14), (23 23), and (24 24).

One of the allele-sharing statistics that we considered is the commonly used autosomal statistic S_all (Whittemore and Halpern 1994). For autosomal loci, S_all is calculated by forming all possible sets consisting of one allele from each affected individual and then summing the numbers of nontrivial permutations of those sets. This definition can be extended straightforwardly to the X chromosome; for example, if we have two females and a male, with alleles (by descent) labeled 12, 13, and 1, we can form the sets (1 1 1), (1 3 1), (2 1 1), and (2 3 1). Alternatively, males can be treated as homozygous, which has some minor computational advantages and which results in exactly the same statistic. Both Allegro and GENEHUNTER version 1.3 implement S_all for the X chromosome.

All of the other statistics that we consider in this article are “pairs” statistics, formed by scoring allele sharing between each pair of affected individuals in the pedigree and then adding that score over all pairs. The commonly used autosomal statistic S_pairs (e.g., see McPeek ¹⁹⁹⁹) is of this type; it defines the pairwise allele-sharing score for each pair simply as the number of alleles (zero, one, or two) shared IBD. GENEHUNTER version 1.3 and Allegro both implement X-chromosome statistics called “S_pairs,” but we found that the two statistics are not the same: GENEHUNTER treats males as homozygous on the X chromosome, and Allegro treats them as hemizygous, which results in pairwise allele-sharing scores (and, thus, versions of S_pairs) that are not equivalent; for example, if a male-male pair shares an allele IBD, Allegro treats the sharing configuration as (1 1) and gives it a score of 1, whereas GENEHUNTER treats the sharing configuration as (11 11) and gives it a score of 2. Table 2 shows all of the pairwise allele-sharing scores used by each version of S_pairs: the Allegro statistic (S^A_pairs), the GENEHUNTER statistic (S^GH_pairs), and our two new statistics, S_X50 and S_X75 (which are defined below). If we assume that there is no inbreeding, male-male and male-female pairs can share only zero alleles or one allele IBD. Female-female pairs can share zero, one, or two alleles IBD, although a female-female sibling pair can share only either one allele or two alleles. The rationale for our new statistics, S_X50 and S_X75, is as follows: Allegro and GENEHUNTER assign very different relative scores to complete sharing between females (13 13) versus complete sharing between males (1 1): Allegro gives much greater weight to female-female sharing, and GENEHUNTER gives much greater weight to male-male sharing. Our two new statistics give equal scores to male-male and female-female sharing, but the two differ in the scores (0.5 vs. 0.75) that they give to male-female (1 13) sharing.

Table 2.

Pairwise Allele-Sharing Scores Used by Different Statistics

Relative Pair and Configuration	SApairs	SGHpairs	SX75	SX50
Female-female:
(13 13)	2	1	1	1
(13 23)	1	.5	.5	.5
(13 24)	0	0	0	0
Male-male:
(1 1)	1	2	1	1
(1 2)	0	0	0	0
Male-female:
(1 13)	1	1	.75	.5
(2 13)	0	0	0	0

As an alternative to the definitions above, all of the statistics that we considered can be described as scoring functions that assign a score, S, to each possible IBD-sharing configuration, φ, that the entire pedigree takes on (Whittemore and Halpern 1994). Thus, for a single pedigree, the statistic is written as

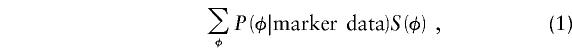where the conditional probabilities of the IBD-sharing configurations, P(φ|marker data), can be computed by whatever method is desired (e.g., by software such as GENEHUNTER). To construct a linkage test, the statistic for each pedigree is normalized by subtracting the null hypothesis mean and dividing by the null hypothesis SD. The normalized statistics are summed over pedigrees, and the sum is asymptotically normally distributed under reasonable regularity conditions. The scores for different pedigrees can also be weighted before they are summed, to reflect different amounts of information contained in pedigrees of different sizes and types. Because of the normalization, additive and multiplicative constants are irrelevant to the definitions of the statistics—that is, any statistics that result in identical normalized coefficients would have identical power; for example, Kruglyak et al. (1996) gave an alternative definition of S_all that is equivalent to Whittemore and Halpern’s definition to a linear transformation.

Table 3 lists the IBD-sharing configurations and scoring functions of all the statistics for an affected sib trio. The scoring functions are normalized as described above, which allows them to be compared directly. Note that a positive normalized score for a given IBD-sharing configuration means that the configuration is considered to be evidence in favor of linkage, whereas a negative normalized score means that the configuration is considered to be evidence against linkage. Table 4 gives the configurations and scoring functions for a family of four affected siblings. We do not present a table for sibling pairs; since each type of sibling pair (male-male, male-female, and female-female) has only two possible IBD-sharing configurations, all of the statistics are equivalent to each other for sibling pairs. Tables 5–8 give the normalized scoring functions for the extended pedigrees that we considered. For each pedigree, the order of the individuals in the IBD-sharing configuration is from first generation to last and from left to right, in each generation (see figs. 1 and 2). The IBD-sharing configurations in each table are ordered from greatest sharing to least, although this ordering is not necessarily well defined, since different ways of quantifying IBD sharing are possible.

Table 3.

Normalized Sibship Statistics for Three Affected Siblings

	Normalized Coefficient for Statistic
IBD Configurationa	SApairs	SGHpairs	Sall	SX75	SX50
Three males:
(1 1 1)	1.73	1.73	1.73	1.73	1.73
(1 1 2)	−.58	−.58	−.58	−.58	−.58
Two males–one female:
(1 1 13)	1.73	1.63	1.70	1.71	1.63
(2 2 13)	−.58	.00	−.24	−.34	.00
(1 2 13)	−.58	−.82	−.73	−.69	−.82
One male–two females:
(1 13 13)	1.73	1.67	1.71	1.71	1.73
(1 13 23)	−.58	−.33	−.43	−.43	−.58
(2 13 13)	−.58	−1.00	−.85	−.85	−.58
Three females:
(13 13 13)	1.73	1.73	1.73	1.73	1.73
(13 13 23)	−.58	−.58	−.58	−.58	−.58

^aThe mother's allele labels are 1/2, and the father's allele label is 3.

Table 4.

Normalized Sibship Statistics for Four Affected Siblings

	Normalized Coefficient for Statistic
IBD Configurationa	SApairs	SGHpairs	Sall	SX75	SX50
Four males:
(1 1 1 1)	2.45	2.45	2.62	2.45	2.45
(1 1 1 2)	.00	.00	−.24	.00	.00
(1 1 2 2)	−.82	−.82	−.56	−.82	−.82
Three males–one female:
(1 1 1 13)	2.45	2.32	2.57	2.42	2.32
(2 2 2 13)	.00	.77	.20	.35	.77
(1 1 2 13)	.00	−.26	−.33	−.12	−.26
(1 2 2 13)	−.82	−.77	−.59	−.81	−.77
Two males–two females:
(1 1 13 13)	2.45	2.26	2.51	2.41	2.33
(1 1 13 23)	.00	.52	.16	.27	.33
(1 2 13 13)	.00	−.52	−.48	−.27	−.33
(2 2 13 13)	−.82	−.52	−.48	−.80	−.33
(1 2 13 23)	−.82	−.87	−.69	−.80	−1.00
One male–three females:
(1 13 13 13)	2.45	2.32	2.50	2.40	2.45
(1 13 13 23)	.00	.26	.04	.16	.00
(2 13 13 13)	.00	−.77	−.66	−.48	.00
(2 13 13 23)	−.82	−.77	−.66	−.80	−.82
Four females:
(13 13 13 13)	2.45	2.45	2.55	2.45	2.45
(13 13 13 23)	.00	.00	−.11	.00	.00
(13 13 23 23)	−.82	−.82	−.70	−.82	−.82

^aThe mother's allele labels are 1/2, and the father's allele label is 3.

Table 5.

IBD Configurations and Normalized Coefficients for the MMT Pedigree

	Normalized Coefficient for Statistic
IBD Configuration	SApairs, SX50	SGHpairs	Sall	SX75
(3 13 1 4 14)	1.34	1.39	1.45	1.37
(3 13 1 4 15)	.45	.28	.23	.34
(3 13 2 4 24)	−.45	−.28	−.38	−.34
(3 13 2 4 25)	−1.34	−1.39	−1.30	−1.37

Table 6.

IBD Configurations and Normalized Coefficients for the NMMT Pedigree

	Normalized Coefficient for Statistic
IBD Configuration	SApairs	SGHpairs	Sall	SX75	SX50
(3 13 13 3 34)	1.58	1.61	1.75	1.63	1.60
(3 13 23 3 34)	.95	1.30	1.62	1.18	1.07
(3 13 13 3 14)	.32	.38	−.17	.28	.53
(3 13 13 1 14)	.32	−.23	−.49	.06	.00
(3 13 13 1 34)	.32	−.23	−.49	.06	.00
(3 13 23 3 24)	−.95	−.23	−.42	−.62	−.53
(3 13 23 2 34)	−.95	−1.15	−.81	−1.07	−1.07
(3 13 23 2 24)	−1.58	−1.45	−1.00	−1.52	−1.60

Table 7.

IBD Configurations and Normalized Coefficients for the CSFF Pedigree

	Normalized Coefficient for Statistic
IBD Configuration	SApairs, SGHpairs, SX75, SX50	Sall
(14 14 15 15)	2.56	2.86
(14 14 15 35)	.37	.15
(14 14 35 35)	−.37	−.33
(14 34 15 35)	−.37	−.49
(14 14 25 35)	−1.10	−.81
(14 34 25 35)	−1.10	−.89

Table 8.

IBD Configurations and Normalized Coefficients for the CSMF Pedigree

	Normalized Coefficient for Statistic
IBD Configuration	SApairs	SGHpairs	Sall	SX75	SX50
(1 14 1 15)	2.56	2.41	2.88	2.52	2.49
(1 14 1 35)	.37	.83	.37	.60	.66
(1 14 3 15)	.37	−.12	−.20	.12	.06
(1 34 1 35)	−.37	−.12	−.31	−.36	.06
(1 14 3 35)	−.37	−.44	−.43	−.36	−.55
(3 14 3 25)	−1.10	−.44	−.54	−.84	−.55
(1 14 2 35)	−1.10	−1.07	−.77	−1.08	−1.16
(1 34 2 35)	−1.10	−1.38	−.88	−1.32	−1.16

Power Computations

We computed power for a test of a single marker, assuming perfect IBD information, with varying recombination fractions (θ = 0.0, 0.05, 0.10, and 0.20) between the marker and the trait locus. (The effect that increasing the recombination fraction has on power is very similar to the effect that is produced by reducing the marker informativeness.) For the two-locus models, we used only θ = 0.0. We used analytic methods to calculate power for all the recombination fractions and, in addition, simulation methods for θ = 0.0. The analytic calculations assume normality and thus fail to account for the fact that some statistics have skewed distributions for small sample sizes and, therefore, higher power; however, since that higher power is accompanied by higher false-positive rates, the analytic calculation provides a “fairer” comparison among the statistics, at least asymptotically. We report results primarily from our analytic comparison, but we also comment on what our simulation studies found about increased power and false-positive rates for the more skewed statistics.

For our analytic calculation, we first calculated the probability of each IBD-sharing configuration under each alternative hypothesis, conditional on the set of affected relatives. For the single-locus models, this was done by MENDEL (Lange et al. 1988); for the two-locus models, we wrote a program to simulate families, selected those with the right set of affected individuals, and scored the IBD-sharing configurations. We then used these IBD-sharing–configuration probabilities to compute the mean and variance of each statistic, on the basis of the normalized coefficients. This procedure is discussed in more detail by Sengul et al. (2001). The sample size (number of families) needed to obtain 80% power with a significance level of .001 by a Z-test was computed as follows: sample size = (z_ασ₀ + z_βσ_a )²/(μ_a− μ₀ )², where z_α = 3.0902, z_β = 0.8416, and where μ₀ (σ₀) and μ_a (σ_a) are, respectively, the means (SDs) under the null and the alternative hypotheses. This approach assumes normality of the statistics but allows them to have different variances under the null and alternative hypotheses.

For our simulation studies of the power for small sample sizes, we simulated 10,000 data sets of 10 pedigrees. For the single-locus models, this was done by FASTSLINK (Ott 1989; Weeks et al. ¹⁹⁹⁰), and, for the two-locus models, this was done by our simulation program (described briefly in the preceding paragraph). These simulations were done conditional on the given disease phenotypes. We simulated one marker with distinct founder alleles (perfect IBD information), in complete linkage with the trait locus. We then computed the empirical power and false-positive rate, using the .001 nominal significance cutoff from the normal distribution.

For each genetic model and each pedigree type, we also derived the optimal statistic, by using a grid search to numerically maximize the aforementioned sample-size formula over all possible statistics of the form shown in equation (1). We included these optimal statistics in all of our analytic power studies. This allowed us to potentially identify models and/or pedigrees for which none of the statistics that we evaluated performed well.

Results

Tables 9–11 show the results of our analytic sample-size calculations for the single-locus models, and table 12 shows the results for the two-locus models. For each pedigree type, statistics that are equivalent (i.e., have the same normalized coefficients) are grouped together.

Table 9.

Estimated Sample Sizes for the Extended Pedigrees under Single-Locus Models

	Estimated Sample Sizeb
	Dominant Model				Additive Model				Recessive Model
Pedigree and Statistic(s)a	1	2	3	4	5	6	7	8	9	10	11	12
MMT:
Optimal test	∞	21,975	6,334	351	89	89	89	120	8	8	9	27
Sall	∞	23,008	6,587	358	93	93	92	120	9	10	10	29
SApairs, SX50	∞	24,075	6,855	353	100	99	98	122	11	11	11	31
SGHpairs	∞	22,666b	6,489	354	94	93	93	120	10	10	11	30
SX75	∞	23,106	6,602	352	96	95	94	120	10	11	11	30
NMMT:
Optimal test	13	14	14	23	31	32	33	52	19	20	20	40
Sall	13	14	14	24	32	33	33	53	982	974	963	615
SApairs	23	24	24	37	40	41	42	64	51	52	52	78
SX50	20	20	21	32	37	38	39	58	73	74	75	101
SGHpairs	16	17	17	28	35	35	36	54	146	147	149	169
SX75	18	19	19	30	35	36	37	56	81	82	83	110
CSFF:
Optimal test	32	32	33	51	31	32	33	74	7	7	8	40
Sall	35	35	36	53	31	32	33	74	7	8	8	41
SApairs, SX50, SGHpairs, SX75	39	39	40	57	34	34	35	75	8	8	8	43
CSMF:
Optimal test	9	9	9	16	9	9	9	19	7	8	9	33
Sall	9	9	10	16	9	9	9	19	7	8	9	40
SApairs	10	10	10	17	10	10	10	20	8	9	10	45
SX50	10	10	10	17	10	10	10	20	8	9	10	37
SGHpairs	10	10	10	17	10	10	10	20	9	9	10	35
SX75	10	10	10	17	9	10	10	20	8	9	10	39

^aStatistics are grouped together when they have identical normalized coefficients.

^bA sample size that is the unique maximum among statistics (excluding optimal test) is in boldface italic; a sample size that is the unique minimum among statistics (excluding optimal test) is underlined.

Table 10.

Estimated Sample Sizes for Three Affected Siblings under Single-Locus Models^[Note]

	Estimated Sample Size
	Dominant Model				Additive Model				Recessive Model
Pedigree and Statistic(s)	1	2	3	4	5	6	7	8	9	10	11	12
Three males:
All statistics	11	11	11	22	11	11	11	22	11	11	11	22
Two males–one female:
Optimal test	13	14	14	28	13	13	14	32	11	12	14	48
Sall	13	14	14	28	13	14	14	32	11	12	14	54
SX75	13	14	14	28	13	13	14	32	11	12	14	56
SApairs	13	14	14	29	13	14	14	34	11	12	14	64
SX50, SGHpairs	14	14	15	29	13	14	15	33	12	13	14	50
One male–two females:
Optimal test	20	21	22	52	24	25	26	72	11	11	12	46
Sall, SX75	21	22	23	54	24	25	26	72	11	11	12	47
SApairs, SX50	20	21	22	52	24	25	27	74	11	11	12	46
SGHpairs	22	23	24	56	24	26	27	73	11	12	12	49
Three females:
All statistics	220	224	227	309	237	243	248	429	11	11	11	34

Note.— Notation is as described in the footnotes to table 9.

Table 11.

Estimated Sample Sizes for Four Affected Siblings under Single-Locus Models^[Note]

	Estimated Sample Size
	Dominant Model				Additive Model				Recessive Model
Pedigree and Statistic(s)	1	2	3	4	5	6	7	8	9	10	11	12
Four males:
Optimal test	10	10	10	17	10	10	10	17	10	10	10	17
Sall	10	10	10	17	10	10	10	17	10	10	10	17
SApairs, SX50, SGHpairs, SX75	11	11	11	18	11	11	11	18	11	11	11	18
Three males–one female:
Optimal test	11	11	11	19	11	11	11	20	10	11	11	23
Sall	11	11	12	19	11	11	12	20	10	11	11	26
SApairs	12	12	13	20	12	12	13	21	11	12	12	29
SX50, SGHpairs	12	12	13	20	12	12	13	21	12	12	13	24
SX75	12	12	12	20	12	12	12	21	11	12	12	26
Two males–two females:
Optimal test	14	14	14	25	15	15	16	29	10	10	10	23
Sall	14	15	15	25	15	15	16	29	10	11	11	24
SApairs	16	16	16	26	17	17	17	32	11	11	11	25
SX50	15	15	16	26	16	16	16	30	12	12	12	25
SGHpairs	16	16	16	27	16	16	17	29	12	13	13	26
SX75	15	16	16	26	16	16	17	30	11	11	12	25
One male–three females:
Optimal test	22	24	25	53	32	33	34	65	10	10	10	19
Sall	25	26	27	55	32	33	34	66	11	11	11	20
SApairs, SX50	25	26	28	55	35	36	37	70	11	11	11	20
SGHpairs	28	29	30	60	33	34	35	66	12	12	12	22
SX75	26	27	29	57	33	34	35	66	11	11	12	21
Four females:
Optimal test	334	337	340	404	280	282	284	347	10	10	10	18
Sall	358	360	362	412	282	284	286	348	10	10	11	18
SApairs, SX50, SGHpairs, SX75	384	385	386	429	291	292	293	349	11	11	11	19

Note.— Notation is as described in the footnotes to table 9.

Table 12.

Estimated Sample Sizes for Selected Pedigrees under Two-Locus Disease Models^[Note]

	Estimated Sample Size
Pedigree and Statistic(s)	H-Rare Model	H-Common Model	Additive Model
NMMT pedigree:
Optimal test	27	64	1,927
Sall	28	67	2,175
SApairs	47	102	2,772
SX50	42	92	2,421
SGHpairs	36	82	2,249
SX75	38	86	2,380
CSFF pedigree:
Optimal test	20	170	596
Sall	22	192	617
SApairs, SX50, SGHpairs, SX75	26	222	620
CSMF pedigree:
Optimal test	12	45	2,691
Sall	13	45	2,910
SApairs	15	50	2,819
SX50	16	51	2,905
SGHpairs	16	51	3,085
SX75	15	49	2,888

Note.— Notation is as described in the footnotes to table 9.

Single-Locus Models

Extended pedigrees

For the MMT pedigree, S_all was the best statistic overall (table 9). It gave sample sizes close to optimal for the additive and recessive models, and it was reasonably good for the dominant models as well. Dominant models required very large sample sizes for this pedigree, regardless of the statistic used, because the observed male-to-male transmission becomes increasingly unlikely as the model becomes more dominant and more penetrant. S^A_pairs and S_X50 generally performed poorly for this pedigree. For the recessive models, the simulation results basically agreed with the analytical results, showing that S_all had the best power (and also had the correct false-positive rate). For the additive and dominant models, the simulated sample size of 10 had low power, regardless of the statistic.

For the NMMT pedigree, S_all was the best, with close to optimal sample sizes under the dominant and additive models, whereas S^A_pairs was the worst (table 9). In contrast, the situation was reversed under the recessive models; S_all was the worst, with quite large sample sizes (>600 families), whereas S^A_pairs was the best. The sample sizes for S_all were very close to optimal for the dominant and additive models. However, for the recessive models, we observed large sample-size differences between the optimal tests and the best statistic, S^A_pairs. The simulation results for the NMMT pedigree were consistent with the analytical results. All statistics except S_all had the expected false-positive rate, whereas S_all's false-positive rate was elevated by a factor of 3–4.

For the CSFF pedigree, S_all was the best statistic for all models and had nearly optimal sample-size requirements (table 9), whereas the other four statistics were equivalent to each other. The simulation results also indicated that S_all was the best statistic, although S_all had an elevated false-positive rate of 0.004–0.007, whereas the other statistics had a less elevated false-positive rate, 0.002–0.004.

For the CSMF pedigree, S_all had consistently smaller sample-size requirements than did the other statistics (table 9), except under recessive model 12, which has reduced penetrance and a high phenocopy rate. For model 12, S^GH_pairs was the best, whereas S^A_pairs was the worst. However, the simulation results showed that, for recessive model 12, S_all was the best, closely followed by S^GH_pairs, whereas S^A_pairs was the worst. This difference may have been due to the false-positive rates in the simulation; S_all had an elevated false-positive rate in the range 0.005–0.006, whereas the other statistics had false-positive rates in the range 0.002–0.004.

Nuclear families

For the nuclear families, the sample-size differences between the best and worst statistics within a given sex configuration were quite small (tables 10 and 11)—often the two sample sizes differed by only one (except for the four-female sibships, under certain models). For nuclear families with only two affected siblings, all statistics have identical sample-size requirements within any model, because all statistics produce the same normalized coefficients.

Table 10 shows the sample sizes for three-sibling families, for four different sex combinations. All five statistics are identical to each other for three-female and three-male combinations, since there are only two possible IBD-sharing configurations (table 3). The best statistics for each sex combination performed the same as did the optimal test, except for recessive model 12. All statistics performed almost identically, in most conditions, for two-males–one-female and one-male–two-females combinations. For the two-males–one-female combination, S^GH_pairs and S_X50 performed best for model 12, whereas S^A_pairs performed worst. For the one-male–two-females combination, S^GH_pairs was the worst statistic more often than were the other statistics. Our simulations indicated that S_all had the lowest power for the two-males–one-female combination (for a sample size of 10), in most models. For the one-male–two-females combination, S^A_pairs and S_X50 were the best in most models, whereas S^GH_pairs was the worst; however, as in the analytical results, there were no dramatic power differences within each family type. Across all sex combinations, all statistics had similar elevated false-positive rates of ∼0.003 or ∼0.004, with a range of 0.002–0.005.

For four siblings, S_all was the best statistic more often than were the other statistics (table 11). For the three-males–one-female combination, recessive model 12 was again the exception, with S^GH_pairs and S_X50 being the best statistics under model 12. S^A_pairs, S^GH_pairs, S_X75, and S_X50 were equivalent to each other for four-female and four-male sibships, since they produced the same normalized coefficients (table 4). The best statistics in each sex combination performed very closely to the optimal test in most cases, except for the dominant models for four-female sibships. The simulation results show that S_all was the best in most models, and S^GH_pairs was the worst more often than were the other statistics; however, for the three-males–one-female combination, S^GH_pairs was the best under model 12, whereas S^A_pairs was the worst, a finding that is consistent with the analytical sample-size estimates. Across all sex combinations, all statistics had similar elevated false-positive rates, of ∼0.004 or ∼0.005, with a range of 0.002–0.006.

Note that, under dominant and additive models, all-female sibships (of sizes two to four) had relatively large sample-size requirements for all statistics (as compared to the sample-size estimates for the other sex combinations). In contrast, all-female sibships under recessive models had low sample-size requirements, similar to those of the other sex combinations. In addition, the sample-size requirements increase as the number of females in the sibship increases, under the dominant and additive models, for all five statistics.

Two-Locus Models

Under the two-locus models, only the NMMT, CSFF, and CSMF pedigrees were studied (table 12). For the NMMT pedigree, S_all was consistently the best statistic, and S^A_pairs was the worst, just as for the single-locus models. For the CSFF pedigree also, the two-locus results mirrored the single-locus results. For the CSMF pedigree, S_all was again the best for the heterogeneity models, but it did not perform as well for the additive models.

Discussion

In an attempt to find a robust allele-sharing statistic for X-linked traits that performs well across a variety of genetic models and pedigree structures, we have compared the relative sample-size requirements of five different allele-sharing statistics for X-linked traits. We have considered four different extended pedigrees, as well as all possible sex combinations in nuclear families with two, three, and four affected siblings. As might be expected, we have found that which statistic is best depends on both the true underlying mode of inheritance and the sex and distribution of the affected individuals within the pedigree.

For the extended pedigrees, S_all was found to be the most powerful and the closest to optimal for the majority of the genetic models (whether single locus or two locus). Similarly, for autosomal traits, S_all performs quite well across a large number of models (Feingold et al. 2000). However, this result does depend on the pedigree structure and genetic model, since, under recessive models for the NMMT pedigree, S_all has dramatically less power than do the other statistics (table 9). S_all is most powerful when there is sharing of alleles in common among the whole group of affected individuals, which is unlikely under recessive models for the NMMT pedigree. Similarly, for autosomal traits, Davis et al. (1997) found that, in situations in which the disease allele is likely to have entered the pedigree more than once (i.e., a recessive disease with a fairly common allele), S_all is much worse than S_pairs. However, we did not, as we might have expected, observe this effect when S_all was applied under the two-locus models; for example, in our simulations of the CSFF pedigree under the “H-common” model, 49% of families were segregating disease alleles at both loci, and yet S_all was still the most powerful statistic. On the basis of this observation, we suggest that further exploration of the behavior of S_all is warranted in both the autosomal and the X-linked contexts. We also have seen that S_all is not the best statistic under dominant models for the MMT pedigree (table 9), but in this situation the sample-size requirements become extremely large as the genetic models become “stronger” and more inconsistent with the observed male-to-male transmission in this pedigree. For the recessive models for the NMMT pedigree, the optimal sample sizes were much smaller than the sample sizes obtained when any of the five statistics were used, which indicates that there is room for improved statistics for recessive models (table 9). This is not surprising, since previous studies have shown that most standard statistics do not have good power for autosomal recessive traits and that special recessively oriented statistics do much better (e.g., see Feingold and Siegmund ¹⁹⁹⁷; Feingold et al. ²⁰⁰⁰; Sengul et al. ²⁰⁰¹).

For the nuclear families, we observed only minor power differences among the five statistics, within any given sex configuration (tables 10 and 11); however, under dominant and additive models, the all-female sibships had quite low power, no matter which statistic we used. This result has been observed before, since Cordell et al. (1995) have shown that, under genetic models in which the female dominance variance is small, the power for full sisters is much less than that for other pairs of relatives. Clearly, any two female sibs share either one or two alleles IBD, since they always share the father's allele in common. If the disease allele has entered the sibship only once through the father, then the female sibship will contain no information for linkage. This effect is pronounced under the dominant and additive models, since one disease allele is enough to induce elevated penetrance. We do not observe such a dramatic effect when there is a least one male in the sibship, since the presence of at least one affected male makes it much more likely that the disease allele has entered the family through the mother rather than through the father. Under the recessive models, no matter which sex combinations the sibships have, all statistics result in comparably high power, since they are all based on the same information: the alleles that have been passed on from the mother. Similar but less-pronounced effects help explain the results for the CSFF pedigree (table 9), in which the sample sizes under the dominant and additive models are quite a bit larger than those under most of the recessive models.

Even though, in most cases, S^GH_pairs is the worst statistic, it is the most powerful statistic when male siblings outnumber female siblings (such as in the two-males–one-female and the three-males–one-female combinations) under the recessive model with a high phenocopy rate and reduced penetrance (model 12; see tables 10 and 11). Similarly, we also have observed that, in the CSMF pedigree, S^GH_pairs is the best statistic for model 12 (table 9). Under recessive models with high phenocopy rates, most female cases are phenocopies. Therefore, for such models, a statistic that scores female sharing less and that scores male sharing more would perform the best. S^GH_pairs performs well because it assigns to alleles shared between males a score higher than that assigned by any of the other statistics (table 2).

To complement and verify our analytical power computations, we also performed simulation-based power studies. Although the analytical power computations assume normality and a fixed type I–error rate, 0.001, the simulation studies do not make such assumptions and also permit us to generate empirical type I–error rates. Our simulation results indicate that, for the NMMT, CSFF, and CSMF pedigrees, S_all always has a larger type I–error rate than do the other statistics. This means that the simulation results showing that S_all generally has high power should be interpreted with some caution. This issue has been discussed in more detail by other authors (e.g., McPeek ¹⁹⁹⁹). In the present study, however, the analytical results also show S_all to be the best statistic in most cases, so we can be fairly confident about this general qualitative result.

Sengul et al. (2001) examined the effect of increasing the distance between the marker and the trait locus in their study of linkage statistics for autosomal traits, and they found that the relative power of the statistics changed as θ increased. Therefore, in addition to our results, which assumed a fully informative marker perfectly linked (θ = 0.0) to the trait locus, we also computed estimated sample sizes at several different larger values of θ (i.e., 0.05, 0.10, and 0.20). We found no change in the relative ranking of the statistics for X-linked traits. Also, note that our results are based on a fully informative marker, but, if the marker is not fully informative, the result is very similar to that caused by an increase in θ. This issue is discussed in more detail by Sengul et al. (2000).

Cordell et al. (1995) investigated the power to detect X linkage in various types of affected relative pairs, as functions of the relative risks (λ's). The λ's for sibling pairs for the models that we considered are given in table 1. Our general results regarding which types of pedigrees are most powerful are consistent with those reported by Cordell et al. (1995). Those authors found that, when the female dominance variance is small (as in our additive and dominant models), sister-sister pairs have much lower power than do other types of relative pairs. We found, as discussed above, that this result is also true for larger sibships that consist entirely of females. When there is substantial dominance variance (as in our recessive models), sibships of sisters become roughly as useful as sibships that include brothers. This is because the sister-sister relative risk, λ_ff, includes components due to both additive and dominance variances, whereas both the sister-brother relative risk, λ_mf, and the brother-brother relative risk, λ_mm, are functions of the additive variance only. A similar effect is seen in comparisons of the power that siblings and unilineal relatives have for the mapping of autosomal loci (e.g., see Feingold and Siegmund ¹⁹⁹⁷). Comparing, across sex groups, first-cousin pairs whose parents are sisters, they found that male-male first-cousin pairs are more powerful than female-female first-cousin pairs. This would lead us to the prediction that the CSMF pedigree should have more power to detect linkage than does the CSFF pedigree, because the CSMF pedigree contains both male-male and female-female first-cousin pairs, whereas the CSFF pedigree contains only female-female first-cousin pairs. Our results (table 9) are consistent with this prediction.

It is important to note that affected relatives of the same general relationship (e.g., full siblings) can provide very different power to detect linkage, depending on their sex. This suggests that, for optimal power, one should pay close attention to proper weighting when combining statistics across families with different sex combinations. One could obtain an overall statistic by combining statistics after assigning appropriate weights to different sex pairs and/or pedigree configurations. The optimal weights depend on the genetic model. Although it is not difficult to derive the weights for any given model, the real challenge is to find weights that have robust power—that is, that have reasonably high power for a variety of models. We hope to explore such weighting issues in the future, building on the framework already developed for autosomal traits (e.g., see Sham et al. ¹⁹⁹⁷; Teng and Siegmund ¹⁹⁹⁷). One way to circumvent the weighting problem is to do parametric linkage analysis instead, which essentially imposes a particular set of weights based on the specified model. There have been some reports of good power obtained by parametric analysis of the autosomes for complex traits, by use of either fairly simple genetic models or “best of several models” approaches (e.g., see Abreu et al. ¹⁹⁹⁹; Sham et al. ²⁰⁰⁰). It will be important to study how these approaches compare to nonparametric methods for X-linked loci.

Finally, this study has used a limited set of trait models and a limited set of pedigrees. Since the actual number of trait models and pedigrees that might be of interest is enormous, we cannot claim to have considered all important possibilities. Future work to study more pedigree types and more models would be useful.