Cognitive Inconsistency and Practice-Related Learning in Older Adults

Abstract

The current study examined predictors of individual differences in the magnitude of practice-related improvements achieved by 87 older adults (mean_age 63.52 years) over 18-weeks of cognitive practice. Cognitive inconsistency in both baseline trial-to-trial reaction times and week-to-week accuracy scores was included as predictors of practice-related gains in two measures of processing speed. Conditional growth models revealed that both reaction time and accuracy level and rate-of-change in functioning were related to inconsistency, even after controlling for mean-level, but that increased inconsistency was negatively associated with accuracy versus positively associated with reaction time improvement. Cognitive inconsistency may signal dysregulation in the ability to control cognitive performance or may be indicative of adaptive attempts at functioning.

Introduction

While cognitive decline may be considered a prominent feature of aging, cognitive functioning remains plastic well into late-life (Hertzog, Kramer, Wilson, & Lindenberger, 2008). Achieving late-life cognitive improvements through training appears to remain normatively possible (Ball et al., 2002). However, some of the gains illustrated through these interventions may be the result of practice-related learning (i.e., learning independent of instruction), given that even untrained controls show pre-posttest improvements. In fact, all cognitive training interventions contain substantial practice components. With several notable recent [i.e., practice-related learning focused interventions (Yang & Krampe, 2009; Yang, Krampe, & Baltes, 2006; Yang, Reed, Russo, & Wilkinson, 2009) and process-based interventions (Eschen, 2012; Lustig, Shah, Seidler, & Reuter-Lorenz, 2009; Noack, Lövdén, Schmiedek, & Lindenberger, 2009; Willis & Schaie, 2009)] and historical [i.e., (Baltes, Sowarka, & Kliegl, 1989; Hofland, Willis, & Baltes, 1981)] exceptions, the vast majority of literature examining late-life learning has viewed practice-related improvements in cognitive functioning as a nuisance that needs to be controlled methodologically and statistically [i.e., (Ball et al., 2002; Jaeggi, Buschkuehl, Jonides, & Perrig, 2008)].

Understanding practice-related or process-based learning (i.e., learning independent of focused intervention) can shed light on the “natural” range of improvability; that is, what older adults can achieve on their own, without formal training. Consequently, practice-related learning has been referred to as “a basic form of cognitive plasticity” (Yang et al., 2006), and has been demonstrated to be comparable to intervention-related learning in magnitude and ability to be maintained long-term (Baltes, Kliegl, & Dittmann-Kohli, 1988; Baltes et al., 1989; Yang & Krampe, 2009). As such, it is important to not only understand older adults' responses to repeated practice, but to also understand predictors of that response. However, there have been relatively few studies in the area of elders' practice-related or process-based learning, meaning that questions remain regarding predictors of elders' response to practice (who gains more, and why?). Just as the gerontological cognitive intervention literature is concerned with identifying predictors of individual differences in learning (Hertzog et al., 2008), it is also important to attempt to identify factors related to an individual's ability to benefit from practice.

Cognitive inconsistency represents an intriguing individual difference variable as it has been shown to relate to various aspects of cognitive functioning [e.g., (Allaire & Marsiske, 2005; Hultsch, MacDonald, & Dixon, 2002; Hultsch, Strauss, Hunter, & MacDonald, 2008)] and disease status [e.g., Alzheimer's disease, Traumatic Brain Injury, etc. (Burton, Hultsch, Strauss, & Hunter, 2002; Hultsch, MacDonald, Hunter, Levy-Bencheton, & Strauss, 2000; Hultsch et al., 2008)]. As such, the overarching goal of the current investigation was to examine cognitive inconsistency as an individual difference predictor of both initial level of cognitive functioning as well as improvement in elders' cognitive functioning as a result of repeated practice.

A small number of investigations have examined individual difference variables in relation to practice-related learning in late-life. It has been reported that both age and level of cognitive functioning are related to an elder's rate of gains in processing speed, reasoning, and visual attention (Yang et al., 2006). Younger age and higher levels of initial functioning both have been associated with increased rates of practice-related learning in reasoning and to a lesser extent processing speed (Yang et al., 2006). This finding is consistent with other studies in which similar individual differences in cognitive training-related gains were observed (McArdle & Prindle, 2008). Both stable anxiety (i.e., trait-anxiety) and momentary anxiety (i.e., state-anxiety) have been examined as potential predictors of older adults' response to practice; however, neither type of anxiety significantly predicted patterns of practice-related learning in late-life (Yang et al., 2009). Though not previously examined in this role, cognitive inconsistency represents an intriguing potential individual difference predictor of practice-related learning.

Cognitive inconsistency is characterized by fluctuation in functioning that occurs over a relatively brief time frame and is thought to be highly reversible in nature (Li, Huxhold, & Schmiedek, 2004; Nesselroade, 1991). This type of change has been examined through repeated assessments spaced in close proximity to one another [such as multiple cognitive assessments repeated daily (Allaire & Marsiske, 2005)] and/or examination of inconsistency from trial-to-trial within a given assessment (Hultsch et al., 2002)]. Results of investigations into this type of late-life cognitive change have revealed: (1) that older adults display large amounts of cognitive inconsistency [i.e., (Allaire & Marsiske, 2005; Hultsch et al., 2002; Hultsch et al., 2008; Li, Aggen, Nesselroade, & Baltes, 2001)], and (2) that cognitive inconsistency is usually greater in persons with various impairment conditions [i.e., (Burton et al., 2002; Hultsch et al., 2000)].

The significance of increased cognitive inconsistency in normal, healthy older adults is not without debate. Researchers have correlated estimates of cognitive inconsistency to mean-level performance, operationalized as mean-level functioning in both reaction times and accuracy scores, in attempts to determine the nature of cognitive inconsistency in healthy older adults. Common results from such investigations reveal that heightened levels of cognitive inconsistency in reaction times are related to lower overall levels of cognitive functioning across domains of processing speed, attention, and working memory (Hultsch et al., 2002; Hultsch et al., 2000; Hultsch et al., 2008; Nesselroade & Salthouse, 2004; Salthouse, Nesselroade, & Berish, 2006). Based on such findings, and consistent with theories of homeostatic regulation, cognitive inconsistency is often viewed as being indicative of an underlying dysfunction.

Moving away from reaction time, the meaning of inconsistency in accuracy of performance may be less clear cut. Allaire and Marsiske (2005) reported that increased cognitive inconsistency in accuracy-based scores was associated with increased overall performance in the domains of reasoning, memory, and processing speed. This finding was interpreted as being consistent with the argument that cognitive inconsistency can serve as an adaptive function, especially in the presence of significant learning (Li et al., 2001; Siegler, 1994, 2007). Interestingly, the studies that have shown cognitive inconsistency to be related to poorer overall performance [e.g., (Hultsch et al., 2002; Salthouse et al., 2006)] have typically used indices of inconsistency calculated as trial-to-trial deviations in reaction time, while the studies that have found cognitive inconsistency to be related to better overall level of performance [e.g., (Allaire & Marsiske, 2005; Li et al., 2001)] have examined inconsistency calculated from occasion-to-occasion deviations in performance.

The Current Investigation

Virtually all published studies of cognitive inconsistency (in either reaction time or accuracy) have examined associations between inconsistency and static measures of cognition (i.e., diagnostic criteria or mean-level performance). The current study sought to provide further information regarding the relationship between cognitive inconsistency (examining both reaction times and accuracy in the same group of participants) with level of cognitive functioning. Additionally, a goal of the current study was to extend our understanding of cognitive inconsistency by examining its association with practice-related rate-of-change in reaction time and accuracy over an 18-week study period. Across RT and accuracy, we hypothesized that individuals with greater levels of cognitive inconsistency, on average, would display poorer levels of cognitive functioning, on average. We also hypothesized, again across RT and accuracy, that individuals with greater levels of cognitive inconsistency, on average, would display shallower practice-related gain slopes in functioning across the testing sessions (i.e., would demonstrate less practice-related learning). These hypotheses are based on findings from the majority of previous research and theories that have suggested that higher levels of cognitive inconsistency are generally maladaptive and associated with cognitive vulnerability.

Methods

General Study Design

This study represents a secondary analysis of the Active Adult Mentoring Program (Project AAMP). The primary objective of Project AAMP was to test the efficacy of a social-cognitive lifestyle intervention to increase moderate-intensity exercise in older adults. The full study methods are presented elsewhere (Buman et al., 2011) and are briefly summarized here. Project AAMP included an Active Lifestyle intervention arm that received weekly, group-based behavioral counseling delivered by trained peer counselors, and a Health Education arm that received appropriately matched health education. Both arms received access to an exercise facility during the intervention period. The results presented here were from the initial 18 weeks of the study, including a baseline week of observation prior to group assignment, 16 weeks of intervention, and a subsequent week of observation following the intervention period.

Procedure

Individuals who expressed interest in study participation were initially screened by telephone (see below). Following telephone screening, qualified participants were consented and completed a baseline assessment. This baseline assessment included a computerized cognitive assessment. Next, participants were randomized to either the Active Lifestyle or Health Education arm of the intervention. Each intervention arm consisted of sixteen weekly group meetings [see (Buman, 2008; Buman et al., 2011) for more information]. Either before or after each group meeting all participants completed several computerized cognitive tasks (see below). Lastly, each participant completed a post-treatment assessment that again included the computerized cognitive assessment. Thus, this study included 18-consecutive weeks of computerized cognitive testing.

Inclusion/Exclusion Criteria

All potential participants were screened by telephone to exclude individuals based on the following criteria: severe dementing illness (i.e., likely dementia based on screening scores), history of significant head injury (loss of consciousness for more than 5 minutes), neurological disorders (e.g., Parkinson's disease), inpatient psychiatric treatment, extensive drug or alcohol abuse, use of an anticholinesterase inhibitor (such as Aricept), severe uncorrected vision or hearing impairments, terminal illness with life expectancy less than 12 months, major medical illnesses (e.g., uncontrolled arrhythmias, active cancers etc.), cardiovascular disease, pulmonary disease requiring oxygen or steroid treatment, and ambulation with assistive devices. Telephone screening included the 11-item Telephone Interview for Cognitive Status (TICS), with a cut-off score of 30 points (Brandt, Spencer, & Folstein, 1988). All study participants were required to self-report sedentary lifestyle – defined as not currently meeting minimum physical activity guidelines of ≥150 minutes/week of moderate or vigorous physical activity during the previous 6 months (Physical Activity Guidelines Advisory Committee Report, Part A: Executive Summary, 2009). A note from primary care physicians acknowledging ability to participate in the study prior to formal enrollment was required, and all participants provided written informed consent. These study procedures were approved by the Institutional Review Board at the University of Florida.

Demographic and Descriptive Measures

Each study participant provided demographic data through means of a telephone screening instrument. Information regarding participant age (measured in years since birth), gender (male or female), and education level (years of education) were collected. Participants reported their daily levels of physical activity throughout the entire study period through use of a modified Leisure-Time Exercise Questionnaire (LTEQ; Godin, Jobin, & Bouilon, 1986). Minutes of moderate-to-vigorous physical activity (MVPA) were computed from the LTEQ by adding the number of moderate and strenuous bouts reported and multiplying by 20. Previous research has supported the validity and reliability of LTEQ (Godin et al., 1986). Daily ratings of MVPA were summed for the first third of the study period (i.e., weeks 1-6) and the final third of the study period (weeks 12-18). Change in MVPA was computed by subtracting the final third MVPA from the initial MVPA and was included in all analyses, as physical activity and fitness levels have been shown to impact cognitive functioning in older adults (McAuley, Kramer, & Colcombe, 2004). Additionally, previous reports have reported few baseline to posttest fitness effects by group status (Buman, 2008) and no baseline to posttest cognitive effects by group status (Aiken Morgan, 2008). Thus, group status was not controlled for in subsequent analyses.

Cognitive Measures

Cognitive functioning was repeatedly assessed with both the Symbol Digit and Number Copy tests (Smith, 1982). Symbol Digit and Number Copy tests both assess processing speed; however, the Symbol Digit test is more frontally mediated – encompassing components of executive functions (i.e., attention and working memory). These tests consist of matching symbols that are paired with numbers (Symbol Digit) or numbers paired with same numbers (Number Copy) as quickly as possible. There was a 120-second time limit for each task. Assessments occurred weekly, for 18 total weeks.

Both the Symbol Digit and Number Copy tests were adapted to allow for computer administration. Computerization of the cognitive measures employed the DirectRT experimental generation program, and then were compiled and administered via MediaLab experimental implementation program (Jarvis, 2008a, 2008b). In an attempt to minimize practice effects due to item memorization commonly found in repeated cognitive assessments (Salthouse, Schroeder, & Ferrer, 2004), fourteen alternate forms of each test were used and rotated such that the same version of any given test was not given within 6 weeks of each other. The alternate forms were constructed to be comparable in difficulty and cognitive resources needed to complete them and have been shown to have high test-retest reliabilities (Allaire & Marsiske, 2005; McCoy, 2004). Alternate forms of the Symbol Digit task were created by randomly altering the symbol-digit parings. Alternate forms of the Number Copy task were created by randomly altering the order of digit presentation. Processing speed was selected as the practiced cognitive domain due to its inclusion in previous practice-related learning investigations (Yang & Krampe, 2009; Yang et al., 2006; Yang et al., 2009) and investigations of intraindividual variability in older adults (Hultsch et al., 2002; MacDonald, Hultsch, & Dixon, 2008; Salthouse et al., 2006). Two indices of cognitive inconsistency were calculated from each cognitive measure: (1) trial-to-trial deviations in reaction time during the baseline testing session, and (2) week-to-week deviations in accuracy scores across the 18-week testing period. Reaction time data were coded such that higher values represent slower/worse functioning. Accuracy data were coded such that higher values represent better functioning/more correct responses.

Data Analyses

Preliminary analysis examined the cognitive data (i.e., dependent variables) for normality. All cognitive data were screened for outliers at the intraindividual level (i.e., within person from trial-to-trial) at +/- 3 SDs. Intraindividual outliers were removed from the dataset prior to calculation of occasion-specific values. While outlier trimming in a study of within person fluctuation may appear counterintuitive, outlier trimming has historical grounding in variability studies [i.e., (Bunce, MacDonald, & Hultsch, 2004; Hultsch et al., 2002)]. In fact, such a practice has been deemed a “conservative approach” to examination of within-person fluctuation (Hultsch et al., 2002).

Cognitive inconsistency was operationally defined in two ways, to address gaps in the extant literature. Reaction time (RT) inconsistency was defined as person-specific trial-to-trial variations in reaction times during the initial testing session. Accuracy inconsistency was defined as person-specific variations in week-to-week number of items correctly answered across the 18-week study period. Both RT inconsistency and accuracy inconsistency were computed following procedures to “detrend” the data for linear and quadratic change [i.e., (1) regression of individuals' cognitive scores (over the 18 week period) on linear/quadratic time vectors; (2) saving the resulting time-detrended residuals; (3) computing intra-individual standard deviations (iSD) of these detrended residuals as the index of cognitive inconsistency]. Several variants of this detrended iSD have been used in previous studies of cognitive inconsistency (Allaire & Marsiske, 2005). As a result, estimates of inconsistency represent within-person deviations in RTs and accuracy controlling for any systematic changes in the data due to repeated testing. To determine the relative amount of within-person cognitive inconsistency, an index of between person variability (Sample Standard Deviation, SD) and within-person variability (Individual Standard Deviation, ISD) can computed. These values can then be compared by dividing the ISD by the SD to get the relative amount of within person variability when compared to the between person variability. As the Table 1 footnote shows, these ratios varied from 15% (for Symbol Digit RT) to 200% (for Number Copy RT). These results suggest that intraindividual variability exists, and is worthy of further exploration, for all four dependent variables explored in this study. The relatively little intraindividual variability in Symbol Digit RT may further help explain why that inconsistency variability was the only one not associated with rate of growth in this study.

Table 1. Descriptive Statistics and Measures of Cognitive Inconsistency (N=90).

	Mean	(SD)
Age	63.52	(8.46)
Education	16.12	(2.25)
Gender (% female)	0.82	--
Δ in Physical Activity Level	0.86	(5.06)
Symbol Digit RT Inconsistency1	1726.23	(3303.39)
Symbol Digit Mean RT2	4471.34	(10982.63)
Symbol Digit Accuracy Inconsistency3	1.79	(1.35)
Symbol Digit Mean Accuracy4	26.22	(3.02)
Number Copy RT Inconsistency1	381.27	(219.89)
Number Copy Mean RT2	1138.99	(192.49)
Number Copy Accuracy Inconsistency 3	2.33	(2.80)
Number Copy Mean Accuracy4	44.68	(3.21)

Notes: Age measured in years since birth; Education measured in years of formal education; Δ in Physical Activity Level was calculated as the amount of self-reported minutes engaged in moderate-strenuous physical activity during the final 1/3 of the study period subtracted from the self-reported minutes engaged in moderate-strenuous physical activity during the initial 1/3 of the study period.

¹RT Inconsistency refer to trial-to-trial inconsistency in reaction times during the initial testing session;

²Mean RT refers to the average reaction time over the course of the study period;

³Accuracy Inconsistency refers to the week-to-week inconsistency in the number of items correctly answered;

⁴Mean Accuracy refers to the average number of items correctly answered over the course of the study period.

^*By dividing the means of the inconsistency variables by the standard deviations of the corresponding mean variables, we obtain a ratio of within person variability to between person variability. In these four variables, the ratios for Symbol Digit RT, Symbol Digit Accuracy, Number Copy RT, and Number Copy Accuracy are 0.15, 0.59, 1.98, and 0.72 respectively.

To explore the associations that may exist between cognitive inconsistency and cognitive functioning (both initial level of cognitive functioning and rate-of-change or practice-related learning in cognitive functioning) in older adults, separate (two for each cognitive variable: one for trial-to-trial RT and one for week-to-week accuracy) conditional growth models were parameterized through a multilevel model (MLM) framework (Singer & Willett, 2003). MLM, also referred to as mixed effects modeling or hierarchical linear modeling (HLM; Bryk & Raudenbush, 1992)], is an extension of the general linear model, and does not require observations to be independent. Model building was conducted in a hierarchical manner, such that each dependent variable (cognitive functioning) served as the outcome in four increasingly complex models. Model 1 included no predictor estimates and was parameterized to allow for estimation of subsequent fit statistics (i.e., null model). Model 2 included linear and quadratic estimates of time trends (e.g., gain or decline) to model any systematic growth in the data (i.e., unconditional growth model). Model 3 included the covariates of age, education, gender, and change in physical activity, and change in physical activity by time trends (i.e., conditional model with covariates only), as previous research has suggested that these variables are associated with late-life cognitive functioning. Model 4 included the previously entered variables, with the addition of a mean-level cognitive functioning variable (either mean-level RT or mean-level accuracy) and the mean-level by time trend interactions. Mean-level functioning was included in all models to account for known associations between cognitive inconsistency and mean-level functioning. Model 5 included the previously entered variables, with the addition of a cognitive inconsistency variable (either trial-to-trial deviations in RT or week-to-week deviations in accuracy) and the inconsistency by time trend interactions (i.e., conditional model with predictors of interest). Models were parameterized such that RT inconsistency was used to predict level and rate-of-change in reaction times across the 18-week study period and accuracy inconsistency was used to predict level and rate-of-change in number of correct responses across the 18-week study period. We decided to examine practice-related learning and cognitive inconsistency in two measures of processing speed (i.e., Symbol Digit and Number Copy) to examine consistency of effects across different outcomes.

The final model (Model 5) predicted cognitive functioning with: intercept (β₀₀), linear and quadratic time (β₁₀, β₂₀), demographic variables [age (β₀₁), education (β₀₂), gender (β₀₃), change in physical activity (β₀₄)], change in physical activity*linear time (β ₃₀), change in physical activity*quadratic time (β₄₀), mean-level cognition (β₀₅), mean-level cognition*linear time (β₅₀), mean-level cognition*quadratic time (β₆₀), cognitive inconsistency (β₀₆), cognitive inconsistency*linear time (β₇₀), cognitive inconsistency*quadratic time (β₈₀), and a random residual component (r_oi). The specifics of MLM are beyond the scope of this paper. Interested readers are referred to other sources (Bryk & Raudenbush, 1992; Singer & Willett, 2003). All variables were evaluated based on their significance levels and effects on overall model fit (i.e., 2LL) (Bryk & Raudenbush, 1992; Singer & Willett, 2003). Final model equation was:

$$\begin{array}{l}{\text{Congition}}_{\mathit{\text{it}}}={\beta }_{\mathit{00}}+{\beta }_{\mathit{10}}(\text{Time})+{\beta }_{\mathit{20}}({\text{Time}}^{\mathit{2}}){+\beta }_{\mathit{01}}({\text{Age}}_i)+{\beta }_{\mathit{02}}({\text{Education}}_i){+\beta }_{\mathit{03}}({\text{Gender}}_i)+\\ {\beta }_{\mathit{04}}{(\Delta \text{MVPA}}_i){+\beta }_{\mathit{30}}{(\Delta \text{MVPA}\ast \text{Time})+\beta }_{\mathit{40}}{(\Delta \text{MVPA}\ast \text{Time}}^{\mathit{2}}){+\beta }_{\mathit{05}}{(\text{Mean}‐\text{level Conginition}}_i)\\ +{\beta }_{\mathit{50}}(\text{Mean}‐\text{level Conginition}\ast \text{Time})+{\beta }_{\mathit{60}}(\text{Mean}‐\text{level Conginition}\ast {\text{Time}}^{\mathit{2}})+\\ {\beta }_{\mathit{06}}({\text{Cognitive Inconsistency}}_i)+{\beta }_{\mathit{70}}(\text{Cognitive Inconsistency}\ast {\text{Time})+\beta }_{\mathit{80}}(\text{Cognitive Inconsistency}\ast {\text{Time}}^{\mathit{2}})r_{oi}\end{array}$$

Results

Descriptive Statistics

The final sample included 87 adults aged 50 years and older. Mean age for the entire sample was 63.52 years, range = 50-87 years. The sample was highly educated, average years of education 16.12, and predominately female, 82%. Additionally, whether quantified as trial-to-trial deviations in RT or week-to-week deviations in accuracy, older adults displayed large amounts of cognitive inconsistency. Table 1 provides a summary of participant characteristics.

Model Building

Residual centering (Little, Bovaird, & Widaman, 2006) was employed to ensure the various time trends were independent predictors. This process involved calculation of the quadratic time residualized from linear time. The addition of cognitive inconsistency and cognitive inconsistency*time trends resulted in only marginal improvements in model fit in the Symbol Digit models; however, this step resulted in significant improvements to model fit for Number Copy models (refer to Tables 2 and 3).

Table 2. Conditional Growth Models for Symbol Digit Test.

Predictor Variable	Reaction Time			Accuracy
	B	SE	p	B	SE	p
Fixed Effects
Intercept	632.36	834.09	0.45	-1.67	1.93	0.39
Time	24.25	15.30	0.11	0.28	0.15	0.06
Time2	-10.98	3.24	0.001	-0.03	0.03	0.40
Age	20.27	8.34	0.02	-0.001	0.01	0.90
Education	-7.86	33.45	0.81	-0.01	0.04	0.82
Gender	138.62	187.61	0.46	-0.08	0.23	0.74
Physical Activity	10.34	25.50	0.69	-0.03	0.03	0.42
Time*Physical Activity	-0.16	2.68	0.95	0.002	0.003	0.48
Time2*Physical Activity	-0.05	0.56	0.92	-0.001	0.001	0.39
Mean	0.24	0.01	<.001	1.00	0.05	<.001
Time*Mean†	-0.02	0.001	<.001	-0.001	0.01	0.92
Time2*Mean†	0.005	0.0003	<.001	0.001	0.001	0.44
Inconsistency†	-0.01	0.04	0.86	0.21	0.11	0.06
Time*Inconsistency†	0.002	0.004	0.63	-0.03	0.01	0.03
Time2*Inconsistency†	-0.0004	0.001	0.66	-0.005	0.003	0.06
Model Fit
Pseudo R2a		46.78%			58.06%
Deviance (df)		0.61(3)			7.46(3)∼

^†Note: For the Accuracy Model mean refers to the person average number of correct items across the study period, inconsistency refers to week-to-week deviations in accuracy; For the Reaction Time Model mean refers to the person average reaction time across all trials and all testing sessions, inconsistency refers to week-to-week deviations in reaction time.

^aPseudo R² refers to the concordance between model predicted values and actual values. ∼The addition of inconsistency resulted in marginal model fit improvement (p=.06).

Table 3. Conditional Growth Models for Number Copy Test.

Predictor Variable	Reaction Time			Accuracy
	B	SE	p	B	SE	p
Fixed Effects
Intercept	164.94	132.87	0.21	-5.18	4.17	0.21
Time	0.77	11.11	0.94	0.79	0.37	0.03
Time2	-4.47	2.29	0.05	-0.12	0.08	0.13
Age	3.21	1.04	0.002	-0.005	0.02	0.79
Education	1.74	3.79	0.65	-0.002	0.06	0.97
Gender	26.64	21.74	0.22	-0.08	0.36	0.83
Physical Activity	1.36	2.97	0.65	0.03	0.05	0.52
Time*Physical Activity	-0.03	0.32	0.93	-0.003	0.01	0.53
Time2*Physical Activity	-0.003	0.07	0.96	-0.002	0.001	0.03
Mean	0.56	0.12	<.001	1.07	0.08	<.001
Time*Mean†	-0.0005	0.01	0.97	-0.01	0.01	0.17
Time2*Mean†	0.004	0.002	0.08	0.002	0.002	0.21
Inconsistency†	-0.03	0.10	0.74	0.43	0.09	<.001
Time*Inconsistency†	-0.02	0.01	0.03	-0.06	0.01	<.001
Time2*Inconsistency†	0.0005	0.002	0.82	0.01	0.002	0.002
Model Fit
Pseudo R2a		14.90%			39.19%
Deviance (df)		17.97(3)*			49.81(3)	*

^†Note: For the Accuracy Model mean refers to the person average number of correct items across the study period, inconsistency refers to week-to-week deviations in accuracy; For the Reaction Time Model mean refers to the person average reaction time across all trials and all testing sessions, inconsistency refers to week-to-week deviations in reaction time.

^aPseudo R² refers to the concordance between model predicted values and actual values.

^*The addition of inconsistency resulted in significant model fit improvement (p<0.001).

Symbol Digit Inconsistency

Predictor estimates, significance levels, and model parameters for both the RT Inconsistency Symbol Digit model and the Accuracy Inconsistency Symbol Digit model are presented in Table 2.

RT Inconsistency

The final conditional growth model for RT Inconsistency as a predictor of initial level and rate-of-change in Symbol Digit task is presented on the left side of Table 2. Age, β = 20.27, SE = 8.34, p = .02, and mean-level cognitive functioning, β = 0.24, SE = 0.01, p < .001, were significant between-person predictors, suggesting that both older individuals and individuals with higher mean-level RT had slower than average Symbol Digit performance. At the within-person level Quadratic Time, β = -10.98, SE = 3.24, p = .001, linear time*mean-level cognition interaction, β = -0.02, SE = 0.001, p < .001, and the quadratic time*mean-level cognition interaction, β = 0.005, SE = 0.0003, p < .001, were significant predictors of Symbol Digit performance, suggesting that across the 18-week study period individuals' reaction time became faster (improved) and average-level of RT predicted this improvement. Neither RT inconsistency nor its interaction with time were significant, suggesting that rate of change was not associated with inconsistency. The model explained 47% of the total variance in Symbol Digit performance.

Accuracy Inconsistency

The final conditional growth model for Accuracy Inconsistency as a predictor of initial level and rate-of-change in Symbol Digit task is presented on the right side of Table 2. Mean-level cognitive functioning, β = 1.00, SE = 0.05, p < .001, was a significant between-person predictor, suggesting that individuals with higher levels of mean-level functioning had better than average Symbol Digit performance. At the within-person level the linear time*inconsistency interaction, β = -0.03, SE = 0.01, p = .03, was a significant predictor of Symbol Digit performance, suggesting that across the 18-week study individuals with lower levels of cognitive inconsistency experienced a greater rate of improvement in Symbol Digit performance. The model explained 58% of the total variance in Symbol Digit performance.

Number Copy Inconsistency

Predictor estimates, significance levels, and model parameters for both the RT Inconsistency Number Copy model and the Accuracy Inconsistency Number Copy model are presented in Table 3.

RT Inconsistency

The final conditional growth model for RT Inconsistency as a predictor of initial level and rate-of-change in Number Copy task is presented on the left side of Table 3. Age, β = 3.21, SE = 1.04, p = .002, and mean-level cognitive functioning, β = 0.56, SE = 0.12, p < .001, were significant between-person predictors, suggesting that both older individuals and individuals higher average RTs had slower than average Number Copy performance. At the within-person level the linear time*inconsistency interaction, β = -0.02, SE = 0.01, p = .03, was a significant predictor of Number Copy performance, suggesting that individuals with higher levels of cognitive inconsistency experienced greater improvement in reaction times. The model explained 15% of the total variance in Symbol Digit performance.

Accuracy Inconsistency

The final conditional growth model for Accuracy Inconsistency as a predictor of initial level and rate-of-change in Number Copy task is presented on the right side of Table 3. Mean-level cognitive functioning, β = 1.07, SE = 0.08, p < .001, and inconsistency, β = 0.43, SE = 0.09, p < .001, were significant between-person predictors, suggesting that both individuals with higher average cognitive functioning and individuals with higher levels of inconsistency had better than average Number Copy performance. At the within-person level Linear Time, β = 0.79, SE = 0.37, p = .03, quadratic time*change in physical activity, β = -0.002, SE = 0.001, p = .03, linear time*inconsistency interaction, β = -0.06, SE = 0.01, p < .001, and quadratic time*inconsistency interaction, β = 0.01, SE = 0.002, p = .002, were significant predictors of performance, suggesting that across the 18-week study period individuals' Number Copy performance improved and that individuals with lower levels of cognitive inconsistency experienced greater practice-related improvements in Number Copy performance. The model explained 39% of the total variance in Number Copy performance.

In order to support understanding of the effects of cognitive inconsistency on level and rate-of-change in cognitive functioning, Figure 1 shows the effects of cognitive inconsistency on level and rate-of-change in our four dependent variables. To explicate the time-by-inconsistency interactions, the model predicted values were plotted separately for individuals who evinced either below average or above average levels of cognitive inconsistency. In Figure 1, the Symbol Digit RT and accuracy outcomes are shown on the left, and Number Copy outcomes are on the right. In Figure 1, graphs depicting 18-week change in reaction time are displayed in the first row, and 18-week accuracy change is shown in the second row.

Figure 1. Relationship of 18-week change to level of inconsistency.

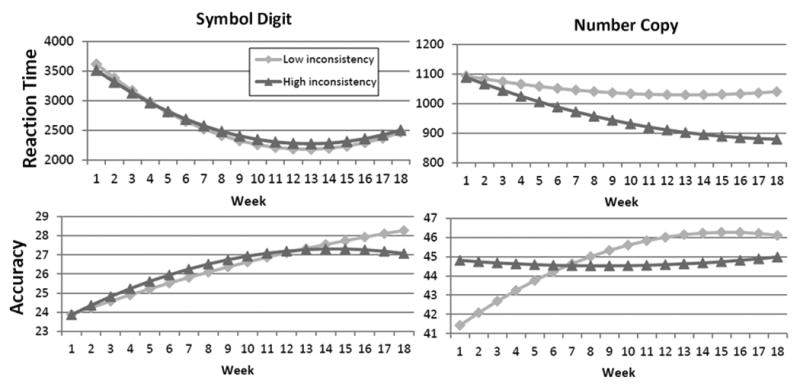
Two levels of inconsistency (low and high), defined as 1 standard deviation below^a and 1 SD above the average level of inconsistency are shown for each dependent measure. For all but Symbol Digit Reaction Time (RT), rate of change interacted significantly with level of inconsistency. For both accuracy measures, greatest improvement was experienced by those with the least inconsistency. For Number Copy RT, greatest improvement was seen for those with the most RT inconsistency.

^a For Symbol Digit RT, and for Number Copy Accuracy, the minimum inconsistency was less than one SD below average inconsistency; thus, minimum inconsistency is plotted instead to represent low inconsistency.

Discussion

As Baltes and colleagues (1986, 1988) have reported, practice-related learning has been shown to compare favorably to tutor-guided cognitive intervention in direct comparisons (Baltes, Dittmann-Kohli, & Kliegl, 1986; Baltes et al., 1988). In line with these previous investigations, we found significant improvements in performance associated with practice alone. In fact, when Step 2 of the model building process (i.e., time parameters only) was re-run with all variables standardized into z-score metric, the gains demonstrated in the current study (i.e., 0.48 – 1.40 standard score increases) were comparable to the average immediate training gains (.48 standard score) in tutor-guided training in ACTIVE 10-sessions (Ball et al., 2002) – and are larger than the estimated age-related decline one might expect over a 14 year period (Yang et al., 2009).

Of importance, due to speculation that practice-related learning may be the result of mere item memorization by older adults (Salthouse et al., 2004), in the current investigation no specific test item was repeated within 6 weeks of itself. Our results corroborate those of Yang and colleagues (2009), who also found significant practice-related learning in the absence of item-specific effects (Yang et al., 2009). Generally, our models revealed the expected results of increased age being associated with slower processing speed and lower mean-level functioning being associated with worse cognitive functioning.

Our growth curve analyses revealed at least one unexpected result. Specifically, increased cognitive inconsistency (in accuracy) was related to better initial level of performance. Individuals who were found to be more inconsistent in their week-to-week accuracy had better than average accuracy-based performances at the beginning of the 18-week study period. These findings are congruent with previous work on cognitive inconsistency in reaction times and inconsistency in accuracy (Allaire & Marsiske, 2005; Li et al., 2001). This positive association between level of performance and inconsistence is also consistent with a number of early life span studies (Siegler, 1994; van Geert & van Dijk, 2002). In child studies, intraindividual variability of performance has been described as reflecting the active exploration and use of differing performance strategies with new tasks (Siegler, 1994). Siegler and Lemaire (1997) suggested a two-component interpretation of inconsistency, which they described as adaptive versus maladaptive variability (Siegler & Lemaire, 1997). Maladaptive intraindividual variability seems to be observed more frequently in reaction time–based tasks that are relatively less likely to show improvement over time. When tasks remain relatively stable over time, inconsistency more likely represents a failure of homeostasis or tight control over repeated performance. Adaptive intraindividual variability, on the other hand, would be most expected in tasks on which individuals improve, perhaps reflecting participants' exploration of alternative performance strategies. This type of intraindividual variability would be expected more often in accuracy measures, where individuals can demonstrate ever-higher levels of performance. Li et al. (2004) argued that there might be a shift when individuals attain asymptotic levels of performance; after this point, consistency is expected, so intraindividual variability would again represent maladaptive processes (Li, et al., 2004).

We failed to observe the common association between increased RT inconsistency and poorer average-RT performance (Hultsch et al., 2002; Hultsch et al., 2000; Hultsch et al., 2008; Nesselroade & Salthouse, 2004; Salthouse et al., 2006), perhaps in part because we controlled for mean levels in all our models. Our results suggest a dissociation between the reaction time/inconsistency relationship and the accuracy/inconsistency relationship in regards to level of functioning.

We also examined cognitive inconsistency as a predictor of practice-related learning. Again, there was a dissociation between accuracy and reaction time findings, and also findings that somewhat contradict the “adaptive variability” expectation from Siegler (1994). Specifically, increased cognitive inconsistency was related to less improvement in Symbol Digit and Number Copy accuracy. Consistent with our initial expectations, for accuracy, individuals with higher levels of cognitive inconsistency experienced smaller benefits of repeated exposure/practice.

Thus, to the extent that practice-related gains can serve as a proxy for learning potential or plasticity (Hertzog et al., 2008; Yang et al., 2006); this study demonstrated that increased cognitive inconsistency may serve as an index of a decreased ability to improve one's performance. Furthermore, in lieu of past research suggesting that cognitive inconsistency is greater in neurologically impaired individuals (Burton et al., 2002; Hultsch et al., 2000) inconsistency in accuracy of performance may serve as a prodromal indicator of difficulties with learning.

In contrast to the accuracy findings, our reaction time findings were more consistent with the view of inconsistency as adaptive. We observed that individuals with higher levels of trial-to-trial RT inconsistency exhibited the most practice-related speed improvement in the Number Copy test. Such a finding was counter our original hypothesis, and also unexpected given previous research. RT inconsistency is typically associated with worse overall functioning and/or negative diagnostic status (Hultsch et al., 2002; Hultsch et al., 2000; Hultsch et al., 2008; Nesselroade & Salthouse, 2004; Salthouse et al., 2006). However, such studies aim to determine the importance/nature of inconsistency through assessing inconsistencies association with a static state (i.e., either mean-level functioning or diagnostic status). It appears that, consistent with the Siegler and Lemaire (1997) expectation that variability can identify individuals who are more actively engaged in trial-and-error explorations in their learning (Siegler & Lemaire, 1997), for Number Copy RT, higher initial inconsistency was associated with greater improvement. This finding remains unexpected, however, because previous work evincing adaptive variability has generally been found in accuracy-related outcomes (Li et al, 2001); in the current study, variability was negatively predictive of improvement in accuracy, but positively predictive of improvement in Number Copy reaction time. Recalling that Siegler and Lemaire (1997) expected adaptive variability in tasks that would not show improvement, and noting that in the current study, participants did show improvement in Number Copy RT, it may be that inconsistency will be predictive of greater gain in RT in those situations where improvement can actually be achieved (Siegler & Lemaire, 1997). Our sedentary sample of older adults improved, on average, about 200 milliseconds in Number Copy item reaction time over the eighteen weeks of the study.

Extrapolating for our accuracy level/inconsistency findings, the current study raises the possibility that inability to consistently produce adequate levels of cognitive performance from occasion-to-occasion could generalize to inconsistency in daily tasks that rely on cognition and support independence, such as driving, medication adherence, and balancing checkbooks. Future research should examine the effects of cognitive training interventions [i.e., (Willis et al., 2006)], which are typically designed to improve level of functioning, on cognitive inconsistency. Given the hypothesized association between cognitive inconsistency and CNS functioning, future research should also examine the effects of increased physical fitness on cognitive inconsistency, given aerobic training's beneficial effect on the cognitive functioning of older adults (McAuley et al., 2004). Future research should also examine the potential cross-associations between RT inconsistency and change in accuracy and accuracy inconsistency and change in RT, as these associations may shed additional light on the nature of cognitive inconsistency in late-life.

There are several limitations to the current study that need to be recognized. The current study was embedded within a larger trial of a lifestyle intervention (Buman, 2008; Buman et al., 2011), and all subjects were given a free gym membership for the length of the investigation. As physical activity and physical fitness has been shown to be related to cognitive functioning in late-life (McAuley et al., 2004), it is possible that some of the variance associated with growth in generalized learning is related to physical activity/fitness levels, and/or changes in physical activity/fitness. However, previous studies have demonstrated an absence of relationships between changes in physical activity/fitness and cognition in the current sample (Aiken Morgan, 2008). We included pre/post change in physical activity and change in physical activity*time interactions in our models to account for any change in cognition related to changes on physical fitness; in general, fitness had little association with level or change in our cognitive measures. Additionally, this study focused on only two closely related-cognitive tasks (i.e., Symbol Digit and Number Copy), both of which are believed to assess aspects of processing speed. It must be acknowledged that our RT inconsistency is likely a more reliable index than our accuracy inconsistency due to its computation from a greater number of trials than the 18-weeks of repeated testing that were used to calculate our accuracy inconsistency. As our RT inconsistency measure was calculated from baseline data and our accuracy inconsistency measure was calculated from data across the 18 sessions, RT and accuracy inconsistency may have rather different meanings given their temporal resolution. In this study, RT inconsistency measured variability of performance within the first session in which participants encountered their task. On the other hand, accuracy inconsistency reflected the heterogeneity of performance over almost five months of assessment. In future work, it would be interesting to explore the inconsistency of mean reaction time over 18 weeks (i.e., to give it a similar temporal resolution to accuracy), and to examine whether some of the dissociations observed in this study between accuracy and RT are an artifact of these resolution differences. We note that, in the current study, we opted for the differing temporal resolutions to be consistent with prior research; RT variability is typically computed within session [e.g., (Hultsch, et al., 2000)], while accuracy variability is typically computed over occasions [e.g, (Allaire & Marsiske, 2005; Li et al., 2001)].

In summary, innovations of the current study included: (a) examination of inconsistency in both reaction time and accuracy (within a single sample); (b) examination of inconsistency over two different temporal resolutions; (c) examination of the influence of inconsistency on both level and improvement slopes in two measures of processing speed; and (d) statistical control a number of background covariates and mean-level of performance in examining the effect of inconsistency. Greater inconsistency is associated with higher initial accuracy of Symbol Digit and Number Copy performance, but also shallower gain slopes. In contrast, for reaction time, inconsistency was relatively less important (and did not predict initial level), but greater inconsistency was associated with more improvement over eighteen weeks. These results affirm previous research on cognitive inconsistency in older adults, in that they suggest that the interpretation of inconsistency must be conditioned on temporal resolution (trial-to-trial or week-to-week), outcome measure (accuracy or reaction time) and growth parameter (initial level or rate-of-change over time). The fact that inconsistency showed a number of significant relationships in these data continues to support the idea that investigators should assess and analyze the effects of inconsistency in future research. Depending on the context, cognitive inconsistency may be a sign of decreased plasticity, a prodromal symptom of cognitive/neurologic impairment, or may signify adaptability. To incorporate inconsistency in future studies, investigators must be sure to employ designs that allow for repeated assessment over several temporal resolutions [e.g., measurement burst designs (Sliwinski, Hoffman, & Hofer, 2010)].