Nonpaternity in Linkage Studies of Extremely Discordant Sib Pairs

Abstract

An approach commonly used to increase statistical power in linkage studies is the study of extremely discordant sibling pairs. This design is powerful under both additive and dominant-gene models and across a wide range of allele frequencies. A practical problem with the design is that extremely discordant pairs that are ostensibly full sibs may be half sibs. Although estimates vary, the population rates of such nonpaternity may be as high as 5%–10%. The proportion in discordant pairs may be much higher. The present article explores this potential inflation as a function of the resemblance of sib pairs and the criteria for discordance used for selection.

Studies of genetic linkage in human populations typically involve pairs or larger groups of relatives. For the analysis of quantitative traits in population-based samples, statistical power is low, unless the gene effect accounts for a large proportion of the variance. Greater statistical power may be obtained by examining larger groups of relatives (Dolan et al. 1999a) or, more commonly, by using selected samples of relatives (Haseman and Elston 1972; Eaves and Meyer 1994; Risch and Zhang 1996; Sham 1997) or by using both approaches. It has been shown that in many cases, the use of extremely discordant pairs—in which, for example, one subject scores in the upper tenth percentile and the sibling scores in the lower tenth percentile—offers the greatest gains in statistical power. Therefore, this type of design is currently popular. It is an integral part of the extremely discordant and concordant design.

At least three problems hamper the use of extremely discordant pairs. First, for traits with a high degree of sibling resemblance, highly discordant pairs are rare. Second, some phenotypes—such as psychiatric disorders—are clearly defined at the upper end of the liability distribution, whereas the lower end (unaffected and low liability) may be difficult or impossible to identify. Third, selection of extremely discordant sib pairs runs the risk of oversampling pairs that are half siblings, rather than full siblings. This last problem is the focus of the present article.

We define “nonpaternity” as the situation in which the ostensible father of a child is not the biological father. Estimates of nonpaternity in the general population vary, ranging from 1% to as high as 20% (Allison 1996). The degree of inflation of the proportion of half sibs in ostensible full-sib pairs is considered here for a variety of nonpaternity base-rates and for various degrees of sibling resemblance. By contrast, with the exception of presumably very rare inadvertent exchanges in hospital nurseries, nonmaternity rates are expected to be zero.

Much of the information in a linkage study of selected-pairs relatives comes from departures of observed levels of allele sharing from expectations. Full sibs have prior expectation of .25, .5, or .25 of sharing zero, one, or two alleles identical by descent, respectively, at a specific locus. Extremely discordant sib pairs are expected to share fewer alleles identical by descent at a trait-relevant locus or at any locus linked to it with a recombination fraction <.5. Half-sibling pairs have a prior expectation of .5 and .5 of sharing zero and one allele identical by descent, respectively. Therefore, contamination of a sample of discordant full-sib pairs with half-sib pairs will increase the type I–error rate, because the average allele sharing will be decreased at all loci.

A number of methods for checking for relationship errors (e.g., incorrectly specifying half sibs as full sibs) have been developed, and software implementations are available (Stringham and Boehnke 1996). In the context of a genome scan, methods that incorporate the information from a large number of microsatellite markers can be particularly useful (Boehnke and Cox 1997; Goring and Ott 1997; Ehm and Wagner 1998). Results presented below indicate that it is critically important to perform these tests when using a design that includes extremely discordant sib pairs. However, when half-sib pairs are correctly identified, there remains the problem that the statistical power is reduced by the presence of half-sib pairs.

The expected proportion of pairs of relatives that are extremely discordant depends on the correlation between relatives and on the definition of discordance. Here, we assume that the trait distribution may be approximated by a normal-distribution curve, and that pairs are designated as discordant if one member has a score >+t and the other has a score <-t, where t is defined in standard normal units. The proportion of extremely discordant pairs depends on the correlation between relatives and is given by the double integral of the bivariate normal distribution:

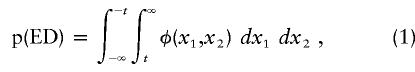where φ is the bivariate normal probability density function:

in which Σ is the covariance matrix and μ_j is the (column) vector of means of the variables, and |Σ| and Σ^-1 denote the determinant and inverse of the matrix Σ, respectively. For our present purposes, we set the mean vector μ to zero and the covariance matrix Σ to have a unit diagonal with correlation r_FS or r_HS for full or half sibs, respectively. These correlations follow from a simple model of phenotypic variation caused by additive-genetic, common-environment, and specific-environment effects. Common-environment effects are defined as those environmental factors that are shared by full siblings and half siblings to the same extent. Specific-environment factors are those that are not shared by members of a sibling pair. additive-genetic factors are correlated .5 in full sibs and .25 in half sibs, according to genetic theory (Mather and Jinks 1977). It is only the additive-genetic variation that causes a difference in the phenotypic correlation between half sibs and full sibs, and it is only when there is a difference in the phenotypic correlation that the proportion of half sibs in the sample will be affected by selection. Therefore, we consider only cases in which A>0.

Let the population proportion of half sibs be π so that proportion of full sibs is 1-π. From equation 1, the posterior proportion of half-sib pairs (π^*) following selection is given by:

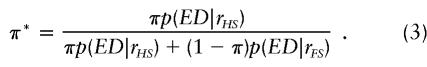We plot this proportion for a variety of values of π, the selection threshold (t), and the additive-genetic variance. Mx (Neale et al. 1999) was used to calculate the predicted proportions.

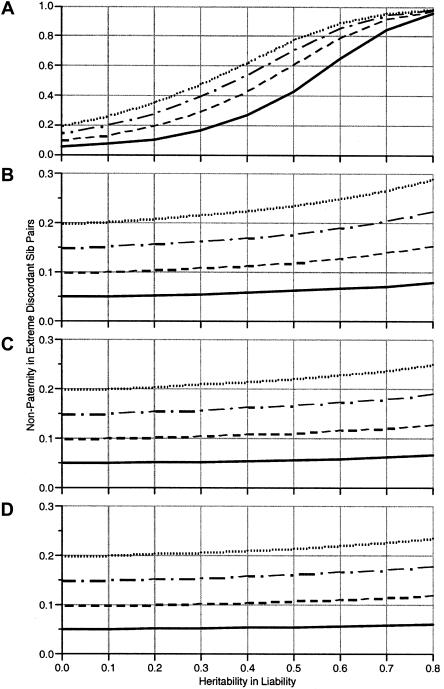
Results are shown in figure 1. Four points are noteworthy. First, if the heritability of liability is zero, there is no increase in the proportion of half siblings (π=π^* at the y-axis).

Figure 1.

Proportion of extremely discordant sibling pairs who are ostensibly full siblings but, in fact, are maternal half siblings. For each panel, the y-axis is the predicted proportion of half-sibling pairs (π*) after selection for extreme discordance, and the x-axis is the heritability of the trait used for selection. The plotted lines indicate π^* for initial proportions of half siblings of π=.05 (solid line), .1 (dashed line), .15 (dash-dot line), and .20 (dotted line). A residual shared environmental correlation of .1 was specified for all traits.

Second, figure 1A shows the proportion of half siblings expected (π^*) when the threshold for selection is very extreme, at 0.1% (t=3.09). When selection is this extreme, there is a very rapid increase in the proportion of half sibs as a function of increasing the additivegenetic variance, such that, for highly heritable traits, almost all sampled pairs of sibs will be half sibs. The larger the overall sibling correlation, the more selection of discordant pairs favors half sibs.

Third, figure 1B–D shows π^* for more moderate selection of 1%, 5%, and 10%, respectively. At the 1% level, the expected proportion of half siblings increases to ∼1.5 times the initial level when the trait is highly heritable. Small increases are seen when the trait is less heritable and when the selection is less extreme.

Fourth, the graphs shown include 10% of shared environmental variance (so the full-sibling correlation is predicted to be .1+.5A), and very little difference was found when we included higher or lower proportions of this source of variance. Therefore, graphs of other values of common-environment effects are not shown.

Linkage studies of extremely discordant sib pairs, including studies of extremely discordant and concordant sib pairs, risk including a proportion of half-sib pairs due to nonpaternity. If undetected, these pairs will contribute to type I errors in a Haseman-Elston analysis by inflating evidence for linkage at all positions on the genome. Therefore, statistical checks (Stringham and Boehnke 1996; Boehnke and Cox 1997; Goring and Ott 1997; Ehm and Wagner 1998) of familial relationship should be performed in all linkage studies that use discordant sibling pairs. Detection of half sibs and reanalysis based on correct family relationships will remove this bias but would lead to a loss of statistical power. In unselected samples, half-sib pairs have power to detect linkage that is approximately one-third as great as that of full-sib pairs. Selection of half-sib pairs to alter their expected 50:50 ratio of IBD 1 and IBD 0 pairs decreases the power of the half-sib study. It is possible to estimate the change in sample size required to overcome the sampling of half sibs. Let the ratio of power of half-sib to full-sib designs be r. A sample of size N will consist of proportions (1-π^*) full-sib pairs and π^* half-sib pairs. The study power will be N(1-π^*+rπ^*), so that the sample size should be increased to N^*=N/(1-π^*+rπ^*).

Our results indicate that the proportion of nonpaternity cases increases dramatically as a function of the trait heritability when the selection of discordant pairs is very extreme. However, it is rare that studies select such extreme pairs; only in very large populations would such pairs be found at all. More reasonable selection criteria, such as 10%, show that the inflation of the proportion of half-sib pairs is much more modest.

The results presented here rely on several assumptions, and, although we do not believe that the conclusions would be substantially altered if the assumptions were incorrect, they should be noted. First, we have assumed normality of trait variation. This assumption will be incorrect if the quantitative trait locus (QTL) effect is large, because a mixture of three normal distributions with equal variances and different means would be expected. However, one would expect approximately similar effects of aggregated selection of the six distinct bivariate normal distributions that would arise from the possible combinations of sib-pair genotypes. Second, we have assumed that residual variation not due to the QTL is also normally distributed.

One alternative to the use of discordant sib pairs is the use of DZ twin pairs. Although DZ twins sometimes have different fathers (James 1993), this appears likely to be far less common than among nontwin siblings. A limitation of this approach is that DZ twins are much less common than nontwin siblings, and the selection of relatively unusual discordant pairs may prove challenging. However, large databases have been established in the United States (e.g., The Mid-Atlantic Twin Registry), and national databases exist in several Scandinavian countries.

The use of extremely discordant full-sib pairs is not the only research design that can increase statistical power. Of particular note is the study of larger sibships, which can confer more power, on average, than even optimally selected sib pairs (in which every pair is either IBD=0 or IBD=2) (Dolan et al. 1999b). Practical concerns remain about studies of large sibships. Such groups may be increasingly rare in modern society, where contraception is common, and they may prove difficult to recruit as a unit. Many sibships (perhaps 5,000) that included four or more members would be required to detect QTL variance of 10% with reasonable power. Augmentation of power from large sibships remains desirable, and selected sampling of large sibships to include extremely discordant pairs could prove to be a valuable research design.